Linear failure criterion for estimating the compressive strength of brittle foliated rocks in response to the loading direction

Abstract

In this study, a failure criterion is proposed for describing the strength variation of foliated rocks that possess inherently anisotropic properties due to the existence of macro weak planes (MWPs). These rocks are typically characterized by the clustering and directional arrangement of needle-flaky minerals, a quasi-interlayered structure composed of weak and strong layers, and a directional arrangement of microcracks. The compressive failure mode of foliated rocks subjected to confining pressure is heavily dependent on the loading direction, which can be divided into two types within a certain range of confining pressures: shear-slip failure along the MWP and macro shear failure oblique to the MWP. From the perspective of the failure mechanism related to rock fabric and macrofailure characteristics, the linear failure criteria available for the two modes are proposed based on fracture mechanics theory, the Mohr–Coulomb criterion and the maximum axial strain criterion. The criteria involve 6 parameters that can be simply determined by a small amount of test data. Among them, the friction coefficient f is closely related to the loading direction corresponding to the minimum compressive strength, and the transversely isotropic parameter n controls the variation form of anisotropic strength with the loading direction. The predicted values of several kinds of exemplary foliated rocks agree well with their measured compressive strengths depending on the confining pressure and loading direction, suggesting a high prediction accuracy for the new criterion. The analysis reveals that the new criterion is suitable for describing the failure of brittle foliated rocks within a certain range of confining pressures.

Introduction

Foliated rocks, including slate, phyllite, schist, and gneiss, generally have characteristic flaky structures. This type of rock is characterized by macro weak planes (MWPs), such as slabs, schistosity, and gneissosity, which are essentially associated with the specific spatial arrangement of minerals that are subjected to recrystallization, deformation, and metamorphic differentiation. The existence of MWPs leads to the mechanical anisotropy of foliated rocks. It is unsound for engineering designs to use constant strength and deformation parameters because tests have found that the mechanical indices of rocks change sensitively with the loading direction. Ignorance of the mechanical anisotropy of rocks often leads to undesirable engineering consequences in the underground engineering of locations with foliated rocks. In previous studies, the strength anisotropy of rocks with MWPs has been widely considered by geotechnical engineers. Extensive experimental research results (Cho et al. 2012; Deng et al. 2018; Kwasniewski 1993; McLamore and Gray 1967; Niandou et al. 1997; Ramamurthy 1993; Singh et al. 1989) have shown that the compressive strength of anisotropic rocks changes with the loading direction angle β in a U-shape, shoulder shape, or wave shape (Fig. 1). In particular, foliated rocks with a group of MWPs often take U-shaped forms.

Fig. 1

Variation curve of compressive strength of anisotropic rock with loading direction angle

Based on an in-depth understanding of the anisotropic properties of rocks, many scholars have further proposed various failure criteria for anisotropic rocks in consideration of engineering applications. Boehler (1987), Pariseau (1968), and Tsai and Wu (1971) established different mathematical continuity models to evaluate the failure of anisotropic materials. Although these models can be applied to numerical simulations, they have failed to become popular in application because they are limited by the complex theories. Moreover, they generated an undesirable fit for foliated rocks with significant anisotropy (Duveau et al. 1998).

Considerable test results have provided necessary data support for some empirical failure criteria of anisotropic rocks. Based on the Mohr–Coulomb theory, Jaeger (1960) established an empirical formula to describe the strength anisotropy of rocks that involved the material cohesion varying with the loading direction. Based on Jaeger’s variable cohesive strength theory, McLamore and Gray (1967) proposed a new failure criterion that accounted for the change in cohesion and internal friction angle with the loading direction. Ramamurthy et al. (1988) created a nonlinear equation to describe the failure envelope of a Mohr circle and proposed an empirical function related to the loading direction to obtain the material parameters in the equation. Saeidi et al. (2014) proposed a modified empirical criterion for estimating the strength of transversely isotropic rocks. Based on the critical state concept stated by Barton (1976), Singh et al. (2015) modified the Mohr–Coulomb criterion to capture the nonlinear variation in anisotropic strength with confining pressure and loading direction.

Striving to solve practical rock engineering problems, Hoek and Brown (1980) established a mature and reliable nonlinear rock (mass) failure criterion and extended the criterion to anisotropic rocks using different material parameters m and s for the rock matrix and weak planes, respectively. However, the determination of the parameters requires a relatively large amount of test data, making application inconvenient. Many scholars have made great efforts to modify the Hoek–Brown criterion for describing the strength of anisotropic rocks (Bagheripour et al. 2011; Li et al. 2018; Saroglou and Tsiambaos 2008; Shi et al. 2016). Saroglou and Tsiambaos (2008) introduced the parameter ${k}_{\beta }$ of strength anisotropy and established a modified Hoek–Brown criterion for anisotropic rocks. Bagheripour et al. (2011) proposed a combined form of the Hoek–Brown criterion involving a polynomial function referring to the reduction rate of anisotropic strength relative to the strength of intact rock.

Indeed, empirical models can generally achieve good agreements with the variation law of strength by determining the empirical parameters, and they are convenient to use. However, these criteria are still controversial due to the unclear physical meaning of the parameters and the lack of mathematical or theoretical background of the model.

By focusing on the failure mechanism of anisotropic rocks, some scholars have established a series of discontinuous weak surface criteria. Jaeger (1960) regarded the anisotropic material as an isotropic body containing a weak plane inside and proposed a single weak surface theory that utilized the Mohr–Coulomb formula with distinct parameter values to evaluate the failure of the isotropic matrix and the weak plane. Although this theoretical criterion proposed by Jaeger is substantial and influential, it still has obvious deficiencies in the prediction effect. Especially near the two boundaries (β = 90° and 0°), there is a notable difference between the predicted and measured values. Kwasniewski (1993) and Duveau and Shao (1998) modified Jaeger’s criterion to improve its fitness with the actual variation law of strength. However, it is difficult for these improved criteria to be universally applicable in anisotropic rocks with different development degrees of MWPs. Walsh and Brace (1964) deemed that the failure of anisotropic rocks under different loading directions was controlled by oriented long cracks and randomly distributed short cracks. The corresponding failure stress formulas were derived from the Griffith theory. Tien and Kuo (2001) and Asadi and Bagheripour (2015) recognized that the strength of bedded rocks would be controlled by weak planes or dominated by rocks in response to different loading directions and proposed sliding and nonsliding failure criteria for inherently anisotropic rock.

There have been consistent efforts to establish a meaningful failure criterion according to the failure mechanism of rocks. However, relevant research is still relatively scant. In recent years, in-depth research on the evolution characteristics and mechanisms of microscopic rock damage has provided a firm foundation for the establishment of more reasonable and reliable failure criteria (Martin 1997; Rawling et al. 2002; Wang et al. 2019). As a typical and widespread anisotropic rock, foliated rock has gained increased research interest regarding its physical and mechanical properties, but awareness of the common fabric characteristics has not been sufficiently clear. An in-depth understanding of rock fabric characteristics is of great significance to precisely analyze the failure mechanism. The establishment of a reliable failure criterion involving the failure mechanism can provide assurance for the stability analysis of foliated rock masses as well as safe engineering construction.

Based on the recognition of the inner link among failure criteria, mechanism, and rock fabric, in this study, the microscopic characteristics of foliated rock and the macroscopic failure mode of rock subjected to triaxial compression were systematically summarized. Furthermore, a compression failure criterion dependent on the brittle failure mechanism and macroscopic failure mode was proposed for foliated rocks. Then, the predictive ability and applicability of this criterion for the compressive strength of foliated rocks were discussed.

Microstructural characteristics of foliated rocks

The minerals in foliated rocks can be divided into layered and nonlayered minerals according to their crystal structure. Nonlayered minerals include multiple types, such as oxide, tectosilicate, and carbonate minerals, represented by quartz, feldspar, and calcite in foliated rocks. Because of metamorphism, these mineral particles are inevitably elongated to a certain extent, commonly presenting a nonequaxial granular shape, and they are tightly interlocked with each other in fresh rock. Layered minerals refer to phyllosilicates, including mica, chlorite, talc, and serpentine. Owing to the inherent layered structure of the crystals, these minerals generally have a set of cleavage planes in the direction parallel to the structure layer. In metamorphic rocks, such minerals commonly take the form of needles or flakes. Complicated regional metamorphism leads to the unique preferential orientation of phyllosilicate minerals (Fig. 2), which essentially contributes to the anisotropy of rocks. In other words, phyllosilicate, as a representative mineral, always exists in foliated rocks. Generally, this type of typical mineral is nonuniformly distributed in space and tends to gather into multiple clusters in a certain directional horizon (Fig. 2). Along the spreading direction of minerals, the adjacent clusters are connected head to tail with different degrees of tightness, forming a micro weak layer. In the direction perpendicular to the extension of oriented minerals, multiple weak layers are distributed at intervals and accompanied by the filling of strong mineral layers (consisting of nonequaxial granular minerals), forming a quasi-interlayered structure composed of weak and strong layers.

Fig. 2

Mineral distribution characteristics of foliated rocks, a slate (Saeidi et al. 2014), b phyllite (Zhou et al. 2019), c schist (Yin et al. 2020), d gneiss (Saroglou and Tsiambaos 2008), muscovite (Ms), mica (Mc), and chlorite (Chl)

In terms of mechanical properties, nonequaxial granular minerals have relatively high rigidity and high strength, whereas needle-flaky minerals exhibit strong toughness and low strength. In a stressed environment, the difference in mechanical properties causes a discontinuity of deformation and stress at the contacts of the two types of minerals, which leads to a concentration of tension or shear stress and further induces cracks in rocks. Therefore, in foliated rocks affected by tectonic stress or engineering disturbance, microcracks are often distributed along the edges of needle-flaky minerals, showing a close spatial dependence of such minerals. Regarding the spreading direction, the microcracks also exhibit obvious consistency depending on the orientation of the representative minerals. The oriented microcracks attached to the edge of needle-flaky minerals enhance the heterogeneity of rock and play an important role in the mechanical anisotropy of foliated rocks (Yin et al. 2021).

In summary, foliated rocks are typically characterized by the clustering and directional arrangement of needle-flaky minerals, a quasi-interlayered structure composed of weak and strong layers and the directional arrangement of microcracks. The microstructure of foliated rocks is generalized according to the types, shapes, distributions, and arrangements of the minerals and main defects, as shown in Fig. 3.

Fig. 3

Microscopic components of foliated rocks

Macroscopic failure modes of foliated rocks

Controlled by the microscopic characteristics of foliated rocks, the macroscopic failure mode of rocks subjected to compression is closely dependent on the loading direction. Triaxial compression tests of foliated rock specimens under low and medium confining pressures (Duveau et al. 1998; Fereidooni et al. 2016; Mclamore and Gray 1967; Nasseri et al. 2003; Zhou et al. 2019) have found that the response of rock failure to the loading direction behaves as follows: at a large angle β between the axial compression and the MWP of the rock specimen (generally 60°–90°), macroscopic shear failure occurs with a main fracture plane skewed across the MWP (Fig. 4a). At a medium angle (generally 15°–60°), shear–slip failure occurs with a fracture plane that develops mainly along the MWP (Fig. 4b). At a small angle β (generally 0°–15°), although the MWP exerts a guiding effect on the propagation of the fracture plane due to a small amount of lateral tensile strain stemming from the lack of sufficiently high confining pressure, macro shear failure still plays a leading role in foliated rocks (Fig. 4c). Notably, the failure mode of foliated rocks is not only related to the loading direction but also affected by the stress environment. When subjected to a higher confining pressure, the rock exhibits weaker brittleness and stronger toughness. Higher confining pressure tends to produce obvious damage, such as kinking and plastic flow (Mclamore and Gray 1967) (Fig. 5). The plastic failure mode of foliated rocks under high confining pressure is not covered in this paper.

Fig. 4

Failure modes of foliated rocks under low and medium confining pressure, a 60° < β ≤ 90°, b 15° ≤ β ≤ 60°, c 0° ≤ β < 15°

Fig. 5

Failure modes of foliated rocks under high confining pressure, a kink failure, b plastic flow failure

Therefore, the compressive failure modes of foliated rocks under low and medium confining pressures can be summarized into two types. For the type corresponding to β = 15°–60°, the MWP has a significant impact on the rock failure, resulting in shear–slip failure (SSF) of the foliated rock along the MWP. For the type corresponding to β = 60°–90° or β = 0°–15°, the lesser influence of MWP on rock failure can be neglected, and foliated rocks exhibit macroscopic shear failure (MSF) characterized by a main fracture plane skewed across the MWP. Subsequently, two failure criteria for the SSF and MSF modes will be established to estimate the compressive strength of foliated rocks.

Failure criterion of foliated rocks with the SSF mode

Failure mechanism

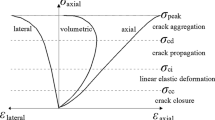
Brittle rock subjected to compression undergoes several deformation stages, such as compaction, linear elasticity, and elastoplastic deformation. In the stage of elastoplastic deformation, new cracks are continuously induced in the rock, followed by gradual propagation and coalescence, and finally connected to a macroscopic fracture plane leading to the failure of the rock. Therefore, the failure of the rock starts with the appearance of new cracks and proceeds through gradual damage associated with crack evolution. As a heterogeneous material, rock subjected to external forces is prone to generate concentrated stress, leading to the initiation of new cracks. Stress concentration often accompanies the internal defects of rock, such as the contact boundary of several minerals with distinct mechanical properties, the internal defects of mineral grains, and the pores and microcracks at the grain boundary. For anisotropic rocks, the location of new cracks also depends on the loading direction. For β = 15°–60°, the shear–slip failure of rock suggests that crack evolution mainly occurs along the MWP (Rawling et al. 2002; Yin et al. 2021). At the MWP, needle-flaky phyllosilicate minerals are likely to aggregate into microscopic weak layers composed of multiple oriented clusters. Moreover, the weak layer is often accompanied by microdefects, including oriented microcracks and inherent mineral cleavage, both of which tend to have consistent spreading directions.

When the compressive load is applied skewed to the spreading direction of microdefects, new cracks are prone to be initiated at the tips of the defects. It is generally believed that the initiation of cracks follows the slip-cracking mode in this case. In this mode, external compression produces normal and shear stress acting on the pre-existing defect surfaces. Once the stress reaches a critical condition, the defect surfaces with adhesion and friction will slide relative to each other, and a locally concentrated tensile stress will be generated at the tips of the defect, leading to the initiation of tensile wing cracks. As the stress increases, the cracks tend to expand toward the direction of the maximum principal stress. Bobet and Einstein (1998) and Sagong and Bobet (2002), among others, pointed out that the tensile stress is gradually released due to the propagation of the wing crack, and when the crack expands to a certain limit, the shear stress concentration will occur at the tips of the original defect, which is likely to induce quasi-coplanar secondary cracks in the spreading direction of the defect. Scanning electron microscopy observations of compressed foliated rock carried out by Rawling et al. (2002) revealed that this type of shear crack truly existed at the tips of the oriented flaky minerals (Fig. 6). Shear cracks propagate and coalesce along the spreading direction of the defect and finally lead to the shear–slip failure of rocks along the MWP. The damage to rock is bound up with the coevolution of tensile and shear cracks. Research results from acoustic emission tests (Chen et al. 2018; Ohtsu et al. 2007; Wang et al. 2019) show that shear cracks generally arise in the later stages of crack evolution and play a key role in the process of crack connection, whereas tensile cracks are continuously initiated and dominate the whole process of rock damage. That is, the damage to rock originates from the generation of tensile cracks. Previous studies (Yin et al. 2020; Zhang et al. 2011) have found that compared to rocks with the MSF mode, rocks with the SSF mode have a fairly rapid crack evolution and relatively short stress history from crack initiation to rock failure, leading to a relatively high stress level of crack initiation (ratio of crack initiation stress to failure stress). Therefore, for foliated rocks with β = 15°–60°, the crack initiation strength can be approximated as the failure strength. Based on the theory of fracture mechanics, the slip-cracking model would be properly utilized to analyze the stress condition of crack initiation to establish an equivalent failure criterion of foliated rocks with the SSF mode.

Fig. 6

Crack distribution at the tip of oriented needle-flaky minerals (this diagrammatic sketch was plotted according to Rawling et al. 2002, represents granular mineral zone, represents needle-flaky minerals)

Failure criterion

As shown in Fig. 7, in a plate under axial pressure and confining pressure, a crack with a length of 2a is subjected to the following far-field stress (Li 2010):

$$\left\{\begin{array}{l}{\sigma }_{\mathrm{x}}^{\infty }=-\frac{{\sigma }_{1}-{\sigma }_{3}}{2}\left(1+\mathrm{cos}\ 2\beta \right)-{\sigma }_{3}\\ {\sigma }_{\mathrm{y}}^{\infty }=-\frac{{\sigma }_{1}-{\sigma }_{3}}{2}\left(1-\mathrm{cos}\ 2\beta \right)-{\sigma }_{3}\\ {\tau }_{\mathrm{xy}}^{\infty }=-\frac{{\sigma }_{1}-{\sigma }_{3}}{2}\mathrm{sin}\ 2\beta \end{array}\right.$$

(1)

where β is the angle between the long axis of the crack and the axial stress.

Fig. 7

New tensile crack at the tip of a single original crack under compressive stress

In this stress state, the crack surface is compressed and closed, so sliding will inevitably occur. It is generally considered to be a type II crack, whose stress intensity factor is

$${K}_{\mathrm{II}}={\tau }_{\mathrm{e}}\sqrt{\pi a}$$

(2)

where ${\tau }_{\mathrm{e}}$ is the equivalent shear stress on the surface of the crack. Taking into account the friction between the surface, ${\tau }_{\mathrm{e}}$ is expressed as

$${\tau }_{\mathrm{e}}={\tau }_{\mathrm{xy}}^{\infty }-f{\sigma }_{\mathrm{y}}^{\infty }$$

(3)

where f is the friction coefficient of the defect surface. Then, Eqs. (1) and (3) are substituted into Eq. (2) to obtain an expression of the stress intensity factor as

$${K}_{\mathrm{II}}=\left\{\frac{\left({\sigma }_{1}-{\sigma }_{3}\right)}{2}\left[\mathrm{sin}\ 2\beta -f\left(1-\mathrm{cos}\ 2\beta \right)\right]-f{\sigma }_{3}\right\}\sqrt{\pi a}$$

(4)

At the beginning of the material fracture, the principal stress difference, called the crack initiation stress, is

$${\sigma }_{ci}={\sigma }_{1i}-{\sigma }_{3i}$$

(5)

According to the theory of fracture toughness, the critical condition for the initiation of crack propagation obeys $\left|{K}_{\mathrm{II}}\right|={K}_{\mathrm{II\ c}}$. Then, the crack initiation stress can be obtained from Eq. (4) as

$${\sigma }_{ci}=\frac{2\left({K}_{\mathrm{II\ c}}/\sqrt{\pi a}+f{\sigma }_{3}\right)}{\mathrm{sin}\ 2\beta -f\left(1-\mathrm{cos}\ 2\beta \right)}$$

(6)

This expression reveals that ${\sigma }_{ci}$ changes nonlinearly with increasing β. ${\sigma }_{ci}$ has a minimum value, and the corresponding angle ${\beta }_{\mathrm{m}}$ can be obtained according to the condition of the minimum value

$${\beta }_{\mathrm{m}}=\frac{1}{2}\ \mathrm{arctan}\ \frac{1}{f}$$

(7)

Then, the minimum value of ${\sigma }_{ci}$ can be determined

$${\sigma }_{ci\ \mathrm{min}}=\frac{2\left({K}_{\mathrm{II\ c}}/\sqrt{\pi a}+f{\sigma }_{3}\right)}{\sqrt{1+{f}^{2}}-f}$$

(8)

When ${\sigma }_{3}=0$, Eq. (8) is transformed into

$${K}_{\mathrm{II\ c}}/\sqrt{\pi a}=\frac{{\sigma }_{ci\ \mathrm{min}}^{0}\left(\sqrt{1+{f}^{2}}-f\right)}{2}$$

(9)

where ${\sigma }_{ci\ \mathrm{min}}^{0}$ is the minimum crack initiation stress of the material subjected to uniaxial compression. Then, Eq. (9) is substituted into Eq. (6) to obtain the final expression of the crack initiation stress

$${\sigma }_{ci}=\frac{{\sigma }_{ci\ \mathrm{min}}^{0}\left(\sqrt{1+{f}^{2}}-f\right)+2f{\sigma }_{3}}{\mathrm{sin}\ 2\beta -f\left(1-\mathrm{cos}\ 2\beta \right)}$$

(10)

At $\beta ={\beta }_{\mathrm{m}}$, ${\sigma }_{ci}$ reaches the minimum, expressed as follows:

$${\sigma }_{ci\ \mathrm{min}}={\sigma }_{ci\ \mathrm{min}}^{0}+\frac{2f{\sigma }_{3}}{\sqrt{1+{f}^{2}}-f}$$

(11)

Equation (10) expresses the change in the critical stress of the material with a single crack as a function of the confining pressure and the crack angle. Although the foliated rock contains a large number of defects, since the crack initiation mode of rock is almost in accord with that of material with a single crack, Eq. (10) can still be used to characterize the response pattern of the crack initiation strength of rock with oriented defects. In this case, the oriented defect in rock, similar to the original crack in the material, preferentially produces tensile wing cracks under compression (Fig. 7). In addition, considering that the crack initiation stress is close to the failure stress for the foliated rock with the SSF mode, we can approximately estimate the failure strength of rock associated with the confining pressure and loading direction by Eq. (10). ${\sigma }_{ci\ \mathrm{min}}^{0}$ and the parameter f in Eq. (10) can be determined by Eq. (11). For this purpose, a group of minimum compressive strengths of foliated rock under different confining pressures need to be measured first, followed by a linear fit to these data. The specific steps for predicting the failure strength of foliated rock with the SSF mode using the above equations are as follows:

• a) ${\beta }_{\mathrm{m}}$ should first be determined. According to previous studies (Behrestaghi et al. 1996; Fereidooni et al. 2016; Nasseri et al. 1997, 2003), the compressive strength of foliated rocks varies with the angle β, and the angle ${\beta }_{\mathrm{m}}$ is generally in the range of 30°–45°. For a certain kind of foliated rock, in the absence of basic test data, ${\beta }_{\mathrm{m}}$ can be approximately taken as an empirical value of 35°.

• b) Next, the triaxial compression test should be carried out to measure the failure stress ${\sigma }_{f\ \mathrm{min}}$ of the cylindrical specimen with ${\beta }_{\mathrm{m}}$ under different confining pressures ${\sigma }_{3}$. Here, ${\sigma }_{f\ \mathrm{min}}$ is approximately equal to ${\sigma }_{ci\ \mathrm{min}}$. Subsequently, the data group (${\sigma }_{3}$, ${\sigma }_{ci\ \mathrm{min}}$) is linearly fitted to determine ${\sigma }_{ci\ \mathrm{min}}^{0}$ and the parameter f depending on Eq. (11). Specifically, ${\sigma }_{ci\ \mathrm{min}}^{0}$ takes the intercept of the fitting line, and f is calculated by the following expression, where m is the slope of the fitting line.

  $$f=\frac{m}{2\sqrt{1+m}}$$

  (12)

• c) Once ${\sigma }_{ci\ \mathrm{min}}^{0}$ and the parameter f have been determined, the critical stress ${\sigma }_{ci}$ (approximate compressive failure strength) as a function of angle β and confining pressure ${\sigma }_{3}$ can be predicted by Eq. (10).

Variation in failure strength with angle β and parameter f

According to Eqs. (10) and (11), the following expression is obtained:

$$\frac{{\sigma }_{ci}}{{\sigma }_{ci\ \mathrm{min}}}=\frac{\sqrt{1+{f}^{2}}-f}{\mathrm{sin}\ 2\beta -f\left(1-\mathrm{cos}\ 2\beta \right)}$$

(13)

where $\frac{{\sigma }_{ci}}{{\sigma }_{ci\ \mathrm{min}}}$ is defined as the strength ratio k_c. This equation shows that k_c changes as a function of angle β and parameter f. The friction coefficient f of the defect surface was taken as several representative values in a range of 0.85–0.3 (Li 2010), and the corresponding k_c–β curves are plotted in Fig. 8.

Fig. 8

Variation of the strength ratio kc with the angle β and the parameter f

As shown in Fig. 8, when the parameter f is fixed, k_c changes in a U-shape with increasing β, suggesting that the theoretical analysis conforms to the test results in terms of the response pattern of the critical failure stress to the angle β. As f decreases from 0.85 to 0.3, the corresponding angle ${\beta }_{\mathrm{m}}$ gradually increases in the range of 25°–45°. This indicates that the angle ${\beta }_{\mathrm{m}}$, which represents the loading direction for foliated rock most prone to shear slip, is closely related to the properties of internal defects in rock. It is concluded that the angle ${\beta }_{\mathrm{m}}$ is generally approximately 35° and varies with different rock types. This is consistent with the theoretical value ${\beta }_{\mathrm{m}}$ = 45°-Φ/2 (Φ is the friction angle of the MWP) given by Nasseri et al. (2003). This conclusion also agrees with the test results of foliated rocks (${\beta }_{\mathrm{m}}$ is generally in the range of 30°–45°).

Failure criterion of foliated rocks with MSF mode

Failure criterion

At β = 0° and β = 90°, MSF occurs in foliated rocks. In this case, the strength is controlled by the mechanical properties of the rock material, which can be regarded as an isotropic medium. The popular Mohr–Coulomb criterion is capable of evaluating the failure strength of isotropic rock. Since the test values of the compressive strength of foliated rocks are usually different between β = 0° and β = 90°, the following expressions can be used to estimate the failure stress of rock under the two loading directions.

$${S}_{f\left(0\right)}=\frac{2\ \mathrm{sin}\ {\phi }_{0}{\sigma }_{3}}{1-\mathrm{sin}\ {\phi }_{0}}+2{c}_{0}\frac{\mathrm{cos}\ {\phi }_{0}}{1-\mathrm{sin}\ {\phi }_{0}}$$

(14)

$${S}_{f\left(90\right)}=\frac{2\ \mathrm{sin}\ {\phi }_{90}{\sigma }_{3}}{1-\mathrm{sin}\ {\phi }_{90}}+2{c}_{90}\frac{\mathrm{cos}\ {\phi }_{90}}{1-\mathrm{sin}\ {\phi }_{90}}$$

(15)

where ${S}_{f\left(0\right)}$ and ${S}_{f\left(90\right)}$ are the critical stresses for the failure of rock at β = 0° and β = 90° (${S}_{f}={\sigma }_{1f}-{\sigma }_{3f}$). ${c}_{0}$, ${c}_{90}$, ${\phi }_{0}$, and ${\phi }_{90}$ represent the cohesion and internal friction angle of rock at β = 0° and β = 90°, respectively.

Previous test results show that when β is close to 0° or 90°, rock specimens exhibit identical failure characteristics as when β = 0° and β = 90°, but the compressive strength increases as β gradually approaches the two boundary values. Some existing failure criteria fail to incorporate the influence of the loading direction on the critical stress of foliated rocks within this angle range. As a result, the predicted strength value changes as a shoulder-shaped curve characterized by two horizontal ends.

Based on the constitutive relation of transversely isotropic materials and the maximum axial strain criterion, Tien and Kuo (2001) deduced the following failure stress expression for stratified rock suffering from MSF.

$${S}_{f\left(\beta \right)}={S}_{f\left(90\right)}\times \frac{k}{{\mathrm{cos}}^{4}\ \beta +k\ {\mathrm{sin}}^{4}\ \beta +2n\ {\mathrm{sin}}^{2}\ \beta\ {\mathrm{cos}}^{2}\ \beta }$$

(16)

$$k=\frac{{S}_{f\left(0\right)}}{{S}_{f\left(90\right)}}$$

(17)

$$n=\left({E}_{\left(90\right)}/2{G}^{^{\prime}}\right)-{v}^{^{\prime}}$$

(18)

where ${E}_{\left(90\right)}$ is the elastic modulus of the rock specimen loaded perpendicular to the transversely isotropic plane. ${G}^{^{\prime}}$ and ${v}^{^{\prime}}$ represent the elastic modulus and Poisson’s ratio, respectively, in the direction perpendicular to the transversely isotropic plane. n is a transversely isotropic parameter that varies with different types of rock samples.

The above failure stress expression not only has a reliable theoretical basis but also includes the effect of loading direction on the compressive strength of foliated rocks. According to the test results of foliated rocks (Behrestaghi et al. 1996; Fereidooni et al. 2016; Nasseri et al. 1997, 2003), the corresponding angle for rock specimens with the MSF mode is generally in the range of 0°–15° or 60°–90°. Within the two angle intervals, the failure strength of foliated rocks can be predicted using Eq. (16). Prior to using this equation, the unknown parameter n needs to be determined. Tien and Kuo (2001) noted that the parameter value can be calculated from the test results of rock specimens with β = 60° or 75°. The specific steps for predicting the failure strength of foliated rock with the MSF mode are as follows:

• (a) Perform triaxial compression tests on the specimens with β = 0°, 90°, and 60° (or 75°), and determine the parameters ${c}_{0}$, ${c}_{90}$, ${\phi }_{0}$, and ${\phi }_{90}$ in Eqs. (14) and (15) by linear fitting to the test values of failure stress.

• (b) Use Eqs. (14) and (15) to obtain the predicted values ${S}_{f\left(0\right)}$ and ${S}_{f\left(90\right)}$ under different confining pressures, which are then substituted into Eq. (17) to calculate the value of k corresponding to each confining pressure.

• (c) Substitute the predicted value ${S}_{f\left(90\right)}$, calculated value k, and test value ${S}_{f\left(60\right)}$ (or ${S}_{f\left(75\right)}$) under different confining pressures into Eq. (16) to determine the parameter n.

• (d) Once the value k corresponding to different confining pressures and the parameter n have been determined, the failure stress ${S}_{f}$ as a function of angle β and confining pressure ${\sigma }_{3}$ can be predicted by Eq. (16).

The key to predicting the failure stress is to properly determine the parameter n. Generally, the parameter n is taken as the average of n values under different confining pressures obtained by step (c). Tien and Kuo (2001) found that parameter n is not sensitive to changes in confining pressure. Therefore, when the test conditions are limited, the parameter n can be obtained using the test results under a specific confining pressure.

Effect of parameter n on the strength variation

When β = 60°–90°, the value of ${\mathrm{cos}}^{4}\beta$ in Eq. (16) is small enough to be ignored, so Eq. (16) evolves into

$$\frac{{S}_{f\left(\beta \right)}}{{S}_{f\left(90\right)}}\approx \frac{k}{k\ {\mathrm{sin}}^{4}\ \beta +2n\ {\mathrm{sin}}^{2}\ \beta\ {\mathrm{cos}}^{2}\ \beta }=\frac{1}{{\mathrm{sin}}^{4}\ \beta +2\left(n/k\right){\mathrm{sin}}^{2}\ \beta\ {\mathrm{cos}}^{2}\ \beta }$$

(19)

Thus, the ratio of failure stress at β = 75° to that at β = 90° abides by the following expression:

$$\frac{{S}_{f\left(75\right)}}{{S}_{f\left(90\right)}}=\frac{1}{0.871+0.125\left(n/k\right)}$$

(20)

According to the test results of foliated rocks (Behrestaghi et al. 1996; Fereidooni et al. 2016; Nasseri et al. 1997, 2003; Wu et al. 2001), the value of k generally ranges from 0.8 to 1.2. Three representative values k = 0.8, 1.0, and 1.2 were selected, and the failure stress ratio ${S}_{f\left(75\right)}/{S}_{f\left(90\right)}$ as a function of parameter n is displayed as the curves in Fig. 9, which shows that for a constant value of k, ${S}_{f\left(75\right)}/{S}_{f\left(90\right)}$ decreases as parameter n increases and that for the same value of n, ${S}_{f\left(75\right)}/{S}_{f\left(90\right)}$ increases with an increase in k. It is thus concluded that in the case of a smaller n and a larger k, ${S}_{f\left(75\right)}$ is closer to ${S}_{f\left(90\right)}$. In this case, within the interval where β approaches 90°, ${S}_{f\left(\beta \right)}$ has an insensitive response to β, and the ${S}_{f\left(\beta \right)}$ curve levels off.

Fig.9

Variation of ${S}_{f\left(75\right)}/{S}_{f\left(90\right)}$ with parameter n

When β = 0°–15°, the value of $k{\mathrm{sin}}^{4}\beta$ in Eq. (16) is small enough to be ignored. Equation (17) is substituted into Eq. (16) to obtain the following expression:

$$\frac{{S}_{f\left(\beta \right)}}{{S}_{f\left(0\right)}}\approx \frac{1}{{\mathrm{cos}}^{4}\ \beta +2n\ {\mathrm{sin}}^{2}\ \beta\ {\mathrm{cos}}^{2}\ \beta }$$

(21)

Then, the ratio of the failure stress at β = 15° to that at β = 0° as a function of parameter n can be obtained:

$$\frac{{S}_{f\left(15\right)}}{{S}_{f\left(0\right)}}=\frac{1}{0.871+0.125n}$$

(22)

The above equation corresponds to the case of k = 1 in Eq. (16). This shows that the smaller the value of n is, the closer ${S}_{f\left(15\right)}$ is to ${S}_{f\left(0\right)}$.

From the above analysis, when k is fixed, the smaller the parameter n is, the closer ${S}_{f\left(\beta \right)}$ is to ${S}_{f\left(0\right)}$ and ${S}_{f\left(90\right)}$ in the interval where β approaches 0° and 90°, respectively. In contrast, the greater the difference between ${S}_{f\left(\beta \right)}$ and ${S}_{f\left(0\right)}$ or ${S}_{f\left(90\right)}$. Therefore, when the parameter n decreases gradually, the failure stress curve will change from a U-shape falling rapidly at both ends to a shoulder shape with flat ends.

Discussion

Predictive ability analysis

In summary, once several sets of data, including the failure stress-confining pressure of rock specimens with β = 0°, 35°, and 90° and the failure stress of the specimen with β = 60° (or 75°) under at least one confining pressure, are obtained through testing, the compressive failure strength of foliated rocks in response to the loading direction and confining pressure can be predicted using Eqs. (10), (11), and (14)–(17).

To verify the practicability of the newly proposed criterion, test data of Angers schist (Duveau et al. 1998), Penrhyn slate (Attewell and Sandford 1974), and Martinsburg slate (Donath 1964) were collected and compared with predicted data. Angers schist, native to France, belongs to a weakly metamorphosed rock formed in the Middle Ordovician. The schist, mainly composed of chlorite, mica, and quartz, is characterized by well-developed schistosity planes, resulting in very strong anisotropy. Penrhyn slate is native to North Wales and belongs to the greenschist facies. The main mineral components are quartz, albite, and mica (Attewell and Taylor 1969). Martinsburg slate, native to Pennsylvania, is a weakly metamorphosed rock formed in the Ordovician. According to Ramamurthy’s classification standard of rock strength (Ramamurthy 2004), the three types of rocks are all high-strength materials with different degrees of brittleness in consideration of the maximum uniaxial compressive strength. The failure stress predicted by the new criterion is shown in Fig. 10. As the angle gradually increases, the predicted value shows a U-shaped change consistent with the test value, which indicates that the new criterion can effectively describe the response pattern of the failure strength of foliated rocks to the loading direction.

Fig. 10

Prediction results of the compressive strength of foliated rocks by the new criterion: a Angers schist, b Penrhyn slate, c Martinsburg slate. The point symbol marks the test data, and the dotted line represents the predicted data

Quantitative analysis was carried out using two error indices, the mean square error (R²) and mean relative error (MAPE), to further understand the predictive ability of the new criterion. These indices were calculated according to the following expressions:

$${R}^{2}=1-\frac{{\sum }_{\mathrm{i}=1}^{N}{\left({S}_{p}-{S}_{t}\right)}^{2}}{{\sum }_{\mathrm{i}=1}^{N}{\left({S}_{t}-{S}_{tm}\right)}^{2}}$$

(23)

$$MAPE=\frac{1}{N}{\sum }_{\mathrm{i}=1}^{N}\left|\frac{{S}_{p}-{S}_{t}}{{S}_{t}}\right|\times 100\%$$

(24)

where N is the total number of data; ${S}_{p}$ and ${S}_{\mathrm{t}}$ are the predicted value and test value of failure stress, respectively; and ${S}_{\mathrm{tm}}$ is the average of all test values. According to the above equations, the higher the R² or the lower the MAPE is, the better the predictive ability of the criterion. The calculation results of the error indices are shown in Table 1.

Table 1 Prediction errors of failure criteria

Scholars have carried out a series of studies on the critical failure condition of anisotropic rocks and established a variety of failure criteria, such as the single weak surface theory and variable cohesive strength theory proposed by Jaeger (1960), the failure criterion involving variable cohesion and friction coefficient created by McLamore and Gray (1967), the Ramamurthy empirical criterion (Ramamurthy et al. 1988), the Walsh–Brace criterion (Walsh and Brace 1964) based on the Griffith theory, and the Hoek–Brown anisotropic failure criterion (Hoek and Brown 1980). The widely recognized Ramamurthy empirical criterion and the modified Hoek–Brown failure criterion (Saroglou and Tsiambaos 2008), which have attracted considerable attention in recent years, were selected to carry out a comparative analysis of prediction accuracy to clarify the predictive ability of the new criterion.

Ramamurthy empirical criterion

Using a large amount of data analysis, Ramamurthy et al. (1988) developed an empirical nonlinear criterion to characterize the critical failure condition of anisotropic rocks:

$$\frac{{\sigma }_{1}-{\sigma }_{3}}{{\sigma }_{3}}={\beta }_{\beta }{\left(\frac{{\sigma }_{c\beta }}{{\sigma }_{3}}\right)}^{{\alpha }_{\beta }}$$

(25)

where ${\sigma }_{c\beta }$ is the uniaxial compressive strength of rock corresponding to the loading direction angle β and ${\beta }_{\beta }$ and ${\alpha }_{\beta }$ are parameters representing the strength anisotropy of rock, which changes with the angle β. The following expressions have been proposed to determine the two parameters:

$$\frac{{\alpha }_{\beta }}{{\alpha }_{90}}={\left(\frac{{\sigma }_{c\beta }}{{\sigma }_{c90}}\right)}^{1-{\alpha }_{90}}$$

(26)

$$\frac{{\beta }_{\beta }}{{\beta }_{90}}={\left(\frac{{\alpha }_{90}}{{\alpha }_{\beta }}\right)}^{0.5}$$

(27)

where ${\sigma }_{c90}$ is the uniaxial compressive strength of rock with β = 90° and ${\alpha }_{90}$ and ${B}_{90}$ correspond to the parameter values at β = 90°.

To predict the failure strength of rock, a compression test under no confining pressure and several groups of confining pressures should first be performed on the specimens with β = 90°, and then the test values of compressive strength can be fitted according to Eq. (25) to obtain ${\alpha }_{90}$ and ${B}_{90}$. Next, Eqs. (26) and (27) can be utilized to determine the parameters ${\alpha }_{\beta }$ and ${\beta }_{\beta }$ corresponding to the angle β. Finally, if ${\sigma }_{c\beta }$ is tested experimentally, the prediction goal will be achieved by Eq. (25).

In the absence of experimental data, ${\sigma }_{c\beta }$ can be estimated according to the following Jaeger–Donath equation (Donath 1964; Jaeger 1960):

$${\sigma }_{c\beta }=A-B\ \mathrm{cos}\ 2\left(\beta -{\beta }_{\mathrm{m}}\right)$$

(28)

where ${\beta }_{\mathrm{m}}$ is the angle β corresponding to the minimum uniaxial compressive strength and A and B are constants, with B related to the anisotropy degree of the rock. The determination of A and B requires uniaxial compression test data from specimens with β = 0°, 30°, and 90° at minimum. Considering the purpose of analyzing and comparing the predictive ability of different criteria, ${\sigma }_{c\beta }$ could be determined using test results of uniaxial compression or linear fitting results of triaxial compression at angle β.

Modified Hoek–Brown failure criterion

Based on the Hoek–Brown failure criterion, Saroglou and Tsiambaos (2008) introduced a parameter characterizing strength anisotropy and established a modified criterion for evaluating the failure stress of rocks with MWPs:

$${\sigma }_{1}={\sigma }_{3}+{\sigma }_{c\beta }{\left({k}_{\beta }{m}_{i}\frac{{\sigma }_{3}}{{\sigma }_{c\beta }}+1\right)}^{0.5}$$

(29)

where ${\sigma }_{c\beta }$ is the uniaxial compressive strength of rock corresponding to the angle β, m_i is a parameter reflecting the properties of rock materials, and ${k}_{\beta }$ characterizes the strength anisotropy of rock and changes with the angle β. When β = 90°, ${k}_{\beta }$ is equal to 1. To predict the compressive strength, uniaxial and triaxial compression tests of specimens with β = 90° should be carried out first. Then, ${\sigma }_{c\beta }$ at β = 90° and ${k}_{\beta }$=1 are substituted into Eq. (29), and the test values of the triaxial compressive strength for the specimen with β = 90° are fitted with Eq. (29) to determine the parameter m_i. Subsequently, the data fitting adhering to Eq. (29) is conducted again to determine the parameter ${k}_{\beta }$ in response to the angle β on the premise of obtaining ${\sigma }_{c\beta }$ and the test values of triaxial compressive strength at the angle β. ${\sigma }_{c\beta }$ can be estimated according to the Jaeger–Donath equation. Once ${k}_{\beta }$, m_i, and ${\sigma }_{c\beta }$ have been obtained, the failure stress of rocks with angle β can be evaluated by Eq. (29).

The prediction errors of the failure stress obtained with the new criterion, Ramamurthy criterion and modified Hoek–Brown criterion, are given in Table 1. In contrast, the new criterion has a higher mean square error and lower mean relative error, indicating that this criterion is superior to the Ramamurthy criterion and modified Hoek–Brown criterion in terms of prediction accuracy. Compared with the other two criteria, the Ramamurthy criterion has a slightly worse predictive ability for the failure stress of foliated rocks. The data from the three rock samples are integrated for an overall comparison of the prediction accuracy of the three criteria, and the difference between the predicted value and the test value is intuitively shown in Fig. 11. It is clear that the failure stress predicted by the new criterion is more approximate to the test values as a whole, whereas the Ramamurthy criterion has significantly small predicted values relative to the actual values under the condition of relatively high confining pressure, resulting in a relatively poor prediction on the whole.

Fig. 11

Comparison between predicted and tested compressive strength value by different failure criteria, a new criterion, b Ramamurthy criterion, and c modified Hoek–Brown criterion

In a comprehensive comparison, the utilization of the Ramamurthy criterion requires the least basic data, which is convenient for the prediction of failure stress. However, as an empirical criterion, it has the disadvantage of a comparatively weak theoretical foundation. In addition, this criterion is slightly worse in prediction accuracy. The key to predicting the failure stress by the modified Hoek–Brown criterion lies in the determination of the anisotropy parameter ${k}_{\beta }$, which varies with the loading direction angle. The parameter values are determined by fitting the triaxial compression data corresponding to the respective loading direction angle, and no convenient and reliable method has been proposed yet to obtain the parameter values. Although the criterion has a well-recognized basis and shows a good predictive ability, it is still limited in promotion and application due to the large amount of basic data required and the relatively cumbersome determination of parameters. Evidently, the new criterion takes into account the advantages of the Ramamurthy criterion and modified Hoek–Brown criterion and performs well in terms of convenience, theoretical basis, and prediction accuracy.

In addition to high prediction accuracy, the new criterion has distinct characteristics compared with other classic failure criteria. In the current study, fracture mechanics and the Mohr–Coulomb theory have been applied to establish new failure criteria matching different failure modes of foliated rocks, showing a good fit with the failure mechanism of rock. The sliding and nonsliding failure criteria proposed by Tien and Kuo (2001) concentrate on the macrofailure pattern of rock material but lack close contact with the microscopic mechanism of rock. Additionally, instead of definite values, some parameters in Tien-Kuo’s criteria need to be determined empirically, which may adversely affect the prediction effect. Recognizing that the strength of anisotropic rocks under different loading directions is controlled by oriented long cracks and randomly distributed short cracks, Walsh and Brace (1964) established a failure criterion based on the Griffith theory. Although this criterion has good agreement with the failure mechanism of anisotropic rock, it is inappropriate to default the crack initiation strength to the peak failure strength in the case in which the load is applied to the oriented cracks at a large angle. The classic Griffith theory was applied to establish the Hoek–Brown criterion, and the relevant modified criteria for anisotropic rocks seem to have a good predictive effect on the compressive strength. However, some parameters in these empirical criteria lack clear physical meaning, and the determination of parameters encounters the same difficulties as Tien-Kuo’s criteria. In general, compared with the above classic failure criteria, the new criterion takes advantage of explicit parameter determination and contributes a good theoretical value for describing the anisotropic strength behavior of foliated rocks.

Application scope of the new criterion

From the above analysis, it is concluded that the new criterion has a reliable theoretical basis and high prediction accuracy. The application of the criterion does not require a large amount of basic data, and the process of determining the parameters is relatively simple. However, its application conditions still require some attention. As seen from Eqs. (10), (14), and (15), the critical stress corresponding to different loading directions is always linearly related to the confining pressure, indicating that this new criterion is a linear failure criterion. In addition, the failure stress formula of foliated rocks with an SSF mode is derived based on the theory of fracture mechanics, which is particularly appropriate for exploring the mechanical behavior of brittle material. The Mohr–Coulomb formula involved in establishing the failure criterion for foliated rocks with an MSF mode also describes the failure of brittle rocks well. Therefore, in theory, the new criterion is applicable to brittle foliated rocks. For apparently ductile rocks, the prediction accuracy of the new criterion will be greatly reduced when the compressive strength exhibits an obvious nonlinear response to the varying confining pressure. In general, the compressive strength of brittle rocks exhibits obvious linear characteristics within a certain range of confining pressures. Therefore, the new criterion has a good predictive ability for the failure stress of three types of brittle rock samples and is superior to the nonlinear Ramamurthy criterion for these cases. Figure 11 shows that the predicted value is generally smaller than the actual value under the condition of relatively high confining pressure, indicating that this empirical criterion is applicable to rocks with a significantly nonlinear response to confining pressure. In comparison, although the modified Hoek–Brown criterion is also a nonlinear criterion, its higher prediction accuracy may be attributed to the accurate fitting of more basic data.

Experimental studies (Behrestaghi et al. 1996; Fereidooni et al. 2016; Nasseri et al. 2003; Ramamurthy et al. 1993) have revealed that the loading direction angle ${\beta }_{\mathrm{m}}$ corresponding to the minimum compressive strength has a relationship with the confining pressure. As the confining pressure increases gradually, ${\beta }_{\mathrm{m}}$ shifts slowly to a somewhat larger value. For example, Nasseri et al. (2003) found that when the confining pressure increases from 5 to 50 MPa, ${\beta }_{\mathrm{m}}$ changes from 30° to 45°. It is worth noting that since parameter f is determined by linear fitting, the prediction result of the new criterion based on this constant parameter cannot conform to the variation regularity of ${\beta }_{\mathrm{m}}$. In fact, if the nonlinear influence of the confining pressure on the critical stress of the specimen with an SSF mode must be considered, the friction coefficient of the defect surface (the parameter f) will not be a constant value. Generally, this parameter tends to decrease slowly with increasing confining pressure (Li 2010). According to the analysis conclusion of Fig. 8, ${\beta }_{\mathrm{m}}$ will increase with decreasing f, indicating that the theoretical result still agrees well with the experimental phenomenon.

In summary, the linear failure criterion established in this study has good applicability for brittle foliated rocks within a certain range of confining pressures. Under the condition of excessively high confining pressure, it is difficult to achieve a satisfactory predictive ability. Furthermore, to describe the effect of confining pressure on failure strength more accurately, a detailed response pattern of parameter f to the confining pressure needs to be further investigated.

Conclusion

• a) The typical microscopic characteristics of foliated rocks involve the clustering and directional arrangement of needle-flaky minerals, the quasi-interlayered structure composed of weak and strong layers, and the oriented arrangement of microcracks distributed on the edge of needle-like minerals, all of which contribute to the mechanical anisotropy of this type of rock. Major microdefects, including microcracks and cleavage of needle-flaky minerals, exist in foliated rocks. The tensile stress is prone to concentrate at the tip of defects under the action of an axial load oblique to the surfaces of defects. The brittle failure of rock stems from the appearance of tensile cracks induced by concentrated stress. However, the critical stress causing crack initiation is closely related to the loading direction.

• b) The failure mode of foliated rocks responds sensitively to the loading direction angle β. In the range of low and medium confining pressures, there are two types of failure modes: shear–slip failure (SSF) along the MWP (at β = 15°–60°) and macro shear failure (MSF) oblique to the MWP (at β = 0°–15° or 60°–90°).

• c) A failure criterion corresponding to each failure mode was proposed for foliated rocks. From the perspective of crack evolution, the critical stress formula was derived based on the slip-cracking model of the original defect to estimate the failure strength of foliated rocks with an SSF mode. Focusing on the macrofailure of rocks, the Mohr–Coulomb criterion and maximum axial strain criterion were utilized to establish a compressive strength formula suitable for foliated rocks with an MSF mode.

• d) The new failure criterion contains 6 parameters, including the friction coefficient f of the defect surface, the two sets of cohesion c and internal friction angle ϕ, and the transversely isotropic parameter n. These parameters can be determined conveniently. Among them, parameter f is closely related to the loading direction angle ${\beta }_{\mathrm{m}}$ corresponding to the minimum compressive strength. As f decreases from 0.85 to 0.3, ${\beta }_{\mathrm{m}}$ gradually increases in the range of 25°–45°. The parameter n controls the curve shape of the compressive strength changing with the loading direction. As n decreases gradually, the curve will change from a U-shape to a shoulder shape.

• e) The new failure criterion is capable of nicely describing the variation regularity of the triaxial compressive strength of foliated rocks with the loading direction. The quantitative analysis of the error between the predicted data and the measured data has been carried out, which suggests a high prediction accuracy of the new failure criterion in the estimation of failure strength. The criterion, suitable for brittle foliated rocks in the range of low and medium confining pressures, captures the linear variation of strength with confining pressure. To describe the effect of confining pressure on failure strength more accurately, a detailed response pattern of parameter f to the confining pressure needs to be further investigated.