Introduction

Large-mass and high-velocity debris flows can be fatal to human society and infrastructures. In particular, the increase in the frequency and intensity of torrential rains caused by global climate change has induced debris flows in the mountains in urban areas (García-Delgado et al. 2019; Jeong et al. 2015). Solving these dynamic problems with extremely large deformations over a short event time is slightly different from traditional problems in geotechnical engineering. It is highly difficult to reproduce debris flows in the field, so lab- or large-scale experiments or numerical simulations are usually carried out to better understand the mechanisms and assess the risks (Chen and Lee 2000; Parsons et al. 2001; Crosta et al. 2009; Iverson et al. 2010, 2011). In South Korea, the real-scale debris flow experiment with terrestrial LiDAR was also attempted to figure out the debris flow mechanisms (Won et al. 2016).

When numerically simulating debris flows, many numerical models are usually based on the Savage-Hutter theory (Savage and Hutter 1989; Iverson 1997; Yavari-Ramshe et al. 2015). Their governing equations take the form of shallow water equations coupled with assumptions that include the incompressibility of materials, a small topology curvature, Coulomb frictional resistance, lateral pressure from the earth pressure coefficient, and a small horizontal momentum dissipation (Hutter et al. 2005). These flow models have to consider constant parameters such as the lateral earth pressure coefficient and the friction angle, which are usually acquired by independent experiments. However, these models are insufficient for reflecting the genuine behaviors of the debris mixture. Previous studies have proposed an effective stress-dependent frictional resistance (Iverson 1997), a μ-parametrization model (Pouliquen and Forterre 2002), a thermo-pore-mechanical model (Vardoulakis 2000), and the velocity-dependent friction law (Liu et al. 2016). In the dilatancy model, Iverson and George (2014) suggested that the pore water pressure induced by a volumetric change of debris mixture can alter the effective stress and corresponding friction resistance. In the μ-parametrization model, the friction coefficient μ (=tanδ) is considered a function of the non-dimensional inertial number. In the thermo-pore-mechanical model, the pore pressure generated by frictional heating alters the frictional resistance at the interface between the debris flow and basal surface. In the velocity-weakening friction model, the friction coefficient μ is interpolated between static and peak friction coefficients by the velocity magnitude.

Some studies have attempted to use a rheological model for non-Newtonian fluids or turbulent flows in shallow water equations to represent debris mixture behavior (Laigle and Coussot 1997; Zanuttigh and Lamberti 2004; Medina et al. 2008; Hong et al. 2019). The rheological model is more flexible in representing the velocity-dependent resistance than the Coulomb friction model. Additionally, previous studies have reported that Coulomb frictional resistance from constant bed friction could be insufficient to dampen debris velocity (Hutter and Greve 1993; Hutter et al. 2005). However, the viscous resistance in the rheological model could be much lower than the Coulomb frictional resistance when the debris flow has some thickness (Iverson 2003), and the estimation of rheological properties in debris mixtures has been less studied than in the Coulomb friction model. Some studies have attempted to estimate the rheological properties of debris mixtures by back analysis (Whipple 1997; Hürlimann et al. 2008). However, a systematic study on overall debris behavior according to various rheological properties is still necessary to verify the potential applicability of the rheological model.

One of the most difficult problems is to measure the rheological properties of the debris flow on the sediment characteristics, let alone the non-Newtonian fluids. The rheological properties of the debris material could be sensitive for solid volume fraction, particle sizes and shapes, etc. (Kaitna et al. 2007; Scotto Di Santolo et al. 2010; Pellegrino and Schippa 2018). Moreover, for a large-particulate debris mixture, conventional small-scale rheometers may be inapplicable and a large-scale rheometer specially designed for the debris should be used (Schatzmann et al. 2009; Pellegrino et al. 2016). The entrainment of basal sediment by the debris is a common process and can cause the change of the solid fraction and corresponding rheological properties of the debris. Also, the mixture density or solid fraction can vary when multiple debris flow with different densities merge at a confluence. Therefore, it is necessary to track the spatial distribution of the solid fraction at least to more realistically reflect the debris rheology in the numerical simulation. However, most previous numerical studies have used single-phase models that assume a constant mixture density (Chen and Lee 2000; Mangeney et al. 2007; Hong et al. 2019).

A few studies have recently suggested two-phase models for debris flows that contain continuity and momentum equations for both the solid and fluid phases (Pudasaini 2012; Li et al. 2018; Pastor et al. 2018). These two-phase models have a high potential to describe debris flow behaviors more realistically and overcome the limitations of current single-phase models. However, a theoretical basis with experimental evidence on the fluid-solid interactions employed in these two-phase models is still insufficient, and the models require greater computational effort and more input parameters than single-phase models.

To solve the shallow water equations for debris flows, many numerical studies have used the smoothed particle hydrodynamics (SPH) method and the finite volume method (FVM) (Xia et al. 2013; Yavari-Ramshe et al. 2015; Wang et al. 2016; Xia and Liang 2018; Han et al. 2019). SPH is a meshless and full Lagrangian-type approach that solves the individual dynamics of fictitious fluid particles by using Newton’s second law. The fluid-fluid and fluid-solid interactions are applied to the particles by volume averaging kernel functions that are macroscopically recovered by shallow water equations. However, SPH requires a sufficient number of particles to obtain an accurate solution, and the computational cost rapidly increases as the number of particles increases. Unlike SPH, the FVM is a mesh-based and Eulerian-type approach based on a divergence theorem that is specialized for computational fluid dynamics. Although SPH is flexible and can be recovered by shallow water equations, the numerical solutions obtained by SPH weakly and asymptotically satisfy the shallow water equations. In contrast, the FVM for debris flows requires sophisticated numerical treatments such as flux difference splitting schemes and can more strictly and accurately produce discontinuous solutions for shallow water equations.

This paper presents a simplified depth-averaged debris flow model for tracking density evolution. The developed model uses Herschel-Bulkley rheology in internal and basal frictions and considers complex terrains and entrainments. In particular, the interaction between solid-fluid phases in the mixture is ignored. A finite volume formulation of the proposed model is presented with relevant numerical schemes to obtain stable and accurate solutions. This work then validates dam-break and multiple debris flow simulations. In addition, the effect of debris rheology is discussed through a parametric study of a United States Geological Survey (USGS) experimental domain.

Methodology

Governing equations

The governing equations derived by depth-averaging the Navier-Stokes equations can facilitate debris flow simulations at a large scale by reducing the computational cost compared to full-scale 3D simulations. The continuity equations for the mixture and solid phases and the momentum equations of the mixture phase for x- and y-axes are given as

$$ \frac{\partial h\rho}{\partial t}+\frac{\partial }{\partial x}\left( h\rho {v}_x\right)+\frac{\partial }{\partial y}\left( h\rho {v}_y\right)=-{\rho}_b\frac{\partial {z}_b}{\partial t} $$
(1)
$$ \frac{\partial {hc}_s}{\partial t}+\frac{\partial }{\partial x}\left({hc}_s{v}_{s,x}\right)+\frac{\partial }{\partial y}\left({hc}_s{v}_{s,y}\right)=-{c}_{bs}\frac{\partial {z}_b}{\partial t} $$
(2)
$$ \frac{\partial h\rho {v}_x}{\partial t}+\frac{\partial h{\rho \alpha}_m{v}_x{v}_x}{\partial x}+\frac{\partial h{\rho \alpha}_m{v}_y{v}_x}{\partial y}=-\frac{\partial h\overline{p}}{\partial x}+\frac{\partial h{\overline{\tau}}_{xx}}{\partial x}+\frac{\partial h{\overline{\tau}}_{yx}}{\partial y}-{p}_b\frac{\partial {z}_b}{\partial x}+{\omega \tau}_b{t}_{b,x} $$
(3)
$$ \frac{\partial h\rho {v}_y}{\partial t}+\frac{\partial h{\rho \alpha}_m{v}_x{v}_y}{\partial x}+\frac{\partial h{\rho \alpha}_m{v}_y{v}_y}{\partial y}=-\frac{\partial h\overline{p}}{\partial y}+\frac{\partial h{\overline{\tau}}_{xy}}{\partial x}+\frac{\partial h{\overline{\tau}}_{yy}}{\partial y}-{p}_b\frac{\partial {z}_b}{\partial y}+{\omega \tau}_b{t}_{b,y} $$
(4)

where h, ρ, and cs are the debris height, mixture density, and solid volume fraction, respectively. vk and vs, k are the k-axis components of depth-averaged velocity for the mixture and solid phases, respectively. ρb and cbs are the mixture density and solid volume fraction of an entrained basal sediment. zb is the surface level of basal sediment. αm is a momentum correction factor. \( {\overline{\tau}}_{ij} \) is the depth-averaged shear stress. \( \overline{p} \) and pb are depth-averaged and basal pressures, respectively. τb is the basal friction stress. tb,k is a direction vector of basal friction. ω is a ratio of the basal surface area to its projection area onto the x-y plane, which can be written as

$$ \omega =\sqrt{{\left(\frac{\partial {z}_b}{\partial x}\right)}^2+{\left(\frac{\partial {z}_b}{\partial y}\right)}^2+1} $$
(5)

The derivation of the governing equation is provided in the Supplementary material in detail. This study assumes that the velocity difference between solid and water phases is sufficiently small and that this assumption is more definite in a high-velocity regime. Therefore, only the mixture velocity is considered as vk ≈ vs, k. By assuming a linear distribution of the pressure along the z-direction and the flow velocity parallel to the basal surface, the bulk pressure p and the apparent gravitational acceleration \( \hat{g} \) are given as (Xia and Liang 2018)

$$ p=\rho \hat{g}\left({z}_b+h-z\right) $$
(6)
$$ \hat{g}=\frac{1}{\omega^2}\left[g+{\mathbf{v}}^{\mathrm{T}}\mathbf{Hv}\right] $$
(7)

in which

$$ \mathbf{v}=\left[\begin{array}{c}{v}_x\\ {}{v}_y\end{array}\right]\kern0.5em \mathrm{and}\kern0.5em \mathbf{H}=\left[\begin{array}{cc}\frac{\partial^2{z}_b}{\partial {x}^2}& \frac{\partial^2{z}_b}{\partial x\partial y}\\ {}\frac{\partial^2{z}_b}{\partial x\partial y}& \frac{\partial^2{z}_b}{\partial {y}^2}\end{array}\right] $$
(8)

where H is the Hessian matrix of the basal surface elevation.

The z-axis component of depth-averaged velocity and the direction vector of basal friction are expressed as

$$ {v}_z={v}_x\frac{\partial {z}_b}{\partial x}+{v}_y\frac{\partial {z}_b}{\partial y} $$
(9)
$$ {t}_{b,k}=-\frac{v_k}{\sqrt{v_x^2+{v}_y^2+{v}_z^2}} $$
(10)

In open channel flow, the velocity profile along the z-direction is necessary to calculate basal viscous friction and is commonly known to be a function of the rheological model, velocity magnitude, and basal surface roughness, but it remains unclarified in the debris flow. For calculating basal friction, previous studies of shallow water equation simulations have used the Manning equation, which is an empirical equation for a relationship among an averaged velocity, a flow area, a channel slope, and a basal roughness (Xia et al. 2017; Hou et al. 2018). However, Manning’s roughness coefficient was originally given for water, so the coefficient is typically corrected depending on the debris rheology. Instead, this study assumes that the debris flow follows the nonlinear velocity profile model proposed by Johnson et al. (2012) as

$$ {u}_k=\left(2-\alpha \right)\left(1-{\left(1-\frac{z-{z}_b}{h}\right)}^{\frac{1}{1-\alpha }}\right){v}_k $$
(11)

where uk is the debris velocity in the 3D space reproduced using a nonlinear velocity profile model and a depth-averaged velocity vk. α is a profile shape parameter ranging between 0 to 1 and is herein set as 0.7. As α approaches 1, the velocity profile moves to a plug-like profile from a linear-like profile. The momentum correction factor and the basal friction stress of the rheological materials can be given as

$$ {\alpha}_m=\frac{4-2\alpha }{3-\alpha } $$
(12)
$$ {\tau}_b=\mu \frac{2-\alpha }{\left(1-\alpha \right)}\frac{\sqrt{v_x^2+{v}_y^2+{v}_z^2}}{h} $$
(13)

where μ is the debris viscosity.

This study uses the Herschel-Bulkley model for the rheology of debris flow as

$$ \mu =\min \left(\left[{\tau}_y+{k}_0{\gamma}^n\right]{\gamma}^{-1},{\mu}_{\mathrm{max}}\right) $$
(14)

where τy is the yield stress, γ is the magnitude of the shear rate, k0 is a consistency index, n is a flow index, and μmax is the maximum viscosity that prevents infinitely high viscosity when the shear rate approaches zero.

The depth-averaged shear strain and stress tensors are approximated as

$$ {\overline{\gamma}}_{ij}\approx \frac{1}{2}\left({\partial}_i{v}_j+{\partial}_j{v}_i\right)\kern0.5em \mathrm{for}\kern0.5em i,j=x,y,\mathrm{and}\kern0.24em z $$
(15)
$$ {\overline{\tau}}_{ij}=\mu {\overline{\gamma}}_{ij}\kern0.5em \mathrm{for}\kern0.5em i,j=x\kern0.24em \mathrm{and}\kern0.24em y $$
(16)

The x- and y-directional derivatives of the depth-averaged velocity in Eq. (16) are approximated by the central difference scheme. The z-directional derivative is assumed as

$$ \frac{\partial {v}_k}{\partial z}\approx \frac{{\left.{u}_k\right|}_{z_b+h}-{\left.{u}_k\right|}_{z_b}}{h}=\left(2-\alpha \right)\frac{v_k}{h} $$
(17)

This study uses the dynamic equilibrium approach for the entrainment of basal sediment proposed by Fraccarollo and Capart (2002) and Medina et al. (2008). The entrainment rate is given as

$$ \frac{\partial {z}_b}{\partial t}=-\frac{\tau_b-{\sigma}_b^{\prime}\tan {\phi}_{bs}-{c}_{bs}}{\rho \sqrt{v_x^2+{v}_y^2+{v}_z^2}} $$
(18)

where ϕbs and cbs are the internal friction angle and cohesion of the basal sediment, respectively.

By implementing a time integration of Eq. (18), we can obtain the erosion position ze, which becomes the new basal surface level after the entrainment as

$$ {z}_b\left(t+\Delta t\right)={z}_e={z}_b(t)+\underset{t}{\overset{t+\Delta t}{\int }}\frac{\partial {z}_b}{\partial t} dt $$
(19)

Our model tracks the local volume fraction of the solid phase, and the debris flow is assumed to be fully saturated regardless of the minimum void ratio of the soil particles. In this sense, to avoid a violation of mass conservation when the mass of eroded sediment at an unsaturated state is mixed with debris at a fully saturated state, the density of the eroded basal sediment ρbs should be evaluated as

$$ {\rho}_{bs}=\frac{1}{z_b-{z}_e}\underset{z_e}{\overset{z_b}{\int }}{\rho}_b(z) dz=\frac{\rho_w{G}_s}{1+e}+\frac{\rho_w}{z_b-{z}_e}\underset{z_e}{\overset{z_b}{\int }}\theta (z) dz $$
(20)

where ρb and θ are the sediment density and the volumetric water content below the basal surface, respectively. Gs is the specific gravity of a soil. ρw is the density of water. 

Model implementation

The physical and mathematical properties of the shallow water equations are analogous to the shock propagation in a compressible fluid in terms of the constant values around one discontinuous interface. This advection-dominant flow is sometimes considered a Riemann problem and is difficult to solve by the traditional numerical differencing schemes used for partial differential equations with a smooth solution. To solve the Riemann problem in computational fluid dynamics, flux-difference splitting or flux-vector splitting schemes are usually implemented. This study also implements the Harten-Lax-van Leer-Contact (HLLC) approximate Riemann solver, which is a powerful flux-difference splitting scheme (Toro 2002).

The governing equation can be rewritten in vector form as

$$ \frac{\partial \mathbf{U}}{\partial t}+\frac{\partial {\mathbf{F}}_x\left(\mathbf{U}\right)}{\partial x}+\frac{\partial {\mathbf{F}}_y\left(\mathbf{U}\right)}{\partial y}=\frac{\partial {\mathbf{T}}_x}{\partial x}+\frac{\partial {\mathbf{T}}_y}{\partial y}+{\mathbf{S}}_s+{\mathbf{S}}_d $$
(21)

where U is a vector of conserved variables. Fx(U) and Fy(U) are advection vectors of U for the x- and y-axes. Tx and Ty are momentum dissipation vectors for the x- and y-axes. Ss is a mass and momentum source vector, and Sd is a drag vector.

Those vector terms are given by

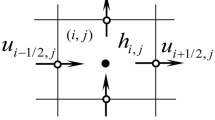
$$ {\displaystyle \begin{array}{l}U=\left\{\begin{array}{c} h\rho \\ {}h{c}_s\\ {} h\rho {v}_x\\ {} h\rho {v}_y\end{array}\right\},{F}_x\left\{\begin{array}{c} h\rho {v}_x\\ {}h{c}_s{v}_x\\ {} h\rho {\alpha}_m{v}_x{v}_x+\frac{1}{2}{\partial}_x\rho \hat{g}{h}^2\\ {} h\rho {\alpha}_m{v}_y{v}_x\end{array}\right\},{F}_y\left\{\begin{array}{c} h\rho {v}_y\\ {}h{c}_s{v}_y\\ {} h\rho {\alpha}_m{v}_x{v}_y\\ {} h\rho {\alpha}_m{v}_y{v}_y+\frac{1}{2}{\partial}_y\rho \hat{g}{h}^2\end{array}\right\}\\ {}{T}_x=\left\{\begin{array}{c}0\\ {}0\\ {} h\mu {\overline{\gamma}}_{xx}\\ {} h\mu {\overline{\gamma}}_{xy}\end{array}\right\},{T}_y=\left\{\begin{array}{c}0\\ {}0\\ {} h\mu {\overline{\gamma}}_{yx}\\ {} h\mu {\overline{\gamma}}_{yy}\end{array}\right\},{S}_s=\left\{\begin{array}{c}-{\rho}_b{\partial}_t{z}_b\\ {}-{c}_{bs}{\partial}_t{z}_b\\ {}-2\overline{p}{\partial}_x{z}_b\\ {}-2\overline{p}{\partial}_y{z}_b\end{array}\right\},{S}_d=\left\{\begin{array}{c}0\\ {}0\\ {}\omega {\tau}_b{t}_{b,x}\\ {}\omega {\tau}_b{t}_{b,y}\end{array}\right\}\end{array}} $$
(22)

The semi-discrete form for the volume integration of Eq. (21) for a rectangular cell at (xi, yj) can be expressed by

$$ {\displaystyle \begin{array}{c}\frac{\partial {U}_{i,j}}{\partial t}=\frac{1}{dA}\left(\varDelta y{F}_x^{i-\frac{1}{2},j}-\varDelta y{F}_x^{i+\frac{1}{2},j}+\varDelta x{F}_y^{i,j-\frac{1}{2}}-\varDelta x{F}_y^{i,j+\frac{1}{2}}\right)\\ {}+\frac{1}{dA}\left(\varDelta y{T}_x^{i-\frac{1}{2},j}-\varDelta y{T}_x^{i+\frac{1}{2},j}+\varDelta x{T}_y^{i,j-\frac{1}{2}}-\varDelta x{T}_y^{i,j+\frac{1}{2}}\right)+{S}_s^{i,j}+{S}_d^{i,j}\end{array}} $$
(23)

where Δx and Δy are the cell edge sizes, dA is the cell area (i.e., ΔxΔy). \( {\mathbf{F}}_x^{i\pm \frac{1}{2},j} \) are advection fluxes passing through cell faces at \( \left({x}_i\pm \frac{1}{2}\varDelta x,{y}_j\right) \). Similarly, \( {\mathbf{F}}_y^{i,j\pm \frac{1}{2}} \) are advection fluxes passing through cell faces at \( \left({x}_i,{y}_j\pm \frac{1}{2}\varDelta y\right) \).

In the HLLC scheme, the cell-faced values of the conserved variables and the advection fluxes are calculated by considering the three characteristic wave speeds as

$$ {\mathbf{U}}^{i+\frac{1}{2},j}=\left\{\begin{array}{cc}{\mathbf{U}}^{i+\frac{1}{2}-,j}& 0\le {S}^{i+\frac{1}{2}-,j}\\ {}{\mathbf{U}}_M^{i+\frac{1}{2}-,j}& {S}^{i+\frac{1}{2}-,j}\le 0\le {S}_M^{i+\frac{1}{2},j}\\ {}{\mathbf{U}}_M^{i+\frac{1}{2}+,j}& {S}_M^{i+\frac{1}{2},j}\le 0\le {S}^{i+\frac{1}{2}+,j}\\ {}{\mathbf{U}}^{i+\frac{1}{2}+,j}& {S}^{i+\frac{1}{2}+,j}<0\end{array}\right. $$
(24)

and

$$ {\mathbf{F}}^{i+\frac{1}{2},j}=\left\{\begin{array}{cc}{\mathbf{F}}^{i+\frac{1}{2}-,j}& 0\le {S}^{i+\frac{1}{2}-,j}\\ {}{\mathbf{F}}_M^{i+\frac{1}{2}-,j}& {S}^{i+\frac{1}{2}-,j}\le 0\le {S}_M^{i+\frac{1}{2},j}\\ {}{\mathbf{F}}_M^{i+\frac{1}{2}+,j}& {S}_M^{i+\frac{1}{2},j}\le 0\le {S}^{i+\frac{1}{2}+,j}\\ {}{\mathbf{F}}^{i+\frac{1}{2}+,j}& {S}^{i+\frac{1}{2}+,j}<0\end{array}\right. $$
(25)

where \( {S}^{i+\frac{1}{2}-,j} \), \( {S}_M^{i+\frac{1}{2},j} \), and \( {S}^{i+\frac{1}{2}+,j} \) are the characteristic wave speeds of the left, middle, and right regions of a cell face at \( \left({x}_i+\frac{1}{2}\varDelta x,{y}_j\right) \). \( {\mathbf{U}}^{i+\frac{1}{2}\pm, j} \) and \( {\mathbf{F}}^{i+\frac{1}{2}\pm, j} \) are conservative variables and advection fluxes extrapolated by using a flux limiter at the left and right sides of a cell face. \( {\mathbf{U}}_M^{i+\frac{1}{2}\pm, j} \) and \( {\mathbf{F}}_M^{i+\frac{1}{2}\pm, j} \) are conservative variables and advection fluxes at the left and right middle regions of a cell face.

The interface values of a quantity ξ at the left and right sides of a cell face at \( \left({x}_i+\frac{1}{2}\varDelta x,{y}_j\right) \) can be extrapolated as

$$ {\xi}^{i+\frac{1}{2}-,j}={\xi}^{i,j}+\frac{\Delta x}{2}\Psi \left({r}^{i,j}\right){\left.\frac{\partial \xi }{\partial x}\right|}_{i,j}^{\mathrm{up}} $$
(26)
$$ {\xi}^{i+\frac{1}{2}+,j}={\xi}^{i+1,j}-\frac{\Delta x}{2}\Psi \left({r}^{i+1,j}\right){\left.\frac{\partial \xi }{\partial x}\right|}_{i+1,j}^{\mathrm{up}} $$
(27)

where ri, j is a ratio of successive gradients, Ψ is a flux limiter function, and \( {\left.{\partial}_x\xi \right|}_{i+1,j}^{\mathrm{up}} \) is an x-directional unlimited gradient of a quantity ζ calculated by the upwind difference scheme.

The ratio of successive gradients is given as

$$ {r}^{i,j}=\frac{\xi^{\mathrm{up}}-{\xi}^{i,j}}{\xi^{i,j}-{\xi}^{\mathrm{down}}} $$
(28)

where ξup and ξdown are upstream and downstream cell-centered values, respectively.

This study uses the van Leer limiter function as

$$ \Psi (r)=\frac{r+\left|r\right|}{1+\left|r\right|} $$
(29)

The basal surface level at a cell face \( {z}_b^{i+\frac{1}{2},j} \) is obtained by the hydrostatic reconstruction method proposed by Audusse et al. (2004) to avoid a negative debris height as

$$ {z}_b^{i+\frac{1}{2},j}=\max \left({\left[{z}_b+h\right]}^{i+\frac{1}{2}-,j}-{h}^{i+\frac{1}{2}-,j},\kern0.36em {\left[{z}_b+h\right]}^{i+\frac{1}{2}+,j}-{h}^{i+\frac{1}{2}+,j}\right) $$
(30)

where \( {h}^{i+\frac{1}{2}\pm, j} \) are calculated by Eqs. (26) and (27).

After the calculation of \( {z}_b^{i+\frac{1}{2},j} \), the interface values of debris height \( {h}^{i+\frac{1}{2}\pm, j} \) are recalculated by

$$ {h}^{i+\frac{1}{2}-,j}=\max \left(0,\kern0.36em {\left[{z}_b+h\right]}^{i+\frac{1}{2}-,j}-{z}_b^{i+\frac{1}{2},j}\right) $$
(31)
$$ {h}^{i+\frac{1}{2}+,j}=\max \left(0,\kern0.36em {\left[{z}_b+h\right]}^{i+\frac{1}{2}+,j}-{z}_b^{i+\frac{1}{2},j}\right) $$
(32)

The characteristic wave speeds considering wet or dry bed condition are given as (Toro 2002)

$$ {S}^{i+\frac{1}{2}-,j}=\left\{\begin{array}{cc}{v}_x^{i+\frac{1}{2}+,j}-2{a}^{i+\frac{1}{2}+,j}& {h}^{i+\frac{1}{2}-,j}=0\\ {}\min \left({v}_x^{i+\frac{1}{2}-,j}-{a}^{i+\frac{1}{2}-,j},{v}_{x,M}^{i+\frac{1}{2},j}-{a}_M^{i+\frac{1}{2},j}\;\right)& {h}^{i+\frac{1}{2}-,j}>0\end{array}\right. $$
(33)
$$ {S}^{i+\frac{1}{2}+,j}=\left\{\begin{array}{cc}{u}_x^{i+\frac{1}{2}-,j}+2{a}^{i+\frac{1}{2}-,j}& {h}^{i+\frac{1}{2}+,j}=0\\ {}\max \left({v}_x^{i+\frac{1}{2}+,j}+{a}^{i+\frac{1}{2}+,j},{v}_{x,M}^{i+\frac{1}{2},j}+{a}_M^{\mathrm{i}+\frac{1}{2},j}\;\right)& {h}^{i+\frac{1}{2}+,j}>0\end{array}\right. $$
(34)

where

$$ {a}^{i+\frac{1}{2}\pm, j}=\sqrt{{\hat{g}}^{i+\frac{1}{2},j}{h}^{i+\frac{1}{2}\pm, j}}\kern0.5em \mathrm{and}\kern0.5em {a}_M^{i+\frac{1}{2},j}=\sqrt{{\hat{g}}^{i+\frac{1}{2},j}{h}_M^{i+\frac{1}{2},j}} $$
(35)

The velocity and height of debris at the middle region are calculated by

$$ {v}_{x,M}^{i+\frac{1}{2},j}=\frac{1}{2}\left({v}_x^{i+\frac{1}{2}-,j}+{v}_x^{i+\frac{1}{2}+,j}\right)+{a}^{i+\frac{1}{2}-,j}-{a}^{i+\frac{1}{2}+,j} $$
(36)
$$ {h}_M^{i+\frac{1}{2},j}=\frac{1}{{\hat{g}}^{i+\frac{1}{2},j}}{\left(\frac{1}{2}\left({a}^{i+\frac{1}{2}-,j}+{a}^{i+\frac{1}{2}+,j}\right)+\frac{1}{4}\left({v}_x^{i+\frac{1}{2}-,j}-{v}_x^{i+\frac{1}{2}+,j}\right)\right)}^2 $$
(37)

The gravitational acceleration at a cell face is taken by the linear interpolation as

$$ {\hat{g}}^{i+\frac{1}{2},j}=\frac{1}{2}\left({\hat{g}}^{i,j}+{\hat{g}}^{i+1,j}\right) $$
(38)

The conservative variables and advection fluxes at the left and right middle regions are interpolated as

$$ {U}_M^{i+\frac{1}{2}\pm, j}=\left(\frac{S^{i+\frac{1}{2}\pm, j}-{v}_x^{i+\frac{1}{2}\pm, j}}{S^{i+\frac{1}{2}\pm, j}-{S}_M^{i+\frac{1}{2},j}}\right)\left[\begin{array}{c}{\rho}^{i+\frac{1}{2}\pm, j}\\ {}{c}_s^{i+\frac{1}{2}\pm, j}\\ {}{\mathrm{S}}_M^{i+\frac{1}{2},j}\\ {}{v}_y^{i+\frac{1}{2}\pm, j}\end{array}\right] $$
(39)
$$ {\mathbf{F}}_M^{i+\frac{1}{2}\pm, j}={\mathbf{F}}^{i+\frac{1}{2}\pm, j}+{S}^{i+\frac{1}{2}\pm, j}\left({\mathbf{U}}_M^{i+\frac{1}{2}\pm, j}-{\mathbf{U}}^{i+\frac{1}{2}\pm, j}\right) $$
(40)

where the middle wave speed \( {S}_M^{i+\frac{1}{2},j} \) is

$$ {S}_M^{i+\frac{1}{2},j}=\frac{S^{i+\frac{1}{2}-,j}{h}^{i+\frac{1}{2}+,j}\left({v}_x^{i+\frac{1}{2}+,j}-{S}^{i+\frac{1}{2}+,j}\right)-{S}^{i+\frac{1}{2}+,j}{h}^{i+\frac{1}{2}-,j}\left({v}_x^{i+\frac{1}{2}-,j}-{S}^{i+\frac{1}{2}-,j}\right)}{h^{i+\frac{1}{2}+,j}\left({v}_x^{i+\frac{1}{2}+,j}-{S}^{i+\frac{1}{2}+,j}\right)-{h}^{i+\frac{1}{2}-,j}\left({v}_x^{i+\frac{1}{2}-,j}-{S}^{i+\frac{1}{2}-,j}\right)} $$
(41)

It is noted that \( {\mathbf{F}}_M^{i+\frac{1}{2}\pm, j} \) and \( {\mathbf{F}}^{i+\frac{1}{2}\pm, j} \) in Eq. (40) only contain advection terms of conserved variables. In other words, these parameters do not include the pressure gradient flux parts. Therefore, the pressure gradient flux needs to be separately calculated by using the cell-faced density and height.

$$ {\left[\rho \hat{g}{h}^2\right]}^{i+\frac{1}{2},j}={\rho}^{i+\frac{1}{2},j}{\hat{g}}^{i+\frac{1}{2},j}{\left({h}^{i+\frac{1}{2},j}\right)}^2 $$
(42)

The cell-faced density and height are also calculated from cell-faced conservative variables obtained by Eq. (24).

$$ {c}_s^{i+\frac{1}{2},j}=\frac{\rho_s{\left[{hc}_s\right]}^{i+\frac{1}{2},j}}{G_s{\left[ h\rho \right]}^{i+\frac{1}{2},j}-{\rho}_s\left({G}_s-1\right){\left[{hc}_s\right]}^{i+\frac{1}{2},j}} $$
(43)
$$ {\rho}^{i+\frac{1}{2},j}={\rho}_s{c}_s^{i+\frac{1}{2},j}+{\rho}_w\left(1-{c}_s^{i+\frac{1}{2},j}\right) $$
(44)
$$ {h}^{i+\frac{1}{2},j}=\frac{{\left[ h\rho \right]}^{i+\frac{1}{2},j}}{\rho^{i+\frac{1}{2},j}} $$
(45)

The momentum dissipation fluxes are discretized by two cell-centered values of shear stress and the cell-faced height as

$$ {\hat{T}}_x^{i\pm \frac{1}{2},j}=\left\{\begin{array}{c}0\\ {}0\\ {}\frac{1}{2}{h}^{i\pm 1,j}\left({\left[{\mu}_{ap}{\overline{\gamma}}_{xx}\right]}^{i\pm 1,j}+{\left[{\mu}_{ap}{\overline{\gamma}}_{xx}\right]}^{i,j}\right)\\ {}\frac{1}{2}{h}^{i\pm 1,j}\left({\left[{\mu}_{ap}{\overline{\gamma}}_{xy}\right]}^{i\pm 1,j}+{\left[{\mu}_{ap}{\overline{\gamma}}_{xy}\right]}^{i,j}\right)\end{array}\right\} $$
(46)

The momentum source term can be simply discretized as

$$ {\left[2\overline{p}{\partial}_x{z}_b\right]}^{i,j}=\frac{1}{2\Delta x}\left({\left[\rho \hat{g}h\right]}^{i+\frac{1}{2}-,j}+{\left[\rho \hat{g}h\right]}^{i-\frac{1}{2}+,j}\right)\left({z}_b^{i+\frac{1}{2},j}-{z}_b^{i-\frac{1}{2},j}\right) $$
(47)

The time marching of Eq. (23) is carried out by the predictor-corrector scheme for a numerical accuracy. To prevent reversing the flow direction by the drag vector, the predictor and corrector steps are given as follows:

In the predictor step:

$$ {\tilde{\mathbf{U}}}^{t+\varDelta t,(0)}={\mathbf{U}}^t+\varDelta t\frac{\partial {\tilde{\mathbf{U}}}^t}{\partial t} $$
(48)
$$ {\tilde{\mathbf{S}}}_{d,3\kern0.24em \mathrm{or}\kern0.24em 4}^t=\left\{\begin{array}{c}{\mathbf{S}}_{d,3\kern0.24em \mathrm{or}\kern0.24em 4}^t\\ {}-\frac{1}{\varDelta t}{\tilde{\mathbf{U}}}_{3\kern0.24em \mathrm{or}\kern0.24em 4}^{t+\varDelta t,(0)}\end{array}\right.\kern0.48em \mathrm{for}\kern0.36em {\displaystyle \begin{array}{c}\sqrt{{\left({\tilde{\mathbf{U}}}_3^{t+\varDelta t,(0)}\right)}^2+{\left({\tilde{\mathbf{U}}}_4^{t+\varDelta t,(0)}\right)}^2}\ge \varDelta t\sqrt{{\left({\mathbf{S}}_{d,3}^t\right)}^2+{\left({\mathbf{S}}_{d,4}^t\right)}^2}\\ {}\mathrm{else}\end{array}} $$
(49)
$$ {\mathbf{U}}^{t+\varDelta t,(0)}={\mathbf{U}}^t+\varDelta t\frac{\partial {\hat{\mathbf{U}}}^t}{\partial t}={\tilde{\mathbf{U}}}^{t+\varDelta t,(0)}+\varDelta t{\tilde{\mathbf{S}}}_d^t $$
(50)

In the corrector step:

$$ {\tilde{\mathbf{U}}}^{t+\varDelta t,(k)}={\mathbf{U}}^t+\frac{\varDelta t}{2}\left(\frac{\partial {\hat{\mathbf{U}}}^t}{\partial t}+\frac{\partial {\tilde{\mathbf{U}}}^{t+\varDelta t,\left(k-1\right)}}{\partial t}\right) $$
(51)
$$ {\overset{\sim }{S}}_{d,3\kern0.24em \mathrm{or}\;\;4}^{t+\varDelta t,\left(k-1\right)}=\left\{\begin{array}{c}{S}_{d,3\kern0.24em \mathrm{or}\;\;4}^{t+\varDelta t,\left(k-1\right)}\\ {}-\frac{2}{\varDelta t}{\overset{\sim }{U}}_{3\kern0.24em \mathrm{or}\;\;4}^{t+\varDelta t,(k)}\end{array}\right.\;\;\;\;\mathrm{for}\;\;\;{\displaystyle \begin{array}{c}\sqrt{{\left({\overset{\sim }{U}}_3^{t+\varDelta t,(k)}\right)}^2+{\left({\overset{\sim }{U}}_4^{t+\varDelta t,(k)}\right)}^2}\ge \frac{\varDelta t}{2}\sqrt{{\left({S}_{d,3}^{t+\varDelta t,\left(k-1\right)}\right)}^2+{\left({S}_{d,4}^{t+\varDelta t,\left(k-1\right)}\right)}^2}\\ {}\mathrm{else}\end{array}} $$
(52)
$$ {\mathbf{U}}^{t+\varDelta t,(k)}={\tilde{\mathbf{U}}}^{t+\varDelta t,(k)}+\frac{\varDelta t}{2}{\tilde{\mathbf{S}}}_d^{t+\varDelta t,\left(k-1\right)} $$
(53)

in which

$$ {\tilde{\mathbf{S}}}_{d,1\kern0.24em \mathrm{or}\kern0.24em 2}={\mathbf{S}}_{d,1\kern0.24em \mathrm{or}\kern0.24em 2} $$
(54)
$$ \frac{\partial \tilde{\mathbf{U}}}{\partial t}=\frac{\partial \mathbf{U}}{\partial t}-{\mathbf{S}}_d $$
(55)

where k is the number of iterations needed for the corrector step to improve an approximated solution of a time marching problem and is herein set as 1. After finishing the iterations of the corrector step, the finally corrected vector Ut + Δt, (k) becomes a conserved quantities vector Ut + Δt at the next time step. Similar to Eqs. (43)–(45), the cell-centered variables of height, density, and velocity at the next time step can be separated from the updated conserved quantities vector. Note that if a numerical scheme is applied that cannot correctly consider a discontinuous solution in the Riemann problem, the mass conservation may be significantly violated during the time marching of our debris flow model. Additionally, our model can capture the evolution of the solid volume fraction during debris flow, but this study does not focus on the rheological properties that depend on the solid volume fraction. The rheological properties are homogeneous and constant during the simulation in the paper.

The time interval Δt is controlled for numerical stability as

$$ \varDelta t=\min \left({CFL}_a\cdot \frac{\min \left(\varDelta x,\varDelta y\right)}{\sqrt{v_x^2+{v}_y^2}+\sqrt{\hat{g}h}},\kern0.48em {CFL}_d\cdot \frac{\min \left(\varDelta {x}^2,\varDelta {y}^2\right)\rho }{4\mu}\right) $$
(56)

where CFLa and CFLd are empirically selected to 0.3 and 0.9 in this study.

Validations

The numerical model proposed in this study is implemented by MATLAB. In this section, three simulations are performed to validate the implemented numerical code. The first simulation is a circular dam-break test of frictionless condition. The second simulation is a dam-break test of non-Newtonian fluid of which the viscosity can follow the Herschel-Bulkley model well. The last one is multiple debris flow with different densities. The test results provide that the implemented code is sufficiently accurate and applicable to simulate the debris flow.

Circular dam-break of frictionless condition

The dam-break test is a famous validation test used to show the shock-capturing capability in numerical modeling (Wang et al. 2010; Xia et al. 2013; Ginting and Mundani 2019). In this section, we conducted a circular dam-break test to validate the shock-capturing capability and the isotropy of the implemented numerical scheme. The domain ranges from [40m, 40m] with a flat basal surface and is discretized by a resolution of 0.1m × 0.1m. The cylindrical dam, with a radius of 2.5m and zero thickness, is placed at the center of the domain. The momentum correction factor is set as unity and the viscosity and corresponding basal friction are ignored. The density is set as 1000kg/m3.

The inside and outside regions of the dam are initially filled with water of 2.5-m and 0.5-m heights with an at-rest condition as

$$ h=\left\{\begin{array}{c}2.5\;m\\ {}0.5\;m\end{array}\kern0.36em \mathrm{for}\kern0.48em \begin{array}{c}\sqrt{x^2+{y}^2}\le 2.5\\ {} else\end{array}\right. $$
(57)

The simulation is run for t = 4.7s. After breaking the dam, the water column isotopically spreads outward, as shown in Fig. 1. The evolution of the water column in the result is consistent with Ginting and Mundani (2019). The water height and velocity profiles for a centerline at t=4.7s are also compared with the analytical solution, as shown in Fig. 2. The results are in overall good agreement with the analytical solutions, although small numerical diffusion occurs near the steep gradient region of the solution.

Fig. 1
figure 1

The configuration of water column after breaking dam t=0.1s (a), t=1.6s (b), and t=4.7s (c). d The water height along the centerline of the domain

Full size image
Fig. 2
figure 2

The water height and velocity along the centerline of the domain at time t=4.7s

Full size image

Dam-break of non-Newtonian fluid

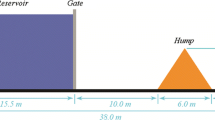
This section simulated a dam-break experiment of a non-Newtonian fluid performed by Ancey and Cochard (2009) to validate the implemented model. The equipment in Ancey and Cochard (2009) is comprised of a reservoir, a gate, and a plate as shown in Fig. 3. The reservoir size is a width of 0.3m and length of 0.51m. The plate size is a width of 1.6m and a length of 2m. The inclination of equipment is herein set as 12°. In the experiment, the gate was inclined orthogonal to the plate, but this study assumed that the gate was standing in the direction of gravity. The initial height of the fluid at the gate is set as 0.34m. The domain is discretized by a resolution of 0.1m × 0.1m. The fluid density is set as 1000kg/m3. The rheological parameters of the fluid are n=0.42, k0=47.68Pa·sn, and τy=89Pa. The simulation is run for t=10s. As similar to the circular dam-break simulation, the gate suddenly disappeared and the stored fluid is accelerated to flow downward. The traveling distance of the fluid front during the simulation was compared to the experimental result and other flow simulations conducted in previous studies as shown in Fig. 3b (Ancey and Cochard 2009; Nikitin et al. 2011; Bernabeu et al. 2014). In the experiment, the initial movement of the fluid (t<~0.05s) was much faster than in all simulations, and the fluid speed decreased sharply afterward. Bernabeu et al. (2014) suspected that this difference could be caused by detailed differences in numerical simulations and experiments. In the early stage, the traveling distance of the fluid front in our simulation was delayed than the experiment but the long-term behavior was in good agreement with the experiment. Therefore, this validation shows that the numerical model developed in this paper is sufficiently accurate to model non-Newtonian fluid behavior for the debris flow.

Fig. 3
figure 3

a Schematic configuration of simulation for the dam-break experiment in Ancey and Cochard (2009). b The traveling distance of the fluid front with time

Full size image

Multiple debris flow

In this section, the density tracking capability is validated by simulating the merging of multiple debris flow. Figure 4 presents the topology of a simulation domain defined as 100 m×34 m that is discretized by a resolution of 0.1 m×0.1 m. The two U-shaped valleys with an included angle of 30° merge into one at a junction at x=20m. The merged valley descends to x=50m with an inclination angle of 15° and then becomes flat. The debris with a radius of 3m and a height of 0.5m is initially placed at the end of the two valleys. The densities of bottom- and top-side debris are 2200 and 1500kg/m3, respectively. The consistency index, flow index, and yield stress in this test are set to 0.3Pa·sn, 0.9, and 100Pa regardless of the debris density. The simulation runs for 12s. Figure 5 displays snapshots of the debris height and density distributions at t=2.5, 4.5, 7, and 12s. As debris started to move, the velocities of the light and heavy debris were similarly developed, but the heavy debris was slightly faster than the light debris.

Fig. 4
figure 4

The topology of multiple debris flow simulation. Initial debris (red circles) with a radius of 3 m and a height of 0.5 m (color bar: debris height (m), contour line: surface level (m))

Full size image
Fig. 5
figure 5

Snapshots of height (a, c, e, g) and density (b, d, f, h) distributions in multiple debris flow (color bar unit: m (left), kg/m3 (right))

Full size image

This result seems to be caused by the differences in debris density. The viscous friction in this study is not a direct function of density. Thus, heavy and light debris under identical conditions lose the same amount of momentums because of the basal friction, and their velocity decreases. However, heavy debris moves relatively faster than the light debris due to its high momentum. The multiple debris flow contacted each other at t=3.6 and then advanced side by side. After the contact of two debris flows, the heavy debris wrapped the light debris, as shown in Fig. 5c and d. Due to the momentum of the heavy debris being higher than the light debris, the advancing debris waved to the upside first, then the downside, and then the upside again. Those vestigial movements remain in Fig. 5e–h, and the result is reasonable when considering the inertial effect.

Figure 6a shows the evolution of cumulative debris volume, which is a summation of low-density debris. As time progresses after contact, the portion of intermediate density debris that is in a contact interface with the heavy and light debris increased. The total volume remains conserved in Fig. 6a. For more clarity in mass conservation, Fig. 6b shows the total mass increase from the initial mass. Although it appears that a sharp increment in total mass occurs at t = 7 s, that is only ~3.5×10−8% of the initial total mass and within a sufficiently tolerable range. Therefore, these results show that the numerical schemes implemented in this paper present mass conservation well and imply that they are sufficiently accurate when considering the numerical stability of the debris flow problem.

Fig. 6
figure 6

a The debris volume cumulated from low density to high density. b Amount of increased mass of the debris

Full size image

Parametric study

This section presents a parametric study of the debris rheology for a large-scale debris flow experiment conducted by Iverson et al. (2010, 2011) whose team is affiliated with the USGS. Previous numerical studies of that experiment used the Coulomb friction model, so the information on the rheological properties of the debris mixture is not well known. This study performs numerical simulations with various model parameters within the same domain of the experiment to provide an understanding of the debris flow behavior according to the rheological properties. Figure 7a illustrates the side view of the experimental setup, in which the downslope channel has a length of 80 m, a width of 2m, a slope angle of 31°, and a slope angle of 5°. The computational domain is herein constructed by a spatial discretization of 0.2m × 0.2m, as shown in Fig. 7b. The no-slip boundary is applied to all sidewalls.

Fig. 7
figure 7

Schematic configuration of the debris flow domain (adopted from Iverson et al. 2010, 2011)

Full size image

The debris, with a volume of 6m3 and a density of 2000kg/m3, is initially placed in the upside of the head gate in the channel. The basal sediment of 12-cm height covers the bed surface at x=5.7–53.5m with a density of 1665kg/m3, a saturation of 0.4, a porosity of 0.45, an internal friction angle of 35°, and no cohesion. The specific gravity of solid particles is 2.7. The total converted debris volume, including the initial debris and basal sediment, is 13.7m3. A modeling series is run for a simulation time of 50s. The input parameters of the rheological model are systematically varied in predefined ranges of consistency index, flow index, and yield stress, as summarized in Table 1. These ranges were selected by considering previous studies on the rheology of debris (Whipple 1997; Sosio and Crosta 2009; Jeong and Park 2016).

Table 1 Ranges of input parameters in the parametric study
Full size table

Figure 8 illustrates the traveling distance of the debris flow front from the opened gate for different consistency and flow indices at four different yield stress τy=0, 100, 400, and 800Pa. The semi-transparent yellowish zone covers the range of experimental results in Iverson et al. (2011) and some cases in low- or high-yield stresses were obviously out of the experiment range. For instance, it was observed that the lower the consistency index and the flow index, the more the traveling distance increases. Considering that a frictionless block could reach on the runout pad at t = ~5.7s (Iverson et al. 2011), the debris front movement of low consistency and flow indices at low-yield stress looks faster than the frictionless block. This is because the debris is not only translated by gravity but also spread by a pressure gradient such as a dam-break. As the yield stress increases, the traveling distance and the front speed decrease, and the curves of low consistency index seem to converge to a virtual upper limit. In addition, when the yield stress is 800Pa (Fig. 8d), the debris stops on the channel regardless of the consistency and flow indices, and the flow quickly converged. Thus, we could infer that the curves of the debris with n=0.1 and k0=0.1Pa·sn for four different yield stresses in Fig. 8 are asymptotically close to the upper limit although the debris property may be unrealistic.

Fig. 8
figure 8

Traveling distance of debris flow fronts in time for different flow and consistency indices at yield stress τy = 0 (a), 100 (b), 400 (c), and 800 Pa (d). The line color and type represent the consistency index and the flow index, respectively. The gray dashed line indicates the start point of the runout pad. The yellowish zone indicates the range of the USGS experiments (Iverson et al. 2011)

Full size image

To further focus on the effect of flow index on the debris flow, profiles of height, speed, density, and basal shear stress of the debris are displayed for three different flow indices (n=0.5, 1, and 1.3) with a constant consistency index (k0=10Pa·sn) and zero yield stress in Fig. 9. Those profiles were obtained along the midplane of the domain at different times. The height of the debris front moving along the downslope channel tended to be higher as the flow index was higher. This seems to be caused by two reasons. One is that the positive feedback owing to the shear-thinning behavior of the debris among low viscosity, high speed (i.e., a high shear rate), and low basal shear stress accelerates spreading the debris front. The other is that the higher basal shear stress and lower speed due to the higher flow index could make greater the entrainment of basal sediment. Note that this study assumes the speed of the debris reduces the erosion rate to the basal sediment according to Eq. (18). The increased density profile can prove that the entrainment predominates in the front of the debris. When entrainment occurs, the debris above the eroded sediment gains in mass but without additional driving momentum, so the debris speed can be reduced or maintained temporarily. Note that this study assumes the debris mixture being saturated. Therefore, the density of the entrained debris mixture is higher than that of the unsaturated basal sediment. Although it seems that the high rate of entrainment causes a rough profile of the debris surface, it may differ from the real profile, because the debris is fully saturated and the turbulence is not considered in this study and because this study does not take into account air entrainment by dilatation and turbulence. As the flow index increases, the entrainment in rear debris may increase, and secondary debris flow may develop. In some of the traveling distance curves in Fig. 8, it is observed that the debris front slows down for a while and then moves again. This is because the secondary debris flow overtook the slowed debris front and the merged one accelerated again.

Fig. 9
figure 9

Profiles of height, speed, density, basal shear stress of the debris for n=0.5 (left), 1 (middle), and 1.3 (right) with k0 =10Pa·sn and zero yield stress along the midplane of the domain

Full size image

Figure 10 presents the averaged front speed of the debris flow at x=60–70m by calculating the secant gradient of the traveling distance curve at x= 60–70m. Note that the measured ranges of averaged speed are 2.4–15m/s in the USGS experiment for post-entrainment flow conditions (Iverson et al. 2011). The front speed in this study increased up to 40m/s as the consistency index and the flow index decreased. In particular, it is observed that the front speed of shear-thinning conditions (n<1) converged to a maximum value when the yield stress τy is smaller than 400Pa.

Fig. 10
figure 10

The averaged front speed at x=60–70m for yield stress τy = 0 (a), 100 (b), 200 (c), and 400 Pa (d)

Full size image

The debris moving through the channel as well as the at-rest debris on the runout pad contains considerable information on rheological behavior. All simulations were run until t=50s, at which point the debris flow could approximately converge to the equilibrium state. Figure 11 illustrates the debris volume on the runout pad at t=50s. There are no data points for the low consistency index and low flow index in Fig. 11 because the debris flow reached the domain boundary of the runout pad before t=50 s, and the simulation stopped. As for the consistency index, the flow index and yield stress increased, and the debris volume on the runout pad at t=50 s decreased. In particular, the debris flow in all cases for τy=800Pa does not reach the runout pad at t=50s, and the debris volume for τy=400Pa cases was smaller than the initial debris volume. Because the total debris volume including basal sediment in this study is smaller than that in the experiment and the debris in the simulation is assumed to be fully saturated, the maximum debris volume on the runout pad in Fig. 11 is also smaller than that in the experiment (8.1–18.3m3) (Iverson et al. 2011). After all simulations, we compared the total mass of debris and basal sediment to the initial total mass. The error was almost ~10−8%, which shows that the implemented code well tracks the density evolution by the entrainment and satisfies the mass conservation of the debris flow.

Fig. 11
figure 11

The debris volume on runout pad at t=50s for yield stress τy = 0 (a), 100 (b), 200 (c), and 400 Pa (d)

Full size image

This study also measured the debris length (L) and width (W) on the runout pad at t = 50s and calculated the debris mobility (M) by M=L/W. Figure 12 presents the contours mapped to the length (L) and mobility (M) on a consistency index and flow index axes for three different yield stresses (τy=0, 100, and 200Pa). The contour regions of the low consistency index, flow index, and yield stress were not rendered because the debris flow reached the domain boundary of the runout pad due to the high flowability and limited domain size. Both the debris length and mobility seem to be inversely proportional to the flow index and the logarithm of the consistency index. For the no-yield stress case (τy=0Pa), the maximum mobility was lower than the case for τy=100 Pa. Additionally, the mobility for τy=100Pa was higher overall than that for τy=200Pa. This is because the yield stress reduces both the longitudinal advancement of the debris flow and its transversal spreading. In the experiment, the debris length and mobility ranged from 2.5–32.3m and 1.8–2.47, respectively (Iverson et al. 2011). Thus, it appears that the ranges of rheological parameters corresponding to the experiment were more limited for τy=0–100Pa than for 200Pa.

Fig. 12
figure 12

The debris length on runout pad and corresponding mobility (=length/width) at t=50s for yield stress τy = 0 (a, b), 100 (c, d), and 200 Pa (e, f). Un-rendered contour regions in (a)–(d) are that the debris flow reached the domain boundary of the runout pad

Full size image

Conclusions

This work developed a simplified debris flow model with Herschel-Bulkley rheology for tracking density evolution. A finite volume formulation of the debris flow model was also proposed for accurate and stable numerical simulations. Both the internal and basal frictions of the debris flow were considered in the model as well as the basal topology effect. To verify the numerical accuracy and stability of the proposed method near a shock front, the circular dam-break benchmark was performed, and the result was in good agreement with the analytical solution and showed sufficient isotropy of the solution. The dam-break of non-Newtonian fluid was also simulated, and the result was sufficiently accurate compared to the experiment and other simulations in the previous studies. The multiple debris flow with different densities was also simulated to verify the tracking of density evolution after debris merging. The total debris mass was well conserved in the simulation, and reasonable debris behavior was observed. These validations indicate that the finite volume schemes implemented in this study are sufficiently appropriate to treat the debris flow model. From the parametric study, the debris behavior depending on various rheological parameters was systematically determined. This could help improve the applicability of the rheology model for debris flow and guide us in determining relevant rheological parameters.