Introduction

It has been recognized that local topography has a significant effect on the ground motion in terms of amplitude and frequency characteristics during earthquakes. In general, convex topographies such as slopes, hills, and ridges aggravate seismic ground motions, while concave topographic features in canyons and slope toes attenuate ground shaking. The topographic amplification or attenuation effect has been witnessed by instrumental recordings and documental observations from destructive seismic events. For example, a peak ground acceleration (PGA) of 1.58 g was recorded during the 1994 Northridge earthquake on the ridge that formed the left dam abutment; however, accelerations in the surrounding areas and at the bottom of the canyon were generally less than 0.50 g (Sergio et al. 2005). In addition, the 1985 Chile earthquake, the 1999 Athens earthquake, and the recent 2008 Wenchuan earthquake, for example, have all shown that that buildings located at the tops of hills, or close to steep slopes, suffer more intensive damage than those located at the base.

In order to better understand, quantify, and predict the topographic amplification effects, a great number of numerical studies have been conducted in the recent past. One of the first numerical investigations on the effect of simple topography on seismic response was carried out by Boore using the finite difference method (Boore 1972). Subsequent studies on the topographic effect were conducted using finite element methods (Sitar and Clough 1983; Assimaki et al. 2005a, b; Lo Presti et al. 2006; Di Fiore 2010; Tripe et al. 2013; Rizzitano et al. 2014), finite difference methods (Bouckovalas and Papadimitriou 2005; Bourdeau and Havenith 2008; Pagliaroli et al. 2011; Lenti and Martino 2012; Hailemikael et al. 2016), boundary element methods (Nguyen and Gatmiri 2007; Pagliaroli et al. 2011, 2015), spectral element methods (Paolucci 2002; Cavallaro et al. 2006; Lee et al. 2009), generalized consistent transmitting boundary methods (Ashford et al. 1997; Ashford and Sitar 1997), and distinct element methods (Gischig et al. 2015).

Among the previous studies, the majority either concerned specific geometries and seismic excitations (Boore 1972; Sitar and Clough 1983; Sepúlveda et al. 2005; Assimaki et al. 2005b; Di Fiore 2010; Tripe et al. 2013; Rizzitano et al. 2014) or evaluated the soil response at the surface, in terms of time history and response spectra (Cavallaro et al. 2006, 2008a, b; Lo Presti et al. 2006; Castelli et al. 2016), or illustrated the important role of soil stratigraphy and material heterogeneity on the aggravation of surface ground motion (Assimaki et al. 2005a; Bouckovalas and Papadimitriou 2005). Geli et al. (1988) made a thorough review of the studies published before 1988, and found that all of them in essence analyzed an isolated two-dimensional (2D) ridge on the surface of a homogeneous half space and that all yielded consistent results: (1) the crest-to-base amplification of acceleration of no more than 2 at the crest, peaking when the wavelength is about equal to the ridge width; and (2) varying amounts of amplification and attenuation along the slope surface from the crest to the base (Ashford et al. 1997). The parametric studies by Ashford et al. (1997) and Ashford and Sitar (1997) provided valuable insights to the effects of slope inclination and height, wave type, and wavelength, as well as the angle of wave incidence. However, the results were presented solely at the crest and at distances equal to H, 2H, and 4H behind the crest (H denotes the slope height). A comprehensive parametric study by Bouckovalas and Papadimitriou (2005) explored the effects of slope angle varying from 10 ° to 90 °, normalized slope height  H/λ  (λ denotes the predominant wave length of the inputs) ranging from 0.05 to 2.00, as well as the dynamic soil properties on seismic ground motion, and provided qualitative and quantitative insights to the amplification effects.

A recent thorough review of studies on seismic response of slopes by Rizzitano et al. (2014) revealed that the values of the horizontal topographic amplification factor were up to 2.75 for linear visco-elastic and homogeneous soil slopes and in the range of 1.30–1.90 for non-linear soil slopes, as obtained using the equivalent-linear approach. It should be noted that the previous studies mostly focused on the seismic response along the slope surface, rather than spatial variation of topographic aggravation.

In spite of extensive numerical studies in the recent past, topographic amplification is still understood imperfectly, and these effects have not been incorporated into most modern seismic codes due to insufficient and incomplete documented evidence. In fact, only some rough ranges on the topographic effects are suggested in modern seismic codes. For example, horizontal topographic amplification factors in a range of 1.1–1.6 for convex topography including steep slopes is suggested by the seismic code of China GB 50011–2010 (2010), and 1.2–1.4 is suggested as the lower limit for slopes by the Eurocode 8 (2004). Moreover, these provisions are very rough and the spatial variation of seismic motion has not yet been considered.

In addition, while it has been found that the topographic effect is of secondary importance to the stratigraphic effect in some soil slopes (Ashford et al. 1997; Tripe et al. 2013), and the topographic and stratigraphic effects are combined in weathered and jointed rock slopes (e.g., Pagliaroli et al. 2011; Hailemikael et al. 2016), it may be a significant source of site amplification on rock slopes and therefore an important factor controlling rock slope stability during strong earthquakes. However, the vast majority of studies paid much attention to the seismic response of soil slopes, and only a few focused on the response of rock slopes (Sepúlveda et al. 2005; Havenith et al. 2003). Moreover, systematic parametric analyses for topographic amplification on seismic response of rock slopes, particularly for spatial variation of topographic aggravation, are extremely insufficient.

In this paper, a new inversion method is proposed to determine the input seismic excitation in numerical modeling based on the white noise analysis. A systematic parametric study on the seismic response of a single-faced homogenous rock slope is then conducted using the commercial finite element program LS-DYNA (2006). The influences of slope geometry and rock material, as well as the magnitude, frequency, and duration of seismic excitations on the seismic ground motion along the free surface, particularly its spatial variation in the slope, are studied in detail. Both qualitative and quantitative insights to the topographic amplification effects on the seismic response of slopes are presented in this study. The results in the present study may provide some guidance for the seismic design of homogeneous rock slopes.

Numerical model

Model setup

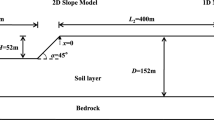
A schematic illustration of the 2D model for a single-faced homogenous rock slope is shown in Fig. 1. The explicit dynamic finite element code LS-DYNA (2006) is adopted for numerical simulation. The element size is selected according to the frequency extent of the incident motion and the shear-wave velocity of rock masses. Generally, the element size in the wave propagation direction is adopted as one-tenth the shortest wavelength (Kuhlemeyer and Lysmer 1973), which can effectively avoid wave distortion during the propagation process and ensure the accuracy of the numerical solution. Additionally, the fully integral formation is adopted for the Gaussian integral of elements in order to avoid hourglassing deformation.

Fig. 1
figure 1

Schematic illustration of the finite element model of a homogenous rock slope. PML perfectly matched layer H slope height M the reference point.

Full size image

The explicit solution is only stable if the maximal time step size Δt is smaller than the critical time step size Δtcr, which can be determined as follows based on the Courant-Friedrichs-Levy criterion (Eq. 1):

$$ \Delta {t}^{\mathrm{cr}}=L/C $$
(1)

where L is the shortest length of elements and C is the wave propagation velocity.

The rock material is assumed to be isotropic and linear elastic in numerical modeling. According to the rock classification scheme in the Standard for Engineering Classification of Rock Masses of China (GB 50218–94) (1994), four representative rock types, namely types I, II, III, and IV, are considered in the simulations, which cover the typical rock types of engineering interest. The rock classification in Chinese Code GB 50218–94 (1994), which considers both the hardness and intactness degree of rock masses, is primarily based on their qualitative characteristics and basic quality (BQ). The BQ ranges for rock masses I, II, III, and IV are > 550, 550–451, 450–351, and 350–251, respectively. The physical and mechanical parameters of the rock materials used in the simulations are listed in Table 1. It should be noted that the rock classification scheme in GB 50218–94 (1994) is different from the ground classification scheme commonly used in seismic code EC8 (2004), which typically classifies the site according to the average shear wave velocity, vs,30 (both vs,20 and depth of the weaker material below the ground surface are used in the Chinese seismic code), since this study merely focuses on the seismic response of rock slopes. For a straightforward view, the mean shear wave velocities of four rock types are also given in Table 1.

Table 1 Parameters of rock masses used in LS-DYNA simulation
Full size table

Boundary conditions and damping

In dynamic analyses, wave reflection may occur at the model boundary, leading to lower accuracy of simulation results. In order to reflect the effect of the truncated infinite far field on the numerical model, the artificial boundary is introduced in the model. In this paper, an artificial absorbing boundary or layer termed the perfectly matched layer (PML) (Basu and Chopraint 2004) is used to simulate wave propagation in an unbounded isotropic and elastic medium, as shown in Fig. 1. A layer of this material may be placed at a boundary of a bounded domain to simulate unboundedness of the domain at that boundary. The waves propagating outward from the domain are absorbed and attenuated by the layer, without any significant wave reflection back into the bounded domain. It is assumed the material in the bounded domain near the artificial absorbing boundary is, or behaves like, an isotropic and linear elastic material, which is the same as the rock material considered in the problem. The high accuracy achievable by PML models is demonstrated by Komatitsch and Tromp (2003).

A constant global damping of 5% is selected according to previous experience involving similar problems.

Determination of input motions

Different to the previous studies (Bouckovalas and Papadimitriou 2005; Assimaki et al. 2005b), which applied harmonic excitations or the Ricker wavelet with a very narrow frequency spectrum at the base of the model, real seismic waves are adopted as seismic excitations in this study in order to better quantify the topographic amplification on seismic response of rock slopes. Two representative seismograms, the E1 Centro and the Taft waves (Fig. 2), are selected as incident motions in the present analyses. The 1940 El Centro earthquake (or 1940 Imperial Valley earthquake; Mw = 6.9) occurred at 21:35 Pacific Standard Time on 18 May in the Imperial Valley in southeastern Southern California near the international border of the USA and Mexico. The peak acceleration of the El Centro north/south (N/S) seismogram was 0.32 g, and the predominant frequencies were between 5 and 6 Hz. The 1952 Kern County earthquake (moment magnitude [Mw] = 7.3) occurred on 21 July in the southern San Joaquin Valley, California, USA. The peak horizontal acceleration of the Taft wave, recorded at the No. 1095 of US Geological Survey (USGS) seismostation, close to the Taft Lincoln School, was 0.18 g, and the predominant frequencies were between 1 and 3 Hz. The frequencies considered in the analyses are between 1 and 6 Hz, which can cover the general range of possible earthquake events.

Fig. 2
figure 2

Seismic excitations used in the numerical analyses: a the El Centro and b the Taft waves

Full size image

It is important to note that the pre-assigned seismic waves or seismograms recorded at ground surface cannot be directly applied to the base of the numerical model in order to obtain the real topographic amplifications on seismic response of slopes. Therefore, the input motions at the base of the model should be appropriately inversed from the recorded or pre-assigned seismograms at ground surface. However, the one-dimensional wave propagation analysis method is only appropriate for horizontally layered soil profiles and not suitable for analyzing the seismic response of local convex and concave topographic features. Thus, an inversion method to determine the accurate input loads is proposed herein based on the white noise analysis and the frequency domain analysis methods due to the fact that the band-limited white noise has identical power spectral density in the frequency range [0, ω0].

The band-limited white noise can be assumed to be an incident motion and applied to the numerical model, and the transfer function of specified location is thus obtained through numerical calculation. Furthermore, the frequency spectrum of the input motion may be amended according to the obtained transfer function, so as to make the frequency extent and the peak value of seismic response consistent with those of the pre-assigned motion at ground surface. The detailed inversion method is illustrated as follows.

Firstly, it is supposed that a Taft wave (or any other available seismic wave) is recorded at point M (as shown in Fig. 1) at ground surface far from the slope toe. Secondly, a band-limited white noise \( \overset{\_}{p}(t) \) with the frequency range [0, 10 Hz] is selected as the input motion and applied to the bottom of the numerical model, considering that the predominant frequency of an earthquake is generally no more than 10 Hz. The dynamic response \( \overset{\_}{u}(t) \) at point M is obtained based on the dynamic time domain analysis, and the corresponding transfer function H(ⅈω) at this point can be determined through the Fast Fourier Transformation. Then, the Fourier spectrum F0(iω) of the predetermined Taft wave at point M is obtained using the Discrete Fourier Transformation. Furthermore, the Fourier spectrum F(iω) of the input motion applied at the bottom of the model is determined as follows (Eq. 2):

$$ F\left( i\omega \right)=\frac{F_0\left( i\omega \right)}{H\left(i\upomega \right)} $$
(2)

Finally, the input motion A(t) applied at the bottom of the model is obtained through the Inverse Fast Fourier Transform as follows (Eq. 3):

$$ A(t)={\mathrm{\mathcal{F}}}^{-1}\left[F\left( i\omega \right)\right] $$
(3)

In order to verify the proposed inversion method, an input motion obtained by the method described above is applied to the base of the model, and the time domain curve at point M is calculated by dynamic analysis and plotted in Fig. 3a (for simplicity, only the first 10 s time history is given). It is found that the time history is almost the same as the pre-assigned Taft wave at point M. Moreover, the two power spectral curves are almost identical to each other (Fig. 3b). Both evidences indicate that the proposed inversion method is feasible and effective.

Fig. 3
figure 3

Comparison of a time domain and b power spectrum curve between the inverted and pre-assigned excitations

Full size image

Definition of amplification factor

It has been commonly recognized that the magnitude of the peak acceleration at the slope toe is slightly smaller than that at the flattened ground surface near the toe. Moreover, the peak acceleration values at the ground surface may significantly differ from each other. Therefore, if the slope toe or any point at the ground surface near the toe is chosen as the reference point, the amplification factors may be overestimated. Generally, the topographic amplification factor was defined as a ratio of the peak acceleration at each point of the ground surface to that of the free-field response in front of the toe or behind the crest of the slope in the previous studies (Rizzitano et al. 2014; Bouckovalas and Papadimitriou 2005). However, the mean peak horizontal acceleration, \( {\overline{a}}_{\mathrm{h}} \), of the points along the ground surface far away from the toe, where the approximate free-field conditions are reached, and is defined herein as in Eq. 4, and the horizontal and vertical topographic amplification factors rh and rv at each point along the slope surface or in the slope are thus evaluated using Eqs. 5 and 6, respectively.

$$ {\overline{a}}_h=\frac{1}{N}\sum \limits_{i=1}^N\max \left(\left|{a}_h\left({\mathrm{M}}_i\right)\right|\right) $$
(4)
$$ {r}_{\mathrm{h}}=\frac{\max \left(\left|{a}_{\mathrm{h}}\right|\right)}{{\overline{a}}_{\mathrm{h}}} $$
(5)
$$ {r}_{\mathrm{v}}=\frac{\max \left(|{a}_{\mathrm{v}}|\right)}{{\overline{a}}_{\mathrm{h}}} $$
(6)

where ah(Mi) is the peak horizontal acceleration at the point Mi along the ground surface far away from the toe; N is the number of point Mi; and max(|ah|) and max(| av|) are the peak horizontal (h) and vertical (v) acceleration at any point along the slope surface or in the slope, respectively.

Parametric analysis

A series of 2D simulations focusing on slope geometry, rock material, and input motion were conducted using the finite element code LS-DYNA to investigate the effects of topographic amplification on the seismic response of the single-faced slope, with emphasis on the topographic amplification at and behind the crest as well as its spatial variation in the slope.

Effects of slope geometry

A complete range of slope heights between 10 and 100 m, with an increment of 10 m, is explored to produce a set of generalized results applicable to rock slopes. The slope angle α varies among 16.7 °, 26.6 °, 35 °, 45 °, 56.3 °, 63.4 °, 76.0 °, and 80.5 °, corresponding to the slope inclination i (i = tanα) 0.3, 0.5, 0.7, 1.0, 1.5, 2.0, 4.0, and 6.0, respectively, which covers the inclination angles mentioned in the Chinese seismic code (GB 50011–2010). It is worth noting that in the present study, the analysis results are directly presented with the slope height H, rather than the normalized height H/λ (λ denotes the predominant wave length of the incident SV waves) commonly used in the previous studies due to the following two reasons: (a) the input motions considered in this study are real seismic waves with varying frequencies, which are different from the harmonic waves with definite frequencies commonly used in the previous studies; and (b) the provisions on the topographic effects on seismic ground motions in the European EC-8 (2004), French (PS-92) (Bouckovalas and Papadimitriou 2005), or the Chinese (GB 50011–2010) seismic codes are presented with the nominal slope height H rather than the normalized height.

The horizontal amplification factors rh at the slope crest with slope inclination i and height H when the slope with rock type I is subjected to the Taft and El Centro waves are plotted in Figs. 4a and b, respectively. It can be found that, generally, rh increases with increasing slope height and inclination. However, after reaching a maximal value of 1.73 at the height of 60 m in case of Taft wave incidence, or 1.63 at the height of 80 m in case of El Centro wave incidence, rh fluctuates with the slope height, rather than increasing monotonically. Additionally, a consistent trend is observed for the amplification factors resulting from the two input motions, although there is a slight difference in magnitude due to the different frequency extents of two excitations.

Fig. 4
figure 4

Horizontal amplification factors rh at the crest of the slope with rock type I subjected to seismic excitations of a Taft and b El Centro waves

Full size image

Figures 5, 6, and 7 present the effects of slope inclination i and height H on the horizontal and vertical amplification factors rh and rv at both the slope and ground surface, when the slope is subjected to the El Centro wave. It is found that the horizontal ground motion is generally amplified near the crest and de-amplified at the toe of the slope. However, the de-amplification effect is not evident for smoother slopes (e.g., i ≤ 0.5), but is obvious for steeper slopes (e.g., i ≥ 0.7) within a short distance away from the toe. The distance is less than about half the slope height. The topographic aggravation may be seriously overestimated if the amplification factor is calculated as the peak seismic ground motion at the crest over that at the toe of the slope. This is the reason why the mean peak horizontal acceleration, \( {\overline{a}}_{\mathrm{h}} \), of the points along the ground surface far from the slope toe, where the approximate free-field conditions are reached, is chosen as the reference value. Additionally, for smoother slopes (e.g., i ≤ 0.5), the horizontal amplification factor may not decrease with increasing horizontal distance away from the crest and may increase at first. However, for steeper slopes (e.g., i ≥ 2.0), rh generally decreases with increasing horizontal distance.

Fig. 5
figure 5

Effect of slope inclination i on the horizontal and vertical amplification factors rh and rv computed at both the slope and ground surface (El Centro excitation, H = 30 m, rock type I): (a) i = 0.3; (b) i = 0.5; (c) i = 0.7; (d) i = 1.0; (e) i = 1.5; (f) i = 2.0; (g) i = 4.0; and (h) i = 6.0

Full size image
Fig. 6
figure 6

Effect of slope inclination i on the horizontal and vertical amplification factors rh and rv at both the slope and ground surface (El Centro excitation, H = 60 m, rock type I): (a) i = 0.3; (b) i = 0.5; (c) i = 0.7; (d) i = 1.0; (e) i = 1.5; (f) i = 2.0; (g) i = 4.0; and (h) i = 6.0

Full size image
Fig. 7
figure 7

Effect of slope inclination i on the horizontal and vertical amplification factors rh and rv at both the slope and ground surface (El Centro excitation, H = 100 m, rock type I): (a) i = 0.3; (b) i = 0.5; (c) i = 0.7; (d) i = 1.0; (e) i = 1.5; (f) i = 2.0; (g) i = 4.0; and (h) i = 6.0

Full size image

The effect of slope inclination i and slope height H on the spatial variation of horizontal and vertical amplification factors rh and rv of the slope subjected to the El Centro wave are also computed and plotted in Figs. 8, 9, 10, 11, 12, and 13. It can be found from Figs. 8 and 9 that, for a slope with a height of 30 m and composed of rock type I, when the slope inclination is less than 0.3 (or the slope angle ≤ 16.7 °), the horizontal amplification factors near the slope crest are generally less than 1.15 and the vertical factors are less than 0.3, which indicates that topographic aggravation on ground motion is not intensive and may be neglected. This is consistent with the observations on earthquake damages of structures on gentle slopes and also the provisions of European EC-8 (2004) for the topographic amplification factors, i.e., for average slope angles less than about 15 °, the topographic effects may be neglected. Moreover, it can be observed that for a slope with a height of 30 m, the vertical amplification factors are significantly less than the horizontal values, and therefore the parasitic vertical amplification effect on ground motion may be neglected, and, of course, this conclusion may be extended to slopes with height less than 30 m.

Fig. 8
figure 8

Effect of slope inclination i on spatial variation of horizontal amplification factor rh of the slope subjected to seismic excitation of El Centro wave: (a) i = 0.3; (b) i = 0.5; (c) i = 2.0; (d) i = 4.0; and (e) i = 6.0 (H = 30 m, rock type I)

Full size image
Fig. 9
figure 9

Effect of slope inclination i on spatial variation of vertical amplification factor rv of the slope subjected to seismic excitation of El Centro wave: (a) i = 0.3; (b) i = 0.5; (c) i = 2.0; (d) i = 4.0; and (e) i = 6.0 (H = 30 m, rock type I)

Full size image
Fig. 10
figure 10

Effect of slope inclination i on spatial variation of horizontal amplification factor rh of the slope subjected to seismic excitation of El Centro wave: (a) i = 2.0; (b) i = 4.0; and (c) i = 6.0 (H = 60 m, rock type I)

Full size image
Fig. 11
figure 11

Effect of slope inclination i on spatial variation of vertical amplification factor rv of the slope subjected to seismic excitation of El Centro wave: (a) i = 2.0; (b) i = 4.0; and (c) i = 6.0 (H = 60 m, rock type I)

Full size image
Fig. 12
figure 12

Effect of slope inclination i on spatial variation of horizontal amplification factor rh of the slope subjected to seismic excitation of El Centro wave: (a) i = 2.0; (b) i = 4.0; and (c) i = 6.0 (H = 100 m, rock type I)

Full size image
Fig. 13
figure 13

Effect of slope inclination i on spatial variation of vertical amplification factor rv of the slope subjected to seismic excitation of El Centro wave: (a) i = 2.0; (b) i = 4.0; and (c) i = 6.0 (H = 100 m, rock type I)

Full size image

Figures 10, 11, 12, and 13 plot the spatial variation of horizontal and vertical amplification factors rh and rv with slope inclination i = 2.0, 4.0, and 6.0, and height H = 60 m (Figs. 10 and 11) and 100 m (Figs. 12 and 13). It can be found that rh reaches the peak value near the slope crest and that rv reaches the peak value near the slope surface. Both rh and rv in the slope increase with increasing slope height and slope inclination. However, compared to the slope height, rh increases relatively slowly with the increment of slope inclination, especially for higher inclinations. Additionally, the spatial distribution characteristics of rh and rv of slopes with the same height and with steeper inclinations (e.g., i = 2.0, 4.0, and 6.0) show relatively high similarities.

Moreover, it is interesting to note that the vertical amplification factor contours are approximately parallel to the slope surface while the horizontal amplification factor contours seem to be parallel to the ground surface, especially for higher (H > 30 m) and steeper slopes (i > 2.0).

It should be noted that, although the response in these figures attenuates with increasing distance from the crest, exact free-field conditions are not reached even at large distances from the crest. The difficulty of attaining free-field conditions was highlighted by Bouckovalas and Papadimitriou (2005), who found that topography effects decrease asymptotically with distance from the slope. This was attributed to the reflection of the incoming SV waves on the inclined free surface of the slope which can result (a) in P and SV waves impinging obliquely at the free ground surface behind the crest and (b) in the generation Rayleigh wave propagation away from the slope.

Effects of rock material

In order to assess the effect of rock material on the topographic amplification factors, analyses were carried out on slopes composed of four different rock types, namely, types I, II, III and IV (Table 1), with the Taft wave as the input motion.

The variation of horizontal amplification factor rh at the crest of the slope with slope height for different rock types is plotted in Fig. 14 (i = 4.0). It can be found that, generally, the seismic response of harder rock masses is less than that of weaker rock masses.

Fig. 14
figure 14

Variation of horizontal amplificationfactor rh with slope height at the crest of slopes subjected to Taft wave for different rock types (i = 4.0)

Full size image

Figures 15 and 16 show the topographic amplification factors rh and rv, respectively, obtained for a slope with height H = 60 m and inclination i = 6.0. It can be found that the distribution characteristics of rh for harder rocks such as types I and II are similar, and those for weaker rocks such as types III and IV are also similar. However, there is a relatively large difference in rh for hard and weak rocks. Additionally, rv increases with the degradation of rock masses and the contour of rv is almost parallel to the slope surface. Moreover, it can be concluded that the vertical amplification effect at the slope crest and along the slope surface cannot be neglected for this condition because the peak values of rv at the crest for rock types I, II, III, and IV are as high as 0.6, 0.8, 1.0, and 1.1, respectively.

Fig. 15
figure 15

Effect of rock types: a I, b II, c III, and d IV on spatial variation of horizontal amplification factor rh of the slope subjected to seismic excitation of the Taft wave (H = 60 m, i = 6.0)

Full size image
Fig. 16
figure 16

Effect of rock types: a I, b II, c III, and d IV on spatial variation of vertical amplification factor rv of the slope subjected to seismic excitation of the Taft wave (H = 60 m, i = 6.0)

Full size image

Effects of input motions

In order to investigate the effect of seismic excitation on the topographic amplification factors, analyses are conducted for input motions with varying magnitudes, frequencies, and durations. The Taft wave is pre-assigned as the seismic excitation at the ground surface. The amplitude of the original Taft history is doubled to generate a Taft wave with higher magnitude and the frequency extents and durations remain unchanged. For different durations, the complete Taft time history (54 s, Fig. 2b) and a truncation of the first 20 s Taft history (Fig. 17a) are considered in the analyses. It should be noted that the left part after truncation in Fig. 17a must cover the main shocks.

Fig. 17
figure 17

Comparison of a time history and b amplitude spectrum of the first 20 s of Taft wave before and after filtering at frequency of 2 Hz

Full size image

Table 2 shows the preliminary analysis results of the horizontal topographic amplification factor rh at the slope crest for a slope composed of rock type II, with inclination i = 4 and height H = 50 and 100 m, subjected to seismic excitations with different magnitudes and durations. It can be found that the magnitude and the duration of input motions have negligible effect on the amplification factors, as would be expected. However, it is worth noticing that the results are obtained based on weak seismic excitations and on the assumptions of homogeneous and elastic rock materials, and may not be applicable to describing the topographic effects associated with strong ground motions.

Table 2 Horizontal amplification factor at the crest of slopes subjected to Taft waves with different magnitudes and durations
Full size table

In order to better assess the effects of frequency extent of input motions, the pre-assigned Taft wave at ground surface is filtered at specified frequencies of 2, 4, and 6 Hz using the filter function proposed by Clough and Penzien (1975), so as to significantly enhance the frequency components near the specified frequencies. Figure 17 compares the time history and the Fourier amplitude spectrum of the first 20 s Taft wave before and after filtering at the frequency near 2 Hz. It is again noteworthy that the input motions applied to the model base are inversed by the method mentioned previously. Figures 18 and 19 show the topographic amplification factors rh and rv of a slope subjected to Taft waves with different frequencies. It can be observed that the horizontal amplification factor rh at the slope crest is 1.60, 1.45, 1.75, and 1.71 under seismic excitations of an unfiltered Taft wave (predominant frequency 2–3 Hz) and a filtered Taft wave at frequency near 2, 4, and 6 Hz, respectively. Both rh and rv increase when the frequency components are enhanced at a higher frequency band of input motions. It is worth noting that there is only a slight difference in the amplification factors of the slope subjected to filtered Taft waves at frequencies between 4 and 6 Hz (see Figs. 18c and d, and 19c and d) due to the fact that the frequency components of Taft wave between 4 and 6 Hz are almost the same as each other, as shown in Fig. 20.

Fig. 18
figure 18

Horizontal application factor rh of slopes subjected to a unfiltered Taft wave, and filtered Taft waves at frequency near b 2 Hz, c 4 Hz, and d 6 Hz

Full size image
Fig. 19
figure 19

Vertical application factor rv of slopes subjected to a unfiltered Taft wave, and filtered Taft waves at frequency near b 2 Hz, c 4 Hz, and d 6 Hz

Full size image
Fig. 20
figure 20

Comparison of amplitude spectrum of filtered Taft waves at frequency near 4 and 6 Hz

Full size image

Discussion

Based on the extensive literature review, the European EC-8 (2004), French PS-92, and Chinese GB 50011–2010 seismic codes are found to contain provisions on topographic amplification factors of slopes. Comparison between the present study and the code provisions may provide valuable conclusions on the overall feasibility of the numerical analysis based predictions in this paper. Specifically, the foregoing range of rh is broadly comparable to the provisions of the European EC-8 (2004) and the French PS-92 seismic codes, which prescribe 20% and 40% increase of the peak horizontal acceleration as the lower limit, respectively, and to those of the Chinese seismic code (2010), which prescribe 60% increase of the peak horizontal acceleration as the upper limit. However, in the present study, the peak value of rh at the crest of the slope (height H = 100 m, rock type III) subjected to the Taft wave is as high as 1.93, and is still no more than 2, which is consistent with previous predictions (Bouckovalas and Papadimitriou 2005; Lee et al. 2009; Ashford et al. 1997; Geli et al. 1988) but significantly greater than the upper limit of 1.60 in the Chinese code (no upper limits of rh are suggested in the European EC-8 and the French PS-92 codes). It is indicated that the Chinese seismic code may significantly underestimate the topographic amplification effects on seismic response of rock slopes. It has also been found that EC-8 underestimates the topographic amplification value by 20–40% for some specific cliffs and ridges (Paolucci 2002; Pagliaroli et al. 2011).

In addition, the three codes provide detailed conditions under which the topographic aggravation can be neglected: H ≤ 10 m and α ≤ 22 ° in the French code PS-92 (Bouckovalas and Papadimitriou 2005), H ≤ 30 m and α ≤ 15 ° in the European code EC-8 (2004), and H < 20 m and α < 16.7 ° in the Chinese code GB 50011–2010 (2010). The results obtained by the present study, i.e., H ≤ 30 m and α ≤ 16.7 °, agree well with these code provisions, which also demonstrates the reasonability of the results in this paper.

It is noteworthy that the parasitic vertical motion component is ignored in the three codes. As mentioned previously, the rv obtained for the slope composed of type IV rock with H = 60 m and i = 6.0 subjected to the Taft wave is as high as 1.1 and thus cannot be neglected.

As discussed previously, the magnitude and duration of input motions have negligible effect on the amplification factors based on weak seismic excitations and on the assumptions of homogeneous and elastic rock materials, and may not be applicable to describing the topographic effects associated with strong ground motions. When the rocks are non-linear and inelastic, the magnitude and duration of input motions may have great effects on the amplification factors.

Conclusions

There is no doubt that local topography plays a critical role in the spatial variation of ground motion and should be explicitly considered in the seismic design of rock slopes. In the present study, a new inversion method for determining the reasonable input loads at the base of the numerical model is proposed based on the white noise analysis and the frequency domain analysis methods. The horizontal and vertical topographic amplification factors both on the free surface and in the slope are then evaluated through a series of parametric studies focusing on slope geometry, rock material, and input motion, using numerical modeling with the 2D finite element code LS-DYNA. By comparison, it is shown that the results obtained in this study are in good agreement with the numerical analyses available in the literature and the relevant provisions in the existing seismic codes. Several valuable conclusions can be drawn, as follows:

  • Both slope geometry and rock material have great influence on horizontal and vertical amplification factors rh and rv. Generally, rh and rv increase with increasing slope height and inclination and degradation of rock material. As for input motion, the magnitude and duration have negligible effect on the amplification factors, but the frequency extent of input motion has great impact on the amplification factors.

  • The topographic effects become important in case of slope height H > 30 m and slope inclination i > 0.3 (16.7 °). Generally, the horizontal and vertical amplification factors near the crest vary between 1.20–1.93 and 0.10–1.10, respectively. As for spatial variation of amplification factors, the horizontal contours seem to be parallel to the ground surface, while the vertical amplification factor contours are approximately parallel to the slope surface, especially for higher (H > 30 m) and steeper (i > 2.0) slopes.

  • The topographic amplification factors recommended by the three modern seismic codes (GB 50011–2010, EC-8, and PS-92) are reasonable to some extent. It seems that the Chinese code has underestimated the horizontal amplification factor, and that all three codes totally neglect the vertical amplification effects, which may bring potential risks for structures subjected to seismic excitations. However, reliable and detailed field measurements are required to improve the provisions of seismic codes, in addition to numerical simulations.

Nonetheless, the results in the present study are obtained based on weak seismic excitations and on the assumptions of homogeneous and elastic rock materials, and may not be applicable to describing the topographic effects associated with strong ground motions. Simulations and experiments concerning the topographic effects for seismic excitations strong enough to cause non-linear and inelastic responses of rock slopes shall be conducted in the near future.