1 Introduction

Fiber optic sensors are competent and widely investigated for many measures depending on their type, possible implementing technique and parameters under investigation [1,2,3,4]. A broad variety of fiber sensors are being developed to monitor desired parameters with high efficiency and optimum costs [5,6,7,8,9]. Fiber Bragg grating (FBG) sensors have shown a great potential for environmental parameters sensing, such as strain, temperature, humidity and vibration in different scientific and industrial applications [10,11,12]. There are limitations reducing their use that one of the most important ones is simultaneous measurement of the parameters [13, 14]. Among them, simultaneous measurement of temperature and strain have received considerable attention from researchers due to their wide applications and higher performance [15, 16]. Monitoring of strain or temperature variations by a FBG sensor is conducted by measuring the Bragg wavelength shift. Since the Bragg wavelength is shifted by both strain and temperature changes, cross-sensitivity compensation is required for their simultaneous measurement [17].

During last years, many techniques have been proposed for simultaneous measurement of temperature and strain using FBG sensors. They have mainly been based on detecting two physical indicators in reflection spectrum of FBG sensors that have different sensitivities to strain and temperature. Since there is only one physical indicator, Bragg wavelength shift, in a reflection spectrum of a FBG, temperature and strain changes which both cause the Bragg wavelength shift, could not be obtained by means of just one FBG [18, 19].

Thus, the proposed techniques can be divided into two categories. In the first category, more than one FBG is used, such as using two FBGs written in fibers of different diameters [20], FBGs written in fibers with different levels of doping elements [21], long-period grating (LPG) and FBG [22], FBGs written in single mode fiber (SMF) and twin core fiber (TCF) [23], four-core fiber combined with a FBG [24], Fabry–Perot interferometer (FPI) and FBG [25], etc. Because using two or more FBGs has several drawbacks including the complexities in setup, overused of spectral sources and the costs, second category techniques were innovated.

In second category, only one special FBG is used for simultaneous measurement of temperature and strain, such as using a superstructure FBG [26], coated FBG [27], FBG in Polarization Maintaining Fiber (PMF) [28], two peanut tapers with embedded FBG [29], Fabry–Perot interferometer cascaded FBG [30], π-Phase-Shifted FBG [31], FBG Inscribed in Dual-Mode Fiber [32], chirped FBG [33], FBG written in PANDA fiber [34], etc. These techniques have drawbacks, such as complexities in fabrication of FBGs and their difficult accessibility, too.

Very recently, in few works, a single FBG has been used for simultaneous measurement of temperature and strain, such as a half of the FBG was bonded on a host structure, while the other half of the FBG was left free. In this work, utilizing the Bragg wavelength shift of unbounded FBG, the temperature can be determined independent of strain and while Bragg wavelength shift of the bonded FBG allows the determination of the strain. As explained in the work, measurements has errors due to the fact that it is assumed that the unbounded FBG does not experience any strain while in reality it experience the strain [35,36,37]. In another article, the side-lobes power of reflection spectrum is used for simultaneous measurement of temperature and strain. This method requires very accurate and sensitive analyzers to be able to correctly distinguish between side-lobes peak power [38].

We propose a use of only one FBG to simultaneous measurement of temperature and strain changes and consider FWHM of reflection spectrum as the second indicator (in addition to Bragg wavelength shift as the first indicator) for the measurement. Uniform temperature and/or strain change only shift/s the Bragg wavelength without any change in FWHM of reflection spectrum of the FBG, while if strain or temperature is non-uniformly distributed along the FBG, each point of the FBG experiences a different strain or temperature, resulting in non-uniformity in its period and consequently changing in the FWHM, in addition to the Bragg wavelength shift. Thus, when a non-uniform strain is applied to a sample, the Bragg wavelength and FWHM of reflection spectrum should be used to straightforwardly obtain temperature and strain changes of the sample at the same time. When a uniform strain is applied to the sample, we propose to fix a tilted cantilever beam on the sample and stuck a single FBG on the cantilever. The cantilever beam converts the uniform applied strain to the sample into non-uniform strain distribution on the cantilever beam and along the FBG. Thus, by creating a non-uniform strain along the FBG, the FWHM of reflection spectrum of the FBG will be sensitive to strain changes.

2 Measurement of temperature and strain

Fiber Bragg grating acts like a wavelength filter that reflects a particular wavelength. This Bragg wavelength (λB) depends on effective refractive index of fiber (neff) and period of grating (Ʌ) and is given as:

$$ \lambda_{B} = 2n_{eff} \Lambda $$
(1)

The main equation of FBG sensors is based on the detection of Bragg wavelength shift that is influenced by the external perturbations, such as temperature and strain, as shown as:

$$ \frac{{\Delta \lambda_{B} }}{{\lambda_{B} }} = (1 - P)\Delta \varepsilon + (\alpha_{\Lambda } + \alpha_{n} )\Delta T $$
(2)

where ∆ε and ΔT are the strain and temperature change, respectively. For silica fiber, P = 0.22 is strain-optic coefficient, αɅ = 0.5 × 10−6/°K is thermal expansion coefficient and αn = 6.9 × 10−6/°K is thermo-optic coefficient. Thus, reflection spectrum from uniform FBG sensor is given as [39]:

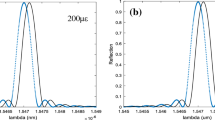
$$ R(\lambda ) = \exp \left[ { - \frac{{4\ln 2[\lambda - \{ (1 - P)\Delta \varepsilon + (\alpha_{\Lambda } + \alpha_{n} )\Delta T + 1\} \lambda_{B} ]^{2} }}{{c^{2} }}} \right] $$
(3)

where c is the FWHM when there is no strain, here c = 0.39. If there is no temperature change and only strain is changed, then just the first part of the Eq. (2) will be used and if the strain is kept constant and temperature is changed, then just the second part of the Eq. (2) is activated. Figure 1(a) and 1(b) show FBG reflection spectra obtained at 100με strain change with constant temperature and 10℃ temperature change with constant strain, respectively, at the Bragg wavelength of 1550 nm.

Fig. 1
figure 1

FBG reflection spectrum in λ = 1550 nm, (a) without external perturbations (point) and only the strain change by 100 με (line), (b) without external perturbations (point) and only the temperature changes by 10 ℃ (line)

Full size image

Thus, sensitivity of a fiber Bragg grating to a uniform temperature change or strain change independently can be obtained as 0.0142 nm/℃ and 0.00121 nm/με, respectively, at the Bragg wavelength of 1550 nm from the graphs which are consistent with FBG standard sensitivities [40].

3 Measurement of strain in a tilted cantilever beam

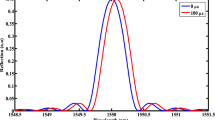
As seen in Fig. 1, a uniformly applied strain or temperature to the FBG resulted only a shift in Bragg wavelength with no change in its FWHM, while if a non-uniform strain distribution is created in the FBG, in addition to the Bragg shift, FWHM of reflection spectrum will change [41]. As shown in Fig. 2, after applying non-uniform strain distribution along a FBG, the reflection spectra shift and their FWHM undergo expansion. This FWHM change besides the Bragg shift is used to obtain simultaneously strain and temperature.

Fig. 2
figure 2

FBG reflection spectra for uniform (point) and non-uniform (line) strain with the values (a) 100 με and (b) 200με

Full size image

A cantilever is a rigid structural and mechanical element, such as a beam or a plate, anchored at one end to a (usually vertical) support from which it protrudes. The important point in the cantilever beam is that strain distribution along this tool, is non-uniform and linear [39, 42].

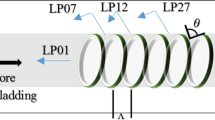
When a uniform strain is applied to the sample, we get the help of cantilever beam concept. In this case, a single FBG is pasted on a tilted cantilever beam which is attached and fixed with a slight angle θ on a sample under test, as shown in Fig. 3. There is a meaningful relation between uniform strain applied to the sample (εs) and strain experienced at each part of the tilted cantilever beam (εc), which depends on the inherent properties, thickness and length of the cantilever beam and the angle θ. Parameter M is considered as an experimental strain coefficient to show this dependency which can be between zero and one. The strain distribution in the cantilever beam is such that the fixed-end of cantilever suffers the most strain (M.εs.cosθ) and decreases linearly to reach 0 at its free end. Depending on the position of the FBG on the cantilever beam, it can be seen that what percentage of a uniform strain applied to the sample under test reaches to the beginning of the FBG and the end of the FBG.

Fig. 3
figure 3

The mechanism of placing the tilted cantilever beam on the sample under test and the FBG on that tilted cantilever beam

Full size image

For example, if the length of FBG and tilted cantilever beam are 2 cm and 6 cm, respectively, and the FBG is attached to the middle third of the cantilever beam, a maximum strain equal to (2/3).(M.εs.cosθ) is arrived at the beginning of the FBG and (1/3).(M.εs.cosθ) is felt at the end of the FBG and the FWHM will change with the strain applied to the sample as shown in Table 1. We assumed that θ = 30 and M = 1 (meaning that all strain applied to the sample is transferred to the fixed- end of the tilted cantilever beam without any loss).

Table 1 Maximum ∆FWHM according to the strain changes applied to the sample, assuming θ = 30 and M = 1
Full size table

As shown in Table 1, the maximum Bragg wavelength shift is linearly correlated with the applied strain on the sample with sensitivity equal to 0.000453 nm/με, while according to Fig. 4, the relationship between the maximum ∆FWHM and applied strain on the sample is nonlinear. Equation (4) shows this relationship:

$$ \Delta FWHM = 6 \times 10^{ - 8} \varepsilon_{s}^{2} - 2 \times 10^{ - 6} \varepsilon_{s} + 0.0002 $$
(4)
Fig. 4
figure 4

Relationship between ∆FWHM and the strain applied to the sample under test

Full size image

As can be seen in Eq. (4), by knowing the maximum FWHM variations, it is straightforward to obtain the strain applied to the sample. It should be noted that the Eq. (4) is obtained for our condition (cantilever beam length, FBG length and position on the cantilever beam), and if the conditions change, the equation’s coefficients will also change. Since non-uniform temperature distribution problem has not been a common issue in sensing by FBGs, we concentrated in our work on strain distribution of on a single FBG. If there was a non-uniformity in the temperature distribution in the FBG in addition to strain distribution, the Eqs. (4) would have temperature dependency, too.

4 Simultaneous measurement of temperature and strain

When uniform strain is applied to the sample as shown in Fig. 3, it led to a FWHM variation (nonlinear) in addition to the Bragg wavelength shift (0.453 pm/με) in reflection spectrum, while a uniform temperature change only results in the Bragg wavelength shift (0.0142 nm/℃). In an environment where both temperature and strain are changing, with obtaining the maximum wavelength shift and FWHM value of the FBG reflection spectrum, both temperature and strain applied to sample under test can be obtained by two equations with two unknowns according to Eq. (5) as:

$$ \begin{gathered} \Delta FWHM = 6 \times 10^{ - 8} \varepsilon_{s}^{2} - 2 \times 10^{ - 6} \varepsilon_{s} + 0.0002 \hfill \\ \Delta \lambda = 0.000453\varepsilon_{s} + 0.0142\Delta T \hfill \\ \end{gathered} $$
(5)

For example, Fig. 5 shows unknown environmental condition for our example and we intend to obtain simultaneously the temperature and strain changes applied to the sample. In this figure, the maximum ∆FWHM is equal to 0.03448 nm and maximum wavelength shift is 0.646 nm. According to Eq. (5), the strain and temperature variations of sample under test are obtained equal to 784.96 με and 20.45 ℃, respectively.

Fig. 5
figure 5

FBG reflection spectrum in constant strain and temperature (point) and in strain and temperature changes (line)

Full size image

The important point in this proposed idea is that, due to the fact that the oscillations of tilted cantilever beam occur very fast, to obtain the maximum ∆FWHM and Bragg wavelength, high data rate analyzers (microseconds) are required.

5 Conclusion

Several methods have been employed for simultaneous measurement of temperature and strain by FBG sensors. They mostly use variety of configurations including two or more FBGs or one special FBG. We propose using FWHM of the reflection spectrum as a cross-sensitivity indicator for simultaneous measurement of temperature and strain using only a single FBG. When a non-uniform strain is applied to a sample which a uniform FBG is stuck on it, in addition to the Bragg wavelength, FWHM of the reflection spectrum changes. This FWHM change besides the Bragg wavelength shift is used to measure simultaneously strain and temperature. When a uniform strain is applied to the sample, we introduce a cantilever beam to our configuration. A single FBG was pasted on a tilted cantilever beam fixed on the sample under test. This can be done with great precision. We exploit a non-uniform strain distribution along a uniform FBG concept resulting in changing in FWHM of reflection spectrum in addition to the Bragg wavelength shift. A uniform strain applied to the sample being distributed non-uniformly on the tilted cantilever beam and on the FBG. The non-uniform strain distribution on the FBG has led to the sensitivity of the FWHM parameter to strain. Temperature and strain changes are detected using Bragg wavelength shift and FWHM changes equations. According to our simulation results, the temperature sensitivity of the FBG sensor to Bragg wavelength shift will be 14 pm/℃ and independent of FWHM changes, while the strain sensitivity of this sensor to Bragg wavelength shift is 0.453 pm/με and is connected to FWHM by a quadratic equation.