1 Introduction

Optical fiber sensors have unique advantages not found in electrical sensors, and are thus expected to be used in various applications [1,2,3]. In particular, sensors using fiber Bragg gratings (FBGs) have further advantages such as localization of the sensor head, and simultaneous measurement of multiple points [4,5,6,7]. FBG sensors for measurement of various physical quantities, such as temperature [8,9,10,11,12,13,14], strain [15,16,17,18,19], sound pressure [20,21,22], and solid vibrations [23,24,25,26,27,28] have been reported.

Multiple point sensing is possible by installing multiple FBGs on one fiber. Such a sensor array is composed of FBGs having different reflection wavelengths [15, 28,29,30,31,32,33,34,35,36,37,38] or FBGs having the same reflection wavelength and low reflectance [39,40,41,42,43,44]. The former is interrogated using a method based on the wavelength division multiplexing (WDM) method [15, 28,29,30,31,32,33,34,35,36,37,38]. The latter is interrogated using a method based on the time division multiplexing (TDM) method [39,40,41,42,43,44] or a method based on the optical frequency domain reflectometry (OFDR) method [45,46,47].

The number of points that can be measured by FBG multi-point sensing is limited by various factors [48]. For example, Yun et al. used a wavelength-swept source with sweep range of 28 nm for WDM based FBG multi-point sensing [49]. The sampling rate of their system was 250 Hz. The reflection wavelength of each FBG must be sufficiently separated. Therefore, assuming that each FBG wavelength shifts by ± 1 nm when operated as a sensor, the difference in the reflection wavelengths must be 2 nm or more. Therefore, it is necessary to limit the number of sensors to 14 or less. As in this example, for the methods based on WDM, the number of measurement points is in a trade-off relationship with the dynamic range of measurement. In the methods based on TDM, the number of measurement points is in a trade-off relationship with the measurement time.

We have previously reported another method for FBG-based multi-point strain sensing in which the number of measurement points is not limited by either the dynamic range or the measurement time. In this method, the sensor head is a Fabry–Perot interferometer (FPI) consisting of low-reflective FBGs (FBG–FPI). A low-reflective FBG-FPI has a spectrum with a sinusoidal structure, where the period is determined by the length of the FBG–FPI. Multiple point sensing is possible by installing multiple low-reflective FBG–FPIs on one fiber and analyzing the reflection spectrum of that fiber by the frequency division multiplexing method. The dynamic range of the measurement is irrelevant to the number of measurement points. In addition, the time required to read out all FBG–FPIs is only the time to read the reflection spectrum of the fiber once, and does not become prolonged in proportion to the number of measurement points.

To precisely acquire the interference signal of a low-reflective FBG–FPI array, the coherence length of the light source must be sufficiently longer than the length of the FBG–FPI. However, the sweep speed of a commercially available wavelength-swept light source that satisfies the condition is only approximately several tens of hertz. Therefore, we propose to conduct wavelength sweeping by injection current modulation of a laser diode. Wavelength sweeping by a modulated laser diode allows fast sweeping at 100 Hz or more, and the sweep range is as narrow as several hundred picometers. The laser linewidth of a laser diode is very thin and the coherence length is sufficiently long. Therefore, by excluding the drawback of a narrow sweep range, a modulated laser diode is suitable for the interrogation of a low-reflective FBG–FPI array.

Here, we propose a method to realize multi-point sensing by the analysis of a partially scanned reflection spectrum of a low-reflective FBG–FPI sensor array. If it is possible to perform the measurement by scanning only a part of the reflection spectrum instead of acquiring the entire reflection spectrum, then it will be possible to realize high-speed measurement using a modulated laser diode for interrogation of a sensor array. Theoretical requirements for successful interrogation using the partial reflection spectrum are discussed. The maximum number of FBG–FPI sensors that can be simultaneously interrogated in the proposed method is also shown theoretically. Experiments are reported to confirm that the proposed method works without problems. In an experiment using only one FBG–FPI, it is confirmed that the linear response to strain can be read using only the partial reflection spectrum. Moreover, in an experiment using two FBG–FPIs simultaneously, it is confirmed that the responses can be read independently, without interference between the two sensors and using only the partial reflection spectrum.

2 Sensor principle

An FBG is fabricated by generating periodic refractive index changes in the core of an optical fiber. Light having a specific wavelength determined by the period of the generated refractive index change and the effective refractive index of the optical fiber is reflected by the FBG. The reflection wavelength is called the Bragg wavelength, which is given by

$$\begin{aligned} \lambda _\mathrm{B}=2n_\mathrm{e}\varLambda , \end{aligned}$$
(1)

where \(n_\mathrm{e}\) is the effective refractive index of the optical fiber and \(\varLambda\) is the period of the generated refractive index change. When strain is applied to the FBG or the ambient temperature changes, the Bragg wavelength shifts according to the relationship shown by

$$\begin{aligned} \varDelta \lambda _\mathrm{B} & = 2\left( n_\mathrm{e}\frac{\partial \varLambda }{\partial T}+\varLambda \frac{\partial n_\mathrm{e}}{\partial T}\right) \varDelta T \nonumber \\&+ 2\left( n_\mathrm{e}\frac{\partial \varLambda }{\partial \mathcal {E}}+\varLambda \frac{\partial n_\mathrm{e}}{\partial \mathcal {E}}\right) \mathcal {E} \end{aligned}$$
(2)
$$\begin{aligned}& = {2n_\mathrm{e}\varLambda (\alpha '\varDelta T+\beta '\mathcal {E}) } = \lambda _\mathrm{B}(\alpha '\varDelta T+\beta '\mathcal {E}), \end{aligned}$$
(3)

where \(\varDelta T\) is the change in temperature, \(\mathcal {E}\) is the strain applied to the FBG, \(\alpha '\) and \(\beta '\) are coefficients for the fractional change of the optical path length. Strain \(\mathcal {E}\) applied to a fiber is given by

$$\begin{aligned} \mathcal {E}=\frac{\varDelta L_\mathrm{f}}{L_\mathrm{f}}, \end{aligned}$$
(4)

where \(\varDelta L_\mathrm{f}\) is the amount of fiber elongation and \(L_\mathrm{f}\) is the initial length of the fiber before the application of strain.

An FPI is an interferometer that consists of two parallel mirrors [50]. When the reflectance of the mirrors is high, the FPI has sharp transmittance peaks due to multiple-beam interference. On the other hand, when the reflectance of the mirrors is low, the FPI has a sinusoidal reflection spectrum due to simple two-beam interference. In the case of an FPI made of low-reflectance mirrors, the reflectance of the FPI is given by

$$\begin{aligned} r_\mathrm{F}(\lambda )& = 2r_\mathrm{M}(1+\cos \phi ) \end{aligned}$$
(5)
$$\begin{aligned}& = 2r_\mathrm{M}\left\{ 1+\cos \left( 2n_\mathrm{F}L_\mathrm{F}\frac{2\pi }{\lambda }\right) \right\} , \end{aligned}$$
(6)

where \(r_\mathrm{M}\) is the reflectance of the mirrors, \(n_\mathrm{F}\) is the refractive index of the medium, \(L_\mathrm{F}\) is the interferometer length, and \(\lambda\) is the light wavelength. For a low-reflective FBG-FPI, Eq. (6) can be rewritten as

$$\begin{aligned} r_\mathrm{F}(\lambda )& = 2r_\mathrm{B}\left\{ 1+\cos \left( 2n_\mathrm{e}L_\mathrm{F}\frac{2\pi }{\lambda }\right) \right\} , \end{aligned}$$
(7)

where \(r_\mathrm{B}\) is the reflectance of the FBGs used instead of the mirrors. \(r_\mathrm{B}\) is a function of \(\lambda\), but it can be approximated by a constant because the range of \(\lambda\) is sufficiently narrow, as described later.

When strain is applied to an FBG–FPI or when the ambient temperature changes, the optical path length of the interferometer changes according to the following equation.

$$\begin{aligned} {n_\mathrm{e}'L_\mathrm{F}'}& = {n_\mathrm{e}L_\mathrm{F}+\left( \frac{\partial }{\partial T}+\frac{\partial }{\partial \mathcal {E}}\right) n_\mathrm{e}L_\mathrm{F}} \end{aligned}$$
(8)
$$\begin{aligned}& = {n_\mathrm{e}L_\mathrm{F}\left( 1+\alpha '\varDelta T+\beta '\mathcal {E}\right) ,} \end{aligned}$$
(9)

where \(n_\mathrm{e}'\) is the effective refractive index and \(L_\mathrm{F}'\) is the interferometer length after the change. Therefore, the reflection spectrum of an FBG–FPI after change is given by

$$\begin{aligned} r'_\mathrm{F}(\lambda )& = 2r_\mathrm{B}\left[ 1+\cos \left\{ 2n_\mathrm{e}L_\mathrm{F}\left( 1+\alpha '\varDelta T+\beta '\mathcal {E}\right) \frac{2\pi }{\lambda }\right\} \right] . \end{aligned}$$
(10)

Assuming that the wavelength shift of the spectrum after change is \(\varDelta \lambda\), the following equation holds.

$$\begin{aligned} r'_\mathrm{F}(\lambda )=r_\mathrm{F}(\lambda -\varDelta \lambda ) \end{aligned}$$
(11)
$$\begin{aligned} r'_\mathrm{F}(\lambda +\varDelta \lambda )=r_\mathrm{F}(\lambda ). \end{aligned}$$
(12)

If the wavelength shift \(\varDelta \lambda\) satisfies \(\varDelta \lambda \ll \lambda\), then the left side of Eq. (12) can be approximated as

$$\begin{aligned} r'_\mathrm{F}(\lambda +\varDelta \lambda ) & \approx 2{r}_\mathrm{B}\left[ 1+\cos \left\{ 2n_\mathrm{e}L_\mathrm{F} \left( 1+\alpha '\varDelta T+\beta '\mathcal {E} \right) \frac{2\pi }{\lambda } \left( 1-\frac{\varDelta \lambda }{\lambda }\right) \right\} \right] \end{aligned}$$
(13)
$$\begin{aligned} & \approx 2{r}_\mathrm{B}\left[ 1+\cos \left\{ 2n_\mathrm{e}L_\mathrm{F}\frac{2\pi }{\lambda }\left( 1+\frac{\lambda (\alpha '\varDelta T+\beta '\mathcal {E})-\varDelta \lambda }{\lambda } \right) \right\} \right] . \end{aligned}$$
(14)

By substituting Eq. (7) and Eq. (14), Eq. (12) is rewritten as

$$\begin{aligned}&2{r}_\mathrm{B}\left[ 1+\cos \left\{ 2n_\mathrm{e}L_\mathrm{F}\frac{2\pi }{\lambda }\left( 1+\frac{\lambda (\alpha '\varDelta T+\beta '\mathcal {E})-\varDelta \lambda }{\lambda } \right) \right\} \right] \nonumber \\&\quad \approx 2r_\mathrm{B}\left\{ 1+\cos \left( 2n_\mathrm{e}L_\mathrm{F}\frac{2\pi }{\lambda }\right) \right\} . \end{aligned}$$
(15)

Therefore, the following expression holds.

$$\begin{aligned} 2n_\mathrm{e}L_\mathrm{F}\frac{2\pi }{\lambda }\left( 1+\frac{\lambda (\alpha '\varDelta T+\beta '\mathcal {E})-\varDelta \lambda }{\lambda } \right) =2n_\mathrm{e}L_\mathrm{F}\frac{2\pi }{\lambda } \end{aligned}$$
(16)
$$\begin{aligned} \frac{\lambda (\alpha '\varDelta T+\beta '\mathcal {E})-\varDelta \lambda }{\lambda } =0. \end{aligned}$$
(17)

Thus, \(\varDelta \lambda\) is given by

$$\begin{aligned} \varDelta \lambda =\lambda (\alpha '\varDelta T+\beta '\mathcal {E}). \end{aligned}$$
(18)

\(\alpha '\) and \(\beta '\) are determined by their dependence on the temperature and strain, respectively, of the optical fiber itself; therefore, the dependence coefficients of the FBG and FPI coincide. Therefore, the amount of wavelength shift of the reflection spectrum for the FPI is the same as the Bragg wavelength shift.

3 Interrogation based on partial scanning frequency division multiplexing

A low-reflective FBG–FPI sensor array can be interrogated by scanning a partial reflection spectrum. The partial reflection spectrum, i.e., the part of the reflection spectrum of an FBG–FPI scanned by sweeping a light wavelength from \(\lambda _0\) to \(\lambda _1\), is given by

$$\begin{aligned} r_\mathrm{M}(\lambda )=h(\lambda )r_\mathrm{F}(\lambda ), \end{aligned}$$
(19)

where h is a transfer function. The transfer function is dependent on \(\lambda _0\) and \(\lambda _1\), and can be described as

$$\begin{aligned} h(\lambda )=h'\left( \frac{\lambda -\lambda _0}{\lambda _1-\lambda _0}-0.5\right) =h'\left( \frac{\lambda -0.5\lambda _1-0.5\lambda _0}{\lambda _1-\lambda _0}\right) , \end{aligned}$$
(20)

where \(h'(x)\) is a transfer function independent of \(\lambda _0\) and \(\lambda _1\). Partial scanning is described mathematically by adopting a truncate function as the transfer function \(h'(x)\). The truncate function is given by

$$\begin{aligned} h'(x)=\mathrm{rect}(x), \end{aligned}$$
(21)

where rect(x) is the rectangular function and is given by

$$\begin{aligned} \mathrm{rect}(x)= {\left\{ \begin{array}{ll} 1 & \quad \left( |x|<\frac{1}{2}\right) \\ \frac{1}{2} & \quad \left( |x|=\frac{1}{2}\right) \\ 0 & \quad \left( |x|>\frac{1}{2}\right) .\\ \end{array}\right. } \end{aligned}$$
(22)

The Fourier transform for the partial reflection spectrum \(r_\mathrm{M}\) can be expressed by

$$\begin{aligned} R_\mathrm{M}(\omega )=\int 2r_\mathrm{B}h(\lambda )\left\{ 1+\cos \left( 2n_\mathrm{e}L_\mathrm{F}\frac{2\pi }{\lambda }\right) \right\} e^{-i\omega \lambda } {\text {d}}\lambda . \end{aligned}$$
(23)

\(\lambda _1-\lambda _0\) is sufficiently smaller than \(\lambda _0\); therefore, the following approximate expression holds.

$$\begin{aligned} \frac{1}{\lambda }& = \frac{1}{\lambda _0}+\frac{1}{\lambda }-\frac{1}{\lambda _0} \end{aligned}$$
(24)
$$\begin{aligned}& = \frac{1}{\lambda _0}+\frac{\lambda _0-\lambda }{\lambda \lambda _0} \end{aligned}$$
(25)
$$\begin{aligned} & \approx \frac{1}{\lambda _0}+\frac{\lambda _0-\lambda }{\lambda _0^2} \end{aligned}$$
(26)
$$\begin{aligned}& = \frac{2}{\lambda _0}-\frac{\lambda }{\lambda _0^2}. \end{aligned}$$
(27)

The cosine function is an even function, so that using Eqs. (27), (23) can be approximated by

$$\begin{aligned} R_\mathrm{M}(\omega )\approx \int 2r_\mathrm{B}h(\lambda ) \left\{ 1+\cos \frac{4n_\mathrm{e}L_\mathrm{F}\pi }{\lambda _0} \left( \frac{\lambda }{\lambda _0}-2\right) \right\} e^{-i\omega \lambda } {\text {d}}\lambda . \end{aligned}$$
(28)

Here, if the Fourier transform of \(r_\mathrm{B}h(\lambda )\) is \(R_\mathrm{H}(\omega )\), then Eq. (28) can be rewritten by

$$\begin{aligned} R_\mathrm{M}(\omega )=2R_\mathrm{H}(\omega )+R_\mathrm{H}(\omega -\omega _\mathrm{F})e^{i\varPhi _\mathrm{F}}+R_\mathrm{H}^*(\omega +\omega _\mathrm{F})e^{-i\varPhi _\mathrm{F}}, \end{aligned}$$
(29)

where the \(*\) superscript indicates the complex conjugate, \(\omega _\mathrm{F}=4\pi n_eL_\mathrm{F}/\lambda _0^2\), and \(\varPhi _\mathrm{F}\) is the initial phase. Equation (29) shows that the function \(R_\mathrm{M}(\omega )\) has peaks in the vicinity of the direct current component and angular frequencies \(\pm \omega _\mathrm{F}\). Let \(r'_\mathrm{M}\) be a partial reflection spectrum measured after wavelength shift due to temperature change or strain application; \(r'_\mathrm{M}\) and its Fourier transform result \(R'_\mathrm{M}\) are then expressed by

$$\begin{aligned} r'_\mathrm{M}(\lambda )& = h(\lambda )r'_\mathrm{F}(\lambda )=h(\lambda )r_\mathrm{F}(\lambda -\varDelta \lambda ) \end{aligned}$$
(30)
$$\begin{aligned} R'_\mathrm{M}& = \int r'_\mathrm{M}(\lambda ) e^{-i\omega \lambda } {\text {d}}\lambda \end{aligned}$$
(31)
$$\begin{aligned}& = 2R_\mathrm{H}(\omega )+R_\mathrm{H}(\omega -\omega _\mathrm{F})e^{i(\varPhi _\mathrm{F}+\varDelta \varPhi )}+R_\mathrm{H}^*(\omega +\omega _\mathrm{F})e^{-i(\varPhi _\mathrm{F}+\varDelta \varPhi )}, \end{aligned}$$
(32)

where \(\varDelta \varPhi\) is the phase shift that corresponds to the wavelength shift \(\varDelta \lambda\) and is given by

$$\begin{aligned} \varDelta \varPhi =-\omega _\mathrm{F}\varDelta \lambda . \end{aligned}$$
(33)

A reflection spectrum from a sensor array consisting of FBG–FPIs with different lengths installed on one fiber is expressed by

$$\begin{aligned} r_\mathrm{A}(\lambda )=2r_\mathrm{B}\sum _{j}{\left\{ 1+\cos \left( 2n_\mathrm{e}L_{\mathrm{F}j} \frac{2\pi }{\lambda }\right) \right\} }, \end{aligned}$$
(34)

where \(L_{\mathrm{F}j}\) is the interferometer length of the jth FBG–FPI. The result of Fourier transform of a partial reflection spectrum of the FBG–FPI array is expressed by

$$\begin{aligned} R_\mathrm{AM}& = \int h(\lambda )r_\mathrm{A}(\lambda ) e^{-i\omega \lambda } {\text {d}}\lambda \end{aligned}$$
(35)
$$\begin{aligned}& = \sum _j {\left\{ 2R_\mathrm{H}(\omega )+R_\mathrm{H}(\omega -\omega _{\mathrm{F}j})e^{i\varPhi _{\mathrm{F}j}}+R_\mathrm{H}^*(\omega +\omega _{\mathrm{F}j})e^{-i\varPhi _{\mathrm{F}j}}\right\} }, \end{aligned}$$
(36)

where \(\omega _{\mathrm{F}j}=4\pi n_eL_{\mathrm{F}_j}/\lambda _0^2\), and \(\varPhi _{\mathrm{F}_j}\) is the initial phase that corresponds to the jth FBG–FPI. Here, it is assumed that the function \(R_{H}\) has a sharp peak near the origin and its sidelobes are sufficiently small. Under this assumption, the following expression is satisfied.

$$\begin{aligned} \max _j {\{|}R_\mathrm{H}(\omega _{\mathrm{F}j}){|\}}\ll & {|}R_\mathrm{H}(0){|} \end{aligned}$$
(37)
$$\begin{aligned} \max _{s,t} {\{|}R_\mathrm{H}(\omega _{\mathrm{F}s}-\omega _{\mathrm{F}t}){|\}}\ll & {|}R_\mathrm{H}(0){|}. \end{aligned}$$
(38)

Therefore, the following approximate expression holds.

$$\begin{aligned} R_\mathrm{AM}(\omega _{\mathrm{F}j})& = {\sum _s \left\{ 2R_\mathrm{H}(\omega _{\mathrm{F}j})+R_\mathrm{H}(\omega _{\mathrm{F}j}-\omega _{\mathrm{F}s})e^{i\varPhi _{\mathrm{F}s}}+R_\mathrm{H}^*(\omega _{\mathrm{F}j}+\omega _{\mathrm{F}s})e^{-i\varPhi _{\mathrm{F}s}}\right\} }\nonumber \\ & \approx R_\mathrm{H}(0)e^{i\varPhi _{\mathrm{F}j}}. \end{aligned}$$
(39)

Let W be the minimum value of \(|\omega _{\mathrm{F}s}-\omega _{\mathrm{F}t}|/(2\pi )\) under the condition that Eq. (38) is satisfied. Thus, W is the minimum value that satisfies the following expression.

$$\begin{aligned} |R_\mathrm{H}(\omega )|\ll |R_\mathrm{H}(0)| \left( W<\frac{|\omega |}{2\pi }\right) . \end{aligned}$$
(40)

W and the maximum number of sensors that can be mounted on the array then have the following relationship:

$$\begin{aligned} N_\mathrm{max}\le \frac{B}{W}, \end{aligned}$$
(41)

where \(N_\mathrm{max}\) is the maximum number of sensors and B is the bandwidth of \(R_\mathrm{AM}\) in the frequency domain. The bandwidth B is given by

$$\begin{aligned} B=\frac{M}{2(\lambda _1-\lambda _0)}, \end{aligned}$$
(42)

where M is the number of sampling points of the partial reflection spectrum \(h(\lambda )r_\mathrm{A}(\lambda )\). \(r_\mathrm{B}\) is assumed to be a constant; therefore, \(R_\mathrm{H}\) is given by

$$\begin{aligned} R_\mathrm{H}(\omega )=r_\mathrm{B}H(\omega )=(\lambda _1-\lambda _0)r_\mathrm{B}H'\{(\lambda _1-\lambda _0)\omega \}\exp \{-i\omega (0.5\lambda _1+0.5\lambda _0)\}, \end{aligned}$$
(43)

where H and \(H'\) are the Fourier transforms of h and \(h'\), respectively. Equation (40) is rewritten using \(H'\) as

$$\begin{aligned} |H'\{(\lambda _1-\lambda _0)\omega \}|\ll |H'(0)| \left( W<\frac{|\omega |}{2\pi }\right) . \end{aligned}$$
(44)

Let \(W_0\) be the minimum value that satisfies the following expression.

$$\begin{aligned} |H'(\omega ')|\ll |H'(0)| \left( W_0<\frac{|\omega '|}{2\pi }\right) . \end{aligned}$$
(45)

\(W_0\) is a constant determined by the form of the function \(h'\), and it is not dependent on other parameters. From Eqs. (44) and (45), W is given using \(W_0\), as shown by the following equation.

$$\begin{aligned} W=\frac{W_0}{\lambda _1-\lambda _0}. \end{aligned}$$
(46)

Therefore, the maximum number of sensors is given by

$$\begin{aligned} N_\mathrm{max}\le \frac{M}{2W_0}. \end{aligned}$$
(47)

Equation (47) shows that the maximum number of sensors is not dependent on the scanning range of the light wavelength, but is dependent on the number of sampling points of the partial reflection spectrum. It is worth noting that this conclusion is based on the assumption that the sweep range is narrower than the reflection band of the FBG–FPI and \(r_\mathrm{B}\) can be approximated to a constant.

Let us consider the conditions that \(\lambda _1-\lambda _0\) must satisfy when the conditions of the FBG–FPIs to be used are determined in advance. The approximation that \(r_\mathrm{B}\) is a constant is reasonable only when \(\lambda _1-\lambda _0\) is narrower than the reflection band of the FBG–FPIs. That is, the following expression must be satisfied.

$$\begin{aligned} \lambda _1-\lambda _0<W_\mathrm{B}, \end{aligned}$$
(48)

where \(W_\mathrm{B}\) is the reflection bandwidth. From the definition of the parameter W, the following expressions must also be satisfied.

$$\begin{aligned} W\le \frac{\min _{s,t}(|\omega _{\mathrm{F}s}-\omega _{\mathrm{F}t}|)}{2\pi }, \end{aligned}$$
(49)
$$\begin{aligned} \frac{2\pi W_0}{\lambda _1-\lambda _0}\le \min _{s,t}(|\omega _{\mathrm{F}s}-\omega _{\mathrm{F}t}|), \end{aligned}$$
(50)
$$\begin{aligned} \lambda _1-\lambda _0\ge \frac{2\pi W_0}{\min _{s,t}(|\omega _{\mathrm{F}s}-\omega _{\mathrm{F}t}|)}. \end{aligned}$$
(51)

The Fourier transform result of the partial reflection spectrum measured after a change in temperature and application of strain to each FBG–FPI is expressed by

$$\begin{aligned} R'_\mathrm{AM}=\sum _j 2R_\mathrm{H}(\omega )+R_\mathrm{H}(\omega -\omega _{\mathrm{F}j})e^{i(\varPhi _{\mathrm{F}j}+\varDelta \varPhi _j)}+R_\mathrm{H}^*(\omega +\omega _{\mathrm{F}j})e^{-i(\varPhi _{\mathrm{F}j}+\varDelta \varPhi _j)}, \end{aligned}$$
(52)

where \(\varDelta \varPhi _j\) is the phase shift that corresponds to the wavelength shift \(\varDelta \lambda _j\) of the jth FBG–FPI, which is given by

$$\begin{aligned} \varDelta \varPhi _j=-\omega _{\mathrm{F}j}\varDelta \lambda _j. \end{aligned}$$
(53)

For the partial reflection spectrum after the shift, the same approximation as in Eq. (39) is applied and the following equation is obtained.

$$\begin{aligned} R'_\mathrm{AM}(\omega _{\mathrm{F}j})\approx R_\mathrm{H}(0)e^{i(\varPhi _{\mathrm{F}j}+\varDelta \varPhi _j)}. \end{aligned}$$
(54)

Therefore, the wavelength shift \(\varDelta \lambda _j\) that corresponds to the jth FBG–FPI can be obtained by

$$\begin{aligned} \varDelta \lambda _j= {\frac{1}{\omega _{\mathrm{F}j}}} \tan ^{-1}\frac{{\mathrm{Im}}[R_\mathrm{AM}(\omega _{\mathrm{F}j})R'^*_\mathrm{AM}(\omega _{\mathrm{F}j})]}{{\mathrm{Re}}[R_\mathrm{AM}(\omega _{\mathrm{F}j})R'^*_\mathrm{AM}(\omega _{\mathrm{F}j})]}. \end{aligned}$$
(55)

4 Experiment

Two low-reflective FBG–FPIs were prepared for multi-point sensing. The FBG–FPIs had a reflectance of approximately 1% and a length of approximately 1 mm. In the first FBG-FPI (FBG-FPI1), the distance between the FBGs was 20 mm, and in the second FBG–FPI (FBG-FPI2), the distance was 25 mm. Both reflection spectra of the two FBG–FPIs had a sinusoidal structure. The periods of the sine waves were 41 pm for FBG–FPI1 and 33 pm for FBG–FPI2. The difference in the frequencies of the sine waves corresponding to \(|\omega _\mathrm{F1}-\omega _\mathrm{F2}|\) was 5.9 nm\(^{-1}\). The full width at half maximums (FWHMs) of the envelopes of the sinusoidal waves were approximately 6 nm. The center wavelength of the envelope was approximately 1550 nm.

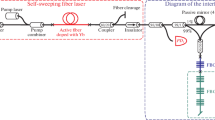
A schematic diagram of the experimental setup for the FBG–FPI array interrogation system is shown in Fig. 1. The center wavelength of the reflection spectrum of the FBG–FPI is 1550 nm; therefore, a laser diode with a lasing wavelength of 1550 nm was used as the light source. Light emitted from the laser diode is split by an optical fiber coupler and travels along two paths. Light passing through one path passes through an asymmetric Mach-Zehnder interferometer and is detected by a photodetector (PD1). Light passing through another path enters an FBG–FPI array through an optical circulator, and reflected light from the FBG–FPI array passes through the optical circulator again and is detected by another photodetector (PD2). The injection current and temperature of the laser diode were adjusted using a laser diode controller.

The initial injection current was 200 mA. The laser driver modulated the injection current by a sawtooth wave with a frequency of 100 Hz and an amplitude of 100 mA. Under this condition, the laser wavelength shifts by approximately 6 pm mA\(^{-1}\) with respect to the change in the current. Therefore, the wavelength sweep range, \(\lambda _1-\lambda _0\), was approximately 1.2 nm. The FWHMs of the reflection spectra for the FBG–FPIs were approximately 6 nm; therefore, the requirement expressed by Eq. (48) for the range was satisfied. The frequency difference of the FBG–FPIs was 5.9 nm\(^{-1}\), the reciprocal of which was 0.17 nm. According to Eq. (51), if the coefficient \(W_0\) is 7 or less, then the peaks that correspond to the sensors can be separated in the frequency domain. The laser driver can drive the laser diode with a temperature stability of 0.004 \(^\circ\)C over 1 h. The temperature dependence of the laser diode wavelength was approximately 0.1 nm \(^\circ\)C\(^{-1}\); therefore, the drift of the wavelength was less than 0.4 pm over 1 h.

Fig. 1
figure 1

Experimental setup of interrogation system for FBG–FPI array; OC optical circulator

Full size image

Strain was measured by connecting only one FBG–FPI to the system to confirm operation of the interrogation system. To apply the strain to the FBG–FPI1, one end of an optical fiber containing the FBG–FPI1 was fixed to a fixed stage and the other end was fixed to a moving stage. The length of the fiber between the two ends was 1347 mm prior to application of strain. Strain was applied to the FBG–FPI1 by moving the stage at an interval of 10 \(\upmu\)m from 0 to 1 mm, which pulled the fiber.

Figure 2 shows the outputs of the photodetectors. The photodetector outputs have sawtooth-shaped envelopes. The reason for this waveform is that the light intensity is changed by modulating the current of the laser diode. The change in the light intensity responds linearly to a change in the current. On the other hand, a change in the wavelength responds nonlinearly to a change in the current. Figure 3 shows an enlarged view of the output of PD1. The change in the phase of the interference signal by the asymmetric interferometer is proportional to the change in the wavelength of the light.

The phase information can be extracted from the interference signal using a Hilbert transform. The change in the laser wavelength estimated using the extracted phase information is shown in Fig. 4. From 1 ms, the change in the wavelength increases monotonically with time and reaches 1200 pm. The change of the output of PD2 due to the laser intensity was compensated, and the compensation result was resampled in the wavelength direction using the change in the wavelength shown in Fig. 4.

A partial reflection spectrum of the FBG–FPI1 obtained through compensation and resampling is shown in Fig. 5. This is a spectrum obtained by scanning a part of the reflection spectrum in the section from 1540 to 1560 nm. The envelope of the sinusoidal wave is a substantially horizontal straight line, which confirms that the assumption set in the previous section, that \(r_\mathrm{B}\) can be approximated by a constant, is satisfied.

The partial reflection spectrum shown in Fig. 5 corresponds to the output of PD2 for the section from 1.8 to 9.8 ms. The sampling rate for PD1 and PD2 was 2.5 MS s\(^{-1}\); therefore, the number of sampling points from 1.8 to 9.8 ms was 20,000. The number of sampling points of the partial spectrum obtained by resampling was also approximately the same. The wavelength sweep range is 1176 pm in the section; therefore, the frequency bandwidth B, of the partial reflection spectrum is 8500 nm\(^{-1}\).

Fig. 2
figure 2

Outputs of photodetectors a for reflected light from FBG–FPI1 and b for transmitted light through the asymmetric Mach–Zehnder interferometer

Full size image
Fig. 3
figure 3

Outputs of photodetectors for transmitted light through the asymmetric Mach–Zehnder interferometer in the range from 4 to 6 ms

Full size image
Fig. 4
figure 4

Change in laser wavelength estimated by fringe analysis

Full size image
Fig. 5
figure 5

Partial reflection spectrum of FBG–FPI1 estimated from the photodetector output

Full size image

The result of the Fourier transform for the partial reflection spectrum is shown in Fig. 6. The frequency bandwidth of the partial reflection spectrum is very wide; however, to clearly show around the peaks, an enlarged view near the origin is shown in Fig. 6. A peak appears at the frequency of the sinusoidal wave. However, the sidelobes around the peak have a non-negligible value. The sidelobes are caused by the narrow wavelength sweep section. The presence of the sidelobes prevents the approximations of Eqs. (39) and (54) from being established. Therefore, to suppress the sidelobes, the Hanning window function was applied [51]. Application of the window function corresponds to replacement of the transfer function \(h(\lambda )\) as

$$\begin{aligned} h(\lambda )= {\left\{ \begin{array}{ll} 0.5 -0.5\cos 2\pi x & (\lambda _0\le \lambda \le \lambda _1)\\ 0 & \text {(otherwize),} \end{array}\right. } \end{aligned}$$
(56)

where x is given by

$$\begin{aligned} x=\frac{\lambda -\lambda _0}{\lambda _1-\lambda _0}-0.5. \end{aligned}$$
(57)

The result for the Fourier transform after application of the window function is shown in Fig. 7. The sidelobes are clearly suppressed by application of the window function.

The width of the peak is spread after application of the window function. The FWHM of the peak is 1.7 nm\(^{-1}\). Assuming that this FWHM is equivalent to W, the maximum number of sensors readable by the present sensor system is given by \(B/W=8500\) nm\(^{-1}\)/1.7 nm\(^{-1}\) = 5000. In our previous systems [48], a light source capable of sweeping with a resolution of 0.1 pm and a sufficiently wide wavelength range was used. In this case, the width of the peak appearing after the Fourier transform is determined by the reflection bandwidth of the FBG-FPIs. The FWHMs of the reflection spectral envelopes of the FBG-FPIs are approximately 6 nm. If the envelope can be approximated by a Gaussian function, then the FWHM of the peak appearing after the Fourier transform would be 0.29 nm\(^{-1}\). In this case, \(B=1/(2\times 0.1 ~\mathrm{pm})=5000~\mathrm{nm}^{-1}\); therefore, the maximum number of sensors readable by the previous system is given by \(B/W=5000\) nm\(^{-1}\)/0.29 nm\(^{-1}\) = 17,000. Thus, the number of sensors available in the proposed system is less than one-third of the number in the previous system.

Fig. 6
figure 6

Fourier transform of the partial reflection spectrum of FBG–FPI1

Full size image
Fig. 7
figure 7

Fourier transform after application of the window function to the partial reflection spectrum of FBG–FPI1

Full size image

The phase shift was read from the peak obtained by the Fourier transform. The phase shift was wrapped from \(-\pi\) to \(\pi\); therefore, phase unwrapping was applied to the phase shift. The wavelength shift was estimated according to the relation shown in Eq. (33) after the application of phase unwrapping. A linear response of the wavelength shift to strain was obtained. The response coefficient of the wavelength shift to strain was 1.2 pm/\(\upmu \upepsilon\). A similar strain application experiment was also performed on FBG–FPI2. As in the experiment using FBG–FPI1, a linear response of the wavelength shift to strain was obtained, and the response coefficient was 1.2 pm/\(\upmu \upepsilon\). Thus, it was confirmed that the linear response of the sensor could be read without problem, even when using the partial reflection spectrum, as with the entire reflection spectrum.

An experiment of simultaneous multi-point strain measurement using the two FBG–FPIs was performed. Figure 8 shows a schematic diagram of the experimental setup around the FBG–FPIs. The fiber containing FBG–FPI1 and the fiber containing FBG–FPI2 were connected. One end of the fiber containing FBG–FPI1 was fixed to a fixed stage and the other end was fixed to a moving stage. The length of the fiber between the two ends before the application of strain was 1347 mm. Similarly, one end of the fiber containing FBG–FPI2 was fixed to a fixed stage and the other end was fixed to a moving stage. The length of the fiber between the two ends before the application of strain was 1410 mm.

Fig. 8
figure 8

Experimental setup around the FBG–FPIs

Full size image

The strain applied to each FBG–FPI was varied according to the following four-step procedure. The moving stage was first moved by 500 \(\upmu\)m at intervals of 10 \(\upmu\)m and only FBG–FPI1 was pulled. Next, only FBG–FPI2 was pulled by moving the stage by 500 \(\upmu\)m at intervals of 10 \(\upmu\)m. FBG–FPI1 was then further pulled by moving the stage further by 500 \(\upmu\)m at intervals of 10 \(\upmu\)m. The moving stage fixed with the end of the fiber containing FBG–FPI2 was then finally moved back to the initial position at 10 \(\upmu\)m intervals to relax the strain of FBG–FPI2 to 0.

The partial reflection spectrum for the FBG–FPI array was measured before and after strain application. Figure 9 shows the partial reflection spectrum measured before strain application. The reflection spectrum has a structure in which two sinusoidal waves are superposed. Figure 10 shows the result of Fourier transform after application of the window function to the partial reflection spectrum. Two peaks appear at the positions that correspond to the FBG–FPIs. The phase changes of the peaks were extracted and phase unwrapping was applied to the extracted phase changes. Figure 11 shows the wavelength shifts estimated according to the relation shown in Eq. (53) after the application of phase unwrapping to the phase changes.

Fig. 9
figure 9

Partial reflection spectrum of the FBG–FPI array

Full size image
Fig. 10
figure 10

Fourier transform after application of the window function to the partial reflection spectrum of the FBG–FPI array

Full size image
Fig. 11
figure 11

Wavelength shifts of the reflection spectra for each FBG–FPI calculated using the phase changes

Full size image

The wavelength shift of each FBG–FPI corresponds one-to-one with the applied strain. In the first 50 steps, only FBG–FPI1 responds, and then in the subsequent 50 steps, only FBG–FPI2 responds. After that, only FBG–FPI1 responds for the next 50 steps, and then only FBG–FPI2 responds for the last 50 steps. Each wavelength shift responds only to the applied strain and there is no crosstalk with each other. This result confirms that even when using a partial reflection spectrum, it is possible to read multiple sensors without interference, as with use the entire reflection spectrum.

5 Conclusions

Interrogation using partial spectrum scanning for a low-reflective FBG–FPI sensor array was proposed. A part of the reflection spectrum of an FBG–FPI sensor array is measured over a short time with a fast but narrow range wavelength sweep provided by a modulated laser diode. Frequency peaks that uniquely correspond to each FBG–FPI are obtained by Fourier transform, and unnecessary sidelobes are suppressed by application of the Hanning window function. The wavelength shift generated for each FBG–FPI is read from the phase change of the corresponding peak.

It was theoretically shown that interrogation is possible from the result of scanning only a part of the reflection spectrum instead of acquiring the entire reflection spectrum. The requirements for the scanning range were also shown. The formula that gives the maximum number of sensors that can be read out from the partial reflection spectrum was also derived. The maximum number of sensors was not dependent on the scanning range but was dependent on the number of sampling points of the partial reflection spectrum.

Experiments confirmed that the proposed method works well and without problems. In an experiment using only one FBG–FPI, it was confirmed that the linear response to strain can be read using only the partial reflection spectrum. In an experiment using two FBG–FPIs simultaneously, it was confirmed that the responses can be read independently and without interference between the two sensors using only the partial reflection spectrum.

The periods of the sine waves were 41 pm for one FBG–FPI and 33 pm for the other FBG–FPI. The FWHMs of the reflection spectra for the FBG–FPIs were approximately 6 nm. The scanning range of the light source was approximately 1.2 nm. In the system used in these experiments, it was possible to collectively read up to 5,000 FBG–FPIs at one time.

The time for strain measurement was 10 ms, which demonstrated that shortening of the measurement time was achieved using the proposed method. It is possible to further increase the modulation speed of a laser diode; therefore, it is expected that the measurement could be performed in an even shorter time. For such fast measurements, the number of available sensors is maintained by sampling a partial reflection spectrum at a high rate.