Introduction

Groundwater resources are essential as a part of water supply systems and in management planning for the sustainability of any community. Although surface-water resources seem to be prominent in many countries and societies, in the long run, groundwater resources are the most viable alternative to the solution of water resource problems. Groundwater resources can be split, in general, into two categories: fossil and replenishable. The former includes paleo-geological groundwater storages, which were formed during pluvial geological periods, especially in arid and semi-arid regions such as the Arabian Peninsula, where deep aquifers are either in the form of sandstone, dolomite or limestone formations as karstic aquifers; connection of these deep aquifers to present-day rainfall is often not possible except at outcrop locations (Baciewicz et al. 1982; Şen and Al-Dakheel 1986; Hötzl 1995). Outcropping aquifers are connected to present-day rainfall events through infiltration and percolation, i.e., mechanisms of groundwater recharge. They are at the earth surface or at shallow depths, and in many parts of the world they exist in the form of karstic formations with intriguing networks of subsurface flow paths (Angelini and Dragoni 1997; Akdim and Amyay 1999; Screaton et al. 2004; Guo et al. 2013; Kavousi and Raesis 2015).

Karstic aquifers are important for water supply worldwide. In Europe they cover almost 35% of the land surface, providing 50% of the water supply in some countries (European Commission 2008). Although karstic aquifers are vulnerable to pollution (Goldscheider et al. 2001) and need special protection, their water supply potential is important, and apart from the nonrainy periods, the recharge response after each rainfall event exposes interesting and important information. For example, Vias et al. (2006) employed the flow concentration, overlying layers and precipitation (COP) approach for the assessment of karstic (carbonate) aquifer intrinsic vulnerability in Europe and they considered carbonate aquifers in the south of Spain.

Bonacci (1993) provided extensive analysis and explanation on recession curves by means of the recession coefficient given in Maillet (1905). Bonacci (1993) simulated the karstic aquifer as a linear reservoir coefficient relating it to the recession coefficient. The final result is that the linear reservoir coefficient changes with time along with changes of the flow conditions in the karstic aquifer.

Dewandel et al. 2003) addressed numerical simulation models for proving the robustness of the Boussinesq (1904) approach under conditions far from the simplifying assumptions that were used to integrate the diffusion equation. They also suggested that the quadratic equation is valid for hydrograph recession, but such an equation is not valid for generalization of karstic aquifer discharge. Furthermore, they stated that an exponential form is closer to the recession limb of the karstic aquifer and closer to the quadratic flow expression in case of horizontal flow dominance.

Criss and Winston (2008) provided a rainfall-driven theoretical hydrograph derivation on the basis of Darcy’s law and the diffusion equation for springs and small rivers from rainfall records. Fiorillo (2014) analysed karst spring hydrographs from sites in southern Italy based on annual daily discharge measurements over 10 years during extensive droughts. Annual spring discharge recession coefficients were calculated from semi-logarithmic plots between the discharge and time, which appeared as a straight line. Each year’s recession coefficient was different from other years. Fiorillo (2014) concluded that, depending on the increase or decrease of this coefficient, karst aquifer discharge empties the aquifer storage slowly or more quickly.

Recently, Jakada et al. (2019) pointed to the hazards of karstic aquifer calculations, because most often they are modelled as nonkarstic watersheds. They compared a karst and nonkarst watershed by elucidating their geomorphological characteristics and their potential impact on the spatio-temporal availability and quality of groundwater. Quantitatively, morphometric mapping and hydrograph recession analysis were used to estimate hydrographs, and hence to define the recession coefficient and the influence of karst drainage attributes. The streamflow components were identified based on the hydrograph recession limbs (segments) and taking account of geomorphological factors.

Adji et al. (2019) presented work on determination of the spatial degree of karstification, based on the Malik (2007) karstification degree index, in springs and underground rivers, in addition to hydrograph recession curves from eight water-level gauges in the Rengel karstic area, Java, Indonesia. The determination of the aquifer karstification degree of the spring was carried out using recession-curve analysis, which is based on the formula and classification proposed by Malik and Votjkova (2010, 2012), who demonstrated that the recession-curve has several subregimes of flow, which are expressed as a laminar flow and a turbulent flow (Adji et al. 2019). As mentioned by Fiorillo (2014) this approach has one or more subregimes during the recession part. Adji et al. (2019) calculated the subregime coefficient of laminar flow according to the Maillet (1905) formula in the form of an exponential expression between the discharge and time.

Daly et al. (2002) provided specific concepts of karstic area vulnerability for the assessment of groundwater resources or water resource through springs and wells in Europe. The main source of groundwater in these cases is the karstic aquifer (below ground) during dry periods, but during rainy periods the response of the karstic springs at the foot hills provides surface-water discharge depending on the additional hydraulic head generation after each rainfall occurrence. The spring flow is the consequence of vertical and horizontal flow combinations through the complex solution cavity network. In the European regions studied, depending on the climate-change projections, maps can be used for environmental management through use of tracer techniques for conceptual understanding of hydrogeology in the karstic terrain (Bruyere et al. 2001; Jeannin et al. 2001; Goldscheider et al. 2001; Perrin et al. 2004; Şen 2015).

Karstic aquifer management is particularly important in tropical developing countries, but unfortunately protection and conservation measures are missing in many countries (Day 1993, 2007; Day and Koenig 2002). Karstic aquifers need special attention because there are many uncertainties with respect to their complex and heterogeneous underground flow paths and bifurcations, their extensive recharge areas, and the variations in aquifer and groundwater depth. Recharge area definition is another uncertain variability. Karst aquifer management is a very complicated matter, and how to manage pollution, karst hazards, and human impacts on karst landscapes is a question worthy of discussion (Parise et al. 2009).

White (1969) classified karstic aquifer flow regimes into three categories: diffuse, mixed and conduit. A diffuse regime has rather weak influence on groundwater movement in the solution cavity network (Shuster and White 1971; Atkinson 1977), whereas groundwater movement is dominated by the larger solution cavity system in conduit aquifers (White 1988). In general, in any karstic terranes, all the three types of water movement take place. The combination of them all provides significant local variation in the transmissivity of the aquifer, which is exemplified by Şen (2018) for Floridian (USA) karstic aquifer data provided by Li et al. (2016). In general, it is very difficult to have a single value for aquifer parameters such as the storage and transmissivity coefficients, in karstic aquifers. In the literature overwhelmingly most of the papers have descriptive information, but the most recent quantitative and detailed modeling work is presented by Li et al. (2016) based on descriptive information.

The main purpose of this paper is to present a general formulation by a power law model for a karstic aquifer spring hydrograph recession limb with an exponent that is not 0.5. The exponent 0.5 is documented in the literature, but it cannot represent all of the karstic spring hydrographs in the world (Li et al. 2016; Jakada et al. 2019). As discussed in the literature, exponent 0.5 does not provide flexibility in karstic aquifer hydrograph modeling. The mathematical difficulty in the general formulation is addressed through a series expansion by means of a division procedure, and hence, an alternative power law model is provided with a power different from 0.5. The recession limb is modeled by means of two functions representing the power law for early times and linear law for late times; however, in the literature they are modelled by the square root and exponential laws, respectively. Another model presented in this paper is based on the logarithmic normal function, which is capable of modeling both rising and recession limbs, and especially, the whole recession limb is modelled by a single expression. A comparison of the suggested methodology with the existing restrictive alternatives in the literature is presented. Finally, the application is applied to data from Wakulla Springs, Florida, USA, in the form of a karst spring hydrograph recession limb or by means of a dimensionless hydrograph (Li et al. 2016; Criss and Winston 2008).

Karstic spring hydrograph

Many researchers argue that the characteristics of the recession limb are strongly influenced by the development of the karst aquifers, which is closely related to the geological conditions. Karstic springs are the result of chemical processes associated with solution cavities in different geological formations such as limestone, dolomite, evaporate, overall gypsum, anhydrite and quartzite. In this paper, karst formations in carbonate rocks are taken into consideration due to their economic groundwater-resource potential and their dynamic karst structure functions. Most of the karstic carbonates are recharged at the outcrop regions, which are either in the form of hills or foothills, where springs are at the end of sinkholes; however, most springs are connected with karst conduits of caves, which may not be at the end of sinkholes. Ford and Williams (1989) stated that about 12% of the world’s land is occupied by carbonate rocks and only about 7–10% of it is in the form of actual groundwater-rich karst. Karstic formations are ranked second, next down from alluvium aquifers, in the provision of groundwater resources exploitation in the world.

Figure 1 illustrates a representative karstic medium with irregularly scattered connective solution cavities leading to a subsurface water regime, in turn leading to a sinkhole spring outlet at the foot hills. Figure 2 indicates various parts of a karstic domain hydrograph that can be observed, in general, at the bottom of a sinkhole spring. Prior to the rainfall occurrence, at the spring there is almost constant base-flow discharge, which does not give any information about the behavior of the karstic aquifer. This can be represented as\( {Q}_{\mathrm{SP}}^{\mathrm{B}} \), with Q as discharge (B labels base flow and SP is spring).

Fig. 1
figure 1

Representative karstic aquifer and a spring. hS is the hydraulic head, hSB is the sinkhole base head

Full size image
Fig. 2
figure 2

Representative karst spring hydrograph

Full size image

At the start of a storm rainfall event, the spring discharge starts rising up to a peak flow discharge, \( {Q}_{\mathrm{SP}}^{\mathrm{P}} \), during the time to peak (tP). From the peak onward, the storm rainfall stops, and consequently the spring discharge starts to recede to the level of base flow discharge during recession time (tr). In general, for any given time 0 < t < tP + tr, the spring discharge is \( {Q}_{\mathrm{SP}}^{\mathrm{B}}<{Q}_{\mathrm{SP}}<{Q}_{\mathrm{SP}}^{\mathrm{P}} \) (where superscript P implies peak). The summation of these two durations is equal to the karstic aquifer recharge duration (tR) which is

$$ {t}_{\mathrm{R}}={t}_{\mathrm{P}}+{t}_{\mathrm{r}} $$
(1)

The more interconnections in the medium and the higher the transmissivity coefficient, the shorter the two time durations. On the other hand, the peak discharge is directly proportional to the rainfall intensity, but nonlinearly. These two factors provide qualitative information as for the shape of the karstic sinkhole spring hydrographs. The peak discharge, \( {Q}_{\mathrm{SP}}^{\mathrm{P}} \), is equal to the summation of the base discharge, \( {Q}_{\mathrm{SP}}^{\mathrm{B}} \), and maximum discharge, \( {Q}_{\mathrm{SP}}^{\mathrm{PM}} \), due to the storm rainfall.

$$ {Q}_{\mathrm{SP}}^{\mathrm{P}}={Q}_{\mathrm{SP}}^{\mathrm{B}}+{Q}_{\mathrm{SP}}^{\mathrm{P}\mathrm{M}} $$
(2)

Physically, the time to peak and the recession time are directly related to the complex configuration and interconnectedness of the solution cavity network of the karstic aquifer.

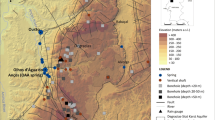
In this paper, the case of Wakulla Springs, Florida, is considered. The karstic aquifer and spring are considered as part of Wakulla River catchment; the major source, Wakulla Springs, is at the upstream tributary to St. Marks River (as explained in Li et al. (2016) and displayed in Fig. 3. As for the reliability and various features of the data, there is detail in Li et al. (2016) and the data are taken to be valid for the purposes of this study. The water flux has been measured by the US Geological Survey (USGS 2015a, b) at a gaging station on the Wakulla River. Total discharge change by time is given in Fig. 4.

Fig. 3
figure 3

The study area location, in Wakulla County, USA

Full size image
Fig. 4
figure 4

Wakulla Springs hydrograph (Şen 2018)

Full size image

It is obvious from Fig. 4 that with the start of storm rainfall, there is rapid groundwater replenishment up to the peak, and then subsequently, a recession limb takes place with comparatively longer time than time to peak. One can identify the base flow part approximately as \( {Q}_{\mathrm{SP}}^{\mathrm{B}} \) = 18.10 m3/s, which is useful for the dimensionless effective hydrograph identification. In general, the karst hydrograph can be thought of as two parts: one is the karstic base flow at the spring level prior to storm rainfall and the other is in addition to this base flow, QSP, which starts with the rainfall occurrence, which is referred to in this paper as effective karstic flow. It has also been indicated by Şen (2018) that the exponent 0.5 in the power model by Li et al. (2016) does not pass through the centroid of the given karstic data. Şen (2018) suggested that n = 0.5 is not the most convenient power, but the integration of the valid expressions as stated by Li et al. (2016) is not possible by means of simple mathematical operations. Even in the integration with n = 0.5, Li et al. (2016) had to ignore some of the terms to accommodate simplification and the comparatively insignificant contribution to the overall equation. In the following sections, the complete integration methodology is presented whether or not the power value n is 0.5.

Karstic aquifer models

It is well-known that the quantification of groundwater flow in karstic media is far more difficult than quantification in porous and fractured media. In the following two subsections, power and the logarithmic normal (log-normal) models are proposed for sinkhole spring discharge quantification.

Power model

In Fig. 1 the sinkhole base head (hSB) represents the situation prior to storm rainfall occurrence, and hS indicates the hydraulic head at any time during the groundwater recharge period. The effect on the spring flux can be expressed in general either as a difference (hS – hSB) or as the ratio hS/hSB. In modeling studies, the ratio is preferable, because its value ranges between 0 and 1, and hence, a nondimensional calculation methodology can be developed

$$ {Q}_{\mathrm{S}\mathrm{P}}^{\mathrm{R}}=\mathrm{f}\left({h}_{\mathrm{S}}-{h}_{\mathrm{S}\mathrm{B}}\right) $$
(3)

or

$$ {Q}_{\mathrm{S}\mathrm{P}}^{\mathrm{R}}=\mathrm{f}\left({h}_{\mathrm{S}}/{h}_{\mathrm{S}\mathrm{B}}\right) $$
(4)

Furthermore, as an implicit logical expression, one can relate the difference or ratio to \( {Q}_{\mathrm{SP}}^{\mathrm{R}} \), which is the spring discharge, similar to the Li et al. (2016) model, but with n ≠ 0.5. Along the same lines, some other authors have also given information (Bonacci 1993; Dewandel et al. 2003; Fiorillo 2014; Malik 2007). In practical applications, explicit forms of these expressions are necessary. For this purpose, in this paper, dimensionless ratios are preferred for use; hence, the logical and rational concepts suggest that in general, there is a nonlinear relationship between the discharge and hydraulic head ratios:

$$ \frac{Q_{\mathrm{S}\mathrm{P}}}{Q_{\mathrm{S}\mathrm{P}}^{\mathrm{B}}}={\left(\frac{h_{\mathrm{S}}}{h_{\mathrm{S}\mathrm{B}}}\right)}^{\mathrm{n}} $$
(5)

Li et al. (2016) considered n = 0.5, because it provides an easy way for later integration works; however, the mathematical explanation of an adaptation to 0.6, instead of 0.5, has been explained in detail by Şen (2018). In Eq. (5) the spring flow is composed of two added components, namely, spring base and spring rainfall flows.

$$ {Q}_{\mathrm{SP}}={Q}_{\mathrm{SP}}^{\mathrm{B}}+{Q}_{\mathrm{SP}}^{\mathrm{R}} $$
(6)

The rainfall recharges the karstic aquifer directly, and therefore, the spring flow due to rainfall can be related to the hydraulic head change by time, dhS/dt, as a percentage of surface solution cavity area (∅) and groundwater recharge area (AS) (Li et al. 2016).

$$ {Q}_{\mathrm{S}\mathrm{P}}^{\mathrm{R}}=-\varnothing {A}_{\mathrm{S}}\frac{\mathrm{d}{h}_{\mathrm{S}}}{\mathrm{d}t} $$
(7)

Herein, the minus sign is for the inverse relationship between the discharge and hydraulic head change. The substitution of Eq. (7) into Eq. (5) and consideration of Eq. (6) leads to the following expression after some algebraic manipulations.

$$ \frac{\mathrm{d}y}{y^n-1}=-\frac{Q_{\mathrm{S}\mathrm{P}}^{\mathrm{B}}}{\varnothing_{\mathrm{s}}{A}_{\mathrm{S}}{h}_{\mathrm{S}\mathrm{B}}}\mathrm{d}t $$
(8)

where 0 < y = hS/hSB < 1. The left hand side of this expression can be expanded into a series by division operator application, which leads to,

$$ \frac{1}{y^n-1}={y}^{-n}+{y}^{-2n}+{y}^{-3n}+.\kern0.5em .\kern0.5em .\kern0.5em .={\sum}_{i=1}^m{y}^{- in} $$
(9)

where m indicates the number of iterations. The integration of this expression with respect to y leads to the following series with many terms, but only three of them are shown explicitly with integration constant (C).

$$ \int \frac{dy}{y^n-1}={\sum}_{i=1}^m\frac{1}{\left(1- in\right)}{y}^{1- in}+C $$
(10)

In light of the last two series, the integration of Eq. (8) using the initial condition (t = 0, hS = h0) leads to

$$ {\sum}_{i=1}^m\frac{1}{\left(1- in\right)}{y}^{1- in}-{\sum}_{i=1}^m\frac{1}{\left(1- in\right)}{\left(\frac{h_0}{h_{\mathrm{S}\mathrm{B}}}\right)}^{1- in}=-\frac{Q_{\mathrm{S}\mathrm{P}}^{\mathrm{B}}}{\varnothing_{\mathrm{s}}{A}_{\mathrm{S}}{h}_{\mathrm{S}\mathrm{B}}}t $$
(11)

or

$$ {\sum}_{i=1}^m\frac{1}{\left(1- in\right)}\left[\ {y}^{1- in}-{\left(\frac{h_0}{h_{\mathrm{S}\mathrm{B}}}\right)}^{1- in}\right]=-\frac{Q_{\mathrm{S}\mathrm{P}}^{\mathrm{B}}}{\varnothing_{\mathrm{s}}{A}_{\mathrm{S}}{h}_{\mathrm{S}\mathrm{B}}}t $$
(12)

One can obtain the y and h0/hSB corresponding values from Eq. (3) after some algebraic manipulations as follows.

$$ y={\left(\frac{Q_{\mathrm{SP}}}{Q_{\mathrm{SP}}^{\mathrm{B}}}\right)}^{1/n} $$
(13)

and

$$ \frac{h_0}{h_{\mathrm{SB}}}={\left(\frac{Q_{\mathrm{SP}}^{\mathrm{Max}}}{Q_{\mathrm{SP}}^{\mathrm{B}}}\right)}^{1/n} $$
(14)

The substitution of these last two expressions into Eq. (12) leads to the final form in terms of the karstic aquifer hydrograph recession model as,

$$ {\sum}_{i=1}^m\frac{1}{\left(1- in\right)}\left[{\left(\frac{Q_{\mathrm{S}\mathrm{P}}}{Q_{\mathrm{S}\mathrm{P}}^{\mathrm{B}}}\right)}^{1/n-i}-\kern0.5em {\left(\frac{Q_{\mathrm{S}\mathrm{P}}^{\mathrm{Max}}}{Q_{\mathrm{S}\mathrm{P}}^{\mathrm{B}}}\right)}^{1/n-i}\right]=-\frac{Q_{\mathrm{S}\mathrm{P}}^{\mathrm{B}}}{\varnothing_{\mathrm{s}}{A}_{\mathrm{S}}{h}_{\mathrm{S}\mathrm{B}}}t $$
(15)

In this equation the two variables are QSP and t, and this implies that as time becomes very large the sinkhole discharge due to the rainfall will be diminishingly small. On the other hand, as time goes to infinity the sinkhole hydraulic head and discharge converges to the steady state flow case, which is the sinkhole base flow in this case. Equation (15) can be solved numerically provided that the relevant karstic hydrograph dependent constants are given.

Logarithmic normal function

One can see from the shapes of the sinkhole-spring karstic hydrographs in Figs. 2 and 3 that they are like the probability distribution functions with rising and recession limbs and a peak value (mode) in between. In this paper, the positively skewed (recession limb longer than the rising limb) logarithmic normal distribution function is adopted for modeling the whole hydrograph not only the recession part, as in the literature and as described in the previous section. The general mathematical expression of such a model can be written as follows (Hahn and Shapiro 1994).

$$ {Q}_{\mathrm{SP}}=\frac{2}{t\sigma \sqrt{2\uppi}}\exp \left\{-\frac{\left(\mathrm{Ln}\ t-\mu \right)}{2{\sigma}^2}\right\} $$
(16)

where μ and σ are the model parameters. The lognormal distribution is applicable when the quantity of interest must be positive, since log(x) exists only when x is positive. Implicitly, this function is the mixture of the power and exponential functions in one expression. This point also gives the impression that rather than dealing with the power and exponential models separately, as Li et al. (2016) have shown and also in the previous section, it is more convenient to adapt the lognormal distribution function for sinkhole-spring hydrograph modeling. The log-normal distribution is a two-parameter family of various forms as shown in Fig. 4. Comparison of these curves with the ones in Fig. 1 of Criss and Winston (2008) indicates that although they are similar the graphs in Fig. 4 have lower recession curves, which are more suitable for karstic aquifers. The Fig. 4 curves are based on the classical Darcy law without any power model for the recession curve. Comparison of Fig. 4 with Fig. 2 and then Fig. 5 gives the impression that there are similar functions to the karstic aquifer hydrograph, and therefore, the problem is to identify the best log-normal distribution function for the Wakulla Springs hydrograph data.

Fig. 5
figure 5

Log-normal functions; m is the arithmetic average, and s is the standard deviation

Full size image

Application and comparison with existing models

In order to consider the comparison of the results from Eq. (8) with the power and exponential models suggested by Li et al. (2016), it is necessary first to obtain important constants in Eq. (8) from the karstic sinkhole hydrograph, which has been identified and described in the previous section. Among these constants is the maximum spring discharge, \( {Q}_{\mathrm{SP}}^{\mathrm{Max}}, \) above the base flow, \( {Q}_{\mathrm{SP}}^{\mathrm{B}} \). These two parameters are determined by Li et al. (2016) as \( {Q}_{\mathrm{SP}}^{\mathrm{Max}}=8.4 \)m3/s and \( {Q}_{\mathrm{SP}}^{\mathrm{B}} \) = 12.5 m3/s. It is physically plausible that 11.695 m3/s < QSP < 11.695 + 98.170 = 109.869 m3/s. The same authors proved that ∅ = 2.9 × 10−4 and that the area A = 193 km2. The sinkhole base head was about 1 m, i.e., hSB = 1 m. Equation (8) can be rearranged for time calculation as,

$$ t=-{\sum}_{i=1}^m\frac{1}{\left(1- in\right)}\left[{\left(\frac{Q_{\mathrm{S}\mathrm{P}}}{Q_{\mathrm{S}\mathrm{P}}^{\mathrm{B}}}\right)}^{1/n-i}-\kern0.5em {\left(\frac{Q_{\mathrm{S}\mathrm{P}}^{\mathrm{Max}}}{Q_{\mathrm{S}\mathrm{P}}^{\mathrm{B}}}\right)}^{1/n-i}\ \right]/\frac{Q_{\mathrm{S}\mathrm{P}}^{\mathrm{B}}}{\varnothing_{\mathrm{s}}{A}_{\mathrm{S}}{h}_{\mathrm{S}\mathrm{B}}} $$
(17)

The solution of this expression is given in Fig. 6b, with the Li et al. (2016) power and exponential model solution in Fig. 6a. Comparison of these two graphs indicates that the series expansion model explained in the previous section represents the high total discharge values better than the Li et al. (2016) power (nonexponential) model. One can also notice that for this karstic sinkhole spring discharge flow during the late time, total discharge data in the recession limb can be approximated by a straight line even better than the exponential model. In both this paper and the article by Li et al. (2016), the two pieces of model explanation may not seem satisfactory, because the spring recharge and discharge events take place continuously in time. It is, therefore, necessary to develop a model that represents early, peak, and late-time sinkhole-spring discharge variations by a single model and if possible to represent the complete spring hydrograph.

Fig. 6
figure 6

Karstic spring recession limb discharge two-piece models, a Power and exponential model (Li et al. 2016), b Series approximation and straight-line models

Full size image

As explained in section ‘Logarithmic normal function’, the logarithmic normal model has almost the same shape as the Wakulla Springs total discharge hydrograph in Fig. 4, which is similar to one of the functions in Fig. 5. Although, Eq. (16) is the probability distribution function, in this paper it will not be used as a probability expression. Its adjustment is by a discharge factor, such that its peak (statistically mode) value becomes equal to the maximum total sinkhole spring discharge. Finally, another multiplication procedure is applied by use of a time factor so that the base duration equals the time duration of the same hydrograph. The application of this procedure leads to the theoretical logarithmic normal model, which has been given in Fig. 7 together with the field data measurements. It is obvious that this model is far better than the previous ones, because a single mathematical formulation represents almost all the sinkhole spring hydrograph especially along the recession limb. In this manner, also, the rising limb of the hydrograph is modelled satisfactorily.

Fig. 7
figure 7

Theoretical log-normal model matches the Wakulla Springs data

Full size image

Following this explanation, the complete theoretical log-normal model can be transformed into a dimensionless hydrograph by dividing its discharge values by peak discharge and also time duration by the maximum time duration. This procedure yields a dimensionless hydrograph for the karstic sinkhole spring discharge, as in Fig. 8. If one knows the peak discharge and the time duration of the discharge variation in any karstic aquifer measurement hydrograph, as in Fig. 4, then the dimensionless karstic hydrograph coordinate values can be used for simple calculations to model the karstic medium sinkhole hydrograph. The dimensionless hydrograph coordinates, dimensionless time (td) and dimensionless discharge (qd) are given in Table 1.

Fig. 8
figure 8

Sinkhole spring dimensionless hydrograph for karstic aquifers

Full size image
Table 1 Karstic aquifer dimensionless hydrograph values
Full size table

Comparison of the Criss and Winston (2008) hydrograph with other existing methodologies yields almost the same result but with a simple mathematical procedure. In Fig. 9, their hydrograph for b = 1 (Fig. 1 of Criss and Winston 2008) is converted into a dimensionless hydrograph and shown together with the karstic aquifer dimensionless hydrograph of this study. It is obvious that although there is a good match along the rising limb, their recession hydrograph limb is presented as higher. This is due to the fact that Criss and Winston (2008) used Darcy’s groundwater flow without taking into consideration the karstic aquifer porosity. The comparison of the recession limbs indicates that, in the case of the karstic spring, the recession is faster.

Fig. 9
figure 9

Dimensionless hydrograph: solid line represents from data of this study; broken line is from Criss and Winston (2008)

Full size image

Conclusions

Groundwater resources are important water supply sources in almost all regions of the world, but especially in the arid and semi-arid regions. Quantitative assessment of groundwater resources in karstic terranes presents more difficulties than assessments for porous and fractured media. In this paper, after a review of the relevant literature on karstic sinkhole spring discharge measurements, the early recession limb is modelled by a power model, but with power not equal to 0.5 (as it is in the literature); instead, the exponent value used is equal to 0.6. The result is compared with already existing models and it is observed that the power model in this paper provides significant improvement over the existing ones. However, the late-time recession limb discharge cannot be modelled sufficiently. All models are developed for the recession limb of the karstic sinkhole spring hydrograph, and they have two components: (1) nonlinear (power) and exponential (as in this paper), and (2) a straight-line for early and late time recession durations.

On the other hand, in order to model a karstic aquifer hydrograph completely, a logarithmic normal (log-normal) mathematical expression is converted to match the karstic sinkhole hydrograph. The log-normal model represents uniquely (as one piece) the recession limb of the karstic aquifer with the rising limb. In the paper, a dimensionless karstic-sinkhole spring-discharge hydrograph is proposed which is expected to help practicing engineers, experts and researchers by providing a means of rapid modeling. It is recommended that in future studies the log-normal model parameters can be related to some physical features of the karstic aquifer such as the storativity and transmissivity.