Introduction

Seawater intrusion of coastal aquifers is a major environmental problem caused mainly by overexploitation of natural groundwater resources. Many studies report the current status and highlight the worldwide extend of the problem (Fleury et al. 2007; Daskalaki and Voudouris 2008; Custodio 2010; Steyl and Dennis 2010; Werner 2010; Bauer-Gottwein et al. 2011). Based on predictions, the number of people living within 100 km of the sea will increase by approximately 35 % compared to 1995 (Cincotta and Gorenflo 2011) by the year 2025. Therefore, management of coastal aquifers is of great importance and remains an active area of research. During the few last decades, significant progress has been made to understand, model and manage coastal aquifer systems (Reilly and Goodman 1985; Werner et al. 2013).

Management of coastal aquifers involves decisions regarding the amount of water to be extracted and/or injected into the aquifer. Simulation tools are often used to evaluate the effectiveness of possible decisions. Coastal aquifer models are inherently complex as they involve mixing of seawater and freshwater having different densities. Mixing of the two liquids creates density variations, which leads to a mathematically complex problem. Seawater is more dense and tends to form a seawater wedge below freshwater.

The modeling tools of seawater intrusion are divided into two categories. The sharp-interface models assume that the liquids are separated without mixing; thus, sharp-interface models consider only advective transport processes, and dispersion is neglected. On the other hand, the variable-density models take into consideration the existence of the mixing zone between seawater and freshwater. Variable density models represent the physical system more accurately and are increasingly used in simulation (Xue et al. 1995; Paniconi et al. 2001; Qahman and Larabi 2006; Werner and Gallagher 2006; Narayan et al. 2007; Kopsiaftis et al. 2009; Lin et al. 2009; Cobaner et al. 2012; Lu et al. 2013; Langevin and Zygnerski 2013). The major disadvantage of variable density models, is that they are computationally demanding as they involve an iterative coupled solution of the governing equations of flow and transport. In addition, they require aquifer parameters that are difficult to estimate such as dispersivity, etc.

Despite progress in hardware and software developments, which allow scientists to simulate very complex variable density problems, researchers still develop and use simulation models based on sharp interface approximation (Padilla et al. 1997; Cheng et al. 2000; Mantoglou 2003; Mantoglou et al. 2004; Ataie-Ashtiani 2006; Kacimov and Sherif 2006; Masciopinto 2006; Tber and Talibi 2007; Mantoglou and Papantoniou 2008; Kacimov et al. 2009; Chang and Yeh 2010; Pool and Carrera 2011; Shi et al. 2011; Koussis et al. 2012; Liu and Dai 2012; Mazi et al. 2013). Under different assumptions regarding the geometry and properties of the aquifer (e.g., slope, homogenous porous medium, specific boundary conditions, etc.), researchers developed models based on analytical solutions of the governing equations (Cheng et al. 2000; Mantoglou 2003; Park and Aral 2004; Bakker 2006; Koussis et al. 2012). On the other hand, numerical models allow simulation of more general cases (Willis and Finney 1985; Finney et al. 1992)—for example, Mantoglou et al. (2004) and Mantoglou and Papantoniou (2008), developed a sharp interface model for unconfined aquifers of general geometry, where the simulation domain is divided into two zones. Bakker and Schaars (2005), developed the SWI (Seawater Intrusion) package for MODFLOW based on the work of Bakker (2003), while Bakker and Schaars (2013), proposed a modeling approach to simulate seawater intrusion using single-density groundwater flow codes.

Management of coastal aquifers requires a method to obtain the optimal decision. Optimization algorithms are frequently employed, where the management problem is converted into an optimization problem, (e.g., maximization of pumping, minimization of seawater intrusion, etc.) Optimization algorithms are mathematical tools searching the decision variable space in an efficient way to identify the optimal solution without user intervention. Optimization algorithms have been extensively used in groundwater management (Bau 2012; Mategaonkar and Eldho 2012; Grundmann et al. 2013; Hernandez et al. 2014).

In coastal aquifer management, both sharp interface and variable-density models have been combined with optimization algorithms. Early efforts (Das and Datta 1999) employed the embedded optimization methods, yet those methods suffer from computational limitations. In order to address computational limitations due to large computational runtime, variable density models are frequently substituted by surrogate models (see Razavi et al. 2012; Kourakos and Mantoglou 2009; Sreekanth and Datta 2011; Bhattacharjya and Datta 2005, 2009; Kourakos and Mantoglou 2013). A thorough review of various optimization methods developed during the last decade is presented by Singh (2014). Alternatively, many researchers choose to simplify the problems under certain assumptions. For example, Kourakos and Mantoglou (2011) used a cross section of a variable density model to study the effects of climate changes in coastal aquifer management. The most commonly used simplification is based on the sharp interface assumption. Despite rapid growth of computational power, researchers still use sharp interface models as modeling tools (Park and Aral 2004; and Mantoglou and Papantoniou 2008; Koussis et al. 2012).

This paper extends the aforementioned works which combine sharp-interface models with optimization by developing an efficient coupling of steady-state sharp-interface simulation models with optimization algorithms. The approach of Mantoglou et al. (2004), based on the potential theory of Strack (1976), was adopted here; this approach has the advantage that it linearizes the steady-state unconfined solution of coastal aquifers. The approach considers the management problem involving decisions regarding pumping of the coastal aquifer. While sharp interface models are not as computationally demanding as variable density models, the computational runtime can significantly increase as the number of decision variables increases.

Prior to optimization, system matrices that describe the aquifer response to pumping are determined. The possible solutions are evaluated during optimization without assembling the system matrices again. This leads to fast convergence to the optimal solutions. In addition, if there is available computer memory, the system matrix can be decomposed before optimization, which has the advantage of accelerating the optimization search. In this work, the covariance-matrix-adaptation evolution strategy (CMA-ES; Hansen and Ostermeier 2001; Hansen et al. 2003) was selected to perform the optimum search; however, any optimization algorithm can be also used. The method is applied to the main aquifer of the Greek island of Santorini with very good results.

The paper is divided into five sections. The second section outlines the sharp interface simulation model, the optimization algorithm, and the proposed efficient coupling between these two components. The third section presents an application of the method to the Santorini aquifer. The small execution times based on the proposed framework allowed for the performance of an extensive sensitivity analysis on the impact of the grid size on the optimum solution is presented in the fourth section. The last section summarizes the findings of this study.

Simulation-optimization framework

The study examines a common problem that is encountered in coastal aquifer management. As the groundwater resources are quite limited, it is desirable to maximize the total water pumped from the aquifer, while protecting the aquifer from seawater intrusion. The maximization of pumping capacity is a typical optimization problem in which the pumping rates are used as decision variables. Mathematically the problem can be formulated as follows:

$$ \underset{Q}{ \max }f(Q) = {\displaystyle \sum_{i=1}^{N_{\mathrm{w}}}}{Q}_{\mathrm{i}} $$
(1)

Subject to:

$$ {g}_{\mathrm{i}}(Q)>{b}_{\mathrm{i}} $$
(2)

where Q i is the pumping rate of the i ∈ [1, …, N w] well, g i is a set of constraint functions that express in mathematical terms the environmental criteria which are used to protect the aquifer from seawater intrusion and b i are constraint values that impose limits on the environmental criteria.

Functions g i can take various expressions. Many researchers use constraint functions which express salt concentrations. In that case, the constraints ensure that the extracted water meets certain quality standards such as the maximum salt limit. Other forms impose geometrical constraints that inhibit seawater encroachment. For example, Mantoglou et al. (2004) and Park and Aral (2004) set criteria that do not allow the toe of the seawater wedge to approach the wells closer than a specified distance. In Kourakos and Mantoglou (2009), the constraint function did not allow the seawater interface to approach the bottom of the well screen based on a specified threshold.

Calculation of the objective function (Eq. 1) is straightforward as it involves the summation of the well pumping rates. Constraints (Eq. 2) require an evaluation of the environmental constraint functions. To this end, simulation models are typically used to simulate the aquifer response and subsequently the constraint criteria as a function of pumping rates Q i generated by the optimization algorithm.

In the following section, an outline of the seawater intrusion model chosen for this study is provided, followed by the description of the optimization algorithm. The last subsection describes an efficient coupling between these two components.

Coastal aquifer model

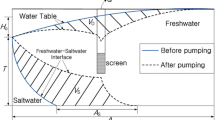
Most sharp interface models are based on the Ghyben-Herzberg assumption, which states that the seawater–freshwater interface below mean sea level, is approximately 40 times the groundwater head above mean sea level. Based on this principle, Mantoglou et al. (2004), and Mantoglou and Papantoniou (2008) developed a steady-state sharp-interface seawater-intrusion model suitable for single-layer unconfined aquifers. The aquifer is divided into two zones where zone 1 contains freshwater only, while zone 2 extends from the toe of the seawater edge to the seawater boundary (Fig. 1). By applying the Strack (1976) transformation, the governing equation in both zones is expressed by:

$$ \frac{\partial }{\partial x}\left({K}_x\frac{\partial \phi }{\partial x}\right) + \frac{\partial }{\partial y}\left({K}_y\frac{\partial \phi }{\partial y}\right) + {Q}_{\mathrm{s}} = 0 $$
(3)

where ϕ is the flow potential (see Strack 1976), K x , K y are components of the hydraulic conductivity tensor aligned with the principal axis x, y, and Q s represent the sources and sinks (e.g., groundwater recharge pumping rates). To obtain the hydraulic head distribution, the flow potential is converted to equivalent head using a different analytic relation for each zone as follows:

$$ \left.\begin{array}{cc}\hfill h=\sqrt{2\phi +\left(1+\delta \right){d}^2} - d,\hfill & \hfill \mathrm{zone}\ 1\hfill \\ {}\hfill h=\sqrt{\frac{2\delta \phi }{1+\delta }},\hfill & \hfill \mathrm{zone}\ 2\hfill \end{array}\right\} $$
(4)

where h is the hydraulic head measured from the sea level, δ expresses the relative density of seawater δ = (ρ s − ρ f)/ρ f, where ρ s, and ρ f are the densities of seawater and freshwater respectively, and d is the depth of the aquifer measured from the mean sea level. Finally, the hydraulic head of zone 2 can be used to calculate the elevation S of the seawater–freshwater interface based on equation S(x, y) = [msl(x, y) − h(x, y)/δ], where msl is the elevation of mean sea level (typically msl = 0) and h(x, y) is the hydraulic head at location (x, y) calculated by Eq. (4).

Fig. 1
figure 1

Typical cross-sections of coastal aquifers. a Coastal aquifer with bedrock. b Coastal aquifer without bedrock, where the freshwater floats above the seawater

Full size image

For a given set of decision variables, this model can be utilized for the prediction of the location of the interface between seawater and freshwater. In this case, the environmental criteria are described in geometrical terms since the model does not compute concentrations. In the application for Santorini Island, the constraints required that the distance between the bottom perforation of the wells and the sharp interface is greater than a specified distance (see also Kourakos and Mantoglou 2009). This formulation is applicable only for non-fully penetrated wells and allows the toe of seawater edge to move below the screen as shown in Fig. 1b. Note also that it is possible that the coastal aquifer consists only of one zone. In that case, the equations related to the freshwater zone are neglected.

Optimization algorithm

The second component of the simulation-optimization methodology is the optimization algorithm. Various optimization algorithms have been used for management of coastal aquifers. While local optimization methods are useful in relatively simple case studies, in general, global optimization methods such as evolutionary algorithms are typically preferred although they require a large number of objective function evaluations to converge to the optimum solution. This paper combines the coastal aquifer simulation model with a relatively new evolutionary optimization algorithm known as the covariance-matrix-adaptation evolution strategy (CMA-ES), which was developed by Hansen et al. (1995) and Hansen and Ostermeier (1996) and is suitable for difficult non-linear non-convex optimization problems in continuous domains. The flowchart of the CMA-ES algorithm is simple and similar to other evolutionary algorithms. The algorithm starts by initializing a number of parameters such as the population number λ, the number of points for recombination μ, the step size σ, the covariance matrix C (which commonly is initialized to the identity matrix), parameters p σ and p c (which are known as evolution paths) and an initial mean x 0m . The next step is the selection of λ independent individuals by sampling a multivariate normal distribution, i.e., \( {x}_{\mathrm{i}}^{g+1} = {x}_{\mathrm{m}}^g+{\sigma}^g\mathcal{N}\left(0,{C}^g\right) \). The i = [1 … λ] individual x gi of each generation g are evaluated based on the objective and constraint functions. The constraint functions require a model execution to return their outcomes. Next, a new mean is calculated based on the weighted objective function measure of the μ best out of λ individuals using user-defined weights w i. Using the updated mean, the evolution path p σ for the step size σ is first updated:

$$ {p}_{\upsigma}=\left(1-{c}_{\mathrm{s}}\right)\ {p}_{\upsigma}+\sqrt{c_{\mathrm{s}}\left(2-{c}_{\mathrm{s}}\right){\mu}_{\mathrm{w}}}{C}_{\mathrm{g}}^{-1/2}\frac{m_{\mathrm{g}+1}-{m}_{\mathrm{g}}}{\sigma_{\mathrm{g}}} $$
(5)

where c s is a constant that controls the update rate of evolution path p σ, μ w is a coefficient that controls the effectiveness of variance, and σ g is a step size, which is initially defined by the user and updated by the algorithm. m g + 1, m g are the mean vectors at generation g + 1 and g, respectively, and C −1/2g is the square root of the inverse covariance matrix. Next the evolution path for the covariance is computed as:

$$ {p}_{\mathrm{c}}=\left(1-{c}_{\mathrm{c}}\right){p}_{\mathrm{c}} + {1}_{\left[0,\upalpha \sqrt{n}\right]}\left(\left\Vert {p}_{\mathrm{s}}\right\Vert \right)\sqrt{c_{\mathrm{c}}\left(2-{c}_{\mathrm{c}}\right){\mu}_{\mathrm{w}}}\frac{m_{\mathrm{g}+1}-{m}_{\mathrm{g}}}{\sigma_{\mathrm{g}}} $$
(6)

where c c is a constant (similar to c s) which controls the update rate of the evolution path p c, and \( {1}_{\left[0,\upalpha \sqrt{n}\right]} \) is the indicator function that returns one if ‖p s‖ < \( \alpha \sqrt{n} \) or zero where n is the number of decision variables. After the updates of the evolution paths, the covariance matrix is computed:

$$ {C}_{\mathrm{g}+1} = \left(1-{c}_1-{c}_{\upmu\ }\right){C}_{\mathrm{g}}+{c}_1\left[{p}_{\mathrm{s}}{p}_{\mathrm{s}}^T+\left(1-{1}_{\left[0,\upalpha \sqrt{n}\right]}\left(\left\Vert {p}_{\mathrm{s}}\right\Vert \right)\right){c}_{\mathrm{c}}\left(2-{c}_{\mathrm{c}}\right){C}_{\mathrm{g}}\right]+{c}_{\upmu}{\displaystyle \sum_{i=1}^{\mu }}{w}_{\mathrm{i}}\frac{x_{\mathrm{i}:\lambda }-{m}_{\mathrm{g}}}{\upsigma_{\mathrm{g}}}{\left(\frac{x_{\mathrm{i}:\lambda }-{m}_{\mathrm{g}}}{\sigma_{\mathrm{g}}}\right)}^T $$
(7)

where c 1, c μ are the learning rates for the rank-one and rank-μ update of the covariance matrix respectively. Finally, the step size σ is updated as follows:

$$ {\sigma}_{\mathrm{g}+1} = {\sigma}_{\mathrm{g}} \exp \Big(\frac{c_{\upsigma}}{d_{\upsigma}}\left(\frac{\left\Vert {p}_{\mathrm{s}}\right\Vert }{E\left\Vert N\left(0,I\right)\right\Vert }-1\right) $$
(8)

Where d σ is a dumping factor commonly chosen very close to one and E‖N(0, I)‖ is the expected value of the norm of a vector with n elements normally distributed with zero mean and one standard deviation. The updated covariance matrix is used to select the new population, and the process is repeated until certain criteria are met.

Efficient coupling of simulation and optimization components

The coupling of simulation models with optimization algorithms is an important part of the overall process, especially when the objective and/or constraint function evaluation requires the solution of a numerical model. In groundwater optimization studies, the majority of numerical codes are used as black box models where users communicate the data between the optimization algorithm and the simulation model using intermediate input–output files. In such cases, the users modify the input files before model execution, e.g., writing the new set of pumping rates. Next, the model reads the input data, assembles the system matrices, solves the system of equations and prints the output to a file. Finally the user reads the model output files which are used to evaluate the objective and constraint functions.

This paper proposes an efficient coupling scheme where the majority of the aforementioned processes required by each model run can be avoided. The proposed method can be applied when the following conditions are valid:

  1. 1.

    The first condition requires linearity of the numerical model. Following discretization into a mesh of nodes, the discretized partial differential equation is written as a system of linear equations in the form of AX = b where X are the piezometric heads or potential. When system matrix A is independent of X, the model is characterized as linear. For example, the equation describing steady-state groundwater flow in confined aquifers is linear, while the equation describing unconfined aquifer flow is non-linear.

  2. 2.

    The second condition requires that decision variables have an impact only on the right hand side b of the preceding equation. In groundwater problems, the right hand side depends on various stresses such as pumping rates and groundwater recharge.

Under the aforementioned conditions, it is possible to implement numerical factorization of matrix A before the optimization phase. Using factorization, matrix A is decomposed into a product of matrices. In LU factorization, matrix A is decomposed to a lower L and upper U triangular matrices so that A = LU. Then the linear system can be solved as L(UX) = b and UX = L − 1 b. This approach avoids the computation of the inverse matrix A − 1, and the solution requires fewer forward substitutions.

The methods based on matrix factorization fall into the category of direct solvers and can be used for problems up to a few hundred thousands of degrees of freedom. Therefore, the proposed coupling scheme is limited to such problems which can be solved using direct solvers.

The method is described as follows. First, the modeling domain is discretized into a grid and the left hand side system matrix A is assembled. Next, matrix A is factorized. This is time intensive, yet this step is executed only once. A weakness of such procedure is that the decomposed matrices are no longer sparse and the memory requirements can be very high. This can be alleviated by taking advantage of recent software developments based on parallel factorization methods.

Following factorization, the optimization method generates candidate solutions which are evaluated by the numerical model. Based on the second problem condition, the decision variables modify only the right hand side vector b of the system. Evaluation of b is very fast and for a particular value of b the system can be solved rapidly using the decomposed matrices. Depending on the problem, different optimization techniques can be used to accelerate convergence—see section ‘Assessment of method in terms of computational cost’.

The proposed coupling scheme eliminates unnecessary writing and reading of input files and does not require assembly of the system matrix multiple times. The simulation step using the decomposed matrices is generally faster compared to iterative methods based on the conjugate gradient method regardless of the preconditioner. This method requires explicit compilation of system matrix A and vector b. Some popular simulation packages such as MODFLOW (Harbaugh 2005), FEFLOW (Trefry and Muffels 2007), HydroGeoSphere (Brunner and Simmons 2012), and SUTRA (Voss and Provost 2002) do not provide access to system matrices so they cannot be utilized in this method. Simulation package such as COSMOL (Li et al. 2009), and numerical libraries deal.II (Bangerth et al. 2013), libMesh (Kirk et al. 2006) and mSim (Kourakos and Harter 2014), on the other hand, can directly provide these matrices or the users can write code at the system level in order to compile these matrices.

The proposed method requires significant user involvement in the numerical computations of the simulation model. Another difficulty is that the two components, i.e., simulation and optimization, are no longer independent because the optimization code has to directly communicate with the numerical modeling code. However, when the two components are developed on the same or compatible programming platforms, this does not impose a problem.

Assessment of method in terms of computational cost

The proposed method, based on the coupling scheme, is applied to a coastal aquifer on the island of Santorini, Greece. Kourakos and Mantoglou (2009) developed a multilayer variable density model for this aquifer yet the aquifer parameters are uniform across the layers. Here, a single-layer sharp-interface model is developed and used instead.

The porous medium of the aquifer consists primarily of volcanic material. The north and south boundaries of the domain are considered impermeable, while the east and west are seawater boundaries with zero constant head. The distribution of hydraulic conductivity and recharge (Fig. 2) is based on a previous study (Mantoglou and Giannoulopoulos 2004). Although the following analysis is based on a real aquifer, the developed aquifer model is treated as a complex hypothetical simulation model rather than a real management case study.

Fig. 2
figure 2

a Study location: the Greek island of Santorini. b Simulation domain outline and boundary conditions. c Hydraulic conductivity distribution. d Groundwater recharge distribution

Full size image

The mSim toolbox (Kourakos and Harter 2014) is used for the simulation of seawater intrusion. mSim is a suite of MATLAB functions for simulation of groundwater flow and contaminant transport. It allows users to access the system matrix; therefore, it is suitable for implementation of the proposed coupling scheme. In addition, a large number of optimization algorithms already exist in MATLAB, which helps to avoid communication issues that could arise when different platforms are used for each simulation-optimization component.

Different meshes, consisting of triangle elements of variable size, are chosen for discretization of the aquifer. The meshes are generated using Gmsh code (Geuzaine and Remacle 2009). Initially, 10 different meshes were generated. Eight meshes were generated using approximately uniformly distributed size elements across the domain with largest element size equal to {200, 150, 100, 75, 50, 30, 15, 10} m. Two additional meshes were generated that have 10 m largest element size with a refinement near the well locations of 1 and 0.1 m respectively. Overall, the coarsest mesh consists of 1,194 nodes, while the finest mesh consists of 643,525 nodes.

In order to compare the proposed coupling scheme with standard methods, where coupling is achieved with the help of intermediate input and output files, nine simulation models are developed based on MODFLOW (Harbaugh 2005). For each model, uniform grids were used with sizes of {200, 150, 100, 75, 50, 30, 20, 15, 10} m. The models were developed using the ModelMuse interface (Winston 2009).

Note that MODFLOW is based on the finite difference method and the well pumping rates are applied to the center of the cells containing the wells. In mSim, based on finite elements, the wells are treated as point sources and the rates are applied to the nearest mesh node for each well.

This study examines the maximization of pumping rates from 41 wells with fixed well locations. The CMA-ES algorithm is used for optimization. The population of CMA-ES is calculated using the formula λ = 4 + ⌊3 log(n)⌋ where n = 41 is the number of decision variables. All runs started with zero initial decision variables and are terminated after 120,000 function evaluations. Note that this is unnecessarily large in practice and it is selected to ensure that all runs have fully converged.

In pumping maximization with fixed well locations, the mesh nodes and the assignment of wells to the nodes remain unchanged during optimization. This aids assembling system matrices during optimization as the new stresses are assigned directly to the right hand side without a need to reassemble it. This led to additional reduction of total optimization time. As expected, the optimization time increases linearly as the degrees of freedom (dof) of the problem increase (Fig. 3).

Fig. 3
figure 3

Comparison between the efficient simulation-optimization coupling (mSim) with the typical coupling using files (MODFLOW). The mSim optimization times are based on the SuperLU solver

Full size image

For the coarsest problem with 1,194 and 1,449 dof for the mSim and MODFLOW, respectively, each function evaluation takes approximately 3.6 × 10−4 and 5 × 10−2 s, respectively, which results in a total optimization time on the order 43 s when the proposed efficient coupling is used and 1.6 h when the standard coupling is used. The finest mesh of the mSim model consists of 643,525 nodes, while the MODFLOW grid consists of 576,925 grid cells. Each function evaluation using MODFLOW takes up ∼16 s while in mSim takes only 0.47 s. This results in an overall optimization time after 120,000 function evaluations on the order of 15.89 h using efficient coupling and 548 h when standard coupling without matrix factorization is used.

Next, various packages are tested in order to investigate their efficiency in solving the linear system Ax = b pertinent to this case study. Solution of linear systems of equations has been the focus of research for at least a century. Recent hardware and software developments have resulted in the development of several numerical libraries which solve linear systems Ax = b. This paper tests the Amesos (Sala et al. 2008) package of the Trilinos project (Heroux et al. 2003), which provides an object-oriented interface to several direct solvers. Four direct solvers were considered, namely KLU (Davis and Palamadai Natarajan 2010), SuperLU (Xiaoye 2005), UMFPACK (Davis 2004) and LAPACK (Anderson et al. 1999). In addition, the direct solvers were compared with the iterative preconditioned conjugate gradient (pcg) solver, using a smoothed aggregated multilevel preconditioner (Gee et al. 2006). Solution of the linear system is divided into two phases. First the system is factorized, which is executed once at the beginning of the optimization. In the case of the iterative pcg solver, this step involves preparation of the multilevel preconditioner. Next, the system is solved using the factorized matrices. Among the selected direct solvers, LAPACK is designed for dense matrices and, therefore, is the least efficient. In fact, for systems with more than 17,000 dof, LAPACK was unable to complete the numerical factorization.

Direct solvers designed for sparse systems appeared significantly faster compared to the iterative pcg solver. In particular, for all simulations setups, the direct solvers (Fig. 4, colored dashed lines) appear 84–95 times faster compared to the iterative solver (Fig. 4, black dashed line). On the other hand, the factorization appears to be a more cpu-time-consuming process compared to the multilevel preconditioner setup (see Fig. 4, solid lines). Nevertheless, this refers to the preparation step that is executed only once during optimization and this time is minimal compared to the overall optimization time. Among the direct solvers, SuperLU, which was designed for symmetric and positive definite systems, was found superior compared to KLU and UMFAPCK in both factorization and solve time.

Fig. 4
figure 4

Comparison of different direct solvers. For the AMG solver the prepare ML refers to the calculation of the multilevel preconditioner

Full size image

Next, eight additional meshes were generated with dof equal to {421,506; 519,196; 657,616; 860,792; 1,172,548; 1,683,548; 2,634,798; 4,683,754}. These meshes were used to examine the potentials of using multiple processors for the solution of the linear system. Each system was solved on 2, 4, 8, 16, 32, 64, and 128 processors using the KLU, SuperLU and UMFPACK solvers (Fig. 5). The factorization procedure using the UMFPACK solver was faster compared to the two other solvers; however, the procedure failed for systems larger than 1.7 million dof due to insufficient memory. On the other hand, SuperLU and KLU solvers were able to factorize all tested systems. Note that the largest system was approximately 4.7 million dof. SuperLU was found faster in this application compared to KLU solver in all cases. The factorization time for systems less than a million dof is less than a minute, while ∼16 min was required for a system with 4.7 × 106 dof. Nevertheless, factorization is executed only once and 16 min can be regarded as acceptable time. While UMFPACK factorization was faster, the solve step was the slowest compared to other two solvers. SuperLU was found to be the best option, as it consistently required the least time for solving the linear system. The most time-consuming case, with 4.7 × 106 dof, was solved in approximately 3 s. Factorization is generally a cpu-memory-consuming operation and a multi-core solution can be used at the expense of increased cpu time, due to the communication requirements between processors. However, one can see that all tested libraries provide very efficient scaling with the number of processors. In most cases the additional computational burden due to the use of more processors is on the order of 1–5 %.

Fig. 5
figure 5

a Factorization time. b Solve time

Full size image

Impact of discretization size

Taking advantage of the small execution time attained by the efficient coupling scheme, a further analysis was performed to investigate the impact of discretization size on the pumping rates from the pumping wells. Due to the random nature of the evolutionary algorithm, the optimization was run 100 times to obtain the average predictions of the method as function of the mesh element size.

The dependence of the total maximum pumping rate on the element size is shown in Fig. 6. Note that as the element size decreases, the maximum pumping rate is initially increased. This is because when very large elements are used, it appears that more than one well is assigned to the same node of the mesh, which has the effect of reducing the number of decision variables; thus, the solution is less optimal due to loss of flexibility.

Fig. 6
figure 6

Total maximum pumping rate as function of mesh element size

Full size image

This trend is reversed for grids with element size smaller than 100 m. In this case, all wells are assigned to different mesh nodes and one observes that the maximum extraction rate decreases as the element size decreases. In this case, as the elements become smaller, the cone of depression is approximated more accurately and the up-coning appears spikier. In Fig. 7, the interface is plotted that corresponds to the optimum solution obtained by an average element size of 15 m. According to the constraints, most of the spikes in Fig. 7c reach (without exceeding) the level of −10 m below msl. The other parts of Fig. 7 show the shape of the interface when different meshes are used to evaluate the optimum solution obtained by the 15-m-average element size. For example, when the 100 and 50-m-average element sizes are tested, the peaks of the spikes appear significantly lower than the −10 m elevation because of the coarse discretization. Therefore, the solution appears suboptimal when evaluated on coarser meshes. On the other hand, when a finer mesh is tested, most of the constraints are violated. Figure 7d shows the spikes which represent the up-coning of seawater intrusion. The majority of the spikes exceed the level of −10 m below msl and, therefore, violate most of the constraints.

Fig. 7
figure 7

Seawater–freshwater sharp interface on various grids. The optimum solution based on the 15-m average element size grid has been evaluated on other grids. The solution appears less optimal on grids with smaller elements, while violating the constraints on grids with smaller elements. Element sizes: a 100 m, b 50 m, c 15 m, and d 10 m

Full size image

To reduce the dependence of the optimization result on the grid size, the next stage was to examine the possibility of introducing a distance parameter from the center of the well where the constraints are evaluated. Note that in analytical models such as Strack (1976), Mantoglou (2003), etc., this distance parameter is taken as the radius of the well, since the equations are not defined on the centers of the wells. This paper evaluates the constrains of the optimization problems by taking the average elevation of the interface between freshwater–seawater of m points around the wells at distance d. While Strack (1976) and Mantoglou (2003) take this distance as the radius of the well, in the application reported here, 10 logarithmically distributed values of distance d, between [0.01, 10], were examined. The optimizations were repeated 100 times for grid sizes {100, 75, 50, 30, 15, 10} to obtain trends of average performance for these cases. For the coarser meshes, e.g. 100–50 m, the maximum pumping rate is relatively independent of distance d and the estimated pumping increases by approximately 1 % when the constrains are evaluated at a distance 10 m from the well center (Fig. 8).

Fig. 8
figure 8

Impact of distance from well center where the constraints are evaluated for different minimum element sizes

Full size image

On the other hand, for relatively fine meshes, the impact of the distance becomes a very important factor. For example, for the finest case where the minimum grid size is equal to 15–10 m, one observes that with a distance of 10 m, the optimization results are of a similar order to those obtained by the coarse mesh.

The preceding discussion illustrates the difficulty that may arise regarding coastal aquifer problems when choosing the appropriate discretization. A very fine discretization should not always be regarded as more accurate for coastal aquifers and can lead to underestimated extraction aquifer capacity. Coarse discretization on the other hand may lead to overestimation of the maximum pumping rate.

Conclusions

In this paper, an efficient coupling scheme is proposed that combines numerical simulation models with optimization algorithms for management of coastal aquifers. The proposed scheme is based on the premise that the numerical model is linear and the decision variables do not affect the matrix of the linear system. In such a case, both developing the simulation model, and arranging the system matrices before optimization, are proposed. In addition, for reasonable sized systems, e.g., less than 1 million dof, it is possible to perform factorization of the system matrix; hence, the model evaluation during optimization is much faster compared to iterative methods.

The method was applied to a case study in the main aquifer of Santorini. A sharp-interface numerical method was used for simulation of seawater intrusion, which has the advantage that it removes the non-linearity of the unconfined simulation. The numerical model was combined with a covariance-matrix-adaptation evolutionary-strategy optimization algorithm, which is suitable for non-linear optimization problems.

The proposed coupling method was compared with a typical coupling scheme where intermediate input/output files are used to communicate the numerical model with the optimization algorithm. The results showed that for each function evaluation, the proposed coupling requires 1–3 % of the time of the typical coupling scheme. In addition, several direct solvers were tested and it was found that the SuperLU direct solver method was the fastest in this application; the approach was able to couple very large numerical models up to ∼5 million dof with optimization without producing unrealistically high overall optimization times.

Finally, the small execution times allowed the study to run multiple optimizations to perform a sensitivity analysis of the effect of grid size on the optimal solution. The results show that the grid size is an important factor and the optimal solution can deviate considerably depending on different grids.