Experimental and numerical investigation of the compression and expansion of a granular bed of repelling magnetic disks

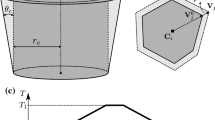
Abstract

We studied experimentally and numerically the compaction and subsequent expansion dynamics of a granular bed composed of cylindrical repelling magnets contained in a two-dimensional cell. The particles are firstly compressed vertically with a piston at a given strain rate until a maximum force is reached. The piston is then removed at the same strain rate while the bed expands due to the magnetic repulsion of the particles. In the experiments, two different initial configurations were generated, a standard and a loose packing bed. The standard packing bed was simulated, and modelling the dry friction between the magnetic particles and the walls of the cell was crucial for the correct description of the compression and expansion dynamics. We found that the force acting on the piston increases continuously and exponentially with the piston stroke during compression, being very sensitive to the initial packing conditions of the bed. In contrast, a history-independent exponential decrease of this force was found during the expansion phase. The hysteresis in the system was quantified in terms of the average displacement of the particles. The continuous compression contrasts with the sudden force drops observed during the compaction of granular materials with direct particle-particle contacts, where stick-slip motion is induced by friction and force chain breakage. Moreover, we found that the short range of magnetic interaction induces density inversion and crystallization of the system. Our results can be useful to develop a new kind of magnetic granular dampers.

Graphical abstract

1 Introduction

The compaction and relaxation response of a granular bed compressed vertically with a piston has been recently studied considering materials with different mechanical properties: rigid, brittle, elastic or hierarchical particles. For rigid glass beads [1,2,3], the force load required to compress the bed increases exponentially, with sudden drops due to stick-slip motion of the particles [2]. The magnitude of these force drops increases with the particle size [3], and the stress relaxation can be characterized by a fast exponential decrease followed by a slow long-time relaxation term [1, 3]. For brittle materials, like snow [4], porous carbonates [5] and cereals [6], propagation of upward compaction bands during vertical compression was reported experimentally, as a consequence of the breakage of particles at the bottom of the bed and further bed rearrangement. Numerical simulations were able to reproduce these propagation bands, and they were used to determine the role of the particle stiffness, elasticity and global damping on the resulting dynamics in terms of two dimensionless groups, the elasto-breakage and the visco-breakage numbers [7]. For the case of elastic particles (specifically, flexible rubber grains), the compression process is characterized by a smooth, rather than periodic, deformation process, with a pronounced compaction near the piston that gradually diffuses with depth [6]. On the other hand, for the case of hierarchical particles (dust conglomerates), a power-law increase of the force load with undulating fluctuations was recently found, which is followed by a continuous relaxation dynamics characterized by different time scales [2]. These undulations result from the combination of elasticity and brittleness of the particles. Extensive studies using different types of sands have been performed to clarify the role of particle rearrangement through interparticle slip and rotation and particle damage, including the yield stress, coefficient of lateral pressure, etc [8].

During vertical compression, the stress generated by the piston is propagated through the granular column primarily along force chains, until reaching the walls and bottom of the container. It is difficult to isolate the mechanism responsible for the sudden drops of the force load, generated by the combination of inter-particle friction, collective rearrangements, stick-slip motion and grain breakage. Here, we introduce a different kind of granular material composed of magnetic repelling grains [9,10,11]. With magnetic grains, the inter-particles contacts are totally suppressed and the interaction is mediated by the repulsive magnetic field. In this manuscript, we use this repelling granular material to test the effect of suppressing the interparticle contacts on the compression and expansion dynamics. We report that for this system the resistance to compression increases nearly exponentially with the piston stroke. Due to the magnetic repulsion, there is enough interstitial space to allow the rearrangement of particles, and sudden force drops or propagating bands are not detected during the compression phase. The results are largely independent on the compression rate. Moreover, we show that the force load during compression is sensitive to the initial packing conditions, but the expansion phase is history-independent, generating hysteresis in the system. A Maxwell model with two decaying exponential terms (with different time scales) is enough to describe the expansion phase. Experimental and numerical results are reported and compared. The observed dynamics resembles the smooth and continuous compression reported for rubber particles [6], reflecting the viscoelastic-like response previously reported for magnetic repelling grains under impact [11]. Our results suggest the possibility of developing two-dimensional magnetic granular dampers or flexible magnetic dampers based on the cell design and the repulsion mechanism reported here.

2 Experiments

A sketch of the experimental setup is shown in Fig. 1. A two-dimensional Hele-Shaw cell with transparent glass walls was fixed vertically and filled with $N=367$ Neodymium (NdFeB) cylindrical magnets of mass $m= 0.625$ g, thickness $\varepsilon =3$ mm, diameter $D=6$ mm, magnetic moment $\mu =0.06$ mAm$^2$ and magnetic field strength $H=5.9$ kG (measured at the surface of the disks according to the supplier [12]). The magnets were introduced into the cell with their magnetic dipoles oriented axially and perpendicular to the confining walls in order to obtain repulsive interaction between the particles. The inner space of the cell is 36 cm wide and 60 cm in height, but the magnets occupy only a fraction of the cell. A separation of $E = 3.1$ mm between the frontal and rear glass walls allows the free motion of magnets in the vertical plane and avoids the inversion of their dipoles. Without this restriction, the interaction between the particles would become attractive and would lead to the collapse of the magnetic bed. The upper wall consists of an acrylic piston that can move freely between the glass walls. This piston and the confining lateral walls are composed of bar magnets that also interact repulsively with the grains. The vertical motion of the piston was controlled using Labview and a step motor attached to a lead screw, which allows to convert the rotational motion of the motor into linear motion, to perform the experiments with four different piston speeds $v=1.47,~3.34,~5.63,~7.35$ and 8.33 mm/s. Each experiment is divided in two phases: compression and expansion. For the compression phase, the piston starts descending from 45 cm above the bottom of the cell at time $t=0$ s, and it stops when the piston stroke, $y_P = v t=33$ cm (i.e. at 12 cm above the bottom of the cell). The level of the granular bed before and after compression is indicated by $y_0$ and $y_F$, respectively, in Fig. 1. So, when $y_P$ approaches $y_0$, the bed starts to feel the compression. This phase lasts until $y_P=y_F$. After that, the piston starts to ascend at constant speed $-v$ until it reaches its initial position. This second part corresponds to the expansion process. The force $F(y_P)$ acting on the piston during the compression and expansion phases was measured using a S-shape load sensor (located between the piston and the step motor) and acquired using a data acquisition system (DAQ) at 100 Hz. Frontal-view videos were taken at 60 fps, and ImageJ was used to determine from these videos the trajectories and the rearrangement of the particles.

Fig. 1

Experimental setup: magnetic repelling particles confined in a Hele-Shaw cell are compressed with a piston at a constant rate v. The initial height of the bed is $y_0$ and it is compressed until reaching $y_F$. The resistance force acting on the piston $F(y_p)$ is measured with a load cell and acquired with a DAQ

To prepare the magnetic bed and avoid history effects, the complete system is turned upside down before each experiment to distribute the grains in the opposite side of the cell, and then suddenly returned to its vertical position. The grains fall under gravity and form a packed bed with initial density of particles of $0.36 \pm 0.02$ magnets/cm$^2$, in a layer of $\sim 28$ cm of height. This bed configuration is called in the following standard packing bed. We also explored a looser configuration obtained by slowly turning upside down the cell at $\sim \pi /10$ rad/s until the disks start to slide from the upper part to the lower part of the cell, which results in a density of $0.21 \pm 0.02$ magnets/cm$^2$ that corresponds to a layer of $\sim 45$ cm of height. From now on, we labelled this second initial configuration as loose packing bed. A more conventional parameter to characterize the density of a two-dimensional granular system is the mean area fraction, $\phi = N A_p/A_c$, defined in this case as the ratio of the area occupied by the N cylindrical magnets of individual area $A_p=\pi D^2/4$ and the available cell area below the piston, $A_c= [36(45-y_P)$] cm$^2$. The initial values of the area fraction are $\phi _{std} \approx 0.11$ and $\phi _{loose} \approx 0.061$ for the standard and loose packing beds, respectively, and these values increase until the final average value $\phi _{max} \approx 0.24$ at the maximum piston stroke. This point corresponds to a maximum density of $0.84\pm 0.02$ magnets/cm$^2$. It is important to remark the very low values of $\phi$ in our system due to the repulsive interaction of the disks, in comparison to the average values expected in two dimensional granular packings with standard non-repelling particles ($\phi >0.60$) [13, 14].

Fig. 2

Snapshots showing the compression and expansion of magnetic repelling grains for two initial conditions of packing fraction: a Standard packing and b Loose packing. c-d Local area fraction profiles obtained from the snapshots shown above. The profiles indicate the area occupied by particles in a row at a given depth y. Note the density inversion observed close to the piston at the maximum compression

3 Experimental results

Snapshots showing the compression-relaxation process for the two initial configurations, standard and loose packing beds, are shown in Fig. 2a and b, respectively. The blue arrows in each snapshot indicate the direction of the piston displacement. In Fig. 2a, it can be noticed that the final state after expansion is very similar to the initial configuration. Nevertheless, for the loose packing bed in Fig. 2b, the grains in the final configuration are considerably more packed than in the initial loose packing state. In fact, this final configuration is practically identical to the one obtained in the standard packing bed. It can be noticed that after reaching the maximum compression, the expansion process is practically the same regardless of the system history. In Fig. 2c and d, we show the local area fraction $\phi _l$ for the standard and loose packing beds, respectively; $\phi _l$ was obtained from the ratio of the area occupied by the magnets in a horizontal narrow band at a given depth y and the total area of the band, determined from the corresponding snapshots in Fig. 2a-b using the software ImageJ. Note that at the beginning of the process the density profile displays a nearly linear dependence with depth (hydrostatic) for the standard packing bed, whereas for the loose packing bed the area fraction is basically constant. The observed oscillations in these profiles indicate that the grains are arranged mostly in rows. During compression, the concentration of magnets only increases at the upper part of the bed due to rearrangements close to the piston, whereas the configuration of grains at the bottom of the bed remains unchanged. This generates a density inversion, with a smaller density at the center of the cell. This can be clearly observed at the maximum compression (central plot in each case). The density inversion is a consequence of the short range of the magnetic interaction and friction with the glass walls. During the expansion phase, the density of grains at the upper part of the cell decreases again, and the final profile looks hydrostatic in both cases.

Fig. 3

Average displacement of the magnets d (in diameters) as a function of the piston position $y_p$ for a standard and b Loose packing conditions. c Snapshot showing the paths of particles during the compression-expansion process. d Mean distance ${\hat{D}}$ between particles normalized by the particle diameter during compression and expansion for the standard (red) and loose (blue) packing beds. The minimum occurs at the maximum compression in each case. Note the same trend for both packing conditions after maximum compression

Although we could expect equilibrium configurations in our system similar to the gravity rainbows produced by magnetized steel spheres [15, 16], the friction between the magnetic disks and the frontal and rear walls plays an important role, avoiding the formation of strictly conformal crystals. In fact, the unstable initial loose packing configuration and the difference between initial and final arrangements are mainly due to friction. This hysteresis during the compression-expansion cycle can be quantified by evaluating the net displacements of the particles. We define the instantaneous average horizontal net displacement of the particles as

$$\begin{aligned} \langle \Delta x \rangle (t) = \frac{1}{N}\sum _{j}\Big [{x_j(t)-x_j(0)}\Big ], \end{aligned}$$

(1)

where $x_j(0)$ is the horizontal coordinate of particle j at the beginning of the compression, $t=0$. Similarly, we define the instantaneous average vertical net displacement of the particles as

$$\begin{aligned} \langle \Delta y \rangle (t) = \frac{1}{N}\sum _{j}\Big [{y_j(t)-y_j(0)}\Big ], \end{aligned}$$

(2)

and the instantaneous average total net displacement of the particles as

$$\begin{aligned} \langle \Delta r \rangle (t) = \frac{1}{N}\sum _{j}{\vert \mathbf{r}_j(t)-\mathbf{r}_j(0)\vert }, \end{aligned}$$

(3)

where $\mathbf{r}_j = (x_j,y_j)$ is the 2D vector denoting the position of the particle j.

We plotted in Fig. 3a-b the average displacement of the particles with respect to their initial positions as a function of $y_P= vt$ for the case $v=8.33$ mm/s. In these plots, d represents the respective displacement normalized with the particle diameter. For the standard bed, the magnets reach a maximum displacement $\langle \Delta r \rangle \approx 9$, while for the loose bed $\langle \Delta r \rangle \approx 24$. This displacement is basically along the vertical direction ($\langle \Delta y \rangle$), whereas the grains are only displaced by approximately one diameter from their initial positions in the horizontal direction ($\langle \Delta x \rangle$). This is confirmed in the snapshot of Fig. 3c, which shows the paths of the particles during one cycle. Note that the particles at the bottom have negligible displacements, and only small deviations from vertical trajectories are observed. The net average displacement of the particles at the end of the process is $\langle \Delta r \rangle \approx 2$ for the standard case, and $\langle \Delta r \rangle \approx 17$ for the loose case, reflecting the considerably larger hysteresis for the latter case. Therefore, as we increase the initial packing fraction, hysteresis decreases.

Another way to assess the hysteresis of the system is to determine the instantaneous mean inter-particle distance, defined as

$$\begin{aligned} {\hat{D}}(t) = \frac{1}{N(N-1)} \sum _{i} \sum _j \vert \mathbf{r}_i(t)-\mathbf{r}_j(t)\vert . \end{aligned}$$

(4)

Figure 3d shows ${\hat{D}}$ given in Eq. 4, as a function of $y_P$. Although the initial values of ${\hat{D}}$ are very different, the minimum of the curves for both packing conditions at the maximum compression $y_P= y_F=330$ mm coincide, and after this point ${\hat{D}}$ takes practically the same values for both processes. The more symmetric plot around $y_P= 330$ mm for the standard bed reflects less hysteresis in the system.

Fig. 4

$F/F_{max}$ vs $y_p$ measured during compression and expansion. The maximum compression corresponds to $F_{max}=24$ N. Results for the standard and loose packing bed are shown. Although the compression phase is sensitive to the initial packing condition, the expansion curves are superimposed, indicating a history-independent response for the expansion phase. The average area fraction is also indicated

Fig. 5

a $F/F_{max}$ vs $y_P$ for different compression speeds and for the two initial conditions of packing fraction. Here $F_{max}=24$ N. b $\ln F/F_{max}$ vs $y_P$ indicating an exponential dependence. c $F/F_{max}$ vs $y_P$ during the expansion process with piston velocity $v=8.33$ mm/s. The inset shows that the expansion process is well described by the Maxwell model with two different time scales (or length scales, since $\phi \propto y_p=vt$)

Figure 4 shows the force exerted by the magnets against the piston, F, normalized by the maximum force $F_{max}=24$ N reached at maximum compression ($y_F=330$ mm), as a function of $y_P$. Since the separation r between particles decreases as the piston descends, and considering that the magnetic force between two cylindrical magnets in our configuration is $F_{pp} \propto 1/r^4$, the resistance to compression F must increase with $y_P$. Note that $F/F_{max}$ increases faster for the standard case, although it starts growing after $y_P\approx 200$ mm, while for the loose case the force increases more slowly but starts from $y_P=0$. At the maximum compression, when the magnets adopt almost a hexagonal close packing configuration, the measured forces in both cases converge to the same value, $F_{max}= 24$ N. Then, $F/F_{max}$ decreases during the expansion process following the same trend for both cases, as a consequence of the history-independent process.

For the compression phase, Fig. 5a shows $F/F_{max}$ vs $y_P$ for different compression rates v (indicated by different colors) and for the two initial conditions of packing. Note that there is no significant effect of the compression speed on the measured force, at least in the range studied in this work (all the curves are superimposed for the same packing condition). This indicates that both the magnetic interactions among particles and the friction forces between the particles and the walls of the cell are not dependent on the velocity of the particles. Furthermore, at these low compression velocities, the particles have enough time to adjust to an instantaneous equilibrium.

The observed dependence suggests an exponential increase of $F(y_P)$. This is confirmed in Fig. 5b, where the compression force is well described by a relation of the form $F/F_{max} \approx A e^{(y_P-y_0)/\lambda }$, where $A=F/F_{max}(y_P=y_0)$ and $\lambda$ is a free characteristic length. The dotted lines correspond to the average fitting parameters $A=0.1, y_0=215, \lambda =37$ for the standard packing bed, and $A=0.1, y_0=113, \lambda =71$ for the loose packing bed. Note that $\lambda$ is considerably larger for the loose packing bed, indicating that the piston stroke required to reach a given force load is larger. On the other hand, Fig. 5c shows that during the expansion, the decrease of F is better described considering the Maxwell model with two exponential terms [3], in the form $F/F_{max} \approx A e^{(\phi -\phi _0)/\kappa _1} + B e^{(\phi -\phi _0)/\kappa _2}$; only one compression rate is shown because, as it was discussed above, the value of v is not relevant in the dynamics and neither is the initial configuration of the bed. Since $\phi$ decreases with time during expansion, the measurements indicate that the force on the piston decays exponentially in time, with two characteristic time scales: one short timescale that manifests itself in the early relaxation of the force, linked to the very fast relaxation of the particles once the expansion motion of the piston starts, and a longer timescale that governs the force relaxation to zero once the piston is moved far from the particles.

4 Numerical simulations

The system described above was simulated numerically using extensions of the models used in [10, 17]. The evolution of the system is determined by a set of N coupled equations that are obtained by applying Newton’s Second law of motion:

$$\begin{aligned} m\frac{d^2{\mathbf {r}}_i}{dt^2} = \mathbf{F}_M^i + \mathbf{F}_F^i + \mathbf{F}_g^i, \end{aligned}$$

(5)

where m denotes the mass of the particles, considered identical for all particles, ${\mathbf {r}}_i(t) = (x_i(t),y_i(t))$ their position, $\mathbf{F}_M^i$ the magnetic forces acting on particle i, $\mathbf{F}_F^i$ is the friction that opposes the motion of particle i and, finally, the weight $\mathbf{F}_g^i = m_i {{\mathbf {g}}}$ of particle i, with $|{\mathbf {g}} |=9.8$ m/s$^2$. The magnetic force $\mathbf{F}_M^i$ can be separated into two contributions: the particle-particle interaction, $\mathbf{F}_{pp}^i$, and the particle-walls interactions, $\mathbf{F}_{pw}^i$. Note that the rotation of the particles is not important in this system and, therefore, is neglected in this work. We describe, in the following, the magnetic and the friction forces that appear in Eq. 5.

4.1 Magnetic forces: particle-particle interactions

The particle-particle interactions are calculated considering that each particle j is a dipole with magnetic moment $\varvec{\mu }_j = \mu \varvec{\hat{\mu }}_j$, with $\mu = |\varvec{\mu }_j |$, taken to be identical for all particles j. Following [17, 18], the dipole-dipole magnetic force on the particle i caused by all the other j particles is given by:

$$\begin{aligned} \begin{aligned} {\mathbf {F}}_{pp}^i = \dfrac{3\mu _0\mu ^2}{4\pi r_{ij}^4} \sum _{j\ne i} \Big [&( {\hat{\mathbf {r}}}_{ij} \cdot \varvec{\hat{\mu }}_i ) \varvec{\hat{\mu }}_j + ( {\hat{\mathbf {r}}}_{ij} \cdot \varvec{\hat{\mu }}_j ) \varvec{\hat{\mu }}_i \\ + ( \varvec{\hat{\mu }}_i \cdot \varvec{\hat{\mu }}_j ) {\hat{\mathbf {r}}}_{ij}&- 5( {\hat{\mathbf {r}}}_{ij} \cdot \varvec{\hat{\mu }}_i ) ( {\hat{\mathbf {r}}}_{ij} \cdot \varvec{\hat{\mu }}_j ){\hat{\mathbf {r}}}_{ij} \Big ], \end{aligned} \end{aligned}$$

(6)

where $\mu _0$ is the vacuum magnetic permeability, ${\mathbf {r}}_{ij} = {\mathbf {r}}_i - {\mathbf {r}}_j$ represents the vector joining the centers of the particles, $r =|{\mathbf {r}}|$ and the unit vector ${\hat{\mathbf {r}}}_{ij} = {\mathbf {r}}_{ij}/r_{ij}$.

Since we consider a 2D configuration in which the magnetic moments of the particles are aligned perpendicularly to the plane of motion, ${\hat{\mathbf {r}}}_{ij} \cdot \varvec{\hat{\mu }}_j = 0 ~\forall ~i,j$ in Eq. 6. Then, the particle-particle magnetic forces are repulsive and, assuming that the magnetic particles are identical and possess the same magnetic moment $\mu$, they are simply given by:

$$\begin{aligned} {\mathbf {F}}_{pp}^i = \dfrac{3\mu _0\mu ^2}{4\pi } \sum _{j\ne i}\dfrac{{\hat{\mathbf {r}}}_{ij}}{r_{ij}^4}. \end{aligned}$$

(7)

4.2 Magnetic forces: particle-wall interactions

The magnetic forces that originate from the particle-walls interactions can be modeled from the magnetic interaction between an infinite magnetic bar and a point dipole. We assume that the infinite bar has a magnetic moment per unit length given by M and we further assume M is such that $M=\mu /D$, that is, an element of length equal to the particle diameter has the same magnetic moment intensity as one of the particles. A quick calculation reveals that, if we consider that particle i is separated from the wall j, with $j=$ left, right, bottom or top, by a distance $w_{ij}$ measured perpendicularly to the wall, then the particle-wall magnetic interaction is given by:

$$\begin{aligned} \mathbf{F}_{p{w}_{\infty }}^i = \frac{\mu _0\mu M}{\pi } \sum _{j} \frac{\hat{\mathbf {w}}_{ij}}{w_{ij}^3}, \end{aligned}$$

(8)

where $\hat{\mathbf {w}}_{ij}$ is the unit wall normal vector pointing towards the particle. Note that this force is the force expected when an infinite magnetic bar is interacting with a dipole. In our case, the walls are not infinite and, therefore, the interaction force in Eq. 8 gives an approximation of the real value of the force. In fact, the finite length of the magnet bars of the walls effectively changes the power law dependence of the force on the distance between the wall and the particles such that it can be different from 3, as well as changing the coefficient appearing in Eq. 8. Therefore, the particle-wall magnetic interaction can be given by a general law:

$$\begin{aligned} \mathbf{F}_{p{w}}^i = \frac{\mu _0\mu Mk}{\pi } \sum _{j}\frac{\hat{\mathbf {w}}_{ij}}{w_{ij}^{\alpha }}, \end{aligned}$$

(9)

where we assume $3< \alpha < 4$ for finite length bars (note that $\alpha =4$ comes from the dipole-dipole limit, as in Eq. 7), and where k is an adjustment factor of the coefficient. In this work, we have taken $\alpha = 3.5$ and $k=1/2$ as these were the values that best fitted the experimental results.

4.3 Friction forces

In the experiments, the motion of the particles in the Hele-Shaw cell is not frictionless. There is friction between the particles and the glass walls of the cell. This happens because the particles are (marginally) thinner than the gap between the walls and, therefore, they have room to tilt and touch the glass walls. Particles can tilt either because they are not perfectly homogeneous or due to local irregularities of the glass walls, for example. When the particles are touching the glass walls, their magnetic moment is no longer aligned perpendicularly to the wall and, therefore, they exert a non-zero torque on the other particles that can also make them tilt and touch the glass walls. The friction between the particles and the glass walls slows the particles down and dissipates kinetic energy and, therefore, has to be considered in order to accurately describe the behavior of the system. In this work, we consider two different friction models: the first one is a linear viscous damping force, proportional to the velocity of the particles, and the second one is a dry friction model that is independent of the particle velocities that also tries to resolve the static/dynamic transition of the motion of the particles more accurately.

4.3.1 Viscous friction force

This model, which was used in our previous works [9, 10], assumes that the friction force is proportional to the velocity of the particle and that opposes its motion. Therefore, we have that:

$$\begin{aligned} \mathbf{F}_F^i = - \gamma _v \mathbf{v}_i, \end{aligned}$$

(10)

where $\mathbf{v}_i = d\mathbf{r}_i/dt$ is the velocity of the particles and $\gamma _v$ is the viscous friction coefficient. We note that this viscous friction model is directly dependent on the velocity of the particles. Therefore, the consequence is that there will be a dependence of the results on the speed of compression and expansion of the bed, which was not observed in the experiments. However, because of the simplicity of this model, and its success in other similar problems, we have decided to test it in our model.

4.3.2 Dry friction force

The viscous friction model is a phenomenological model that includes a resistance to motion and energy dissipation. However, it is unable to capture the static-dynamic transition of the initiation of the motion of particles at rest and, most importantly, it does not provide a velocity independent friction force. We have chosen, therefore, to implement a dry friction model based on the regularized Coulomb model as proposed in [19, 20]. In this model, the friction force is given by

$$\begin{aligned} \mathbf{F}_F^i = \left\{ \begin{array}{l} -{\mathbf {F}}_T^i, ~~~\text {if } |{\mathbf {F}}_T^i |\le \mu _e N_i ~~\text {and} ~~|\mathbf{v}_i|< v_t\\ \qquad \\ -\mu _d N_i\dfrac{\mathbf{v}_i}{|\mathbf{v}_i|}, ~~~\text {otherwise}\\ \end{array}\right. , \end{aligned}$$

(11)

where ${\mathbf {F}}_T^i = {\mathbf {F}}_M^i + {\mathbf {F}}_g^i$, $\mu _e$ and $\mu _d$ are the static and dynamic friction coefficients, respectively, and $N_i= \vert \mathbf{N}_i \vert$ is the normal force acting on the contacts of the particles with the walls. Furthermore, $\mathbf{v}_i$ is the velocity of the particle i and $v_t$ is a small number that is used to characterize that the motion of the particle is negligible. In the numerical implementation of the second condition, $v_t$ is added to the denominator to avoid a potential division by zero.

Fig. 6

Schematic diagram of a magnetic disk of diameter D and thickness $\varepsilon$ tilted between the glass walls of the cell separated by $E > \varepsilon$. The particle’s tilt (here exaggerated for clarity) is generated by the torque produced by the rest of the magnets on the disk, producing two contact points $P_1$ and $P_2$ between the disk and the glass walls

The calculation of the normal force ${\mathbf {N}}_i$ involves the geometry of the system, as described in Fig. 6. The angle $\varphi$ is defined by the ratio between the thickness $\varepsilon$ of the particles and the separation E of the walls, while the rotation angle $\theta$ that leads to contact is related to these two variables and also to the particle diameter D. These angles are, respectively, given by:

$$\begin{aligned} \varphi = \arctan \left( \frac{\varepsilon }{D} \right) , \quad \theta = \arcsin \left( \frac{E}{\sqrt{\varepsilon ^2 + D^2}} \right) - \varphi . \end{aligned}$$

(12)

The magnetic torques generated on the particle i by another particle j, are given by [17]:

$$\begin{aligned} \varvec{\tau }_{ij} = \frac{\mu _0 \mu ^2}{4\pi r_{ij}^3} \left[ 3( \varvec{\hat{\mu }}_j \cdot \hat{\mathbf {r}} ) ( \varvec{\hat{\mu }}_i \times \hat{\mathbf {r}} ) + ( \varvec{\hat{\mu }}_i \times \varvec{\hat{\mu }}_j ) \right] . \end{aligned}$$

(13)

We will assume, as a first order approximation, that the contribution to the torque from the term $\vert \varvec{\hat{\mu }}_i \times \varvec{\hat{\mu }}_j\vert$ is negligible. From the angles defined in Eq. 12, we can simplify Eq. 13 to

$$\begin{aligned} \tau _{ij} = \frac{3\mu _0 \mu ^2}{8\pi r_{ij}^3}\sin (2\theta ). \end{aligned}$$

(14)

If we now take the torque contributions from all other particles j of the system, and determine the torque balance on the particle j, with the help of some geometrical relations obtained from Fig. 6, we obtain that the normal force acting on each magnetic particle is approximately given by

$$\begin{aligned} N_i = \frac{3\mu _0 \mu ^2}{8\pi }\frac{\sin (2\theta )}{\cos (\varphi + \theta )\sqrt{D^2 + \varepsilon ^2}}\sum _{j\ne i} \dfrac{1}{r_{ij}^3}. \end{aligned}$$

(15)

Note that the normal force is composed of three factors of different nature. The first one is related to the intensity of the magnetic dipoles of the particles, while the second one is given by the geometry of the system and the third one is given by the instantaneous arrangement of the particles. Therefore, Eq. 15 reveals that as the area packing of the particles increases, and the average distance between particles decreases, the normal forces and, consequently the friction force acting on the particles, increase. This simple model, in fact, helps to further explain the reason why the force measurements for compression and expansion follow different paths with the stroke of the piston.

5 Numerical results

In the following, we show the results that were obtained from the numerical simulations using the model presented in Sect. 4. We have reproduced in the numerical experiments the geometry of the experiments described in Sect. 2, and we have also considered the same size and mass of the particles. The values of the other parameters of the model, unless otherwise stated, are given by (in the corresponding adequate units):

$$\begin{aligned} \begin{array}{c} B_r = 1.3 , ~~\gamma _v = 1.0,\\ v_t = 10^{-8}, ~~ \mu _e = 0.6, ~~ \mu _d = 0.45,\\ \end{array} \end{aligned}$$

(16)

where $B_r$ is the residual magnetization of the particles, which is linked to the magnetic moment of the particles by $\mu = B_rV_p/\mu _0$, where $V_p$ is the volume of the particles. The value of $\mu$ (or $B_r$) was determined so that the magnetic bed with $N= 367$ particles had the same height (28 cm) as the bed in the experiments. The model was implemented in the code used in Ref. [17] originally for the simulations of sistems of few magnetic particles and, therefore, we kept the original ${\mathcal {O}}(N^2)$ algorithm to calculate magnetic forces for simplicity. A full simulation, including the generation of the initial condition, the compression and the expansion phases, such as the ones whose results are presented in the following, would typically take 24h to run.

Fig. 7

Snapshots showing the compression and expansion of magnetic repelling grains obtained in the numerical simulations using the dry friction model given by Eq. 11 and $v=8.33$ cm/s. These results should be compared with the experimental results presented in Fig. 2a,b. The values on the vertical and horizontal axes refer to particle diameters, e.g. $60D = 36$cm for this simulation. The color of the particles, according to the color bar on the right, indicates the total force acting on them, normalized with respect to the maximum force obtained in simulations. The scale T is the compression/expansion time, $T = y_F/v$

We have not attempted to reproduce, in the numerical simulations, the loose configuration presented described in Sect. 2. This is due to the fact that the loose configuration, which is obtained when the Hele Shaw cell is tilted upside-down and then slowly tilted back to its original upright position, can only be obtained when full dry friction between the surface of the particles and the glass walls is taken into account. When the cell is nearly horizontal, particles will be supported by one of the glass walls, and friction and gravity control the dynamics of the stick-and-slip motion of the particles at that stage. This kind of dry friction, which dominates the process of the generation of the loose packing bed, is not considered in our two-point friction model derived in Sect. 4.3.2. Therefore, the loose packing bed remains to be investigated numerically in future works.

The simulations start with the particles organized in a slightly perturbed ordered array that is placed inside the computational Hele-Shaw cell between 120D and 250D from the bottom of the cell. Each particle starts with identical, non-zero kinetic energies, but their velocities have initial random orientations. The piston is initially located very far from the base of the cell. The particles are let to naturally evolve to an equilibrium state in which they are at rest. The arrays can be slightly perturbed to generate beds with slightly different static equilibrium states. The piston is instantaneously placed at 45 cm from the bottom of the cell (this initial position is taken as $y_0=0$ in the simulations) and then moved at a constant speed, until it reaches the same maximum stroke $y_f$ as in the experiments. At that point, the motion is reversed and the piston moves upwards with the same speed as in the compression phase. Figure 7 shows the sequence of compression and expansion of the bed obtained in the numerical simulations. The similarity of these results with the experimental ones is outstanding. Note that in Fig. 7, the particles were plotted with colors associated to the sum of the absolute values of all the forces acting on the particles: the more intense the red of the particles, the larger this sum of the forces acting on them is. This is a measure of the (magnetic) pressure the particles are subjected to and indicates that the pressure is maximum at the maximum compression state. The hysteresis of the system can also be observed here: at the initial configuration, the magnetic pressure is roughly homogeneous, whereas in the end of the compression/expansion cycle, the particles at the bottom are subjected to a larger magnetic pressure.

Fig. 8

Density profiles obtained from the numerical simulation results presented in Fig. 7. a The vertical density profiles. Note the density inversion of the maximum compression state and the similarity with the experimental results presented in Fig. 2c,d. b The horizontal density profiles. The scales of the axes are expressed in particle diameters

The density profiles extracted from the results presented in Fig. 7 are shown in Fig. 8. The vertical density profiles are plotted in Fig. 8a, and the resemblance to the experimental results is again very good. The particles are initially roughly organized in horizontal lines of particles that get closer to each other at the lower parts of the cell. As the motion of the piston begins, the grains near the top are compressed as they are pushed downwards. The density inversion observed in the experiments is also observed in the numerical simulations, and it is also maximum at the maximum compression state. As the piston moves up, the bed of particles expands and returns to a looser configuration that is more disorganized in the top and more concentrated in the bottom when compared to the initial state. Figure 8b shows the horizontal concentration profiles for the results presented in Fig. 7. Similarly to the vertical density profiles, the initial horizontal profiles indicate that the bed of particles was also arranged primarily in vertical lines, almost homogeneously (note that the peaks are roughly of equal value and are roughly equidistant one to the other). As the compression cycle starts, particles are pushed from the center of the cell towards the walls. At the maximum compression state, the particles are now randomly arranged in the central zone of the cell and an almost uniform density profile is observed. Finally, at the end of the expansion cycle, most of the initial horizontal structure is lost, the particles are more homogeneously distributed near the center and more concentrated towards the walls. This is an evidence of the hysteresis of the system during the compression/expansion cycle.

Fig. 9

Trajectories of the particles for the compression/expansion cycle shown in Fig. 7. The particles are plotted at their final configuration

Figure 9 shows the trajectories of the particles for the simulation presented in Fig. 8. The particles are plotted in their final state configuration, after the end of the compression/expansion cycle. Similarly to the experimental observation, the particles do not reach the same initial height at the end of the expansion phase and they develop almost vertical trajectories, with some lateral fluctuations. It is also interesting to observe that the trajectories of the particles near the bottom are very short and they almost have negligible displacements.

So far, we have shown that the numerical model with dry friction is qualitatively in agreement with the experimental observations. Figure 10a shows the behavior of the average net particle displacements, calculated from Eqs. 1–3, as functions of the dimensionless time $tv/y_F$, for the piston velocity $v= 8.33$ mm/s and for both the dry and the viscous friction models. The compression starts at $tv/y_F =0$ and lasts for one dimensionless time, i.e. $y_F$ is reached at $tv/y_F =1$. At the maximum compression state, the particles are, on average, just under $\langle \Delta y \rangle \approx 15$ diameters far from their original positions. We observe that, on average, the particles shift horizontally by about $\langle \Delta x \rangle \approx 1.25$ particle diameters at the end of the cycle, for both the dry and the viscous friction models, whereas their vertical net displacement is, on average, approximately equal to $\langle \Delta y \rangle \approx 4.5$ particle diameters for the simulation with the dry friction model, and approximately $20\%$ smaller for the viscous friction model. If we compare these results with the experimental results, they are surprisingly more similar to the ones obtained in the loose bed configuration than in the standard packing bed configuration.

Fig. 10

a Average net displacements of the particles calculated from Eqs.1, 2 and 3 for the results presented in Fig. 8 with the dry friction (dashed lines) and with the viscous friction model (heavy lines). The results are given in terms of particle diameters and as functions of the dimensionless time $tv/y_F$. All parameters of the simulations are given in Eq. 16). The value of $\langle \Delta z \rangle$ obtained for different piston velocities are plotted in b for the dry friction model, and in c for the viscous friction model

The results in Fig. 10a, as discussed above, indicate that the choice of the friction model causes significant changes to the response of the system. The differences in the final average net displacements indicate that, when the viscous friction model is considered, the particles end the cycle in positions closer to their original positions. This shows that the dry friction model effectively imposes an extra resistance to the motion of the particles when compared to the viscous friction model. The response of the system to the velocity of the piston also changes according to the friction model used. Fig. 10b shows the effect of the piston velocity on the average total net displacement of the particles for the dry friction model. The larger the piston velocity, the larger the final value of $\langle \Delta z \rangle$ is, indicating large hysteresis on the system. This trend is surprisingly reversed in the viscous case: it seems that the slow motion of the piston allows the particles to rearrange in a more stable, yet more different arrangement with respect to the initial arrangement when the viscous friction model is used.

Figure 11a shows the result for the mean inter-particle distance obtained from the simulation presented in Fig. 8. During the compression phase, the mean inter-particle distance decreases almost steadily to its minimum value at the maximum stroke of the piston, ${\hat{D}} \approx 11$. Then, as the expansion process starts, the mean inter-particle distance does not return to its original value, but to a value around ${\hat{D}} \approx 14-15$, depending on the velocity of the piston. We observe that the larger the piston velocity is, the smaller the final inter-particle distance is, with a minimum of just under ${\hat{D}} \approx 14$ for $v = 8.33$mm/s, indicating a larger hysteresis in the system with larger velocities. This overall behavior is, once again, very similar to the experimental results obtained for the loose packing bed, as observed in Fig. (3). However, the values obtained for ${\hat{D}}$ in the simulations are smaller than the ones obtained in the experiments (for both standard and loose packing initial configurations). Figure 11b shows the result for the viscous friction model. In this case, the piston velocity changes the evolution of the mean inter-particle distance during the expansion phase, but all systems seem to evolve to a very similar value, which is slightly smaller than the value at the initial condition. This indicates that the viscous friction model is not able to capture most of the hysteresis that this system undergoes during the compression/expansion cycle.

The insets on the plots in Fig. 11 show the evolution of ${\hat{D}}$ during the numerical generation of the initial condition. For the dry friction model, at $tv/y_F=-5$, the particles are placed in the ordered array on the computational domain and are let to evolve to the physical initial state, which is obtained shortly after the initiation of the motion of the particles. However, it takes much longer for the particles to achieve the physical initial state when the viscous friction model is used. In both cases, the mean inter-particle distance increases to its maximum due to the strong repulsion of the particles in the ordered array, and then decays, due to gravity, to just under ${\hat{D}} \approx 15$ as they settle to the physical initial condition just before the initiation of the compression phase. Note that, during this phase, the piston does not move and the dependency on the piston velocity of the results presented in the insets is only due to the choice of the time normalization.

Fig. 11

Average mean inter-particle distance calculated from Eq. 4 for the results presented in Fig. 8 with the dry friction model a and the viscous friction model b. The insets in each plot show the evolution of the average mean inter-particle distance of the ordered array to the initial condition just before the initiation of the compression phase

Despite the results presented in Figs. 8 and 9 show a good qualitative agreement with the experimental observations, quantitatively the results for mean displacements and mean inter-particle distance presented in Fig. 10 do not match perfectly those obtained in the experiments. In addition to the uncertainty on the choice of many of the model parameters, and of the particle-wall interaction force, Eq. 9, the friction model might be at the heart of this disagreement. The sensitivity of the numerical results to the friction model is investigated in the following.

Fig. 12

The force on the piston for the simulations performed with the parameters defined on Eq. 16 and for different values of the velocity of the piston. In a, The results obtained with the viscous friction model are presented, while in b The results for the dry friction model are presented. The black line with crosses represent, in both plots, exponential fits for the case $v = 8.33$mm/s. In the inset of b, one can notice the force fluctuations generated by local rearrangements when the dry friction model is considered

Figure 12 shows the results of the force on the piston measured on the numerical simulations for the two proposed friction models. In both cases, as a general trend, we observe the same asymmetry of the compression and expansion phases, with the forces on the former being larger, as also observed on the experiments. Figure 12a shows the results for the viscous friction model. Note that, as expected, the measured force on the piston is dependent on its velocity. This is due to the fact that, as the particles are pushed with a given piston velocity, the resistance to their motion depends on their velocity and, therefore, the evolution of local arrangements of the particles will be resolved slower or faster depending on the piston velocity. Note that the faster the piston moves, the larger the difference between the forces of the compression and expansion phases is. For the slowest velocity, the difference is very small, since the particles have enough time and little resistance to readjust to the instantaneous minimum energy configuration for a given packing fraction.

On the other hand, the results for the dry friction model in Fig. 12b show that the force on the piston is independent on the compression and expansion velocities, reproducing qualitatively the experimental results presented in Sect. 3. This indicates that the simple dry friction model that we have derived in Sect.  4 is able to capture the necessary features of the friction between the particles and the walls of the Hele-Shaw cell. We note that, for the slowest piston velocity, the force measured during the expansion phase was different from the ones obtained for the other velocities. In this case, since the piston moves very slowly, the particles closer to the piston have enough time to catch up with the moving piston as they are pushed upwards by the other particles within the cell and, therefore, the piston will feel a stronger force exerted from the particles. This feature is an indication that the dry friction model, despite being enough to reproduce the overall qualitative behavior of the system, is probably not only underestimating the actual friction force on the particles, but additionally is not accurately capturing all the necessary features of friction forces for a more precise quantitative agreement with the experiments.

The black lines with crosses in Fig. 12 show the exponential fits obtained for both the dry and the viscous friction models, and for $v = 8.33$mm/s. Following the experimental results, we were able to fit one exponential of the form $F/F_{max} \approx A e^{(y_P/y_F-y_0)/\lambda }$ for the compression phase, with $A= 1.5791, ~y_0 = 1.0946$ and $\lambda = 0.1899$ for the dry friction model, whereas we obtained $A= 1.5785, ~y_0 = 1.0969$ and $\lambda = 0.1854$ for the viscous friction model. Here the parameters $y_0$ and $\lambda$ have been normalized accordingly. Note that, despite the similarity of the fitting parameters, the fitting for the viscous friction model does not capture correctly the early and final stages of the compression, whereas the final stage is very well captured by the exponential model in the dry friction case. The expansion phases were fitted by two exponentials, similarly to the experiments, that is, $F/F_{max} \approx A e^{(y_P/y_F-y_0)/\lambda _1} + B e^{(y_P/y_F-y_0)/\lambda _2}$. The parameters obtained were: $A= 1.2209, ~B=0.6117 , ~y_0 = 1.0167, ~\lambda _1 = 0.01421$ and $\lambda _2 = 0.1373$ for the dry friction model, and $A= 1.1189, ~B=1.1172 , ~y_0 = 1.0555, ~\lambda _1 = 0.02817$ and $\lambda _2 = 0.1485$ for the viscous friction model. As with the compression phase, the exponential model fits better the expansion phase for the dry friction case, indicating that the dry friction model is crucial to correctly describe the experimental system near the maximum stroke of the piston.

Fig. 13

Comparison between the experimental and numerical results for the normalized force on the piston as a function of the piston stroke for $v=8.33$mm/s. The experimental results are plotted in heavy lines, whereas the numerical model with viscous friction is plotted with dashed lines and the numerical model with dry friction is plotted with dotted lines

Figure 13 shows the comparison of the experimental force measurements with the results obtained from the numerical simulations. The results indicate that, despite the general trend and asymmetry of the compression and expansion curves are recovered by the numerical model, the force measured on the experiments is smaller than the force measured on the numerical simulations for both viscous and dry friction models. We believe that there are three main reasons for that.

Firstly, as discussed previously, the numerical model is based on friction force models that only approximately account for the real friction of the particles and the walls of the cell. Note that, in the experiments, there is a sharp decay of the force at the beginning of the expansion regime, which is caused by static friction holding up the particles still while the piston is moving away from them. The dry friction model improves the early time response of the expanding system when compared to the viscous friction model, but only partially. Secondly, in the numerical model proposed in this work, only the forces caused by the particles in the piston are considered, i.e. the walls do not interact with the piston. In the experiment, this is certainly not the case and the forces from the other walls on the piston may have an important influence on the force measured by the load sensor. Finally, we assume that the interaction of the particles with the walls is governed by Eq. 9, which is derived for the interaction of a dipole with an infinite bar. The actual power law dependence of this force could be any power between 3 and 4, as discussed in Sect. 4.2. Different particle-wall interaction forces would change local particle arrangements, especially near the walls, and consequently, the overall force acting the piston.

6 Discussion

Let us first compare our results with those of previous studies using non-magnetic grains. Sudden drops of $F(y_P)$ were measured during the compression of granular columns composed of rigid or brittle particles [2, 4] (also observed during compression of ice blocks [21]). Note the absence of these drops for our system with repulsive magnets. This indicates that the average force acting on the piston is much larger than the force fluctuations produced by the local rearrangement of some particles. Moreover, although friction with the frontal-rear glass walls exists, this is small and not enough to produce significant stick-slip motion of a large number of magnets. These results indicate that the compression response of the repulsive bed is more similar to the case of flexible particles confined into a cylinder with smooth walls [6], where a smooth increase of the force load was also measured during compression, and where the compaction of particles also increases near the piston, which in our case is the consequence of the density inversion observed in Fig. 2c-d. Therefore, the magnetic bed does not support localized compaction propagation, corroborating that grain breakage and inter-particle friction are required for the emergence of compaction bands or sudden drops in the force load.

It is important to point out that, despite no significant drops of the force are observed in the magnetic granular bed, localized rearrangements of individual particles as the piston moves are indeed observed (these can be seen in the videos in the Supplementary Material). Although the consequences of these rearrangements cannot be observed on the experimental force measurements, because they are comparable to the instrumental noise, they are noticeable in the numerical results presented in the inset of Fig. 12b: when the dry friction model is used, the force measurements fluctuate and these fluctuations are correlated to the local (sudden) rearrangements that happen in the bed and become more important near the maximum stroke of the piston. On the other hand, there are no fluctuations in the results corresponding to the viscous friction model (see inset in Fig. 12a), as this model does not allow for stick and slip motion of the particles and all rearrangements are “smooth” in time, causing only small amplitude undulations on the resistance force experienced by the piston.

The fact that the bed expands as the piston is removed also reveals an elastic response of the magnetic bed that, together with the smooth increase of the force load without marked force drops, are features that can be exploited to design a new type of granular damper. A granular damper is a device used to attenuate mechanical vibrations based on the dissipative nature of granular materials [22, 23], where kinetic energy is dissipated through friction and collisions between particles. These devices have been used to attenuate the vibrations of oscillatory tools [24] and impacts [25]. Although in our case there are no contacts between the particles, there is friction with the glass walls induced by the magnetic interactions. The repulsive magnetic energy stored during the compression generates an elastic response of the system that is independent of the initial distribution of particles. This makes plausible the use of magnetic repelling grains to build a magnetic granular damper.

Another good reason to consider the magnetic assembly in a two dimensional cell is that the lateral magnetic walls cannot generate a vertical force on the magnets, or it is negligible. The interaction is purely repulsive and an arch cannot start from the walls (this explains the hydrostatic linear increase of density of particles with depth in Fig. 2c). Therefore, a sudden increase of compression force is not required to break an arch and rearrange the particles. This is not true for the case of non-magnetic walls [2, 6]. On the other hand, with non-repulsive particles, for instance glass beads, the width of the cell must be a multiple of the particle diameter so that a crystalline array can be formed. For magnetic grains, the “magnetic size" of the grains self-adapts to the size of the Hele-Shaw cell and, as the bed is compressed, the particles are softly rearranged in the cell until they reach an almost a crystalline array [15, 16]. These two features of our system can explain why there are no jumps in the force curve as a function of the stroke of the piston, as it is typically observed during granular compaction of hard steel spheres [2], brittle materials [6], or ice blocks [21], in which cases there is stick-slip particle motion induced by friction, geometry, arches and force chain breakage. An additional important fact is that $F(y_p)$ is not univocally determined during compression and depends strongly on the preparation of the bed, which is produced by the difference in initial volume fraction. For the same value of $\phi$, we have measured two different values of the force on the piston. This could be attributed, firstly, to the hysteresis on the system and, secondly, to the different configuration of the particles within the Hele-Shaw cell in each phase (note that $\phi$ is an average, as opposed to a locally measured property of the bed). Nevertheless, the expansion phase is independent of this initial history, which is relevant, as previously mentioned, for damping applications.

7 Conclusion

We have presented experimental and numerical results of the compaction-expansion dynamics of a granular bed composed of cylindrical repelling magnets contained in a two-dimensional cell. In the experiments, the compression dynamics was found to be sensitive to the initial packing conditions of the grains. In contrast, a history-independent response was found for the expansion phase. This hysteresis in the system was quantified in terms of the average particle displacement. The force response on the piston was found to be independent on its velocity, at least for the range of velocities tested.

We have proposed a numerical model that can account for the basic features and dynamics of the system. The model has to consider a dry friction interaction between the magnetic particles and the confining walls. Using this model, the independence of the force on the piston in terms of its velocity can be reproduced numerically. The characterization of the hysteresis of the system shows the same qualitative features as those obtained in the experiments, but they do not match quantitatively. The numerical results indicate that both the friction model and the particle-wall interaction model have to be improved to account for a more precise agreement with the experimental results, in addition to a more detailed parametric study to define more adequately the model parameters. Nevertheless, the results obtained with the numerical model proposed in this work are robust enough to be used to study and to understand the basic dynamics of this system. Therefore, in the future we want to study the same system under different conditions that cannot be achieved in the laboratory: more particles, faster piston velocities and particles with different magnetic moments. Finally, we also want to explore other systems based on repelling magnetic particles, such as two-dimensional magnetic granular dampers or flexible magnetic dampers. Our numerical simulations will be of great relevance to test the damping efficiency for different designs of such devices.