1 Introduction

Rotating drums are commonly used to process granular materials in numerous industries as mixing, drying, coating, granulation and so on with diversity of size, from large particles of minerals to food powders and pharmaceutical ingredients. Heat transfer plays a significant role in many of these processes in which granular materials are heated indirectly through the rotating wall. When particles with different properties such as size, density, and shape are handled in the rotating drum, the undesirable segregation phenomenon occurs. Segregation causes non-uniformity in the granular bed and affects the heat transfer efficiency of the bed. For example, in the pyrolysis industry, the segregation can lead to reduce the efficiency of the process and affect the produced fuel properties. Due to the importance of heat transfer in the rotating drums, many researches were carried out to investigate heat transfer inside rotating drums for several past decades [1, 2].

It is well-known that the distribution of particle size and the density of particles have significant effects on segregation [3, 4]. Jain et al. [4] presented an experimental study in order to investigate how the combination of size and density of granular materials affects the mixing and segregation. They reported that proper mixing can be achieved instead of segregation if denser beads are bigger and also if the ratio of particle size is greater than the ratio of particle density. Yamamoto et al. [5] used Discrete Element Method (DEM) simulation to analyze the influence of particle density on mixing behavior. They claimed that particles with lower density could move easily in comparison with higher density particles. They also indicated that the difference between the mobilities of particles causes the segregation. The effect of particle shape on the segregation was studied as well. Dubé et al. [6] found that particles with aspect ratio of greater than two led to significant deviations in velocity profile and residence time. Also, they observed that mixing of different shaped particles led to unexpected core segregation patterns. In addition, the effect of baffles on segregation control was investigated [7, 8]. Maione et al. [9] investigated the effects of internal baffles and wood chip particle shape on segregation. They showed that the presence of baffles imposes a cyclic behavior on the solid bed. Arntz et al. [10] studied the phase behavior of granular beds of bidisperse hard spherical particles in a rotating horizontal drum by DEM simulations. They found strong correlations between the flow regime and segregation pattern of the bed. Soni et al. [11] analyzed mixing of particles in a rotating drum with fill levels greater than 50%. It was found that packing arrangement and particle size significantly affect the formation of a dead zone.

On the other hand, several researchers experimentally and numerically studied heat transfer within a rotating drum. Ding et al. [12] assessed heat transfer in rotating drums operating in a rolling mode. They showed that heat transfer from the covered wall to the particulate bed is the dominant mechanism in supplying heat to the bed. Heat transfer between the freeboard gas and the exposed surface of the free cascading layer accounts only for a small portion. Figueroa et al. [13] studied the effects of mixing rate on heat transfer of the granular material by changing cross-sectional shape and operating parameters of the tumbler. Herz et al. [14, 15] experimentally investigated heat transfer by making contact between the covered inner wall surface and the particulate bed in the rotary drum. They estimated the effects of operational parameters of the drum such as rotation speed, fill angle and solid bed parameters such as particle diameter and thermo physical properties on the contact heat transfer coefficient. Nafsun and Herz [16] empirically examined temperature distribution inside the solid bed of a rotating drum. They reported that the temperature gradient in the upper part is less than the lower part of the boundary layer due to mixing of particles. Nafsun et al. [17] experimentally investigated the transversal thermal mixing in the batch rotary drum and reported that thermal mixing time decreases with higher rotation speed and lower filling angle.

The discrete element method has been widely used to investigate the granular beds because this approach provides important information for each particle behavior [18, 19]. Kwapinska et al. [20] simulated the mixing of free flowing particles in horizontal rotating drums without inlets by using DEM in two dimensions under different operating parameters. Kwapinska et al. [21] reported that the results of thermal version of DEM are in qualitative agreement with existing experimental data and with the classical penetration model for three limiting cases: heat transfer controlled by a contact resistance at the wall of the drum, heat transfer to agitated beds with significant bed-side resistance, and heat transfer to the stagnant bed. The last limiting case can be used as a calibration between DEM and the penetration model. Shi et al. [22] studied the transition from convection to conduction-dominated heat transfer. They found that at higher particle conductivities, solid–solid conduction plays a more important role, but heat transfer is controlled by gas–solid conduction at lower particle conductivities. Chaudhuri et al. [23] investigated the effects of thermal conductivity, specific heat capacity, vessel rotation speed and fill level and observed faster heating for materials with higher conductivities and lower heat capacities. They showed that while rotation speed decreases both heat transfer and temperature uniformity of the granular bed for calciner increase on per revolution basis. Chaudhuri et al. [24] simulated various baffle configurations (rectangular and L-shaped flights) in the calciner and investigated their effects on the flow and heat transfer of granular materials. Gui et al. [25] investigated mixing and heat conduction of granular particles in a rotating drum by DEM simulation and particle–particle heat conduction model. Gui and Fan [26] studied heat conduction of particles in wavy rotating drums by discrete element method coupled with a thermal version.

Many reputable researchers have investigated the segregation phenomenon or the mono-dispersed heat transfer in the rotary drum separately. But the simultaneous study of segregation and heat transfer has not been investigated yet. In this study, the previous work by Chaudhuri et al. [23] has been extended to the binary-sized particles of a granular system conducted by using discrete element method and conduction heat transfer model inside the horizontal rotating drum. The particulate system is formed by the mixture of particles with different diameters. The main objective of the present work is to investigate the effects of characteristics of binary-sized particles (i.e. volume and diameter ratio) and operating conditions (i.e. rotation speed and fill level) on the heat transfer. In order to fulfill this objective, the heating time and mixing entropy are calculated and discussed.

2 Numerical model

2.1 Discrete element method

Discrete Element Method (DEM) which was initially proposed by Cundall and Strack [27] is one of the most promising methods to determine the particle behavior in a particulate system using Newton equation of motion. The particle–particle and particle–wall contact forces are computed, and the position of each particle is subsequently obtained from the particle–particle and particle–wall collisions. In this work, a soft-sphere approach is employed for simulating the particles as rigid bodies that are permitted to overlap at the contact points. The non-linear spring-dashpot model of Hertz-Mindlin contact theory is used to model the collisions. The translational and rotational motions of each particle can be described by:

$$ m_{i} \frac{{d\overrightarrow{V}_{\!\!i} }}{dt} = \mathop \sum \limits_{i = 1}^{n} (\overrightarrow{F}_{\!\!n,ij} + \overrightarrow{F}_{\!\!t,ij} ) + m_{i} \overrightarrow{g} $$
(1)
$$ I_{i} \frac{{d \overrightarrow{\omega_{i} }}}{dt} = \mathop \sum \limits_{i = 1}^{n}\overrightarrow {M_{i}} $$
(2)

where \( m_{i} \) and \( \overrightarrow{V}_{\!\!i} \) are the mass and linear velocity of particle \( i \), respectively, \( \overrightarrow{g} \) is the gravity acceleration constant and \( I_{i} \), \( \overrightarrow{\omega}_{\!i} \) and \( \overrightarrow{M}_{\!i} \) are the moment of inertia, angular velocity of particle \( i \) and torque acting on the particle respectively. \( \overrightarrow{F}_{\!\!n,ij} \) and \( \overrightarrow{F}_{t,ij} \) are the normal and tangential forces, respectively resulting from the contact of the particle \( i \) with particle \( j \) and can be expressed by:

$$ \overrightarrow{F}_{\!\!n,ij} = (k_{n} \delta_{n}){\mathbf{\widehat {n}_{\varvec{ij}}}} - (\eta_{n} V_{n,ij}) {\mathbf{\widehat {n}_{\varvec{ij}}}}$$
(3)
$$ \overrightarrow{F}_{\!\!t,ij} = (k_{t} \delta_{t}) {\mathbf{\widehat{t}_{\varvec{ij}}}} - (\eta_{t} V_{t,ij}){\mathbf{\widehat{t}_{\varvec{ij}}}}$$
(4)

where \( k_{n} \), \( k_{t} \) are the normal and tangential stiffness coefficients, respectively. \( \eta_{n} \) and \( \eta_{t} \) are the visco-elastic damping coefficients and \( \delta_{n} \) and \( \delta_{t} \) are the normal and tangential displacement, respectively. The magnitude of the tangential force is limited by the Coulomb frictional limit \( \left( {F_{n} < \mu F_{t} } \right) \); where \( \mu \) is the particle–particle friction coefficient.

The stiffness coefficient in the normal and tangential directions can be calculated by the following equations [9]:

$$ k_{n} = \frac{4}{3}E_{eff} \sqrt {r_{eff} \delta_{n} } $$
(5)
$$ k_{t} = 8G_{eff} \sqrt {r_{eff} \delta_{n} } $$
(6)

The visco-elastic damping coefficients in the normal and tangential directions are calculated according to the following equations [9]:

$$ \eta_{n} = - 2\sqrt {\frac{5}{6}} \beta \sqrt {\frac{3}{2}k_{n} m_{eff} } $$
(7)
$$ \eta_{t} = - 2\sqrt {\frac{5}{6}} \beta \sqrt {k_{t} m_{eff} } $$
(8)

where \( E_{eff} \) and \( G_{eff} \) are the effective Young’s modulus and effective shear modulus, respectively. The \( r_{eff} \) and \( m_{eff} \) are the effective radius and effective mass and expressed by \( 1/r_{eff} = 1/r_{i} + 1/r_{j} \) and \( 1/m_{eff} = 1/m_{i} + 1/m_{j} \), respectively where \( r \) and \( m \) are radius and mass of the particle, respectively. The subscript \( i \) and \( j \) stand for the two particles in contact.

The relation between the damping ratio (\( \beta \)) and the coefficient of restitution (\( e \)) is defined as:

$$ \beta = \frac{\ln \left( e \right)}{{\sqrt {\text {ln}^{2} \left( e \right) + \pi^{2} } }} $$
(9)

The effective Young’s modulus between the pair of particle–particle or particle–wall collisions can be calculated as:

$$ \frac{1}{{E_{eff} }} = \frac{{\left( {1 - \nu_{i}^{2} } \right)}}{{E_{i} }} + \frac{{\left( {1 - \nu_{j}^{2} } \right)}}{{E_{j} }} $$
(10)

where \( \nu \) is the Poisson's ratio. The effective shear modulus of two colliding individuals is calculated by:

$$ \frac{1}{{G_{eff} }} = \frac{{2\left( {2 - \nu_{i} } \right)\left( {1 + \nu_{i} } \right)}}{{E_{i} }} + \frac{{2\left( {2 - \nu_{j} } \right)\left( {1 + \nu_{j} } \right)}}{{E_{j} }} $$
(11)

2.2 Heat transfer model

The linear heat condition model is used for heat transfer between two particles in contact [23, 28]. The heat transfer rate is calculated as:

$$ Q_{ij} = h_{c,i - j} \left( {T_{j} - T_{i} } \right) $$
(12)

where \( Q_{ij} \) is the heat transfer rate between the two particles, \( i \) and \( j \), with temperature \( T_{i} \) and \( T_{j} \), respectively, which are in contact. The heat transfer coefficient of colliding particles \( h_{c,i - j} \) can be expressed as [29]:

$$ h_{c,i - j} = \frac{{4K_{i} K_{j} }}{{K_{i} + K_{j} }}\sqrt {A_{c,i - j} } $$
(13)

where the \( K_{i} \) is the thermal conductivity of particle \( i \) and \( A_{c} \) is the contact area between the two particles. Temperature variation of particle \( i \) can be expressed as:

$$ C_{pi} m_{i} \frac{{dT_{i} }}{dt} = \mathop \sum \limits_{i = 1}^{n} Q_{ij} $$
(14)

where \( C_{pi} \) is the specific heat of the particle \( i \). In this model, it was assumed that thermal conduction inside a particle is very fast and temperature gradient inside the particle is negligible (Biot number is smaller than 0.1). This assumption is relatively reasonable when the heat conduction resistance inside the particle is remarkably smaller than of which between the particles (Vargas and McCarthy [28]). In the present work, it is assumed that convection heat transfer is negligible; because the fluid is stagnant inside the drum and accordingly, the heat transfer rate by convection mechanism is considerably smaller than the heat transfer rate by conduction mechanism. To characterize and compare heat transfer rate in different simulation cases, the heating time was defined as the time when \( {{\left( {T_{s} - T_{s,0} } \right)} \mathord{\left/ {\vphantom {{\left( {T_{s} - T_{s,0} } \right)} {\left( {T_{w} - T_{s,0} } \right)}}} \right. \kern-0pt} {\left( {T_{w} - T_{s,0} } \right)}} \) equals 0.9 in which \( T_{s} \) is the mean temperature of all particles in time \( t \). \( T_{s,0} \) and \( T_{w} \) are the temperature of solid bed when \( t \) = 0 s and the temperature of wall of rotating drum, respectively. By the way of interpretation, lower values of the heating time indicate higher heat transfer rates.

2.3 Entropy of mixing

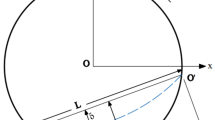
Several approaches are proposed to determine the mixing or segregation intensity [5, 7, 30]. In the present study, the entropy of mixing is used [10, 31, 32]. In this approach, a grid that overlaps the entire bed is defined (Fig. 1). The local entropy of mixing \( \varvec{s}\left( \varvec{k} \right) \) for each grid cell \( \varvec{k} \) is defined as follows [10]:

$$ s\left( k \right) = \mathop \sum \limits_{i = 1}^{n} x_{i} \left( {\text{k}} \right){ \ln }x_{i} \left( {\text{k}} \right) $$
(15)

where \( x_{i} \) is the volume concentration of particles of type \( i \), in the cell \( k \) and \( n \) is the number of particles type. The local mixing entropy is equal to zero if all particles in the cell are identical. Entropy of mixing is defined by:

$$ S\left( t \right) = \frac{1}{{s_{\infty } V}}\mathop \sum \limits_{k} s\left( {k,t} \right)v\left( {k,t} \right) $$
(16)

where \( v \) is the volume occupied by the particles in cell \( k \). The entropy of the perfectly mixed state, \( s_{\infty } \), is defined by \( s_{\infty } = \mathop \sum \nolimits x_{i,s} lnx_{i,s} \), where \( x_{i,s} \) is the volume concentration of particles of type \( i \), in the solid bed. The higher value for \( S\left( t \right) \) is an indicator of the better mixing.

Fig. 1
figure 1

Schematic of the rotating drum

Full size image

Initially, specified number of particles is randomly inserted into the rotating drum with 180 mm diameter and 10 mm length where they are considered to be settled under only the gravity force. Thus, at first, a short simulation is done until the kinetic energy of the system is equal to zero and the bed reaches mechanical equilibrium. Then, the drum is rotated around its horizontal axis at a constant rotation speed. The input parameters for the DEM simulation adopted from the reported data by Chaudhuri et al. [23], are listed in Table 1. In addition, the time step for simulation has been selected equal at most 10% of the critical Rayleigh time-step [33].

Table 1 Simulations parameters
Full size table

The simulation was performed by the open source DEM software LIGGGHTS. LIGGGHTS stands for “LAMMPS Improved for General Granular and Granular Heat Transfer Simulations” and is based on LAMMPS [29]. Simulations were performed on an Intel Core i7-4790 K CPU processor (4.00 GHz) with 16 GB of RAM.

3 Results and discussion

3.1 Verification of simulation results

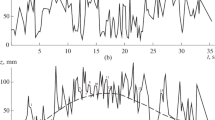
This study is the extended of previous work carried out by Chaudhuri et al. [23]. In order to verify the heat transfer simulation, the results are compared with the reported DEM simulation [23]. The rotating drum with 180 mm diameter and 10 mm length without baffle is loaded by 16,000 mono-dispersed particles of 2 mm diameter. The initial temperature of all particles (i.e., \( T_{s,0} \)) is considered to be 298 \( {\text{K}} \) whereas the temperature of the drum wall (i.e., \( T_{w} \)) is considered to be 1298 \( {\text{K}} \). Also, the drum is rotated at 20 rpm and thermal radiation heat transfer is ignored [23, 24]. Figure 2 demonstrates the comparison of the simulation results concerning the mean bed temperature with the data reported by Chaudhuri et al. [23]. According to Fig. 2, the simulation results are in reasonable agreement with data reported by Chaudhuri et al. [23].

Fig. 2
figure 2

Comparison simulation results for mean temperature of the particulate bed with the data reported [23] in rotating drum filled with mono-dispersed particles with 1 mm radius rotating at 20 rpm

Full size image

3.2 The effect of binary mixing

Either granular flow dynamics or heat transfer in the rotating drum is governed by particle size distribution. In this section, the effect of the particle volume ratio with different diameters has been investigated on the heat transfer. Figure 3 presents six snap-shots of temperature distribution for the rotating drum at the rotation speed of 20 rpm. As the segregation occurred, the large particles are gathered in the outer layer of the bed and smaller particles are collected in the core of the bed. So, the large particles are heated up directly due to contact with the hot wall of the rotating drum, while the small particles are heated up indirectly due to contact with large particles. In the other words, the heat from the hot wall of rotating drum through the large particles is transferred to the small particles (the core of the solid bed). Therefore, the large particles are heated up faster and small particles are heated up gradually. Variation of the heating time of the rotating drum with different volume ratios is presented in Fig. 4. Total mass of the bed is identical in all cases. It is notable that, when the bed consists only large particles (i.e., volume ratio is 0.0), all particles are circulated continuously and it helps to improve the heat transfer rate. On the other hand, when a small amount of the small particles is presented in the bed (i.e., volume ratio of 0.1), these particles are surrounded by large particle and are forced to be collected in the center of the bed with no considerable circulation. In this case, the large particles resist the heat up of small particles. Thus the mean temperature of small particles will increase very slowly in comparison with large particles and consequently, it is expected that the heat transfer of the volume ratio of 0.1 is less than volume ratio of 0.0. The enhancement of the heat transfer rate at the higher volume ratios, i.e., volume ratios more than 0.1, is due to the following facts: First, the total number of particles is increased, which leads to an increase in the rate of contacts and an improvement in mixing. Second, the number of larger particles having higher thermal resistance than small particles is decreased. It is clear from Fig. 4 that in spite of expectation, the heating time of the bed is not linearly depended on the volume ratio, particularly when the diameter ratio is high.

Fig. 3
figure 3

Six snapshots of the temperature distribution in the rotating drum rotating at 20 rpm and containing 8000 particles with 1 mm radius and 1000 particles with 2 mm radius (\( v_{r} \) = 0.5, \( d_{r} \) = 2.0)

Full size image
Fig. 4
figure 4

Variation of the heating time for different volume ratios (\( v_{r} \)) of particles at rotation speed of 20 rpm

Full size image

3.3 The effect of rotation speed

Rotation speed plays an important role in particle dynamics [34] and heat transfer along the solid bed [35]. Particles with lower temperature move towards the wall and are heated up to reach approximately the temperature of the wall. According to the segregation phenomenon, small particles are concentrated in the inner layer and have less chance to be in contact with the wall. Thus, the small particles are heated through contact with large particles. Consequently, on the contrary to the large particles, temperatures of small particles increase gradually.

Figure 5 demonstrates the mixing entropy of the bed (when \( v_{r} \) = 0.5 and \( d_{r} \) = 2.0) by varying the rotation speed from 10 rpm (\( Fr \) = 0.010) up to 40 rpm (\( Fr \) = 0.161). The flow regime of the solid bed is mainly rolling/cascading because particles fall down due to gravity instead of rising up due to inertia. The first notable point is that with increasing rotation speed, the mixing of particles was improved, as shown in Fig. 5. The second point is that by increasing the rotation speed, the circulation and the contact rate of particles with the drum wall are improved and temperatures of the small and large particles are increased and consequently, it is expected that mixing improves heat transfer rate. Figure 6 presents the temperature difference between particles with larger diameter (i.e., radius of 2 mm) and smaller diameter (i.e., radius of 1 mm) in the bed rotated at various rotation speeds. When the segregation occurred, the larger particles are located in the outer layer of the bed and near the hot wall, consequently, the temperature of the larger particles are more than smaller ones. As can be seen from this figure, the temperature difference between larger and smaller particles at various rotation speeds become different approximately after 7 s, which is similar to the time when the entropy of mixing become different as presented in Fig. 5. The interesting point is that according to Fig. 5, by increasing the rotation speeds, the entropy of mixing or the degree of segregation is decreased. Accordingly, temperature difference between larger and smaller particles decreased by increasing the rotation speed as a result of the segregation impact on temperature profile.

Fig. 5
figure 5

Variation of mixing entropy (\( v_{r} \) = 0.5 and \( d_{r} \) = 2.0)

Full size image
Fig. 6
figure 6

Variation of temperature difference between particles with larger diameter and smaller diameter (\( v_{r} \) = 0.5 and \( d_{r} \) = 2.0)

Full size image

Enhancing heat transfer by mixing is illustrated in Fig. 7 for different rotation speeds. Due to larger gaps between larger particles, they have lower number of contacts in comparison to small particles and consequently, larger particles have higher thermal contact resistance. The increment the rotation speed increases the number of contacts and improves the heat transfer rate. This improvement for larger particles is more significant than for small particles because of higher thermal contact resistance of the larger ones.

Fig. 7
figure 7

Variation of the heating time for different rotating speeds (\( v_{r} \) = 0.5)

Full size image

3.4 The effect of filling ratio

The drum included particles (\( v_{r} \) = 0.5 and \( d_{r} \) = 2.0) is rotated at 10 rpm. The standard deviation of temperature is shown in Fig. 8. The standard deviation of temperature,\( \upsigma_{T} \), determines the temperature distribution uniformity of particles inside the particulate bed.\( \upsigma_{T} \) is defined as follows:

$$ \upsigma_{T} = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {T_{i} - T_{s} } \right)^{2} } $$
(17)

where \( T_{i} \) is the temperature of each particle (either small or large particle) in time \( t \) and \( T_{s} \) is the mean temperature of solid bed in time t. \( N \) is the number of all particles in the bed. Initially, the temperature of all particles are 298 K and so the standard deviation of temperature equals to zero. After approximately 3 s the non-uniformity of particles reaches the maximum value. Then, by approaching the temperature of all particles to the temperature of the hot wall of rotating drum (i.e., 1298 K), the non-uniformity of particles decreased gradually and finally, the temperature of all particles become equals. At higher filling levels, particles circulate inside a larger space of the particulate bed and they have higher circulation time and lower mixing rate, which cause an increase in the standard deviation of temperature. In other words, the bed is derived thermally non-uniform. Figure 9 depicts the heating time for different fill levels with the same particle volume ratio (i.e., \( v_{r} \) = 0.5) and two diameter ratios (i.e., \( d_{r} \) = 1.5 and 2.0). As the filling level increases, the chance of contact of particles with the hot wall of rotating drum reduces, and the bed heats up slower and consequently, the heat transfer rate is decreased.

Fig. 8
figure 8

Standard deviation of all particle temperature in different fill levels of the bed rotated at 10 rpm (\( v_{r} \) = 0.5 and \( d_{r} \) = 2.0)

Full size image
Fig. 9
figure 9

Variation of the heating time for different fill levels of the bed rotated at 10 rpm (\( v_{r} \) = 0.5)

Full size image

3.5 The effect of particle diameter ratio

In this section, the heating time for different values of particle diameter ratio, \( d_{r} \), was studied. The drum was rotated at 10 rpm. For all cases, the particle volume ratios and also the masses of particle beds were identical. Figure 10 shows snapshots of segregation phenomenon in the rotating drum for different particle diameter ratios. It is clearly seen that for the particle ratio of 1.25, the segregation phenomenon occurs slightly in comparison with other cases. Increasing the particle diameter ratio intensifies the segregation. Figure 11 shows the dimensionless mean temperature (i.e., \( {{\left( {T - T_{s,0} } \right)} \mathord{\left/ {\vphantom {{\left( {T - T_{s,0} } \right)} {\left( {T_{w} - T_{s,0} } \right)}}} \right. \kern-0pt} {\left( {T_{w} - T_{s,0} } \right)}} \)) of small, large and all particles at \( t \)= 10 \( {\text{s}} \). In a constant volume ratio and filling level, when the diameter ratio is increased, the mean temperature of large particles is increased while the mean temperatures of small and all particles (including small and large particles) are decreased. The reason for this is with increasing the diameter ratio, the segregation is intensified (Table 2). Therefore, by increasing the \( d_{r} \) more large particles are located near the hot wall and more small particles are collected in the center of the bed, and consequently, large particles heat up faster than small particles. The point worth to mention is that when \( d_{r} \) is increased, the diameter of particles with large diameter is increased (Table 2). Accordingly, the thermal resistance of the solid bed (i.e., mixture of small and large particles) is increased, which leads to decrease in the mean temperature of all particles.

Fig. 10
figure 10

Snapshots of the segregation phenomenon in the rotating drum for rotation speed of 10 rpm, volume ratio of 0.5 and a–d \( d_{r} \) = 1.25, e–h \( d_{r} \) = 1.5, i–l \( d_{r} \) = 1.75

Full size image
Fig. 11
figure 11

Variation of dimensionless temperature for rotation speed of 10 rpm at \( t \) = 10 s (\( v_{r} \) = 0.5)

Full size image
Table 2 Variation of mixing entropy
Full size table

Figure 12 shows heating time for different particle diameter ratios. Larger particles have higher thermal resistance than smaller particles and when segregation occurs and larger particles move towards the outer layer of the bed, they resist heat penetration into the inner layer of the bed. Accordingly, increasing the diameter ratio causes decreasing the heat transfer rate.

Fig. 12
figure 12

Variation of the heating time for different diameter ratios (\( d_{r} \)) of particles at rotation speed of 10 rpm (\( v_{r} \) = 0.5)

Full size image

4 Conclusions

Heat transfer was studied by using discrete element method (DEM) and conductive heat transfer model inside horizontal rotating drum filled with binary-sized particles. Heat transfer and segregation phenomena were taking place simultaneously. To characterize heat transfer and radial segregation phenomenon, the heating time and the mixing entropy were used. In the radial segregation, large particles tend to move towards the outer layer of the bed since small particles tend to move towards the central core of the bed. As particulate bed was heated from the outer wall, larger particles heat up faster than smaller ones. In this simulation, the effects of mixture characteristics such as volume and diameter ratio on the heat transfer rate were investigated. It was found, that at high volume ratios, by increasing the number of small particles and decreasing the number of large particles the heat transfer rate improved. However, the heating time is not linearly dependent on the volume ratio. Also, increasing the diameter ratio led to heat up the particulate bed slowly; since the mean temperature difference between large and small particles was increased and the bed became more non-uniform. Furthermore, the effects of operating parameters such as rotation speed and filling level on heat transfer were investigated in the binary sized particulate bed. Higher rotation speed enhanced the mixing of the particulate bed and therefore, the heat transfer rate was increased. Increasing the filling level caused decreasing of heat transfer rate because the contact rate of particles with the hot wall decreased.