Deconvolution of a Cumulative Distribution Function with Some Non-standard Noise Densities

Abstract

Let X be a continuous random variable having an unknown cumulative distribution function F. We study the problem of estimating F based on i.i.d. observations of a continuous random variable Y from the model Y = X + Z. Here, Z is a random noise distributed with known density g and is independent of X. We focus on some cases of g in which its Fourier transform can vanish on a countable subset of ℝ. We propose an estimator $\hat F$ for F and then investigate upper bounds on convergence rate of $\hat F$ under the root mean squared error. Some numerical experiments are also provided.

1 Introduction

Consider the model

$$ Y= X+ Z, $$

(1)

where Y, X, and Z are univariate continuous random variables with densities h, f, and g, respectively. The random variables X and Z are assumed to be independent and not observed. The quantity Z is considered as a random noise, so we call g the noise density. Let Y₁,…, Y_n be i.i.d. observations of Y. Our aim is to estimate the unknown cumulative distribution function (cdf, for short) $F(x): = \mathbb {P}(X\leq x)$ of X on the basis of the observations. This problem can be viewed as a deconvolution problem of cdf’s.

In practice, the noise density g is often unknown; however, it can be empirically estimated by some additional data drawn from the noise distribution, see, e.g., Diggle and Hall [5], Neumann [19], Comte and Lacour [3], and Kappus and Mabon [15]. Therefore, to simplify the presentation as well as the statistical analysis, we assume that the noise density g is exactly known throughout the present paper.

In general, the difficulty of the deconvolution problem depends heavily on the smoothness of the noise density g, which is often characterized by the decay of the function $g^{\text {ft}}(t): = {\int }_{-\infty }^{\infty } g(x)e^{itx}dx$, called the Fourier transform of g, at the infinity. Ordinary smooth and supersmooth are the most common types of the smoothness. We give an overview of some research concerning the problem in the literature. As the pioneering result, Gaffey [12] established a consistent estimator for F when the random noise Z has a normal distribution with zero mean and known variance. Fan [10] proposed an estimator for F based on integration of a density deconvolution kernel estimator. In the case of supersmooth noise densities, he proved that this estimator attains minimax optimal convergence rate over a Hölder class of target cdf’s. However, a minimax result for the case of ordinary smooth noise densities was not presented. Cordy and Thomas [2] focused on the model that the distribution of X is a mixture of a finite number of known distributions and the random variable Z has a normal distribution with zero mean and known variance. Dattner et al. [7] proposed an estimator based on a direct inversion formula for continuous cdf’s and studied minimax complexity of this estimator over a Sobolev class of target cdf’s when the noise density g is assumed to be ordinary smooth. After that, Dattner and Reiser [8] considered theoretical properties of the estimator in the case of supersmooth g and also studied practical aspects of this estimator. Note also that the deconvolution problem is closely related to the problem of estimating linear functionals $T_{\varphi }(f) = {\int }_{-\infty }^{\infty }{\varphi (u)f(u)du}$ studied by Butucea and Comte [1] and Pensky [20] in the cases of ordinary smooth and supersmooth noise densities. This problem reduces to the estimation of F(x) if φ is the indicator function of (−∞, x].

In all mentioned papers, the Fourier transform g^ft is assumed to be non-vanishing on ℝ. This assumption is quite standard in topics on density deconvolution. However, there are also many usual densities violating this assumption, for example, uniform densities, triangular densities, self-convolved uniform densities, or convolution of a uniform density with another density. Hence, it is necessary to consider the cases where the function g^ft may have zeros on ℝ, which are informally called non-standard cases of g. In the context of density deconvolution, there exist some papers mentioning some non-standard cases of g, such as Devroye [4], Hall and Meister [13], Meister [17, 18], Delaigle and Meister [6], Trong et al. [21], and Trong and Phuong [22]. However, to the best of our knowledge, the nonparametric estimation of the cdf F with the non-standard noise density g has still not been considered much. In the present paper, we fill partly the gap by considering the following non-standard cases of g:

• 1⁰) The density g satisfies the condition

  $$ \frac{c_{1}|\sin(\eta t)|^{\mu} e^{-\kappa|t|^{\beta}}}{(1+|t|)^{\nu}} \leq \left|g^{\text{ft}}(t) \right| \leq \frac{c_{2} e^{-\kappa|t|^{\beta}}}{(1 + |t|)^{\nu}} \quad\text{ for all }t\in\mathbb{R}, $$

  (2)

  where c₁, c₂, η, ν, β > 0, $\mu \in \mathbb {Z}^{+}$ and κ ≥ 0. In addition, there exist c, ξ, t_∗ > 0 such that

  $$ 1 - \left|g^{\text{ft}}(t)\right|^{2} \leq c t^{\xi} \quad \text{ for all } t\in [0, t_{\ast}]. $$

  (3)

• 2⁰) The density g satisfies the condition

  $$ {\int}_{- \infty}^{\infty} g(x) e^{k|x|^{\gamma}} dx \leq M $$

  (4)

  with k, γ, M > 1.

Condition (2) is a combination of conditions (2.2) and (2.3) in Delaigle and Meister [6]. Clearly, under the condition, the function g^ft can have isolated zeros at non-zero integer multiples of π/η. Examples for condition (2) with κ = 0 include uniform densities, self-convolved uniform densities, or convolution of uniform densities with ordinary smooth densities, whereas convolution of uniform densities with supersmooth densities is a standard example for condition (2) with κ > 0. Condition (3) describes the local behavior of the function g^ft in a neighborhood of t = 0 and satisfies if g^ft is smooth at the point. This condition was also used in Dattner et al. [7] and Dattner and Reiser [8].

Condition (4) has been less studied in the statistical literature, but it is not very strict. For example, it is satisfied with uniform densities, triangular densities, normal densities (1 < γ < 2), or compactly supported densities. Under condition (4), the function g^ft is the restriction of a non-trivial analytic function on ℂ and is allowed to vanish at some isolated points on ℝ. As we will see in Lemma 3, if the density g satisfies condition (4), then it also holds condition (3). In fact, condition (4) was also considered in Trong et al. [21]; however, this paper is only focused on nonparametric estimation of the unknown density f.

The rest of the present paper is organized as follows. In Section 2, we introduce our estimator. In Section 3, we consider mean consistency as well as upper bounds on convergence rate of the proposed estimator under the root mean squared error (RMSE). Some numerical experiments are performed in Section 4. Finally, proofs of all results in Section 3 are given in Section 5.

For convenience, we introduce some notations. For $\varphi \in L^{1}(\mathbb {R})$, the notation ∥φ∥₁ denotes the usual $L^{1}(\mathbb {R})$-norm of φ. The convolution of two functions u and v is defined by $(u \ast v)(x) = {\int }_{-\infty }^{\infty } u(x - t)v(t)dt$. The numbers Re{z}, Im{z}, and $\overline {z}$ denote the real part, the imaginary part, and the conjugate number of a complex number z, respectively. The number λ(A) is the Lebesgue measure of a measurable set A ⊂ ℝ. For two sequences of positive real numbers {a_n}_n and {b_n}_n, the notation a_n ≤ O(b_n) means a_n ≤const ⋅ b_n for large n.

2 Estimator

Since the cdf F is continuous on ℝ, one has (see, e.g., Gil-Pelaez [11])

$$ F(x) = \frac{1}{2} - \frac{1}{\pi }{\int}_{0}^{\infty} \frac{1}{t}\text{Im} \left\{e^{- itx}f^{\text{ft}}(t)\right\}dt, \quad x\in\mathbb{R}, $$

(5)

where the integral is understood as an improper Riemann integral. In view of the equality (5), we first construct an estimator for the unknown function f^ft and then replace f^ft by the proposed estimator to derive an estimator for F.

In order to construct an estimator for f^ft, we use the relation

$$ h = f \ast g $$

(6)

deduced from the assumption on the independence of X and Z in the model (1). Taking the Fourier transform to both sides of (6) yields the equality h^ft = f^ftg^ft.

Put Z(g^ft) = {t > 0 : g^ft(t) = 0}. If Z(g^ft) = ∅, we have f^ft(t) = h^ft(t)/g^ft(t) for all t > 0. Then, using $\widehat {h^{\text {ft}}}(t): = n^{-1}{\sum }_{j = 1}^{n} e^{it Y_{j}}$ as an estimator for h^ft(t), we can estimate f^ft(t) by the quantity $\widehat {h^{\text {ft}}}(t)/ g^{\text {ft}}(t)$. However, the quantity $\widehat {h^{\text {ft}}}(t)/ g^{\text {ft}}(t)$ is unstable if Z(g^ft) ≠ ∅. It is because $\lim _{t \to s}\widehat {h^{\text {ft}}}(t)/ g^{\text {ft}}(t) = \infty$ for s ∈ Z(g^ft), and in addition, $\lim _{t \to \infty }\widehat {h^{\text {ft}}}(t)/ g^{\text {ft}}(t) = \infty$. Thus, another suitable estimator for f^ft(t) is required.

To avoid divisions by zero or by numbers very close to zero, we propose to replace the quantity $\widehat {h^{\operatorname {ft}}}(t)/ g^{\operatorname {ft}}(t)$ by the quantity

$$\widehat{f^{\text{ft}}}(t) : = \frac{g^{\text{ft}}(- t)}{\delta t^{a} + \left| g^{\text{ft}}(t)\right|^{2}}\widehat{h^{\text{ft}}}(t), \quad t>0, $$

where a > 0 is a given parameter, and δ > 0 is a regularization parameter which will be chosen later. For every δ > 0, the function $\widehat {f^{\text {ft}}}$ is bounded on (0, ∞), and for each t > 0, we have $\mathbb {E}[\widehat {f^{\text {ft}}}(t)] \to f^{\text {ft}}(t)$ as δ → 0. Moreover, if δ ≡ δ(n) satisfies δ → 0 and nδ →∞ as n →∞, then $\widehat {f^{\text {ft}}}(t) \to f^{\text {ft}}(t)$ almost surely, as n →∞. Hence, we can use $\widehat {f^{\text {ft}}}(t)$ to estimate f^ft(t). Substituting f^ft(t) in (5) by $\widehat {f^{\text {ft}}}(t)$ yields an estimator for F(x) of the final form

$$ \hat F(x; Y_{1}, \ldots, Y_{n}) = \frac{1}{2} - \frac{1}{\pi }{\int}_{0}^{\infty} \frac{1}{t}\text{Im} \left\{e^{- itx}\frac{g^{\text{ft}}(- t)}{\delta t^{a} + \left|g^{\text{ft}}(t) \right|^{2}}\frac{1}{n}\sum\limits_{j = 1}^{n} e^{it Y_{j}} \right\}dt. $$

(7)

Note that the estimator $\hat F(x)$ is well-defined for all values of x ∈ ℝ because the integral in the right-hand side of (7) is convergent for a > 0.

3 Mean Consistency and Rates of Convergence of $\hat F$

In this section, we consider mean consistency and rates of convergence of the estimator $\hat F$ in (7) under the RMSE. First, the following proposition gives general upper bounds for the quantity $\sup _{x \in \mathbb {R}}\sqrt {\mathbb {E}| \hat {F}(x) - F(x)|^{2}}$.

Proposition 1

Let$\hat {F}$be as in (7) with 0 < a ≤ a₀, wherea₀ ≥ 1 is a fixed realnumber. Suppose${\int }_{s}^{\infty } \frac {|f^{\text {ft}}(t)|}{t}dt <\infty$forsomes > 0.

• (a) Ifg satisfies condition (3) and$h^{\text {ft}}\in L^{1}(\mathbb {R})$, then for 0 < δ < 1/(4max{t_∗; 1}) we have

  $$\begin{array}{@{}rcl@{}} \sup\limits_{x \in \mathbb{R}}\sqrt{\mathbb{E}|\hat{F}(x) - F(x)|^{2}} &\leq& \left( D_{0}+\frac{E_{0}}{a}\right)\left( \delta + {\int}_{t_{0}}^{\infty} \frac{\delta t^{a - 1}\left|f^{\text{ft}}(t) \right|}{\delta t^{a} + \left|g^{\text{ft}}(t)\right|^{2}}dt + \frac{1}{\sqrt{n}} \right.\\ &&\left. + \sqrt{\frac{1}{n}{\int}_{t_{0}}^{\infty} \frac{|g^{\text{ft}}(t)|^{2}}{t^{2}(\delta t^{a} + |g^{\text{ft}}(t)|^{2})^{2}}dt}\right), \end{array} $$

  wheret₀ = min{(4c)^− 1/ξ; t_∗; 1}, $D_{0} = \pi ^{-1}\max \{4+\xi ^{-1}\ln {2};\sqrt {2\|h^{\text {ft}}\|_{1}}\}$, E₀ = 4/(3π).

• (b) Ifg satisfies condition (4), then for 0 < δ < 1/4 wehave

  $$\sup_{x \in \mathbb{R}}\sqrt{\mathbb{E}|\hat{F}(x) - F(x)|^{2}} \leq \left( D_{1}+\frac{E_{1}}{a}\right)\left( \delta + {\int}_{t_{1}}^{\infty} \frac{\delta t^{a - 1}|f^{\text{ft}}(t)|}{\delta t^{a} + |g^{\text{ft}}(t)|^{2}}dt + \frac{1}{\delta\sqrt{n}}\right), $$

  where t₁ = (4c₀)^− 1, c₀ = 2[e − 1 + M/(k − 1)] + [e − 1 + M/(k − 1)]², D₁ = π^− 1(4 + ln2) and $E_{1} = \pi ^{-1}[\ln {2}+\sqrt {2}(4c_{0})^{a_{0}}]$.

Remark 1

In Proposition 1, the condition ${\int }_{s}^{\infty } \frac {|f^{\text {ft}}(t)|}{t}dt <\infty$ for some s > 0 implies

$${\int}_{t_{j}}^{\infty} \frac{\delta t^{a - 1}\left|f^{\operatorname{ft}}(t)\right|}{\delta t^{a} + \left|g^{\operatorname{ft}}(t)\right|^{2}}dt<\infty \quad\text{for } j = 1,2. $$

The condition 0 < a ≤ a₀ is to ensure that the parameter a cannot become very large. In fact, for every δ > 0, we have

$$\liminf\limits_{a \to \infty} {\int}_{t_{j}}^{\infty} \frac{\delta t^{a - 1}\left|f^{\operatorname{ft}}(t) \right|}{\delta t^{a} + \left|g^{\operatorname{ft}}(t)\right|^{2}}dt \geq \liminf\limits_{a \to \infty} {\int}_{1}^{\infty} \frac{\delta t^{a - 1}\left|f^{\operatorname{ft}}(t)\right|}{\delta t^{a} + \left|g^{\operatorname{ft}}(t) \right|^{2}}dt = {\int}_{1}^{\infty}\frac{|f^{\text{ft}}(t)|}{t}dt. $$

Hence, the upper bounds of $\sup _{x \in \mathbb {R}}\sqrt {\mathbb {E}|\hat {F}(x) - F(x)|^{2}}$ in Proposition 1 would not converge to zero if we let a →∞.

On the basis of Proposition 1, we establish the mean consistency of the estimator $\hat F$ in the following theorem.

Theorem 1

Suppose the assumptions of Proposition1 hold. Moreover, supposeδis a positive parameter depending on the sample sizen in such a way thatδ → 0 and$\delta \sqrt {n} \to \infty$asn → ∞.

• (a) Ifg satisfies (2), (3), and$h^{\text {ft}}\in L^{1}(\mathbb {R})$, then$\sup _{x \in \mathbb {R}} \sqrt {\mathbb {E}|\hat {F}(x) - F(x)|^{2}} \to 0$asn → ∞.

• (b) Ifg satisfies (4), then$\sup _{x \in \mathbb {R}} \sqrt {\mathbb {E}|\hat {F}(x) - F(x)|^{2}} \to 0$asn → ∞.

In order to study rates of convergence of the estimator $\hat F$, we need the following definition.

Definition 1

For α > − 1/2 and L > 0, the class $\mathcal {F}_{\alpha , L}$ is the set of all cdf’s Φ such that Φ has a Lebesgue density ϕ on ℝ satisfying ${\int }_{ - \infty }^{\infty } |\phi ^{\operatorname {ft}}(t)|^{2} (1 + t^{2})^{\alpha } dt \leq L$.

The class $\mathcal {F}_{\alpha , L}$ contains the cdf’s of normal, Cauchy, Laplace, and gamma distributions, among others. The parameter α describes degree of smoothness of densities corresponding to the cdf’s in $\mathcal {F}_{\alpha , L}$. The class $\mathcal {F}_{\alpha , L}$ for α > − 1/2 contains continuous cdf’s, whereas the class $\mathcal {F}_{\alpha , L}$ for α > 1/2 contains cdf’s with bounded continuous densities. The class was also considered in some papers, such as Dattner et al. [7], Dattner and Reiser [8], and Dattner [9].

Remark 2

If f is the density corresponding to $F\in \mathcal {F}_{\alpha , L}$, then ${\int }_{r}^{\infty } \frac {|f^{\text {ft}}(t)|}{t}dt <\infty$ for all r > 0. Thus, f satisfies the condition in Proposition 1.

For the estimator $\hat {F}(\cdot ; Y_{1}, \ldots , Y_{n})$, we denote

$$\mathcal{R}[\hat{F}; \mathcal{F}_{\alpha ,L}] = \sup\limits_{F \in \mathcal{F}_{\alpha ,L}}\sup\limits_{x \in \mathbb{R}} \sqrt{\mathbb{E}|\hat{F} (x; Y_{1}, \ldots, Y_{n}) - F(x)|^{2}}. $$

This quantity is called maximal risk of F over the class $\mathcal {F}_{\alpha , L}$ with respect to the RMSE.

Remark 3

In the present paper, we focus on the deconvolution problem of cdf’s with some non-standard cases of g. However, to show that our estimator is reasonable, we list here convergence rates of the estimator in the cases of ordinary smooth and the supersmooth noise densities which are the same as the existing results in the literature.

First, suppose the noise density g is supersmooth of order θ > 0, i.e., there exist c₃, c₄, d > 0 such that

$$c_{3} e^{- d|t|^{\theta}} \leq \left|g^{\operatorname{ft}}(t)\right| \leq c_{4}e^{- d|t|^{\theta}}\quad\textrm{for all } t\in\mathbb{R}. $$

In addition, suppose g satisfies condition (3). Then, for α > − 1/2, L > 0, 0 < a ≤ a₀ and δ = n^{−(2σ+ 1)/4}(lnn)^−a/(2θ) with 0 < σ < 1/2, we obtain from Proposition 1(a) that

$$\mathcal{R}[\hat{F}; \mathcal{F}_{\alpha ,L}] \leq O\left( \frac{1}{\min\{a;1\}}(\ln n)^{-(\alpha + 1/2)/\theta} \right). $$

Clearly, this convergence rate is the same as the optimal one established in Dattner and Reiser [8] for the same conditions on g.

Next, we consider the case where g is ordinary smooth of order σ > 0, i.e., there exist c₅, c₆ > 0 such that

$$c_{5} (1+|t|)^{-\sigma} \leq |g^{\text{ft}}(t)| \leq c_{6} (1+|t|)^{-\sigma} \quad\text{ for all } \ t\in\mathbb{R}. $$

Moreover, suppose g satisfies condition (3). Let L > 0, α > − 1/2 and max{α + 1; 1}≤ a ≤ a₀. Then, based on Proposition 1(a), we derive the following results:

• (i) if 0 < σ < 1/2 and α + σ > 1/2, then for δ = n^{−(2α+ 1)/(4α+ 4σ)} we obtain

  $$\mathcal{R}[\hat{F}; \mathcal{F}_{\alpha, L}] \leq O\left( n^{-1/2} \right). $$

• (ii) if σ = 1/2 and α + σ > 1/2, then for δ = n^{−(a+ 1)/(2α+ 1)} we obtain

  $$\mathcal{R}[\hat{F}; \mathcal{F}_{\alpha, L}]\leq O\left( n^{-1/2}(\ln{n})^{1/2}\right). $$

• (iii) If σ > 1/2 and α + σ > 1/2, then for δ = n^{−(a+ 2σ)/(2α+ 2σ)} we obtain

  $$\mathcal{R}[\hat F;\mathcal{F}_{\alpha ,L}] \leq O\left( n^{-(2\alpha+ 1)/(4\alpha + 4\sigma)} \right). $$

We realize that all the mentioned convergence rates coincide with the convergence rates given in Theorem 2.1 of Dattner et al. [7] for the case of ordinary smooth noise densities.

We now turn to the non-standard cases of g that are main subject of our paper. We derive upper bounds on convergence rate of $\mathcal {R}[\hat {F}; \mathcal {F}_{\alpha ,L}]$ in the following theorem.

Theorem 2

Letα > − 1/2, L > 0 andleta₀beas in Proposition1.

• (a) Supposeg satisfies both condition (3) and condition (2) withκ = 0, ν + α > 1/2. When 0 < a < 1, we obtainfor

  $$\delta = n^{-[2a + (2\alpha + 1)(2\mu + 1) + 4(\nu + \mu)]/[4a + 4(2\alpha + 1)(\mu + 1) + 8(\nu + \mu)]} $$

  that

  $$\mathcal{R}[\hat F;\mathcal{F}_{\alpha ,L}] \leq O\left( \frac{1}{a} n^{-(\alpha + 1/2)/[2a + 2(2\alpha + 1)(\mu + 1) + 4(\nu + \mu)]} \right). $$

  When 1 ≤ a ≤ a₀, the following results hold:

  • If − 1/2 < α < 1/2, then for δ = n^{−[a+(2α+ 1)μ+ 2(ν + μ)]/[2a+(2α+ 1)(2μ+ 1)+ 4(ν + μ)]}we have

    $$\mathcal{R}[\hat{F};\mathcal{F}_{\alpha ,L}] \leq O\left( n^{-(\alpha + 1/2)/[2a + (2\alpha + 1)(2\mu + 1) + 4(\nu + \mu)]} \right). $$

  • If α = 1/2, then forδ = n^{−(4a+ 1 + 16μ+ 8ν)/(8a+ 10 + 32μ+ 16ν)}we have

    $$\mathcal{R}[\hat{F};\mathcal{F}_{\alpha ,L}] \leq O\left( n^{- 2/(4a + 5 + 16\mu + 8\nu)} \right). $$

  • If α > 1/2, then forδ = n^{−[2a− 2+(2α+ 1)(2μ+ 1)+ 4(ν + μ)]/[4a− 4 + 4(2α+ 1)(μ+ 1)+ 8(ν + μ)]}we have

    $$\mathcal{R}[\hat{F};\mathcal{F}_{\alpha,L}] \leq O\left( n^{-(\alpha + 1/2)/[2a - 2 + 2(2\alpha + 1)(\mu + 1) + 4(\nu + \mu)]}\right). $$

• (b) Suppose g satisfies both condition (3) and condition (2) with κ > 0. Then for 0 < a ≤ a₀and δ = n^−ζ (0 < ζ < 1/2), we obtain

  $$\mathcal{R}[\hat{F}; \mathcal{F}_{\alpha ,L}] \leq O\left( \frac{1}{\min\{a;1\}} (\ln n)^{- (\alpha + 1/2)/\beta} \right). $$

• (c) Suppose gsatisfies condition (4). Then, for 0 < a ≤ a₀and

  $$\delta = n^{-(\omega + 1/4)}\left( \frac{\ln n}{\sqrt{\ln(\ln n)}} \right)^{-a/2}\quad \text{ with } 0<\omega<1/4, $$

  we obtain

  $$\mathcal{R}[\hat{F};\mathcal{F}_{\alpha ,L}] \leq O\left( \frac{1}{\min\{a;1\}}(\ln n)^{- 2(\gamma - 1)(2\alpha + 1)/[\gamma(2\alpha + 7)]} \right). $$

  In particular, ifgis compactly supported, then

  $$\mathcal{R}[\hat{F}; \mathcal{F}_{\alpha ,L}] \leq O\left( \frac{1}{\min\{a;1\}} (\ln n)^{- 2(2\alpha + 1)/(2\alpha + 7)} \right). $$

In Theorem 2, all the convergence rates depend on the parameter α. The larger α is, the faster convergence rates will be. The convergence rates in the part (a) are faster than those of the parts (b) and (c). Unlike the results in the part (a), the convergence rate in the part (b) is independent of μ, η, and ν, which implies the existence of isolated zeros of the function g^ft does not effect in this rate. For the part (c), the first logarithm rate will decrease if the parameter γ is increased; in particular, the found convergence rate in the case of compactly supported g is independent of γ and corresponds to the first one as γ → ∞.

Remark 4

In the parts (b) and (c) of Theorem 2, the choices of the regularization parameter δ are independent of α, so we can compute the estimator $\hat F$ without any knowledge on α.

Remark 5

Under the condition $|g^{\text {ft}}(t)| \leq c_{7} e^{-d|t|^{\theta }}$ for all $t\in \mathbb {R}$, with c₇, d, θ > 0, it is shown in Dattner and Reiser [8] that there exists c₈ > 0 independent of n such that $\inf _{\tilde F}\mathcal {R}[\tilde {F}; \mathcal {F}_{\alpha ,L}] \geq c_{8} (\ln n)^{-(\alpha + 1/2)/\theta }$, for L > 0 sufficiently large and α > 1/2. Here, the infimum is taken over all possible estimators $\tilde F$ of F based on the data Y₁,…, Y_n. Combining this result with the result of Theorem 2(b) gives that if the noise density g satisfies both condition (3) and the condition

$$\frac{c_{1}|\sin(\eta t)|^{\mu} e^{-\kappa |t|^{\beta}}} {(1 + |t|)^{\nu}} \leq \left|g^{\operatorname{ft}}(t)\right| \leq c_{9} e^{-\kappa|t|^{\beta}} \quad\text{ for all } t\in\mathbb{R}, $$

in which c₁, c₉, η, ν, β, κ > 0 and $\mu \in \mathbb {Z}^{+}$, then O ((lnn)^{−(α+ 1/2)/β}) with α > 1/2 is the minimax optimal convergence rate of deconvolution estimators for F over the class $\mathcal {F}_{\alpha , L}$.

In Theorem 2(a), we derive some upper bounds on convergence rate of $\mathcal {R}[\hat {F};\mathcal {F}_{\alpha ,L}]$ in several different cases of a and α. We can see that the upper bound obtained for 0 < a < 1 is the best when a = a_n, where

$$ a_{n} = \frac{2{\ell_{0}^{2}}}{k_{0}\ln n-2\ell_{0}+\sqrt{{k_{0}^{2}}(\ln n)^{2}- 4k_{0}\ell_{0}\ln n}} $$

(8)

with

$$ k_{0}=(2\alpha+ 1)/4, \quad \ell_{0}=(2\alpha+ 1)(\mu+ 1)+ 2(\nu+\mu). $$

(9)

In the case 1 ≤ a ≤ a₀, the upper bounds are the best as possible when a is also the smallest as possible, namely a = 1. Since the parameter a is fixed, we need to compare these two best cases to give user-choices of a. The following corollary provides a solution for this problem.

Corollary 1

Letα > − 1/2 andL > 0. Supposeg satisfies the assumptions of Theorem2(a). Leta_n, k₀, ℓ₀bedefined as in (8) and (9). The following results hold:

• If − 1/2 < α ≤ 1/2, thenfor$\delta \! =\! n^{-[2a_{n} + (2\alpha + 1)(2\mu + 1) + 4(\nu + \mu )]/[4a_{n} + 4(2\alpha + 1)(\mu + 1) + 8(\nu + \mu )]}$theconvergence rate of the upper bound is fastest asa = a_nand

  $$\inf\limits_{a>0}\mathcal{R}[\hat{F};\mathcal{F}_{\alpha ,L}] \leq O\left( \frac{1}{a_{n}}n^{-k_{0}/(a_{n}+\ell_{0})}\right). $$

• If α > 1/2, then for δ = n^{−[(2α+ 1)(2μ+ 1)+ 4(ν + μ)]/[4(2α+ 1)(μ+ 1)+ 8(ν + μ)]}the convergence rate of the upper bound is fastest as a = 1 and

  $$\inf\limits_{a>0}\mathcal{R}[\hat{F};\mathcal{F}_{\alpha ,L}] \leq O(n^{-k_{0}/\ell_{0}}). $$

4 Numerical Experiments

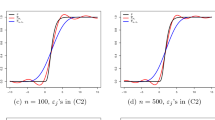
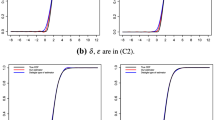
We now perform some numerical experiments to confirm the convergence of the estimator $\hat {F}$ in (7). We assume that the target random variable X has the gamma distribution with the shape parameter 3 and the scale parameter $1/\sqrt {3}$. Denote by σ_X and σ_Z the standard deviations of X and Z, respectively. The random noise Z is chosen such that we have a specific noise to signal ratio σ_Z/σ_X. We are interested in the values σ_Z/σ_X = 0.2,0.5, corresponding to 20%, 50% noise contamination, respectively. We consider the case where Z has the uniform distribution on [−𝜖, 𝜖], denoted by Z ∼ Uniform(−𝜖, 𝜖), where $\epsilon =\sqrt {3}/5$ (20% contamination) and $\epsilon = \sqrt {3}/2$ (50% contamination).

We generate 1000 independent samples (X_p,1, … , X_{p, n}), p = 1, … , 1000, of size n from the distribution of X, and each of the results is then added by a sample of noises (Z_p,1,…, Z_{p, n}) generated from the distribution of Z to obtain a sample (Y_p,1,…, Y_{p, n}). We then approximate the RMSE $\sqrt {\mathbb {E}{{| {\hat F(x) - F(x)}|}^{2}}}$ at every x by empirical RMSE

$$\vartheta(x) = \sqrt{\frac{1}{1000}\sum\limits_{p = 1}^{1000} |\hat{F}_{p}(x) - F(x)|^{2}}, $$

where

$$ \hat{F}_{p}(x) = \frac{1}{2} - \frac{1}{\pi}{\int}_{0}^{\infty} \frac{1}{t}\text{Im} \left\{e^{-itx}\frac{g^{\operatorname{ft}}(- t)}{\delta t^{a} + \left|g^{\operatorname{ft}}(t)\right|^{2}}\frac{1}{n}\sum\limits_{j = 1}^{n} e^{it Y_{p,j}} \right\}dt. $$

Here, the parameter a is given, whereas the regularization parameter δ is chosen as in Theorem 2(c), i.e.,

$$\delta = n^{-(\omega + 1/4)} \left( \frac{\ln n}{\sqrt{\ln(\ln n)}}\right)^{-a/2}\quad \text{with } 0<\omega<1/4. $$

In the setup, we take ω = 1/8. Note that we only compute the empirical RMSE 𝜗(x) at q_0.1, q_0.25, q_0.5, q_0.75, and q_0.9, which correspond to the percentiles 0.1, 0.25, 0.5, 0.75, and 0.9 of the distribution of X.

Tables 1 and 2 present the empirical RMSE 𝜗(x) when $Z\sim \operatorname {Uniform}(-\sqrt {3}/5, \sqrt {3}/5)$ and $Z\sim \operatorname {Uniform}(-\sqrt {3}/2, \sqrt {3}/2)$, respectively. In these tables, the values of 𝜗(x) are evaluated with respect to different values of n and a, where n = 100 and 500, a = 0.01, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 50, and 100. We can see from the tables that at every x ∈{q_0.1, q_0.25, q_0.5, q_0.75, q_0.9} and n ∈{100,500}, the values of 𝜗(x) for the case 20% contamination are smaller than those of 𝜗(x) for the case 50% contamination. For every value of a, the values of 𝜗(x) are uniformly decreased when increasing n, i.e., n = 100 and 500. The results are compatible with the mean consistency of the estimator $\hat {F}$. However, for every value of n, the values of 𝜗(x) are quite mixed when increasing a. For instance, when increasing a, the values of 𝜗(x) are uniformly decreased at the points q_0.25, q_0.75 and are relatively increased at the point q_0.5. When a nears zero, the values of 𝜗(x), except at q_0.5, become large. For large a, for example a = 100, the obtained results of 𝜗(x) are also quite mixed.

Table 1 The empirical RMSE 𝜗(x) × 100 when $Z\sim \operatorname {Uniform}(-\sqrt {3}/5, \sqrt {3}/5)$

Table 2 The empirical RMSE 𝜗(x) × 100 when $Z\sim \operatorname {Uniform}(-\sqrt {3}/2, \sqrt {3}/2)$

5 Proofs

In order to prove Proposition 1, we need the three following lemmas.

Lemma 1

For every$t,s,x\in \mathbb {R}$, we have

$$\begin{array}{@{}rcl@{}} Q&:=&\left|{\int}_{-\infty}^{\infty} \operatorname{Im}\left\{e^{it(y - x)} g^{\operatorname{ft}}(- t)\right\}\operatorname{Im} \left\{e^{is(y - x)}g^{\operatorname{ft}}(- s)\right\}h(y)dy\right|\\ &\leq& \frac{1}{2}\left|g^{\operatorname{ft}}(t)\right|\left|g^{\operatorname{ft}}(s)\right|\left( \left|h^{\operatorname{ft}}(t - s)\right| + \left|h^{\operatorname{ft}}(t + s)\right| \right). \end{array} $$

Proof

Using the Fubini theorem, we have

$$\begin{array}{@{}rcl@{}} Q &=&\left|{\int}_{- \infty}^{\infty} \left( {\int}_{- \infty}^{\infty} g(u)\sin(t(y - x - u))du \right)\left( {\int}_{-\infty}^{\infty} g(v)\sin(s(y - x - v))dv \right)h(y)dy\right|\\ & =&\left|{\int}_{-\infty}^{\infty} {\int}_{-\infty}^{\infty} g(u)g(v)\left( {\int}_{-\infty}^{\infty} h(y)\sin(t(y - x - u))\sin(s(y - x - v))dy \right)dudv\right|. \end{array} $$

By the equality $\sin (u)\sin (v) = \frac {1}{2}[\cos (u-v) - \cos (u+v)]$ for $u,v\in \mathbb {R}$, we have

$$\begin{array}{@{}rcl@{}} &&{\int}_{-\infty }^{\infty} h(y)\sin(t(y - x - u))\sin(s(y - x - v))dy\\ && = \frac{1}{2}{\int}_{-\infty}^{\infty} h(y)\cos((t - s)(y - x) + sv - tu)dy\\ &&\quad - \frac{1}{2}{\int}_{- \infty}^{\infty} h(y)\cos((t + s)(y - x) - sv - tu)dy\\ &&= \frac{1}{2}\operatorname{Re} \left\{{\int}_{-\infty}^{\infty} h(y)e^{i((t - s)(y - x) + sv - tu)}dy \right\} - \frac{1}{2}\operatorname{Re}\left\{{\int}_{- \infty}^{\infty} h(y) e^{i((t + s)(y - x) - sv - tu)}dy \right\}\\ && = \frac{1}{2}\operatorname{Re} \left\{e^{i(-(t - s)x + sv - tu)}{h^{\operatorname{ft}}}(t - s) \right\} - \frac{1}{2}\operatorname{Re} \left\{e^{i(-(t + s)x - sv - tu)}h^{\operatorname{ft}}(t + s)\right\}. \end{array} $$

Thus,

$$\begin{array}{@{}rcl@{}} Q & =& \frac{1}{2}\left|\operatorname{Re}\left\{g^{\operatorname{ft}}(- t)\left[e^{- i(t - s)x} h^{\operatorname{ft}}(t - s)g^{\operatorname{ft}}(s) - e^{- i(s + t)x}h^{\operatorname{ft}}(t + s) g^{\operatorname{ft}}(- s)\right]\right\} \right|\\ &\leq& \frac{1}{2}\left|g^{\operatorname{ft}}(t)\right|\left|g^{\operatorname{ft}}(s) \right|\left( \left|h^{\operatorname{ft}}(t - s) \right| + \left|h^{\operatorname{ft}}(t + s)\right| \right), \end{array} $$

and this completes the proof. □

Lemma 2

Leta > 0, δ > 0 andt₀be as in Proposition1(a). If$h^{\text {ft}} \in L^{1}(\mathbb {R})$, then

$$\begin{array}{@{}rcl@{}} I &:=&{\int}_{t_{0}}^{\infty} {\int}_{t_{0}}^{\infty} \frac{\left|g^{\operatorname{ft}}(t)\right| \left|g^{\operatorname{ft}}(s)\right|\left( \left|h^{\operatorname{ft}}(t - s)\right| + \left|h^{\operatorname{ft}}(t + s)\right|\right)}{ts(\delta t^{a} + \left|g^{\operatorname{ft}}(t) \right|^{2}) (\delta s^{a} + \left|g^{\operatorname{ft}}(s)\right|^{2})}dsdt\\ &\leq& 2\|h^{\operatorname{ft}}\|_{1}{\int}_{t_{0}}^{\infty} \frac{\left|g^{\operatorname{ft}}(t) \right|^{2}}{t^{2}(\delta t^{a} + \left|g^{\operatorname{ft}}(t)\right|^{2})^{2}}dt. \end{array} $$

Proof

We have

$$\begin{array}{@{}rcl@{}} I & =& {\int}_{t_{0}}^{\infty} {\int}_{t_{0}}^{\infty} \frac{|g^{\operatorname{ft}}(t)| |g^{\operatorname{ft}}(s)| |h^{\operatorname{ft}}(t - s)|} {ts(\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}) (\delta s^{a} + |g^{\operatorname{ft}}(s)|^{2})}dsdt\\ && + {\int}_{t_{0}}^{\infty} {\int}_{t_{0}}^{\infty} \frac{|g^{\operatorname{ft}}(t)| |g^{\operatorname{ft}}(s)| |h^{\operatorname{ft}}(t + s)|} {ts(\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}) (\delta s^{a} + |g^{\operatorname{ft}}(s)|^{2})}dsdt =: I_{1} + I_{2}. \end{array} $$

(10)

Using the Cauchy–Schwarz inequality and the Fubini theorem, we obtain

$$\begin{array}{@{}rcl@{}} I_{1} &\leq& \sqrt{{\int}_{t_{0}}^{\infty} {\int}_{t_{0}}^{\infty} \frac{|g^{\operatorname{ft}}(t)|^{2} |h^{\operatorname{ft}}(t - s)|} {t^{2} (\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2})^{2}}dsdt \cdot {\int}_{t_{0}}^{\infty} {\int}_{t_{0}}^{\infty} \frac{|g^{\operatorname{ft}}(s)|^{2} |h^{\operatorname{ft}}(t - s)|} {s^{2} (\delta s^{a} + |g^{\operatorname{ft}}(s)|^{2})^{2}}dtds}\\ & =& \sqrt {{\int}_{t_{0}}^{\infty} \frac{|g^{\operatorname{ft}}(t)|^{2}}{t^{2}(\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2})^{2}}\left( {\int}_{t_{0}}^{\infty} |h^{\operatorname{ft}}(t - s)|ds \right)dt}\\ &&\times \sqrt {{\int}_{t_{0}}^{\infty} \frac{|g^{\operatorname{ft}}(s)|^{2}} {s^{2}(\delta s^{a} + |g^{\operatorname{ft}}(s)|^{2})^{2}}\left( {\int}_{t_{0}}^{\infty} |h^{\operatorname{ft}}(t - s)|dt \right)ds}\\ & \leq& \|h^{\text{ft}}\|_{1} {\int}_{t_{0}}^{\infty} \frac{|g^{\operatorname{ft}}(t)|^{2}}{t^{2}(\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2})^{2}}dt. \end{array} $$

The same bound holds for I₂. Combining (10) with the bounds of I₁ and I₂, we obtain the desired conclusion. □

Lemma 3

If the noise densityg satisfies condition (4) , then1 − |g^ft(t)|² ≤ c₀tfor all 0 < t ≤ 1, wherec₀ = 2[e − 1 + M/(k − 1)] + [e − 1 + M/(k − 1)]².

Proof

Fix 0 < t ≤ 1. We have

$$ g^{\operatorname{ft}}(t) = {\int}_{- \infty}^{\infty} \sum\limits_{l = 0}^{\infty} \frac{(itx)^{l}}{l!}g(x)dx. $$

(11)

For l = 0, 1, … , we have

$$\begin{array}{@{}rcl@{}} {\int}_{- \infty}^{\infty} |x|^{l} g(x)dx & \leq& 1 + {\int}_{|x| > 1} |x|^{l} e^{- k|x|^{\gamma}} e^{k|x|^{\gamma}} g(x)dx\\ &\leq& 1 + \frac{l!}{k^{l}}{\int}_{|x| > 1} \frac{1}{|x|^{(\gamma - 1)l}} e^{k|x|^{\gamma}}g(x)dx \leq 1 + M\frac{l!}{k^{l}}, \end{array} $$

where we have used the inequality e^u ≥ u^l/l! (with u > 0, l = 0, 1, …) and condition (4). Hence,

$$\begin{array}{@{}rcl@{}} \sum\limits_{l = 0}^{\infty} {\int}_{- \infty}^{\infty} \left|\frac{(itx)^{l}}{l!} g(x)\right|dx &=& \sum\limits_{l = 0}^{\infty} \frac{t^{l}}{l!}{\int}_{- \infty}^{\infty} |x|^{l} g(x)dx \leq \sum\limits_{l = 0}^{\infty} \frac{1}{l!}\left( 1 + M\frac{l!}{k^{l}} \right)\\ & =& e + M\sum\limits_{l = 0}^{\infty} \left( \frac{1}{k}\right)^{l} = e + \frac{Mk}{k - 1}<\infty. \end{array} $$

Therefore, we can interchange between the integration and the summation in (11) to derive

$$g^{\operatorname{ft}}(t) = \sum\limits_{l = 0}^{\infty} \frac{(it)^{l}}{l!}{\int}_{- \infty}^{\infty} x^{l} g(x)dx = 1 + t\phi(t), $$

where

$$\phi(t) = \sum\limits_{l = 1}^{\infty} \frac{i^{l}}{l!}\left( {\int}_{- \infty}^{\infty} x^{l} g(x)dx\right) t^{l - 1}. $$

Then, we have

$$\begin{array}{@{}rcl@{}} 1 - |g^{\operatorname{ft}}(t)|^{2} &=& 1- [1 + t\phi(t)][1 + t \overline{\phi(t)}] = - t [\phi(t) + \overline{\phi(t)}] - t^{2} |\phi(t)|^{2} \\ & =& - 2t\operatorname{Re}\{\phi(t)\} - t^{2}|\phi(t)|^{2} \leq (2|\phi(t)| + |\phi(t)|^{2})t. \end{array} $$

(12)

Moreover,

$$ |\phi(t)| \leq \sum\limits_{l = 1}^{\infty} \frac{1}{l!}{\int}_{- \infty}^{\infty} |x|^{l} g(x)dx \leq \sum\limits_{l = 1}^{\infty} \frac{1}{l!}\left( 1 + M\frac{l!}{k^{l}} \right) = e - 1 + \frac{M}{k - 1}. $$

(13)

Thus, from (12) and (13), we deduce 1 −|g^ft(t)|² ≤ c₀t, where c₀ is as in the statement of the present lemma. □

Proof of Proposition 1

Put $B(x)=|\mathbb {E}\hat {F}(x) - F(x)|$ and $V(x)=\operatorname {Var} \hat {F}(x)$.

(a) Using the Fubini theorem, the equality (5), the equality h^ft = f^ftg^ft, and the inequality |Im{z}|≤|z| for $z\in \mathbb {C}$, we obtain

$$\begin{array}{@{}rcl@{}} B(x) &=& \left|\frac{1}{\pi}{\int}_{0}^{\infty} \frac{1}{t}\operatorname{Im} \left\{e^{-itx}\frac{|g^{\operatorname{ft}}(t)|^{2}}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}} f^{\operatorname{ft}}(t)\right\}dt - \frac{1}{\pi}{\int}_{0}^{\infty} \frac{1}{t}\operatorname{Im} \left\{e^{-itx} f^{\operatorname{ft}}(t) \right\}dt \right|\\ &\leq& \frac{1}{\pi}{\int}_{0}^{\infty} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt\\ & =&\frac{1}{\pi}\left( {\int}_{0}^{t_{0}} \frac{\delta t^{a - 1} |f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt + {\int}_{t_{0}}^{\infty} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt \right). \end{array} $$

For all 0 < t < t₀, we deduce from condition (3) that |g^ft(t)|² ≥ 3/4, so

$${\int}_{0}^{t_{0}} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt \leq \frac{4}{3}\delta {\int}_{0}^{t_{0}} t^{a - 1}dt = \frac{4{t_{0}^{a}}}{3a}\delta \leq \frac{4}{3a}\delta. $$

Thus,

$$ B(x) \leq \frac{1}{\pi}\left( \frac{4}{3a}\delta + {\int}_{t_{0}}^{\infty} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt \right). $$

(14)

Next, we bound V (x). In fact, we have

$$\begin{array}{@{}rcl@{}} V(x) &=& \frac{1}{n \pi^{2}}\operatorname{Var} \left( {\int}_{0}^{\infty} \frac{1}{t}\operatorname{Im} \left\{e^{it(Y_{1} - x)}\frac{g^{\operatorname{ft}}(- t)}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}} \right\}dt \right) \\ &\leq&\frac{1}{n\pi^{2}}\mathbb{E}\left|{\int}_{0}^{\infty} \frac{1}{t}\operatorname{Im} \left\{e^{it(Y_{1} - x)}\frac{g^{\operatorname{ft}}(- t)}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}} \right\}dt \right|^{2}\\ & \leq& \frac{2}{n\pi^{2}}[V_{1}(x) + V_{2}(x)], \end{array} $$

(15)

where

$$\begin{array}{@{}rcl@{}} V_{1}(x) &=& \mathbb{E}\left|{\int}_{0}^{t_{0}} \frac{1}{t}\operatorname{Im} \left\{e^{it(Y_{1} - x)}\frac{g^{\operatorname{ft}}(- t)}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}} \right\}dt \right|^{2},\\ V_{2}(x) &=& \mathbb{E}\left|{\int}_{t_{0}}^{\infty} \frac{1}{t}\operatorname{Im} \left\{e^{it(Y_{1} - x)}\frac{g^{\operatorname{ft}}(- t)}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}} \right\}dt \right|^{2}. \end{array} $$

We first bound V₁(x). For all 0 < t < t₀, using condition (3), we have

$$|\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2} - 1| \leq \delta t^{a} + 1 - |g^{\operatorname{ft}}(t)|^{2} \leq \delta + c t^{\xi} < \frac{1}{4} + ct^{\xi} \leq \frac{1}{2}, $$

so

$$\frac{1}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}} = \frac{1}{1 + (\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2} - 1)} = 1 + \sum\limits_{l = 1}^{\infty} (1 - |g^{\operatorname{ft}}(t)|^{2} - \delta t^{a})^{l}. $$

Then,

$$\begin{array}{@{}rcl@{}} V_{1}(x) &=& \mathbb{E} \left|{\int}_{0}^{t_{0}} \frac{1}{t}\operatorname{Im} \left\{e^{it(Y_{1} - x)} g^{\operatorname{ft}}(- t)\left[1 + \sum\limits_{l = 1}^{\infty} (1 - |g^{\operatorname{ft}}(t)|^{2} - \delta t^{a})^{l} \right] \right\}dt \right|^{2}\\ &\leq& 2[V_{1,1}(x) + V_{1,2}(x)], \end{array} $$

where

$$\begin{array}{@{}rcl@{}} V_{1,1}(x) &=& \mathbb{E} \left|{\int}_{0}^{t_{0}} \frac{1}{t}\operatorname{Im} \left\{e^{it(Y_{1} - x)} g^{\operatorname{ft}}(- t)\right\}dt \right|^{2},\\ V_{1,2}(x) &=& \mathbb{E} \left|{\int}_{0}^{t_{0}} \frac{1}{t}\operatorname{Im} \left\{e^{it(Y_{1} - x)} g^{\operatorname{ft}}(- t)\right\}\sum\limits_{l = 1}^{\infty} (1 - |g^{\operatorname{ft}}(t)|^{2} - \delta t^{a})^{l} dt\right|^{2}. \end{array} $$

By the Fubini theorem, we have

$$\begin{array}{@{}rcl@{}} V_{1,1}(x) &=& \mathbb{E} \left|{\int}_{0}^{t_{0}} \frac{1}{t}{\int}_{- \infty}^{\infty} g(u)\sin (t(Y_{1} - x - u))du dt \right|^{2}\\ &\leq& \mathbb{E} \left( {\int}_{- \infty}^{\infty} g(u)\left|{\int}_{0}^{t_{0}(Y_{1} - x - u)} \frac{\sin v}{v}dv \right|du \right)^{2} \leq 4, \end{array} $$

where we have used the inequality $\left |{\int }_{0}^{t_{0}(Y_{1} - x - u)} \frac {\sin v}{v}dv \right | \leq 2$ (see Lemma 2.6.2, Section 2.6 in Kawata [14]). Also, by the inequality (u + v)^p ≤ 2^p− 1(u^p + v^p) for u, v ≥ 0, p ≥ 1 and by condition (3), we have

$$\begin{array}{@{}rcl@{}} V_{1,2}(x) &\leq& \left( {\int}_{0}^{t_{0}} \frac{1}{t}\sum\limits_{l = 1}^{\infty} \left( 1 - |g^{\operatorname{ft}}(t)|^{2} + \delta t^{a}\right)^{l} dt \right)^{2}\\ &\leq& \left( {\int}_{0}^{t_{0}} \frac{1}{t}\sum\limits_{l = 1}^{\infty} 2^{l - 1}\left[(c t^{\xi})^{l} + (\delta t^{a})^{l}\right] dt \right)^{2}\\ &=& \left( \sum\limits_{l = 1}^{\infty} 2^{l - 1} c^{l}{\int}_{0}^{t_{0}} t^{\xi l - 1}dt + \sum\limits_{l = 1}^{\infty} 2^{l - 1} \delta^{l}{\int}_{0}^{t_{0}} t^{al - 1}dt \right)^{2}\\ &=& \left( \frac{1}{2\xi}\sum\limits_{l = 1}^{\infty} \frac{(2ct_{0}^{\xi})^{l}}{l} + \frac{1}{2a}\sum\limits_{l = 1}^{\infty} \frac{(2\delta {t_{0}^{a}})^{l}}{l}\right)^{2}. \end{array} $$

Note that $0<2\delta {t_{0}^{a}}\leq 2\delta \leq 1/2$ for a ≥ 1, and

$$0<2\delta {t_{0}^{a}}\leq 2\delta t_{\ast}^{a} \leq 2\delta (\max\{t_{\ast}; 1\})^{a} \leq 2\delta \max\{t_{\ast}; 1\} \leq 1/2 $$

for 0 < a < 1. Moreover, $0< 2c t_{0}^{\xi } \leq 1/2$. Therefore, we derive

$$V_{1,2}(x) \leq \left( \frac{1}{2\xi}\sum\limits_{l = 1}^{\infty} \frac{(1/2)^{l}}{l} + \frac{1}{2a}\sum\limits_{l = 1}^{\infty} \frac{(1/2)^{l}}{l} \right)^{2} = \frac{(\ln{2})^{2}}{4} \left( \frac{1}{\xi} + \frac{1}{a} \right)^{2}, $$

where we have used the equality ${\sum }_{m = 1}^{\infty }\frac {u^{m}}{m} = -\ln (1-u)$ for all 0 < u < 1. From the bounds of V_1,1(x) and V_1,2(x), we deduce

$$ V_{1}(x) \leq 8 + \frac{(\ln{2})^{2}}{2} \left( \frac{1}{\xi} + \frac{1}{a}\right)^{2}. $$

(16)

We next bound V₂(x). Indeed, using the Fubini theorem, Lemma 1, and Lemma 2, we have

$$\begin{array}{@{}rcl@{}} V_{2}(x) & =& {\int}_{-\infty}^{\infty} \left( {\int}_{t_{0}}^{\infty} \frac{1}{t}\operatorname{Im} \left\{e^{it(y - x)}\frac{g^{\operatorname{ft}}(- t)}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}} \right\}dt\right)^{2} h(y)dy \\ &\leq& {\int}_{t_{0}}^{\infty} {\int}_{t_{0}}^{\infty} \frac{\left|{\int}_{- \infty}^{\infty} \operatorname{Im}\left\{e^{it(y - x)} g^{\operatorname{ft}}(- t)\right\}\operatorname{Im} \left\{e^{is(y - x)} g^{\operatorname{ft}}(- s) \right\}h(y)dy \right|}{ts(\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2})(\delta s^{a} + |g^{\operatorname{ft}}(s)|^{2})}dsdt \\ & \leq& \frac{1}{2}{\int}_{t_{0}}^{\infty} {\int}_{t_{0}}^{\infty} \frac{|g^{\operatorname{ft}}(t)| |g^{\operatorname{ft}}(s)| (|h^{\operatorname{ft}}(t - s)| + |h^{\operatorname{ft}}(t + s)|)}{ts(\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}) (\delta s^{a} + |g^{\operatorname{ft}}(s)|^{2})}dsdt \\ & \leq& \|h^{\text{ft}}\|_{1} {\int}_{t_{0}}^{\infty} \frac{|g^{\operatorname{ft}}(t)|^{2}}{t^{2} (\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2})^{2}}dt. \end{array} $$

(17)

It follows from (15), (16), and (17) that

$$ V(x) \leq \frac{1}{\pi^{2}}\left[16 + (\ln{2})^{2} \left( \frac{1}{\xi} + \frac{1}{a}\right)^{2} \right] \frac{1}{n} + \frac{2\|h^{\text{ft}}\|_{1}}{\pi^{2} n}{\int}_{t_{0}}^{\infty} \frac{|g^{\operatorname{ft}}(t)|^{2}}{t^{2}(\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2})^{2}}dt. $$

(18)

From the inequality $\sqrt {\mathbb {E} |\hat {F}(x) - F(x)|^{2}} \leq B(x) + \sqrt {V(x)}$, (14), (18), and the inequality $\sqrt {u+v} \leq \sqrt {u} + \sqrt {v}$ for u, v ≥ 0, we deduce

$$\begin{array}{@{}rcl@{}} \sup_{x \in \mathbb{R}} \sqrt{\mathbb{E}|\hat{F}(x) - F(x)|^{2}} &\leq&C_{0}\left( \delta + {\int}_{t_{0}}^{\infty} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt + \frac{1}{\sqrt{n}} \right.\\ &&\left. + \sqrt{\frac{1}{n}{\int}_{t_{0}}^{\infty} \frac{|g^{\operatorname{ft}}(t)|^{2}}{t^{2}(\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2})^{2}}dt}\right) \end{array} $$

(19)

with

$$C_{0} = \frac{1}{\pi}\max\left\{4+ \frac{\ln{2}}{\xi} + \frac{4}{3a}; \sqrt {2\| h^{\text{ft} }\|_{1}}\right\}. $$

Note that C₀ ≤ D₀ + E₀/a, where D₀, E₀ are as in the statement of the present proposition. Combining this with (19) yields the result of this part.

(b) According to Lemma 3, we see that when g satisfies (4), it also satisfies (3) with c ≡ c₀ > 2, ξ ≡ 1 and t_∗≡ 1. Hence, for t₀ = min {(4c)^− 1/ξ;t_∗;1} = (4c₀)^− 1 =: t₁ and 0 < δ < 1/(4max{t_∗;1}) = 1/4, the bounds for B(x) and V₁(x) in the part (a) are still preserved. More precisely, we derive

$$B(x) \leq \frac{1}{\pi}\left( \frac{{4}}{3a}\delta + {\int}_{t_{1}}^{\infty} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt \right), \quad V_{1}(x) \leq 8 + \frac{(\ln{2})^{2}}{2} \left( 1 + \frac{1}{{a}} \right)^{2}. $$

For the quantity V₂(x) in the part (a), we have some changes in its estimation. In fact,

$$V_{2}(x) \leq \left( {\int}_{t_{1}}^{\infty} \frac{|g^{\operatorname{ft}}(t)|}{t(\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2})}dt \right)^{2} \leq \frac{t_{1}^{- 2a}}{a^{2} \delta^{2}} = \frac{(4c_{0})^{2a}}{a^{2}\delta^{2}} \leq \frac{(4c_{0})^{2a_{0}}}{a^{2}\delta^{2}}. $$

Combining the estimate $V(x) \leq \frac {2}{\pi ^{2} n}[V_{1}(x) + V_{2}(x)]$ with the bounds of V₁(x), V₂(x) yields

$$V(x) \leq \frac{1}{\pi^{2}}\left[16 + (\ln{2})^{2}\left( 1 + \frac{1}{a} \right)^{2} + \frac{2(4c_{0})^{2a_{0}}}{a^{2}} \right]\frac{1}{n\delta^{2}} . $$

From the inequality $\sqrt {\mathbb {E}|\hat {F}(x) - F(x)|^{2}} \leq B(x) + \sqrt {V(x)}$, the bounds of B(x), V (x) and the inequality $\sqrt {u+v} \leq \sqrt {u} + \sqrt {v}$ for u, v ≥ 0, we deduce

$$\sup_{x \in \mathbb{R}}\sqrt{\mathbb{E}|\hat{F}(x) - F(x)|^{2}} \leq C_{1}\left( \delta + {\int}_{t_{1}}^{\infty} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt + \frac{1}{\delta\sqrt{n}}\right) $$

with

$$C_{1} =\frac{1}{\pi}(4+\ln{2})+ \frac{1}{\pi}[\ln{2} + \sqrt 2 {{\left( {4{c_{0}}} \right)}^{a_{0}}}]\frac{1}{a} = : D_{1} +E_{1}\frac{1}{a}. $$

The proof of this part has completed. □

Proof of Theorem 1

(a) From condition (2), we deduce $Z(g^{\text {ft}}) \subset \{j\eta /\pi : j\in \mathbb {Z}^{+}\}$, which implies λ(Z(g^ft)) = 0. Therefore,

$$ {\int}_{t_{0}}^{\infty} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt = {\int}_{(t_{0},\infty)\backslash Z(g^{\operatorname{ft}})} \frac{\delta t^{a-1}|f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt \to 0 \quad\text{ as } \delta\to 0, $$

(20)

we have used the Lebesgue dominated convergence theorem. Moreover,

$$ \frac{1}{n}{\int}_{t_{0}}^{\infty} \frac{|g^{\operatorname{ft}}(t)|^{2}}{t^{2}(\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2})^{2}}dt \leq \frac{1}{n \delta^{2}}{\int}_{t_{0}}^{\infty} \frac{1}{t^{2 + 2a}}dt \leq \frac{t_{0}^{-(2a + 1)}}{(2a + 1)n\delta^{2}}. $$

(21)

Combining Proposition 1(a) with (20), (21) and the assumptions on the parameter δ, we obtain the desired conclusion.

(b) Put $G(z) = {\int }_{-\infty }^{\infty } g(x) e^{izx}dx$ with z ∈ ℂ. Under condition (4), we can check that G is a non-trivial analytic function on ℂ. This implies G has only isolated zeros on ℂ. Combining this with the fact that G(t) = g^ft(t) for all t ∈ ℝ yields λ(Z(g^ft)) = 0. Hence, by the same arguments as in the part (a), we have ${\int }_{t_{1}}^{\infty } \frac {\delta t^{a - 1}|f^{\operatorname {ft}}(t)|}{\delta t^{a} + |g^{\operatorname {ft}}(t)|^{2}}dt$ as δ → 0. Combining this with Proposition 1(b) and the assumptions on the parameter δ, we obtain the conclusion. □

To prove Theorem 2, we need the three following important lemmas.

Lemma 4

Suppose the noise densityg satisfies condition (2). ForR > 1 andε > 0, put$B_{g^{\text {ft}}; R, \varepsilon } = \{0< t\leq R: |g^{\text {ft}}(t)| \leq \varepsilon \}$. Then thereexistsC₂ ≡ C₂(c₁, η, ν, μ) > 0 suchthat

$$\lambda \left( B_{g^{\operatorname{ft}};R,\varepsilon} \right) \leq C_{2} \varepsilon^{1/\mu} R^{\nu /\mu + 1} e^{\kappa^{\ast} R^{\beta}} $$

with κ^∗ = (κ/μ)(1 + 2π/η)^β.

Proof

Put $D_{g^{\text {ft}}; R, \varepsilon } = \{t\in [-R, R]: |g^{\text {ft}}(t)| \leq \varepsilon \}$. For every $t\in D_{g^{\text {ft}}; R, \varepsilon }$, there exists an integer number j such that (2j − 1)π/(2η) ≤ t < (2j + 1)π/(2η), which gives |t − (jπ)/η| ≤ π/(2η). Since $t\in D_{g^{\text {ft}}; R, \varepsilon }$, we have |t| ≤ R and |g^ft(t)|≤ ε. Using condition (2) and the inequality |sinu| ≥ 2|u|/π for |u| ≤ π/2, we have

$$\begin{array}{@{}rcl@{}} |g^{\operatorname{ft}}(t)| &\geq& c_{1}\left|\sin\left( \eta \left( t - \frac{j\pi}{\eta}\right) \right) \right|^{\mu} (1 + |t|)^{-\nu} e^{-\kappa |t|^{\beta}}\\ &\geq& c_{1}\left( \frac{2\eta}{\pi}\left|t - \frac{j\pi}{\eta} \right| \right)^{\mu} (1 + |t|)^{- \nu} e^{- \kappa|t|^{\beta}}. \end{array} $$

It implies

$$c_{1}\left( \frac{2\eta}{\pi}\left|t - \frac{j\pi}{\eta}\right| \right)^{\mu} (1 + |t|)^{-\nu} e^{- \kappa|t|^{\beta}} \leq \varepsilon, $$

so

$$\left|t - \frac{j\pi}{\eta}\right| \leq \frac{\pi}{2\eta} c_{1}^{-1/\mu} \varepsilon^{1/\mu}(1 + |t|)^{\nu /\mu} e^{(\kappa /\mu)|t|^{\beta}}. $$

Since

$$|t| \leq \left|t - \frac{j\pi}{\eta}\right| + \left|\frac{j\pi}{\eta}\right| \leq \left( \frac{1}{2} + |j|\right)\frac{\pi}{\eta}, $$

we deduce

$$\left|t - \frac{j\pi}{\eta}\right| \leq \frac{\pi }{2\eta} c_{1}^{- 1/\mu} \varepsilon^{1/\mu} \left[1 + \left( \frac{1}{2} + |j|\right)\frac{\pi}{\eta}\right]^{\nu /\mu} e^{(\kappa /\mu)[(1/2 + |j|)(\pi/\eta)]^{\beta}}. $$

It follows that t ∈ I_j, where

$$\begin{array}{@{}rcl@{}} I_{j} &=& \left[\frac{j\pi}{\eta } - \frac{\pi}{2\eta} c_{1}^{-1/\mu} \varepsilon^{1/\mu} \left[1 + \left( \frac{1}{2} + |j|\right)\frac{\pi}{\eta}\right]^{\nu/\mu} e^{(\kappa/\mu)[(1/2 + |j|)(\pi/\eta)]^{\beta}},\right.\\ &&\left.\frac{j\pi}{\eta} + \frac{\pi}{2\eta} c_{1}^{-1/\mu} \varepsilon^{1/\mu} \left[1 + \left( \frac{1}{2} + |j|\right)\frac{\pi }{\eta} \right]^{\nu/\mu} e^{(\kappa/\mu)[(1/2 + |j|)(\pi/\eta)]^{\beta}} \right]. \end{array} $$

Moreover, we have |(jπ)/η| ≤|t − (jπ)/η| + |t| ≤ π/(2η) + R, so |j| ≤ 1/2 + (Rη)/π. We deduce therefore t ∈∪_{|j| ≤ 1/2+(Rη)/π}I_j, which gives

$$D_{g^{\text{ft}}; R, \varepsilon} \subset \bigcup_{|j|\leq 1/2 + (R\eta )/\pi} I_{j}. $$

From the relation, we obtain

$$\begin{array}{@{}rcl@{}} \lambda \left( D_{g^{\operatorname{ft}};R,\varepsilon} \right) & \leq& \sum\limits_{|j| \leq 1/2 + (R\eta)/\pi} \lambda(I_{j})\\ & =&\sum\limits_{|j| \leq 1/2 + (R\eta)/\pi} \frac{\pi}{\eta} c_{1}^{-1/\mu} \varepsilon^{1/\mu} \left[1 + \left( \frac{1}{2} + |j|\right)\frac{\pi}{\eta}\right]^{\nu /\mu} e^{(\kappa/\mu)[(1/2 + |j|)(\pi /\eta)]^{\beta}}\\ & \leq& \frac{2\pi}{\eta} c_{1}^{-1/\mu} \varepsilon^{1/\mu} \sum\limits_{0 \leq j \leq 1/2 + (R\eta)/\pi} \left[1 + \left( \frac{1}{2} + j\right)\frac{\pi}{\eta}\right]^{\nu/\mu} e^{(\kappa/\mu)[(1/2 + j)(\pi /\eta)]^{\beta}}\\ & \leq& \frac{2\pi}{\eta} c_{1}^{-1/\mu} \varepsilon^{1/\mu} {\int}_{0}^{3/2 + (R\eta)/\pi} \left[1 + \left( \frac{1}{2} + u\right)\frac{\pi}{\eta} \right]^{\nu /\mu} e^{(\kappa /\mu)[(1/2 + u)(\pi /\eta)]^{\beta}}du \\ & \leq& \frac{2\pi}{\eta} c_{1}^{-1/\mu} \varepsilon^{1/\mu} \left( 1 + \frac{2\pi}{\eta} + R\right)^{\nu /\mu} e^{(\kappa /\mu)(2\pi /\eta + R)^{\beta}}\left( \frac{3}{2} + \frac{R\eta}{\pi} \right)\\ & \leq& \frac{2\pi}{\eta} c_{1}^{- 1/\mu} \left( 2 + \frac{2\pi}{\eta}\right)^{\nu /\mu}\left( \frac{3}{2} + \frac{\eta}{\pi} \right) \varepsilon^{1/\mu} R^{\nu /\mu + 1} e^{(\kappa/\mu)(1 + 2\pi /\eta)^{\beta} R^{\beta}}. \end{array} $$

Finally, using the estimate $\lambda (B_{g^{\operatorname {ft}};R,\varepsilon }) \leq \frac {1}{2}\lambda (D_{g^{\operatorname {ft}};R,\varepsilon })$ gives the conclusion. □

Lemma 5

Suppose the noise densityg satisfies condition (4). For everyε > 0, we put

$$ s_{\varepsilon} = \inf \left\{s \geq 1:{\int}_{|x| \geq s} g(x)dx \leq \varepsilon\right\}. $$

(22)

Let q > 1. For every ε > 0 small enough, let R_ε > 0 satisfy

$$ 2e s_{\varepsilon} R_{\varepsilon} \ln(15 e^{3} R_{\varepsilon}^{q}) = \ln \left( \frac{1}{4\varepsilon} \right). $$

(23)

Then, we have

$$ C_{3} \left( \ln\left( \frac{1}{\varepsilon} \right)\right)^{\frac{2(\gamma - 1)}{\gamma (q + 2)}} \leq R_{\varepsilon} \leq C_{4} \frac{\ln\left( \frac{1}{\varepsilon}\right)}{\sqrt{\ln \left( \ln\left( \frac{1}{\varepsilon}\right) \right)}} $$

(24)

for ε > 0 small enough, where

$$C_{3} = \left( \frac{1}{4e\sqrt{15 e^{3}}}\left( \frac{k}{2}\right)^{\frac{1}{\gamma}} \right)^{\frac{2}{q + 2}},\qquad C_{4} = \frac{1}{4e}\sqrt{\frac{\gamma(q + 2)}{(\gamma - 1)q\ln(15 e^{3})}}. $$

Furthermore, we have

$$ \lambda \left( B_{g^{\operatorname{ft}}; R_{\varepsilon}, \varepsilon} \right) \leq R_{\varepsilon}^{1 - q}, $$

(25)

where the set$B_{g^{\operatorname {ft}}; R_{\varepsilon },\varepsilon }$is defined as in Lemma 4.

In addition, if the noise density gis compactly supported on [−S, S] with S > 0, then

$$ C_{5} \left( \ln\left( \frac{1}{\varepsilon}\right)\right)^{\frac{2}{q + 2}} \leq R_{\varepsilon} \leq C_{6} \frac{\ln\left( \frac{1}{\varepsilon}\right)}{\sqrt{\ln\left( \ln \left( \frac{1}{\varepsilon} \right) \right)}} $$

(26)

for ε > 0 small enough, where

$$C_{5} = \left( \frac{1}{4eS\sqrt{15 e^{3}}}\right)^{\frac{2}{q + 2}},\quad C_{6} = \frac{1}{4e}\sqrt{\frac{q + 2}{q\ln(15e^{3})}}. $$

Proof

The proof is divided into two steps. In Step 1, we give the existence of R_ε satisfying (23) and verify the estimates (24) and (26). In Step 2, we check the estimate (25).

• Step 1. First, from the definition of s_ε in (22), we deduce ${\int }_{|x| \geq s_{\varepsilon }} g(x)dx = \varepsilon$. On the other hand, since g satisfies (4), we have ${\int }_{|x| \geq s_{\varepsilon }} g(x)dx \leq Me^{- k(s_{\varepsilon })^{\gamma }}$. Hence, $Me^{- k(s_{\varepsilon })^{\gamma }} \geq \varepsilon$, which gives

  $$ s_{\varepsilon} \leq \left( \frac{1}{k}\ln \left( \frac{M}{\varepsilon}\right)\right)^{\frac{1}{\gamma}}. $$

  (27)

Next, consider the function φ_ε(R) = 2es_εR ln(15e³R^q) + ln(4ε), R > 0. Clearly, the function φ_ε is strictly increasing on (0, ∞). Moreover, φ_ε(R) →∞ as R →∞, and as R → 0⁺, φ_ε(R) → ln(4ε) < 0 for ε > 0 small enough. Hence, there exists a unique R_ε > 0 such that ψ_ε(R_ε) = 0, i.e., R_ε satisfies (23). Also, it follows from (23), the inequality $\ln (u) \leq \sqrt {u}$ for u > 0 and the inequality $\ln (\frac {1}{4\varepsilon }) \geq \frac {1}{2}\ln (\frac {1}{\varepsilon })$ for all ε > 0 small enough that

$$ R_{\varepsilon}^{(q + 2)/2} \geq \frac{1}{2es_{\varepsilon}\sqrt{15 e^{3}}} \ln \left( \frac{1}{4\varepsilon} \right) \geq \frac{1}{4es_{\varepsilon}\sqrt {15e^{3}}}\ln \left( \frac{1}{\varepsilon}\right) $$

(28)

for ε > 0 small enough. Thus, we obtain from (27) and (28) that

$$R_{\varepsilon}^{(q + 2)/2} \geq \frac{k^{1/\gamma}}{4e\sqrt{15e^{3}}} \left( \ln\left( \frac{M}{\varepsilon} \right)\right)^{-\frac{1}{\gamma}}\ln\left( \frac{1}{\varepsilon} \right). $$

Combining the latter inequality with the fact that $\ln \left (\frac {M}{\varepsilon } \right ) \leq 2\ln \left (\frac {1}{\varepsilon } \right )$ for ε > 0 small enough, we derive

$$R_{\varepsilon}^{(q + 2)/2} \geq \frac{1}{4e\sqrt{15e^{3}}} \left( \frac{k}{2} \right)^{\frac{1}{\gamma}} \left( \ln\left( \frac{1}{\varepsilon} \right) \right)^{1 - \frac{1}{\gamma}}, $$

which gives

$$ R_{\varepsilon} \geq \left( \frac{1}{4e\sqrt{15e^{3}}} \left( \frac{k}{2}\right)^{\frac{1}{\gamma}}\right)^{\frac{2}{q + 2}} \left( \ln\left( \frac{1}{\varepsilon} \right)\right)^{\left( 1 - \frac{1}{\gamma}\right)\left( \frac{2}{q + 2}\right)} =: C_{3} \left( \ln\left( \frac{1}{\varepsilon}\right)\right)^{\frac{2(\gamma - 1)}{\gamma(q + 2)}}. $$

(29)

Besides, from the equality (23), the Cauchy inequality, and the fact that s_ε ≥ 1, we have

$$ R_{\varepsilon} \leq \frac{\ln\left( \frac{1}{4\varepsilon} \right)}{4e s_{\varepsilon} \sqrt{\ln(15e^{3})q\ln(R_{\varepsilon})}} \leq \frac{\ln\left( \frac{1}{\varepsilon}\right)}{4e\sqrt{\ln(15e^{3})q\ln(R_{\varepsilon})}}. $$

(30)

However, for ε > 0 small enough, we infer from (29) that

$$\ln(R_{\varepsilon}) \geq \ln\left[C_{3}\left( \ln\left( \frac{1}{\varepsilon}\right)\right)^{\frac{2(\gamma - 1)}{\gamma(q + 2)}} \right]\geq \frac{\gamma - 1}{\gamma(q + 2)}\ln\left( \ln\left( \frac{1}{\varepsilon}\right)\right), $$

so

$$ R_{\varepsilon} \leq \frac{1}{4e\sqrt{\frac{(\gamma - 1)q}{\gamma(q + 2)}\ln (15e^{3})}} \cdot \frac{\ln \left( \frac{1}{\varepsilon}\right)}{\sqrt{\ln\left( \ln\left( \frac{1}{\varepsilon}\right) \right)}} =: C_{4}\frac{\ln\left( \frac{1}{\varepsilon}\right)}{\sqrt{\ln \left( \ln\left( \frac{1}{\varepsilon}\right)\right)}}. $$

(31)

Combining (29) and (31) gives (24).

Now, we consider the case where g is compactly supported on [−S, S]. In this case, we have s_ε ≤ S, for all ε > 0 small enough. Then, we obtain from the estimate (28) that

$$R_{\varepsilon}^{(q + 2)/2} \geq \frac{1}{4eS\sqrt{15e^{3}}} \ln\left( \frac{1}{\varepsilon} \right), $$

which yields

$$ R_{\varepsilon} \geq \left( \frac{1}{4eS\sqrt {15e^{3}}}\right)^{\frac{2}{q + 2}} \left( \ln \left( \frac{1}{\varepsilon} \right)\right)^{\frac{2}{q + 2}} =: C_{5} \left( \ln\left( \frac{1}{\varepsilon} \right)\right)^{\frac{2}{q + 2}}. $$

(32)

From the estimate (32), we deduce

$$\ln(R_{\varepsilon}) \geq \ln \left[C_{5} \left( \ln\left( \frac{1}{\varepsilon}\right)\right)^{\frac{2}{q + 2}} \right] \geq \frac{1}{q + 2}\ln\left( \ln\left( \frac{1}{\varepsilon} \right)\right). $$

From the latter estimate and the estimate (30), we obtain

$$ R_{\varepsilon} \leq \frac{1}{4e}\sqrt{\frac{q + 2}{q\ln(15e^{3})}} \cdot \frac{\ln \left( \frac{1}{\varepsilon}\right)}{\sqrt{\ln \left( \ln \left( \frac{1}{\varepsilon} \right) \right)}} = :C_{6} \frac{\ln \left( \frac{1}{\varepsilon} \right)}{\sqrt{\ln \left( \ln \left( \frac{1}{\varepsilon} \right)\right)}}. $$

(33)

Combining (32) with (33) gives (26).

• Step 2. Consider the function $\tilde {\Phi }_{\varepsilon } (z)= |{\Phi }_{\varepsilon }(0)|^{-1} {\Phi }_{\varepsilon }(z)$ with z ∈ ℂ, where

  $${\Phi}_{\varepsilon}(z)={\int}_{-s_{\varepsilon}}^{s_{\varepsilon}} g(x) e^{izx}dx. $$

We see that $\tilde {\Phi }_{\varepsilon }$ is a non-trivial analytic function on ℂ, $\ln (\max _{|z| = 2eR_{\varepsilon }} |\tilde {\Phi }_{\varepsilon }(z)|) \leq 2e s_{\varepsilon } R_{\varepsilon }$ and $|\tilde {\Phi }_{\varepsilon }(0)| = 1$. Hence, using [16, Section 11.3, Theorem 4] with $\eta \equiv R_{\varepsilon }^{-q}$ and R ≡ R_ε, we obtain

$$\begin{array}{@{}rcl@{}} |\tilde{\Phi}_{\varepsilon}(z)| &>& \exp \left\{-\ln \left( \frac{15e^{3}}{R_{\varepsilon}^{-q}}\right)\ln\left( \max_{|z| = 2eR_{\varepsilon}} |\tilde{\Phi}_{\varepsilon}(z)| \right) \right\}\\ & \geq& \exp \left\{- 2es_{\varepsilon} R_{\varepsilon} \ln(15e^{3}R_{\varepsilon}^{q}) \right\} = 4\varepsilon \end{array} $$

for all |z| ≤ R_ε, except a set of disks {B(z_{j, ε}, r_{j, ε})}_j∈J with ${\sum }_{j \in J} r_{j,\varepsilon } \leq \eta R = R_{\varepsilon }^{1 - q}$, where we recall $B(z_{j,\varepsilon },r_{j,\varepsilon }) = \{z \in \mathbb {C}:|z - z_{j,\varepsilon }| < r_{j,\varepsilon }\}$. Therefore,

$$\{z \in \mathbb{C}:~|z| \leq R_{\varepsilon}, |\tilde{\Phi}_{\varepsilon} (z)| \leq 4\varepsilon\} \subset \bigcup\limits_{j \in J} B(z_{j,\varepsilon}, r_{j,\varepsilon}). $$

This leads to

$$\{z \in \mathbb{R}:~|z| \leq R_{\varepsilon}, |{\Phi}_{\varepsilon}(z)| \leq 4|{\Phi}_{\varepsilon}(0)| \varepsilon\} \subset \bigcup\limits_{j \in J} [B(z_{j,\varepsilon},r_{j,\varepsilon}) \cap \mathbb{R}]. $$

Note that $|{\Phi }_{\varepsilon }(0)| = \left |1 - {\int }_{|x| \geq s_{\varepsilon }} g(x)dx\right | \geq 1 - \varepsilon \geq 1/2$ for small ε > 0. Hence, we have

$$\{z \in \mathbb{R}:~|z| \leq R_{\varepsilon},|{\Phi}_{\varepsilon}(z)| \leq 2\varepsilon\} \subset \bigcup\limits_{j \in J} [B(z_{j,\varepsilon},r_{j,\varepsilon}) \cap \mathbb{R}], $$

which gives

$$ \lambda (\{z \in \mathbb{R}:~|z| \leq R_{\varepsilon},|{\Phi}_{\varepsilon} (z)| \leq 2\varepsilon\}) \leq 2\sum\limits_{j \in J} r_{j,\varepsilon} \leq 2R_{\varepsilon}^{1 - q}. $$

(34)

Next, for all $z\in \mathbb {R}$, we have

$$|{\Phi}_{\varepsilon} (z)| \leq |{\Phi}_{\varepsilon} (z) - g^{\operatorname{ft}}(z)| + |g^{\operatorname{ft}}(z)| \leq {\int}_{|x| \geq s_{\varepsilon}} g(x)dx + |g^{\operatorname{ft}}(z)| \leq \varepsilon + |g^{\operatorname{ft}}(z)|, $$

so

$$ \{z \in \mathbb{R}:~|z| \leq R_{\varepsilon}, |g^{\operatorname{ft}}(z)| \leq \varepsilon\} \subset \{z \in \mathbb{R}:~|z| \leq R_{\varepsilon},|{\Phi}_{\varepsilon}(z)| \leq 2\varepsilon\}. $$

(35)

Combining (34) with (35), we deduce

$$\lambda(\{z \in \mathbb{R}:~|z| \leq R_{\varepsilon},|g^{\operatorname{ft}}(z)| \leq \varepsilon\}) \leq 2R_{\varepsilon}^{1 - q}. $$

Finally, using the estimate $\lambda (B_{g^{\operatorname {ft}}; R_{\varepsilon },\varepsilon }) \leq \frac {1}{2}\lambda (\{z \in \mathbb {R}:|z| \leq R_{\varepsilon },|g^{\operatorname {ft}}(z)| \leq \varepsilon \})$ gives (25). The lemma is proved. □

Lemma 6

Suppose$F\in \mathcal {F}_{\alpha , L}$withα > − 1/2 andL > 0. Lett₀be as in Proposition1(a).Then for anyT > 1, wehave

$${\int}_{T}^{\infty} \frac{|f^{\operatorname{ft}}(t)|}{t}dt \leq C_{7} T^{-(2\alpha + 1)/2}, \qquad {\int}_{t_{0}}^{T} \frac{|f^{\operatorname{ft}}(t)|}{t}dt \leq C_{8}, $$

where

$$\begin{array}{@{}rcl@{}} C_{7} &=& \left\{ \begin{array}{ll} \sqrt {\frac{L}{2(2\alpha + 1)}},&\quad \alpha \geq 0,\\ \sqrt {\frac{2^{-(\alpha + 1)}L}{2\alpha + 1}},& \quad - 1/2 < \alpha < 0, \end{array} \right.\\ C_{8} &=& \left\{ \begin{array}{ll} \sqrt {\frac{L}{2(2\alpha + 1)}t_{0}^{-(2\alpha + 1)}},&\quad \alpha \geq 0,\\ \sqrt {\frac{2^{-\alpha}(\alpha + 1)L}{2\alpha + 1}}, &\quad - 1/2 < \alpha < 0. \end{array} \right. \end{array} $$

Proof

Using the Cauchy–Schwarz inequality and the assumption $F\in \mathcal {F}_{\alpha , L}$ gives

$${\int}_{T}^{\infty} \frac{|f^{\operatorname{ft}}(t)|}{t}dt = {\int}_{T}^{\infty} \frac{|f^{\operatorname{ft}}(t)|}{t} (1 + t^{2})^{\alpha/2}(1 + t^{2})^{-\alpha/2}dt \leq \sqrt {\frac{L}{2}{\int}_{T}^{\infty} \frac{1}{t^{2}} (1 + t^{2})^{-\alpha}dt}. $$

If α ≥ 0, then

$${\int}_{T}^{\infty} \frac{|f^{\operatorname{ft}}(t)|}{t}dt \leq \sqrt {\frac{L}{2} {\int}_{T}^{\infty} \frac{1}{t^{2 + 2\alpha}}dt} = \sqrt {\frac{L}{2(2\alpha + 1)} T^{-(2\alpha + 1)}}. $$

If − 1/2 < α < 0, then

$${\int}_{T}^{\infty} \frac{|f^{\operatorname{ft}}(t)|}{t}dt \leq \sqrt{2^{-(\alpha+ 1)}L{\int}_{T}^{\infty} t^{-(2\alpha + 2)}dt} = \sqrt {\frac{2^{-(\alpha + 1)}L}{2\alpha + 1}T^{-(2\alpha + 1)}}. $$

Combining the bounds of ${\int }_{T}^{\infty } \frac {|f^{\operatorname {ft}}(t)|}{t}dt$ in the cases α ≥ 0 and − 1/2 < α < 0, we derive the first statement of the lemma.

We now verify the second statement. By the Cauchy–Schwarz inequality and the assumption $F\in \mathcal {F}_{\alpha , L}$, we have

$${\int}_{t_{0}}^{T} \frac{|f^{\operatorname{ft}}(t)|}{t}dt \leq \sqrt {\frac{L}{2}{\int}_{t_{0}}^{T} \frac{1}{t^{2}} (1 + t^{2})^{-\alpha}dt}. $$

If α ≥ 0, then

$${\int}_{t_{0}}^{T} \frac{|f^{\operatorname{ft}}(t)|}{t}dt\leq \sqrt {\frac{L}{2}{\int}_{t_{0}}^{T} t^{-(2\alpha+ 2)}dt} \leq \sqrt {\frac{L}{2(2\alpha + 1)}t_{0}^{-(2\alpha + 1)}}. $$

If − 1/2 < α < 0, then

$$\begin{array}{@{}rcl@{}} {\int}_{t_{0}}^{T} \frac{|f^{\operatorname{ft}}(t)|}{t}dt &\leq& \sqrt {\frac{L}{2}\left( {\int}_{t_{0}}^{1} \frac{1}{t^{2}} (1 + t^{2})^{-\alpha}dt + {{\int}_{1}^{T}} \frac{1}{t^{2}} (1 + t^{2})^{- \alpha}dt\right)}\\ &\leq& \sqrt{\frac{L}{2}\left( 2^{- \alpha}{\int}_{t_{0}}^{1} \frac{1}{t^{2}}dt + 2^{-\alpha}{{\int}_{1}^{T}} t^{-(2\alpha + 2)}dt\right)}\\ & \leq& \sqrt {2^{-(\alpha + 1)}L\left( 1 + \frac{1}{2\alpha + 1} \right)\frac{1}{t_{0}}}. \end{array} $$

Combining the bounds of ${\int }_{t_{0}}^{T} \frac {|f^{\operatorname {ft}}(t)|}{t}dt$ in the cases α ≥ 0 and − 1/2 < α < 0, we derive the second statement of the lemma. □

Proof of Theorem 2

(a) Suppose $F\in \mathcal {F}_{\alpha , L}$. First, under the assumptions α + ν > 1/2 and $F\in \mathcal {F}_{\alpha , L}$, there exists C_∗,1 ≡ C_∗,1(L, α, ν) > 0 so that ∥h^ft∥₁ ≤ C_∗,1. This implies

$$D_{0} \leq \pi^{-1}\max\{4+\xi^{-1}\ln{2};\sqrt{2C_{\ast, 1}}\} : = D_{0,1}, $$

where the constant D₀ is as in Proposition 1(a).

As in (21), we have

$$Q_{1}:=\frac{1}{n}{\int}_{t_{0}}^{\infty} \frac{|g^{\operatorname{ft}}(t)|^{2}}{t^{2}(\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2})^{2}}dt \leq \frac{t_{0}^{-(2a + 1)}}{(2a + 1)n\delta^{2}} \leq \frac{t_{0}^{-(2a + 1)}}{n\delta^{2}}. $$

Moreover, it follows from the definition of t₀ and the assumption 0 < a ≤ a₀ that

$$t_{0}^{-(2a + 1)}\leq \max\left\{(4c)^{(2a + 1)/\xi}; 1; t_{\ast}^{-(2a + 1)}\right\} \leq \max\left\{(4c)^{(2a_{0}+ 1)/\xi}; 1; t_{\ast}^{-(2a_{0}+ 1)}\right\}. $$

Hence,

$$ Q_{1} \leq \max\left\{(4c)^{(2a_{0}+ 1)/\xi}; 1; t_{\ast}^{-(2a_{0}+ 1)}\right\} \frac{1}{n\delta^{2}}. $$

(36)

For R > 1 and 0 < ε < 1, we have

$$\begin{array}{@{}rcl@{}} Q_{2} &:=& {\int}_{{t_{0}}}^{\infty} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt \\ & \leq& {\int}_{t_{0} \leq t \leq R, |g^{\operatorname{ft}}(t)|\leq \varepsilon} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt + {\int}_{t_{0} \leq t \leq R, |g^{\operatorname{ft}}(t)| > \varepsilon} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt\\ && + {\int}_{R}^{\infty} \frac{|f^{\operatorname{ft}}(t)|}{t}dt\\ & =:& Q_{2,1} + Q_{2,2} + Q_{2,3}. \end{array} $$

We define the set $B_{g^{\operatorname {ft}};R,\varepsilon }$ as in Lemma 4. Applying Lemma 4 with κ = 0, we infer

$$Q_{2,1} \leq \frac{1}{t_{0}}\lambda \left( B_{g^{\operatorname{ft}};R,\varepsilon} \right) \leq \frac{C_{2}}{t_{0}} \varepsilon^{1/\mu} R^{\nu/\mu + 1}. $$

For Q_2,3, applying Lemma 6 gives Q_2,3 ≤ C₇R^{−(2α+ 1)/2}. For Q_2,2, we have

$$Q_{2,2}\leq {\int}_{t_{0}}^{R} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\varepsilon^{2}}dt. $$

Thus,

$$ Q_{2} \leq \frac{C_{2}}{t_{0}} \varepsilon^{1/\mu} R^{\nu/\mu + 1} + {\int}_{t_{0}}^{R} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\varepsilon^{2}}dt + C_{7} R^{- (2\alpha + 1)/2}. $$

(37)

Case 1

0 < a < 1.

In this case, it follows from (37) and Lemma 6 that

$$ Q_{2} \leq \frac{C_{2}}{t_{0}} \varepsilon^{1/\mu} R^{\nu/\mu + 1} + C_{8} \frac{\delta R^{a}}{\varepsilon^{2}} + C_{7} R^{-(2\alpha + 1)/2}. $$

(38)

Combining Proposition 1(a) with (36) and (38), we obtain for 0 < δ < 1/(4min{t_∗;1}) that

$$\mathcal{R}[\hat F;\mathcal{F}_{\alpha ,L}] \leq C_{9} \frac{1}{a}\left( \varepsilon^{1/\mu} R^{\nu/\mu + 1} + \frac{\delta R^{a}}{\varepsilon^{2}} + R^{-(2\alpha + 1)/2} + \frac{1}{\delta \sqrt{n}} \right) $$

with

$$C_{9} = 2(D_{0,1} + E_{0})\sqrt{\max\left\{\max\left\{(4c)^{(2 a_{0} + 1)/\xi};1; t_{\ast}^{-(2a_{0} + 1)}\right\}; \frac{C_{2}}{t_{0}};C_{8};C_{7} \right\}}. $$

Choosing ε = R^{−[(2α+ 1)μ+ 2(ν + μ)]/2} and δ = n^− 1/4R^{−[a+(2α+ 1)μ+ 2(ν + μ)]/2}, we derive

$$\mathcal{R}[\hat F;\mathcal{F}_{\alpha ,L}] \leq O\left( \frac{1}{a} \left( R^{-(2\alpha + 1)/2} + n^{-1/4} R^{[a + (2\alpha + 1)\mu + 2(\nu + \mu)]/2}\right) \right). $$

Then for R = n^{1/[2a+ 2(2α+ 1)(μ+ 1)+ 4(ν + μ)]}, we obtain

$$\mathcal{R}[\hat F;\mathcal{F}_{\alpha,L}] \leq O\left( \frac{1}{a} n^{-(\alpha + 1/2)/[2a + 2(2\alpha + 1)(\mu + 1) + 4(\nu + \mu)]} \right). $$

Case 2

1 ≤ a ≤ a₀.

We have

$$\begin{array}{@{}rcl@{}} {\int}_{t_{0}}^{R} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\varepsilon^{2}}dt &\leq& \frac{\delta R^{a - 1}}{\varepsilon^{2}} {\int}_{t_{0}}^{R} |f^{\operatorname{ft}}(t)|(1 + t^{2})^{\alpha/2} (1 + t^{2})^{-\alpha/2}dt\\ &\leq& \frac{\delta R^{a - 1}}{\varepsilon^{2}}\sqrt{\frac{L}{2}{\int}_{t_{0}}^{R} (1 + t^{2})^{-\alpha}dt}. \end{array} $$

Moreover, we have

$${\int}_{t_{0}}^{R} (1 + t^{2})^{-\alpha}dt \leq \left\{ \begin{array}{ll} \left( \frac{2 - 2\alpha}{1 - 2\alpha}\right)\max\{1;2^{-\alpha}\} R^{1 - 2\alpha},&\quad - 1/2 < \alpha < 1/2,\\ 2\ln{R}, &\quad \alpha= 1/2,\\ \frac{t_{0}^{1 - 2\alpha}}{2\alpha - 1},&\quad\alpha >1/2. \end{array} \right. $$

Hence,

$${\int}_{t_{0}}^{R} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\varepsilon^{2}}dt \leq \left\{ \begin{array}{ll} \sqrt{L\left( \frac{1 - \alpha}{1 - 2\alpha}\right)\max\{1;2^{-\alpha}\}} \frac{\delta R^{a - \alpha - 1/2}}{\varepsilon^{2}},&\quad- 1/2 < \alpha < 1/2,\\ \sqrt{L}\frac{\delta R^{a-1} \sqrt{\ln{R}}}{\varepsilon^{2}},&\quad\alpha = 1/2,\\ \sqrt{\frac{L t_{0}^{1-2\alpha}}{2(2\alpha - 1)}} \frac{\delta R^{a - 1}}{\varepsilon^{2}},&\quad\alpha >1/2. \end{array} \right. $$

From (37) and the latter estimate, we deduce

$$ Q_{2} \leq \left\{ \begin{array}{ll} C_{10}\left( \varepsilon^{1/\mu} R^{\nu/\mu + 1} + \frac{\delta R^{a - \alpha - 1/2}}{\varepsilon^{2}} + R^{-(2\alpha + 1)/2} \right),&\quad - 1/2 < \alpha < 1/2,\\ C_{10}\left( \varepsilon^{1/\mu} R^{\nu/\mu + 1} + \frac{\delta R^{a-1} \sqrt{\ln{R}}}{\varepsilon^{2}} + R^{-1} \right),&\quad \alpha = 1/2,\\ C_{10}\left( \varepsilon^{1/\mu} R^{\nu/\mu + 1} + \frac{\delta R^{a - 1}}{\varepsilon^{2}} + R^{-(2\alpha + 1)/2} \right), &\quad\alpha >1/2 \end{array} \right. $$

(39)

with C₁₀ ≡ C₁₀(C₂, C₇, t₀, α, L) > 0.

From Proposition 1(a), (36), and (39), we obtain for 0 < δ < 1/(4min{t_∗;1}) that

$$\mathcal{R}[\hat{F}; \mathcal{F}_{\alpha,L}] \!\leq\! \left\{\!\! \begin{array}{ll} C_{11}\!\left( \varepsilon^{1/\mu} R^{\nu/\mu + 1} + \frac{\delta R^{a - \alpha - 1/2}}{\varepsilon^{2}} + R^{-(2\alpha + 1)/2} +\! \frac{1}{\delta\sqrt{n}}\right),&\!\!\quad - 1/2 < \alpha < 1/2,\\ C_{11}\!\left( \varepsilon^{1/\mu} R^{\nu/\mu + 1} + \frac{\delta R^{a-1}}{\varepsilon^{2}}\sqrt{\ln{R}} + R^{-1} + \frac{1}{\delta\sqrt{n}} \right),&\!\!\quad\alpha = 1/2,\\ C_{11}\!\left( \varepsilon^{1/\mu } R^{\nu/\mu + 1} + \frac{\delta R^{a - 1}}{\varepsilon^{2}} + R^{-(2\alpha + 1)/2} + \frac{1}{\delta\sqrt{n}} \right),&\!\!\quad\alpha >1/2, \end{array} \right. $$

where

$$C_{11} = 2(D_{0,1} + E_{0})\max\left\{C_{10};\sqrt{\max\left\{(4c)^{(2a_{0}+ 1)/\xi}; 1; t_{\ast}^{-(2a_{0}+ 1)}\right\}} \right\}. $$

• For − 1/2 < α < 1/2, choosing ε = R^{−[(2α+ 1)μ+ 2(ν + μ)]/2}, δ = n^− 1/4R^{−[2a+(2α+ 1)(2μ− 1)+ 4(ν + μ)]/4}, we obtain

  $$\mathcal{R}[\hat F;\mathcal{F}_{\alpha,L}] \leq O\left( R^{-(2\alpha + 1)/2} + n^{- 1/4} R^{[2a + (2\alpha + 1)(2\mu - 1) + 4(\nu + \mu)]/4}\right). $$

  Then for R = n^{1/[2a+(2α+ 1)(2μ+ 1)+ 4(ν + μ)]}, we derive

  $$\mathcal{R}[\hat F;\mathcal{F}_{\alpha,L}] \leq O\left( n^{-(\alpha + 1/2)/[2a + (2\alpha + 1)(2\mu + 1) + 4(\nu + \mu)]}\right). $$

• For α = 1/2, using the inequality $\ln {u} \leq \sqrt {u}$ for u > 0, we obtain

  $$\mathcal{R}[\hat F;\mathcal{F}_{\alpha,L}] \leq O\left( \varepsilon^{1/\mu} R^{\nu/\mu + 1} + \frac{\delta R^{a - 3/4}}{\varepsilon^{2}} + R^{- 1} + \frac{1}{\delta \sqrt{n}} \right). $$

  Choosing ε = R^{−(2μ + ν)} and δ = n^− 1/4R^{−(a− 3/4 + 4μ+ 2ν)/2} gives

  $$\mathcal{R}[\hat F;\mathcal{F}_{\alpha ,L}] \leq O\left( R^{-1} + n^{-1/4} R^{(a - 3/4 + 4\mu + 2\nu)/2}\right). $$

  Then for R = n^{2/(4a+ 5 + 16μ+ 8ν)}, we derive

  $$\mathcal{R}[\hat F;\mathcal{F}_{\alpha,L}] \leq O\left( n^{- 2/(4a + 5 + 16\mu + 8\nu)} \right). $$

• For α > 1/2, choosing ε = R^{−[(2α+ 1)μ+ 2(ν + μ)]/2} and δ = n^− 1/4R^{−[a− 1+(2α+ 1)μ+ 2(ν + μ)]/2} gives

  $$\mathcal{R}[\hat F;\mathcal{F}_{\alpha,L}] \leq O\left( R^{-(2\alpha + 1)/2} + n^{- 1/4} R^{[a - 1 + (2\alpha + 1)\mu + 2(\nu + \mu)]/2}\right). $$

  Then for R = n^{1/[2a− 2 + 2(2α+ 1)(μ+ 1)+ 4(ν + μ)]}, we derive

  $$\mathcal{R}[\hat F;\mathcal{F}_{\alpha,L}] \leq O\left( n^{-(\alpha + 1/2)/[2a - 2 + 2(2\alpha + 1)(\mu + 1) + 4(\nu + \mu)]} \right). $$

(b) Since $\|h^{\text {ft}}\|_1 \leq {\int }_{-\infty }^{\infty }|g^{\text {ft}}(t)|dt$ and $|g^{\text {ft}}(t)| \leq c_2 e^{-\kappa |t|^{\beta }}$ for all $t\in \mathbb {R}$, there exists C_∗,2 ≡ C_∗,2(c₂, κ, β) > 0 so that ∥h^ft∥₁ ≤ C_∗,2. This implies

$$D_{0} \leq \pi^{-1}\max\left\{4+\xi^{-1}\ln{2};\sqrt {2C_{\ast, 2}}\right\} : = D_{0,2}, $$

where the constant D₀ is as in Proposition 1(a).

Suppose $F\in \mathcal {F}_{\alpha , L}$. For R > 1 and 0 < ε < 1, we have

$$\begin{array}{@{}rcl@{}} {\int}_{t_{0}}^{\infty} \frac{\delta t^{a - 1} |f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt &\leq& {\int}_{t_{0}}^{R} \frac{\delta t^{a-1}|f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt + {\int}_{R}^{\infty} \frac{|f^{\operatorname{ft}}(t)|}{t}dt\\ &\leq& \frac{1}{t_{0}}\lambda \left( B_{g^{\operatorname{ft}};R,\varepsilon}\right) + {\int}_{t_{0}}^{R} \frac{\delta t^{a - 1}|f^{\text{ft}}(t)|}{\varepsilon^{2}}dt + {\int}_{R}^{\infty} \frac{|f^{\operatorname{ft}}(t)|}{t}dt, \end{array} $$

where the set $B_{g^{\operatorname {ft}};R,\varepsilon }$ is defined as in Lemma 4. Applying Lemma 4 and Lemma 6, we have

$$\begin{array}{@{}rcl@{}} \frac{1}{t_{0}}\lambda \left( B_{g^{\operatorname{ft}};R,\varepsilon}\right) &\leq& \max\left\{(4c)^{1/\xi}; 1; t_{\ast}^{-1}\right\} C_{2} \varepsilon^{1/\mu} R^{\nu/\mu + 1} e^{\kappa^{\ast}R^{\beta}},\\ {\int}_{t_{0}}^{R} \frac{\delta t^{a - 1}|f^{\text{ft}}(t)|}{\varepsilon^{2}}dt &\leq& \frac{\delta R^{a}}{\varepsilon^{2}}{\int}_{t_{0}}^{R}\frac{|f^{\text{ft}}(t)|}{t}dt \leq C_{8} \frac{\delta R^{a}}{\varepsilon^{2}},\\ {\int}_{R}^{\infty} \frac{|f^{\operatorname{ft}}(t)|}{t}dt &\leq& C_{7} R^{-(2\alpha + 1)/2}. \end{array} $$

Hence, with $C_{12} = \max \{\max \{(4c)^{1/\xi }; 1; t_{\ast }^{-1}\} C_2; C_8; C_7\}$, we derive

$$ {\int}_{t_{0}}^{\infty} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|} {\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt \leq C_{12} \left( \varepsilon^{1/\mu} R^{\nu/\mu + 1} e^{\kappa^{\ast}R^{\beta}} + \frac{\delta R^{a}}{\varepsilon^{2}} + R^{-(2\alpha + 1)/2} \right). $$

(40)

Next, as in (36), we have

$$\frac{1}{n}{\int}_{t_{0}}^{\infty} \frac{|g^{\operatorname{ft}}(t)|^{2}}{t^{2}(\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2})^{2}}dt \leq \max\left\{(4c)^{(2a_{0}+ 1)/\xi}; 1; t_{\ast}^{-(2a_{0}+ 1)}\right\} \frac{1}{n\delta^{2}}. $$

From Proposition 1(a), (40), and the latter estimate, we obtain for 0 < δ < 1/(4min{t_∗;1}) that

$$ \mathcal{R}[\hat{F}; \mathcal{F}_{\alpha,L}] \leq C_{13}\frac{1}{\min\{a;1\}} \left( \varepsilon^{1/\mu} R^{\nu/\mu + 1} e^{\kappa^{\ast}R^{\beta}} + \frac{\delta R^{a}}{\varepsilon^{2}} + R^{-(2\alpha + 1)/2} + \frac{1}{\delta\sqrt{n}}\right) $$

(41)

with

$$C_{13}= 2(D_{0,2} + E_{0}) \max\left\{1; C_{12}; \sqrt{\max\{(4c)^{(2a_{0}+ 1)/\xi}; 1; t_{\ast}^{-(2a_{0}+ 1)}\}} \right\}. $$

From (41), letting δ = n^−ζ, ε = n^−𝜗, R = (ρ lnn)^1/β with 0 < ζ < 1/2, 0 < 𝜗 < ζ/2 and 0 < ρ < 𝜗/(μκ^∗), we derive the desired conclusion.

(c) Suppose $F\in \mathcal {F}_{\alpha , L}$. For every ε > 0 small enough, let R_ε be defined by the equality (23) of Lemma 5, where we take q = 3/2 + α. Then, the inequality (24) becomes

$$C_{3}\left( \ln\left( \frac{1}{\varepsilon}\right)\right)^{\frac{4(\gamma - 1)}{\gamma(2\alpha + 7)}} \leq R_{\varepsilon} \leq C_{4}\frac{\ln \left( \frac{1}{\varepsilon}\right)}{\sqrt {\ln\left( \ln\left( \frac{1}{\varepsilon} \right) \right)}}. $$

By the similar arguments as in the part (b), we obtain

$$\begin{array}{@{}rcl@{}} {\int}_{t_{1}}^{\infty} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|} {\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt &\leq& \frac{1}{t_{1}}\lambda\left( B_{g^{\operatorname{ft}};R_{\varepsilon},\varepsilon} \right) + {\int}_{t_{1}}^{R_{\varepsilon}} \frac{\delta t^{a - 1}|f^{\text{ft}}(t)|}{\varepsilon^{2}}dt + {\int}_{R_{\varepsilon}}^{\infty} \frac{|f^{\operatorname{ft}}(t)|}{t}dt\\ &\leq& 4c_{0}\lambda \left( B_{g^{\operatorname{ft}};R_{\varepsilon},\varepsilon} \right) + \frac{\delta R_{\varepsilon}^{a}}{\varepsilon^{2}}{\int}_{t_{1}}^{R_{\varepsilon}} \frac{|f^{\text{ft}}(t)|}{t}dt + {\int}_{R_{\varepsilon}}^{\infty} \frac{|f^{\operatorname{ft}}(t)|}{t}dt. \end{array} $$

According to Lemma 5, $\lambda \left (B_{g^{\operatorname {ft}};R_{\varepsilon },\varepsilon } \right ) \leq R_{\varepsilon }^{1 - q} = R_{\varepsilon }^{-(1 + 2\alpha )/2}$. Moreover, applying Lemma 6 gives ${\int }_{t_1}^{R_{\varepsilon }} \frac {|f^{\text {ft}}(t)|}{t}dt \leq C_8$ and ${\int }_{R_{\varepsilon }}^{\infty } \frac {|f^{\operatorname {ft}}(t)|}{t}dt \leq C_7 R_{\varepsilon }^{-(2\alpha + 1)/2}$. Thus,

$$\begin{array}{@{}rcl@{}} {\int}_{t_{1}}^{\infty} \frac{\delta t^{a - 1}|f^{\operatorname{ft}}(t)|}{\delta t^{a} + |g^{\operatorname{ft}}(t)|^{2}}dt &\leq& (4c_{0} + C_{7}) R_{\varepsilon}^{-(1 + 2\alpha)/2} + C_{8} \frac{\delta R_{\varepsilon}^{a}}{\varepsilon^{2}} \\ & \leq& (4c_{0} + C_{7}) (C_{3})^{-(1 + 2\alpha)/2}\left( \ln\left( \frac{1}{\varepsilon} \right)\right)^{-\frac{2(\gamma - 1)(2\alpha + 1)}{\gamma(2\alpha + 7)}}\\ && + C_{8} \max\{(C_{4})^{a_{0}}; 1\}\frac{\delta}{\varepsilon^{2}} \left( \frac{\ln \left( \frac{1}{\varepsilon} \right)}{\sqrt{\ln\left( \ln\left( \frac{1}{\varepsilon}\right)\right)}}\right)^{a}. \end{array} $$

Combining the latter estimate with Proposition 1(b) yields

$$\begin{array}{@{}rcl@{}} &&\mathcal{R}[\hat F; \mathcal{F}_{\alpha, L}]\\ && \leq O\left( \frac{1}{\min\{a;1\}}\left( \left( \ln\left( \frac{1}{\varepsilon} \right)\right)^{-\frac{2(\gamma - 1)(2\alpha + 1)}{\gamma(2\alpha + 7)}} + \frac{\delta}{\varepsilon^{2}} \left( \frac{\ln\left( \frac{1}{\varepsilon}\right)}{\sqrt{\ln\left( \ln \left( \frac{1}{\varepsilon} \right) \right)}} \right)^{a} + \frac{1}{\delta \sqrt n}\right) \right). \end{array} $$

Substituting ε = n^−ω (0 < ω < 1/4) to the right-hand side of the latter estimate gives

$$\mathcal{R}[\hat F; \mathcal{F}_{\alpha, L}] \leq O\left( \frac{1}{\min\{a;1\}}\left( (\ln{ n})^{-\frac{2(\gamma - 1)(2\alpha + 1)}{\gamma(2\alpha + 7)}} + n^{2\omega} \left( \frac{\ln n}{\sqrt{\ln(\ln n)}}\right)^{a} \delta + \frac{1}{\delta\sqrt {n}} \right) \right). $$

Choosing $\delta = n^{-(\omega + 1/4)}\left ((\ln {n})/\sqrt {\ln {(\ln {n})}}\right )^{- a/2}$ gives the conclusion of this part.

Finally, if the noise density g is compactly supported, then for q = 3/2 + α the estimate (26) becomes

$$C_{5}\left( \ln\left( \frac{1}{\varepsilon}\right)\right)^{\frac{4}{2\alpha + 7}} \leq R_{\varepsilon} \leq C_{6}\frac{\ln\left( \frac{1}{\varepsilon} \right)}{\sqrt{\ln\left( \ln{ \left( \frac{1}{\varepsilon}\right)}\right)}}. $$

Then, arguments for deriving the convergence rate of $\mathcal {R}[\hat F; \mathcal {F}_{\alpha , L}]$ are similar as above. □

Proof of Corollary 1

With the defined notations, we rewrite the result of Theorem 2(a) in the case 0 < a < 1 as $\mathcal {R}[\hat F;\mathcal {F}_{\alpha ,L}] \leq O(\rho (a))$, where $\rho (a)=n^{-k_0/(a+\ell _0)}/a$. For 0 < a < 1, by taking the first derivative of the function ρ with respect to a, we obtain

$$\rho^{\prime}(a)=\frac{1}{a}n^{-k_{0}/(a+\ell_{0})}\left( -\frac{1}{a}+\frac{k_{0}\ln n}{(a+\ell_{0})^{2}}\right). $$

Solving the equation ρ^′(a) = 0 on (0,1) gives a = a_n, where a_n is defined as in (8). Moreover, we see that ρ^′(a) < 0 as 0 < a < a_n and ρ^′(a) > 0 as a_n < a < 1. Hence, the function ρ attains its minimum on (0,1) at a = a_n. This leads to

$$\inf_{0<a<1}\mathcal{R}[\hat F;\mathcal{F}_{\alpha ,L}] \leq O(\rho(a_{n})). $$

We consider the case − 1/2 < α < 1/2. In this case,

$$\inf_{1\leq a \leq a_{0}}\mathcal{R}[\hat F;\mathcal{F}_{\alpha ,L}] \leq O\left( n^{-(\alpha + 1/2)/[2 + (2\alpha + 1)(2\mu + 1) + 4(\nu + \mu)]} \right)=O\left( n^{-2k_{0}/(1-2\alpha+ 2\ell_{0})}\right). $$

Since $\lim _{n\to \infty } n^{-2k_0/(1-2\alpha + 2\ell _0)}/\rho (a_n) = \lim _{n\to \infty }a_n n^{k_0(1-2\alpha -2a_n)/[(a_n + \ell _0)(1-2\alpha + 2\ell _0)]} = \infty$, we obtain $\inf _{a>0}\mathcal {R}[\hat F;\mathcal {F}_{\alpha ,L}] \leq O(\rho (a_n))$.

For the case α = 1/2, we have $\rho (a_n)=\frac {1}{a_n}n^{-1/(2a_n + 8\mu + 4\nu + 4)}= \frac {1}{a_n}n^{-2/(4a_n + 16\mu + 8\nu + 8)}$ and

$$\inf_{1\leq a \leq a_{0}}\mathcal{R}[\hat F;\mathcal{F}_{\alpha ,L}] \leq O\left( n^{- 2/(9 + 16\mu + 8\nu)}\right). $$

Since $\lim _{n\to \infty }n^{- 2/(9 + 16\mu + 8\nu )}/\rho (a_n)=\infty$, we obtain $\inf _{a>0}\mathcal {R}[\hat F;\mathcal {F}_{\alpha ,L}] \leq O(\rho (a_n))$.

For the case α > 1/2, we have

$$\inf_{1\leq a \leq a_{0}}\mathcal{R}[\hat F;\mathcal{F}_{\alpha ,L}] \leq O\left( n^{-(\alpha + 1/2)/[2(2\alpha + 1)(\mu + 1) + 4(\nu + \mu)]}\right) = O\left( n^{-k_{0}/\ell_{0}}\right). $$

Since $\lim _{n\to \infty }n^{-k_0/\ell _0}/\rho (a_n)= 0$, we obtain $\inf _{a>0}\mathcal {R}[\hat F;\mathcal {F}_{\alpha ,L}] \leq O(n^{-k_0/\ell _0})$. □