Bending strength of oil-lubricated cylindrical plastic gears

Abstract

Oil-lubricated plastic gears enable significantly higher power transmission compared to dry-running gears. One of the most relevant damage mechanisms herein is tooth root breakage. Due to the high elasticity of thermoplastics, load-induced deflections strongly affect the tooth root stresses. In this work, a modified method for calculating the tooth root stresses is used to increase the accuracy of the bending strength calculation of plastic gears. Experimental results with steel-plastic spur gear pairings prove that load-induced deflections and dynamic tooth forces are not yet adequately considered in VDI 2736. In doing so, it was to some extent possible to validate and confirm the POM fatigue strength data in accordance with VDI 2736.

1 Current knowledge

The state of the art load carrying capacity calculation of plastic gears is summarized in VDI 2736 [1]. The approach to calculate the bending strength according to VDI 2736 [1] is based on DIN 3990 [2] Method C and therefore does not consider elastokinematic effects on tooth root stresses. Fürstenberger [5] indicated the importance of load-induced deflections and modified the calculation methods according to VDI 2736 [1] by replacing the transverse contact ratio $\varepsilon _{\alpha}$ with the actual contact ratio $\varepsilon _{\alpha ,w}$. This particularly affects both bending strength calculation methods and tooth and flank temperature calculation methods according to [1]. The actual contact ratio is calculated using an empirical equation that is taken from Rettig [13].

2 Aim of this work

The aim of this work is to validate the current state of the art calculation methods according to VDI 2736 [1] including the maximum root strength ($\sigma _{\text{FG}}$) data for POM by comparison with own test results for injection molded test gears made of a homopolymer POM (Delrin® 100NC010 by DuPont™) material. The challenge in this context is, that on the one hand many notable influence factors are not yet considered in the bending strength calculation of VDI 2736 [1] and on the other hand, the underlying test conditions and test gears used for the determination of the fatigue strength data ($\sigma _{\text{FlimN}}$) of POM included in [1] are unknown. Hence, this work is also an approach towards correlating the bending strength of state of the art injection molded POM gears with existing fatigue strength data according to VDI 2736 [1].

3 Modified calculation of tooth root stress

In prior work [8,9,10], the impact of the gear geometry, especially the number of teeth (compare Thoma [6]) of pinion and wheel, on the increase in contact ratio under load is evaluated. As the approach to calculating the actual contact ratio $\varepsilon _{\alpha ,w}$ according to Fürstenberger [5] does not consider the geometric effects of the number of teeth, a modified analytic-iterative method called ACORA (=Actual Contact Ratio) is derived in [8]. The results for $\varepsilon _{\alpha ,w}$ according to ACORA are in good correlation with results of numeric calculations (finite element method). However, because ACORA must be implemented as a calculation program for practical applications, an extension of the empirical equation according to Fürstenberger [5] is proposed in [10] to enable the consideration of the influence of the number of teeth by a simplified approach. Calculation of the tooth root stress $\sigma _{\text{F0},\text{ACR}}$ (Eq. (1)) considering the actual contact ratio $\varepsilon _{\alpha ,w}$ is called ACORARS (=ACORA Root Stress) [9] and contains a modified description of the contact ratio factor which is given in Eq. (2) as $Y_{\varepsilon ,\text{ACR}}$ according to [9].

$$\sigma _{\text{F0},\text{ACR}}=Y_{\text{Fa}}\cdot Y_{\text{Sa}}\cdot Y_{\varepsilon ,\text{ACR}}\cdot Y_{\beta}\cdot \frac{F_{\text{t}}}{b\cdot m_{n}}$$

(1)

$$Y_{\varepsilon ,\text{ACR}}=a_{\text{ACR}}+\frac{1-a_{\text{ACR}}}{\varepsilon _{\alpha ,w}}$$

(2)

$$a_{\text{ACR}}=\max\left (\min\left (\left (2.6-\varepsilon _{\alpha ,w}\right )\cdot \frac{0.25}{0.8},\ 0.25\right ),\ 0\right )$$

(3)

Furthermore, the calculation of the mesh stiffness is an input parameter for the iterative calculation method ACORARS [9] as well as for the calculation of the resonance speed [2]. It is parametrized analogously using the auxiliary factor $a_{\text{ACR}}$ (Eq. (3)) and calculated according to Eq. (4).

$$c_{\gamma ,\text{ACR}}=c^{\prime}\cdot \left (\left (1-a_{\text{ACR}}\right )\cdot \varepsilon _{\alpha ,w}+a_{\text{ACR}}\right )$$

(4)

4 Permissible root stress in the context of VDI 2736

One important disadvantage regarding bending strength calculation of plastic gears is the lack of material specific fatigue strength data. VDI 2736 [1] contains fatigue strength data for two common thermoplastic materials – PA66 and POM. While the data for PA66 is taken from Hachmann/Strickle [11], the most elementary gear geometry parameters (number of teeth, pressure angle) are known. However, where the POM data is concerned, neither the geometry of the test gears nor the details of the test rig and the test conditions are known. Furthermore, the underlying probability of failure remains unknown in both cases.

The ignoring of load-induced deflections for calculating tooth root stresses according to VDI 2736 [1] implies that the fatigue strength data ($\sigma _{\text{FlimN}}$), which at the time were evaluated using test results, contain a certain amount of load sharing of the test gears used at that time. Hence, to use the fatigue strength data with a calculation method (see Sect. 3), that considers the geometry dependent and Young’s modulus dependent load sharing, the contact ratio factor of the test gears has to be considered when calculating the maximum root strength $\sigma _{\text{FG}}$. Therefore, the contact ratio factor of the test gears $Y_{\varepsilon \text{T}}$ is considered to calculate the modified maximum root strength $\sigma _{\text{FG},\text{VDI}\rightarrow \text{ACR}}$ according to Eq. (5).

$$\sigma _{\text{FG},\text{VDI}\rightarrow \text{ACR}}=\sigma _{\text{FlimN}}\cdot Y_{\text{ST}}\cdot Y_{\varepsilon \text{T}}$$

(5)

To estimate the amount of load-induced increase in the contact ratio contained in the fatigue strength data, a gear geometry must be assumed. As the macrogeometry of the FZG-C [12] test gear is mentioned in Hachmann/Strickle [11] and bending strength test results [5] with this gear geometry confirm the good correlation with the predictions of VDI 2736 [1], this geometry is also assumed as the test gear geometry underlying the POM fatigue strength data according to [1].

Fig. 1

Estimation of the contact ratio factor of the test gears $Y_{\varepsilon \text{T}}$ used for the determination of the fatigue strength under pulsating stress $\sigma _{\text{FlimN}}$ of POM according to VDI 2736 [1]

By equating the Equations for $\sigma _{\text{F}}$ and $\sigma _{\text{FG}}$ ($S_{\text{Fmin}}=1$) according to [1], the nominal tangential force $F_{\text{t}}$ as a function of $\sigma _{\text{FlimN}}\left (\vartheta _{\text{Fu{\ss}}},N_{\text{L}}\right )$ can be determined. Furthermore, this also enables the calculation of the contact ratio factor according to ACORARS [9] for the presumed test gear geometry $Y_{\varepsilon \text{T}}$ as a function of $\vartheta _{\text{Fu{\ss}}}$ and $N_{\text{L}}$. Fig. 1 shows the characteristics of $Y_{\varepsilon \text{T}}$. $Y_{\varepsilon \text{T}}$ can be estimated using Eq. (6) (parameters see Table 1) and is also plotted in Fig. 1 as $Y_{\varepsilon \text{T},\text{est}}$.

$$Y_{\varepsilon \text{T},\text{est}}\approx a+b\cdot \vartheta _{\text{Fu{\ss}}}^{\text{be}}+c\cdot N_{\text{L}}^{\text{ce}}+\left (\vartheta _{\text{Fu{\ss}}}\cdot N_{\text{L}}\right )^{d}$$

(6)

Table 1 Constant parameters to estimate $Y_{\varepsilon \text{T}}$ according to Eq. (6)

Fig. 2

Injection molded plastic test gear [10]

5 Essential results of recent gear tests

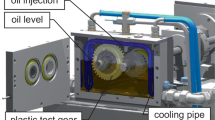
Experimental bending strength tests are conducted using back-to-back test rigs according to DIN ISO 14635-1 [4] with ground steel pinions meshing with injection molded plastic gears (Fig. 2). Details regarding the development of the injection molded test gears are reported in [7]. During testing, the test gears are lubricated using a temperature controlled oil bath. In prior tests [10], the increase in tooth temperature relative to the oil temperature was measured depending on speed and torque. Based on this knowledge, the oil temperature during fatigue testing is controlled to enable a constant tooth temperature level for each test condition.

Table 2 contains the investigated gear geometries. Primary data of the tooth root breakages occurring and further details of the test results are documented in [10].

Table 2 Test gear geometries; steel = 16MnCr5e (case hardened and ground)

The test results are evaluated in Fig. 3 by correlating the calculated nominal tooth root stress $\sigma _{\text{F0}}$ for each tooth root breakage that occurred according to VDI 2736 [1] as well as ACORARS [9]. Despite all tests being performed using test gears from identical POM material, the tolerable tooth root stress level according to VDI 2736 [1] differs significantly for each gear geometry. The main reason for this is the negligence of the load-induced increase in contact ratio in the calculation method of VDI 2736 [1].

Fig. 3

Nominal tooth root stress for different gear geometries kst-A, kst-B, kst-C according to VDI 2736 [1] and ACORARS [9]; $\vartheta _{\text{Fu{\ss}}}\approx$ 80 °C ; see [10]

Fig. 4

Calculated actual contact ratio for the test results shown in Fig. 3 according to ACORA [8]

Fig. 4 shows the calculated values of the actual contact ratio $\varepsilon _{\alpha ,w}$ according to ACORA [8] for the test results given in Fig. 3. Due to the geometric effect of the number of teeth on the increase in contact ratio under load, significantly higher actual contact ratios result for gear geometries with higher numbers of teeth. The right-hand plot in Fig. 3 shows that the calculated tooth root stresses according to ACORARS [9] result in a common level of tolerable tooth root stress for the given material and temperature ($\vartheta _{\text{Fu{\ss}}}\approx 80^{\circ} C$). As kst-C contains cavities in the tooth root area (see [10]), which as would be expected affect the load capacity, it is plausible that the level of kst-C in Fig. 3 by tendency is below kst-A or kst-B.

To estimate the probability of failure for the test gears, the referenced load level is evaluated according to Rossow [14] and illustrated in Fig. 5 as a normal probability plot. It is expected that the higher amount of scattering of kst‑C compared to kst‑A or kst‑B is due to the already mentioned cavities in the root area of kst‑C. As kst‑A has twice as much teeth compared to kst‑B, a higher probability of failure for kst‑A, as seen in Fig. 5, is reasonable.

Fig. 5

Probability of failure due to root breakage evaluated according to Rossow [14]

6 Influence of the resonance ratio on bending strength of POM

In general, gear pairings are vibrating systems. Depending on the vibrational state, the tooth loads may be higher due to dynamic forces, compared to the static model underlying the analytic tooth root stress calculation methods. Therefore, according to DIN 3990 [2]/ISO 6336 [3], operation at the resonance speed $n_{\text{E}}$ must be avoided. For ranges near the main resonance speed, the additional dynamic forces can approximately be allowed for by the dynamic factor $K_{\text{v}}$.

Like the fundamental frequency, the resonance speed is proportional to the square root of the stiffness divided by the mass of the system under consideration [2, 3]. Because of the low Young’s moduli of thermoplastic materials, the mesh stiffness $c_{\gamma }$ of a steel-plastic pairing is about 1/50 of the stiffness of a steel-steel pairing. Additionally high performance plastic gears often feature a steel hub (compare Fig. 2), which results in a relatively high mass. According to DIN 3990 [2]/ISO 6336 [3] the dynamic operating condition is expressed as the resonance ratio $N$ which is defined as the operational rotational speed of the gear under consideration divided by the resonance speed $n_{\text{E}}$ (compare Eq. (7)).

$$N=\frac{n_{1}}{n_{\text{E1}}}=\frac{n_{1}\cdot \pi \cdot z_{1}}{30000}\sqrt{\frac{m_{\text{red}}}{c_{\gamma ,\text{ACR}}}}$$

(7)

Hence by calculation, the resonance speed of test gear kst-B is about 1100 rpm. To check whether dynamic forces can have a significant effect on the bending strength of plastic gears, fatigue tests are performed at approximately equal torque levels, but at different rotational speeds and therefore different resonance ratios.

Fig. 6

Nominal tooth root stresses for different resonance ratio test cases; kst-B; according to ACORARS [9]

Fig. 6 shows the tooth root stress values $\sigma _{\text{F0},\text{ACR}}$ according to ACORARS [9] corresponding to the failures due to tooth root breakage/crack. Tests at a resonance ratio of $N\approx 0.8$ fail at significantly lower numbers of cycles compared to tests at a more subcritical resonance ratio of $N\approx 0.6$. Highest fatigue durability is obtained in the supercritical range ($N\geq 1.4$), while the differences between tests at $N\approx 1.4$ and $N\approx 2.8$ are almost negligible. Therefore, it can be stated that supercritical operation can have a positive effect on the bending strength of plastic gears.

7 Interpretation of the test results and integration into state of the art bending strength calculations according to VDI 2736

The maximum root strength $\sigma _{\text{FG},\text{VDI}\rightarrow \text{ACR}}$ according to Sect. 4 is plotted in Fig. 6. Obviously $\sigma _{\text{FG},\text{VDI}\rightarrow \text{ACR}}$ correlates well with the subcritical test results. This indicates that the permissible root stress according to VDI 2736 [1] is valid for subcritical operation near the resonance speed ($N\approx 0.8$). In contrast, for supercritical conditions the permissible tooth root stress can be higher. To consider this for the calculation of the maximum root strength $\sigma _{\text{FG},\text{ACR}}$ according to Eq. (8), a dynamic factor of the test gears $K_{\text{vT}}$ is used to consider the fact that $\sigma _{\text{FG},\text{VDI}\rightarrow \text{ACR}}$ correlates with subcritical operation near the resonance speed and can be higher for supercritical conditions.

$$\sigma _{\text{FG},\text{ACR}}=\sigma _{\text{FlimN}}\cdot Y_{\text{ST}}\cdot Y_{\varepsilon \text{T}}\cdot K_{\text{vT}}$$

(8)

Consequently, when calculating $\sigma _{F,\text{ACR}}$, according to Eq. (9), the resonance ratio has to be considered by the dynamic factor $K_{\text{v}}$. Here, the dynamic factor is empirically estimated based on the test results according to Fig. 6 and determined conservatively according to Table 3.

$$\sigma _{F,\text{ACR}}=K_{\text{v}}\cdot Y_{\text{Fa}}\cdot Y_{\text{Sa}}\cdot Y_{\varepsilon ,\text{ACR}}\cdot Y_{\beta }\cdot \frac{F_{\text{t}}}{b\cdot m_{n}}$$

(9)

Table 3 Experimentally derived $K_{\text{v}}$ for POM

8 Comparison of test results with bending strength data according to VDI 2736

Following the assumptions of the previous sections, the permissible tooth root stress values based on VDI 2736 [1] are compared to the test results in Fig. 7.

Fig. 7

Comparison of maximum root strength $\sigma _{\text{FG},\text{ACR}}$ and root strength according to experimental tests of gear geometries kst-A and kst-B according to ACORARS [9]

The test results are plotted as a semi logarithmic partial regression line considering an estimated probability of failure of 10% according to Eq. (10) by assuming $f_{xF,50\% \rightarrow 10\% }=0.95$ (see Fig. 5). Here, a failure probability of 10% is chosen rather than 1% (see [2, 3]), because of the limited number of tests per variant.

$$\sigma _{F,10\% }=f_{xF,50\% \rightarrow 10\% }\cdot \sigma _{F,50\% }=0.95\cdot \sigma _{F,50\% }$$

(10)

Fig. 7 indicates very good correlation of the evaluated test results of kst-A and kst-B for a tooth temperature $\vartheta _{\text{Fu{\ss}}}\approx 80^{\circ} \mathrm{C}$ and therefore confirms the sufficient accuracy of the tooth root stress $\sigma _{F,\text{ACR}}$ calculation method. Furthermore, the test results for $\vartheta _{\text{Fu{\ss}}}\approx 80^{\circ} \mathrm{C}$ and $\vartheta _{\text{Fu{\ss}}}\approx 60^{\circ} \mathrm{C}$ correlate well with $\sigma _{\text{FG},\text{ACR}}$, which is based on $\sigma _{\text{FlimN}}$ according to VDI 2736 [1]. However, the spot check tests for $\vartheta _{\text{Fu{\ss}}}\approx 100^{\circ} \mathrm{C}$ indicate a significantly higher permissible stress level for this temperature level.

9 Summary

A modified method, called ACORARS [9], is introduced to consider load-induced deflections for calculating the tooth root stresses of cylindrical steel-plastic gear pairings. Experimental tests confirm the necessity to take deflections into account as, according to VDI 2736 [1], the permissible tooth root stress levels for test gears with different gear geometries, but made of the same material, partially deviate by values greater than 100%. Furthermore, experimental results show that the resonance ratio may also affect the bending strength of POM gears and therefore has to be considered in load carrying capacity calculation. Tests performed at a speed close to the resonance speed ($N\approx 0.8$) correlate with the maximum root strength data derived from VDI 2736 [1]. At higher speeds ($N\geq 1.4$), the experimentally tolerable stress is about 20% higher compared to the maximum root strength derived from VDI 2736 [1]. Therefore, it is important to note that for the chosen POM material with adequate cooling/lubrication provided, higher speeds in the supercritical range are not critical but even result in higher durability when compared to subcritical operation. The presented calculation method includes, by extending an approach based on VDI 2736 [1], the effects of load-induced deflection as well as dynamic tooth forces and furthermore allows maintaining of the known fatigue strength data $\sigma _{\text{FlimN}}$ according to [1].

Appendix

1.1 Nomenclature

 

$a_{\text{ACR}}$	–	Auxiliary factor used to calculate$Y_{\varepsilon ,\text{ACR}}$	[9]
$b$	mm	Face width	–
$c^{\prime}$	N/(mm ⋅ µm)	Single stiffness	[2]
$c_{\gamma ,\text{ACR}}$	N/(mm ⋅ µm)	Modified mesh stiffness according to ACORA	[9]
$\varepsilon _{\alpha }$	–	Transverse contact ratio	[2]
$\varepsilon _{\alpha ,w}$	–	Actual contact ratio	[8]
$F_{\text{t}}$	N	Nominal tangential load	–
$K_{\text{v}}$	–	Dynamic factor	[2]
$K_{\text{vT}}$	–	Dynamic factor of the test gears	–
$m_{n}$	mm	Normal module	–
$m_{\text{red}}$	kg/mm	Relative mass of a gear pair	[2]
$n_{1}$	$\text{min}^{-1}$	Rotation speed of pinion	[2]
$n_{\text{E1}}$	$\text{min}^{-1}$	Resonance speed of pinion	[2]
N	–	Resonance ratio	[2]
$N_{\text{L}}$	–	Number of load cycles	–
$S_{\text{Fmin}}$	–	Minimum required safety factor for tooth root stress	[1]
$\sigma _{\text{F0},\text{ACR}}$	MPa	Nominal tooth root stress according to ACORARS	[9]
$\sigma _{F,\text{ACR}}$	MPa	Tooth root stress according to ACORARS	–
$\sigma _{\text{FG}}$	MPa	Maximum root strength	[1]
$\sigma _{\text{FG},\text{ACR}}$	MPa	Maximum root strength according to ACORARS	–
$\sigma_{\text{FG},\text{VDI}\rightarrow \text{ACR}}$	MPa	Maximum root strength derived from VDI 2736
$\sigma _{\text{FlimN}}$	MPa	Fatigue strength under pulsating stress	[1]
$\vartheta _{\text{Fu{\ss}}}$	°C	Root temperature	[1]
$Y_{\varepsilon ,\text{ACR}}$	–	Modified contact ratio factor according to ACORA	[9]
$Y_{\varepsilon \text{T}}$	–	Contact ratio factor of the test gears	–
$Y_{\beta }$	–	Helix angle factor	[1]
$Y_{\text{Fa}}$	–	Form factor (DIN 3990 Method C)	[2]
$Y_{\text{Sa}}$	–	Stress correction factor (DIN 3990 Method C)	[2]
$Y_{\text{ST}}$	–	Stress correction factor of the test gears	[1]