Abstract
Writing correct programs for weak-memory models such as the C11 memory model is challenging because of the weak consistency guarantees these models provide. The first program logics for the verification of such programs have recently been proposed, but their usage has been limited thus far to manual proofs. Automating proofs in these logics via first-order solvers is non-trivial, due to features such as higher-order assertions, modalities and rich permission resources. In this paper, we provide the first encoding of a weak-memory program logic using existing deductive verification tools. Our work enables, for the first time, the (unbounded) verification of C11 programs at the level of abstraction provided by the program logics; the only necessary user interaction is in the form of specifications written in the program logic and, in rare cases, ghost operations. We tackle three recent program logics: Relaxed Separation Logic and two forms of Fenced Separation Logic, and show how these can be encoded using the Viper verification infrastructure. In doing so, we illustrate several novel encoding techniques which could be employed for other logics. Our work is implemented, and has been evaluated on examples from existing papers as well as the Facebook open-source Folly library.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Reasoning about programs running on weak memory is challenging, because weak-memory models admit executions that are not sequentially consistent, that is, cannot be explained by a sequential interleaving of concurrent threads. Moreover, weak-memory programs employ a range of operations to access memory, which require dedicated reasoning techniques. These operations include fences as well as read and write accesses with varying degrees of synchronisation. The complexity of the underlying memory model and the non-existence (in general) of a single ordering of events consistent with the observations of all program threads makes writing and reasoning about code combining these primitives extremely difficult.Footnote 1
Some of these challenges are addressed by the first program logics for weak-memory programs, in particular, Relaxed Separation Logic (RSL) [43], GPS [41], Fenced Separation Logic (FSL) [13], and FSL \({+}{+}\) [14]. These logics apply to interesting classes of C11 programs, but their tool support has been limited to embeddings in Coq. Verification based on these embeddings requires substantial user interaction, which is an obstacle to applying and evaluating these logics.
In this paper, we present a novel approach to automating deductive verification for weak-memory programs. We encode large fractions of RSL, FSL, and FSL\({+}{+}\) (collectively referred to as the RSL logics) into the intermediate verification language Viper [26], and use the existing Viper verification backends to reason automatically about the encoded programs. This encoding reduces all concurrency and weak-memory features as well as logical features such as higher-order assertions and custom modalities to a much simpler sequential logic.
Defining a verification technique via an encoding into Viper is much more lightweight than developing a dedicated verifier from scratch, since we can reuse the existing automation for a variety of advanced program reasoning features. Compared to an embedding into an interactive theorem prover such as Coq, our approach leads to a significantly higher degree of automation than that typically achieved through tactics. Moreover, it allows users to interact with the verifier on the abstraction level of source code and annotations, without exposing the underlying formalism. Verification in Coq can provide foundational guarantees, whereas in our approach, errors in the encoding or bugs in the verifier could potentially invalidate verification results. We mitigate the former risk by a soundness argument for our encoding and the latter by the use of a mature verification system. We are convinced that both approaches are necessary: foundational verification is ideal for meta-theory development and application areas such as safety-critical systems, whereas our approach is well-suited for prototyping and evaluating logics, for making a verification technique applicable by a wider user base, and for applying it more efficiently.
The contributions of this paper are:
-
1.
The first automated deductive verification approach for weak-memory logics. We demonstrate the effectiveness of this approach on examples from the literature, which are available online [28].
-
2.
An encoding of large fractions of RSL, FSL, and FSL\({+}{+}\) into Viper. Various aspects of this encoding (such as the treatment of higher-order features and modalities, as well as the overall proof search strategy) are generic and can be reused to encode other advanced separation logics.
-
3.
A prototype implementation, which is available online [32, 33].
-
4.
A proof sketch for the soundness of our encoding.
This paper is an extended version of our TACAS paper [38]. It provides details of our support for rewriting atomic invariants (Sect. 3.3) and of our encoding of compare and swap operations (Sect. 5), an extension of our core techniques to support ghost state as employed in FSL\({+}{+}\) (Sect. 4.3), as well as a proof sketch of soundness and a discussion of completeness relative to the RSL logics (Sect. 6).
1.1 Related work
The existing weak-memory logics RSL [43], GPS [41], FSL [13], and FSL\({+}{+}\) [14] have been formalised in Coq; Kaiser et al. [19] also encoded RSL into Iris [21]. These formalisations were used to verify small examples. The proofs were constructed mostly manually, whereas our approach automates most of the proof steps. As shown in our evaluation, our approach reduces the overhead by more than an order of magnitude. The degree of automation in Coq could be increased through logic-specific tactics (e.g. [9, 35]), whereas our approach benefits from Viper’s automation for the intermediate language, which is independent of the encoded logic.
Jacobs [17] proposes a program logic for the TSO memory model that has been encoded in VeriFast [18]. Applying this encoding requires a substantial amount of annotations, whereas our approach provides a higher degree of automation and handles the more-complex C11 memory model.
Alglave et al. [3] propose a proof method for parallel or distributed programs running on weakly consistent memory, which allows one to prove invariants such as mutual exclusion of a synchronisation algorithm. The method relies on a so-called communication semantics that characterises the permitted inter-process communications. The proof is then decomposed into showing that the communication semantics implies the intended invariants, and that all executions permitted by the weakly consistent memory comply with the communication semantics. Alglave et al. focus on a theoretical exposition, whereas our work aims to automate proofs for weak-memory programs.
Dan et al. [12] combine a static program analysis together with a program transformation to over-approximate all possible executions under weak memory into a single sequentially consistent program execution. The resulting program can then be verified using standard verification techniques for sequential consistency. Travkin et al. [40] apply a similar approach, without using static analysis. Both approaches reflect all possible executions of a weak-memory program, for instance, to support subsequent model checking. However, they do not enable modular reasoning principles for weak memory such as those provided by the RSL logics that we automate.
Weak-memory reasoning has been addressed using model checking (e.g. [1, 2, 7]), by enumerating thread interleavings and taking into account the reorderings permitted by weak memory. To improve the scalability of model checking, Kokologiannakis et al. [20] propose an alternative approach, which enumerates all consistent execution graphs of a program up to a bound. This approach has been implemented in a stateless model checker for C11. These approaches are fully automatic, but do not analyse code modularly, which is e.g. important for verifying libraries independently from their clients. Deductive verification enables modular proofs by requiring specifications at function boundaries. Such specifications can preserve arbitrarily precise information about the (unboundedFootnote 2) behaviour of a program’s constituent parts.
Automating logics via encodings into intermediate verification languages is a proven approach, as witnessed by the many existing verifiers (e.g. [10, 11, 23, 24]) which target Boogie [4] or Why3 [5]. Our work is the first that applies this approach to logics for weak-memory concurrency. Our encoding benefits from Viper’s native support for separation-logic-style reasoning and several advanced features such as quantified permissions and permission introspection [25, 26], which are not available in other intermediate verification languages.
An overview of verification challenges and techniques for weak memory, in particular, causally consistent memory, is provided by Lahav [22].
Syntax for memory accesses. na indicates a non-atomic operation; \(\tau \) indicates an atomic access mode (as defined in C11), discussed in later sections. \(\rho \), and assertions A and invariants \(\mathcal {Q}\) are program annotations, needed as input for our encoding. Expressions e include boolean and arithmetic operations, but no heap accesses (as is standard for separation logics). We assume that source programs are type-checked
1.2 Outline
The next four sections present our encoding for the core features of the C11 memory model: we discuss non-atomic locations in Sect. 2, release-acquire accesses in Sect. 3, fences in Sect. 4, and compare and swap in Sect. 5. We discuss soundness and completeness of our encoding in Sect. 6; this includes details of the restrictions of our work compared with general manual proofs based on the original logics. We evaluate our approach in Sect. 7 including a comparison with all available pre-existing examples using the original papers; Sect. 8 then concludes. Further details of our encoding and examples are available in our accompanying technical report [39]. A prototype implementation of our encoding (with all examples) is available as an artefact [32, 33].
2 Non-atomic locations
We present our encoding for a small imperative programming language similar to the languages supported by the RSL logics. C11 supports non-atomic memory accesses and different forms of atomic accesses. The access operations are summarised in Fig. 1. We adopt the common simplifying assumption [41, 43] that memory locations are partitioned into those accessed only via non-atomic accesses (non-atomic locations), and those accessed only via C11 atomics (atomic locations). Read and write statements are parameterised by a mode \(\sigma \), which is either na (non-atomic) or one of the atomic access modes \(\tau \). We focus on non-atomic accesses in this section and discuss atomics in subsequent sections.
Assertion syntax of the RSL logics. The top row of constructs are standard for separation logics; those in the second row are specific to the RSL logics, and explained throughout the paper. Invariants \(\mathcal {Q}\) are functions from values to assertions (cf. Sect. 3)
2.1 RSL proof rules
Non-atomic memory accesses come with no synchronisation guarantees; programmers need to ensure that all accesses to non-atomic locations are data-race free. The RSL logics enforce this requirement using standard separation logic [27, 31]: programs that race on non-atomic locations cannot be verified. We show the syntax of assertions in Fig. 2, which will be explained throughout the paper. A points-to assertion \({l}\overset{\scriptscriptstyle {k}}{\mapsto }{e}\) denotes a transferrable resource, providing permission to access the location l, and expressing that l has been initialised and its current value is e. Here, k is a fraction \(0 < k \le 1\); \(k=1\) denotes the full (or exclusive) permission to read and write location l, whereas \(0< k < 1\) provides (non-exclusive) read access [8]. Points-to resources can be split and recombined, but never duplicated or forged; when transferring such a resource to another thread it is removed from the current one, avoiding data races by construction. The RSL assertion \(\textsf {Uninit}(l)\) expresses exclusive access to a location l that has been allocated, but not yet initialised; l may be written to but not read from. The main proof rules for non-atomic locations, adapted from RSL [43], are shown in Fig. 3. The latter two rules included are the frame rule, used for locally reasoning about only the relevant logical resources (and preserving information about the others) in any given proof step, and the rule for parallel composition, which allows modular proofs about parallel threads. Other statement-level rules for e.g. sequential composition or if-conditions are standard, and their encodings into Viper straightforward; we refer the reader to [43] for a full set of these additional proof rules.
Adapted RSL rules for non-atomics, along with the frame and parallel composition rules. Read access requires a non-zero permission. Write access requires either write permission or that the location is uninitialised. The underscore \(\_\) stands for an arbitrary value. Here and throughout the paper, permission amounts k are strictly positive: \(0 < k \le 1\)
2.2 Encoding
The Viper intermediate verification language [26] supports an assertion syntax based on that of Implicit Dynamic Frames [36], a program logic related to separation logic [29], but which separates permissions from value information. Viper is object-based; the only memory locations are field locations e.f (in which e is a reference, and f a field name). Permissions to access these heap locations are described by accessibility predicates of the form

, where k is a fraction as for points-to predicates above (k defaults to 1). Assertions that do not contain accessibility predicates are called pure. Unlike in separation logics, heap locations may be read in pure assertions.
We model C-like memory locations l using a field
 of a Viper reference l. Consequently, a separation logic assertion
\({l}\overset{\scriptscriptstyle {k}}{\mapsto }{e}\) (denoting k permission to the location l storing value e) is represented in Viper as
of a Viper reference l. Consequently, a separation logic assertion
\({l}\overset{\scriptscriptstyle {k}}{\mapsto }{e}\) (denoting k permission to the location l storing value e) is represented in Viper as

. We assume that memory locations have type
 , but a generalisation is trivial. Viper’s conjunction
, but a generalisation is trivial. Viper’s conjunction
 treats permissions like a separating conjunction, requiring the sum of the permissions in each conjunct, and acts as logical conjunction for pure assertions (just as
\(*\) in separation logic).
treats permissions like a separating conjunction, requiring the sum of the permissions in each conjunct, and acts as logical conjunction for pure assertions (just as
\(*\) in separation logic).
Viper provides two main statements for encoding proof rules:

adds the permissions denoted by the assertion A to the current state, and assumes pure assertions in A. This can be used to model gaining new resources, e.g. acquiring a lock in the source program. Dually,

checks that the current state satisfies A (otherwise a verification error occurs), and removes the permissions that A denotes; the values of any locations to which no permission remains are havoced (assigned arbitrary values). For example, when forking a new thread, its precondition is exhaled to transfer the necessary resources from the forking thread. Inhale and exhale statements can be seen as the permission-aware analogues of the assume and assert statements of first-order verification languages [24]. Viper also provides an
 statement; analogous to
statement; analogous to
 ,
,
 A checks that the current state satisfies A, but does not remove any permissions.
A checks that the current state satisfies A, but does not remove any permissions.
Viper encoding of the RSL assertions and the rules for non-atomic memory accesses from Fig. 3
The encoding of the rules for non-atomics from Fig. 3 is presented in Fig. 4.
 denotes the encoding of an RSL assertion A as a Viper assertion, and analogously
denotes the encoding of an RSL assertion A as a Viper assertion, and analogously
 for source-level statements s.
for source-level statements s.
The first two lines introduce two fields,
 and
and
 . Since Viper does not have a built-in notion of initialisation, we use the boolean
. Since Viper does not have a built-in notion of initialisation, we use the boolean
 field to reflect whether a memory location has been initialised. The assertion encodings use both fields and the corresponding permissions. Allocation is modelled by obtaining a fresh reference (via
field to reflect whether a memory location has been initialised. The assertion encodings use both fields and the corresponding permissions. Allocation is modelled by obtaining a fresh reference (via
 ) and inhaling permissions to its
) and inhaling permissions to its
 and
and
 fields; assuming
fields; assuming
 reflects that the location is not yet initialised. Viper implicitly checks the necessary permissions for field accesses (verification fails otherwise). Hence, the translation of a non-atomic read needs to check explicitly only that the read location is initialised before obtaining its value. Analogously, the translation of a non-atomic write only stores the value and records that the location is now initialised.
reflects that the location is not yet initialised. Viper implicitly checks the necessary permissions for field accesses (verification fails otherwise). Hence, the translation of a non-atomic read needs to check explicitly only that the read location is initialised before obtaining its value. Analogously, the translation of a non-atomic write only stores the value and records that the location is now initialised.
Note that Viper’s implicit permission checks are both necessary and sufficient to encode the RSL rules in Fig. 3. In particular, the assertions
\({l}\overset{\scriptscriptstyle {1}}{\mapsto }{\_}\) and
\(\textsf {Uninit}(l)\) both provide the permissions to write to location l. By including

 in the encoding of both assertions,Footnote 3 we avoid the disjunction of the RSL rule.
in the encoding of both assertions,Footnote 3 we avoid the disjunction of the RSL rule.
Like the RSL logics, our approach requires programmers to annotate their code with access modes for locations (as part of the
 statement), and specifications such as pre and post-conditions for methods and threads (as well as loop invariants and, in rare cases, ghost statements). Given these inputs, Viper constructs the proof automatically. In particular, it automatically proves entailments, and splits and combines fractional permissions (hence, the equivalence in Fig. 3 need not be encoded). Automation can be increased further by inferring some of the required assertions, but this is orthogonal to the encoding presented in this paper.
statement), and specifications such as pre and post-conditions for methods and threads (as well as loop invariants and, in rare cases, ghost statements). Given these inputs, Viper constructs the proof automatically. In particular, it automatically proves entailments, and splits and combines fractional permissions (hence, the equivalence in Fig. 3 need not be encoded). Automation can be increased further by inferring some of the required assertions, but this is orthogonal to the encoding presented in this paper.
3 Release-acquire atomics
The simplest form of C11 atomic memory accesses are release write and acquire read operations. They can be used to synchronise the transfer of ownership of (and information about) other, non-atomic locations, using a message passing idiom, illustrated by the example in Fig. 5. This program allocates two non-atomic locations a and b, and an atomic location l (initialised to 0), which is used to synchronise the three threads that are spawned afterwards. The middle thread makes changes to the non-atomics a and b, and then signals completion via a release write of 1 to l; in the separation logic sense of reasoning about this program, the thread gives up ownership of the non-atomic locations via this signal. The other threads loop attempting to acquire read a non-zero value from l. Once they do, they each gain ownership of one non-atomic location via the acquire read of 1 and access that location. The release write and acquire reads of value 1 enforce ordering constraints on the non-atomic accesses, preventing the left and right threads from racing with the middle one.
3.1 RSL proof rules
The RSL logics capture message-passing idioms by associating a location invariant \(\mathcal {Q}\) with each atomic location. Such an invariant is a function from values to assertions; we represent such functions as assertions with a distinguished variable symbol \(\mathcal {V}\) as parameter. Location invariants prescribe the intended ownership that a thread obtains when performing an acquire read of value \(\mathcal {V}\) from the location, and that must correspondingly be given up by a thread performing a release write. The main proof rules [43] are shown in Fig. 6.
When allocating an atomic location for release/acquire accesses (first proof rule), a location invariant \(\mathcal {Q}\) must be chosen (as an annotation on the allocation). The assertions \(\textsf {Rel}(l,\mathcal {Q})\) and \(\textsf {Acq}(l,\mathcal {Q})\) record the invariant to be used with subsequent release writes and acquire reads. To perform a release write of value e (second rule), a thread must hold the \(\textsf {Rel}(l,\mathcal {Q})\) assertion and give up the assertion \(\mathcal {Q}[e/\mathcal {V}]\). For example, the line \([l]_{\texttt {rel}}~{:=}~1\) in Fig. 5 causes the middle thread to give up ownership of both non-atomic locations a and b. The assertion \(\textsf {Init}(l)\) represents that atomic location l is initialised; both \(\textsf {Init}(l)\) and \(\textsf {Rel}(l,\mathcal {Q})\) are duplicable assertions: once obtained, they can be passed to multiple threads.
Multiple acquire reads might read the value written by a single release write operation; RSL prevents ownership of the transferred resources from being obtained (unsoundly) by multiple readers in two ways. First, \(\textsf {Acq}(l,\mathcal {Q})\) assertions cannot be duplicated, only split by partitioning the invariant \(\mathcal {Q}\) into disjoint parts. For example, in Fig. 5, \(\textsf {Acq}(l,\mathcal {Q}_1)\) is given to the left thread, and \(\textsf {Acq}(l,\mathcal {Q}_2)\) to the right. Second, the rule for acquire reads adjusts the invariant in the \(\textsf {Acq}\) assertion such that subsequent reads of the same value will not obtain any ownership.
Adapted RSL rules for release-acquire atomics. Location invariants \(\mathcal {Q}\) are parameterised by the value read from or written to the location. This value is represented by the free variable \(\mathcal {V}\) in location invariants. \(\mathcal {Q}(e)\) denotes \(\mathcal {Q}\) with e substituted for \(\mathcal {V}\)
3.2 Encoding
A key challenge for encoding the above proof rules is that \(\textsf {Rel}\) and \(\textsf {Acq}\) are parameterised by the invariant \(\mathcal {Q}\); higher-order assertions are not directly supported in Viper. However, for a given program, only finitely many such parameterisations will be required, which allows us to apply defunctionalisation [30], as follows. Given an annotated program, we assign a unique index to each syntactically-occurring invariant \(\mathcal {Q}\) (in particular, in allocation statements, and as parameters to \(\textsf {Rel}\) and \(\textsf {Acq}\) assertions in specifications). This allows us to parameterise Viper-level assertions with indices rather than other assertions and, thus, avoids higher-order assertions. Furthermore, we assign unique indices to all immediate conjuncts of these invariants, which allows us to refer to individual conjunctions when an \(\textsf {Acq}\) assertion is split according to the penultimate line of Fig. 6. We write \(\textit{indices}\) for the set of indices used in the current example. For each i in \(\textit{indices}\), we write \({\textit{inv}}{i}\) for the invariant which i indexes. For an invariant \(\mathcal {Q}\), we write \({\langle }{\mathcal {Q}}{\rangle }\) for its index, and  for the set of indices assigned to its immediate conjuncts.
for the set of indices assigned to its immediate conjuncts.
Our encoding of the RSL rules from Fig. 6 is summarised in Fig. 7. In contrast to non-atomic locations, RSL uses an \(\textsf {Init}(l)\), but no \(\textsf {Uninit}(l)\) assertion for atomic locations l; that is, it tracks only positive initialisation information. We represent the fact that a location is initialised by the presence of some permission to the
 field; the value of this field is irrelevant. To encode duplicable assertions such as \(\textsf {Init}(l)\), we use fractional permissions. We represent \(\textsf {Init}(l)\) with some non-zero permission to l
field; the value of this field is irrelevant. To encode duplicable assertions such as \(\textsf {Init}(l)\), we use fractional permissions. We represent \(\textsf {Init}(l)\) with some non-zero permission to l
 . Since the concrete fraction is irrelevant, we use Viper’s wildcard permissions [26], which represent unknown positive permission amounts. When exhaled, these amounts are chosen such that the amount exhaled will be strictly smaller than the amount held (verification fails if no permission is held) [16]. So after inhaling an \(\textsf {Init}(l)\) assertion (that is, a
. Since the concrete fraction is irrelevant, we use Viper’s wildcard permissions [26], which represent unknown positive permission amounts. When exhaled, these amounts are chosen such that the amount exhaled will be strictly smaller than the amount held (verification fails if no permission is held) [16]. So after inhaling an \(\textsf {Init}(l)\) assertion (that is, a
 permission), it is possible to exhale two
permission), it is possible to exhale two
 permissions, corresponding to two \(\textsf {Init}(l)\) assertions.
permissions, corresponding to two \(\textsf {Init}(l)\) assertions.
We represent a \(\textsf {Rel}(l,\mathcal {Q})\) assertion using an additional Viper field
 : Permission to this field represents the \(\textsf {Rel}\) assertion for some invariant, while
: Permission to this field represents the \(\textsf {Rel}\) assertion for some invariant, while
 ’s value indicates the index of the specific invariant \(\mathcal {Q}\). Since \(\textsf {Rel}\) is duplicable, we employ again a
’s value indicates the index of the specific invariant \(\mathcal {Q}\). Since \(\textsf {Rel}\) is duplicable, we employ again a
 permission in the
permission in the
 macro.Footnote 4 The encoding of a release write uses this macro to assert that some \(\textsf {Rel}\) assertion is held, according to Fig. 6. It subsequently branches on the value of the
macro.Footnote 4 The encoding of a release write uses this macro to assert that some \(\textsf {Rel}\) assertion is held, according to Fig. 6. It subsequently branches on the value of the
 field to exhale the appropriate invariant.
field to exhale the appropriate invariant.
Analogously to \(\textsf {Rel}\), we represent an \(\textsf {Acq}\) assertion via an additional Viper field
 . However, to support splitting, we represent the invariant in a more fine-grained way, by recording individual conjuncts separately. Each conjunct i of the invariant is modelled as a predicate instance AcqConjunct(l , i), which can be inhaled and exhaled individually. A predicate instance represents a resource (just like a field permission), but can be parameterised by multiple parameters (here, the location and the invariant index).
. However, to support splitting, we represent the invariant in a more fine-grained way, by recording individual conjuncts separately. Each conjunct i of the invariant is modelled as a predicate instance AcqConjunct(l , i), which can be inhaled and exhaled individually. A predicate instance represents a resource (just like a field permission), but can be parameterised by multiple parameters (here, the location and the invariant index).
 is an abstract predicate, that is, has no definition; this reflects that the predicate serves merely as a resource to track and prescribe which invariants are inhaled during a subsequent acquire read.
is an abstract predicate, that is, has no definition; this reflects that the predicate serves merely as a resource to track and prescribe which invariants are inhaled during a subsequent acquire read.
Representing an invariant via multiple
 instances handles the common case that invariants are split along top-level conjuncts, as in Fig. 5. More complex splits can be supported through additional annotations, as explained in Sect. 3.3. To enable splitting, we encode the \(\textsf {Acq}\) assertion for some invariant using a
instances handles the common case that invariants are split along top-level conjuncts, as in Fig. 5. More complex splits can be supported through additional annotations, as explained in Sect. 3.3. To enable splitting, we encode the \(\textsf {Acq}\) assertion for some invariant using a
 permission (the
permission (the
 macro), analogously to \(\textsf {Rel}\). However, since \(\textsf {Acq}\) is not duplicable for any given invariant, we use full permissions to the
macro), analogously to \(\textsf {Rel}\). However, since \(\textsf {Acq}\) is not duplicable for any given invariant, we use full permissions to the
 predicates representing the invariant conjuncts.
predicates representing the invariant conjuncts.
Allocation of an atomic location obtains a fresh reference and inhales the \(\textsf {Rel}\) and \(\textsf {Acq}(\)) predicates for the chosen location invariant \(\mathcal {Q}\).
A release write is encoded by checking that some \(\textsf {Rel}\) assertion is held, and then exhaling the associated invariant for the value written. The \(\textit{foreach}\) statement is unrolled statically; together with the if-statement, it determines the invariant to be exhaled by comparing all possible invariant indices to the index stored in the
 field of the updated location. Moreover, the encoding records that the location is initialised.
field of the updated location. Moreover, the encoding records that the location is initialised.
The RSL rule for acquire reads adjusts the \(\textsf {Acq}\) invariant by obliterating the assertion for the value read. Instead of directly representing the adjusted invariant (which would complicate our numbering scheme), we track the set of values read as state in our encoding. For each AcqConjunct(l , i) predicate, we record the values that have been read from l and for which the invariant with index i was already claimed. To avoid mutable maps in our encoding, we complement each
 predicate instance with an (uninterpreted) Viper function
predicate instance with an (uninterpreted) Viper function

, returning a set of values, and update information about this function explicitly when a value is read.
An acquire read checks that the location is initialised and that we have some \(\textsf {Acq}\) assertion for the location. It assigns an unknown value to the lhs variable x, which is subsequently constrained by the invariant associated with the \(\textsf {Acq}\) assertion as follows: We check for each index whether we both currently hold an
 predicate for that index,Footnote 5 and if so, have not previously read the value x from that conjunct of our invariant. If these checks succeed, we inhale the indexed invariant for x, and then include x in the values read. Viper’s heap-dependent functions are mathematical functions of their parameters and the resources stated in their preconditions (here, AcqConjunct(l , i)). Consequently, exhaling and re-inhaling the function’s precondition removes all prior information about the function value, which is then constrained to be the union of its previous value (stored in variable
predicate for that index,Footnote 5 and if so, have not previously read the value x from that conjunct of our invariant. If these checks succeed, we inhale the indexed invariant for x, and then include x in the values read. Viper’s heap-dependent functions are mathematical functions of their parameters and the resources stated in their preconditions (here, AcqConjunct(l , i)). Consequently, exhaling and re-inhaling the function’s precondition removes all prior information about the function value, which is then constrained to be the union of its previous value (stored in variable
 ) and the newly read value
) and the newly read value
 .
.
3.3 Rewriting invariants
The encoding described so far supports automatically splitting and conjoining the invariants of \(\textsf {Acq}\) assertions according to the penultimate line of Fig. 6. Beyond that, it is sometimes necessary to rewrite these invariants using general entailment reasoning according to the final line of Fig. 6, for instance, when two programmer-annotated assertions are equivalent, but not syntactically identical.
We support rewriting invariants by providing a ghost statement \(\texttt {rewrite }\textsf {Acq}(l,\mathcal {Q})\texttt { as }\textsf {Acq}(l,\mathcal {Q}')\) which programmers can manually insert to express that invariant \(\mathcal {Q}\) should be rewritten to \(\mathcal {Q}'\). This statement gives rise to a proof obligation that checks the entailment between the original invariant \(\mathcal {Q}\) and the new invariant \(\mathcal {Q}'\), for all values of \(\mathcal {V}\) and in all states.
In RSL, rewriting invariants is a side condition of a standard rule of consequence step (cf. Fig. 6). Such side conditions can be encoded in Viper via a conditional statement, where one branch checks the side condition and the other verifies the implementation under the assumption that the side condition holds. Since the verifier explores both branches, it will verify the code and prove the side condition. The encoding in Fig. 8 uses a non-deterministic
 statement for this purpose. To encode the side condition, that is, the entailment check, for all values of \(\mathcal {V}\) and all states, the
statement for this purpose. To encode the side condition, that is, the entailment check, for all values of \(\mathcal {V}\) and all states, the
 -branch removes all permissions from the current state, obliterating all information that the verifier had about any heap locations, and havoc an integer variable, representing the arbitrary value of \(\mathcal {V}\). We
-branch removes all permissions from the current state, obliterating all information that the verifier had about any heap locations, and havoc an integer variable, representing the arbitrary value of \(\mathcal {V}\). We
 the original invariant \(\mathcal {Q}\) (using our indexing as usual), and
the original invariant \(\mathcal {Q}\) (using our indexing as usual), and
 the new invariant \(\mathcal {Q}'\). If the
the new invariant \(\mathcal {Q}'\). If the
 succeeds then the entailment holds. Since the then-branch encodes a side condition, we kill it by adding an
succeeds then the entailment holds. Since the then-branch encodes a side condition, we kill it by adding an
 to ensure that only the other branch (in which no changes were made) will be considered for further verification. Lastly, we perform the rewriting itself by discarding all of the original
to ensure that only the other branch (in which no changes were made) will be considered for further verification. Lastly, we perform the rewriting itself by discarding all of the original
 instances, and replacing them with the new ones. Verification can then proceed as usual.
instances, and replacing them with the new ones. Verification can then proceed as usual.
3.4 Multiple copies of invariant conjuncts
The encoding of \(\textsf {Acq}(l,\mathcal {Q})\) assertions in Fig. 7 expresses that no value has been read for the conjuncts of invariant \(\mathcal {Q}\) (valsRead(l, i)==Set()). This is unsound if a program inhales an \(\textsf {Acq}(l,\mathcal {Q})\) conjunct, then performs an acquire read, and then inhales another \(\textsf {Acq}(l,\mathcal {Q})\) conjunct, for instance, due to joining a thread. In that case, the second
 re-constrains \(\texttt {valsRead(l, }i\texttt {)}\) to be the empty set, even though values have been written. We avoid this unsoundness simply by inhaling valsRead(l, i)==Set() only if the newly acquired conjunct was not already held. This is easy to check using Viper’s
re-constrains \(\texttt {valsRead(l, }i\texttt {)}\) to be the empty set, even though values have been written. We avoid this unsoundness simply by inhaling valsRead(l, i)==Set() only if the newly acquired conjunct was not already held. This is easy to check using Viper’s
 expressions analogously to Fig. 8.
expressions analogously to Fig. 8.
The encoding presented so far allows us to automatically verify annotated C11 programs using release writes and acquire reads (e.g. the program of Fig. 5) without any custom proof strategies [28]. In particular, we can support the higher-order \(\textsf {Acq}\) and \(\textsf {Rel}\) assertions through defunctionalisation and enable the splitting of invariants through a suitable representation.
4 Relaxed memory accesses and fences
In contrast to release-acquire accesses, C11’s relaxed atomic accesses provide no synchronisation: threads may observe reorderings of relaxed accesses and other memory operations. Correspondingly, RSL’s proof rules for relaxed atomics provide weak guarantees, and do not support ownership transfer. Memory fence instructions can eliminate this problem. Intuitively, a release fence together with a subsequent relaxed write allows a thread to transfer away ownership of resources, similarly to a release write. Dually, an acquire fence together with a prior relaxed read allows a thread to obtain ownership of resources, similarly to an acquire read. This reasoning is justified by the ordering guarantees of the C11 model [13].
4.1 FSL proof rules
FSL and FSL\({+}{+}\) provide proof rules for fences (see Fig. 9). They use modalities \(\bigtriangleup \) (“up”) and \({\bigtriangledown }\) (“down”) to represent resources that are transferred through relaxed accesses and fences. An assertion \(\bigtriangleup {A}\) represents a resource A which has been prepared, via a release fence, to be transferred by a relaxed write operation; dually, \({\bigtriangledown }{A}\) represents resources A obtained via a relaxed read, which may not be made use of until an acquire fence is encountered. The proof rule for relaxed write is identical to that for a release write (cf. Fig. 6), except that the assertion to be transferred away must be under the \(\bigtriangleup \) modality; this can be achieved by the rule for release fences. The rule for a relaxed read is the same as that for acquire reads, except that the gained assertion is under the \({\bigtriangledown }\) modality. The modality can be removed by a subsequent acquire fence. As shown in the last lines of the Figure, assertions may be rewritten under modalities, and both modalities distribute over all other logical connectives. Finally, FSL\({+}{+}\) allows additional non-atomic heap locations to be added to the programs as ghost locations. These are typically employed in proofs to facilitate additional transfer of information between the atomic invariants and threads interacting with them. In particular, as the last line of the Figure shows, assertions depending only on ghost locations can be freely moved in and out of the modalities.
Figure 10 shows an example program, which is a variant of the message-passing example from Fig. 5. Comparing the left-hand one of the three parallel threads, a relaxed read is used in the spin loop; after the loop, this thread will hold the assertion \({\bigtriangledown }{{a}\overset{\scriptscriptstyle {1}}{\mapsto }{42}}\). The subsequent \(\texttt {fence}_{\texttt {acq}}\) statement allows the modality to be removed, allowing the non-atomic location a to be accessed. Dually, the middle thread employs a \(\texttt {fence}_{\texttt {rel}}\) statement to place the ownership of the non-atomic locations under the \(\bigtriangleup \) modality, in preparation for the relaxed write to l.
4.2 Encoding
The main challenge in encoding the FSL rules for fences is how to represent the two new modalities. Since these modalities guard assertions that cannot be currently used and/or combined with modality-free assertions, we model them using two additional heaps to represent the assertions under each modality. That is, the assertions A, \({\bigtriangledown }{A}\), and \(\bigtriangleup {A}\) are all encoded like assertion A, but refer to a “real” heap, a “down” heap, and an “up” heap, respectively. The program heap (along with associated permissions) is a built-in notion in Viper, and so we cannot directly employ three heaps. Therefore, we construct the additional “up” and “down” heaps, representing each source location through three references in Viper’s heap (rather than one reference in three heaps). For this purpose, we axiomatise bijective mappings \(\texttt {up}\) and \(\texttt {down}\) between a real program reference and its counterparts in these heaps. Assertions \(\bigtriangleup {A}\) are then represented by replacing all reference-typed variables r in the encoded assertion A with their counterpart \(\texttt {up}{r}\). We write \(\lceil A\rceil ^{\textit{up}}\) for the transformation which performs this replacement. For example,  is transformed to
is transformed to  . Analogously, we write \(\lceil A\rceil ^{\textit{down}}\) for the corresponding transformation for the \(\texttt {down}\) function.
. Analogously, we write \(\lceil A\rceil ^{\textit{down}}\) for the corresponding transformation for the \(\texttt {down}\) function.
The extension of our encoding is shown in Fig. 11. We employ a Viper domain to introduce and axiomatise the mathematical functions for our \(\texttt {up}\) and \(\texttt {down}\) mappings. A Viper domain represents a mathematical theory, consisting of uninterpreted functions and axioms over them. By axiomatising inverses for these mappings, we guarantee bijectivity. Bijectivity allows Viper to conclude that (dis)equalities and other information is preserved under these mappings. Consequently, we do not have to explicitly encode the last two rules of Fig. 9; they are reduced to standard assertion manipulations in our encoding. An additional \(\texttt {heap}\) function labels references with an integer identifying the heap to which they belong (
 for real references,
for real references,
 and
and
 for their “down” and “up” counterparts); this labelling provides the verifiers with the (important) information that these notional heaps are disjoint. For all reference-typed variables and expressions in the source program, we add the assumption that the references they store (if non-null) belong to heap
for their “down” and “up” counterparts); this labelling provides the verifiers with the (important) information that these notional heaps are disjoint. For all reference-typed variables and expressions in the source program, we add the assumption that the references they store (if non-null) belong to heap
 .
.
Our handling of relaxed reads and writes is almost identical to that of acquire reads and release writes in Fig. 7; this similarity comes from the proof rules, which only require that the modalities be inserted for the invariant. Our encoding for release fences requires an annotation in the source program to indicate which assertion to prepare for release by placing it under the \(\bigtriangleup \) modality.
Our encoding for acquire fences does not require any annotations. Any assertion under the \({\bigtriangledown }\) modality can (and should) be converted to its corresponding version without the modality, because \({\bigtriangledown }{A}\) is strictly less-useful than A itself. To encode this conversion, we find all permissions currently held in the down heap, and transfer these permissions and the values of the corresponding locations over to the real heap. These steps are encoded for each field and predicate separately; Fig. 11 shows the steps for the
 field. We first define a set
field. We first define a set
 to be precisely the set of all references
to be precisely the set of all references
 to which some permission to
to which some permission to
 is currently held, i.e.,
is currently held, i.e.,
 . For each such reference, we
. For each such reference, we
 exactly the same amount of permission to the corresponding
exactly the same amount of permission to the corresponding
 location, equate the heap values, and then remove the permission to the locations in the “down” heap.
location, equate the heap values, and then remove the permission to the locations in the “down” heap.
With our encoding based on multiple heaps, reasoning about assertions under modalities inherits all of Viper’s native automation for permission and heap reasoning. We will reuse this idea for a different purpose in the following section.
4.3 Ghost locations
Ghost locations are handled analogously to regular locations, but the encoding needs to be adapted to reflect the equivalence in the last line of Fig. 9. The adapted encoding is given in Fig. 13.
Firstly, we add an uninterpreted boolean function
 on references, to identify whether or not a location is ghost. For each reference-typed parameter employed in the encoding of a source program, we add assumptions defined by the macros
on references, to identify whether or not a location is ghost. For each reference-typed parameter employed in the encoding of a source program, we add assumptions defined by the macros
 Footnote 6 or
Footnote 6 or
 ; these both constrain that the reference’s value is on the “real” heap in the sense of Sect. 4.2, and then add the
; these both constrain that the reference’s value is on the “real” heap in the sense of Sect. 4.2, and then add the
 or
or
 assumption, depending on whether the parameter was declared ghost in the source program.
assumption, depending on whether the parameter was declared ghost in the source program.
To obtain the equivalence in the last line of Fig. 9, we adapt our multiple-heaps encoding for ghost locations. Concretely, we replace the domain
 from Fig. 11 with the version from Fig. 13. This version requires the \(\texttt {up}\) and \(\texttt {down}\) mappings to act as the identity for ghost locations (correspondingly, the result of \(\texttt {heap}\) is no longer constrained to be different after applying these mappings to a ghost reference). This immediately gives us that, for assertions depending only on ghost locations in the heap, \(\bigtriangleup {A}\), A and \({\bigtriangledown }{A}\) are handled equivalently; they will be encoded as provably equivalent assertions.
from Fig. 11 with the version from Fig. 13. This version requires the \(\texttt {up}\) and \(\texttt {down}\) mappings to act as the identity for ghost locations (correspondingly, the result of \(\texttt {heap}\) is no longer constrained to be different after applying these mappings to a ghost reference). This immediately gives us that, for assertions depending only on ghost locations in the heap, \(\bigtriangleup {A}\), A and \({\bigtriangledown }{A}\) are handled equivalently; they will be encoded as provably equivalent assertions.
Finally, we add an assumption of
 to our existing statements for allocating references, and add a new ghost allocation statement, for which the analogous
to our existing statements for allocating references, and add a new ghost allocation statement, for which the analogous
 assumption is added. These details are summarised in Fig. 13.
assumption is added. These details are summarised in Fig. 13.
5 Compare and swap
C11 includes atomic read-modify-write operations, which are commonly used to implement high-level synchronisation primitives such as locks. FSL\({+}{+}\) [14] provides proof rules for compare and swap (CAS) operations. An atomic compare and swap \(\texttt {CAS}_{\tau }(l,e,e')\) reads and returns the value of location l; if the value read is equal to e, it also writes the value \(e'\) to location l (otherwise we say that the CAS fails). The annotation \(\tau \) indicates an atomic access mode, see Fig. 1.Footnote 7
5.1 \(\text {FSL{+}{+}}\) proof rules
FSL\({+}{+}\) does not support general combinations of atomic reads and CAS operations on the same location; the way of reading must be chosen at allocation via the annotation \(\rho \) on the allocation statement (see Fig. 1). \(\text {FSL{+}{+}}\) provides an assertion \(\textsf {RMWAcq}(l,\mathcal {Q})\), which is similar to \(\textsf {Acq}(l, \mathcal {Q})\), but is used for CAS operations instead of acquire reads (that is, when \(\rho =\texttt {RMW}\)). In contrast to the \(\textsf {Acq}\) assertions used for atomic reads, \(\textsf {RMWAcq}\) assertions can be freely duplicated and their invariants need not be adjusted for a successful CAS: when using only CAS operations, each value read from a location corresponds to a different write. A successful CAS both obtains ownership of an assertion via its read operation and gives up ownership of an assertion via its write operation.
Our presentation of the relevant proof rules is shown in Fig. 12. Allocating a location with annotation \(\texttt {RMW}\) provides a \(\textsf {Rel}\) and a \(\textsf {RMWAcq}\) assertion, such that the location can be used for release writes and CAS operations.
For the CAS operation, we present a single, general proof rule instead of four rules for the different combinations of access modes in FSL\({+}{+}\). The rule requires that l is initialised (since its value is read), \(\textsf {Rel}\) and \(\textsf {RMWAcq}\) assertions, and an assertion \(P'\) that provides the resources needed for a successful CAS. If the CAS fails (that is, \(x\not = e\)), its precondition is preserved.
If the CAS succeeds, it has read value e and written value \(e'\). Assuming for now that the access mode \(\tau \) permits ownership transfer, the thread has acquired \(\mathcal {Q}[e/\mathcal {V}]\) and released \(\mathcal {Q}[e'/\mathcal {V}]\). As illustrated in Fig. 14i, these assertions may overlap. Let T denote the assertion characterising the overlap; then assertion A denotes \(\mathcal {Q}[e/\mathcal {V}]\) without the overlap, and P denotes \(\mathcal {Q}[e'/\mathcal {V}]\) without the overlap. The net effect of a successful CAS is then to acquire A and to release P, while T remains with the location invariant across the CAS. Automating the choice of T, A, and P is one of the main challenges of encoding this rule. Finally, if the access mode \(\tau \) does not permit ownership transfer (that is, fences are needed to perform the transfer), A and P are put under the appropriate modalities.
5.2 Encoding
Our encoding of CAS operations reuses several of our ideas and techniques presented in earlier sections. The details of this encoding are shown in Fig. 15. We represent \(\textsf {RMWAcq}\) assertions analogously to our encoding of \(\textsf {Acq}\) assertions (see Sect. 3), but set the acq field to false in order to differentiate holding one from the other.Footnote 8 Since \(\textsf {RMWAcq}\) assertions are duplicable (cf. Fig. 12), we employ
 permissions for the corresponding
permissions for the corresponding
 predicates; this allows the \(\textsf {RMWAcq}\) assertions, along with their full invariants to be freely duplicated, in contrast to \(\textsf {Acq}\) assertions (whose invariants must be split when the \(\textsf {Acq}\) assertion is split).
predicates; this allows the \(\textsf {RMWAcq}\) assertions, along with their full invariants to be freely duplicated, in contrast to \(\textsf {Acq}\) assertions (whose invariants must be split when the \(\textsf {Acq}\) assertion is split).
The encoding of allocation is straightforward; it inhales the \(\textsf {Rel}\) and \(\textsf {RMWAcq}\) predicates; the latter includes the information that the new location is accessed via compare and swaps (by setting its
 field to false.
field to false.
The proof rule for CAS operations from Fig. 12 is complex to encode. We initially check that we indeed hold the required \(\textsf {Init}\), \(\textsf {RMWAcq}\) and \(\textsf {Rel}\) assertions for the location, according to the precondition of the rule. In case the CAS fails, nothing else needs to be done. Otherwise, in the case of a successful CAS operation, the key challenge is how to select an appropriate assertion T to satisfy the premises of the rule, while retaining maximal information for future proof steps. Maximising the overlap represented by T is desirable in practice since this reduces the resources to be transferred, which must interact in some cases (when the access mode is not \(\texttt {rel\_acq}\)) with the modalities. Our Viper encoding indirectly computes this largest-possible T as follows.
Reusing the notion of multiple heaps employed in Sect. 4, we introduce yet another heap (“tmp”) in which we inhale the invariant \(\mathcal {Q}[e/\mathcal {V}]\) for the value read; the functions and axioms for the “tmp” heap are shown in Fig. 13. We proceed in three steps (see Fig. 14ii for a high-level illustration).
Firstly, we inhale the newly gained resources (corresponding to \(\mathcal {Q}[e/\mathcal {V}]\)) into the tmp heap.
Secondly, we attempt to exhale the assertion \(\mathcal {Q}[e'/\mathcal {V}]\) for the value written, but adapt the assertions as follows: for each permission in the invariant, we take the maximum possible amount from our “tmp” heap; these permissions correspond to T. Any remainder is taken from the current heap (either the real or the “up” heap, depending on \(\tau \)); these correspond to P. This adaptation of the assertion (which splits the taken permission amounts across the two heaps) is denoted by the \(\lceil .\rceil ^{\textit{tmp/real}}\) and \(\lceil .\rceil ^{\textit{tmp/up}}\) mappings; if the values of heap locations are also mentioned in the parameter assertions, these heap dereferences must also be rewritten to a dereference in the corresponding heap (e.g. x.val == 4 might become
 ). In case permission to the corresponding location is taken partly from both heaps, the extra assumption that the two values are the same is explicitly added by these mappings.
). In case permission to the corresponding location is taken partly from both heaps, the extra assumption that the two values are the same is explicitly added by these mappings.
Finally, any permissions remaining in the “tmp” heap after this exhale correspond to the assertion A and are moved (in a way similar to our \(\texttt {fence}_{\texttt {acq}}\) encoding in Fig. 11) to either the real or “down” heap (depending on \(\tau \)).
Summary of our encoding of source-level assertions. Our technique is agnostic as to the precise language of pure expressions; we assume a suitable encoding of pure expressions into Viper, which can typically be the identity mapping. Note that for examples which potentially employ multiple copies of the same conjunct in an \(\textsf {Acq}(\)) predicate’s invariant, some additional care needs to be taken about when exactly to make the \(\texttt {valsRead(l, }i\texttt {)}==Set()\) assumption, see Sect. 3.4
This combination of techniques results in an automatic support for the proof rule for CAS statements. This completes the core of our Viper encoding, which now handles the complete set of memory access constructs from Fig. 1. We summarise the encoding of the general source language of assertions in Fig. 16.
6 Soundness and completeness
In this section, we give soundness arguments (as an outlined proof sketch) for our encoding, and also discuss completeness compared with a manual proof effort.
6.1 Soundness overview
Soundness means that if the Viper encoding of a program and its specification verifies, then there exists a proof of the program and specification using the RSL logics. We outline the soundness of our encoding via three key ingredients.
Firstly (Sect. 6.3), we identify invariants on the states of the Viper programs which are in the image of our encoding. They encode fairly basic properties, such as the fact that the amounts of permission held to the
 and
and
 fields of a non-atomic location are always the same. We can show straightforwardly that these invariants are preserved by the Viper programs generated by our encoding.
fields of a non-atomic location are always the same. We can show straightforwardly that these invariants are preserved by the Viper programs generated by our encoding.
Secondly (Sect. 6.4), for Viper states satisfying these invariants, we define a mapping from the state to an assertion of the RSL logics. Conceptually, this mapping can be thought of as capturing where we are in the construction of a Hoare Logic proof in the original formalism. This is connected to our soundness argument by then showing that, if one compares the initial and final states of the encoding of any source-level statement, and applies our mapping to each, the assertions represent a Hoare triple derivable in the original logics provided that the Viper-encoded program has no verification errors. Thus, we connect verification at the Viper level with proof construction at the Hoare logic level.
Finally (Sect. 6.5), we explain how we can be sure that Viper does not, e.g. deduce inconsistency at points in a proof where this would not be justified in the original logic. In general, we need to know that any entailments between assertions in a single state which Viper can justify automatically, reflect entailments which were justified in the original logic.
Putting these three ingredients together, we know that the verification of an encoded Viper program will imply the existence of a Hoare Logic derivation in the original logics; in other words, our technique will only verify (encoded) properties for which a proof exists in the RSL logics; our technique is sound.
6.2 Viper states and semantics
The states of a Viper program are triples \((H,P,\sigma )\) of a heap H (mapping pairs of references and field names to values), a permission map P (mapping such pairs, as well as predicate instances to permission amounts, which can be considered non-negative rational values; for field locations, these cannot exceed 1), and an environment \(\sigma \), mapping variable names to values. We write H[r, f] and P[r, f] for lookups in these maps; for looking up e.g. predicate instances p(r) in the permission map, we write P[p(r)].
The semantics of Viper’s core logic follows Parkinson and Summers [29]; in particular, the semantics of heap-dependent expressions such as heap dereferences x.f comes with a well-definedness condition; such heap dereferences are allowed only in states in which non-zero permission is held (i.e. \(P[x,f] > 0\)). The treatment of functions and predicates in the logic follows Summers and Drossopoulou [37].
Verification of a Viper program amounts to: (1) Symbolically tracking knowledge of changes to the Viper state elements (heap values, permissions held, variable values). For example, an inhale operation can add permissions to the permission map P. (2) Checking that all assert and exhale statements describe provable assertions (both are sources of verification failures; the difference is that any permissions or predicates in the assertion of an exhale statement are removed from the current state). (3) Checking that all expressions employed in the program are well-defined: for heap dereferences this means checking that some permission to the corresponding location is held; for applications of specification functions (such as
 in our encoding), this means checking that their preconditions hold where they are applied. Some assertions are defined via specifications: for example, a method post-condition must be shown to hold at the end of the method body.
in our encoding), this means checking that their preconditions hold where they are applied. Some assertions are defined via specifications: for example, a method post-condition must be shown to hold at the end of the method body.
6.3 Encoding invariants
Our encoding maintains invariants on the states of Viper programs, which hold before and after (but not necessarily during) the code-fragments generated by the encoding of a single source-level statement. In particular, our argument depends on the following invariant on states \((H,P,\sigma )\), guaranteed to hold at the start and end of each block of Viper code representing the encoding of a single source-level statement (assuming we reach the end of the block without verification errors):
This states that we always hold the same amount of permission to the \(\texttt {val}\) and \(\texttt {init}\) fields of an encoded non-atomic location, and if we hold such permissions and the corresponding \(\texttt {init}\) field is false, then the only possibility is that we hold the full permissions. This corresponds to the fact that the \(\textsf {Uninit}(l)\) assertion in the RSL logics is not splittable, whereas once a non-atomic location is initialised, its ownership can be shared.
In explaining our soundness argument we make use implicitly of the fact (also assumed at the source level, and in the RSL logics themselves) that locations are known to be either non-atomic or atomic locations; this is indirectly reflected at the Viper level in terms of which permissions or predicates are held for the locations, but is only explicitly relevant for constructing the soundness argument itself.
It is straightforward to show that the above invariant is preserved by our statement encodings, i.e. if we assume it in the Viper state prior to the translation of a source-level statement, we can show that (barring verification errors, or reaching an inconsistent state) it will be still be true in the state after the Viper statements generated by the source-level statement’s encoding. This can be checked per statement encoded; here we summarise the overall argument applicable to all cases.
Consider first the first conjunct of the invariant. Allocation of a non-atomic location provides full permission to both \(\texttt {val}\) and \(\texttt {init}\) fields. These permissions can be subsequently modified as a result of program statements which add or remove RSL logic assertions A, e.g. forking and joining threads. Each of these results in a corresponding

 or
or

 operation in the encoded Viper program. The definition of
operation in the encoded Viper program. The definition of  (cf. Fig. 16) only concerns these permission amounts in two cases:
(cf. Fig. 16) only concerns these permission amounts in two cases:  and
and  ; in both cases, the permissions to the two fields come together in identical amounts.
; in both cases, the permissions to the two fields come together in identical amounts.
We now consider preservation of the second conjunct of the invariant; that is, we show preservation of \((P[l,\texttt {val}] > 0 \wedge H[l,\texttt {init}] = \textit{false}\Rightarrow P[l,\texttt {val}] = 1)\). We use the fact discussed above: that permissions to the two fields are only ever added or removed in sync with each other. We also observe that no encoding of a statement results in assigning \(\textit{false}\) to any \(\texttt {init}\) field; the only way of adding knowledge that an \(\texttt {init}\) field is \(\textit{false}\) is via the . We now consider two cases on properties of the prior Viper state \((H,P,\sigma )\):
-
(Case \(P[l,\texttt {val}]= 0\)): Then either the encoding of the statement doesn’t change this fact (the invariant conjunct remains trivially true), or it adds non-zero permissions to the field locations \(l.\texttt {val}\) and \(l.\texttt {init}\). This can only be done by an inhale of
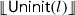 or of (perhaps several times)
or of (perhaps several times)  for some e, k (cf. Fig. 4). In the former case, the invariant conjunct is true, since \(P[l,\texttt {val}] = 1\) is guaranteed after inhaling
for some e, k (cf. Fig. 4). In the former case, the invariant conjunct is true, since \(P[l,\texttt {val}] = 1\) is guaranteed after inhaling  . In the latter case, the invariant conjunct holds vacuously, since \(H[l,\texttt {init}] = \textit{true}\) after such an inhale.
. In the latter case, the invariant conjunct holds vacuously, since \(H[l,\texttt {init}] = \textit{true}\) after such an inhale. -
(Case \(P[l,\texttt {val}]> 0\)): Then we have \(P[l,\texttt {init}] > 0\). If this permission is fully removed from the Viper state as a result of the encoded statement in question, we can subsequently argue according to the previous case. If it is never removed, the value of \(H[l,\texttt {init}]\) must remain stable across the translation of the statement, except if that translation directly modifies it. Now, if \(P[l,\texttt {val}] = P[l,\texttt {init}] < 1\) then, since we assumed the invariant conjunct true in the prior state, we must have \(H[l,\texttt {init}] = \textit{true}\), and this will remain the case, since we never assign \(\textit{false}\) to such a field. This leaves us to consider the remaining case (\(P[l,\texttt {val}] = P[l,\texttt {init}] = 1\)): we are left to consider the possibility that we modify the value of \(H[l,\texttt {init}]\) directly in the Viper code corresponding to the translated statement. This happens only in the case of encoding a non-atomic write: \({[l]_{\texttt {na}}~{:=}~e}\) (cf. Fig. 4). In this case, it is guaranteed that the final state will satisfy \(H[l,\texttt {init}] = \textit{true}\), and so the invariant conjunct in question holds vacuously.
We require similar “sanity” invariants on Viper states for the encodings of atomic locations. In particular:
This states that a readable \(\texttt {rel}\) field always stored the index of one of the atomic invariants from the current example being encoded, and analogously for the index parameters of \(\texttt {AcqConjunct}\) predicate instances held. Showing these invariants to be preserved is also straightforward; we omit the details here, for brevity.
Having established these basic invariants over the Viper states corresponding to the beginning and end of each encoded statement, we turn to how to map what Viper checks back to the existence of a proof in the RSL logics.
6.4 Mapping and Hoare triples
We next define the mapping  from a reference l in a Viper state \((H,P,\sigma )\) (which is assumed to satisfy the invariants in Sect. 6.3) to assertions from the RSL logics; the corresponding mapping for the entire Viper state is then the iterated separating conjunction [31] over the assertion for each reference to which at least some permission is held.
from a reference l in a Viper state \((H,P,\sigma )\) (which is assumed to satisfy the invariants in Sect. 6.3) to assertions from the RSL logics; the corresponding mapping for the entire Viper state is then the iterated separating conjunction [31] over the assertion for each reference to which at least some permission is held.
We deal concretely with the simplified case of the logics without the \(\bigtriangleup \) and \({\bigtriangledown }\) modalities, and then explain how to extend the definitions.
For non-atomic locations l, the mapping is defined as follows:

For atomic locations l, the mapping is more involved:

Here, we rewrite \(\langle {\texttt {valsRead}(l,i)}\rangle _{H,P,\sigma }\) for the semantics of this function application in the given state; i.e. the set of integer values it represents.
The above mapping reconstructs appropriate \(\textsf {Init}(\)), \(\textsf {Rel}(\)), and either \(\textsf {Acq}(\)) or \(\textsf {RMWAcq}(\)) assertions for the corresponding location, according to the permissions (and predicates) held in the state. By conjoining these assertions per location together with separating conjunctions (skipping those for which \(\textit{true}\) is the result), we obtain an assertion from the RSL logics corresponding to the logical resources held at this particular point in a corresponding proof in the RSL logics.
The mappings above can be generalised to the full logics with modalities by reflecting on the \(\texttt {heap}\) numbering of the reference in question (cf. Sect. 4); where \(\texttt {heap}{l} = 0\), the above definitions apply, while for 1 or \(-1\) the resulting assertion must be placed under the \(\bigtriangleup \) or \({\bigtriangledown }\) modalities, respectively.
For each source language statement, one can now show that if the encoded Viper statements verify, the beginning and end states of the Viper program describe (when mapped to RSL assertions according to these definitions) a provable Hoare triple in the original logic. For example, consider the encoding of a release write statement \([l]_{\texttt {rel}}~{:=}~e\) from the middle of Fig. 7, following  . Due to the initial
. Due to the initial
 statement, this code will only verify if the current state has at least some permission to the location’s \(\texttt {rel}\) field; i.e. if \(P[l,\texttt {rel}] > 0\). Based on the invariants from the previous subsection, we then know that \(H[l,\texttt {rel}]\) will be the value of a valid index i in \(\textit{indices}\). Suppose \(Q = {\textit{inv}}{i}\) is the corresponding invariant for this index, as defined in the original program. Correspondingly, one of the
statement, this code will only verify if the current state has at least some permission to the location’s \(\texttt {rel}\) field; i.e. if \(P[l,\texttt {rel}] > 0\). Based on the invariants from the previous subsection, we then know that \(H[l,\texttt {rel}]\) will be the value of a valid index i in \(\textit{indices}\). Suppose \(Q = {\textit{inv}}{i}\) is the corresponding invariant for this index, as defined in the original program. Correspondingly, one of the
 conditions will evaluate to \(\textit{true}\), forcing an
conditions will evaluate to \(\textit{true}\), forcing an
 of
of  . In particular, this will also cause a verification failure, unless the Viper state also satisfies this assertion. In this case, the relevant permissions and predicate instances will be removed by the exhale. Finally,
. In particular, this will also cause a verification failure, unless the Viper state also satisfies this assertion. In this case, the relevant permissions and predicate instances will be removed by the exhale. Finally,  will be inhaled, corresponding to adding \(\textsf {Init}(l)\) in the post-state of this operation.
will be inhaled, corresponding to adding \(\textsf {Init}(l)\) in the post-state of this operation.
Combining this analysis with our  definition, we know we must have
definition, we know we must have  for some A (whose definition depends on whether e.g. \(\textsf {Init}(l)\) assertions are also held for the same location). More generally, the assertion obtained by pointwise conjoining
for some A (whose definition depends on whether e.g. \(\textsf {Init}(l)\) assertions are also held for the same location). More generally, the assertion obtained by pointwise conjoining  for all location’s l must be equivalent to \(Q[e/\mathcal {V}] *\textsf {Rel}(l,Q) *A'\) for some assertion \(A'\), for the analysed Viper code to be free of verification errors; the resulting Viper state will be analogous except that the assertions corresponding to \({\textit{inv}}{i}[e/\mathcal {V}]\) will have been removed, and those corresponding to \(\textsf {Init}(l)\) will have been added. If no verification errors occur, the following analogous derivation therefore exists in the RSL logics:
for all location’s l must be equivalent to \(Q[e/\mathcal {V}] *\textsf {Rel}(l,Q) *A'\) for some assertion \(A'\), for the analysed Viper code to be free of verification errors; the resulting Viper state will be analogous except that the assertions corresponding to \({\textit{inv}}{i}[e/\mathcal {V}]\) will have been removed, and those corresponding to \(\textsf {Init}(l)\) will have been added. If no verification errors occur, the following analogous derivation therefore exists in the RSL logics:

6.5 Entailment correspondence
In addition to the encoding of individual statements, it is important to consider which entailments Viper can automatically prove about the encoded assertions from the original logics. For the assertions describing non-atomic locations, Viper’s built-in field permissions are used in a standard manner; the relationship between the handling of these permissions in such a logic and a typical concurrent separation logic presentation is well-understood to give an isomorphism [29]. In particular, Viper imposes the same assumptions for field permissions (that no more than 1 permission can be held) as in a standard separation logic.
For the encoding of atomic locations, the Viper representation is largely in terms of duplicable (wildcard) permissions, and abstract predicates. Wildcard permissions, as discussed in Sect. 3, model a duplicable resource exactly as desired. Abstract predicates, on the other hand, are treated as unknown resources in Viper; these are counted in and out when inhaled and exhaled, but no additional facts will be deduced from holding them in a particular state. Our modelling of atomic invariants with \(\texttt {AcqConjunct}\) predicates can, in some cases, provide entailments between the encodings of different \(\textsf {Acq}(\)) predicates, but these are always instances of the general rules of the logic. However, not all entailments valid in the logic are available automatically to the Viper verifiers according to our encoding: for rewriting atomic invariants, we require an explicit annotation (cf.Sect. 3.3); in the next subsection we discuss other potential sources of incompleteness.
6.6 Completeness
Completeness means that all programs provable in the RSL logics can be verified via their encoding into Viper. As part of the design of our work, we intentionally chose not to support certain features of the RSL logics; each of these is technically a source of incompleteness, although in most cases our decision was based on the fact that the expressiveness lost is not actually useful in practical examples.
Rust reference counting variant with strengthened access modes (RustARCStronger in our evaluation). Compared to the original code [14], we modified the write in new to use a release rather than relaxed mode, and the update in clone to use acquire rather than relaxed. As discussed in Sect. 7, the original version of the example is proved in [14] using features which are not yet supported by our encoding. We do, however, verify a slightly less-efficient variant of the original code (which does not require the custom monoid employed in [14]) here; this example requires our support for CAS operations and fences. We write \(\textit{rd}\) for a read permission, in the sense of counting permissions [6]. In this example, g is a ghost location. We model the free statement by exhaling the corresponding permissions
By systematically analysing each rule of the RSL logics, we identify the following sources of incompleteness of our encoding: (1) It does not allow strengthening the invariant in a \(\textsf {Rel}{}\) assertion; strengthening the requirement on writing does not allow more programs to be verified, and has never been useful in practice [42]. Conceptually, it amounts to forcing a writer to live up to a more difficult requirement than the atomic invariant really relies on; e.g. forcing one to give up more permissions than will ever be obtainable via subsequent reads of the location. (2) For a \(\texttt {fence}_{\texttt {acq}}\), our encoding removes all assertions from under a \({\bigtriangledown }\) modality. As mentioned when we introduce our encoding of this feature (cf. Sect. 4), the ability to choose not to remove the modality is not useful in practice; conceptually, the modality blocks the usage of resources (such as ownership of non-atomic locations) underneath it until they moved out from the modality at a memory fence. Technically, an incompleteness could arise for modular proofs if one uses the \({\bigtriangledown }\) modality in a function precondition (effectively promising to insert an appropriate fence in the function’s implementation) but a particular caller has already employed a memory fence, removing the modality. However, this modality doesn’t appear to be used or useful across such modularity boundaries. The fact that libraries exploiting these weak-memory primitives are written with very precise synchronisation strategies in mind means that this kind of division of synchronisation responsibility between caller’s and callee’s doesn’t arise. (3) For simplicity, our encoding doesn’t address quantifiers (although these are supported in Viper; an extension should be straightforward). We also don’t allow the \(\bigtriangleup \) and \({\bigtriangledown }\) modalities to be used in atomic invariants themselves. This restriction is largely inherited from FSL and FSL\({+}{+}\)[13], but a slightly weaker technical requirement (called normalisability) is employed there. This difference doesn’t appear significant for examples in practice. (4) The ghost state employed in FSL\({+}{+}\) can be defined over a custom permission structure (a partial commutative monoid), which is not possible in Viper. For examples whose proof relies on a custom monoid which is not known to be encodable in Viper, a proof possible in the RSL logics cannot be obtained via our techniques (Viper natively supports only fractional permissions, although some additional models such as counting permissions can be encoded). This is the only incompleteness of our encoding arising in practice; we will discuss an example in Sect. 7.
7 Examples and evaluation
We evaluated our work with a prototype front-end tool [32, 33], and some additional experiments directly at the Viper level [28]. Our front-end tool accepts a simple input language for C11 programs, closely modelled on the syntax of the RSL logics. It supports all features described in this paper, with the exception of invariant rewriting ((cf. Sect. 3.3 of the TR [39]) and ghost state (Sect. 4.3 of the TR), which will be simple extensions. We encoded examples which require these features, additional theories, or custom permission structures manually into Viper, to simulate what an extended version of our prototype will be able to achieve.
Our encoding supports several extra features which we used in our experiments but mention only briefly here: (1) We support the FSL\({+}{+}\) rules for ghost state: see Sect. 4.3 of the TR. (2) Our encoding handles common spin loop patterns without requiring loop invariant annotations. (3) We support fetch-update instructions (e.g. atomic increments) natively, modelled as a CAS which never fails.
Examples We took all examples with specifications from the RSL [43] and FSL [13] papers, along with variants in which we seeded errors, to check that verification fails as expected (and in comparable time). We also encoded the Rust reference-counting (ARC) library [34], which is the main example from FSL\({+}{+}\) [14]. The proof there employs a custom permission structure (using the custom ghost state supported in the FSL\({+}{+}\) paper [14]), which is not yet supported by Viper; we can only encode this exact example directly by omitting the corresponding ghost state, without which its proof fails as expected. However, following the suggestion of one of the authors [42], we were able to fully verify two variants of the example, in which some access modes are strengthened, making the code slightly less efficient but enabling a proof using a simpler permission model. For these variants, we required counting permissions [6], which we expressed with additional background definitions (see [28] for details, and Fig. 17 for the code). Note that we encode more examples than have been mechanised in the pre-existing papers: we speculate that not all examples were mechanised due to the substantial work and time required to construct the Coq-based proofs.
Finally, we tackled seven core functions of a reader-writer-spinlock from the Facebook Folly library [15]. We were able to verify five of them directly. The other two employ code idioms which are beyond the scope of the RSL logics without employing sophisticated custom ghost state: a similar situation to that of the unmodified ARC example. Again similarly, for both functions we also wrote and verified alternative implementations in which some atomic access modes are strengthened, enabling a slightly less complex proof explainable using counting permissions. The Rust and Facebook examples demonstrate a key advantage of building on top of Viper; both require support for extra theories (counting permissions as well as modulo and bitwise arithmetic), and we were able to exploit Viper’s features to integrate support for these additional complementary verification aspects easily.
Performance We measured the verification times on an Intel Core i7-4770 CPU (3.40 GHz, 16 Gb RAM) running Windows 10 Pro and report the average of 5 runs. A snapshot of all dependencies and experiments (including all source examples) is provided online [32, 33]. For those examples supported by our front-end, the times include the generation of the Viper code. As shown in Table 1, verification times are reasonable (generally around 10 sec, and always under a minute).
Automation Each function (and thread) must be annotated with an appropriate pre and post-condition, as is standard for modular verification. In addition, some of our examples require loop invariants and other annotations (e.g. on allocation statements and, for the hand-crafted FencesDblMsgPassAcqRewrite example, for rewriting invariants according to Sect. 3.3). The abstraction level and annotation overhead can be roughly judged from e.g. Fig. 10; up to mild syntactic differences this closely follows the input language of our tool, except that the parallel blocks show up as explicit fork and join statements in the input language of our tool.
Critically, the number of required annotations is consistently very low. In particular, our annotation overhead is between one and two orders of magnitude lower than the overhead of existing mechanised proofs (using the Coq formalisations for [14, 43] and a recent encoding [19] of RSL into Iris [21]). Such ratios are consistent with other recent Coq-mechanised proofs based on separation logic (e.g. [44]), which suggests that the strong soundness guarantees provided by Coq have a high cost when applying the logics. By contrast, once the specifications are provided, our approach is almost entirely automatic.
8 Conclusions and future work
We have presented the first encoding of modern program logics for weak-memory models into an automated deductive program verifier. The encoding enables programs (with suitable annotations) to be verified automatically by existing back-end tools. We have implemented a front-end verifier and demonstrated that our encoding can be used to verify weak-memory programs efficiently and with low annotation overhead. As future work, we plan to tackle other weak-memory logics such as GPS [41]. Building practical tools that implement such advanced formalisms will provide feedback that inspires further improvements of the logics.
Notes
For a general introduction to these reasoning challenges and issues in defining the model itself, we refer the reader to [43].
i.e. verifying all program behaviours, without bounding the number of threads, loop iterations, heap size and so on.
By convention, we use math-font variables for meta/logical variables and those from source programs (e.g. in \(\textsf {Uninit}(l)\); we use corresponding code-font variables for the Viper variables corresponding to these source-level variables (e.g. in

 .
.Viper macros can be defined for assertions or statements, and are syntactically expanded (and their arguments substituted) on use.
A
 expression yields the permission fraction held for a field or predicate instance.
expression yields the permission fraction held for a field or predicate instance.For historical reasons, in our artefact examples, the
 macro is actually called
macro is actually called
 ; we renamed this subsequently due to potential confusion with the notion of the “real heap” employed in Sect. 4.2.
; we renamed this subsequently due to potential confusion with the notion of the “real heap” employed in Sect. 4.2.In the RSL logics, extended CAS proof rules are also supported (e.g. in the “Appendix” of FSL\({+}{+}\) [14]) allowing the specification of a different access mode for when a CAS operation fails; we omit this for simplicity, and use the same access mode for both cases. An extension would be straightforward, but this flexibility has not yet appeared necessary for any examples.
Instead of distinguishing the two cases via the value of the
 field, it would also be possible to introduce another field to represent \(\textsf {RMWAcq}\) assertions.
field, it would also be possible to introduce another field to represent \(\textsf {RMWAcq}\) assertions.
References
Abdulla, P.A., Atig, M.F., Jonsson, B., Leonardsson, C.: Stateless model checking for POWER. In: CAV 2016 Proceedings Part II, pp. 134–156 (2016). https://doi.org/10.1007/978-3-319-41540-6_8
Abdulla, P.A., Atig, M.F., Bouajjani, A., Ngo, T.P.: The benefits of duality in verifying concurrent programs under TSO. CoRR (2017). arXiv:1701.08682
Alglave, J., Cousot, P.: Ogre and Pythia: an invariance proof method for weak consistency models. In: POPL 2017, pp. 3–18. ACM, New York, NY, USA, POPL (2017). https://doi.org/10.1145/3009837.3009883
Barnett, M., Chang, B.Y.E., DeLine, R., Jacobs, B., Leino, K.R.M.: Boogie: a modular reusable verifier for object-oriented programs. In: Proceedings of the 4th International Conference on Formal Methods for Components and Objects, pp. 364–387. Springer, Berlin, FMCO’05 (2006). https://doi.org/10.1007/11804192_17
Bobot, F., Filliâtre, J.C., Marché, C., Paskevich, A.: Why3: shepherd your herd of provers. In: Boogie 2011: First International Workshop on Intermediate Verification Languages, Wrocław, Poland, pp. 53–64 (2011). http://proval.lri.fr/publications/boogie11final.pdf
Bornat, R., Calcagno, C., O’Hearn, P., Parkinson, M.: Permission accounting in separation logic. In: Proceedings of POPL’05, pp. 259–270. ACM, New York, NY, USA (2005). https://doi.org/10.1145/1040305.1040327
Bouajjani, A., Derevenetc, E., Meyer, R.: Checking and enforcing robustness against TSO. In: ESOP 2013, pp. 533–553. Springer, Berlin, ESOP’13 (2013). https://doi.org/10.1007/978-3-642-37036-6_29
Boyland, J.: Checking Interference with Fractional Permissions, vol. 2694, pp. 55–72. Springer, Berlin (2003)
Chlipala, A.: Mostly-automated verification of low-level programs in computational separation logic. In: Proceedings of the 32nd ACM SIGPLAN Conference on Programming Language Design and Implementation, pp. 234–245. ACM, New York, NY, USA, PLDI’11 (2011). https://doi.org/10.1145/1993498.1993526
Cohen, E., Dahlweid, M., Hillebrand, M., Leinenbach, D., Moskal, M., Santen, T., Schulte, W., Tobies, S.: VCC: A Practical System for Verifying Concurrent C, pp. 23–42. Springer, Berlin (2009). https://doi.org/10.1007/978-3-642-03359-9_2
Cuoq, P., Kirchner, F., Kosmatov, N., Prevosto, V., Signoles, J., Yakobowski, B.: Frama-C. In: SEFM, pp. 233–247. Springer, Berlin (2012). https://doi.org/10.1007/978-3-642-33826-7_16
Dan, A., Meshman, Y., Vechev, M., Yahav, E.: Effective abstractions for verification under relaxed memory models. In: VMCAI 2015, pp. 449–466. Springer, Berlin (2015). https://doi.org/10.1007/978-3-662-46081-8_25
Doko, M., Vafeiadis, V.: A program logic for C11 memory fences. VMCAI, Springer, Lecture Notes in Computer Science 9583, 413–430 (2016)
Doko, M., Vafeiadis, V.: Tackling real-life relaxed concurrency with FSL++. In: ESOP 2017, pp. 448–475. Springer, Berlin (2017)
Facebook Folly: Reader–writer spinlock implementation (2018). https://github.com/facebook/folly/blob/master/folly/RWSpinLock.h
Heule, S., Leino, K.R.M., Müller, P., Summers, A.J.: Abstract read permissions: fractional permissions without the fractions. VMCAI, Springer, Lecture Notes in Computer Science 7737, 315–334 (2013)
Jacobs, B.: Verifying TSO programs. CW Reports CW660, Department of Computer Science, KU Leuven, (2014). https://lirias.kuleuven.be/handle/123456789/452373
Jacobs, B., Smans, J., Piessens, F.: A quick tour of the VeriFast program verifier. APLAS, Springer, LNCS 6461, 304–311 (2010)
Kaiser, J.O., Dang, H.H., Dreyer, D., Lahav, O., Vafeiadis, V.: Strong logic for weak memory: reasoning about release-acquire consistency in Iris. In: ECOOP 2017, Schloss Dagstuhl–Leibniz, LIPIcs, vol. 74, pp. 17:1–17:29, (2017). https://doi.org/10.4230/LIPIcs.ECOOP.2017.17, http://drops.dagstuhl.de/opus/volltexte/2017/7275
Kokologiannakis, M., Lahav, O., Sagonas, K., Vafeiadis, V.: Effective stateless model checking for C/C++ concurrency. In: PACMPL, vol. 2(POPL), pp. 17:1–17:32 (2018). https://doi.org/10.1145/3158105, https://doi.org/10.1145/3158105
Krebbers, R., Jung, R., Bizjak, A., Jourdan, J.H., Dreyer, D., Birkedal, L.: The essence of higher-order concurrent separation logic. In: ESOP, pp. 696–723, Springer, New York, Inc., New York, NY, USA (2017). https://doi.org/10.1007/978-3-662-54434-1_26, https://doi.org/10.1007/978-3-662-54434-1_26
Lahav, O.: Verification under causally consistent shared memory. SIGLOG News 6(2), 43–56 (2019). https://doi.org/10.1145/3326938.3326942
Leino, K.R.M.: Dafny: an automatic program verifier for functional correctness. In: Proceedings of LPAR’10, pp. 348–370, Springer, Berlin (2010). http://dl.acm.org/citation.cfm?id=1939141.1939161
Leino, K.R.M., Müller, P.: A basis for verifying multi-threaded programs. In: Castagna, G. (ed.) ESOP, Springer-Verlag, LNCS, vol. 5502, pp. 378–393 (2009)
Müller, P., Schwerhoff, M., Summers, A.J.: Automatic verification of iterated separating conjunctions using symbolic execution. CAV, Springer-Verlag, LNCS 9779, 405–425 (2016)
Müller, P., Schwerhoff, M., Summers, A.J.: Viper: a verification infrastructure for permission-based reasoning. In: Jobstmann, B., Leino, K.R.M. (eds.) VMCAI, Springer-Verlag, LNCS, vol. 9583, pp. 41–62 (2016)
O’Hearn, P.W., Reynolds, J.C., Yang, H.: Local reasoning about programs that alter data structures. In: Proceedings of CSL’01, pp. 1–19. Springer, London, UK (2001). http://dl.acm.org/citation.cfm?id=647851.737404
Online Appendix: Viper-encoded examples (2019). http://viper.ethz.ch/onlineappendix-rsl-encoding/
Parkinson, M.J., Summers, A.J.: The relationship between separation logic and implicit dynamic frames. Log. Methods Comput. Sci. 8(3:01), 1–54 (2012)
Reynolds, J.C.: Definitional interpreters for higher-order programming languages. In: ACM Annual Conference—Volume 2, pp. 717–740. ACM, ACM’72 (1972)
Reynolds, J.C.: Separation logic: a logic for shared mutable data structures. In: LICS, IEEE Computer Society Press (2002)
RSL Front-End: RSL to Viper Front-End; TACAS 2018 Artifact Version (2018). https://figshare.com/articles/RSL_to_Viper_Front_end/5900233
RSL Front-End Zip Files: RSL to Viper Front-End Zip Files (updated since TACAS 2018; Windows, Linux, Mac versions available) (2019). https://www.pm.inf.ethz.ch/research/viper/prototype-rsl-encoding.html
Rust Library: ARC (Atomic Reference Counting) (2019). https://doc.rust-lang.org/std/sync/struct.Arc.html
Sergey, I., Nanevski, A., Banerjee, A.: Mechanized verification of fine-grained concurrent programs. In: Proceedings of PLDI’15, pp. 77–87. ACM, New York, NY, USA (2015). https://doi.org/10.1145/2737924.2737964
Smans, J., Jacobs, B., Piessens, F.: Implicit dynamic frames. ACM Trans Program Lang Syst 34(1), 2:1–2:58 (2012)
Summers, A.J., Drossopoulou, S.: A formal semantics for isorecursive and equirecursive state abstractions. ECOOP, Springer, LNCS 7920, 129–153 (2013)
Summers, A.J., Müller, P.: Automating deductive verification for weak-memory programs. Tools and Algorithms for the Construction and Analysis of Systems (TACAS), LNCS, pp. 190–209. Springer, Berlin (2018)
Summers, A.J., Müller, P.: Automating deductive verification for weak-memory programs (extended version) (2018)
Travkin, O., Wehrheim, H.: Verification of concurrent programs on weak memory models. In: Sampaio, A., Wang, F. (eds.) Theoretical Aspects of Computing (ICTAC). Lecture Notes in Computer Science, vol. 9965, pp. 3–24. Springer, Berlin (2016)
Turon, A., Vafeiadis, V., Dreyer, D.: GPS: navigating weak memory with ghosts, protocols, and separation. In: OOPSLA, pp. 691–707. ACM (2014)
Vafeiadis, V.: Personal communication (2016)
Vafeiadis, V., Narayan, C.: Relaxed separation logic: a program logic for C11 concurrency. In: OOPSLA, pp. 867–884. ACM (2013)
Xu, F., Fu, M., Feng, X., Zhang, X., Zhang, H., Li, Z.: A practical verification framework for preemptive OS kernels. In: CAV Proceedings Part II, Springer International Publishing, Cham, pp. 59–79 (2016). https://doi.org/10.1007/978-3-319-41540-6_4
Acknowledgements
We are grateful to Viktor Vafeiadis and Marko Doko for many explanations of the RSL logics and helpful discussions about our encoding. We thank Christiane Goltz for her work on the prototype tool, and Malte Schwerhoff for implementing additional features. We thank Marco Eilers for his assistance with the online appendix, and Arshavir Ter-Gabrielyan for automating our artefact assembly for various operating systems. We also thank Andrei Dan, Lucas Brutschy, Malte Schwerhoff and the anonymous TACAS 2018 and STTT Special Issue reviewers for feedback on earlier versions of this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Summers, A.J., Müller, P. Automating deductive verification for weak-memory programs (extended version). Int J Softw Tools Technol Transfer 22, 709–728 (2020). https://doi.org/10.1007/s10009-020-00559-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10009-020-00559-y










 in our evaluation (Sect.
in our evaluation (Sect. 

 field will be explained in Sect.
field will be explained in Sect. 
 is empty)
is empty)

 ) in Sect.
) in Sect. 


 domain from Fig.
domain from Fig.  and
and
 , as well as the corresponding axioms will be explained in Sect.
, as well as the corresponding axioms will be explained in Sect. 


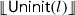 or of (perhaps several times)
or of (perhaps several times)  for some e, k (cf. Fig.
for some e, k (cf. Fig.  . In the latter case, the invariant conjunct holds vacuously, since
. In the latter case, the invariant conjunct holds vacuously, since 

 .
. expression yields the permission fraction held for a field or predicate instance.
expression yields the permission fraction held for a field or predicate instance. macro is actually called
macro is actually called
 ; we renamed this subsequently due to potential confusion with the notion of the “real heap” employed in Sect.
; we renamed this subsequently due to potential confusion with the notion of the “real heap” employed in Sect.  field, it would also be possible to introduce another field to represent
field, it would also be possible to introduce another field to represent