Modeling investigation of Sm_0.5Sr_0.5CoO_3−δ–Ce_0.8Sm_0.2O_2−δ cathode for proton-conducting ceramic fuel cell

Abstract

Simulation of proton ceramic fuel cell is of great importance in understanding their working mechanisms. Cathode activation polarization is a critical concern in the simulation. In this paper, Sm_0.5Sr_0.5CoO_3−δ–Ce_0.8Sm_0.2O_2−δ cathode is selected as studied case. The effective reaction order, which is the exponential of the oxygen partial pressure in cathode Butler-Volmer equation, is determined via our model. The dominant process in cathode reaction is investigated and identified. Among the involved reaction steps, model result points out that the surface diffusion of absorbed oxygen ion is dominant, which is in accord with the report. Moreover, single button cells with BaCe_0.7Zr_0.1Y_0.2O_3−δ electrolyte and Sm_0.5Sr_0.5CoO_3−δ–Ce_0.8Sm_0.2O_2−δ cathode are prepared, and the measured cell output voltages are compared with the simulated ones. The predicted cell outputs via our full cell simulation match the measurements under diverse experimental settings, suggesting that the method and parameters in our simulation are applicable. Our models facilitate both the analysis of experimental results and the development of proton-conducting solid oxide fuel cell model.

Introduction

The increasing demand for clean, low-cost, and powerful energy stimulates considerable research interests on the solid oxide fuel cell (SOFC) fed with hydrogen. Previously, oxygen-ion conductor such as yttrium-stabilized zirconia (YSZ) is used as electrolyte for oxygen conducting SOFC (O-SOFC). However, the high operating temperature reduces the fuel utilization efficiency and makes the sealing of the cell stack difficult [1]. To decrease the cell operating temperature, proton conductor is introduced as the electrolyte material for the proton-conducting fuel cells (H-SOFC) operating at intermediate or low temperature [2,3,4]. Zr- and Y-doped BaCeO₃ (BZCY) is widely used as electrolyte material of H-SOFC [3].

The cathode material plays a crucial role in determining the cell capacity. Enormous efforts have been made in order to find a stable and high-activity cathode [5]. Lanthanum strontium cobalt ferrite perovskite (LSCF) is a classical and promising cathode material for H-SOFC [6]. Fuel cells with La_0.4Sr_0.6Co_0.2Fe_0.8O_3−δ–BaZr_0.1Ce_0.7Y_0.2O_3−δ cathode on BZCY electrolyte is fabricated by Yang [7]. Relatively high performance is achieved in that report. Cobalt-free cathodes have also been discovered and applied to H-SOFC in consideration of material stability and cost. For instance, Ba_0.95Ca_0.05Fe_0.9−xSn_xY_0.1O_3−δCe_0.8Sm_0.2O_2−δ cathode was developed, and satisfactory power density of 949 mW/cm² at 700 °C was reported [8]. A novel cathode of Ba_0.95Ca_0.05Fe_0.85Sn_0.05Y_0.1O_2.9−δF_0.1 was prepared via introducing anion F as dopant [9]. Desirable stability and oxygen activity was achieved owing to the anions and cations co-doping strategy. At 700 °C, the cell output power density reached as high as 1050 mW/cm².

Cathode reaction is extensively studied via both experimental and theoretical approaches. For instance, cathode reaction mechanisms of Sm_0.5Sr_0.5CoO_3−δ–Ce_0.8Sm_0.2O_2−δ (SSC–SDC) and Sm_0.5Sr_0.5CoO_3−δ–BaCe_0.8Sm_0.2O_3−δ composite cathodes were explored [10,11,12]. Rate limiting steps have been found by analyzing the impedance spectra of half cells measured under various testing conditions. First principle calculations have been introduced to the simulation of oxygen reduction reaction (ORR) mechanism in La_1−xSr_xMnO_3−δ cathode [13]. They found that surface oxygen vacancy concentration for the (La,Sr) O termination is much smaller than MnO₂, which is attributed to the drastic decrease of ORR rates. ORR mechanism of Sr₃Fe₂O₇ cathode for H-SOFC has been explored [14], and energy barrier of the proton migration was calculated and discussed.

Among enormous reported cathode materials, SSC–SDC not only is a typical cathode for O-SOFC [15] but also proves to be ideal when applied to H-SOFC owing to the reduced cathode activation polarization. This phenomenon was firstly recovered in [12]. Rational explanation was elucidated there, mainly because SSC exhibits higher oxygen ion conductivity and better chemical compatibility with SSC than with BZCY for H-SOFC, leading to faster oxygen ion migration in SSC–SDC than in SSC–BZCY. This advantage of SDC would effectively compensate for the lack of active sites in SSC–SDC cathode [12]. Dual porosity structured SSC–SDC composite cathode was fabricated in [16], and the electrochemical enhancement was compared with the conventional cathode. They found that new structure becomes more effective for diffusion process. In [17], electrolyte-free fuel cell based on SDC–SSC composite was invented, and it gained better performance over the SDC electrolyte. They found that the SDC–SDC layer can replace the electrolyte to make the cell work when the ionic and electronic conductivities are balanced. In [15], SDC-embedded SSC composite fibers were successfully fabricated, and maximum power densities of 360 and 1250 mW/cm² were reported at 550 and 700 °C.

The reaction model of this cathode for H-SOFC was put forward by Zhao [10] via analyzing the impedance spectra. They discovered that there are two rate-determining steps, and thus, a complex formula was used to describe the relationship between the current density and cathode activation overpotential. Moreover, reaction orders of surface diffusion as well as other possible elementary reaction steps for the H-SOFC involved in the cathode activation process were derived theoretically there. Brief introduction about the deduction of the reaction order value is described as follows. First, one of the elementary steps is assumed as the rate-determining one, and other steps are treated as quasi-equilibrium. Then, the net cathode reaction rate is expressed as the difference between forward and backward reaction rates of that rate-determining step. The forward and backward reaction rates of other quasi-equilibrium steps are equal; thus, the concentration of the involved species could be expressed by these relationships. Finally, combining these equations together, and noticing that the net reaction rate is 0 when the balanced electromotive force is applied, the relation between the reaction rate and the electrode overpotential could be deduced. The exponential of the partial pressures, i.e., reaction orders, would appear as part of the deduced formula. Repeat this process; the reaction order of each elementary step could be figured out, as listed in Table 1 of [10]. Note that the assignment of the actual reaction order of the elementary step discussed in this work below is based on the result of that table.

Table 1 Settings in our experiments

Charge transfer for the oxygen reduction reaction is known as a rate determining step for typical cathodes of O-SOFCs, while it is different in SSC–SDC cathodes used in the H-SOFC. It could be attributed to the relatively high surface exchange activity of SSC [10, 12, 19] and the synergistic effect of SDC [10, 20]. SDC proves to be very effective in reducing the interfacial polarization resistance and enhancing the surface exchange processes in the cathode.

Here, the Butler–Volmer (B–V) equation which is common in the SOFC simulation [21] is adopted to depict the activation polarization of SSC–SDC cathode, instead of the complex one in Zhao’s work [10] mentioned above. This is not only for the consideration of generality but also for the convenience of numerical computing. Since multiple rate-determining steps may appear in this kind of cathode, the effective reaction order (ERO), namely the exponential of the oxygen partial pressure in B–V equation, has to be determined experimentally.

Mention that the term ERO in this work is slightly different from the actual reaction order of each elementary step discussed in [10]. In that paper, reaction order is a constant for each elementary reaction step, while in this model, another term—effective reaction order—is used. It reflects the overall apparent effect which stems from the possible rate-determining elementary steps. If there is only one rate-determining step, ERO here equals to the reaction order of the corresponding rate-determining step. Yet if there are two rate-determining steps, ERO here could be viewed as the apparent reaction order of these dominant steps, and thus, its value is between the actual values of the reaction orders of these two dominant steps. This parameter is introduced to facilitate the parametric evaluation and numerical simulation.

According to Zhao’s theory [10], ERO is 0 if the rate-determining step is oxygen ion transportation from the triple phase boundary (TPB) in cathode to the interface of the electrolyte and cathode, and it is 0.25 if the rate-determining step is surface diffusion of absorbed oxygen ion. If there are multiple rate-determining steps, ERO may vary between 0 and 0.25, depending on which step is more dominant under the working condition. Thus, ERO could be viewed as an indicator of the cathode reaction mechanism. It is a vital parameter for the determination of cathode overpotential but is seldom discussed in the fully developed SOFC model to the best of our knowledge.

In this paper, a model is utilized to extract the value of ERO of SSC–SDC cathode from the measured cell i–v curves under varied oxygen partial pressures. The dominant step in SSC–SDC cathode is identified via the model results. Then, the determined ERO is adopted to simulate the cell output i–v curves, and the simulated output voltages are examined by our measured ones.

This model has several advantages to the earlier one in [10]. First, in that paper, the explicit expression of the related exchange current density (i₀₃ and i₀₆) is not given, and the parameters for calculating them are also missing. Since exchange current densities vary with partial pressures, they need to be fitted by half-cell measurements under each partial pressure. It is inconvenient for numerical modeling. Second, more empirical parameters are needed in that model in the aspect of modeling, which is also disadvantage to the simulation. Besides, in our model, i–v curves of the full cell are used, and half-cell testing in [10] is not necessary. It also simplifies the experiment. This model is useful for understanding the rate-determining step of the cathode reaction and evaluating this key parameter in the full-cell simulation.

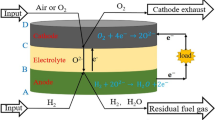
Model and experiment description

In our experiments and simulations, button cells are used. The current along radial direction in the electrolyte and electrodes is neglected, because the thicknesses of electrolyte and electrodes are much smaller than the cell diameter.

Electrode polarization and electrolyte ohmic loss

B–V equation is used to evaluate the electrode polarization in our model. For cathode, if the charge transfer coefficient β is evaluated as 0.5 in common [10], B–V equation reads:

$$ {i}_{\mathrm{tot}}={i}_{0.\mathrm{c}}{\left(\frac{p_{\mathrm{O}2}}{p_0}\right)}^m\exp \left(-\frac{E_{\mathrm{c}}}{RT}\right)\sinh \frac{0.5_{n\mathrm{F}{\eta}_{\mathrm{c}}}}{RT} $$

(1)

Here, i_tot is total current density through the fuel cell, η_c is the cathode activation overpotential, p_O2 is the oxygen partial pressure at cathode side, n is the number of electrons involved per reaction, and i_0,c (p_O2/p₀)^mexp(− E_c/RT) is the exchange current density. Variable m is the exponential of oxygen partial pressure and is called the effective reaction order (ERO) in our model.

The anode activation overpotential could be written in a similar way [22, 23]:

$$ {i}_{\mathrm{tot}}={i}_{0.\mathrm{a}}\exp \left(-\frac{E_{\mathrm{a}}}{RT}\right)\frac{{\left({p}_{\mathrm{H}2}/{p}_{\ast}\right)}^{1/4}}{1+{\left({p}_{\mathrm{H}2}/{p}_{\ast}\right)}^{1/2}}\sinh \frac{0.5_{n^1\mathrm{F}{\eta}_{\mathrm{a}}}}{RT} $$

(2)

where i_tot and η_a are the total current density and the anode activation overpotential, and p_* is the equilibrium hydrogen partial pressure [23].

The voltage drop in the electrolyte due to ohmic resistance is as follows:

$$ {\eta}_{\mathrm{ohm}}={i}_{\mathrm{tot}}\frac{l}{\sigma_{\mathrm{H}}} $$

(3)

where σ_H is the proton conductivity of the electrolyte, and l is the electrolyte thickness.

Determination of effective reaction order

The effective reaction order of oxygen partial pressure, which is denoted as m in Eq. (1), is not only an important parameter to figure out the cathode activation polarization but also a signpost of the cathode reaction mechanism, as illustrated in the “Introduction.”

ERO is the exponential of oxygen partial pressure and thus should be determined via the knowledge of cell output voltages under varied partial pressures. Here, a model is described below so that we can deal with the experimental results and evaluate the value of ERO for a given cathode under certain testing condition.

Equation (1) which is related to cathode activation overpotential is rewritten in the logarithm form, where m is the ERO to be determined:

$$ \ln \left({i}_{\mathrm{tot}}\right)=\ln \left({i}_{0,\mathrm{c}}\right)+m\ln \left(\frac{p_{\mathrm{O}2}}{p_0}\right)-\frac{E_{\mathrm{c}}}{RT}+\ln \left(\sinh \frac{0.5n\mathrm{F}{\eta}_{\mathrm{c}}}{RT}\right) $$

(4a)

Note that i_tot is the total current density, which includes both external current density and leakage current density through the electrolyte. The cathode activation overpotential η_c is as follows:

$$ {\eta}_{\mathrm{c}}={E}_{\mathrm{e}\mathrm{q}}-V-{\eta}_{\mathrm{a}}-{\eta}_{\mathrm{e}}-{\eta}_{\mathrm{c}\mathrm{on}} $$

(4b)

where V is the measured cell output voltage, and η_con is the electrode concentration overpotentials. Simulation results show that both anode and cathode concentration polarizations are less than 0.01 V under working conditions and thus are ignorable for this kind of SOFC [18]. Hence, η_con is safely omitted for simplicity.

Suppose two experimental records are measured under the same temperature and external current density, but under varied oxygen partial pressures at cathode side. Their anode activation polarization is identical, because the current through the anode and the hydrogen partial pressure at anode are almost the same for these two records. Here, we define an intermediate variable A as follows:

$$ A={E}_{\mathrm{eq}}-V-{\eta}_{\mathrm{ohm}} $$

(4c)

where E_eq and η_ohm are the EMF of the cell and the ohmic loss of the cell electrolyte, respectively, and V is the output voltage of the cell under divergent oxygen partial pressures. Hence:

$$ {\eta}_{\mathrm{c},1}-{\eta}_{\mathrm{c},0}={E}_{\mathrm{e}\mathrm{q},1}-{\eta}_{\mathrm{e},1}-{V}_1\left({E}_{\mathrm{e}\mathrm{q},0}-{\eta}_{\mathrm{e},0}-{V}_0\right)={A}_1-{A}_0 $$

(5)

where the subscripts (0 and 1) represent these two different records above. The variables A₀ and A₁ could be computed by the measured cell output (V₀ and V₁) using Eqs. (3) and (4c).

Meanwhile, Eq. (4a) could be rewritten as follows:

$$ \ln \frac{i_{\mathrm{tot},1}}{i_{\mathrm{tot},0}}=m\ln \left(\frac{p_{\mathrm{O}2,1}}{p_{\mathrm{O}2,0}}\right)+\ln \left(\sinh \frac{0.5n\mathrm{F}{\eta}_{\mathrm{c},1}}{RT}\right)-\ln \left(\sinh \frac{0.5n\mathrm{F}{\eta}_{\mathrm{c},0}}{RT}\right) $$

(6)

Since the differences of the cathode overpotentials (η_c,1 − η_c,0) between the two records are relatively small, the 2nd and 3rd items in the right side of Eq. (6) could be approximated via the Taylor expansion to 1st order:

$$ \ln \frac{i_{\mathrm{tot},1}}{i_{\mathrm{tot},0}}\approx m\ln \left(\frac{p_{\mathrm{O}2,1}}{p_{\mathrm{O}2,0}}\right)+\frac{0.5n\mathrm{F}}{RT}\left({\eta}_{\mathrm{c},1}-{\eta}_{\mathrm{c},0}\right)\coth \frac{0.5n\mathrm{F}{\eta}_{\mathrm{c},0}}{RT} $$

(7)

The 2nd and higher order Taylor expansions are much smaller than the 1st one and thus are ignored in this equation.

Equation (7) is further simplified based on the approximation that coth(x) approaches one when x is large enough. In our SOFC cases, this approximation could be easily satisfied under relatively high current density (and thus relatively high cathode polarization η). For instance, under 600 °C, coth(∙) in Eq. (7) is 1.03 when η_c = 0.15 V and is 1.01 when η_c = 0.2 V. This approximation becomes more precise under lower temperature and higher external current density.

Then, substituting Eq. (5) into Eq. (7) and applying the above approximation:

$$ \ln \left({i}_{\mathrm{tot},1}\right)-\ln \left({i}_{\mathrm{tot},0}\right)\approx m\left[\ln {p}_{\mathrm{O}2,1}-\ln {p}_{\mathrm{O}2,0}\right]+\frac{0.5n\mathrm{F}}{RT}\left({A}_1-{A}_0\right) $$

(8)

Finally, we rewrite Eq. (8) to make it convenient for data processing. Variable J is defined as follows:

$$ J=\ln \left({i}_{\mathrm{tot}}\right)-\frac{0.5n\mathrm{F}}{RT}. $$

(9a)

By using two experimental records (denoted as subscript 0 and 1) measured under identical external current density but different oxygen partial pressures (p_O2,1 and p_O2,2 below), the following equation is used to determine the parameter m (ERO):

$$ {J}_1-{J}_0=m\left[\ln \left({p}_{\mathrm{O}2,1}\right)-\ln \left({p}_{\mathrm{O}2,0}\right)\right]. $$

(9b)

To summarize, the method is described as follows. To determine the ERO under a certain temperature, the experiment is conducted at a fixed temperature and external current density. Different oxygen partial pressures have to be applied because the measured data under these conditions are necessary in this model. First, the output voltages under diverse oxygen partial pressures are recorded, and the corresponding variables A and J can be computed for each record under different oxygen partial pressures. Then, we pick up a pair of records, and calculate the differences of their variables J and ln (p_O2). Repeat this step until all possible pairs are collected. Finally, dot all these collected ΔJ = J₁− J₀ (Y coordinates) and Δlnp_O2= ln (p_O2,1) − ln (p_O2,0) (X coordinates) data points together in a ΔJ vs Δlnp_O2 plot and apply linear least square regression (LLSR) to find a regression curve. Its slope is the value of ERO under current experimental settings.

Extended model

As to the SSC–SDC cathode adopted here, the possible rate-determining steps (step 3 and 6 in [10]) are independent with water partial pressure p_H2O [10]. Thus, only p_O2 needs to be considered; and in the discussion section below, model in “Determination of effective reaction order” is used.

Nevertheless, in general, the reaction is not only controlled by p_O2 but possibly by p_H2O. To take the effect of p_H2O into consideration, the model above could be extended as follows.

The cathode activation overpotential expressed by Eq. (1) is rewritten as follows:

$$ {i}_{\mathrm{tot}}={i}_{0,\mathrm{c}}{\left(\frac{p_{\mathrm{O}2}}{p_0}\right)}^m{\left(\frac{p_{\mathrm{H}2\mathrm{O}}}{p_0}\right)}^t\exp \left(-\frac{E_{\mathrm{c}}}{RT}\right)\sinh \frac{0.5n\mathrm{F}{\eta}_{\mathrm{c}}}{RT}, $$

(10)

where t is the ERO of water vapor, and it also needs to be determined by the model.

Similarly, the final formula Eq. (9b) of this model is rewritten as follows:

$$ {J}_1={J}_0=m\left[\ln \left({p}_{\mathrm{O}2.1}\right)-\ln \left({p}_{\mathrm{O}2,0}\right)\right]+t\left[\ln \left({p}_{\mathrm{H}2\mathrm{O},1}\right)-\ln \left({p}_{\mathrm{H}2\mathrm{O},0}\right)\right]. $$

(11)

In the aspect of experiment, i–v curves under diverse oxygen and water vapor pressures are necessary. In the aspect of data processing, to determine parameters m and t, multiple linear regression has to be performed, instead of LLSR in “Determination of effective reaction order.”

Cell output simulation

The output voltages under varied operating conditions are calculated once the polarizations and ohmic loss are determined. The electromotive force of the proton-conducting cell is determined using equation in [24]. The electrolyte ohmic loss is expressed in Eq. (3), and cathode and anode activation polarizations are expressed in Eqs. (1) and (2). The leakage current through the electrolyte is calculated using the model in [18]. The concentration polarizations of cathode and anode are calculated using the method brought forward in [25].

Our simulation code is written in C language, and the GNU Scientific Library (GSL) is used when performing non-linear optimization. The GCC compiling tool chain and adopted libraries are free and open-source under the GNU Public License.

Experiment

The cathode, electrolyte, and anode materials were Sm_0.5Sr_0.5CoO_3−δ–Ce_0.8Sm_0.2O_2−δ, BaZr_0.1Ce_0.7Y_0.2O_3−δ, and BaZr_0.1Ce_0.7Y_0.2O_3−δ–Ni. To synthesize these materials, citric acid–nitrate gel combustion method was used. The powder was calcined under 1000 °C for 4 h to eliminate the carbon residues. To prepare the anode powder, the BZCY, NiO, and graphite powders were mixed in ethanol and ball-milled for 24 h, and the weight ratio was 55:45:10. To prepare the cathode slurry, SSC powder, SDC powder, and ethylcellulose–terpineol binder were mixed, and the weight ratio was 6:4:1. The anode and electrolyte powders were co-pressed as a pellet under 200 MPa. Then, it was sintered at 1350 °C for 6 h to densify the electrolyte. Finally, the cathode slurry was painted onto the electrolyte, and then sintered at 950 °C for 3 h to form a porous cathode. Figure 1 a and b were the cross section of the cell and the microstructure of the cathode. The electrolyte was about 48 μm thick and was already densified. The cathode was firmly attached to the electrolyte, and its particle diameter was around 0.9 μm.

Fig. 1

Cross section of the cell (a), microstructure of the cathode (b), XRD patterns of BZCY (c), and SSC–SDC (d). Peaks related to SSC and SDC are marked as “plus sign” and “multiplication sign,” respectively

Figure 1 c and d were the XRD patterns of the electrolyte and cathode powders respectively. Pure BZCY phase was synthesized since no impurity peak was found in the electrolyte pattern. Peaks related to SSC and SDC were identified in the cathode pattern and marked in the figure, indicating that desired cathode composition was achieved. The indices of lattice planes of these XRD peaks are also marked in the plot. According to the XRD peaks, crustal structure of BZCY, SSC, and SDC is cubic-perovskite, orthorhombic-perovskite, and cubic-fluorite, respectively.

Cells were operated under 550 ~ 700 °C, using humidified hydrogen with 3% H₂O vapor as fuel at a flow rate of 30 sscm. To measure the cell output voltages under varied oxygen partial pressures, the oxygen was mixed with nitrogen to obtain the required oxygen concentration. The i–v curves of the cell were measured with a DC electronic load (ITech Electronics IT8511). Impedance spectra were recorded using impedance analyzer (Chenhua CHI614e).

Results and discussions

Results of the ERO of the SSC–SDC cathode

To determine the ERO for SSC–SDC cathode, the output voltages of the cell sample are measured under several oxygen partial pressures, i.e., 0.05 atm, 0.10 atm, 0.21 atm, 0.40 atm, and 0.60 atm. Then, the model described in “Determination of effective reaction order” is applied to handle these data. Based on Eq. (9b), Fig. 2a–d are plotted, which show the regression lines under 550 °C, 600 °C, 650 °C, and 700 °C respectively. The dotted markers are the results calculated by our model, using the experimentally recorded voltages and current densities, while the solid lines are the results of LLSR.

Fig. 2

LLSR plots for diverse temperatures: 550°C (a), 600°C (b), 650°C (c) and 700°C (d). The dotted points are the data calculated by this model using measured voltages, and the solid lines are the least-square fitting

The plots in these figures exhibit a clear linear character, as expected in “Determination of effective reaction order.” EROs under varied temperatures are determined via the slopes of the plots. For 550 °C, 600 °C, 650 °C and 700 °C, they are 0.251, 0.245, 0.240 and 0.216, respectively. These values are adopted in the following simulations.

Note that variable ΔJ = J₁− J₀ = ln (i_tot,1/i_tot,0) − 0.5nF/(RT)∙(A₁− A₀) is dimensionless by its definition in Eqs. (4c) and (9a), because the unit of variable A is volt, and both i_tot,1/i_tot,0 and nF/(RT)∙A are dimensionless. Consequently, the unit of the Y-axis is not presented in this figure.

The ERO is around 0.25 and could be explained as follows. According to Zhao’s work [10], two rate-determining steps are identified since there are two arcs in the impedance spectra. For high-frequency and low-frequency arcs, they are attributed to the transport of oxygen ion from the TPB in cathode to the electrolyte-cathode interface, and the surface diffusion of absorbed oxygen ion, respectively. The actual reaction orders are 0 and 0.25 for these elementary processes corresponding to high-frequency and low-frequency arcs, respectively [10]. The ERO given by our model is close to 0.25 at 550 ~ 650 °C. This matches Zhao’s result [10]. In Fig. 4 of that reference, the resistance of the low-frequency process exceeds the high-frequency one within this temperature range, implying that the former one is more dominant. Since the actual reaction order of the low-frequency arc is 0.25 in that reference, it is consistent with our model result. It implies that surface diffusion process is the actual bottleneck of the cathode reaction within 550 ~ 650 °C. Moreover, the resistances of high-frequency and low-frequency processes become comparable at about 700 °C in their report [10], suggesting that the influence of high-frequency process becomes more significant. As a result, ERO at 700 °C is lower than 0.25. The calculated EROs are in accord with the reported temperature-dependent trend.

To further explore the behavior and trend of the impedance spectra described in [10], experiment about symmetrical cell was conducted, and impedance spectra under 600 and 700 °C were recorded under 21% O₂ and 3% H₂O, as shown in Fig. 3 a and b. The equivalent circuit is also given in the figure, where CPE is the constant phase element, R_L and R_H are the equivalent resistances of low-frequency and high-frequency arcs, and R_e is the resistance of the electrolyte. The expression of the impedance of CPE element is 1/[(jω)^αQ], and α is 0.9 here to achieve better parametric fitness. The fitted R_L and R_H are 3.29 and 1.42 Ω cm² at 600 °C, and 0.54 and 0.63 Ω cm² at 700 °C. Clearly, under 700 °C, both steps related to low- and high-frequency arcs are competitive, while under 600 °C, low-frequency step is the dominant one. It is consistent with both results of this model and [10].

Fig. 3

Impedance spectra of symmetrical cell with SSC–SDC cathode under 600 °C (a) and 700 °C (b). The equivalent circuit is also presented

Moreover, to make the studied cases more persuasive, another cathode based on proton-conducting material, Sm_0.5Sr_0.5CoO_3−δ–BaZr_0.1Ce_0.7Y_0.2O_3−δ, is also adopted in the H-SOFC. Following the same procedure, LLSR plots are obtained and discussed, as presented in Appendix, Fig. 6.

Simulated and measured output voltages of H-SOFC

In this section, the output voltages of the tested samples under varied pressures, temperatures, and currents are simulated by applying the full H-SOFC model described in “Cell output simulation.”

The pre-exponential factor of exchange current density (i_c.0) and cathode reaction activation energy (E_c) in Eq. (1) is evaluated by non-linear optimization from the experimental i–v curves of the cell. The activation energy and pre-exponential factor of the exchange current density of SSC–SDC cathode are 1.17 eV and 4.27 × 10⁴ A cm⁻² respectively. Note that the cathode reaction activation energy derived here is comparable to the reported one of 1.29 eV for low-frequency arc in [10]. This result is in accord with the conclusion above that the corresponding step is the dominant one under experimental conditions.

The input parameters adopted in this simulation, involving the geometric sizes and the operating settings, are presented in Table 1. In our experiment, the output voltages are recorded under varied external current densities, oxygen partial pressures, and temperatures. In Fig. 4 a and b, the experimental results along with the model-predicted ones are plotted together for comparison, under oxygen partial pressures of 0.05 atm and 0.60 atm respectively.

Fig. 4

Calculated and experimental i–v curves of cell sample, under oxygen partial pressures of 0.05 atm (a) and 0.60 atm (b)

Generally, the predicted cell output voltages fit well with the experiments for the studied cases under diverse working conditions. Therefore, the parameters acquired by our model are reasonable for this kind of cell. Moreover, this simulation points out that the universal and standard B–V equation could rationally describe the activation polarization of SSC–SDC cathode and thus is still numerically applicable to the simulation of H-SOFC, apart from the complex formula given in [10]. The computation of cathode polarization is therefore greatly simplified by using our methods and parameters.

Polarization and ohmic loss

The involved polarizations under varied operating conditions are computed based on the model in “Cell output simulation.” For our tested cells, the electrolyte ohmic loss, along with the anode and cathode activation overpotentials, is figured out, as presented in Fig. 5 a and b, for oxygen partial pressures of 0.05 atm and 0.60 atm, respectively. The calculated electrode concentration overpotentials at both sides are around 0.01 ~ 0.03 V under varied current densities and temperatures. They are tiny and are not plotted in this figure.

Fig. 5

Overpotentials of the cell under oxygen partial pressures of 0.05 atm (a) and 0.60 atm (b). Here, “act” means activation polarizations, “ohm” means ohmic loss, and “a” and “c” mean anode and cathode

Figure 5 shows that the major losses of the cells are from the electrolyte ohmic resistance and the cathode activation overpotential for the tested cells under intermediate temperature. It is clear that they are sensitive to the cell working temperature. Both of them decrease rapidly with testing temperature, owing to the evident improvement of electrolyte proton conductivity and cathode reaction rates.

Conclusions

In this article, the effective reaction order of SSC–SDC cathode is determined and compared with other reported results. The calculated ERO is around 0.25, indicating that the most dominant step in cathode reaction is the surface diffusion within intermediate temperature for H-SOFC. It is compatible with Zhao’s work. By adopting the derived empirical parameters, the calculated output i–v curves are simulated. Simulation results are in accord with our experiments under different operating conditions. Next, activation polarization, concentration polarization, and electrolyte ohmic loss are judged based on the full cell model. It turns out that the electrolyte ohmic loss and the cathode activation polarization are the manor ones for these samples. Since ERO of the cathode is essential to compute the cathode activation polarization and predict cell output, our method is practical when evaluating related vital parameters in simulation and probing rate-limiting steps of the cathode processes.

Appendix

Sm_0.5Sr_0.5CoO_3−δ–BaZr_0.1Ce_0.7Y_0.2O_3−δ (SSC–BZCY) cathode are also selected as another studied case to illustrate the application of this model. LLSR plots under 550 °C and 650 °C are drawn in Fig. 6. The calculated ERO (slope of the LLSR curve) values are around 0.25. The behavior of SSC–BZCY is similar, indicating that the surface diffusion step is also the dominant one, and it matches the conclusion made in [11].

Fig. 6

LLSR plots of SSC–BZCY under 550 °C and 650 °C