Introduction

In various emerging technology applications, a fundamental understanding of fluid flow through solid surfaces is essential. Self-cleaning surfaces, de-icing coatings for aeronautical control surfaces, and drag-reducing/antifouling marine coatings are just a few examples. The fluid flow over bulk solids is likely different from micro-/nano-counterparts [1]. The nanomaterials have motivated researchers to develop a fundamental understanding of various phenomena associated with them. Wettability is one such phenomenon that is characterized by idiosyncratic properties such as extreme water repellency, large slip, and low viscous drag [2,3,4]. At micro-/nanoscales, the combination of hydrophobic surface chemistry and micro/nanosurface topography can lead to superhydrophobicity. Nature provides several examples of superhydrophobic surfaces, including the leaves of lotus plants and the shell of the desert beetle that collects water from the morning mist [5].

At the nanoscale, where the surface to volume ratio is very large, the role of hydrodynamic boundary conditions on liquid velocity profiles becomes dominant [6, 7]. The typical no-slip assumption does not always apply to micro-/nanoengineered surfaces, and the velocity slip at a surface is required to predict the overall flow behaviour [8]. The general Navier boundary condition for a finite slip velocity at a planar bounding wall is given by \({V}_{wall}=b\epsilon {|}_{wall}\), where \(\epsilon {|}_{wall}=dV/dy\) is the velocity gradient normal to the wall (say, in the y direction) and \(b\) is the slip length, i.e. the normal distance beyond the fluid–solid interface at which the velocity profile would become zero (Fig. 1a). The slip length is a phenomenological variable that governs the surface-fluid friction characteristics. Hydrophilic and hydrophobic surfaces produce nanometric slip lengths (b ≈1–30 nm) [9], which are too small to generate any practical viscous drag reduction. Superhydrophobic surfaces, however, have shown evidence of ~ O(100) µm slip lengths [10, 11], making them stronger candidates for drag-reducing coatings. In practice, even on atomic or molecular dimensions, a flawlessly smooth solid surface is unachievable. Early studies attempted to link surface roughness to interfacial slip in order to better understand the influence of rough surfaces on liquid flow. In different systems and under different situations, roughness can have opposing effects on interfacial slip. The atomic-scale roughness increases the liquid–solid interaction by increasing contact sites and decreases slippage at the solid surface for liquid flow in a rough nanochannel. Several rough wall geometrical patterns, such as sinusoidal, triangular, rectangular, and random distributions, were investigated in this regard, and it was discovered that surface roughness has a significant role in reducing interfacial slip at the solid boundary.

Fig. 1
figure 1

Illustration of a boundary layer flow over a rough surface: a without a coating, and b with a coating, exemplifying a superhydrophobic surface with an improved slip

Full size image

There has been growing interest in superhydrophobic surfaces that entrap air pockets within micro-/nanostructures in the past few years, as shown schematically in Fig. 1b. The interstitial air pockets between the micro- or nanostructures [12], or the micro-/nanobubbles trapped on the surface [13,14,15,16], are believed to generate a mixed boundary condition, consisting of large slip at the gas–liquid interface and a much lower slip at the liquid–solid interfaces; collectively, these contribute towards an overall greater slippage [17,18,19]. Various experiments on slip flows of water on superhydrophobic surfaces have been reported, including longitudinal flows over micro-ridges [12], micro-posts [10], microgrates [11], needle-like structures [20], and carbon nanotube forests [21].

The molecular-scale interactions within multiphase and multiscale interfaces cannot be ignored when considering fluid slip over surfaces of different materials and morphologies. Several factors influence the slip length, including the surface material chemistry, structure/roughness, and the physics at the fluid interfaces. At the micro-/nanoscale, non-continuum phenomena potentially play a crucial role, such as slip, molecular ordering, higher stability of nanobubbles, electrostatic charges at interfaces, and changes in surface tension. Choi and Kim [20] created a nanostructured superhydrophobic surface with a minimal liquid–solid contact area, allowing the liquid to flow mostly over a layer of air, resulting in significant slip effects. Water slippage through superhydrophobic carbon nanotube forests in microchannels was explored by Joseph et al. [21] and discovered that boundary slippage on the Cassie superhydrophobic state was linked with slip lengths of a few microns. Furthermore, Choi et al. [22] looked into the liquid flow in nanograted superhydrophobic microchannels. The air nanostrips in the grate troughs under the liquid cause effective slip and friction reduction for water moving parallel over the hydrophobic nanogrates. Theoretical models have been developed to help interpret the experimental results [23,24,25]. These models do not always capture important molecular effects. Molecular dynamics (MD) can play an important role in complementing both experiments and analytical models.

This study aims to present a fixed-stress technique to consistently enable low-noise measurements of the slip lengths of surfaces. The technique is first validated for graphene-only surfaces. Then, the investigation is focused on surface coatings comprising carbon nanotubes (CNTs) with entrapped gas and tested the model for the analogous problem of slip lengths in longitudinal flows over micro-/nanoridges [26, 27]. The protocol is demonstrated using the MD simulations, based on which the reliability is assessed.

Molecular dynamics methods for calculating slip length

The potential parameters used in the molecular dynamics simulations are listed in Table 1. Water is modelled using the rigid TIP4P/2005 force field [28], consisting of the (12–6) Lennard–Jones (LJ) potential for pair-wise interactions between the oxygen atoms smoothly truncated Coulomb potential for electrostatic interactions between pairs of water molecules [29]. The H–O-H bond angle and the O–H bond length in a water molecule are fixed at 104.53° and 0.095 nm, respectively, using Hamilton’s quaternions.

Table 1 Lennard–Jones and Coulomb potential parameters for water, nitrogen, carbon (graphene/CNT), and platinum molecules in our NEMD simulations
Full size table

The platinum substrate is modelled using FCC (100 face orientation) rigid atoms with lattice constant of 0.392 nm. We list the platinum’s LJ interactions in Table 1 for completeness, as these are needed for the Lorentz-Berthelot mixing rules [30]. Surface coatings are modelled with either graphene or single-walled carbon nanotubes. A three-site model with two nitrogen atoms and a massless site with a positive charge represent the nitrogen molecules inside the air pockets [31].

We use the LJ and the smoothly truncated Coulomb potentials for the bonded and the nonbonded interactions, respectively. A cutoff radius of 1 nm is used in all our simulations for the LJ and the Coulomb force calculations. The Lorentz-Berthelot mixing rules derive interactions between atomic sites of different molecules [32]. However, the carbon–carbon LJ parameters are calibrated using the values σCO = 0.319 nm and εCO = 0.427 kJ mol−1 for the oxygen-carbon interactions, as these values have been found to produce hydrophobic properties in contact with water [29, 33].

Current methods

Equilibrium molecular dynamics (EMD) and non-equilibrium molecular dynamics (NEMD) are the two simulation methods that can calculate slip lengths of solid surfaces. Linear response theory is used in the EMD approach to compute the solid–fluid friction coefficient from the correlation function of microscopic fluctuating quantities [34,35,36,37], from which the slip length can then be determined. However, the focus of this study is on the NEMD approach, which can characterize the slip of a liquid flowing over a nanostructured surface within which a gas or vapour has been trapped, typically in either Couette- or Poiseuille-type flow configurations [21, 26, 34, 35, 38,39,40].

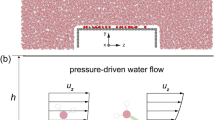
The Poiseuille approach in NEMD is most often generated by applying a constant body force on all fluid molecules within a pipe or channel with an internal surface one wishes to test, as shown in Fig. 2a. The body force generates a fluid shear stress that varies in the direction normal to the surface. The steady-state velocity profile is measured, and a slip length is obtained by least-squares fitting to determine the local tangent at the point in the liquid velocity profile closest to the wall. The major drawback of this method is that it assumes that the variation in shear stress throughout the gas region is unimportant and that slip measurement at a single location (i.e. at the fluid–solid interface) is sufficient to describe the slip flow phenomenon overall. This surely is a poor assumption and may lead to severe errors in slip length estimation. For simple dilute gas flows, such as in the example of gas bubbles entrapped between the structures on a super hydrophobic surface (Fig. 2), the existence of wall-normal gradients in shear stress can affect the near-interface Knudsen layers, and hence also the slip boundary conditions that must incorporate them. Therefore, unless slip lengths are needed for pressure-driven flows through a specific channel or pipe geometries, Poiseuille flow configurations are not ideal for investigating slip surfaces, and the discussions on them are ignored in this study.

Fig. 2
figure 2

Schematics of three NEMD simulations for obtaining the slip length at a nanostructured surface with entrapped gas pockets: a Poiseuille flow in a channel/pipe, b Couette shear flow, and c our proposed fixed-stress method

Full size image

A Couette flow configuration provides a way of generating constant shear stress in a fluid confined between two surfaces (see Fig. 2b). The widely adopted NEMD setup consists of one wall in motion at a target velocity, followed by measurements (after steady-state is reached) of the wall-normal velocity profile, strain rate, slip velocity, and slip length. The Couette flow approach does, however, have some drawbacks itself. The first minor one is that the slip characteristics of the surface prevent us from knowing beforehand what shear stress is being generated, which makes controlled comparisons (i.e. at fixed shear stresses, and hence drag) of various slip surfaces difficult. A far greater problem with the Couette flow configuration is that when used for high-slip systems (characteristic of superhydrophobic surfaces), it creates non-normally distributed noise, resulting in large statistical errors. The “Noise and accuracy improvements” section covers a rigorous discussion on these errors.

The fixed-stress method

Owing to the drawbacks of current methods, a technique for use with NEMD simulations to measure the slip characteristics of external liquid flows over different surface topographies has been presented. The proposed method (hereby called the fixed-stress method; see Fig. 2c) avoids the deficiencies of the Couette- and Poiseuille-type flow configurations. First, unlike in Couette flow, this approach imposes controlled shear stress to a flow over a surface, enabling a comparison of slip and drag reduction to be made across various surface materials and morphologies. Second, unlike the Couette flow approach, the level of noise-related errors in the proposed NEMD setup is independent of the slip length and remains normally distributed, as we demonstrate using pseudo-data in the “Noise and accuracy improvements” section. This ensures the applicability of the method to high-slip systems. It also has the benefit of being simple to implement and run in most molecular dynamics software. More importantly, this technique is easy to use in concurrent multiscale simulations to enable two-way coupling between molecular dynamics and CFD solvers as it is appropriate to use stress instead of velocity condition.

Figure 3 shows a schematic of the NEMD computational domain for flow over an arbitrary coated surface. Near-wall, bulk/measurement, and forcing zones are the three zones that make up the liquid region. The system is treated as periodic in the \(x\) and \(z\) directions but non-periodic in the \(y\) direction for computing efficiency. The top boundary in contact with the fluid is configured to be a zero-shear stress specular wall, which means that molecules hitting with it conserve tangential velocity, while their normal components are reversed, resulting in perfect slip. The flow in the \(x\) direction is enabled by imposing a constant shear stress \({\tau }_{xy}\) to the fluid, with a magnitude chosen large enough to have a reasonable signal-to-noise ratio in the particle ensemble, but much below the magnitude at which strain varies nonlinearly with stress and the critical stress at which the slip length diverges.

Fig. 3
figure 3

Schematic of the proposed NEMD setup for flows over coated surfaces

Full size image

Imposing such constant shear stress to the fluid requires prescribing a body force that can then be applied to the equations of motion of all the fluid molecules in the forcing zone. Based on the assumption of steady, incompressible, and low Reynolds number flows, the one-dimensional momentum balance for the system in Fig. 3 is:

$$\frac{d{\tau }_{xy}}{dy}=-{\rho }_{n}{f}_{x}(y)$$
(1)

where \({\rho }_{n}\) is the number density of the liquid, and \({f}_{x}\) is a body force applied to each liquid molecule that varies in the \(y\) direction. This body force is, for simplicity, confined to the forcing zone, such that it takes the form:

$$f_x\left(y\right)=\left\{\begin{array}{l}F if\;Y_F\leq y\leq Y_{R,}\\0 \;otherwise.\end{array}\right.$$
(2)

Integrating Eq. (1) from \(y = {Y}_{F}\) (where \({\tau }_{xy}\) is prescribed and constant below \({Y}_{F}\)) to the top boundary \(y = {Y}_{R}\) (where \({\tau }_{xy}=0\), due to the specular boundary) and from the step forcing in Eq. (2):

$${\tau }_{xy}={\rho }_{n}F{\int }_{{ Y}_{F}}^{{ Y}_{R}}dy={\rho }_{n}F\Delta Y$$
(3)

where \(\Delta Y={Y}_{R}-{Y}_{F}\) is the forcing zone thickness. Rearranging gives the force that needs to be applied in the equations of molecular motion:

$$F=\frac{{\tau }_{xy}}{{\rho }_{n}\Delta Y}$$
(4)

A steady-state flow over the surface is generated with a known shear stress with this forcing.

The slip length measured at an arbitrary reference plane in the surface is termed as effective slip length, \({b}_{eff}\) However, the adsorption of molecules onto the surface, molecular ordering of the fluid next to the surface, and the flow around complex topographical surfaces make it very challenging to obtain meaningful measurements of slip velocities near the wall. In the current approach, we assume that these effects are sufficiently confined to the near-wall region such that the strain rate in the bulk/measurement zone is constant throughout, with a velocity profile that resembles the standard Couette form [41]. The need to measure the average streaming velocity \(\langle \overline{V }\rangle\) over the entire bulk/measurement zone can be simplified using standard techniques. With a finite slip \({V}_{slip}\) defined at the reference plane, the strain rate can be written as:

$$\epsilon =\frac{dV}{dy}=\frac{\langle \overline{V }\rangle -{V}_{slip}}{H}$$
(5)

where \(H\) represents the distance between the reference plane and the bulk measurement zone’s midpoint (see Fig. 3). The effective slip length \({b}_{eff}\) can now be deduced by substituting the Navier slip condition, \({V}_{slip}={\epsilon b}_{eff}\), and the Newtonian stress–strain relationship \({\tau }_{xy}=\mu \epsilon\), into Eq. (5), and rearranging:

$${b}_{eff}=\frac{{\mu }_{1}\langle \overline{V}\rangle }{{\tau }_{xy}}-H$$
(6)

where \({\mu }_{1}\) is the viscosity of the liquid in the bulk zone. It can be noted that it is not essential that the fluid be Newtonian, but the viscosity for a given strain is a prerequisite (obtained from known fluid tables or MD pre-simulations).

Provided that the definition of a reference plane within the surface is consistent, slip lengths using Eq. (6) for various NEMD simulations of surfaces can be compared independent of the contact surface area and the thickness of any coating. Therefore, this can serve as a useful tool for comparing various proposed drag-reducing coatings on a substrate or comparing average slip quantities between different surface topographies and heterogeneities, as we demonstrate in the rest of this paper.

Noise and accuracy improvements

The fixed-stress method described in the previous section can alleviate the drawbacks of the Couette flow approach since it (a) imposes a known and spatially uniform stress field and (b) performs much better in managing noise-related errors for high-slip systems. The alleviations are demonstrated in this section. In order to circumvent running multiple expensive NEMD simulations, a simple pseudo-model of the output of a Couette flow configuration is created that mimics the results obtained in a typical NEMD simulation, as shown in Fig. 4. The following assumptions are made in this pseudo-model: (a) there is no gas/liquid interface (i.e. the channel height is occupied by only one fluid); (b) there is a slip velocity at the stationary wall; (c) there is no-slip at the moving wall; and (d) the fluid velocity response caused by the wall shear is linear in a central measurement zone.

Fig. 4
figure 4

Couette flow setup in a typical molecular dynamics simulation

Full size image

In a typical NEMD simulation, the fluid velocity profile is obtained by measuring velocities in \(N\) bins (see Fig. 4). To mimic the NEMD simulation in the pseudo-model, the output of each bin is taken as a sample from an equivalent linear velocity profile subject to normally distributed noise, i.e.:

$${V}_{i}={V}_{slip}+{\epsilon }_{xy}{y}_{i}+{N}_{i}\left(0,{\sigma }^{2}\right),$$
(7)

where \({y}_{i}\) is the centre position of the \({i}^{th}\) bin, \({V}_{slip}\) is the slip velocity, \({\epsilon }_{xy}=dV/dy\) is the strain rate, and \({N}_{i}\) are normally distributed random variables with variance \({\sigma }^{2}\). This equation assumes that the velocity profile is known exactly. However, it is only used here to generate MD-like values for \({V}_{i}\), in order to prevent us having to run expensive simulations for this error analysis; of course, a NEMD simulation would produce the measurements of \({V}_{i}\) directly.

A least-squares fit applied to the data of Vi provides an estimate of the actual \({V}_{slip}\) and \({\epsilon }_{xy}\) from the observed bin velocities, viz.:

$${\widehat{V}}_{slip}=\overline{\mathrm{V} }-{\widehat{\varepsilon }}_{xy}\overline{y }$$
(8)
$${\widehat{\varepsilon }}_{xy}=\frac{\overline{V y} -\overline{V}\overline{y}}{\overline{{y }^{2}}-{\overline{y} }^{2}}$$
(9)

where an overline \(\overline{x }=\left(\frac{1}{N}\right){\sum }_{i=1}^{N}{x}_{i}\) denotes an average over the \(N\) bins for one set of random bin samples, and an over-hat \(\widehat{x}\) represents the coefficients obtained from the least-squares fit of one statistical realization. The slip length estimate for this Couette flow problem is finally obtained from:

$$\widehat{b}=\frac{{\widehat{V}}_{slip}}{{\widehat{\epsilon }}_{xy}}$$
(10)

To estimate the noise in these variables from a NEMD simulation of a Couette flow configuration, Eqs. (7) to (10) are solved with M statistical realizations of the \(N\) random variables, and the root-mean-square error (RMSE) of the estimates for slip velocity and slip length is calculated, respectively, i.e.:

$$RMSE\left({\widehat{V}}_{slip}\right)=\sqrt{\frac{1}{M}\sum_{i=1}^{M}{\left({\left.{\widehat{V}}_{slip}\right|}_{i}-{V}_{slip}\right)}^{2}}$$
(11)
$$RMSE\left(\widehat{b}\right)=\sqrt{\frac{1}{M}\sum_{i=1}^{M}{\left({\left.\frac{{\widehat{V}}_{slip}}{{\widehat{\epsilon }}_{xy}}\right|}_{i}-\frac{{V}_{slip}}{{\epsilon }_{xy}}\right)}^{2} }$$
(12)

As an example, the following values with arbitrary units \({Y}_{1}=1\), \({Y}_{2}=2\), \({V}_{slip}=1\), \(\sigma =0.1\), \(N=100\), and \(M=\mathrm{10,000}\) are chosen. In Fig. 5a, the RMSE of the slip velocity estimate, normalized by the slip velocity, using red circles is plotted. It is reasonably constant (< < 1) for all slip lengths considered. However, the normalized RMSE of the estimated slip length in Fig. 5b increases very rapidly with the actual slip length (note: the \(y\)-axis is a logarithmic scale). The problem is worse than even this implies because the distribution of \(b\) becomes non-normal at higher \(b\), as shown in Fig. 6a and b, meaning that the probability of poor prediction increases when flows with greater slip lengths are simulated. This manifests itself in the kinks in the curve in Fig. 5b at high \(b\).

Fig. 5
figure 5

Normalized root-mean-square error (RMSE) of a the slip velocity and b the slip length in a pseudo-NEMD simulation of the Couette flow method and in the proposed method

Full size image
Fig. 6
figure 6

a Probability density function Pr of the sampled slip lengths for the Couette flow configuration against normalized slip lengths, and b sample skewness of Pr for both Couette and fixed-stress methods. Slip lengths are measured from the pseudo-NEMD simulations, with the following values with arbitrary units: Y1 = 1, Y2 = 2, Vslip = 1, σ = 0.1, N = 100, M = 10,000. This figure indicates the progressively non-normal distribution of noise in the Couette flow method for high-slip surfaces.

Full size image

In the proposed fixed-stress method, a body force is applied to molecules within a forcing zone located away from the surface, which allows controlling accurately the hydrodynamic shear applied to the fluid across the entire domain. In combination with a shear viscosity \(\mu\), obtained from accurate prior simulation or from published data, the mean strain rate \({\epsilon }_{xy}\) can be calculated. This can be used to simplify and improve the least-squares estimate given in Eqs. (8) and (10) to:

$$\widehat{V}_{\mathrm{slip}}=\overline{\mathrm{V} }-\frac{{\tau }_{xy}\overline{y}}{\mu }$$
(13)

and

$$\widehat{b}=\frac{\mu {\widehat{V}}_{slip}}{{\tau }_{xy}}$$
(14)

where \(\overline{V}\) is the velocity measured in one large bin, i.e. in the measurement zone of the liquid. The pseudo-method was again used to solve Eqs. (13) and (14) for illustration purposes. The RMSE of these two estimates, normalized with the actual slip velocity and slip length, is plotted as blue squares in Fig. 5.

A significant improvement is seen for all slip velocities and slip lengths measured compared to the conventional Couette flow method. Furthermore, the probability distribution of slip lengths for the fixed-stress method is normal, as shown in Fig. 6b.

Molecular dynamics simulations

The NEMD simulations are performed to measure slip lengths for different nanostructured surface coatings, using the fixed-stress method described in the “The fixed-stress method” section. All the simulations are performed using the mdFOAM solver [42, 43], a highly parallelized molecular dynamics code implemented within the open-source OpenFOAM C +  + libraries. The simulations are performed on ARCHER, the UK’s national supercomputer. The mdFOAM solver has previously been validated for several micro-nano-flow problems [44, 45].

Figure 7 shows a technologically relevant test case considered fully in the “CNT coatings with and without entrapped interstitial gas pockets” section. Because of its significance in marine engineering and recent advancements in superhydrophobic drag-reducing surfaces, water was chosen as the contact liquid. Platinum is chosen as the substrate because its wetting properties are well defined both experimentally and theoretically [46] and through molecular dynamics simulations [47, 48]. The CNTs are adopted as coating materials because of their low frictional properties and as we wish to investigate the effect of gas bubbles entrapped in the interstitial gaps. This could change drag in two ways: shielding the water from the platinum surface and providing a gas–liquid interface that increases liquid slip [49]. Nitrogen is chosen as the gas because it is the least soluble in water of all the species in air [50].

Fig. 7
figure 7

Example of one of the configurations considered in this work: coating of carbon nanotubes on a platinum surface, with water flowing longitudinally over the coating

Full size image

The size of the computational domain in the \(x\) direction is Lx = 4.62 nm, while extents in the y and z directions depend on the nature of the coating. For instance, in the case of CNT coatings, Ly is the sum of the CNT diameter and height of the water layer (∼10 nm) above the coating, while Lz is the sum of the CNT diameter and gap between CNTs. The slip reference plane is taken as the first layer of atoms of the solid surface (unless stated otherwise), as shown in the inset in Fig. 7. Newton’s equations of motion for all the molecules are integrated using the velocity-Verlet scheme, with a time step of 2 fs.

Using a Berendsen thermostat, the lattices of the solid, gas, and liquid zones are first initialized and allowed to equilibrate at a temperature of \(T=300\,\mathrm{K}\). The water density in bulk is tuned to \({\rho }_{M}=1000 \,\mathrm{kg/{m}^{3}}\) during this equilibration stage using the FADE insertion/deletion protocol [51]. After the system reached equilibrium, the flow simulation proceeds by imposing a constant shear stress of \({\tau }_{xy}=0.69 \,\mathrm{MPa}\), via the uniform force F in Eq. (4), to the water molecules in the forcing zone. This forcing drives the flow over the coated surface. For simulation, a velocity-unbiased Berendsen thermostat is applied in bins of width 0.8 nm within the fluid region.

Validation

The fixed-stress method is validated in NEMD by calculating slip length for water over graphene sheet.

The velocity and density profiles for water over the graphene-only surface are shown in Fig. 8. This figure highlights the three zones (forcing, bulk, and near-wall) which have been correctly set to confine the molecular structuring within the near-wall zone, and the strain rate is constant within the bulk zone. This setup is repeated for the rest of our NEMD simulations. The slip length obtained from the graphene-only simulation is 61 ± 2 nm, which compares well with other MD simulations: 60 ± 6 nm [52] and 54 nm [53]. Kannam et al. [54] have extensively reviewed the experimental, theoretical, and simulation values of slip lengths reported in the literature for graphene and found that these vary substantially. It should be noted that other MD results for the slip length of water on graphene might differ because of the differences in the force field models used (i.e. the adopted water model and the water-graphene potentials). Due to experimental uncertainty, the intermolecular potentials for graphene are still an open problem [29].

Fig. 8
figure 8

Validation case of flow over a graphene sheet: a the molecular system configuration; b the velocity profile in solid red line (dotted blue line represents a fit through the bulk data); and c the fluid density profile

Full size image

CNT coatings with and without entrapped interstitial gas pockets

For the first time, the current study reports molecular dynamics simulations of water slip over CNT coatings with nitrogen gas bubbles trapped in the gaps, producing a Cassie state. The importance of entrapped gas pockets on slip performance is highlighted by presenting slip length results of CNT coatings in the Wenzel state (fully wetted) without gas pockets. The external flow direction is taken along the tube axis in all the simulations.

While water flows around completely submerged CNTs of various diameters have been simulated using both EMD and NEMD by [37], here, the aligned CNTs coating a platinum substrate in the Wenzel state are considered (see Fig. 9), with the external flow directed along the tube axis. Three cases (C1–C3) are investigated: C1 is for (10, 10) CNTs of radius 0.68 nm, C2 is for (32, 32) CNTs of radius 2.17 nm, and C3 is for (58, 58) CNTs of radius 3.93 nm. The gap between CNTs in all 3 cases is approximately 2.5 nm. It is found that the slip lengths are much smaller than for a pristine graphene coating, with values ranging between beff = 2–8 nm. Note that these are effective slip lengths, which are better estimates for coating comparisons; the intrinsic slip lengths defined at the upper surface of the CNTs can be obtained by adding, in each case, the CNT diameter (thus, 3–16 nm). The slip lengths are found to increase with CNT diameter, and the observation is in line with the findings in the literature [34]. However, in the present simulations, the platinum surface plays an additional role.

Fig. 9
figure 9

Cases (C1–C3) with aligned CNTs coating a platinum substrate in the Wenzel state

Full size image

CNTs do not perform well as a slip-inducing coating in the Wenzel state because there are still significant intermolecular forces between the platinum and the water that drastically diminish the overall performance of the coating. Placing the CNTs very close together to completely de-wet the substrate would require the gap between successive CNTs to be less than 1.36 nm, agreeing with the findings in the literature [55]. Technologically speaking, such a small gap may be practically unachievable in coatings. It is expected that if CNT-coated surfaces remain in the Wenzel state, no matter how large the CNT diameters are, the coating may not be able to retrieve the same slip performance as a pure graphene surface.

Furthermore, four cases are considered with varying bubble sizes within the CNT gaps that successively reduced the water-CNT contact area (and from which an increase in the effective slip length is expected). Cases D1–D4 consisted of CNTs of radius 2.17 nm (the same as in case C2), with several nitrogen molecules (659, 792, 1320, and 2375, respectively) in the gap between CNTs. Cases D1 and D2 had a gap of 5.44 nm between adjacent CNTs, while cases D3 and D4 had gaps of 10.2 nm and 17 nm, respectively. Increasing the gas density and changing the gap extents changed the size and pinning location of the nano-gas bubble at the CNT.

Figure 10 shows the measured slip lengths for cases D1–D4 and compares them with cases C1–C3. It is evident that the major cause of the larger slip lengths (viz. 40–130 nm, compared to 5 nm in the fully wetted case C2) is the gas pockets shielding the water from the platinum surface. In these cases, the CNT-water interactions became the key contributor to drag, as verified by increasing the bubble size; there was an increase in slip length for smaller CNT-water contact areas.

Fig. 10
figure 10

Effective slip lengths of platinum coated with CNTs with nitrogen gas bubbles entrapped in the interstices (cases D1–D4). These results are plotted alongside results for CNT coatings in the Wenzel state (cases C1–C3). Note: in all cases, the flow is in the x direction, and the NEMD snapshots have been cropped in the y direction for visualization purposes

Full size image

Cottin-Bizonne et al. [26, 27] developed a model for estimating the effective slip length for flow over surface coatings with air pockets trapped in rectangular nanoscale grooves. To our knowledge, this model has not previously been compared with molecular dynamics simulations of surface coatings with entrapped gas, so its validity down to the nanoscale can be explored here for the first time. With the gas–liquid area fraction defined as \(\phi_{\mathrm{g}}={A}_{g}/{A}_{T}\) (where \({A}_{g}\) is the cross-sectional area of the gas–liquid interface in the \(xz\) plane, and \({A}_{T}={L}_{x}\times {L}_{z}\) is the total surface area; refer to Fig. 7), the effective slip length beff can then be calculated as:

$$\frac{1}{{b}_{eff}}=\frac{1-\phi_{\mathrm{g}}}{{b}_{sl}}+\frac{\phi_{\mathrm{g}}}{{b}_{gl}}$$
(15)

which depends on two additional parameters: the intrinsic slip lengths for the solid–liquid and gas–liquid surfaces, \({b}_{sl}\) and \({b}_{gl}\), respectively. This model is appropriate when the intrinsic slip lengths \({b}_{sl},{b}_{gl}> {L}_{z}/10\) [26, 27].

While the model is for surfaces coated with rectangular-shaped pillars, the NEMD results can be used to check the applicability of Eq. (15) to flow over surfaces nano-patterned with CNTs. The distances between the gas–liquid interface and the slip reference plane for cases D1 and D2 are \(y=\) 3.9 ± 0.5 nm and \(y=\) 4.7 ± 0.5 nm, respectively, which are estimated from the surface-normal density profile as the point at which the fluid density is 50% of the bulk value. Various values for \(\phi_{\mathrm{g}}\) are calculated with successively larger gaps between the CNTs; the number of nitrogen molecules is increased until the same gas thickness is approximately obtained for each gap adjustment. Note that we do not consider cases D3 and D4 in this part of the analysis because in these there is significant curvature in the gas–liquid interfaces.

In these simulations, the mass density for nitrogen is chosen to be ∼360 kg/m3 (one-third the density of water) as lower densities would introduce much larger fluctuations and longer simulation times. The slip lengths from these NEMD simulations are plotted against \(\phi_{\mathrm{g}}\) in Fig. 11 using circle and square symbols for the two cases. For model Eq. (15), the intrinsic slip lengths for the solid–liquid \({b}_{sl}\) and gas–liquid \({b}_{gl}\) cases are determined from two additional NEMD simulations, shown outset in Fig. 11. For the calculation of \({b}_{sl}\), a simulation of water flowing on a CNT with an interstitial gap is performed. The gap is so small that the system is maintained in the Cassie state. For the calculation of \({b}_{gl}\), where \(\phi_{\mathrm{g}}=1\), a water flow simulation over a gas layer of a thickness consistent with the previous cases (4.4 ± 0.5 nm, ρg = 360 kg/m3) is run. The intrinsic slip lengths are found to be \({b}_{sl}\) = 19.4 ± 3.8 nm and \({b}_{gl}\) = 134 ± 1 nm, enabling Eq. (15) to be plotted as the solid black line in Fig. 11.

Fig. 11
figure 11

Effective slip lengths are varying with gas–liquid area fraction for cases D1 (squares) and D2 (circles) with increasing CNT spacing and intrinsic slip lengths (diamonds). Error bars are smaller than the size of the symbols and have been omitted. In all cases, the flow is in the x direction, and the NEMD snapshots have been cropped for visualization purposes. The analytical Eq. (15) [26, 27] is also plotted (solid line) using the corresponding intrinsic slip lengths bsl = 19.4 nm and bgl = 134 nm obtained from our NEMD simulations

Full size image

It is seen that there is reasonably good agreement between the observed MD simulations and the theoretical models [26, 27]. What is clear from both the NEMD results and the theoretical model is that beff increases very gradually with increasing \(\phi_{\mathrm{g}}\) up to \(\phi_{\mathrm{g}}=\) 1.0 (where the separation between CNTs is very large), which indicates that the solid–liquid intermolecular interactions play a significant role, even if hydrophobic CNT surfaces are used as a drag-reducing component in the coating. Figure 11 also indicates that in order to obtain substantial slip lengths, the best choice for the solid nanostructure is a material with a large intrinsic slip length, i.e. large \({b}_{sl}\). The disadvantage of these types of surfaces, though, is that while operating at greater than 90–95% of bubble coverage produces the largest slip gains, whether these gas bubbles remain hydrodynamically stable still needs to be investigated.

Conclusions

With a fixed-stress technique to control the flow, non-equilibrium molecular dynamics (NEMD) simulations of slip flow over different nanostructured surfaces were developed. The approach was validated for water flow over a graphene surface and compared the result with slip lengths from benchmark molecular dynamics predictions. Furthermore, the slip lengths of flows over carbon nanotube (CNT) coatings in both the Wenzel and Cassie states on a no-slip platinum substrate were investigated. The slip length was found to increase with increasing CNT radius, and for CNT coatings with interstitial gas, we found that the presence of the gas pockets increases the slip compared to surfaces in the Wenzel state. Slip increased with increasing gas area fraction, and the effective slip length was mainly dictated by the CNT-water friction. It was found that the surfaces coated with CNTs with entrapped gas may offer significant drag reduction only if the gas surface coverage is above 95%. This is likely to be very challenging to produce in reality, although generating myriad micro-/nanobubbles at the surface to produce ultra-thin and stable pseudo-films may offer a technological solution to this open problem in the long term.