Multigrid methods with space–time concurrency

Abstract

We consider the comparison of multigrid methods for parabolic partial differential equations that allow space–time concurrency. With current trends in computer architectures leading towards systems with more, but not faster, processors, space–time concurrency is crucial for speeding up time-integration simulations. In contrast, traditional time-integration techniques impose serious limitations on parallel performance due to the sequential nature of the time-stepping approach, allowing spatial concurrency only. This paper considers the three basic options of multigrid algorithms on space–time grids that allow parallelism in space and time: coarsening in space and time, semicoarsening in the spatial dimensions, and semicoarsening in the temporal dimension. We develop parallel software and performance models to study the three methods at scales of up to 16K cores and introduce an extension of one of them for handling multistep time integration. We then discuss advantages and disadvantages of the different approaches and their benefit compared to traditional space-parallel algorithms with sequential time stepping on modern architectures.

1 Introduction

The numerical solution of linear systems arising from the discretization of partial differential equations (PDEs) with evolutionary behavior, such as parabolic (space–time) problems, hyperbolic problems, and equations with time-like variables is of interest in many applications including fluid flow, magnetohydrodynamics, compressible flow, and charged particle transport. Current trends in supercomputing leading towards computers with more, but not faster, processors induce a change in the development of algorithms for these type of problems. Instead of exploiting increasing clock speeds, faster time-to-solution must come from increasing concurrency, driving the development of time-parallel and full space–time methods.

In contrast to classical time-integration techniques based on a time-stepping approach, i.e., solving sequentially for one time step after the other, time-parallel and space–time methods allow simultaneous solution across multiple time steps. As a consequence, these methods enable exploitation of substantially more computational resources than standard space-parallel methods with sequential time stepping. While classical time-stepping has optimal algorithmic scalability, with best possible complexity when using a scalable solver for each time step, space-time-parallel methods introduce more computations and/or memory usage to allow the use of vastly more parallel resources. In other words, space–time parallel methods remain algorithmically optimal, but with larger constant factors. Their use provides a speedup over traditional time-stepping when sufficient parallel resources are available to amortize their increased cost.

Research on parallel-in-time integration started about 50 years ago with the seminal work of Nievergelt [38]. Since then, various approaches have been explored, including direct methods such as [8, 20, 34, 37, 41], as well as iterative approaches based on multiple shooting, domain decomposition, waveform relaxation, and multigrid including [2, 7, 9, 10, 13, 17, 21, 24,25,26,27, 29, 32, 33, 35, 36, 43,44,45,46]. A recent review of the extensive literature in this area is [16].

There are now many available parallel-in-time methods that allow for faster time-to-solution in comparison with classical time-stepping approaches, given enough computational resources. However, a comparison of the different space-time-parallel approaches does not exist. A comprehensive comparison of all proposed parallel-in-time methods is a far greater task than could be covered in a single manuscript; here, we focus on representative approaches of multigrid type on space–time grids, including both semicoarsening approaches and those that coarsen in both space and time. More specifically, we compare space–time multigrid with point-wise relaxation (STMG) [26], space–time multigrid with block relaxation (STMG-BR) [17], space–time concurrent multigrid waveform relaxation with cyclic reduction (WRMG-CR) [27], and multigrid-reduction-in-time (MGRIT) [13] for time discretizations using backward differences of order k (BDF-k).

The goal of our comparison is not to simply determine the algorithm with the fastest time-to-solution for a given problem. Instead, we aim at determining advantages and disadvantages of the methods based on comparison parameters such as robustness, intrusiveness, storage requirements, and parallel performance. We recognize that there is no perfect method, since there are necessarily trade-offs between time-to-solution for a particular problem, robustness, intrusiveness, and storage requirements. One important aspect is the effort one has to put into implementing the methods when aiming at adding parallelism to an existing time-stepping code. While MGRIT is a non-intrusive approach that, similarly to time stepping, uses an existing time propagator to integrate from one time to the next, both STMG methods and WRMG-CR are invasive approaches. On the other hand, the latter three approaches have better algorithmic complexities than the MGRIT algorithm. In this paper, we are interested in answering the question of how much of a performance penalty one might pay in using a non-intrusive approach, such as MGRIT, in contrast with more efficient approaches like STMG and WRMG-CR. Additionally, we demonstrate the benefit compared to classical space-parallel time-stepping algorithms in a given parallel environment.

This paper is organized as follows. In Sect. 2, we review the three multigrid methods with space–time concurrency, STMG (both the point-wise and the block relaxation version), WRMG-CR, and MGRIT, including a new description of the use of MGRIT for multistep time integration. In Sect. 3, we construct a simple model for the comparison. We introduce a parabolic test problem, derive parallel performance models, and discuss parallel implementations as well as storage requirements of the three methods. Section 4 starts with weak scaling studies, followed by strong scaling studies comparing the three multigrid methods both with one another and with a parallel algorithm with sequential time stepping. Additionally, we include a discussion of insights from the parallel models as well as an overview of current research in the XBraid project [47] to incorporate some of the more intrusive, but highly efficient, aspects of methods like STMG. Conclusions are presented in Sect. 5.

2 Multigrid on space–time grids

The naive approach of applying multigrid with standard components, i.e., point relaxation and full coarsening, for solving parabolic (space–time) problems typically leads to poor multigrid performance (see, e.g. [26]). In this section, we describe three multigrid algorithms that represent the most basic choices for multigrid methods on space–time grids which offer good performance, allowing parallelism in space and time. For a given parabolic problem, the methods assume different discretization approaches using either a point-wise discretization of the whole space–time domain or a semidiscretization of the spatial domain. However, for a given discretization in both space and time, all methods solve the same (block-scaled) resulting system of equations.

2.1 Space–time multigrid

The space–time multigrid methods proposed in [17, 26] treat the whole of the space–time problem simultaneously. The methods use either point or block smoothers and employ parameter-dependent coarsening strategies that choose either semicoarsening in time or in space or full space–time coarsening at each level of the hierarchy.

Let $\varSigma = \varOmega \times [0,T]$ be a space–time domain and consider a time-dependent parabolic PDE of the form

$$\begin{aligned} u_t + \mathcal {L}(u) = b \end{aligned}$$

(1)

in $\varSigma$, subject to boundary conditions in space and an initial condition in time. Furthermore, $\mathcal {L}$ denotes an elliptic operator and $u=u(x,t)$ and $b=b(x,t)$ are functions of a spatial point, $x\in \varOmega$, and time, $t\in [0,T]$. We discretize (1) by choosing appropriate discrete spatial and temporal domains. The resulting discrete problem is typically anisotropic due to different mesh sizes used for discretizing the spatial and temporal domains. Consider, for example, discretizing the heat equation in one space dimension and in the time interval [0, T] on a rectangular space–time mesh with constant spacing $\varDelta x$ and $\varDelta t$, respectively. If we use central finite differences for discretizing the spatial derivatives and backward Euler [also, first-order backward differentiation formula (BDF1)] for the time derivative, the coefficient matrix of the resulting linear system depends on the parameter $\lambda = \varDelta t/(\varDelta x)^2$, which can be considered as a measure of the degree of anisotropy in the discrete operator.

Analogously to anisotropic elliptic problems, in the parabolic case, there are also two standard approaches for deriving a multigrid method to treat the anisotropy: the strategy is to either change the smoother to line or block relaxation, ensuring smoothing in the direction of strong coupling, or to change the coarsening strategy, using coarsening only in the direction where point smoothing is successful. STMG follows the second approach, while STMG-BR is mainly driven by the first approach. The STMG method uses a colored point-wise Gauss–Seidel relaxation, based on partitioning the discrete space–time domain into points of different ‘color’ with respect to all dimensions of the problem. That is, time is treated simply as any other dimension of the problem. For the block-relaxation version of STMG, STMG-BR, damped block Jacobi in time relaxation is used (implemented by using a spatial V-cycle independently on each time-line of the solution).

Relaxation is accelerated using a coarse-grid correction based on an adaptive parameter-dependent coarsening strategy. More precisely, depending on the degree of anisotropy of the discretization stencil, $\lambda$ (e.g., $\lambda = \varDelta t/(\varDelta x)^2$ in our previous example), in STMG, either semicoarsening in space or in time is chosen while in the block-relaxation version, either full space–time coarsening or semicoarsening in time is used. The choice for the coarsening strategy is based on a selected parameter, $\lambda _\text {crit}$, which can be chosen, for example, using Fourier analysis, as was done for the heat equation [26], applying the two-grid methods using either semicoarsening in space (when $\lambda \ge \lambda _{crit}$) or in time (when $\lambda < \lambda _{crit}$). Thus, a hierarchy of coarse grids is created, where going from one level to the next coarser level, the number of points is reduced either only in the spatial dimensions or only in the temporal dimension if the point-wise relaxation version is used. In the case of block relaxation, the number of points is reduced either in all dimensions or only in the temporal dimension. Rediscretization is used to create the discrete operator on each level, and the intergrid transfer operators are adapted to the grid hierarchy. In the case of space-coarsening, interpolation and restriction operators are the standard ones used for isotropic elliptic problems. For time-coarsening, interpolation and restriction are only forward in time, transferring no information backward in time.

Summing up, assuming a discretization on a rectangular space–time grid with $N_x$ points in each spatial dimension and $N_t$ points in the time interval, we consider a hierarchy of space–time meshes, $\varSigma _l$, $l=0,1, \ldots ,L=\log _2(N_xN_t)$. Let $A_l u^{(l)} = g^{(l)}$ be the discrete problem on each grid level and $\lambda _l$ the degree of anisotropy of the discretization stencil defining $A_l$. Then, with $P_x, R_x, P_t$, and $R_t$ denoting interpolation and restriction operators for space-coarsening and time-coarsening, respectively, and for a given parameter $\lambda _\text {crit}$, the STMG(-BR) V-cycle algorithm for solving a linear parabolic problem is given in Algorithm 1.

Note that STMG algorithms of other cycling types such as F- or W-cycles can be defined, which are of particular interest for improving the overall convergence rates [26].

Remark

While for one-step time-discretization methods, such as BDF1, usually a red–black ordering of the grid points is sufficient for the point-relaxation version, for multi-step time discretizations, more colors are needed. As a consequence, the amount of parallelism decreases with relaxation performed on points of one color at a time. Alternatively, a two-color ordering could be used in combination with a Jacobi-like in time approach, i.e., a backward ordering of the grid points in time.

2.2 Multigrid waveform relaxation

Waveform relaxation methods are based on applying standard iterative methods to systems of time-dependent ordinary differential equations (ODEs). Waveform relaxation, used in combination with either multigrid [33, 43] or domain decomposition [3, 18] ideas to treat the spatial problem expands the applicability of standard iterative methods to include time-dependent PDEs. Multigrid waveform relaxation (WRMG) [33] combines red–black zebra-in-time line relaxation with a semicoarsening strategy, using coarsening only in the spatial dimension.

For solving parabolic problems as given in (1), in contrast to STMG described above, the WRMG algorithm uses a method of lines approximation, discretizing only the spatial domain, $\varOmega$. Thus, a semidiscrete problem is generated, i.e., the PDE is first transformed to a system of time-dependent ODEs of the form

$$\begin{aligned} \frac{d}{dt}u(t) + Q(u(t)) = b(t), \quad u(0) = g_0, \quad t\in [0,T], \end{aligned}$$

(2)

where u(t) and b(t) are vector functions of time, $t\in [0,T]$ [i.e., the semidiscrete analogues of the functions u and b in (1)], with (d / dt)u(t) denoting the time derivative of the vector u(t), and where Q is the discrete approximation of the operator $\mathcal {L}$ in (1). In the linear case, considered in the remainder of this section, function $Q(\cdot )$ corresponds to a matrix-vector product. The idea of waveform (time-line) relaxation [31] is to apply a standard iterative method such as Jacobi or Gauss–Seidel to the ODE system (2). Therefore, let $Q=D-L-U$ be the splitting of the matrix into its diagonal, strictly lower, and strictly upper triangular parts; note that D, L,  and U may be functions of time. Then, one step of a Gauss–Seidel-like method for (2) is given by

$$\begin{aligned}&\frac{d}{dt}u^{(\text {new})}(t) + (D-L)u^{(\text {new})}(t) = Uu^{(\text {old})}(t) + b(t),\nonumber \\&u^{(\text {new})}(0) = g_0, \quad t\in [0,T], \end{aligned}$$

(3)

with $u^{(\text {old})}$ and $u^{(\text {new})}$ denoting known and to be updated solution values, respectively. That is, one step of the method involves solving $N_s$ linear, scalar ODEs, where $N_s$ is the number of variables in the discrete spatial domain (e.g., $N_s=N_x^2$ if discretizing on a regular square mesh in 2D). Furthermore, if Q is a standard finite difference stencil and a red–black ordering of the underlying grid points is used, the ODE system decouples, i.e., each ODE can be integrated separately and in parallel with the ODEs at grid points of the same color.

The performance of Gauss–Seidel waveform relaxation is accelerated by a coarse-grid correction procedure based on semicoarsening in the spatial dimensions. More precisely, discrete operators are defined on a hierarchy of spatial meshes and standard interpolation and restriction operators as used for isotropic elliptic problems (e.g., full-weighting restriction and bilinear interpolation for 2D problems), allowing the transfer between levels in the multigrid hierarchy. Parallelism in this algorithm, however, is limited to spatial parallelism. Space–time concurrent WRMG enables parallelism across time, i.e., parallel-in-time integration of the scalar ODEs in (3) that make up the kernel of WRMG. While in the method described in [43] only some time parallelism was introduced by using pipelining or the partition method, WRMG with cyclic reduction (WRMG-CR) [27] enables full time parallelism within WRMG.

The use of cyclic reduction within waveform relaxation is motivated by the connection of multistep methods to recurrence relations. Therefore, let $t_i = i\delta t$, $i=0,1,\ldots ,N_t$, be a temporal grid with constant spacing $\delta t = T/N_t$, and for $i=1,\ldots ,N_t$, let $u_{n,i}$ be an approximation to $u_n(t_i)$, with the subscript $n = 1, \ldots , N_s$ indicating that we consider one ODE of the system. Then, a general k-step time discretization method for a linear, scalar ODE, e.g., one component of the ODE systems in (2) or (3), with solution variable $u_n$ and initial condition $u_n(0) = g_0$ is given by

$$\begin{aligned} u_{n,0}= & {} g_0\nonumber \\ u_{n,i}= & {} \sum \limits _{s=1}^{\min \{i,k\}}a_{i,i-s}^{(n)}u_{n,i-s} + g_{n,i}, \quad i = 1, 2, \ldots , N_t. \end{aligned}$$

(4)

That is, the solution, $u_{n,i}$, at time $t_i$ depends on solution-independent terms, $g_{n,i}$, e.g., related to boundary conditions or source terms or connections to different spatial points, as well as on the solution at the previous k time steps, except at the beginning, where the method builds up from a one-step method involving only the initial condition at time zero. Thus, the time discretization method (4) is equivalent to a linear system of equations with lower triangular structured coefficient matrix, or, equivalently, to a linear recurrence relation of order k. Note that in the case of constant-coefficients, i.e., in the case that coefficients $a_{i,i-s}^{(n)}$ are time-independent, we have $a_{i,i-s}^{(n)} = a_{\mu ,s}^{(n)}$ with $\mu =i$ for each $i<k$ and $\mu =k$ otherwise. In practice, coefficients $a_{\mu ,s}^{(n)}$ are independent of n; however, they may not be, e.g., if using different time discretizations across the spatial domain. Considering this connection to linear recurrences and the fact that linear recurrences can be parallelized efficiently using a cyclic reduction approach [6, 22, 30], motivates using cyclic reduction for integrating the ODEs in (3) and, thus, introducing temporal parallelism in WRMG.

Altogether, assuming a discrete spatial domain with $N_x$ points in each spatial dimension, WRMG-CR uses a hierarchy of spatial meshes, $\varOmega _l$, $l = 0, 1, \ldots , L = \log _2(N_x)$. Let $\frac{d}{dt}u^{(l)} + Q_lu^{(l)} = b^{(l)}, ~u^{(l)}(0) = g_0^{(l)}$ be the ODE system on level l, where $Q_l$ represents a time-independent spatial discretization on the mesh $\varOmega _l$. Furthermore, for $l = 0, 1, \ldots , L$, let $A_lu^{(l)}=g^{(l)}$ be the equivalent linear system of equations for a given linear multistep time discretization method. Note that the linear systems are of the form

$$\begin{aligned} A_lu^{(l)} \equiv (I_{N_s^{(l)}}\otimes J + Q_l\otimes I_{N_t})u^{(l)} = g^{(l)}, \end{aligned}$$

where $I_{N_s^{(l)}}$ and $I_{N_t}$ are identity matrices on the discrete spatial and temporal domains, respectively, and J is the (lower-triangular) matrix describing the discretization in time. With $P_x$ and $R_x$ denoting the interpolation and restriction operators (also used in STMG for space-coarsening), the WRMG-CR V-cycle algorithm for solving (2) is given in Algorithm 2.

Other cycling types can be defined and have been studied, e.g., [27] discusses the use of full multigrid (FMG).

Remark

While we focus on the use of cyclic reduction, which is very efficient for the case of a single-step time discretization ($k=1$), it is clear that any algorithm with good parallel efficiency can be used to solve the banded lower-triangular linear systems in the waveform relaxation step. In particular, for multistep methods ($k\ge 2$), it is computationally more efficient to use the recursive doubling method [23] instead of cyclic reduction (see [27]), but block cyclic reduction (as explained below for multigrid-reduction-in-time) or residual-correction strategies could also be used.

2.3 Multigrid-reduction-in-time

The multigrid-reduction-in-time (MGRIT) algorithm [13] is based on applying multigrid reduction techniques [39, 40] to time integration, and can be seen as a multilevel extension of the two-level parareal algorithm [32]. The method uses block smoothers for relaxation and employs a semicoarsening strategy that, in contrast to WRMG, coarsens only in the temporal dimension. To describe the MGRIT algorithm, we consider a system of ODEs of the form

$$\begin{aligned} u'(t) = f(t,u(t)), \quad u(0) = g_0, \quad t\in [0,T]. \end{aligned}$$

(5)

Note that (5) is a more general form of (2). We choose the form (5) to underline that we do not assume a specific discretization of the spatial domain, allowing a component-wise viewpoint of the ODE system as in the WRMG approach, but consider the discrete spatial domain as a whole. Instead, we choose a discretization of the time interval. For ease of presentation, we first review the MGRIT algorithm for one-step time discretization methods as introduced in [13]. We then explain how to recast multistep methods as block single-step methods, which is the basis for extending MGRIT to multistep methods.

Denoting the temporal grid with constant spacing $\delta t = T/N_t$ again by $t_i = i\delta t$, $i=0,1,\ldots ,N_t$, we now let $u_i$ be an approximation to $u(t_i)$ for $i=1,\ldots ,N_t$. Then, in the case that f is a linear function of u(t), the solution to (5) is defined via time-stepping, which can also be represented as a forward solve of the linear system, written in block form as

$$\begin{aligned} Au \equiv \begin{bmatrix} I\\ -\varPhi _{\delta t}&I\\&\ddots&\ddots \\&-\varPhi _{\delta t}&I \end{bmatrix} \begin{bmatrix} u_0\\ u_1\\ \vdots \\ u_{N_t} \end{bmatrix} = \begin{bmatrix} g_0\\ g_1\\ \vdots \\ g_{N_t} \end{bmatrix} \equiv g, \end{aligned}$$

(6)

where $\varPhi _{\delta t}$ represents the time-stepping operator that takes a solution at time $t_i$ to that at time $t_{i+1}$, along with a time-dependent forcing term $g_i$. Hence, in the time dimension, this forward solve is completely sequential.

MGRIT enables parallelism in the solution process by replacing the sequential solve with an optimal multigrid reduction method using a hierarchy of coarse temporal grids. For simplicity, we only describe the two-level MGRIT algorithm; the multilevel scheme results from applying the two-level method recursively. The coarse temporal grid, or the set of C-points, is derived from the original (fine) temporal grid by considering only every m-th temporal point, where $m>1$ is an integer. That is, the coarse temporal grid consists of $N_t/m$ points, denoted by $T_j = j\varDelta T, ~j=0, 1, \ldots , N_t/m$, with constant spacing $\varDelta T = m\delta t$; the remaining temporal points define the set of F-points.

The MGRIT algorithm uses the block smoother FCF-relaxation, which consists of three sweeps: F-relaxation, then C-relaxation, and again F-relaxation. F-relaxation updates the unknowns at F-points by propagating the values of C-points at times $T_j$ across a coarse-scale time interval, $(T_j, T_{j+1})$, for each $j=0,1,\ldots ,N_t/m-1$. Note that within each coarse-scale time interval, these updates are sequential, but there are no dependencies across coarse time intervals, enabling parallelism. C-relaxation updates the unknowns at C-points analogously, using the values at neighboring F-points. The intergrid transfer operators of MGRIT are injection, $R_I$, and ‘ideal’ interpolation, P, with ‘ideal’ interpolation corresponding to injection from the coarse grid to the fine grid, followed by F-relaxation with a zero right-hand side. The coarse-grid system, $A_\varDelta u_\varDelta = g_\varDelta$, is of the same form as the fine-grid system (6), with $\varPhi _{\delta t}$ replaced by the coarse-scale time integrator $\varPhi _{\varDelta T}$ that takes a solution $u_{\varDelta ,j}$ at time $T_j$ to that at time $T_{j+1}$, along with consistently restricted forcing terms $g_{\varDelta ,j}$. The two-level MGRIT algorithm is given in Algorithm 3.

Multilevel schemes of various multigrid cycling types such as V-, W-, and F-cycles can be defined by applying the two-level method recursively to the system in Step 3. Indeed, it is for this reason that FCF-relaxation is used, in contrast to the two-level algorithm, for which F-relaxation alone yields a scalable solution algorithm. When using F-relaxation in the two-level algorithm, the resulting approach can be viewed as a parareal-type algorithm [12,13,14, 19, 32].

Remark

For nonlinear functions f, the full approximation storage (FAS) approach [5] can be used to extend the MGRIT algorithm [12].

2.3.1 MGRIT for multistep time integration

Consider the system of ODEs in (5) on a temporal grid with time points $t_i$, $i = 0,1,\ldots ,N_t$ as before, but consider the general setting of non-uniform spacing given by $\tau _i = t_i - t_{i-1}$ (in the scheme considered here, this will be the setting on coarse time grids). As before, let $u_i$ be an approximation to $u(t_i)$ for $i = 1,\ldots ,N_t$, where $u_0 = g_0$ is the initial condition at time zero. Then, a general k-step time discretization method for (5) is given by

$$\begin{aligned} u_i= & {} \varPhi _i^{(\mu )}(u_{i-1},u_{i-2},\ldots ,u_{i-\mu }) + g_i\nonumber \\:= & {} \sum \limits _{s=1}^{\mu =\min \{i,k\}}\varPhi _i^{(\mu ,s)}(u_{i-s}) + g_i, \quad i = 1, \ldots , N_t, \end{aligned}$$

(7)

where analogously to (4), the solution, $u_i$, at time $t_i$ depends on solution-independent terms, $g_i$, as well as on the solution at the previous k time steps, except at the beginning, where the method builds up from a one-step method involving only the initial condition at time zero. Note that from a time-stepping perspective, the key is the time-stepping operator, $\varPhi _i^{(\mu )}$, that takes a solution at times $t_{i-1}, t_{i-2}, \ldots , t_{i-\mu }$ to that at time $t_i$ along with a time-dependent forcing term $g_i$ with $\mu = i$ for each $i<k$ and $\mu =k$ otherwise.

Extending the MGRIT algorithm described above to this multistep time discretization setting is based on the idea of recasting the multistep method (7) as a block one-step method. This idea is the key to keeping the MGRIT approach non-intrusive so that only the time-stepping operator, $\varPhi _i^{(\mu )}$, is needed. The approach works in both the linear and nonlinear case; for simplicity, we consider the linear case and describe it in detail.

Fig. 1

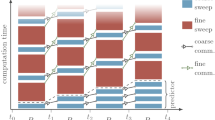
Schematic view of the action of F-relaxation in one coarse-scale time interval for a two-step time discretization method and coarsening by a factor of four; open circle represent F-points and filled square represent C-points. The action of F-relaxation on the individual F-points are distinguished by using different line styles

The idea is to group unknowns into k-tuples to define new vector variables

$$\begin{aligned} \mathbf {w}_n = (u_{kn},u_{kn+1},\ldots ,u_{kn+k-1})^T , \end{aligned}$$

$n = 0, 1,\ldots ,(N_t+1)/k-1$, then rewrite the method as a one-step method in terms of the $\mathbf {w}_n$. For example, in the BDF2 case in Fig. 1, we have

$$\begin{aligned} \mathbf {w}_n= & {} \begin{bmatrix} u_{2n} \\ u_{2n+1}\nonumber \end{bmatrix}\\= & {} \begin{bmatrix} \varPhi _{2n}^{(\mu )}(u_{2n-1},u_{2n-2})+g_{2n} \\ \varPhi _{2n+1}^{(\mu )}\left( \varPhi _{2n}^{(\mu )}(u_{2n-1},u_{2n-2})+g_{2n},u_{2n-1} \right) +g_{2n+1}\nonumber \end{bmatrix} \\= & {} \varvec{\varPsi }_n \left( \begin{bmatrix} u_{2n-2} \\ u_{2n-1} \end{bmatrix} \right) + \begin{bmatrix} g_{2n} \\ g_{2n+1} \end{bmatrix} = \varvec{\varPsi }_n( \mathbf {w}_{n-1} ) + \mathbf {g}_n . \end{aligned}$$

(8)

In the linear case, it is easy to see that the step function $\varvec{\varPsi }_n$ is a block $2\times 2$ matrix ($k \times k$ for general BDF-k) composed from the $\varPhi _i^{(\mu ,s)}$ matrices in (7). In addition, the method yields the same lower bi-diagonal form as (6) with the $\varvec{\varPsi }_n$ matrices on the lower diagonal. Implementing this method in XBraid [47] is straightforward because the step function in (8) just involves making calls to the original BDF2 method, whether in the linear setting or the nonlinear setting. Note that if the $u_{2n}$ result in (8) is saved, it can be used to compute the $u_{2n+1}$ result, hence only two spatial solves are required to compute a step, whereas a verbatim implementation of the block matrix approach in the linear case would require many more spatial solves.

All of this generalizes straightforwardly to the BDF-k setting. Note that, even if we begin with a uniformly spaced grid (as here), this method leads to coarse grids with time steps (between and within tuples) that vary dramatically. In the BDF2 case considered later, this does not cause stability problems. Research is ongoing for the higher order cases, where stability may be more of an issue.

3 Cost estimates

In investigating the differences between the three time-parallel methods, it is useful to construct a simple model for the comparison. In the model, we consider a diffusion problem in two space dimensions discretized on a rectangular space–time grid and distributed in a domain-partitioned manner across a given processor grid.

3.1 The parabolic test problem

Consider the diffusion equation in two space dimensions,

$$\begin{aligned} u_t - \varDelta u = b(x,y,t), ~(x,y)\in \varOmega = [0,\pi ]^2, ~t\in [0,T],\nonumber \\ \end{aligned}$$

(9)

with the forcing term (motived by the test problem in [42]),

$$\begin{aligned} b(x,y,t)&= -\sin (x)\sin (y)\left( \sin (t)-2\cos (t)\right) ,\nonumber \\&\phantom {=~~}(x,y)\in \varOmega , ~t\in [0,T], \end{aligned}$$

(10)

and subject to the initial condition,

$$\begin{aligned} u(x,y,0) = g_0(x,y) = \sin (x)\sin (y), \quad (x,y)\in \varOmega , \end{aligned}$$

(11)

and homogeneous Dirichlet boundary conditions,

$$\begin{aligned} u(x,y,t) = 0, \quad (x,y)\in \partial \varOmega , ~t\in [0,T]. \end{aligned}$$

(12)

The problem is discretized on a uniform rectangular space–time grid consisting of an equal number of intervals in both spatial dimensions using the spatial mesh sizes $\varDelta x = \pi /N_x$ and $\varDelta y = \pi /N_x$, respectively, and $N_t$ time intervals with a time step size $\delta t = T/N_t$, where $N_x$ and $N_t$ are positive integers and T denotes the final time. Let $u_{j,k,i}$ be an approximation to $u(x_j, y_k, t_i)$, $j, k = 0, 1, \ldots , N_x$, $i = 0, 1, \ldots , N_t$, at the grid points $(x_j, y_k, t_i)$ with $x_j = j\varDelta x$, $y_k = k\varDelta y$, and $t_i = i\delta t$. Using central finite differences for discretizing the spatial derivatives and first- (BDF1) or second-order (BDF2) backward differences for the time discretization, we obtain a linear system in the unknowns $u_{j,k,i}$. The BDF1 discretization can be written in time-based stencil notation as

$$\begin{aligned} \begin{bmatrix} -\frac{1}{\delta t}I&\left( \frac{1}{\delta t}I + M\right)&0 \end{bmatrix}, \end{aligned}$$

where M can be written in space-based stencil notation as

$$\begin{aligned} M = \left[ \begin{array}{c} -a_y\\ -a_x 2(a_x+a_y) -a_x\\ -a_y \end{array}\right] , \end{aligned}$$

with $a_x = 1/(\varDelta x)^2$ and $a_y = 1/(\varDelta y)^2$.

For the BDF2 discretization, we use the variably spaced grid with spacing $\tau _i$ introduced in Sect. 2.3.1 since we need it to discretize the coarse grids. In time-based stencil notation, we have at time point $t_i$

$$\begin{aligned} \begin{bmatrix} \frac{r_i^2}{\tau _i(1+r_i)}I&-\frac{(1+r_i)}{\tau _i}I&\left( \frac{(1+2r_i)}{\tau _i(1+r_i)}I + M\right)&0&0 \end{bmatrix}, \end{aligned}$$

where $r_i = \tau _i/\tau _{i-1}$.

3.2 Parallel implementation

For the implementation of the three multigrid methods on a distributed memory computer, we assume a domain-decomposition approach. That is, the space–time domain consisting of $N_x^2\times N_t$ points is distributed evenly across a logical $P_x^2\times P_t$ processor grid such that each processor holds an $n_x^2\times n_t$ subgrid. The distributions on coarser grids are in the usual multigrid fashion through their parent fine grids.

The STMG and WRMG-CR methods were implemented in hypre [28] and for the MGRIT algorithm, we use the XBraid library [47]. The XBraid package is an implementation of the MGRIT algorithm based on an FAS approach to accommodate nonlinear problems in addition to linear problems. From the XBraid perspective, the time integrator, $\varPhi$, is a user-provided black-box routine; the library only provides time-parallelism. To save on memory, only solution values at C-points are stored. Note that the systems approach for the multistep case does not increase MGRIT storage. For BDF2, for example, the number of C-point time pairs is half of the number of C-points when considering single time points. We implemented STMG and WRMG-CR as semicoarsening algorithms, i.e., spatial coarsening is first done in the x-direction and then in the y-direction on the next coarser grid level. Relaxation is only performed on grid levels of full coarsening, i.e., on every second grid level, skipping intermediate semi-coarsened levels. While this approach has larger memory requirements (see Sect. 3.3), it allows savings in communication compared with implementing the two methods with full spatial coarsening. For cyclic reduction within WRMG-CR, we use the cyclic reduction solver from hypre, which is implemented as a 1D multigrid method. The spatial problems of the time integrator, $\varPhi$, in the MGRIT algorithm are solved using the parallel semicoarsening multigrid algorithm PFMG [1, 11], as included in hypre. For comparison to the classical time-stepping approach, we also implemented a parallel algorithm with sequential time stepping, using the same time integrator as in the implementation of MGRIT. In modelling the time integrator as well as for the experiments in Sect. 4, we assume PFMG V(1, 1)-cycles with red–black Gauss–Seidel relaxation.

Remark 1

For the point-relaxation version of STMG, a four-color scheme would be needed in case of the BDF2 time discretization. However, for simplicity of implementation, we use a two-color scheme as in the case of the BDF1 discretization with the difference that updating of grid points is from high t-values to low t-values, i.e., backward ordering of the grid points in time. Thus, point-relaxation is Gauss–Seidel-like in space and Jacobi-like in time. The results in Sect. 4 show that this reduction in implementation effort is an acceptable parallel performance tradeoff.

Remark 2

For the block-relaxation version of STMG, there are three changes to be made to closely match the algorithm proposed in [17]: First, instead of semicoarsening in space, full space–time coarsening is applied. Secondly, interpolation is backward in time instead of forward in time and, thirdly, the key component of the STMG variant is a damped block Jacobi in time smoother. Similarly to STMG and WRMG-CR, we implemented full space–time coarsening in a semicoarsening fashion, i. e., coarsening is done in three steps: first in the x-direction, then in the y-direction on the next coarser grid level and finally in the t-direction on the next coarser grid level. Relaxation is only performed on grid levels of full coarsening. For the damped block Jacobi in time relaxation, a single spatial V-cycle is applied to each time slice. We use PFMG V(1, 1)-cycles with red–black Gauss–Seidel relaxation for the spatial V-cycles. Note that this block-relaxation variant of STMG is similar to but differs from the method proposed in [17]. In [17], a standard finite element discretization in space and a discontinuous Galerkin approximation in time is used. Therefore, spatial interpolation and restriction are transposes of each other as opposed to transposes of each other up to a constant in the finite-difference setting of this paper. Temporal interpolation and restriction come from the finite-element in time basis, which gives restriction forward in time and interpolation backward in time when using piecewise constant-in-time elements corresponding to a BDF1 discretization used in this paper.

Remark 3

In the case of a two-step time discretization method like BDF2, waveform relaxation requires solving linear systems where the system matrix, A, has two subdiagonals. For simplicity of implementation, we approximate these solves by a splitting method with iteration matrix $E = I - M^{-1}A$, where $A = M-N$ with M containing the diagonal and first subdiagonal of A and where N has only entries on the second subdiagonal, corresponding to the entries on the second subdiagonal of $-A$. Since M is bidiagonal we can apply standard cyclic reduction.

However, the use of the splitting method has a profound effect on the robustness of the waveform relaxation method with respect to the discretization grid, restricting the use of this implementation of WRMG-CR for BDF2 to a limited choice of grids. When discretizing the test problem on a regular space–time grid with spatial grid size $\varDelta x$ in both spatial dimensions and time step $\delta t$, the coefficient matrix of the linear system within waveform relaxation with cyclic reduction arising from a BDF2 time discretization depends on the parameter $\lambda = \delta t/(\varDelta x)^2$. The norm of the iteration matrix of the splitting method, E, is less than one provided that $\lambda > 1/4$. Figure 2 shows error reduction factors for the splitting method applied to a linear system with 128 unknowns for different values of $\lambda$. Results show that for values of $\lambda$ larger than 1/4, the method converges with good error reduction in all iteration steps. However, for $\lambda < 1/4$, error reduction rates are greater than one in the first iterations before convergence in later iterations. Thus, the method converges asymptotically, but one or a few iterations are not suitable for a robust approximation within the waveform relaxation method. For the BDF2 time discretization, we therefore do not include WRMG-CR in weak and strong parallel scaling studies in Sect. 4. Note that a block version of cyclic reduction can be useful to avoid this issue (see Remark at the end of Sect. 2.2).

Fig. 2

Error reduction factors per iteration for a splitting method applied to the linear system within waveform relaxation with cyclic reduction arising from a BDF2 time discretization using 128 time steps for different values of $\lambda = \delta t/(\varDelta x)^2$

3.3 Storage requirements

In all of the algorithms, we essentially solve a linear system, $Ax = b$, where the system matrix A is described by a stencil. Thus, considering a constant-coefficient setting, storage for the matrix A is negligible and we only estimate storage requirements for the solution vector. Since STMG(-BR) and WRMG require storing the whole space–time grid, whereas for MGRIT only solution values at C-points are stored, on the fine grid, this requires about $N_x^2N_t$ or $N_x^2N_t/m$ storage locations, respectively, where m denotes the positive coarsening factor in the MGRIT approach. Taking the grid hierarchy of cyclic reduction (1D multigrid in time) within WRMG into account increases the storage requirement by a factor of about two, leading to a storage requirement of about $2N_x^2N_t$ storage locations on the fine grid for WRMG-CR. In STMG(-BR) and WRMG-CR, the coarse grids are defined by coarsening by a factor of two in a spatial direction and/or in the time direction per grid level, while in MGRIT, coarsening by the factor m, only in the time direction is used. Thus, the ratio of the number of grid points from one grid level to the next coarser grid is given by two in STMG(-BR) and WRMG-CR and by m in MGRIT. This leads to a total storage requirement of about $2N_x^2N_t$ for STMG(-BR) and about $4N_x^2N_t$ (taking storage for cyclic reduction into account) for WRMG-CR. For the MGRIT approach, the total storage requirement is about $N_x^2N_t/(m-1)$.

Note that implementing STMG(-BR) and WRMG-CR as full (spatial) coarsening methods, i.e., coarsening in both spatial dimensions or in all dimensions from one grid level to the next coarser grid, instead of the implemented semicoarsening approaches, additional savings can be gained. In particular, the ratio of the number of grid points from one grid level to the next coarser grid is given by four or eight, respectively, instead of two. This reduces the total storage requirement of WRMG-CR to about $(8/3)N_x^2N_t$. The storage requirement of STMG and STMG-BR is bounded by the extreme cases of coarsening only in space or full coarsening, respectively, and coarsening only in time. Thus, implemented with full (spatial) coarsening, the total storage requirement of STMG and STMG-BR is bounded below by $(4/3)N_x^2N_t$ or $(8/7)N_x^2N_t$, respectively, and above by $2N_x^2N_t$. Assuming the initial parameter $\lambda$ is within a factor two of $\lambda _\text {crit}$, coarsening in STMG and STMG-BR alternates between semicoarsening in space or full coarsening, respectively, and semicoarsening in time, yielding an expected total storage requirement of $(10/7)N_x^2N_t$ or $(6/5)N_x^2N_t$, respectively.

3.4 Performance models

In this section, we derive performance models for estimating the parallel complexities of STMG, STMG-BR, WRMG-CR, MGRIT, and a space-parallel algorithm with sequential time stepping applied to the test problem; the resulting formulas will be discussed in Sect. 4.4. In the models, we assume that the total time of a parallel algorithm consists of two terms, one related to communication and one to computation,

$$\begin{aligned} T_\text {total} = T_\text {comm} + T_\text {comp}. \end{aligned}$$

Standard communication and computation models use the three machine-dependent parameters $\alpha , \beta ,$ and $\gamma$. The parameter $\alpha$ represents latency cost per message, $\beta$ is the inverse bandwidth cost, i.e., the cost per amount of data sent, and $\gamma$ is the flop rate of the machine. “Small” ratios $\alpha /\beta$ and $\alpha /\gamma$ represent computation-dominant machines, while “large” ratios characterize communication-dominant machines. On future architectures, the parameters are expected to be most likely in the more communication-dominant regime; a specific parameter set will be considered in Sect. 4.4. In the models, we assume that the time to access n doubles from non-local memory is

$$\begin{aligned} T_\text {comm} = \alpha + n\beta , \end{aligned}$$

(13)

and the time to perform n floating-point operations is

$$\begin{aligned} T_\text {comp} = n\gamma , \end{aligned}$$

(14)

3.4.1 STMG models

As the STMG methods employ parameter-dependent coarsening strategies, for the point-relaxation version, we derive performance models for the extreme cases of coarsening only in space and coarsening only in time. For the block-relaxation version, we model the performance only for the case of semicoarsening in time in terms of units of PFMG V(1, 1)-cycles used within relaxation. The derived model gives an upper bound for the performance of STMG-BR; including spatial coarsening in the model would go beyond the scope of this paper.

For the point-relaxation version, consider performing a two-color point relaxation, where each processor has a subgrid of size $n_x^2 \times n_t$. The time for one relaxation sweep per color can roughly be modeled as a function of the stencil size of the fine- and coarse-grid operators. Since the coarse-grid operators are formed by rediscretization, the stencil size, A ($A=6$ for BDF1 and $A=7$ for BDF2), is constant. Denoting the number of neighbors in the spatial and temporal dimensions by $A_x$ and $A_t$, respectively, the time for one relaxation sweep per color on level l ($l=0$ is finest) can be modeled as

$$\begin{aligned} T_l^{S^{(1/2)}}\approx & {} (A-1)\alpha + \left( \left( 2^{-l}n_xn_t/2\right) A_x + \left( 4^{-l}n_x^2/2\right) A_t\right) \beta \\&+ \, \left( 4^{-l}n_x^2n_t/2\right) (2A-1)\gamma , \end{aligned}$$

in the case of semicoarsening in space and as

$$\begin{aligned} T_l^{S^{(1/2)}}\approx & {} (A-1)\alpha + \left( \left( n_x2^{-l}n_t/2\right) A_x + \left( n_x^2/2\right) A_t\right) \beta \\&+\, \left( n_x^22^{-l}n_t/2\right) (2A-1)\gamma , \end{aligned}$$

in the case of semicoarsening in time. Summing over the two colors and the number of space or time levels, $L_x = \log _2(N_x)$ or $L_t = \log _2(N_t)$, respectively, yields

$$\begin{aligned} T^S_{\text {STMG}-x}\approx & {} 2(A-1)L_x\alpha + \left( 2A_xn_xn_t + (4/3)A_tn_x^2\right) \beta \\&+ \, (4/3)(2A-1)n_x^2n_t\gamma , \end{aligned}$$

in the case of semicoarsening in space and

$$\begin{aligned} T^S_{\text {STMG}-t}\approx & {} 2(A-1)L_t\alpha + \left( 2A_xn_xn_t + A_tL_tn_x^2\right) \beta \\&+ \, 2(2A-1)n_x^2n_t\gamma , \end{aligned}$$

in the case of semicoarsening in time. The time for the residual computation within the STMG algorithm is roughly the same as the time for relaxation.

The time for restriction and interpolation can be modeled as a function of the stencil size of the intergrid transfer operators, $P_x$ and $P_t$, for spatial and temporal semicoarsening, respectively. Note that interpolation and restriction in space only requires communication with neighbors in the spatial dimensions, whereas communication with neighbors in only the temporal dimension is needed in the case of temporal semicoarsening. On level l, the time for interpolation and restriction can be modeled as

$$\begin{aligned} T_l^P \approx T_l^R\approx & {} (P_x-1)\left( \alpha + 2^{-l}n_xn_t\beta \right) \\&+ \, (2P_x-1)2^{-l}n_x^2n_t\gamma /2 \end{aligned}$$

and

$$\begin{aligned} T_l^P \approx T_l^R \approx (P_t-1)\left( \alpha + n_x^2\beta \right) + (2P_t-1)2^{-l}n_x^2n_t\gamma /2, \end{aligned}$$

respectively, where the factor of 1 / 2 in the computation term is due to the fact that restriction is only computed from C-points and interpolation is only to F-points. Summing over the number of space or time levels, $2L_x$ (due to the semicoarsening implementation) or $L_t$, respectively, yields

$$\begin{aligned} T^P_{\text {STMG}-x} \approx T^R_{\text {STMG}-x}\approx & {} (P_x-1)2L_x\alpha + 2(P_x-1)n_xn_t\beta \\&+ \, (2P_x-1)n_x^2n_t\gamma , \end{aligned}$$

in the case of semicoarsening in space and

$$\begin{aligned} T^P_{\text {STMG}-t} \approx T^R_{\text {STMG}-t}\approx & {} (P_t-1)L_t\alpha + (P_t-1)L_tn_x^2\beta \\&+ \, (2P_t-1)n_x^2n_t\gamma , \end{aligned}$$

in the case of semicoarsening in time. Note that $P_x = 3$ and $P_t = 2$ in the algorithm.

The time of one $V(\nu _1, \nu _2)$-cycle of the STMG algorithm with point-wise relaxation can then be modeled as

$$\begin{aligned}&(\nu _1+\nu _2 + 1)T^S_{\text {STMG}-x} + 2T^P_{\text {STMG}-x}\\&\le T_\text {STMG} \le (\nu _1+\nu _2 + 1)T^S_{\text {STMG}-t} + 2T^P_{\text {STMG}-t}. \end{aligned}$$

For the block-relaxation version, the time for one relaxation sweep on level l can be modeled as

$$\begin{aligned} T_l^S \approx T_l^\text {res} + 2^{-l}n_tT_\text {PFMG}, \end{aligned}$$

where $T_l^\text {res}$ denotes the time for the residual computation and $T_\text {PFMG}$ is the time for one PFMG V(1, 1)-cycle. Summing over the number of time levels, $L_t$, yields

$$\begin{aligned} T^S_{\text {STMG-BR}-t} \approx T^S_{\text {STMG}-t} + 2n_t T_\text {PFMG}, \end{aligned}$$

where we make use of the facts that the residual computation is the same as in the point-relaxation version and that the time for the residual computation is roughly the same as the time for point-relaxation. Using the interpolation and restriction models derived above, the time of one $V(\nu _1,\nu _2)$-cycle of the STMG-BR algorithm can then be modeled as

$$\begin{aligned} T_\text {STMG-BR} \le 3T^S_{\text {STMG}-t} + (\nu _1+\nu _2)2n_tT_\text {PFMG} + 2T^P_{\text {STMG}-t}. \end{aligned}$$

3.4.2 WRMG-CR model

The main difference between WRMG-CR and STMG with coarsening only in space is the smoother. The STMG algorithm uses point smoothing, whereas WRMG-CR uses (time-) line relaxation on a spatial subdomain. Consider performing a two-color waveform relaxation where each processor has a subgrid of size $\sigma _xn_x^2 \times n_t, ~0 < \sigma _x \le 1$. In one sweep of a two-color waveform relaxation, for each color, a processor must calculate the right-hand side for the line solves and perform the line solves (i.e., solving a bidiagonal linear system as described in Remark 3 in Sect. 3.2) using cyclic reduction. Modeling the cyclic reduction algorithm as a 1D multigrid method requires two communications and six floating-point operations per half the number of points per grid level. Summing over the number of cyclic reduction levels, $L_t = \log _2(N_t)$, the time of the line solves within waveform relaxation can be modeled as

$$\begin{aligned} T_\text {CR}(\sigma _x) \approx 2L_t\alpha + 2L_t\sigma _xn_x^2\beta + 6\sigma _xn_x^2n_t\gamma . \end{aligned}$$

Calculating the right-hand side for the line solves requires communications with $A_x$ neighbors in space and $A_t$ neighbors in time, where $A_x + A_t = A-2$ with A denoting the (constant) stencil size of the fine- and coarse-grid operators. Note that we consider a 2-point stencil for the cyclic reduction solves. The time for one two-color waveform relaxation sweep on level l can then roughly be modeled as

$$\begin{aligned} T_l^S\approx & {} 2(A_x+A_t)\alpha + \left( 2^{-l}n_xn_tA_x + 4^{-l}n_x^2A_t\right) \beta \\&+ \, 4^{-l}n_x^2n_t\cdot 2(A_x+A_t)\gamma + 2T_\text {CR}(2^{-2l-1}). \end{aligned}$$

Summing over the number of grid levels, $L_x = \log _2(N_x)$, yields

$$\begin{aligned} T^S_\text {WRMG}\approx & {} 2(A_x+A_t)L_x\alpha + \left( 2A_xn_xn_t+(4/3)A_tn_x^2\right) \beta \\&+ \, (4/3)2(A_x+A_t)n_x^2n_t\gamma + \sum \limits _{l=0}^{L_x}2T_\text {CR}(2^{-2l-1})\\\approx & {} 2(A_x+A_t+2L_t)L_x\alpha \\&+ \, \left( 2A_xn_xn_t+(4/3)(A_t+2L_t)n_x^2\right) \beta \\&+ \, (8/3)(A_x+A_t+3)n_x^2n_t\gamma . \end{aligned}$$

The time for the residual computation, interpolation, and restriction is the same as these times within the STMG algorithm with semicoarsening only in space and, thus, the time of one $V(\nu _1,\nu _2)$-cycle of WRMG-CR can be modeled as

$$\begin{aligned} T_\text {WRMG} \approx (\nu _1+\nu _2)T^S_\text {WRMG} + T^S_{\text {STMG}-x} + 2T^P_{\text {STMG}-x}. \end{aligned}$$

3.4.3 MGRIT model

Due to the non-intrusive approach of the MGRIT algorithm, it is natural to derive performance models in terms of units of spatial solves [13]. A full parallel performance model based on the standard communication and computation models (13) and (14) can then be easily developed for a given solver. Assuming that PFMG V(1, 1)-cycles are used for the spatial solves, such a model was derived in [13] which is generalized for a BDF-k time discretization method as follows: Consider solving the spatial problems within relaxation and restriction on the finest grid to high accuracy requiring $\nu _x^{(0)}$ PFMG iterations. Spatial solves within relaxation and restriction on coarse grids as well as within interpolation on all grids are approximated by $\nu _x^{(l)}$ PFMG iterations. Furthermore, assume that each processor has a subgrid of size $n_x^2\times n_t$. Since restriction and interpolation correspond to C- or F-relaxation, respectively, the time per processor for the spatial solves can be approximately modeled as

$$\begin{aligned}&\left( k\cdot 2\nu _x^{(0)} + \frac{k\nu _x^{(l)}(m+1)}{(m-1)}\right) n_tT_\text {PFMG}\\&\quad + \, \frac{2k^2(3m-1)}{(m-1)}n_tn_x^2\gamma , \end{aligned}$$

where $m>0$ denotes the coarsening factor, $T_\text {PFMG}$ is the time of one PFMG V(1, 1)-cycle and the $\gamma$-term represents the time for computing the right-hand side of the spatial problems. Each F- or C- relaxation sweep requires at most one parallel communication of the local spatial problem (of size $kn_x^2$) and, thus, the time of one V(1, 0)-cycle of MGRIT is given by

$$\begin{aligned} T_\text {MGRIT}\approx & {} 5L_t(\alpha + kn_x^2\beta )\\&+ \, \left( k\cdot 2\nu _x^{(0)} + \frac{k\nu _x^{(l)}(m+1)}{(m-1)}\right) n_tT_\text {PFMG}\\&+ \, \frac{2k^2(3m-1)}{(m-1)}n_tn_x^2\gamma , \end{aligned}$$

where $L_t = \log _m(N_t)$ denotes the number of time levels in the MGRIT hierarchy.

3.4.4 Time-stepping model

Sequential time stepping requires computing the right-hand side of the spatial problem and solving the spatial problem at each time step. Thus, the time for sequential time stepping can be modeled as

$$\begin{aligned} T_\text {ts} \approx N_t\left( \nu _x^{(\text {ts})}T_\text {PFMG} + 2kn_x^2\gamma \right) , \end{aligned}$$

where $\nu _x^{(\text {ts})}$ is the number of PFMG iterations for one spatial solve.

4 Parallel results

In this section, we consider weak and strong parallel scaling properties of the three multigrid methods. Furthermore, we are interested in the benefit of the methods compared to sequential time stepping. We apply the three multigrid methods and a parallel algorithm with sequential time stepping to the test problem on the space–time domain $[0,\pi ]^2\times [0,T]$. On the finest grid of all methods, the initial condition is used as the initial guess for $t=0$, and a random initial guess for all other times to ensure that we do not use any knowledge of the right-hand side that could affect convergence. Furthermore, in the case of BDF2 for the time discretization, we use the discrete solution of the BDF1 scheme for the first time step $t=\delta t$. Coarsening in STMG is performed until a grid consisting of only one variable is reached or until a grid with one time step is reached when considering the block-relaxation version; semicoarsening in WRMG-CR and MGRIT stops at three points in each spatial dimension or three time steps, respectively. The convergence tolerance is based on the absolute space–time residual norm and chosen to be $10^{-6}$, measured in the discrete $L_2$-norm unless otherwise specified. We have checked that, for all algorithms, the fixed space–time residual norm for our stopping criterion is sufficient to achieve discretization error for the problems that we consider.

Numerical results in this section are generated on Vulcan, a Blue Gene/Q system at Lawrence Livermore National Laboratory consisting of 24,576 nodes, with sixteen 1.6 GHz PowerPC A2 cores per node and a 5D Torus interconnect.

Notation The space–time grid size and the final time, T, of the time interval uniquely define the step sizes of the discretization using the relationships $\varDelta x = \varDelta y = \pi /N_x$ and $\delta t = T/N_t$. To facilitate readability, only the space–time grid size and final time are specified in the caption of tables and figures, and the following labels are used

FirstOrder2D($\varvec{T=\cdot }$):

test problem with BDF1 time discretization;

SecondOrder2D($\varvec{T=\cdot }$):

test problem with BDF2 time discretization.

4.1 Challenges of a fair comparison

Having implemented STMG, STMG-BR, and WRMG-CR in hypre and MGRIT using XBraid and hypre ensures a similar implementation complexity as all implementations use C and Message Passing Interface (MPI). However, even with this basis, several parameter spaces of both the algorithms themselves and the parallelization make a fair comparison of the three methods challenging. In terms of algorithmic parameters, many choices must be made for each method such as the type of multigrid cycling scheme (e.g., V-cycle vs. F-cycle), the coarsening strategy (e.g., the choice of the parameter, $\lambda _\text {crit}$, determining the coarsening direction in the STMG approaches or the coarsening factor, m, in the MGRIT algorithm), and the relaxation scheme (e.g., the number of pre- and post-relaxation steps in STMG, STMG-BR, and WRMG-CR or the solver and accuracy for the spatial problems of the time integrator, $\varPhi$, in MGRIT). Additionally, for the parallel implementation, the number of processors and their arrangement on a processor grid, i.e., the amount of parallelism in each direction, must be chosen. Since the processor distribution determines the ratio of computation vs. communication on and across processors, one arrangement of the processors can lead to completely different parallel performance than another arrangement. Note that the processor distribution can be restricted by memory requirements of the algorithms.

There is, of course, a very large parameter space for each of these algorithms, considering V-, F-, and W-cycle variants, number of relaxation sweeps, and so forth. In this study, we consider a subset of these possibilities, informed based on experiences with these algorithms reported in the literature, the need for finite effort within implementation, and general practice and experience with multigrid in a parallel environment. Thus, we consider only V-cycle algorithms, known to offer better parallel scaling than F- or W-cycles, even though it is known that F-cycles are needed for algorithmic scalability of STMG [26]. To ensure convergence of WRMG-CR using the splitting method within relaxation in the case of BDF2 for the time discretization, the parameter $\lambda = \delta t/(\varDelta x)^2$ must be greater than 1/4 on all grid levels where relaxation is performed (see Remark 3 in Sect. 3.2). Since only the spatial grid size, $\varDelta x$, increases by a factor of two per grid level in the multigrid hierarchy, $\lambda$ decreases by a factor of four per grid level. As a consequence, the implementation of WRMG-CR using the splitting method within relaxation is not suitable for meaningful strong and weak parallel scaling studies. Consider, for example, the test problem SecondOrder2D $(T=4\pi )$, discretized on a $65^2\times 65$ space–time grid. Then, $\lambda$ is greater than 1/4 on all grid levels where relaxation is performed. In Fig. 3, we plot the accuracy of the approximation, $\max _i\left||e_i \right||$, i.e., the maximum of the errors to the discrete solution of SecondOrder2D $(T=4\pi )$ at each time step, measured in the discrete $L_2$-norm as a function of the compute time. The linear-log scaling of the axes shows typical multigrid convergence. However, if we were to use this example for a proper domain-refinement weak scaling study, on 8 processors (i.e., consistent refinement by a factor of two in each dimension), we have to consider a uniform grid of $\varDelta x = \varDelta y = \pi /128$ and 129 points in time. Then, the condition on $\lambda$ is not fulfilled on all grid levels in the multigrid hierarchy where relaxation is performed and, thus, one iteration of the splitting method within relaxation is not sufficient for convergence. Instead, for V(1, 1)-cycles for example, we need 30 iterations of the splitting method to get reasonable convergence, which is prohibitively costly. For the BDF2 time discretization, we therefore do not include WRMG-CR in weak and strong parallel scaling studies. The block-relaxation version of STMG is also included only for the BDF1 time discretization to match one of the settings of [17] as close as possible with the setting of this paper.

Fig. 3

Accuracy of the approximation to the solution of SecondOrder2D $(T=4\pi )$ on a $65^2\times 65$ space–time grid using WRMG-CR V(1, 1)- and V(2, 1)-cycles and using one iteration of the splitting method within relaxation on a single processor; each open diamond and filled diamond represents one iteration of the V(1, 1)- or V(2, 1)-scheme, respectively

4.2 Weak parallel scaling

We apply several variants of the three multigrid schemes to the test problem. For both time discretization schemes, we look at computation time and iteration counts to demonstrate good parallel scaling. In Sect. 4.3, a subset of this set of variants is then considered for the comparison to sequential time stepping.

Fig. 4

Weak parallel scaling: time to solve FirstOrder2D $(T=\pi ^2/64)$ (top), FirstOrder2D $(T=\pi ^2/32)$ (bottom left), and FirstOrder2D $(T=\pi ^2/128)$ (bottom right) using STMG, WRMG, and MGRIT variants; MGRIT-SC indicates MGRIT with spatial coarsening. The problem size per processor is about $129^2 \times 257$ (top), $65^2 \times 129$ (bottom left) or $129^3$ (bottom right)

Figure 4 shows weak parallel scaling results for several multigrid variants applied to the test problem with BDF1 time discretization on various space–time domains. For the test problem on the space–time domain $[0,\pi ]^2\times [0,\pi ^2/64]$ shown at the top of the figure, for example, the problem size per processor is fixed at (roughly) 129 points in each spatial direction and 257 points in the temporal direction. For proper domain-refinement, we quadruple the number of points in time when doubling the number of points in space. Thus, on one processor, we use a uniform grid of $\varDelta x = \varDelta y = \pi /128$ and 257 points in time while, on 4096 processors, we use a uniform grid of $\varDelta x = \varDelta y = \pi /1024$ and 16,385 points in time; in the bottom row of Fig. 4, domain-refinements of different space–time domains are considered. Note that due to the large memory requirements of our implementation of STMG-BR, we were not able to run the larger weak scaling study at the top of Fig. 4 on our current parallel machine. Shown are results for STMG and WRMG-CR variants with one pre- and one post-smoothing step and with two pre- and one post-smoothing step, as well as STMG-BR with two pre- and two post-smoothing steps. The parameter $\lambda _\text {crit}$ determining the coarsening direction in STMG is chosen to be $\lambda _\text {crit} = 0.6$ or $\lambda _\text {crit} = \sqrt{2}/3$ in the block-relaxation version based on the Fourier analysis results in [17, 26]. Here, $\lambda = 1$ on the finest grid for all three space–time domains, so semicoarsening in space or full space–time coarsening is chosen in STMG or STMG-BR, respectively, to define the first coarse grid. Thus, considering (roughly) 65 points in each spatial dimension and 129 points in the temporal direction on one processor, for example, the space–time grid on the first coarse level consists of (roughly) 33 points in each spatial direction and 129 points in the temporal direction for both STMG and WRMG-CR and (roughly) 33 points in each spatial direction and 65 points in the temporal direction when using STMG-BR; coarse-grid operators are based on rediscretization. For MGRIT, we consider standard FCF-relaxation and a non-uniform coarsening strategy in the temporal direction that coarsens by factors of 16 until fewer than 16 temporal points are left on each processor, then coarsens by factors of 2; details of the benefits of this coarsening strategy are described in [13]. On one processor and a space–time grid (roughly) of size $65^2 \times 129$, for example, the space–time grid on the first coarse level is (roughly) of size $65^2\times 9$. Furthermore, we limit computational work of the spatial solves by limiting the number of PFMG iterations on the fine grid to a maximum of 9 iterations and to a maximum of 2 iterations on coarse grids. Additionally, we consider MGRIT with spatial coarsening, denoted MGRIT-SC in the figure, with space-coarsening using standard bilinear interpolation and restriction operators performed on grid levels with CFL-number $\delta t/(\varDelta x)^2 > 2$. The spatial coarsening thus balances the temporal coarsening. On the first coarse grid, each spatial dimension is coarsened by a factor of four to match the factor of 16 temporal coarsening, yielding a per processor problem size of $17^2 \times 9$ for the above example.

The time curves in Fig. 4 show good parallel scaling for all methods. More precisely, in the weak scaling study shown at the top of the figure, the overall compute time of both STMG variants and MGRIT with spatial coarsening increases by a factor of about 1.3 over 4096-way parallelism, by a factor of about 1.6 when using MGRIT without spatial coarsening and by a factor of about 1.8 for both WRMG-CR variants. Comparing the total time-to-solution of the different approaches with one another, in all three scaling studies, the point-wise version of STMG is fastest, followed by the WRMG-CR variants which are about a factor of two to three times slower. For STMG-BR and the two MGRIT variants, runtimes behave differently in the different weak parallel scaling studies. Interestingly, STMG-BR is slower than MGRIT-SC in the $129^3$ case, but faster than both MGRIT variants for the $65^2 \times 129$ case. We believe that this is because communication costs dominate for these relatively small per processor spatial problem sizes. Given the exceptionally fast MGRIT space–time coarsening factor (256 on the first level), this likely makes MGRIT-SC significantly more communication bound on coarse levels than STMG-BR, which has an overall initial coarsening factor of eight. Thus, MGRIT-SC may be able to better “hide” the extra operations needed for the larger problem size and thus enjoy a scaling advantage over STMG-BR when moving between these two problem sizes.

Table 1 details the results of the weak scaling study on the top in Fig. 4 with timings split up into timings of the setup and solve phases of the algorithms. While the timings of the solve phase show good parallel scaling for all methods with only a slight increase for larger processor counts, due to the increase in the number of multigrid levels and corresponding communication latency costs, this is not the case for the timings of the setup phase. For MGRIT, the setup time is about constant across the number of processors and negligible compared to the solve time. However, for STMG and particularly for WRMG-CR, setup times increase with the number of processors. This is a known implementation inefficiency in hypre that is expected to be fixed at some point in the future and does not need further exploration here, in particular because the added time does not greatly change the overall comparison between these approaches. Results further show that iteration counts are largely independent of the problem size.

Table 1 Weak parallel scaling: setup and solve times and number of iterations for solving FirstOrder2D $(T=\pi ^2/64)$ using STMG, WRMG, and MGRIT variants. The problem size per processor is about $129^{2} \times 257$

The situation is a bit different for the BDF2 time discretization. Table 2 shows weak scaling results for solving SecondOrder2D $(T=2\pi -\delta t)$ using STMG and MGRIT with timings split up into setup and solve times as well as iteration counts. Note that considering a second-order time discretization, matching the accuracy of the spatial discretization, for proper weak scaling we increase the number of processors by factors of eight, as opposed to factors of 16 in the one-step case considered in Fig. 4. Here, on one processor, we use a uniform grid of $\varDelta x = \varDelta y = \pi /128$ and 257 points in time while, on 4096 processors, we use a uniform grid of $\varDelta x = \varDelta y = \pi /1024$ and 2049 points in time. We consider STMG V-cycles with two pre- and one post-smoothing step and parameter $\lambda _\text {crit} = 0.555$; V(1, 1)-cycles do not show reasonable convergence. For MGRIT, V-cycles with FCF-relaxation and the non-uniform coarsening strategy described above are used. We limit the computational cost of the spatial solves to at most 9 PFMG iterations on the fine grid and to at most 4 iterations on all coarse grids. Note that the spatial problems are more difficult to solve than in the one-step case since on the finest grid, the time-step size is of the same order as the spatial grid size and, thus, a higher accuracy of the spatial solves on coarse grids is needed. Additional spatial coarsening in MGRIT is not considered as the CFL-number stays balanced. Table 2 shows that for MGRIT, compute times increase in the beginning but stagnate at higher processor counts. Although stagnation is observed at larger processor counts than in the one-step case, the overall compute time increases by a factor of about 1.6 (the same as in the one-step case) over 4096-way parallelism. Furthermore, Table 2 shows that iteration counts are again independent of the problem size.

Table 2 Weak parallel scaling: setup and solve times and number of iterations for solving SecondOrder2D $(T=2\pi -\delta t)$ using STMG and MGRIT. The problem size per processor is about $129^2 \times 257$

For the STMG method, however, compute times increase by a factor of about 2.4 over 4096-way parallelism and iteration counts do not appear to be perfectly bounded independently of the problem size. The increase in iteration counts indicates that the implementation is not robust with respect to the discretization grid which is consistent with results in [26]. For a robust implementation, F-cycles have to be considered; however, this implementation effort would go beyond the scope of this paper and the factor of 1.5 in iterations with V-cycles almost certainly outweighs the worse parallel scalability expected to be seen with F-cycles.

4.3 Strong parallel scaling

The above results show that the three multigrid methods obtain good weak parallel scalability, particularly for the BDF1 time discretization. Now, we focus on the performance of these methods compared with one another and to traditional space-parallel algorithms with sequential time stepping.

Figure 5 shows compute times for solving FirstOrder2D $(T=\pi ^2)$ on a $128^2\times 16{,}384$ space–time grid using a subset of the set of STMG, STMG-BR, WRMG-CR, and MGRIT variants considered in the weak parallel scaling study in Fig. 4 and a space-parallel algorithm with sequential time stepping. For the time-stepping approach, the spatial domain is distributed evenly such that each processor’s subdomain is approximately a square in space. When using 16 processors, for example, each processor owns a square of approximately $32 \times 32$. Since considering 16 processors for distributing the spatial domain appears to be an efficient use of computational resources with respect to benefits in runtime, for the space–time approaches, we parallelize over 16 processors in the spatial dimensions, with increasing numbers of processors in the temporal dimension. That is, with $P_t$ denoting the number of processors used for temporal parallelism, the space–time domain is distributed across $16P_t$ processors such that each processor owns a space–time hypercube of approximately $32^2 \times 16{,}384/P_t$. Note that due to the storage requirements of STMG, STMG-BR, and WRMG-CR, at least eight processors for temporal parallelism must be used in order to avoid memory issues in the given parallel computational environment. For MGRIT, even $P_t = 1$ would be possible, but the required compute time is much larger than for any of the other methods, due to the computational overhead inherent in the MGRIT approach; thus, Fig. 5 only presents results for MGRIT with $P_t \ge 4$. Additionally, since on the one hand, the spatial problem size of $128^2$ points is reasonably small in terms of storage requirements and, on the other hand, the number of time steps is sufficiently large, we also include results for the methods with time-only parallelism (dashed lines in Fig. 5).

Results demonstrate the large computational overhead of the MGRIT approach in contrast with STMG, WRMG-CR, and traditional time stepping. However, this extra work can be effectively parallelized at very large scales with excellent strong parallel scalability. While on smaller numbers of processors, MGRIT is slower than time stepping we see good speedup at higher processor counts particularly when considering space–time parallelism. For example, considering 64 processors, the space-parallel algorithm with sequential time stepping is faster than the space-time-concurrent MGRIT algorithm by a factor of about nine or by a factor of about seven when considering MGRIT with spatial coarsening. Increasing the number of processors to 16,384, however, MGRIT is faster with a speedup of up to a factor of about 30 compared to sequential time stepping with 16 processors used for spatial parallelism. The benefit of using MGRIT over the time stepping approach can be extended to include benefit at smaller processor counts by changing the space–time processor decomposition. For example, considering 64 processors, time stepping with space-only parallelism is fastest, but the factor in comparison with MGRIT can be decreased from nine or seven when considering MGRIT without or with spatial coarsening, respectively, to a factor of about 1.6 or 1.2, respectively, when using MGRIT with time-only parallelism. Thus, for this problem, changing from space–time concurrency to time-only parallelism in the MGRIT algorithm leads to faster runtimes by up to a factor of 5.8. At 1024 processors, time-parallel MGRIT without or with spatial coarsening is faster with a speedup of a factor of about 8.5 or 16 compared to 16-way space-parallel time stepping. However, the scalability of MGRIT with time-only parallelism is limited by the temporal problem size, analogously to the limits placed by the spatial problem size on sequential time stepping. Here, for 1024-way temporal parallelism, the number of time steps per processor is 16 corresponding to the coarsening factor and, thus, time-parallel MGRIT has exhausted the available temporal parallelism and cannot scale to a larger number of processors. Changing the coarsening factor from 16 to two allows pushing the scalability limit to larger processor counts and leads to a speedup of up to a factor of about 53. Note, however, that this algorithmic choice should only be made for MGRIT with spatial coarsening since the cost of solving the spatial problems of the time integrator, $\varPhi$, in the MGRIT algorithm dominates for small numbers of local time steps arising at high levels of temporal parallelism.

Fig. 5

Strong parallel scaling: total time to solve FirstOrder2D $(T=\pi ^2)$ on a $128^2\times 16{,}384$ space–time grid using space-parallel time-stepping, STMG, STMG-BR, WRMG-CR, and MGRIT. Solid lines are results for space–time concurrent runs and dashed lines represent runtimes for time-only parallelism

With STMG and WRMG-CR, we can benefit over the time stepping approach at even smaller scales. Considering 128 processors, i.e., adding eight-way temporal parallelism to 16-way spatial parallelism, STMG is already faster than 16-way space-parallel time stepping, with a speedup of a factor of about seven. For WRMG-CR, the speedup is about a factor of two. Using all 128 processors for temporal parallelism leads to faster runtimes, with a speedup of a factor of about 11 for STMG and of four for WRMG-CR. Increasing the number of processors to 16,384 results in a speedup, measured relative to the time for time stepping with 16-way spatial parallelism, of up to a factor of 33 for WRMG-CR and of 325 for STMG. Scaling properties of the two approaches are excellent at the beginning, with poorer scaling at larger processor counts, especially for time-only parallelism and for the WRMG-CR method. For higher levels of temporal parallelism, the number of time steps per processor is small and cyclic reduction becomes problematic which can be explained by the performance models developed in Sect. 3.4, as will be discussed in Sect. 4.4. For the block-relaxation version of STMG, compute times have very similar qualitative properties as STMG with point relaxation, but quantitatively, the block-relaxation version differs significantly from the point-relaxation version with slower runtimes of a factor of about seven when considering space–time concurrency and of about six for time-only parallelism. Considering 128 processors, space–time parallel STMG-BR is about as fast as 16-way space-parallel time stepping while with time-only parallelism STMG-BR is already twice as fast as space-parallel time stepping. Increasing the number of processors to 16,384 results in a speedup of up to a factor of about 53. Furthermore, note that for this problem, runtimes of MGRIT with spatial coarsening and factor-2 coarsening in time are similar to those of STMG with block relaxation when considering time-only parallelism underlining the similarities of the two approaches.

Figure 6 details “effective” parallel efficiencies, i.e., parallel efficiencies relative to sequential time stepping on a single processor, for the space-time-parallel variant of each time-integration approach considered in Fig. 5 as well as for STMG-BR and MGRIT with time-only parallelism. For both STMG variants, the numbers are very steady out to 2048 cores, and then despite modest degradation, better than the other methods for large processor counts out to 16K processors. For WRMG-CR, the numbers are less steady, but still acceptable relative to time-stepping. For space-time-concurrent MGRIT, the effective efficiencies are small, but almost perfectly steady out to 16K cores, demonstrating its excellent strong scaling. Effective efficiencies of MGRIT with time-only parallelism are higher for small processor counts, but demonstrate the scalability limit when temporal parallelism has been exhausted.

Fig. 6

Strong scaling efficiencies of sequential time-stepping, STMG, STMG-BR, WRMG-CR, and MGRIT applied to FirstOrder2D $(T=\pi ^2)$ on a $128^2\times 16{,}384$ space–time grid. For each method, parallel efficiency is measured relative to time stepping on a single processor as $T (1)/(P\cdot T(P))\cdot 100$, where T(P) is the wall-clock time required for solution on P processors

In the case of the BDF2 time discretization, compute times have very similar qualitative properties. Figure 7 shows compute times of a space-parallel algorithm with sequential time stepping, as well as the STMG and MGRIT variants considered in Fig. 4 applied to SecondOrder2D $(T=4\pi -\pi /512)$ on a space–time grid of size $513^2\times 4096$. Here, for STMG and MGRIT, we consider adding temporal parallelism to two different levels of spatial parallelism, i.e., we look at using 64 and 256 processors for distributing the spatial domain. If we denote the number of processors used for temporal parallelism in the two multigrid schemes by $P_t$, when using 64-way parallelism in space, the space–time domain is distributed across $64P_t$ processors such that each processor owns a space–time hypercube of approximately $64^2\times 4096/P_t$. Analogously, considering 256-way parallelism in space, the space–time domain is distributed across $256P_t$ processors such that each processor owns a space–time hypercube of approximately $32^2\times 4096/P_t$. The time curves show that the crossover point for which it becomes beneficial to use MGRIT for this particular problem and the speedup compared to time stepping at large processor counts depends on the levels of spatial and temporal parallelism. More precisely, for this particular problem, for MGRIT to break even with sequential time stepping using a fixed level of spatial parallelism, we need to add about 16-way parallelism in time. For 64-way parallelism in space, for example, we need about 1024 processors for MGRIT to break even with sequential time stepping. Increasing the number of processors to 8192 results in a speedup of a factor of seven compared to sequential time stepping with 64-way parallelism. A similar comparison can be made for 256-way parallelism in space. Note that for MGRIT with 64-way parallelism in space and 8192 processors in total, the number of time-step pairs per processors is 16 corresponding to the coarsening factor and, thus, further increasing the number of processors is not beneficial.

Fig. 7

Strong parallel scaling: time to solve SecondOrder2D $(T=4\pi -\pi /512)$ on a $513^2 \times 4096$ space–time grid using sequential time-stepping, STMG, and MGRIT

The dependency of compute times on the levels of spatial and temporal parallelism is not as pronounced in the STMG approach as in the MGRIT approach. While for smaller numbers of processors it is slightly beneficial to use fewer processors for spatial parallelism, on larger processor counts compute times of both variants are very similar. Comparing to the space-parallel algorithm with sequential time stepping, the maximum speedup of STMG is about a factor of 15 larger than that of MGRIT.

Figure 8 details “effective” parallel efficiencies, i.e., parallel efficiencies relative to sequential time stepping on a single processor, for the time-integration approaches considered in Fig. 7. For both STMG and MGRIT, numbers are about steady out to large processor counts. Comparing the two multigrid approaches, the difference in effective parallel efficiencies diminishes when going from the BDF1 to the BDF2 time discretization. More precisely, while in Fig. 6, efficiencies for STMG are between 15 and 40% and for MGRIT about 1%, in Fig. 8, efficiencies for STMG are between 11 and 16% and for MGRIT between 1 and 3%.

Fig. 8

Strong scaling efficiencies of sequential time-stepping, STMG, and MGRIT applied to SecondOrder2D $(T=4\pi -\pi /512)$ on a $513^2 \times 4096$ space–time grid. For each method, parallel efficiency is measured relative to time stepping on a single processor as $T (1)/(P\cdot T(P))\cdot 100$, where T(P) is the wall-clock time required for solution on P processors

4.4 Insights from the parallel models

The above results demonstrate that the two intrusive approaches show somewhat poorer parallel scalability than the MGRIT algorithm. To better understand the parallel scalability, we use the models developed in Sect. 3.4. Based on data in [15, Table 2], we choose the set of machine parameters given by

$$\begin{aligned} \alpha = 1 ~\mu s, ~\beta = 0.74 \text { ns/double}, ~\gamma = 0.15 \text { ns/flop}, \end{aligned}$$

(15)

characterizing a modern communication-dominant machine. To define the parameter set, we have set $\alpha = 1 ~\mu s$ and chosen $\beta$ and $\gamma$ such that the ratios $\alpha /\beta$ and $\alpha /\gamma$ are equal to the maximum ratios from [15, Table 2]. Figure 9 shows predicted times to solve FirstOrder2D $(T=\pi ^2)$ on a $128^2\times 16{,}384$ space–time grid using sequential time stepping, STMG, STMG-BR, WRMG-CR, and MGRIT. The parameters in the models are chosen as in the strong parallel scaling study in Fig. 5. Note that for STMG, models for the extreme cases of coarsening only in space and of coarsening only in time are used and that for STMG-BR, only the semicoarsening in time case is modeled. Results show that predicted time curves behave qualitatively very similar to experimentally measured runtimes depicted in Fig. 5.

Fig. 9

Predicted times to solve FirstOrder2D $(T=\pi ^2)$ on a $128^2\times 16{,}384$ space–time grid using sequential time-stepping, STMG, WRMG-CR, and MGRIT

The models also explain the somewhat poorer parallel scalability of STMG and WRMG-CR at higher processor counts in this specific parallel scaling study. For WRMG-CR, cyclic reduction becomes problematic introducing an additional logarithmic factor in the communication cost. More precisely, assuming that the space–time grid of size $N_x^2\times N_t$ is distributed evenly such that each processor’s subdomain is approximately of size $n_x^2\times n_t$, the $\beta$-term in the WRMG-CR-model of $\nu _\text {WRMG}$ $V(\nu _1,\nu _2)$-cycles is given by

$$\begin{aligned} T_\beta ^{(\text {WRMG})}&\approx \nu _\text {WRMG}\left[ 8(\nu _1+\nu _2+(5/2))n_xn_t\right. \\&\quad + \, (4/3)((2\log _2(N_t)+1)\\&\left. (\nu _1+\nu _2)+1)n_x^2\right] \beta . \end{aligned}$$

If we fix $n_x$ as in the strong scaling study of the numerical experiment, the second term is constant and becomes dominant as $n_t$ decreases. Thus, we expect poorer scalability when

$$\begin{aligned} n_t < \frac{\left( (2\log _2(N_t)+1)(\nu _1+\nu _2)+1\right) }{8\left( \nu _1+\nu _2+(5/2)\right) }n_x. \end{aligned}$$

For the problem considered in Figs. 5 and 9 and one pre- and one postrelaxation sweep within WRMG-CR, the $\beta$-term causes loss in parallel scalability for $n_t < 2.19n_x$, which is the case for about 4096 processors and higher processor counts. The loss in parallel scalability for STMG at higher numbers of processors when fixing $n_x$ can be similarly explained by considering the $\beta$-term in the STMG model with temporal semicoarsening.

Having validated the models with experimental data, we now use the models for estimating the parallel scalability of the four time integration approaches on modern large-scale machines. In the models, we assume a communication-dominant environment with machine parameters given in (15). We consider a domain refinement of the problem in Figs. 5 and 9, i.e., we consider solving FirstOrder2D $(T=\pi ^2)$ on a space–time grid of size $1024^2\times 131{,}072$ instead of on a $128^2\times 16{,}384$ space–time grid. Analogously to the numerical experiment, for the space-parallel algorithm with sequential time stepping, we assume that the spatial domain is evenly distributed such that each processor holds approximately a square in space. For the space-parallel multigrid approaches, we add temporal parallelism to 64-way spatial parallelism, as 64 processors are effectively utilized in the time-stepping approach.

Figure 10 shows expected parallel scaling for solving FirstOrder2D $(T=\pi ^2)$ on a $1024^2\times 131{,}072$ space–time grid using the four time-integration approaches. The models indicate a similar scaling behavior on large numbers of processors as seen in numerical experiments at small scale. We note that the expected good parallel scalability of the three space-time-concurrent multigrid approaches partially relies on the assumption of large communication-to-computation ratios on modern large-scale computers.

Fig. 10

Predicted times to solve FirstOrder2D $(T=\pi ^2)$ on a $1024^2\times 131{,}072$ space–time grid using sequential time-stepping, STMG, WRMG-CR, and MGRIT

4.5 Potential improvements to XBraid

The purpose of this paper is to compare WRMG, STMG, and MGRIT, as implemented in their “pure” forms, i.e., to compare the three parallel-in-time strategies that (1) only semicoarsen in space, (2) only semicoarsen in time and (3) coarsen in both space and time. Not surprisingly, the most efficient solution is to coarsen in both space and time (STMG). The slowest (at least for many problem sizes) is to coarsen only in time (MGRIT).

To address this, current research in the XBraid project is considering approaches for incorporating aspects of STMG into XBraid. This will allow XBraid to be more intrusive, but to also achieve efficiencies closer to those of STMG. The ultimate goal is to allow the user to choose the level of intrusiveness that his/her application can tolerate, and to enjoy the maximum benefit of time parallelism for that application. In other words, the more intrusive the chosen parallel-in-time implementation, the better the potential speedup.

One such improvement is faster residual computations. The computation of the residual from (6) requires a matrix inversion for the application of $\varPhi _{\delta t}$ at every time point. In other words, the computation of the residual is as expensive (in terms of FLOPS) as the entire traditional time-stepping approach. The alternative used by STMG is to form the residual based on the matrix stencil $[ -I \quad \varPhi _{\delta t}^{-1} ]$ rather than the MGRIT stencil $[ -\varPhi _{\delta t} \quad I]$. Note that here the matrix $\varPhi _{\delta t}^{-1}$ is sparse and relatively cheap to evaluate, and as such, this alternate residual has the potential to save significant compute and messaging time. Taking the largest test case for $P=4096$ from Table 1, for example, the time spent computing residuals in MGRIT is 21 s out of the total time of 172 s. This change would largely eliminate this cost.

Another example improvement is to allow for variable storage in XBraid. Allowing for storage at every time point allows for user-implemented point-wise relaxation, as in STMG. Current F(CF)-relaxation involves expensive matrix inversions and therefore, cheap point-wise relaxation could offer similar speedups as those available from faster residual computations. Lastly, full storage of every time point would allow for improved initial guesses to the (non)linear solvers called by implicit methods.

5 Conclusion

Current trends in computer architectures leading towards systems with more, but not faster processors, induce a change in the development of algorithms for evolutionary problems. Instead of exploiting increasing clock speeds, faster time-to-solution must come from increasing concurrency, driving the development of algorithms with space–time concurrency. Motivated by this development, the comparison of three multigrid methods with space–time concurrency, STMG(-BR), WRMG-CR, and MGRIT, is considered.

Parallel results show that all three multigrid methods with space–time concurrency considered in this paper are effective solvers for diffusion problems. In the case where many more processors are available than can be effectively utilized by sequential time-stepping, performance of all multigrid methods with space–time concurrency is better than that of space-parallel time stepping. However, the crossover point at which it becomes beneficial to use one of the three multigrid methods differs significantly. While the invasive STMG and WRMG-CR approaches are already faster than space-parallel time stepping at small numbers of processors, due to a large computational overhead, MGRIT and STMG-BR require more processors to benefit over time stepping. This result was confirmed both practically and through the performance models. Changing from space–time concurrency to time-only parallelism leads to faster runtimes of all multigrid methods. The decrease in runtimes is particularly pronounced for the MGRIT algorithms and allows shifting the crossover point to a smaller number of processors for achieving similar performance to STMG with block relaxation.

While STMG and WRMG-CR offer best speedup over sequential time-stepping at small processor counts, these intrusive approaches show poorer parallel scalability than the MGRIT algorithm. The scalability of STMG with block relaxation is better than that of the point-relaxation version, but considering the slower runtimes of the block-relaxation version, STMG-BR does not seem to give great benefit over STMG with point relaxation, at least not as with the implementation used for this paper. On the other hand, MGRIT offers some key practical advantages. While the generalization to problems in three space dimensions is straightforward with the non-intrusive MGRIT approach, the effort for a parallel implementation of the two intrusive approaches STMG(-BR) and WRMG-CR is immense. Furthermore, MGRIT allows for memory savings equal to the coarsening factor (here 16$\times$), which is another appealing advantage over the two invasive approaches.¹ Since the MGRIT algorithm offers a clear advantage in terms of its nonintrusive nature, we believe further research into performance improvements of MGRIT, particularly adding intrusiveness (see Sect. 4.5), is warranted.

Extending the comparison presented in this paper to include other time-dependent problems is exceedingly difficult, due to the intrusiveness of STMG(-BR) and WRMG-CR. Although benefits in runtime are likely much smaller with the MGRIT approach, its non-intrusiveness easily allows effective exploitation of substantially more computational resources than with space-parallel time stepping. More concretely, since MGRIT uses the same time-integration operator as algorithms based on a time-stepping approach, problem-specific time-integration operators are handled naturally. On the other hand, it is not clear how to extend STMG and WRMG-CR to other problem types in cases where specific time-integration schemes are crucial for convergence of time stepping.

Extending the comparison presented in this paper to include other space–time parallel methods is also difficult, due to the complexities of generating fair comparisons for methods that may be best applied on certain computational platforms or architectures, or for specific classes of problems. A natural next step in the comparison presented here would be to consider the parallel full approximation scheme in space and time (PFASST) [10, 35], another popular method in the literature. PFASST uses a specific spectral deferred correction time integrator, but has recently been shown to be equivalent to a multigrid method [4, 36]. Extending the comparison presented in this paper to include the PFASST algorithm is a subject of future work.