Prospective strict no-arbitrage and the fundamental theorem of asset pricing under transaction costs

Abstract

In discrete-time markets with proportional transaction costs, Schachermayer (Math. Financ. 14:19–48, 2004) showed that robust no-arbitrage is equivalent to the existence of a strictly consistent price system. In this paper, we introduce the concept of prospective strict no-arbitrage that is a variant of the strict no-arbitrage property from Kabanov et al. (Finance Stoch. 6:371–382, 2002). The prospective strict no-arbitrage condition is slightly weaker than the robust no-arbitrage condition, and it implies that the set of portfolios attainable from zero initial endowment is closed in probability. A weak version of prospective strict no-arbitrage turns out to be equivalent to the existence of a consistent price system. In contrast to the fundamental theorem of asset pricing of Schachermayer (Math. Financ. 14:19–48, 2004), the consistent frictionless prices may lie on the boundary of the bid–ask spread. On the technical level, a crucial difference to Schachermayer (Math. Financ. 14:19–48, 2004) and Kabanov et al. (Finance Stoch. 7:403–411, 2003) is that we prove closedness without having at hand that the null-strategies form a linear space.

1 Introduction

In frictionless financial market models in finite discrete time, the absence of arbitrage opportunities is equivalent to the existence of an equivalent probability measure under which the discounted price processes are martingales. This result is called the fundamental theorem of asset pricing (FTAP). In the case of a finite probability space, it goes back to the work of Harrison and Pliska [8]. The extension to arbitrary probability spaces is known as the Dalang–Morton–Willinger theorem [3], whose original proof was subsequently refined by several authors; see e.g. [13, 21]. In the later proofs, the implication that in frictionless markets, the absence of arbitrage opportunities implies that the set of hedgeable claims attainable from zero endowment is closed in probability is identified as the key lemma.

For a finite probability space, Kabanov and Stricker [14] extend the FTAP of Harrison and Pliska to models with proportional transaction costs. They consider a general “currency model” with finitely many currencies (assets), which we also use in the current paper. It allows buying any asset by paying with any other asset. In this general framework, there need not exist an asset which can play the role of a bank account, i.e., an asset which can be involved in every transaction at minimal costs. Kabanov and Stricker show that no-arbitrage (NA) is equivalent to the existence of a so-called consistent price system (CPS), which is a multidimensional martingale under the objective probability measure taking values within the dual of the cone of solvent portfolios at each point in time. For infinite probability spaces, this equivalence fails; Schachermayer [22] provides an example for an arbitrage-free market which allows an approximate arbitrage, i.e., a nonzero and nonnegative portfolio which is the limit in probability of a sequence of portfolios attainable from zero endowment, and consequently a CPS cannot exist (see Example 3.1 therein). This raises the obvious question under which stronger no-arbitrage conditions the existence of a CPS can be guaranteed. Schachermayer [22] introduces the concept of robust no-arbitrage (NA^r) – a no-arbitrage condition which is robust with respect to small changes in the bid–ask spreads. Loosely speaking, if the bid–ask spread (of a pair of assets) does not vanish, there have to exist more favourable bid–ask prices, leading to a smaller spread, such that the modified market still satisfies (NA). Schachermayer shows that (NA^r) implies that the set of hedgeable claims attainable from zero endowment, in the following denoted by $\mathcal{A}$, is closed in probability, and that (NA^r) is equivalent to the existence of a strictly consistent price system (SCPS), that is, a martingale taking values within the relative interior of the dual of the cone of solvent portfolios at each point in time.

An alternative condition is the strict no-arbitrage property (NA^s) introduced by Kabanov et al. [10]. Loosely speaking, a market model satisfies (NA^s) if any claim which is attainable from zero endowment up to some intermediate time $t$ and can be liquidated in $t$ for sure can also be attained from zero endowment by trading at time $t$ only. Property (NA^s) alone does not imply the existence of a CPS (see [22, Example 3.3] for the existence of an approximate arbitrage under (NA^s)); but together with the Penner condition (4.1) due to I. Penner [18], this implication holds (see Kabanov et al. [11, Theorem 2]). Loosely speaking, the Penner condition postulates that any “free round-trip” of exchanging assets that can be carried out in the next period for sure – given the information of the current period – can already be carried out in the current period. Together with (NA^s), it allows showing that the so-called null-strategies, i.e., the increments of self-financing portfolio processes with vanishing terminal value, form a linear space. This is also a crucial argument in [22] to show closedness of $\mathcal{A}$, which is the main step to show the existence of a CPS. Indeed, it is shown by Rokhlin [20] that the vector space property of the set of null-strategies is equivalent to (NA^r).

A different approach to study the occurrence of an approximate arbitrage is followed in Jacka et al. [9]. They provide a necessary and sufficient condition for $\mathcal{A}$ to be closed in probability and construct adjusted trading prices such that the corresponding cone of hedgeable claims attainable from zero endowment either contains an arbitrage or equals the closure of $\mathcal{A}$. Put differently, they postulate the (weak) no-arbitrage condition for an adjusted trading model instead of postulating a stronger no-arbitrage condition for the original one (cf. also Remark 4.4 below).

Furthermore, it is important to note that the closedness of $\mathcal{A}$ is not necessary for the existence of a CPS. In the case of only two assets (e.g. a bank account and one risky stock), it is shown by Grigoriev [7] that (NA) already implies the existence of a CPS, although $\mathcal{A}$ need not be closed (see [7, Example 1.3] and Lépinette and Zhao [17, Proposition 3.5] for the non-closedness of the set of attainable liquidation values). This means that already in dimension two, additional conditions are required to guarantee that the set of attainable liquidation values is closed. For this, Lépinette and Zhao [17] provide an intuitive and easy to verify condition (Condition E) that takes the postponing of trades into consideration. Their proof uses the existence of a CPS that is guaranteed by Grigoriev [7] in the case of an arbitrage-free model with two assets. On the other hand, already for three assets, there is a counterexample showing that (NA) does not imply the existence of a CPS (see [16, Example 4.6]).

The goal of the current paper is twofold:

– We want to provide an (easy to interpret) no-arbitrage condition which is as weak as possible and under which the set $\mathcal{A}$ of terminal portfolios attainable from zero endowment is closed in probability.

– We want to establish an FTAP with CPSs which are not necessarily strict as in the FTAP of Schachermayer [22].

For this, we introduce a variant of (NA^s) that we call prospective strict no-arbitrage (NA^ps) and that turns out to be sufficient to guarantee that $\mathcal{A}$ is closed in probability (see Theorem 2.6). We say that the market model satisfies (NA^ps) if any claim which is attainable from zero endowment by trading up to some time $t$ and can subsequently be liquidated for sure can also be attained from zero endowment in the subsequent periods (here, “subsequent” is not understood in a strict sense). This means that in contrast to the (NA^s) criterion, we do not distinguish between a trade that can be realised at time $t$ and a trade from which we know at time $t$ for sure that it can be realised in the future. In the special case of efficient friction (i.e., positive bid–ask spreads, cf. Definition 2.5), (NA^ps) and (NA^s) are equivalent (see Proposition 2.20).

In our proofs, we cannot rely on the vector space property of the null-strategies, which was central in the arguments of Schachermayer and Kabanov et al. Indeed, it was shown by Rokhlin [20] that this property is equivalent to (NA^r) which is strictly stronger than (NA^ps). Our proof relies on a decomposition of the trading possibilities into “reversible” and “purely nonreversible” transactions at each point in time, where we call a transaction “reversible” if the resulting portfolio can be liquidated in the later periods for sure. This decomposition can be seen as a nonlinear, only positively homogeneous generalisation of the projection on the set of null-strategies that is used in the case that the null-strategies form a vector space. Given a trading strategy, we then consider only the “purely nonreversible” part at each point in time and postpone the “reversible” part to later points in time, where more information is available. This is possible by (NA^ps), and as it turns out, sufficient to assert that $\mathcal{A}$ is closed in probability. Consequently, (NA^ps) implies the existence of a CPS.

On the other hand, as described above, a CPS can exist even if the set $\mathcal{A}$ is not closed. Consequently, the existence of a CPS cannot be equivalent to (NA^ps). But for a weak version of (NA^ps), called weak prospective strict no-arbitrage (NA^wps), we obtain equivalence to the existence of a CPS (see Theorem 2.11). A market satisfies (NA^wps) if there exists an at least as favourable market which satisfies (NA^ps). Since the second market need not be strictly more favourable than the original one, (NA^ps) implies (NA^wps). Hence we establish an FTAP which complements those of Schachermayer [22] and Kabanov et al. [10, 11]. The main difference is that the resulting CPS may lie on the relative boundary of the bid–ask spread. In Sect. 4, Fig. 1 illustrates this in a very simple example. Alternatively, one may think of an actually frictionless market with one risky stock that is written as a model with efficient friction in the following way. Each point in time is split into two points. Under the same information, at the first point, the investor can only buy, and at the second point, she can only sell (arbitrary quantities of) the stock. If the frictionless market satisfies (NA), the artificial market with friction has a CPS, but not an SCPS. Thus, at least from a conceptual point of view, it is desirable to have an FTAP with arbitrary CPSs as well.

Fig. 1

Deterministic model satisfying (NA^ps) and (NA^s), but not (NA^r). At $t=0$, the bid price $\underline{S}_{0}$ equals $1/2$ and the ask price $\overline{S}_{0}$ equals 1; at $t=1$, the market is frictionless with price $\underline{S}_{1}=\overline{S}_{1}=1$.

In the case of a finite probability space, (NA^wps) is equivalent to (NA), which means that our version of the FTAP can be seen as a generalisation of the above-mentioned FTAP by Kabanov and Stricker [14] (see part 2 of Theorem 1 therein) to the case of arbitrary probability spaces. Finally, we motivate the (NA^wps) condition by an example which shows that (NA^wps) cannot be replaced by a further weakening of the (NA^ps) condition (see Example 4.3).

The remainder of the paper is organised as follows. In Sect. 2, we introduce the framework of financial modelling, the prospective strict no-arbitrage condition, and the weak prospective strict no-arbitrage condition. We relate these properties to the robust no-arbitrage and the strict no-arbitrage condition and state the main results of the paper (Theorems 2.6 and 2.11). The proofs can be found in Sect. 3. In Sect. 4, we give two very simple examples that illustrate the differences between the above no-arbitrage conditions, and a more sophisticated example (Example 4.3) that shows the effect of a possible “cascade” of approximate hedges.

2 Prospective strict no-arbitrage and consistent price systems

We now introduce the market model and the relevant notation. We work on a probability space $(\Omega,\mathcal{F},\mathbb{P})$ equipped with a discrete-time filtration $(\mathcal{F}_{t})_{t=0}^{T}$, $T\in\mathbb{N}$, such that $\mathcal{F}_{T}=\mathcal{F}$. The space (of equivalence classes) of $\mathcal{F}_{t}$-measurable $d$-dimensional random vectors is denoted by $L^{0}(\mathcal{F}_{t};\mathbb{R}^{d})$. For a set-valued mapping $\omega\mapsto N(\omega)\subseteq\mathbb {R}^{d}$, we denote by $L^{0}(\mathcal{F}_{t} ; N):=\{v\in L^{0}(\mathcal {F}_{t} ; \mathbb{R}^{d}): v(\omega)\in N(\omega)\ \mathrm{for\ a.e.}\ \omega\in\Omega\}$ the set of $\mathcal{F}_{t}$-measurable selectors of $N$. As usual, the spaces are equipped with the topology of convergence in probability, and we write $L^{0}(N):=L^{0}(\mathcal{F}_{T} ; N)$.

We work with the market model with proportional transaction costs from Schachermayer [22], where the reader may find a discussion about its economic meaning and its connection to the models of [10] and [14]. There are $d\in\mathbb{N}$ traded assets (one of which may, but need not, be a money market account), and a $d\times d$-matrix $\Pi=(\pi^{ij})_{1\leq i,j\leq d}$ is called bid–ask matrix if

• (i) $0<\pi^{ij}<\infty$ for $1\leq i,j\leq d$;

• (ii) $\pi^{ii}=1$ for $1\leq i\leq d$;

• (iii) $\pi^{ij}\leq\pi^{ik}\pi^{kj}$ for $1\leq i,j,k\leq d$.

The terms of trade of the $d$ assets are specified by a bid–ask process$(\Pi_{t})_{t=0}^{T}$, i.e., an adapted $d\times d$-matrix-valued process such that $\Pi_{t}(\omega)$ is a bid–ask matrix for each $\omega\in\Omega$ and $t\in\{0,\dots,T\}$. The random matrix $\Pi_{t}=(\pi^{ij}_{t})_{1\leq i,j\leq d}$ specifies for each $t\in\{0,\dots,T\}$ the exchanges available to the investor at time $t$. More precisely, the entry $\pi^{ij}_{t}$ denotes the number of units of asset $i$ for which an agent can buy one unit of asset $j$ at time $t$. Therefore, the set of portfolios attainable at zero endowment at time$t$, which in this context consists of $\mathcal{F}_{t}$-measurable $\mathbb{R}^{d}$-valued random variables, is modelled by the convex cone

$$ \bigg\{ \sum_{1\leq i,j\leq d}\lambda^{ij}(e^{j}-\pi^{ij}_{t}e^{i})-r : (\lambda^{ij})_{1\leq i,j\leq d}\in L^{0}(\mathcal{F}_{t} ; \mathbb {R}^{d\times d}_{+}),\ r\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d}_{+})\bigg\} , $$

(2.1)

where $e^{i}$ denotes the $i$th unit vector of $\mathbb{R}^{d}$. This means that each portfolio is the result of an order $\lambda=(\lambda ^{ij})_{1\leq i,j\leq d}\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$, where $\lambda^{ij}$ denotes the units of asset $j$ ordered in exchange for asset $i$, and some nonnegative amount $r\in L^{0}(\mathcal {F}_{t} ; \mathbb{R}^{d}_{+})$, which corresponds to the decision of the investor to “throw away” some nonnegative physical quantities of each asset. Next, we define for each $\omega\in\Omega$ the polyhedral cone

$$\begin{aligned} K\big(\Pi_{t}(\omega)\big):=\mathrm{cone}\big(\{\pi^{ij}_{t}(\omega )e^{i}-e^{j}\}_{1\leq i,j\leq d}, \{e^{i}\}_{1\leq i\leq d}\big), \end{aligned}$$

which we abbreviate as $K_{t}(\omega):=K(\Pi_{t}(\omega))$. In Lemma 3.1 below, we briefly verify the intuitively obvious fact that the set given in (2.1) coincides with the set $L^{0}(\mathcal{F}_{t} ; -K_{t})$ of $\mathcal{F}_{t}$-measurable selectors of the set-valued mapping $\omega\mapsto-K_{t}(\omega)$. We use this equality throughout the paper and refer to $L^{0}(\mathcal{F}_{t} ; -K_{t})$ as the set of portfolios attainable from zero endowment at time $t$.

Definition 2.1

An $\mathbb{R}^{d}$-valued adapted process $\vartheta=(\vartheta _{t})_{t=0}^{T}$ is called a self-financing portfolio process for the bid–ask process $(\Pi_{t})_{t=0}^{T}$ if

$$\vartheta_{t}-\vartheta_{t-1}\in L^{0}(\mathcal{F}_{t} ; -K_{t})\qquad \mbox{for all }t=0,\ldots,T, $$

where $\vartheta_{-1}:=0$. Consequently, for each pair $(s,t)$ with $s,t\in\{0,\ldots,T\}$ and $s\le t$, the convex cone of hedgeable claims attainable from zero endowment between$s$and $t$ is denoted by $\mathcal{A}_{s}^{t}$ and defined to be

$$\begin{aligned} \mathcal{A}_{s}^{t}:=\sum_{k=s}^{t}L^{0}(\mathcal{F}_{k} ; -K_{k}). \end{aligned}$$

For an alternative bid–ask process $(\widetilde{\Pi}_{t})_{t=0}^{T}$, the corresponding set is denoted by $\widetilde{\mathcal{A}}_{s}^{t}$, where $\widetilde {K}_{t}(\omega):=K(\widetilde{\Pi}_{t}(\omega))$ for all $\omega\in \Omega$ and $t=0,\dots,T$.

The primary object of interest in this paper is the cone $\mathcal {A}_{0}^{T}$ of hedgeable claims attainable from zero endowment between 0 and $T$. However, we still need the following auxiliary notions. The convex cone $L^{0}(\mathcal{F}_{t} ; K_{t})$ is called the set of solvent portfolios at time$t$ and the (polyhedral) cone $K_{t}(\omega )$ is called the solvency cone corresponding to the bid–ask matrix $\Pi_{t}(\omega)$. Indeed, for each portfolio $v\in L^{0}(\mathcal {F}_{t} ; K_{t})$ the portfolio $-v\in L^{0}(\mathcal{F}_{t} ; -K_{t})$ is attainable at price zero; thus the portfolio $v$ can be liquidated to zero and consequently is solvent. Similarly, let $K^{0}_{t}(\omega ):=K_{t}(\omega)\cap-K_{t}(\omega)$ for each $\omega\in\Omega$; then $L^{0}(\mathcal{F}_{t} ; K^{0}_{t})$ denotes the space of portfolios which are attainable at zero endowment and are also solvent, i.e., can be liquidated to the zero portfolio.

Before we introduce our new no-arbitrage condition, we recall the concepts of no-arbitrage from the literature; compare to [11] and [22].

Definition 2.2

(i) The bid–ask process $(\Pi_{t})_{t=0}^{T}$ satisfies the no-arbitrage property (NA) if

$$\mathcal{A}_{0}^{T}\cap L^{0}(\mathbb{R}^{d}_{+})=\{0\}. $$

(ii) The bid–ask process $(\Pi_{t})_{t=0}^{T}$ satisfies the strict no-arbitrage property (NA^s) if

$$\mathcal{A}_{0}^{t}\cap L^{0}(\mathcal{F}_{t} ; K_{t})\subseteq L^{0}(\mathcal {F}_{t} ; K^{0}_{t})\qquad \mbox{for all }t=0,\ldots,T. $$

(iii) The bid–ask process $(\Pi_{t})_{t=0}^{T}$ satisfies the robust no-arbitrage condition (NA^r) if there is a bid–ask process $(\widetilde{\Pi}_{t})_{t=0}^{T}$ with smaller bid–ask spreads, in the sense that the interval $[1/\widetilde{\pi}_{t}^{ji}(\omega),\widetilde{\pi}_{t}^{ij}(\omega )]$ is contained in the relative interior of $[1/\pi^{ji}_{t}(\omega ),{\pi_{t}}^{ij}(\omega)]$ for all $1\leq i,j\leq d$, $t\in\{0,\dots,T\}$ and almost all $\omega \in\Omega$, and such that $(\widetilde{\Pi}_{t})_{t=0}^{T}$ satisfies the no-arbitrage condition (NA).

We note that in the case of vanishing bid–ask spreads, the choice of $\widetilde{\Pi}=\Pi$ has smaller bid–ask spreads than $\Pi$, i.e., frictionless markets are not excluded in Definition 2.2(iii).

It is well known that although each of the cones $L^{0}(\mathcal{F}_{t} ; -K_{t})$ is closed with respect to convergence in probability, the cone $\mathcal{A}_{0}^{T}$ may fail to be closed. As already mentioned, neither (NA) nor (NA^s) are strong enough to guarantee that $\mathcal{A}_{0}^{T}$ is closed (see [22, Examples 3.1 and 3.3]). This is in contrast to the frictionless case, where (NA) is sufficient (see e.g. [6, Theorem 6.9.2]). In the present context, Schachermayer [22] showed that the robust no-arbitrage condition (NA^r) is strong enough to ensure that $\mathcal{A}_{0}^{T}$ is closed. We now introduce a slight weakening of (NA^r), called prospective strict no-arbitrage (NA^ps), which is still sufficient to guarantee that $\mathcal{A}_{0}^{T}$ is closed.

Definition 2.3

The bid–ask process $(\Pi_{t})_{t=0}^{T}$ satisfies the prospective strict no-arbitrage property (NA^ps) if

$$\begin{aligned} \mathcal{A}_{0}^{t}\cap(-\mathcal{A}_{t}^{T})\subseteq\mathcal {A}_{t}^{T}\qquad \mbox{for all }t=0,\ldots,T. \end{aligned}$$

Remark 2.4

The property (NA^ps) has the following interpretation: Any claim $v\in\mathcal{A}_{0}^{t}$ attained by trading up to time $t$ which can be reduced to the zero portfolio in $t$ or in the subsequent periods, i.e., $-v\in\mathcal{A}_{t}^{T}$, must be attainable by trading between $t$ and $T$ only, i.e., $v\in\mathcal {A}_{t}^{T}$. It is a variant of the (NA^s) condition, which postulates that any claim $v\in\mathcal{A}_{0}^{t}$ which can be liquidated at time $t$, i.e., $-v\in\mathcal{A}_{t}^{t}$, must be attainable at time $t$ as well, i.e., $v\in\mathcal{A}_{t}^{t}$. The difference is that we do not distinguish between a trade at time $t$ and a trade about which one knows for sure at time $t$ that it can be realised in the future.

Put differently, for every $t$, we review the trading up to time $t$. Either one does not gain advantage from the trading since the same terminal position can be achieved for sure by starting to trade at $t$, or one takes some risk by the trading up to time $t$ since the position cannot be liquidated for sure in the future.

Definition 2.5

The bid–ask process $(\Pi_{t})_{t=0}^{T}$ satisfies efficient friction (EF) if

$$\begin{aligned} K^{0}_{t}(\omega):=K_{t}(\omega)\cap\big(-K_{t}(\omega)\big)=\{0\} \qquad \mbox{for all $t=0,\dots,T$ and $\omega\in\Omega$.} \end{aligned}$$

The bid–ask process $(\Pi_{t})_{t=0}^{T}$ satisfies (EF) if and only if $\pi^{ij}_{t}(\omega)\pi^{ji}_{t}(\omega)>1$ for all $1\leq i\neq j\leq d$, $t=0,\dots,T$ and $\omega\in\Omega$ (see Proposition 2.19). Under efficient friction, the conditions (NA^ps) and (NA^s) coincide (see Proposition 2.20). We can already formulate the first main result of the paper:

Theorem 2.6

If the bid–ask process$(\Pi_{t})_{t=0}^{T}$has the prospective strict no-arbitrage property (NA^ps), then the convex cone$\mathcal{A}_{0}^{T}$is closed with respect to convergence in probability.

The theorem above has obvious consequences for the existence of dual variables. For a given bid–ask matrix $\Pi$, the (positive) dual cone $K^{\star}$ of the solvency cone $K=K(\Pi)$ is defined by $K^{\star}:=\{w\in\mathbb{R}^{d}: \langle v,w\rangle\geq 0 \ \text{for all}\ v\in K\}$. For the bid–ask process $(\Pi_{t})_{t=0}^{T}$, this induces the set-valued process $(K^{\star}_{t})_{t=0}^{T}$ of dual cones. We can now define the notion of a consistent price system, which is dual to the notion of a self-financing portfolio process and plays a similar role as the notion of an equivalent martingale measure in the frictionless theory. Once again, we refer to [22] for a detailed discussion of the economic interpretation.

Definition 2.7

An adapted $\mathbb{R}^{d}_{+}$-valued process $Z=(Z_{t})_{t=0}^{T}$ is called a consistent price system (CPS) for the bid–ask process $(\Pi _{t})_{t=0}^{T}$ if $Z$ is a martingale under ℙ and $Z_{t}\in L^{0}(\mathcal{F}_{t} ; K^{\star}_{t}\setminus\{0\})$, i.e., $Z_{t}(\omega )\in K^{\star}_{t}(\omega)\setminus\{0\}$ for a.e. $\omega\in\Omega$ and each $t\in\{0,\dots,T\}$.

We have the following consequence of Theorem 2.6.

Corollary 2.8

If the bid–ask process$(\Pi_{t})_{t=0}^{T}$satisfies the prospective strict no-arbitrage condition (NA^ps), then it admits a consistent price system (CPS). More generally, for any strictly positive$\mathcal {F}_{T}$-measurable function$\varphi:\Omega\to(0,1]$, there is a CPS$Z=(Z_{t})_{t=0}^{T}$with$\vert Z_{T}\vert\leq M\varphi$a.s. for some$M\in\mathbb{R}_{+}\setminus\{0\}$.

Remark 2.9

An abstract version of (NA^ps) reads as follows: If a strategy up to time $t$ can be extended to a strategy without losses at $T$, then any other extension beyond $t$ can be dominated at $T$ by a strategy that does not trade before $t$.

This scheme can be formalised in a quite canonical way in diverse market models including e.g. capital gains taxes, uncertainty about the execution of limit orders or dividend paying assets, where the basic problem from Schachermayer [22, Example 3.1] can also occur (see e.g. [16, Example 4.5]). The arguments of our proofs may be adapted to these models to show that the set of attainable terminal portfolios is closed.

For example, in the context of optimal investment problems with utility functions on the positive real line, this means, roughly speaking, that the set $\mathcal{C}$ of nonnegative random variables dominated by the liquidation value of an attainable portfolio (with a given initial endowment) is also closed in probability. Hence, defining the set of dual variables $\mathcal{D}$ as the polar set of $\mathcal{C}$, the abstract versions of the duality results in Kramkov and Schachermayer [15, Theorem 3.1 and 3.2] may also be applied to these models.

The converse of Corollary 2.8 fails to be true. More generally, by [12, Sect. 3.2.4, Example 1], there cannot exist a no-arbitrage criterion that both guarantees closedness of $\mathcal{A}^{T}_{0}$ and is equivalent to the existence of a CPS; cf. also the discussion in Remark 2.13 below. We can, however, establish an equivalence if we pass from (NA^ps) to a weaker notion of prospective strict no-arbitrage.

Definition 2.10

The bid–ask process $(\Pi_{t})_{t=0}^{T}$ satisfies the weak prospective strict no-arbitrage property (NA^wps) if there is a bid–ask process $(\widetilde{\Pi}_{t})_{t=0}^{T}$ with $\widetilde{\Pi}_{t}\leq\Pi_{t}$ a.s. for all $t=0,\dots,T$ such that $(\widetilde{\Pi}_{t})_{t=0}^{T}$ satisfies the prospective strict no-arbitrage condition (NA^ps).

The condition (NA^wps) is obviously a weakening of (NA^ps) since the bid–ask process $(\widetilde{\Pi }_{t})_{t=0}^{T}$ in Definition 2.10 need not be strictly more favourable than $(\Pi_{t})_{t=0}^{T}$. The difference between the two conditions is illustrated in Example 4.2 below; see also Remark 2.13 below. Our second main result is the following fundamental theorem of asset pricing.

Theorem 2.11

A bid–ask process$(\Pi_{t})_{t=0}^{T}$satisfies the weak prospective strict no-arbitrage condition (NA^wps) if and only if it admits a consistent price system (CPS).

Remark 2.12

Theorem 2.11 extends part 2 of Theorem 1 in Kabanov and Stricker [14] to the case of infinite probability spaces. Combining these two theorems, it can be seen that (NA^wps) possesses the nice property that it is equivalent to (NA) if $|\Omega|<\infty$. In addition, (NA) and (NA^wps) coincide in the case of only two assets on arbitrary probability spaces, which follows from the equivalence of (NA) and the existence of a CPS derived by Grigoriev [7].

Remark 2.13

In the following discussion, we identify an “absence of arbitrage” criterion $\mathcal{C}$ with the set of bid–ask processes which satisfy the criterion and call it monotone if for all bid–ask processes $\widetilde {\Pi }\le\Pi$, $\widetilde{\Pi}\in\mathcal{C}$ implies that $\Pi\in \mathcal{C}$. Monotonicity is obviously satisfied by the simple (NA) condition. The more sophisticated criteria (NA^s), (NA^r) and (NA^ps) are in general only monotone if bid–ask matrices without efficient friction are excluded from the consideration, i.e., $\pi^{ij}\pi ^{ji}\ge\widetilde{\pi}^{ij}\widetilde{\pi}^{ji}>1$ for all $i\not=j$ (cf. Proposition 2.19). On the one hand, the equivalence to the existence of a CPS can only hold for a monotone criterion. Indeed, it follows directly from Definition 2.7 that a CPS for $\widetilde{\Pi}$ is also a CPS for $\Pi$ with $\Pi\ge \widetilde{\Pi}$. On the other hand, the closedness of the set of attainable portfolios does not transfer to a market with a less favourable bid–ask process (see e.g. [12, Sect. 3.2.4, Example 1] and [9, Example 2.1]). Thus, to guarantee closedness e.g. in the context of optimal investment problems, a limitation to monotone criteria would be unduly restrictive.

The (NA^wps) criterion can be characterised as the “strongest monotone criterion which is weaker than (NA^ps)”, i.e., it follows directly from Definition 2.10 that

$$(NA^{\textrm{wps}}) = \bigcap_{(NA^{\textrm{ps}})\subseteq\mathcal {C},\ \mathcal {C}\text{ is monotone }}\mathcal{C}. $$

In the special case of a frictionless market, the criteria (NA^ps) and (NA^wps) coincide (see Proposition 2.17 below).

We stress that the picture cannot be as clear-cut as in the frictionless case. In discrete-time frictionless markets, (NA) already implies closedness (see Schachermayer [21, Lemma 2.1]). In continuous-time frictionless markets, Delbaen and Schachermayer [5] derived closedness in an appropriate topology under the economically meaningful assumption of “no free lunch with vanishing risk” (NFLVR) that is also necessary for the existence of an equivalent martingale measure. Under transaction costs, the FTAP of Delbaen and Schachermayer [5] cannot hold. In fact, Schachermayer [22, Example 3.1] satisfies (NFLVR) defined for multivariate portfolio processes, i.e., we have $\overline{\mathcal{A}_{0}^{T}}^{\infty}\cap L^{\infty}(\Omega ,\mathcal{F}_{T},\mathbb{P};\mathbb{R}^{d}_{+})=\{0\}$, where $\overline {\mathcal{A}_{0}^{T}}^{\infty}$ denotes the closure of $\mathcal {A}_{0}^{T}\cap L^{\infty}(\Omega,\mathcal{F}_{T},\mathbb{P};\mathbb {R}^{d})$ with respect to the topology of uniform convergence; but a CPS nevertheless does not exist.

Definition 2.14

An element $v\in L^{0}(\mathbb{R}^{d}_{+})$ with $v\neq0$ is called an approximate arbitrage (in probability) if there is a sequence $(v^{n})_{n\in\mathbb{N}}\subseteq\mathcal{A}_{0}^{T}$ such that $v^{n}\to v$ in probability.

In general, (NA) does not guarantee the absence of an approximate arbitrage, i.e., $\overline{\mathcal{A}^{T}_{0}}\cap L^{0}(\mathbb {R}^{d}_{+})=\{0\}$. On the other hand, even though the (NA^wps) property is not sufficient to ensure that $\mathcal{A}_{0}^{T}$ is closed in probability, we have the following easy consequence of Theorem 2.11.

Corollary 2.15

If a bid–ask process$(\Pi_{t})_{t=0}^{T}$satisfies the weak prospective strict no-arbitrage condition (NA^wps), then we have$\overline{\mathcal{A}^{T}_{0}}\cap L^{0}(\mathbb{R}^{d}_{+})=\{0\}$.

The (short) proof is also deferred to Sect. 3.

Remark 2.16

(NA^wps) postulates the existence of a bid–ask process $(\widetilde{\Pi}_{t})_{t=0}^{T}$ such that $\widetilde{\Pi }_{t}\leq\Pi_{t}$ a.s. for all $t=0,\dots,T$ and

$$\begin{aligned} \widetilde{\mathcal{A}}_{0}^{t}\cap(-\widetilde{\mathcal {A}}_{t}^{T})\subseteq\widetilde {\mathcal{A}}_{t}^{T}\qquad \mbox{for all }t=0,\dots,T. \end{aligned}$$

(2.2)

One may ask if one can replace this condition with the following slightly weaker condition: there exists a bid–ask process $(\widetilde {\Pi }_{t})_{t=0}^{T}$ satisfying (NA) such that $\widetilde{\Pi}_{t}\leq\Pi _{t}$ a.s. for all $t=0,\dots,T$ and

$$\begin{aligned} \mathcal{A}_{0}^{t}\cap(-\widetilde{\mathcal{A}}_{t}^{T})\subseteq \widetilde{\mathcal {A}}_{t}^{T}\qquad \mbox{for all }t=0,\dots,T. \end{aligned}$$

(2.3)

Indeed, by Proposition 2.17 below, (2.2) implies that $\widetilde{\Pi}$ satisfies (NA), which means that the second condition is a weakening of the first one. In condition (2.3), the position at time $t$ is achieved by trading in the original market; only its “evaluation” is made in the more favourable market model $\widetilde{\Pi}$. But maybe surprisingly, it turns out that (2.3) does not exclude the existence of an approximate arbitrage, and thus a CPS need not exist (see Example 4.3 below).

Proposition 2.17

We have the following implications:

$$\begin{aligned} (NA^{\textrm{r}})\quad \Longrightarrow \quad (NA^{\textrm{ps}})\quad \Longrightarrow \quad (NA^{\textrm{wps}})\quad \Longrightarrow \quad (NA). \end{aligned}$$

(2.4)

Remark 2.18

All implications in (2.4) are strict. For the first two, see Examples 4.1 and 4.2 below; for (NA) ⇏ (NA^wps), consider an arbitrage-free model with an approximate arbitrage, e.g. [22, Example 3.1], and apply Corollary 2.15.

Proof Proposition 2.17

(NA^r) ⇒ (NA^ps). Assume that the bid–ask process $(\Pi_{t})_{t=0}^{T}$ satisfies (NA^r) and let $v\in\mathcal{A}_{0}^{t}$ be such that $-v\in\mathcal{A}_{t}^{T}$. We have to show that $v\in\mathcal{A}_{t}^{T}$. According to our assumption, we have $v=\sum_{s=0}^{t}\widetilde{\xi _{s}}$ with $\widetilde{\xi}_{s}\in L^{0}(\mathcal{F}_{s} ; -K_{s})$ for $s=0,\ldots,t$ and $-v=\sum_{s=t}^{T}\widehat{\xi}_{s}$ with $\widehat{\xi}_{s}\in L^{0}(\mathcal{F}_{s} ; -K_{s})$ for $s=t,\ldots,T$. Hence we define $\xi _{s}\in L^{0}(\mathcal{F}_{s} ; -K_{s})$ by

$$\begin{aligned} \xi_{s}:= \textstyle\begin{cases} \widetilde{\xi}_{s}, &\quad s< t,\\ \widetilde{\xi}_{s}+\widehat{\xi}_{s}, &\quad s=t,\\ \widehat{\xi}_{s}, &\quad s>t, \end{cases}\displaystyle \end{aligned}$$

and notice that $\sum_{s=0}^{T}\xi_{s}=v-v=0$. From [12, Lemma 3.2.12], it follows that $\xi_{s}\in L^{0}(\mathcal{F}_{s} ; K^{0}_{s})$ for all $s=0,\dots,T$. In particular, we have $\widehat{\xi}_{s}\in L^{0}(\mathcal{F}_{s} ; K_{s})$ for $s> t$. In addition, we have $\widehat{\xi}_{t}=-\widetilde{\xi}_{t}+\xi_{t}\in L^{0}(\mathcal{F}_{t} ; K_{t}) + L^{0}(\mathcal{F}_{t} ; K_{t}) = L^{0}(\mathcal{F}_{t} ; K_{t})$. This implies that $v=\sum_{s=t}^{T}(-\widehat{\xi}_{s})\in\mathcal{A}_{t}^{T}$, which concludes the proof of the first implication.

(NA^ps) ⇒ (NA^wps). Obvious.

(NA^wps) ⇒ (NA). Assume that the bid–ask process $(\Pi_{t})_{t=0}^{T}$ satisfies (NA^wps), i.e., there exists a bid–ask process $(\widetilde{\Pi }_{t})_{t=0}^{T}$ with $\widetilde{\Pi}_{t}\leq\Pi_{t}$ a.s. for all $t=0,\dots,T$ and such that $(\widetilde{\Pi}_{t})_{t=0}^{T}$ satisfies (NA^ps). Let $v\in\mathcal{A}_{0}^{T}\cap L^{0}(\mathbb{R}^{d}_{+})\subseteq\widetilde {\mathcal{A}}_{0}^{T}\cap L^{0}(\mathbb{R}^{d}_{+})$. This obviously implies that $-v\in L^{0}(\mathcal{F}_{T} ; -\widetilde{K}_{T})$ and hence by (NA^ps) of $\widetilde{\Pi}$ that $v\in L^{0}(\mathcal {F}_{T} ; -\widetilde{K}_{T})$. Together with $(-\widetilde{K}_{T}(\omega))\cap\mathbb{R}^{d}_{+}=\{0\}$ for each $\omega\in\Omega$, which holds by the properties of a bid–ask matrix, this implies that $v=0$ a.s. Thus the bid–ask process $(\Pi _{t})_{t=0}^{T}$ satisfies (NA). □

Proposition 2.19

The bid–ask process$(\Pi_{t})_{t=0}^{T}$satisfies efficient friction (EF) if and only if

$$\begin{aligned} \pi^{ij}_{t}(\omega)\pi^{ji}_{t}(\omega)>1\qquad \textit{for all}\ 1\leq i\neq j\leq d,\ t=0,\dots,T\ \textit{and}\ \omega\in\Omega. \end{aligned}$$

Proof

If $\pi^{ij}_{t}(\omega)\pi^{ji}_{t}(\omega)=1$ for some $1\leq i\neq j\leq d$, $t\in\{0,\dots,T\}$ and $\omega\in\Omega$, we find

$$\begin{aligned} e^{j}-\pi^{ij}_{t}(\omega)e^{i}+\frac{1}{\pi^{ji}_{t}(\omega)}\big(e^{i}-\pi ^{ji}_{t}(\omega)e^{j}\big)=\frac{1}{\pi^{ji}_{t}(\omega)}\big(1-\pi ^{ij}_{t}(\omega)\pi^{ji}_{t}(\omega)\big)e^{i}=0. \end{aligned}$$

This implies that $e^{j}-\pi^{ij}_{t}(\omega)e^{i}=-\frac{1}{\pi ^{ji}_{t}(\omega)}(e^{i}-\pi^{ji}_{t}(\omega)e^{j})\in(-K_{t}(\omega))\cap K_{t}(\omega)$ and thus (EF) is not satisfied. This shows the “only if” part.

For the converse implication, we assume $\pi^{ij}_{t}(\omega)\pi ^{ji}_{t}(\omega)>1$ for all $1\leq i\neq j\leq d$, $t=0,\dots,T$ and $\omega\in\Omega$. Suppose that (EF) does not hold, i.e., for some $t\in\{0,\dots,T\}$ and $\omega\in\Omega$, there is $v\in(-K_{t}(\omega))\cap K_{t}(\omega)$ with $v\neq0$. By the definition of $-K_{t}(\omega)$, we have $v=\sum_{1\leq i\neq j\leq d}\lambda^{ij}(e^{j}-\pi^{ij}_{t}(\omega)e^{i})-\sum_{i=1}^{d}\beta^{i}e^{i}$ with $\lambda^{ij},\beta^{i}\geq0$. Let $\pi^{1}_{t}(\omega):=(\pi ^{11}_{t}(\omega),\dots,\pi^{1d}_{t}(\omega))^{T}$ and note that $\pi ^{1}_{t}(\omega)\in K_{t}^{\star}(\omega)$ by the property (iii) of a bid–ask matrix. We have $\langle v,\pi^{1}_{t}(\omega)\rangle=0$ as $v\in(-K_{t}(\omega))\cap K_{t}(\omega)$. Property (iii) of a bid–ask matrix implies $\lambda^{ij}(\pi^{1j}_{t}(\omega)-\pi^{1i}_{t}(\omega )\pi^{ij}_{t}(\omega))\leq0$ for all $1\leq i\neq j\leq d$, which yields

$$\begin{aligned} 0&=\langle v, \pi^{1}_{t}(\omega)\rangle\\ &= \sum_{1\leq i\neq j\leq d}\lambda^{ij}\big(\pi^{1j}_{t}(\omega )-\pi^{1i}_{t}(\omega)\pi^{ij}_{t}(\omega)\big)-\sum_{i=1}^{d}\beta ^{i}\pi^{1i}_{t}(\omega) \leq-\sum_{i=1}^{d}\beta^{i}\pi^{1i}_{t}(\omega) \end{aligned}$$

and thus $\beta^{i}=0$ for $i=1,\dots,d$. Therefore, $v\neq0$ implies $\lambda^{k\ell}>0$ for at least one pair $1\leq k\neq\ell\leq d$. Applying the same arguments now with the vector $\pi^{\ell}_{t}(\omega):=(\pi^{\ell1}_{t}(\omega),\dots,\pi^{\ell d}_{t}(\omega ))^{T}\in K^{\star}_{t}(\omega)$, we get

$$\begin{aligned} 0&=\langle v, \pi^{\ell}_{t}(\omega)\rangle=\sum_{1\leq i\neq j\leq d}\lambda^{ij}\big(\pi^{\ell j}_{t}(\omega)-\pi^{\ell i}_{t}(\omega )\pi^{ij}_{t}(\omega)\big)\\&\leq\lambda^{k\ell}\big(\pi^{\ell \ell}_{t}(\omega)-\pi^{\ell k}_{t}(\omega)\pi^{k\ell}_{t}(\omega)\big)=\lambda^{k\ell}\big(1-\pi^{\ell k}_{t}(\omega)\pi^{k\ell }_{t}(\omega)\big)< 0, \end{aligned}$$

which is a contradiction. □

Proposition 2.20

Assume that the bid–ask process$(\Pi_{t})_{t=0}^{T}$satisfies efficient friction (EF). Then we have the equivalence

$$(NA^{\textrm{ps}})\quad \Longleftrightarrow \quad (NA^{\textrm{s}}). $$

Remark 2.21

In general, (NA^s) is neither necessary nor sufficient for (NA^ps). Indeed, (NA^ps) ⇏ (NA^s) is straightforward and (NA^s) ⇏ (NA^ps) follows from [22, Example 3.3].

However, it is also well known that under efficient friction, (NA^r) and (NA^s) are equivalent (cf. [10, Theorem 1] and [22, Theorem 1.7]). Thus in this case, (NA^r), (NA^s) and (NA^ps) coincide.

Proof of Proposition 2.20

In view of Proposition 2.17 and the preceding remark, it is sufficient to show (NA^ps) ⇒ (NA^s). Hence we assume that (NA^ps) holds. Let us show by backward induction on $t=T,T-1,\dots,0$ that $\mathcal{A}_{0}^{t}\cap L^{0}(\mathcal{F}_{t} ; K_{t})=\{0\}$. Let $t=T$ and $v\in\mathcal{A}_{0}^{T}\cap L^{0}(\mathcal {F}_{T} ; K_{T})$; then (NA^ps) implies that $v\in L^{0}(\mathcal{F}_{T} ; -K_{T})$, i.e., $v\in L^{0}(\mathcal{F}_{T} ; K_{T}\cap (-K_{T}))$, which under (EF) is tantamount to $v=0$ a.s.

For the induction step $t+1\leadsto t$, we let $t< T$ and assume $A_{0}^{s}\cap L^{0}(\mathcal{F}_{s} ; K_{s})=\{0\}$ for $s=t+1,\dots,T$. Given $v\in\mathcal{A}_{0}^{t}\cap L^{0}(\mathcal{F}_{t} ; K_{t})$, we may write $v=\sum_{s=t}^{T}\xi_{s}$ for $\xi_{s}\in L^{0}(\mathcal{F}_{s} ; -K_{s})$ by (NA^ps). Since $-v\in L^{0}(\mathcal{F}_{t} ; -K_{t})$ and $-v+\sum_{s=t}^{T-1}\xi _{s}=-\xi_{T}$, we obtain $-v+\sum_{s=t}^{T-1}\xi_{s}\in\mathcal {A}_{0}^{T}\cap L^{0}(\mathcal{F}_{T} ; K_{T})$. Thus by the induction hypothesis, $-v+\sum_{s=t}^{T-2}\xi_{s}=-\xi _{T-1}$. Hence $-v+\sum_{s=t}^{T-2}\xi_{s}\in\mathcal{A}_{0}^{T-1}\cap L^{0}(\mathcal{F}_{T-1} ; K_{T-1})$, and again by the induction hypothesis, $-v+\sum_{s=t}^{T-3}\xi_{s}=-\xi_{T-2}$. Continuing inductively, we get $-v+\xi_{t}=0$; but this means that $v\in L^{0}(\mathcal{F}_{t} ; K_{t}\cap(-K_{t}))$ and thus $v=0$ a.s. by (EF). □

Remark 2.22

With Theorem 2.6, the superhedging result in Schachermayer [22] (see Theorem 4.1 therein) and its proof hold one-to-one under the slightly weaker assumption that $(\Pi_{t})_{t=0}^{T}$ satisfies (NA^ps) instead of (NA^r) — only without the statement with “strictly consistent price systems” in the brackets.

3 Proofs of the main results

This section is devoted to the proof of Theorem 2.6. The other results of Sect. 2 are standard consequences of $\mathcal{A}_{0}^{T}$ being closed, and thus we mainly refer to the known results in the literature and highlight the minor adjustments. This is postponed to the end of the section.

The main hurdle in the proof of Theorem 2.6 is that we do not have at hand that the null-strategies, i.e., the tuples $(\xi_{0},\dots,\xi_{T})\in L^{0}(\mathcal{F}_{0} ; -K_{0})\times\dots \times L^{0}(\mathcal{F}_{T} ; -K_{T})$ with $\sum_{t=0}^{T}\xi_{t}=0$ a.s., form a linear space. Namely, it is shown by Rokhlin [20] that the implication

$$\begin{aligned} &\sum_{t=0}^{T}\xi_{t}=0\ \mbox{a.s.}~\text{with}\ \xi_{t}\in L^{0}(\mathcal {F}_{t} ; -K_{t}) \\ & \Longrightarrow \quad \xi_{t}\in L^{0}(\mathcal{F}_{t} ; K^{0}_{t})\ \mbox{for all}\ t=0,\dots,T \end{aligned}$$

(3.1)

is equivalent to (NA^r), which is strictly stronger than (NA^ps). Thus in the following, we propose a new proof method which overcomes this hurdle.

Before starting with the main proof, we show that $L^{0}(\mathcal{F}_{t} ; -K_{t})$ coincides with the set given in (2.1). This allows us to argue directly with orders $\lambda\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$ and vectors $r\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d}_{+})$ instead of the resulting elements of $L^{0}(\mathcal{F}_{t} ; -K_{t})$. In order to ease notation, we define for all $t=0,\ldots,T$ the mapping

$$\begin{aligned} L_{t}:L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+}) \to L^{0}(\mathcal {F}_{t} ; \mathbb{R}^{d}) \end{aligned}$$

by

$$\begin{aligned} L_{t}(\lambda_{t})=\sum_{1\leq i,j\leq d}\lambda^{ij}_{t}(e^{j}-\pi ^{ij}_{t}e^{i})\qquad \mbox{for all } \lambda_{t}=(\lambda^{ij}_{t})_{1\leq i,j\leq d}\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+}). \end{aligned}$$

Lemma 3.1

Let$\Pi=(\Pi_{t})_{t=0}^{T}$denote a bid–ask process. Then we have

$$\begin{aligned} L^{0}(\mathcal{F}_{t} ; -K_{t})=\{L_{t}(\lambda_{t})-r_{t}: \lambda_{t}\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+}), r_{t}\in L^{0}(\mathcal {F}_{t} ; \mathbb{R}^{d}_{+})\} \end{aligned}$$

(3.2)

for all$t=0,\dots,T$, and consequently, for all$0\leq s\leq t\leq T$,

$$\begin{aligned} \mathcal{A}_{s}^{t}=\bigg\{ \sum_{k=s}^{t}L_{k}(\lambda_{k})-r: \lambda _{k}\in L^{0}(\mathcal{F}_{k} ; \mathbb{R}^{d\times d}_{+}),\ k=s,\dots,t,\ r\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d}_{+})\bigg\} . \end{aligned}$$

(3.3)

Proof

For all $\lambda_{t}\in L^{0}(\mathcal{F}_{t} ; \mathbb {R}^{d\times d}_{+})$, $r_{t}\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d}_{+})$, the random vector $L_{t}(\lambda_{t})-r_{t}$ is an element of $L^{0}(\mathcal{F}_{t} ; -K_{t})$. So we only have to show that for each $v\in L^{0}(\mathcal{F}_{t} ; -K_{t})$, we can find $\lambda_{t}\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$ and $r_{t}\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d}_{+})$ such that $v=L_{t}(\lambda_{t})-r_{t}$ a.s.

For this, let $v\in L^{0}(\mathcal{F}_{t} ; -K_{t})$, i.e., $v(\omega)\in -K_{t}(\omega)$ for each $\omega\in\Omega\setminus N$, where $N\in \mathcal{F}_{t}$ is a set of measure zero. Then satisfies $\widetilde{v}=v$ a.s. and $\widetilde{v}(\omega)\in -K_{t}(\omega)$ for all $\omega\in\Omega$. Next, we define the set-valued mapping $\omega\mapsto P(\omega)\subseteq\mathbb {R}^{d\times d}\times\mathbb{R}^{d}$ by

$$\begin{aligned} P(\omega):=\bigg\{ (\lambda,r)\in\mathbb{R}^{d\times d}\times \mathbb{R}^{d}: \lambda,r \geq0, \! \sum_{1\leq i,j\leq d} \lambda ^{ij}\big(e^{j}-\pi^{ij}_{t}(\omega)e^{i}\big)-r=\widetilde{v}(\omega )\bigg\} . \end{aligned}$$

Then $P(\omega)\neq\emptyset$ for each $\omega\in\Omega$ by virtue of $\widetilde{v}(\omega)\in-K_{t}(\omega)$ for each $\omega \in\Omega$. In addition, the mapping $\omega\mapsto\sum_{1\leq i,j\leq d} \lambda ^{ij}(e^{j}-\pi^{ij}_{t}(\omega)e^{i})-r$ is $\mathcal{F}_{t}$-measurable for each $(\lambda,r)\in\mathbb{R}^{d\times d}_{+}\times \mathbb{R}^{d}_{+}$, and the mapping $(\lambda,r)\mapsto\sum_{1\leq i,j\leq d} \lambda^{ij}(e^{j}-\pi^{ij}_{t}(\omega)e^{i})-r$ is continuous for each $\omega\in\Omega$. Hence we may apply [19, Theorem 14.36] to find $\lambda_{t}\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$ and $r_{t}\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d}_{+})$ such that $(\lambda _{t}(\omega),r_{t}(\omega))\in P(\omega)$ for all $\omega\in \Omega$. This yields $\widetilde{v}(\omega)=\sum_{1\leq i,j\leq d} \lambda ^{ij}_{t}(\omega)(e^{j}-\pi^{ij}_{t}(\omega)e^{i})-r(\omega)$ for each $\omega\in\Omega$ and consequently, we have $v=L_{t}(\lambda_{t})-r_{t}$ a.s. Finally, (3.3) follows directly from (3.2). □

Definition 3.2

For any $t\in\{0,\dots,T-1\}$, we define the (convex) cone of reversible orders at time $t$ by

$$\begin{aligned} \mathcal{R}_{t}:=\{\lambda\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+}): -L_{t}(\lambda)\in\mathcal{A}_{t+1}^{T}\}. \end{aligned}$$

The following lemma establishes a decomposition of the elements of $L^{0}(\mathcal{F}_{t} ; \!\mathbb{R}^{d\times d}_{+})$ into reversible and “purely nonreversible” orders. For the decomposition, one needs that $\mathcal{R}_{t}$ is closed in probability. To achieve this, the lemma assumes that $\mathcal{A}_{t+1}^{T}$ is closed in probability, a property that is not yet shown at this point.

Lemma 3.3

Let$t\in\{0,\dots,T-1\}$and assume that$\mathcal{A}_{t+1}^{T}$is closed in probability. Then for any$\lambda\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$, there is a unique (up to null sets) pair consisting of$\lambda_{1}\in\mathcal{R}_{t}$and$\lambda_{2}\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$with$\lambda=\lambda _{1}+\lambda_{2}$such that for any decomposition$\lambda=\widetilde {\lambda}_{1}+\widetilde{\lambda}_{2}$with$\widetilde{\lambda}_{1}\in \mathcal{R}_{t}$, $\widetilde{\lambda}_{2}\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$, we have

$$\begin{aligned} \vert\lambda_{2}\vert\leq\vert\widetilde{\lambda}_{2}\vert \quad \mathbb{P}\textit{-a.s.}, \end{aligned}$$

(3.4)

where the inequality is strict ℙ-a.s. on$\{\lambda_{2}\neq \widetilde{\lambda}_{2}\}$and$\vert \cdot\vert$denotes the Euclidean norm on$\mathbb{R}^{d\times d}$. In addition, the mappings

$$\begin{aligned} p_{t}:L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})\to\mathcal {R}_{t}\quad\textit{and}\quad q_{t}:L^{0}(\mathcal{F}_{t} ; \mathbb {R}^{d\times d}_{+})\to L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+}) \end{aligned}$$

defined by$p_{t}(\lambda)=\lambda_{1}$and$q_{t}(\lambda)=\lambda_{2}$have the following properties:

• (i) For all$\lambda\in L^{0}(\mathcal {F}_{t} ; \mathbb{R}^{d\times d}_{+})$and$\mu\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}_{+})$, we have$p_{t}(\mu\lambda)=\mu p_{t}(\lambda)$;

• (ii) $\mathrm{Im}(q_{t})=\{\lambda\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+}): q_{t}(\lambda)=\lambda \}$;

• (iii) $\mathrm{Im}(p_{t})\cap\mathrm {Im}(q_{t})=\{0\}$.

We refer to $p_{t}(\lambda)$ and $q_{t}(\lambda)$ as the reversible and the purely nonreversible part of the order $\lambda\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$, respectively. The following continuity of the decomposition is the last ingredient for the proof of Theorem 2.6.

Lemma 3.4

Let$t\in\{0,\dots,T-1\}$and assume that$\mathcal{A}_{t+1}^{T}$is closed in probability. Let$(\lambda_{n})_{n\in\mathbb{N}}\subseteq L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$converge$\mathbb {P}\textit{-a.s.}$to some$\lambda\in L^{0}(\mathcal{F}_{t} ; \mathbb {R}^{d\times d}_{+})$. Then$p_{t}(\lambda_{n})\to p_{t}(\lambda)$and$q_{t}(\lambda_{n})\to q_{t}(\lambda)$$\mathbb{P}\textit{-a.s.}$for$n\to\infty$. In particular, $\mathrm{Im}(q_{t})$is closed in probability.

We postpone the proofs of Lemmas 3.3 and 3.4 and first comment on their use. By the prospective strict no-arbitrage property (NA^ps), reversible orders can be postponed to later periods $s\in\{t+1,\dots ,T\}$. Thus any order at time $t$ can be replaced by its purely nonreversible part at time $t$. On the other hand, if a sequence in $\mathcal{A}_{t}^{T}$ converges, we can show, by leading a possible explosion to a contradiction, that the sequence of purely non-reversible orders at time $t$ must stay bounded. The mapping $p_{t}$ plays the role of the projection in [22] of an arbitrary self-financing strategy onto the set of null-strategies. There, the null-strategies form a linear subspace, which implies that the orthogonal part is automatically self-financing. This property is not available here, and thus we cannot argue with a projection, but need a more complicated decomposition.

Alternatively, the decomposition in Lemma 3.3 could also be defined on the level of portfolio changes $\vartheta_{t} - \vartheta_{t-1}\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d})$. But in the proof of Lemma 3.4, we have to argue directly with the orders $\lambda$.

For the convenience of the reader, we recall a lemma on the existence of a measurable subsequence that is applied several times in the following proofs (see e.g. [22] and [13]).

Lemma 3.5

[22, Lemma A.2]Let$t\in\{0,\ldots,T\}$. For any sequence$(f_{n})_{n\in\mathbb{N}}$in$L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$, there is a random subsequence$(\tau_{k})_{k\in\mathbb{N}}$, i.e., a strictly increasing sequence of ℕ-valued$\mathcal {F}_{t}$-measurable random variables, such that the sequence of random variables$(g_{k})_{k\in\mathbb{N}}$given by$g_{k}(\omega):=f_{\tau _{k}(\omega)}(\omega)$, $k\in\mathbb{N}$, converges a.s. in the one-point compactification$\mathbb{R}^{d\times d}_{+}\cup\{\infty\}$to a random variable$f\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+}\cup\{\infty\})$. In fact, we may find the subsequence such that

$$\begin{aligned} \vert f\vert=\limsup_{n\to\infty}\vert f_{n}\vert \qquad \mathbb {P}\textit{-a.s.}, \end{aligned}$$

where$\vert\infty\vert=\infty$.

Proof of Lemma 3.3

First, we show the existence and uniqueness of the decomposition satisfying (3.4). Fix $\lambda\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$ and define the nonempty set

$$\begin{aligned} X_{\lambda}:=\{\widetilde{\lambda}\in\mathcal{R}_{t} : \lambda -\widetilde{\lambda}\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})\}, \end{aligned}$$

which consists of the first components of the possible decompositions of $\lambda$. Under the assumptions made, the convex cone $\mathcal{R}_{t}$ is closed in probability and closed under multiplication with nonnegative $\mathcal{F}_{t}$-measurable scalars. This implies that $X_{\lambda}$ is closed in probability and closed under measurable convex combinations. We have to show that

$$\begin{aligned} x:=\operatorname*{ess\,inf}_{\widetilde{\lambda}\in X_{\lambda}}\vert\lambda -\widetilde{\lambda}\vert \end{aligned}$$

is attained and the minimiser is unique. To that end, notice that the set of random variables $\{\vert\lambda-\widetilde{\lambda}\vert: \widetilde{\lambda}\in X_{\lambda}\}$ is downward directed. Indeed, for each $\lambda_{1},\lambda_{2}\in X_{\lambda}$, one has $\vert\lambda-\lambda_{3}\vert= \vert\lambda-\lambda_{1}\vert\wedge \vert\lambda-\lambda_{2}\vert$, where

Hence there is a sequence of random variables $(\lambda_{n})\subseteq X_{\lambda}$ such that $\vert\lambda-\lambda_{n}\vert\to x$$\mathbb {P}\text{-a.s.}$ for $n\to\infty$. From the parallelogram law (see e.g. [1, Lemma 6.51]) of the Euclidean norm on $\mathbb{R}^{d\times d}$ and the convexity of $X_{\lambda}$, we obtain

$$\begin{aligned} \vert\lambda_{n}-\lambda_{m}\vert^{2} & = 2\vert\lambda-\lambda_{n}\vert ^{2}+2\vert\lambda-\lambda_{m}\vert^{2}-4 \bigg\vert \lambda-\frac {\lambda_{n}+\lambda_{m}}{2}\bigg\vert ^{2} \\ &\leq2\vert\lambda-\lambda_{n}\vert^{2}+2\vert\lambda-\lambda _{m}\vert^{2}-4x\qquad \mathbb{P}\text{-a.s.}, \end{aligned}$$

(3.5)

implying that $(\lambda_{n})_{n\in\mathbb{N}}$ converges $\mathbb {P}\text{-a.s.}$ to some element of $L^{0}(\mathcal{F}_{t} ; \mathbb {R}^{d\times d}_{+})$. By the closedness of $X_{\lambda}$, one derives the existence. Uniqueness in the postulated sense also follows from the estimate (3.5). This means that the mappings $p_{t}$ and $q_{t}$ are well defined, and it remains to show that they satisfy the claimed properties.

(i) Let $\mu\geq0$ be an $\mathcal {F}_{t}$-measurable random variable. As a consequence of $\mathcal{R}_{t}$ and $L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$ being closed under multiplication with nonnegative $\mathcal{F}_{t}$-measurable random variables, we have $X_{\mu\lambda}= \{\mu\widetilde{\lambda }:\widetilde{\lambda}\in X_{\lambda}\}$. Then the assertion follows from the construction of $p_{t}$ from above.

(ii) Let $\lambda\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$. We have $p_{t}(\lambda)+p_{t}(q_{t}(\lambda ))\in\mathcal{R}_{t}+\mathcal{R}_{t}\subseteq\mathcal{R}_{t}$ and $\lambda-(p_{t}(\lambda)+p_{t}(q_{t}(\lambda)))=q_{t}(\lambda )-p_{t}(q_{t}(\lambda))\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$ by the definition of $p_{t}$, and thus in particular

$$\begin{aligned} p_{t}(\lambda)+p_{t}\big(q_{t}(\lambda)\big)\in X_{\lambda}. \end{aligned}$$

(3.6)

On the other hand, one has

$$\begin{aligned} \Big\vert \lambda-\Big(p_{t}(\lambda)+p_{t}\big(q_{t}(\lambda)\big)\Big)\Big\vert &=\big\vert q_{t}(\lambda)-p_{t}\big(q_{t}(\lambda)\big)\big\vert \\ &\leq\vert q_{t}(\lambda)\vert =\left\vert\lambda-p_{t}\left(\lambda\right)\right\vert\quad \mathbb{P}\text{-a.s.}, \end{aligned}$$

(3.7)

where the inequality holds since $p_{t}(q_{t}(\lambda))$ is the optimal reversible part of $q_{t}(\lambda)$. By (3.7), (3.6) and the uniqueness of the optimal reversible part in the decomposition of $\lambda$, it follows that $p_{t}(\lambda)+p_{t}(q_{t}(\lambda)) =p_{t}(\lambda)$$\mathbb {P}\text{-a.s.}$ and thus

$$\begin{aligned} \mathrm{Im}(p_{t}\circ q_{t})=\{0\}. \end{aligned}$$

(3.8)

The assertion immediately follows from (3.8).

(iii) This follows immediately from (ii). □

Proof of Lemma 3.4

We have to show that

$$\begin{aligned} \lambda_{n}\to\lambda\quad\mathbb{P}\text{-a.s.}\quad\implies \quad p_{t}(\lambda_{n})\to p_{t}(\lambda)\quad\mathbb{P}\text{-a.s.} \end{aligned}$$

(3.9)

The property that $\mathrm{Im}(q_{t})$ is closed in probability directly follows from Lemma 3.3 (ii) and (3.9) by passing to an almost surely converging subsequence. To show (3.9), we define for each $n\in\mathbb{N}$ the $\mathcal{F}_{t}$-measurable real-valued random variable

$$\begin{aligned} \mu_{n}(\omega):= 1\wedge\inf_{\substack{1\leq i,j\leq d\\ {p_{t}(\lambda)}^{ij}(\omega)>0}}\frac{\lambda_{n}^{ij}(\omega )}{{p_{t}(\lambda)}^{ij}(\omega)}. \end{aligned}$$

(3.10)

One has that $\mu_{n} p_{t}(\lambda)\in\mathcal{R}_{t}$ and $\lambda _{n}-\mu_{n} p_{t}(\lambda)\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$, i.e., $\mu_{n} p_{t}(\lambda)\in X_{\lambda_{n}}$. This means that we compress the transfer matrix $p_{t}(\lambda)$ to use it for a (in general not optimal) decomposition of $\lambda_{n}$ into a reversible and a nonreversible part. Note that in the trivial case where $p_{t}(\lambda )^{ij}(\omega)=0$ for all $(i,j)$, the compression is irrelevant because here one has $\mu_{n}(\omega)=1$. As $p_{t}(\lambda_{n})$ is the optimal reversible part of $\lambda_{n}$, it follows that

$$\begin{aligned} \vert\lambda_{n}-p_{t}(\lambda_{n})\vert \le\vert\lambda_{n}-\mu_{n} p_{t}(\lambda)\vert \qquad \mathbb {P}\text{-a.s., } \forall n\in\mathbb{N}. \end{aligned}$$

(3.11)

In addition, due to $\lambda^{ij}\ge p_{t}(\lambda)^{ij}\ge0$ for all $i,j=1,\ldots,d$ and $\lambda_{n}\to\lambda$, we have that $\mu_{n}\to1$$\mathbb {P}\text{-a.s.}$ Combining this with the triangle inequality of the Euclidean norm, we arrive at

$$\begin{aligned} \limsup_{n\to\infty}\vert\lambda-p_{t}(\lambda_{n})\vert&= \limsup_{n\to\infty}\vert\lambda_{n}-p_{t}(\lambda_{n})\vert\\ &\le \limsup_{n\to\infty}\vert\lambda_{n}-\mu_{n} p_{t}(\lambda)\vert= \vert\lambda-p_{t}(\lambda)\vert \qquad \mathbb{P}\text{-a.s.}, \end{aligned}$$

where the inequality follows from (3.11). Since $p_{t}(\lambda)$ is the optimal reversible part of $\lambda$, this just means that

$$\begin{aligned} \vert\lambda-p_{t}(\lambda_{n})\vert\longrightarrow \vert\lambda -p_{t}(\lambda )\vert \qquad \text{as $n\to\infty, \mathbb{P}$-a.s.} \end{aligned}$$

(3.12)

To complete the proof, we define the $\mathcal{F}_{t}$-measurable random variable

$$\begin{aligned} {\varepsilon}(\omega):=\sup\left\{1/k:k\in\mathbb{N}, \vert p_{t}\left(\lambda_{n}\right)-p_{t}\left(\lambda\right)\vert (\omega)\ge1/k\ \mbox{for infinitely many}\ n\right\} \end{aligned}$$

which is strictly positive on the set $A:=\{p_{t}(\lambda_{n})\not\to p_{t}(\lambda)\}\in\mathcal{F}_{t}$. Then we construct the random subsequence $(\tau_{k})_{k\in\mathbb{N}}$ recursively by setting $\tau_{0}:=0$ and

$$\tau_{k}:= \inf\{n\in\mathbb{N}:n>\tau_{k-1}, \vert p_{t}(\lambda _{n})-p_{t}(\lambda)\vert\ge{\varepsilon}\} \qquad \text{on $A$} $$

and $\tau_{k}:=k$ on $\Omega\setminus A$. By construction, we have that

$$\begin{aligned} \mathbb{P}\left[ \vert p_{t}(\lambda_{\tau_{k}})-p_{t}(\lambda)\vert\ge {\varepsilon},\ \forall k\in\mathbb{N}\, \big| A\right]=1. \end{aligned}$$

(3.13)

Due to $\lambda_{n}\to\lambda$ and $0\le p_{t}(\lambda_{n})^{ij}\le \lambda^{ij}_{n}$, one has $\sup_{n\in\mathbb{N}}\vert p_{t}(\lambda _{n})\vert \le\sup_{n\in\mathbb{N}}\vert\lambda_{n}\vert<\infty$$\mathbb {P}\text{-a.s.}$ Thus by Lemma 3.5, there exist a random subsequence $(\widetilde{\tau}_{k})_{k\in\mathbb {N}}$ of $(\tau_{k})_{k\in\mathbb{N}}$ and an $f\in L^{0}(\mathcal{F}_{t} ; \mathbb {R}^{d\times d}_{+})$ such that $p_{t}(\lambda_{\widetilde{\tau}_{k}})\to f\ \mathbb{P}\text{-a.s.}$ Together with (3.12), this implies that $\vert\lambda -f\vert= \vert\lambda-p_{t}(\lambda)\vert\ \mathbb{P}\text{-a.s.}$. In addition, we have $f\in X_{\lambda}$. On the other hand, by (3.13), $f\not= p_{t}(\lambda)$ on $A\ \mathbb{P}\text{-a.s.}$ Since $p_{t}(\lambda)$ is the unique optimal reversible part of $\lambda$ in the sense of Lemma 3.3, these two properties can only hold simultaneously if $\mathbb{P}[A]=0$ and we are done. □

Remark 3.6

We note that for the proof of Theorem 2.6, we only need the weaker assertion that $\mathrm{Im}(q_{t})$ is closed in probability. To show this assertion, one can restrict oneself to sequences with $\lambda_{n}=q_{t}(\lambda _{n})$, i.e., $p_{t}(\lambda_{n}) = 0$, for all $n\in\mathbb{N}$, and the above proof would already be completed with (3.12).

We are now in the position to prove Theorem 2.6. As in Kabanov et al. [11], we argue by induction on the periods. The key difference is that reversible orders are postponed to later periods, instead of being executed and compensated in the same period. The later is not possible since the null-strategies do not form a linear space.

Proof of Theorem 2.6

Assume that the bid–ask process $(\Pi_{t})_{t=0}^{T}$ satisfies (NA^ps). Let us prove by a backward induction on $t=T,T-1,\ldots,0$ that $\mathcal{A}_{t}^{T}$ is closed in probability. The induction basis $t=T$ is trivial since $\mathcal{A}_{T}^{T}$ coincides with $L^{0}(\mathcal{F}_{T} ; -K_{T})$ which is closed in probability.

Induction step $t+1\leadsto t$. We assume that $\mathcal{A}_{t+1}^{T}$ is closed in probability for some $t\leq T-1$ and have to show that $\mathcal{A}_{t}^{T}$ is closed too. Therefore, let $(\xi_{n})_{n\in \mathbb{N}}$ be a sequence in $\mathcal{A}_{t}^{T}$ which converges to some $\xi\in L^{0}(\mathbb{R}^{d})$ in probability. Obviously, we may assume that $\xi_{n}\to\xi$ almost surely by passing to a subsequence. We have to show that $\xi\in\mathcal{A}_{t}^{T}$.

Step 1. According to Lemma 3.1, we may write

$$\begin{aligned} \xi_{n}=\sum_{s=t}^{T}L_{s}(\lambda_{s}^{n})-r^{n}, \qquad n\in\mathbb{N}, \end{aligned}$$

(3.14)

where $(\lambda_{s}^{n})_{n\in\mathbb{N}}\subseteq L^{0}(\mathcal{F}_{s} ; \mathbb{R}^{d\times d}_{+})$ for each $s=t,\dots,T$ and $(r^{n})_{n\in \mathbb{N}}\subseteq L^{0}(\mathbb{R}^{d}_{+})$. Recall that $L^{0}(\mathbb{R}^{d}_{+}) = L^{0}(\mathcal{F}_{T} ; \mathbb {R}^{d}_{+})$ by convention. Under the induction hypothesis that $\mathcal{A}_{t+1}^{T}$ is closed in probability, we apply Lemma 3.3 in order to decompose $\lambda_{t}^{n}$ into $p_{t}(\lambda_{t}^{n})+q_{t}(\lambda_{t}^{n})$ and thus

$$\begin{aligned} L_{t}(\lambda_{t}^{n})=L_{t}\big(p_{t}(\lambda_{t}^{n})\big)+L_{t}\big(q_{t}(\lambda _{t}^{n})\big), \end{aligned}$$

where $p_{t}(\lambda_{t}^{n})$ is reversible and $q_{t}(\lambda_{t}^{n})$ is purely nonreversible. This means that

$$\begin{aligned} L_{t}\big(p_{t}(\lambda^{n}_{t})\big)\in\mathcal{A}_{0}^{t}\cap(-\mathcal {A}_{t+1}^{T}). \end{aligned}$$

The prospective strict no-arbitrage property (NA^ps) implies that

$$\mathcal{A}_{0}^{t}\cap(-\mathcal{A}_{t+1}^{T})\subseteq\mathcal {A}_{0}^{t+1}\cap(-\mathcal{A}_{t+1}^{T})\subseteq\mathcal{A}_{t+1}^{T} $$

and thus $L_{t}(p_{t}(\lambda_{t}^{n}))\in\mathcal{A}_{t+1}^{T}$. This allows us to rewrite (3.14) as

$$\begin{aligned} \xi_{n}= L_{t}\big(q_{t}(\lambda_{t}^{n})\big)+L_{t}\big(p_{t}(\lambda_{t}^{n})\big) +\sum_{s=t+1}^{T}L_{s}(\lambda_{s}^{n})-r^{n} =: L_{t}\big(q_{t}(\lambda_{t}^{n})\big) +x_{n} \end{aligned}$$

with $x_{n}\in\mathcal{A}_{t+1}^{T}$. Hence from now on, we can assume without loss of generality that $(\lambda_{t}^{n})_{n\in\mathbb{N}}\subseteq\mathrm{Im}(q_{t})$.

Step 2. Our next goal is to show that

$$\begin{aligned} \mathbb{P}[A]=0,\qquad \mbox{where } A:=\Big\{ \limsup_{n\to \infty}\vert\lambda^{n}_{t}\vert=\infty\Big\} . \end{aligned}$$

(3.15)

By Lemma 3.5, we may pass to a measurable subsequence $(\tau_{k})_{k\in\mathbb{N}}$ such that for a.e. $\omega\in A$, we have $\lambda^{\tau_{k}(\omega)}_{t}(\omega )\neq0$ for all $k\in\mathbb{N}$ and $\lim_{k\to\infty}\vert \lambda ^{\tau_{k}(\omega)}_{t}(\omega)\vert=\infty$. Then by the stability of $\mathrm{Im}(q_{t})$ under multiplication with $\mu\in L^{0}(\mathcal {F}_{t} ; {\mathbb {R}}_{+})$ (see Lemma 3.3 (i)), we find that belongs to $\mathrm {Im}(q_{t})$, and in addition, we define

We have a.s. Now we may apply once again Lemma 3.5 to find a measurable subsequence $(\sigma _{k})_{k\in\mathbb{N}}$ such that

$$\widetilde{\lambda}_{t}:=\lim\limits_{k\to\infty}\widetilde {\lambda}^{\sigma_{k}}_{t} $$

exists and $\vert\widetilde{\lambda}_{t}\vert=\lim\limits_{k\to \infty}\vert\widetilde{\lambda}^{\sigma_{k}}_{t}\vert$. Consequently, $L_{t}(\widetilde{\lambda}^{\sigma_{k}}_{t})\to L_{t}(\widetilde{\lambda}_{t})$ and thus the sequence

$$\begin{aligned} \bigg(\sum_{s=t+1}^{T}L_{s}(\widetilde{\lambda}^{\sigma _{k}}_{s})-\widetilde{r}^{\sigma_{k}}\bigg)_{k\in\mathbb{N}}\subseteq \mathcal{A}_{t+1}^{T} \end{aligned}$$

converges to $-L_{t}(\widetilde{\lambda}_{t})$. Since $\mathcal{A}_{t+1}^{T}$ is closed and due to Lemma 3.1, the limit can be written as $\sum_{s=t+1}^{T}L_{s}(\widetilde{\lambda}_{s})-\widetilde{r}$, i.e., we have

$$\begin{aligned} L_{t}(\widetilde{\lambda}_{t})+\sum_{s=t+1}^{T}L_{s}(\widetilde{\lambda }_{s})-\widetilde{r}=0\qquad \mathbb{P}\text{-a.s.} \end{aligned}$$

with $\widetilde{\lambda}_{s}\in L^{0}(\mathcal{F}_{s} ; \mathbb {R}^{d\times d}_{+})$ and $\widetilde{r}\in L^{0}(\mathcal{F}_{s} ; \mathbb{R}^{d}_{+})$. Thus we have that $\widetilde{\lambda}_{t}$ is reversible, i.e., $\widetilde {\lambda}_{t}\in\mathcal{R}_{t}=\mathrm{Im}(p_{t})$. But on the other hand, the sequence $(\widetilde{\lambda}^{\sigma_{k}}_{t})_{k\in\mathbb {N}}$ belongs to $\mathrm{Im}(q_{t})$; thus by Lemma 3.4, $\widetilde{\lambda}_{t}\in\mathrm{Im}(q_{t})$. Therefore $\widetilde{\lambda}_{t}\in\mathrm{Im}(p_{t})\cap \mathrm{Im}(q_{t})$, hence $\widetilde{\lambda}_{t}=0$ a.s. according to Lemma 3.3 (iii). Since $\mathbb{P}[A]=\mathbb{P}[\widetilde{\lambda}_{t}\neq0]$, this is only possible if $\mathbb{P}[A]=0$, i.e., (3.15) holds true.

Step 3. According to Step 2, we can apply Lemma 3.5 to find a measurable subsequence $(\tau _{k})_{k\in\mathbb{N}}$ such that $\lambda^{\tau_{k}}_{t}\to\lambda_{t} \in L^{0}(\mathcal{F}_{t} ; \mathbb{R}^{d\times d}_{+})$ ℙ-a.s. for $k\to\infty$, and consequently $L_{t}(\lambda^{\tau _{k}}_{t})\to L_{t}(\lambda_{t})$ a.s. Hence $\sum_{s=t+1}^{T}L_{s}(\lambda _{s}^{\tau_{k}})-r^{\tau_{k}}$ converges a.s. to $\xi-L_{t}(\lambda_{t})$, which by the induction hypothesis belongs to $\mathcal{A}_{t+1}^{T}$. This implies that $\xi\in\mathcal{A}_{t}^{T}$. □

Finally, we finish up the remaining proofs. Notice that every result is a standard consequence of the set $\mathcal{A}_{0}^{T}$ being closed in probability under the (NA^ps) condition; hence we only give the respective references and point out where some changes are needed.

Proof of Corollary 2.8

It suffices to repeat the arguments of the proof of [22, Theorem 2.1] (page 29, lines 5–33) with $\mathcal{A}_{0}^{T}$ (instead of $\widetilde {\mathcal{A}}_{T}$), which is closed by Theorem 2.6. □

Proof of Theorem 2.11

(NA^wps) ⇒ $\exists$ CPS. According to the condition (NA^wps), there is a bid–ask process $(\widetilde{\Pi}_{t})_{t=0}^{T}$ with $\widetilde{\Pi}_{t}\leq \Pi_{t}$ a.s. for all $t=0,\dots,T$ and satisfying (NA^ps). Corollary 2.8 implies that $(\widetilde {\Pi}_{t})_{t=0}^{T}$ admits a CPS, which is obviously a CPS for $(\Pi _{t})_{t=0}^{T}$ as well.

$\exists$ CPS ⇒ (NA^wps). It is again sufficient to repeat the arguments of the proof of [22, Theorem 2.1] (page 30, lines 1–12) to define a frictionless bid–ask process $(\widetilde{\Pi }_{t})_{t=0}^{T}$, i.e., $\widetilde{\pi}_{t}^{ij}=1/\widetilde{\pi }_{t}^{ji}$, with $\widetilde{\Pi}_{t}\leq\Pi_{t}$ a.s. for all $t=0,\dots,T$ and satisfying (NA), which in the frictionless case coincides with (NA^ps) by Proposition 2.17. Thus $(\Pi_{t})_{t=0}^{T}$ satisfies (NA^wps). □

Proof of Corollary 2.15

This is a well-known consequence of the existence of a consistent price system. Indeed, we may use [12, Proposition 3.2.6] to see that the existence of a consistent price system implies $\overline{\mathcal{A}_{0}^{T}}\cap L^{0}(\mathcal{F}_{T} ; K_{T})\subseteq L^{0}( \mathcal{F}_{T} ; \partial K_{T})$. To complete the proof, we observe that $\partial K_{T}\cap\mathbb{R}^{d}_{+}=\{0\}$. Indeed, due to $\pi^{ij}<\infty$, the existence of a $v\in\mathbb{R}^{d}_{+}\setminus \{0\}$ and a sequence $(v_{n})_{n\in\mathbb{N}}\subseteq\mathbb {R}^{d}\setminus K_{T}(\omega)$ with $v_{n}\to v$ can easily be led to a contradiction. □

Remark 3.7

Our results can be extended to the Kabanov model as defined in [12, Sect. 3.2], which in addition to the barter market considered here also covers a wider range of models, e.g. models of a barter market where a bank account is charged the transaction costs, and models where baskets of assets are exchanged. To see this, we briefly highlight the minor adjustments. On the other hand, the proofs of Lemmas 3.3 and 3.4 are heavily based on the polyhedral structure of the solvency cones. The key argument that the sequence $(\mu_{n})$ defined in (3.10) converges to 1 does not work for general closed solvency cones.

The Kabanov model is defined as follows. Let $((X_{t}^{i})_{t=0}^{T})_{i\in \mathbb{N}}$ be a sequence of adapted $\mathbb{R}^{d}$-valued processes such that for all $t$ and $\omega$, the set $\{i\in\mathbb{N}: X^{i}_{t}(\omega)\neq0\}$ is nonempty and finite, and set

$$\begin{aligned} K_{t}(\omega):= \mathrm{cone}\big(-X^{i}_{t}(\omega): i\in\mathbb {N}\big). \end{aligned}$$

In this case, $K=(K_{t})_{t=0}^{T}$ is called a cone-valued process. In addition, we assume $\mathbb{R}^{d}_{+}\setminus\{0\}\subseteq\mathrm {int } K_{T}(\omega)$ for all $\omega$ (which corresponds to the possibility to freely dispose of assets and $\pi^{ij}_{T}<\infty$ for all $i,j$ in the base model) and $-K_{T}(\omega)\cap\mathbb{R}^{d}_{+} = \{ 0\}$ (which corresponds to $\pi^{ij}_{T}\le\pi^{ik}_{T}\pi^{kj}_{T}$ and $\pi ^{ii}_{T}=1$ for all $i,j,k$). The cone of hedgeable claims attainable from zero endowment by trading between $s$ and $t$ is given by $\mathcal{A}_{s}^{t}=\sum_{k=s}^{t}L^{0}(\mathcal{F}_{k} ; -K_{k}),\ s\leq t$. The conditions (NA) and (NA^ps) are defined accordingly. We now sketch how the arguments of the previous proofs can be applied in this more general setting. Let $I_{t}(\omega):=\sup \{n\in\mathbb{N}: X^{n}_{t}(\omega)\not=0\}$ for $\omega\in\Omega$ and $t=0,\dots,T$. The assumptions above guarantee that $I_{t}$ is an ℕ-valued $\mathcal{F}_{t}$-measurable random variable. Because $\Omega=\bigcup_{I\in\mathbb{N}}\{I_{t}=I\}$, the arguments from Lemmas 3.1, 3.3 and 3.4 can be separately applied on the sets $\{ I_{t}=I\}$ for $I\in\mathbb{N}$. In particular, portfolio changes can be represented by $L_{t}(\lambda_{t}):= \sum_{i=1}^{I_{t}}\lambda^{i}_{t}X^{i}_{t}$, where $\lambda ^{i}_{t}\in L^{0}(\mathcal{F}_{t} ; \mathbb{R}_{+})$. The Euclidean norm on $\mathbb{R}^{d\times d}$ that is used for the decomposition of an order into the reversible and the purely nonreversible part is replaced by

$$\begin{aligned} \vert\lambda\vert:=\sqrt{\sum_{i=1}^{I}(\lambda^{i})^{2}}\qquad \text{on}\ \{I_{t}=I\}. \end{aligned}$$

With these adjustments, Theorem 2.6 extends to the Kabanov model by arguing along the lines of the original proofs. We note again that it is crucial that for fixed $\omega$, only linear combinations from finitely many $X^{i}_{t}(\omega)$ need to be considered.

Finally, we say that $K=(K_{t})_{t=0}^{T}$ satisfies the property (NA^wps) if there is a cone-valued process $\widetilde {K}=(\widetilde{K}_{t})_{t=0}^{T}$ with the property (NA^ps) such that $K_{t}(\omega)\subseteq\widetilde{K}_{t}(\omega)$ for all $\omega$ and $t$. Then Theorem 2.11 holds true in the Kabanov model as well. Indeed, (NA^wps) implies the existence of a consistent price system for $K=(K_{t})_{t=0}^{T}$, and on the other hand, given a CPS $Z=(Z_{t})_{t=0}^{T}$, the cone-valued process $\widetilde{K}=(\widetilde{K}_{t})_{t=0}^{T}$ defined by $\widetilde {K}_{t}(\omega):=(\mathbb {R}_{+}Z_{t}(\omega))^{\star}$ satisfies (NA^ps) and $K_{t}(\omega)\subseteq\widetilde{K}_{t}(\omega)$ for all $t$ and $\omega$, i.e., $K$ satisfies (NA^wps).

In addition, our reasoning to show the closedness of $\mathcal{A}_{0}^{T}$ can also be applied to models with incomplete information such as those considered in [2, 4], where arguing on the level of orders is quite natural.

4 (Counter-)Examples

We start with two very simple examples that illustrate the difference between (NA^r), (NA^ps) and (NA^wps) and the need to consider CPSs which do not lie in the relative interior of the bid–ask spread.

Example 4.1

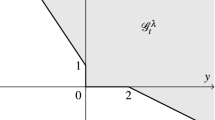
(NA^ps) ⇏ (NA^r). We consider a deterministic two-asset one-period model with the bid–ask process given by

$$\Pi_{t} = \begin{pmatrix} 1 & \overline{S}_{t}\\ 1/\underline{S}_{t} & 1 \end{pmatrix} ,\qquad t=0,1, $$

where the deterministic processes $(\underline{S}_{t})_{t=0,1}$ and $(\overline{S}_{t})_{t=0,1}$ are illustrated in Fig. 1. This is just a two-asset model with a bank account that does not pay interest and one stock with bid price $(\underline{S}_{t})_{t=0,1}$ and ask price $(\overline{S}_{t})_{t=0,1}$.

Here, we have $K_{t}=\mathrm{cone}(\overline{S}_{t}e^{1}-e^{2}, e^{2}-\underline{S}_{t}e^{1}, e^{1},e^{2})$, and its dual is given by $K^{\star}_{t}=\{(y^{1},y^{2})\in\mathbb{R}^{2}_{+}: \underline{S}_{t}y^{1}\leq y^{2}\leq \overline{S}_{t} y^{1}\}$ for $t=0,1$. Since $\Omega$ is a singleton, a CPS must be constant in time. Thus the market admits the unique (up to scalar multiples) CPS $Z=(Z^{1}_{t}, Z^{2}_{t})_{t=0,1}$ given by $Z_{t}=(1,1)$ for $t=0,1$.

Recall that a strictly consistent price system (SCPS, for short) is a CPS which has $Z_{t}\in L^{0}(\mathcal{F}_{t} ; \mathrm{ri~}K^{\star}_{t})$ for all $t$, where $\mathrm{ri~}K^{\star}_{t}$ denotes the relative interior of $K^{\star}_{t}$, and that (NA^r) is equivalent to the existence of a SCPS (see Schachermayer [22, Theorem 1.7]). We have $\mathrm {ri~}K^{\star}_{t}=\{(y^{1},y^{2})\in\mathrm{int}(\mathbb{R}^{2}_{+}): y^{2}/y^{1}\in\mathrm{ri}[\underline{S}_{t},\overline{S}_{t}]\}$ for $t=0,1$ (see e.g. Rokhlin [20, Eq. (3.2)]). Thus $Z$ is not a SCPS since $Z^{2}_{0}/Z^{1}_{0}=1\notin(1/2,1)$. Hence the model cannot satisfy (NA^r). Also the Penner condition

$$\begin{aligned} L^{0}(\mathcal{F}_{t-1} ; K^{0}_{t})\subseteq L^{0}(\mathcal{F}_{t-1} ; K^{0}_{t-1})\qquad \mbox{for all }t=1,\dots,T \end{aligned}$$

(4.1)

is not satisfied. On the other hand, we have that

$$\mathcal{A}_{0}^{0}\cap(-\mathcal{A}_{1}^{1}) =\mathrm {cone}(e^{2}-e^{1})\subseteq\mathrm{cone}(e^{2}-e^{1}, e^{1}-e^{2}, -e^{1}, -e^{2}) = \mathcal{A}_{1}^{1}, $$

i.e., only a long stock position built up at time 0 can be liquidated without losses at time 1, but the purchase of the stock (asset 2) can also be postponed to time 1. Thus the model satisfies (NA^ps).

Example 4.2

(NA^wps) ⇏ (NA^ps). We consider a variant of Example 4.1, where the processes $(\underline{S}_{t})_{t=0,1}$ and $(\overline {S}_{t})_{t=0,1}$ are given in Fig. 2. The market still admits the unique (up to scalar multiples) CPS $Z_{t}=(1,1)$ for $t=0,1$, but now fails (NA^ps) since

$$\mathcal{A}_{0}^{0}\cap(-\mathcal{A}_{1}^{1}) =\mathrm{cone}(e^{2}-e^{1})\not \subseteq\mathrm{cone}(e^{2}-2 e^{1}, e^{1}-e^{2}, -e^{1}, -e^{2}) = \mathcal{A}_{1}^{1}. $$

On the other hand, the model satisfies (NA^wps) since the more favourable bid–ask process in Fig. 1 satisfies (NA^ps).

Fig. 2

Deterministic model satisfying (NA^wps), but not (NA^ps). One has $\underline{S}_{0}=1/2$, $\overline{S}_{0}=1$, $\underline{S}_{1}=1$ and $\overline{S}_{1}=2$.

Finally, we provide an example showing that (NA^wps) cannot be replaced by the “next weaker” condition that there exists a more favourable market, i.e., a bid–ask process $(\widetilde {\Pi}_{t})_{t=0}^{T}$ with $\widetilde{\Pi}_{t}\leq\Pi_{t}$ for each $t=0,\dots,T$, such that $(\widetilde{\Pi}_{t})_{t=0}^{T}$ satisfies (NA) and

$$\begin{aligned} \mathcal{A}_{0}^{t}\cap(-\widetilde{\mathcal{A}}_{t}^{T})\subseteq \widetilde{\mathcal{A}}_{t}^{T}\qquad \mbox{for all } t=0,\dots ,T \end{aligned}$$

(4.2)

(cf. Remark 2.16). We show that there is a bid–ask process $(\Pi_{t})_{t=0}^{3}$ with four assets satisfying (4.2) which allows an approximate arbitrage (see Definition 2.14). In the spirit of the basic Example 3.1 of Schachermayer [22], which can be used to achieve an approximate arbitrage, the example is based on the idea of two consecutive approximate hedges. An approximate hedge is a sequence of trading strategies that hedge a given portfolio position in the limit. There exists a more favourable bid–ask process $(\widetilde{\Pi }_{t})_{t=0}^{3}$ such that (4.2) holds, but which only turns the first approximate hedge into a perfect hedge and thus the model still satisfies (NA).

The example highlights the importance of a possible “cascade” of approximate hedges, which is to the best of our knowledge a phenomenon not discussed in the previous literature. It is also of interest for the discussion of adjusted bid–ask processes as introduced in Jacka et al. [9](see Remark 4.4).

Example 4.3

A cascade of approximate hedges

Let $T=3$, $\Omega=\mathbb{N}^{2}\times\{-1/2,1/2\}^{2}$, $\mathcal {F}=2^{\Omega}$ and all states have positive probability. In addition, the information structure is given by $\mathcal{F}_{0}=\{ \emptyset,\Omega\}$,

$$\begin{aligned} \mathcal{F}_{1}&=\sigma\Big(\Big\{ \big\{ (n,m,i,j): (m,i,j) \in \mathbb{N}\times\{-1/2, 1/2\}^{2}\big\} : n\in\mathbb{N}\Big\} \Big),\\ \mathcal{F}_{2}&=\sigma\big( \big\{ \{(n,m,i,-1/2), (n,m,i,1/2)\} : (n,m,i)\in\mathbb{N}^{2}\times\{-1/2,1/2\}\big\} \big), \end{aligned}$$

and $\mathcal{F}_{3}=2^{\Omega}=\mathcal{F}$. This means that $n$ is revealed at time 1, $m$ and $i$ are revealed at time 2 and finally $j$ is revealed at time 3. Next, we define a bid–ask process $(\Pi _{t})_{t=0}^{3}$ depending on a parameter $a>0$ for $t=0,1$ by

$$\begin{aligned} &\Pi_{0}= \begin{pmatrix} 1 & 1 & 1 & 1\\ a & 1 & \cdot& \cdot\\ a & \cdot& 1& \cdot\\ a & \cdot& \cdot&1 \end{pmatrix} ,\qquad \Pi_{1}\equiv \begin{pmatrix} 1 & a & a & a\\ a & 1 & \cdot& \cdot\\ a & \cdot& 1& \cdot\\ 1 & \cdot& \cdot& 1 \end{pmatrix} \end{aligned}$$

and for $t=2,3$ depending on the state $(n,m,i,j)\in\mathbb {N}^{2}\times\{-1/2,1/2\}^{2}$ as

$$\begin{aligned} \Pi_{2}(n,m,i,j)= \begin{pmatrix} 1 & a & a & a\\ a & 1& \cdot& \cdot\\ \frac{1}{1+i} & \cdot& 1& \cdot\\ \frac{1}{1-\frac{i}{n}} & \cdot& \cdot& 1 \end{pmatrix} ,\qquad \Pi_{3}(n,m,i,j)= \begin{pmatrix} 1 & a & a & a\\ \frac{1}{1+\frac{1}{4}+j} & 1 & \cdot& \cdot\\ \frac{1}{1+i}\frac{1}{1-\frac{j}{m}} & \cdot& 1& \cdot\\ a & \cdot& \cdot& 1 \end{pmatrix} . \end{aligned}$$

The missing entries are specified via the direct transfer over the first asset, i.e., $\pi^{ij}_{t}:=\pi^{i1}_{t}\pi^{1j}_{t}$ for $2\leq i\neq j\leq4$. This means that the first asset plays the role of a money market account and the assets 2,3, and 4 represent risky stocks. Finally, we choose the parameter $a$ prohibitively high such that the corresponding transfers are unattractive; more precisely, we set $a:=5>4$.

This market is actually frictionless with special short- and long-selling constraints. Asset 2 yields the random return $1/4+j$, $j\in\{-1/2,1/2\}$. It can be approximately hedged, yielding an extra profit, by the return $-j/m$ of asset 3 between times 2 and 3. On the other hand, asset 3 must be bought already at time 0 which leads to the prior random return $i\in\{-1/2,1/2\}$. The latter return can be approximately hedged by asset 4. This means that there is a cascade of approximate hedges – hedge asset 2 by asset 3 and asset 3 by asset 4 – leading to an approximate arbitrage.

To exclude an arbitrage, it is crucial that assets 2, 3 and 4 have to be bought already at time 0, without the knowledge of $n$ and $m$. If $n$ and $m$ were known at time 0, the return of asset 3 between times 0 and 2 could be perfectly hedged by asset 4 with hedging ratio $n$, and then asset 2 could be perfectly hedged by the return of asset 3 between times 2 and 3 with a hedging ratio exploding with $m$. On the other hand, asset 4 can be sold at its initial purchasing price at time 1 after $n$ is revealed, and the same holds for the portfolio of one asset 3 and $n$ assets 4 at time 2 after $m$ is revealed. Thus one can buy large quantities of assets 4 and 3 at time 0 and sell the units which are not needed later at their initial prices. But since there is no a priori upper bound for $n$ and $m$, there remains the risk that one does not have enough quantities of assets 4 and 3. Thus buying more and more units at time 0 only leads to an approximate arbitrage.

The extension from $\Pi$ to $\widetilde{\Pi}$ in (4.3) below allows the investor to postpone the purchase of assets 3 and 4 by one period to time 1. This means that she can now use her knowledge of $n$ to perfectly hedge the return of asset 3 up to time 2 by asset 4. On the other hand, $m$ is still not known at the time when assets 2 and 3 must be purchased. Thus the extension only turns the first of the two consecutive approximate hedges into a perfect hedge. This is the reason why (4.2) holds and $\widetilde{\Pi}$ satisfies (NA). In the following, these ideas are worked out in detail.

Step 1. Let us show that $(\Pi_{t})_{t=0}^{3}$ allows an approximate arbitrage in the sense that $\overline{\mathcal{A}_{0}^{3}}\cap L^{0}(\mathbb{R}^{4}_{+})\supsetneq \{0\}$. To that end, we define for fixed $k\in\mathbb{N}$ the following strategy. For $t=0$, we set

$$\begin{aligned} \xi_{0}^{k}= e^{2}-e^{1}+k(e^{3}-e^{1})+k^{2}(e^{4}-e^{1})\in-K_{0}. \end{aligned}$$

For $t=1$, we define

$$\begin{aligned} \xi_{1}^{k}(n,m,i,j)=\big(k^{2}-(k\wedge n)k\big)(e^{1}-e^{4})\in-K_{1}(n,m,i,j). \end{aligned}$$

For $t=2$, we define

$$\begin{aligned} \xi_{2}^{k}(n,m,i,j)&=(k\wedge n)k\bigg(1-\frac{i}{n}\bigg)\bigg(e^{1}-\frac{1}{1-\frac{i}{n}}e^{4}\bigg)\\ &\phantom{=:}+\bigg(k-\frac{m}{1+i}\wedge k\bigg)(1+i)\bigg(e^{1}-\frac{1}{1+i}e^{3}\bigg)\in-K_{2}(n,m,i,j). \end{aligned}$$

Finally, at $t=3$, we liquidate the remaining positions in the assets 2 and 3. Thus we define

$$\begin{aligned} \xi_{3}^{k}(n,m,i,j)&=\bigg(1+\frac{1}{4}+j\bigg)\bigg(e^{1}-\frac {1}{1+\frac{1}{4}+j}e^{2}\bigg)\\ &\phantom{=:}+ \bigg(\frac{m}{1+i}\wedge k\bigg)(1+i)\bigg(1-\frac {j}{m}\bigg)\bigg(e_{1}-\frac{1}{1+i}\frac{1}{1-\frac{j}{m}}e^{3}\bigg), \end{aligned}$$

which belongs to $-K_{3}(n,m,i,j)$. Thus $v^{k}=\xi_{0}^{k}+\xi_{1}^{k}+\xi _{2}^{k}+\xi_{3}^{k}$ belongs to $\mathcal{A}_{0}^{T}$ and we have

$$\begin{aligned} v^{k}(n,m,i,j)=\Bigg(\frac{1}{4}+ik\Big(1-\frac{n\wedge k}{n}\Big)+j\bigg(1-\frac{1+i}{m}\Big(\frac{m}{1+i}\wedge k\Big)\bigg)\Bigg)e^{1}. \end{aligned}$$

Finally, letting $k\to\infty$, we obtain $v\in\overline{\mathcal {A}_{0}^{T}}$ given by

$$\begin{aligned} v(n,m,i,j)=\lim\limits_{k\to\infty}v^{k}(n,m,i,j)=\frac{e^{1}}{4}, \end{aligned}$$

which is the desired asymptotic arbitrage. Hence the model cannot admit a CPS (see [12, Proposition 3.2.6.]).

Next, we introduce the bid–ask process $(\widetilde{\Pi}_{t})_{t=0}^{3}$ given by $\widetilde{\Pi}_{0}=\Pi_{0}$, $\widetilde{\Pi}_{2}=\Pi_{2}$, $\widetilde{\Pi}_{3}=\Pi_{3}$, and

$$\begin{aligned} \widetilde{\Pi}_{1}\equiv \begin{pmatrix} 1 & a & 1 & 1\\ a & 1 & \cdot& \cdot\\ a & \cdot& 1& \cdot\\ 1 & \cdot& \cdot& 1 \end{pmatrix} , \end{aligned}$$

(4.3)

which satisfies $\widetilde{\Pi}_{t}\leq\Pi_{t}$ for all $t=0,1,2,3$. We want to show that $(\widetilde{\Pi}_{t})_{t=0}^{3}$ has the property (NA) and satisfies $\mathcal{A}_{0}^{t}\cap-\widetilde{\mathcal {A}}_{t}^{T}\subseteq\widetilde{\mathcal{A}}_{t}^{T}$ for $t=0,1,2,3$.

Step 2. We start with the property (NA) for $(\widetilde{\Pi }_{t})_{t=0}^{T}$. Let $\widetilde{v}\in\widetilde{\mathcal{A}}_{0}^{3}$ with $\widetilde {v}^{i}=0$ for $i=2,3,4$ and $\widetilde{v}^{1}\ge0$ a.s. We have to show that this already implies $\widetilde{v}^{1}=0$ a.s. We may pass to a $v\in\widetilde{\mathcal{A}}_{0}^{3}$ with $v^{i}=0$ for $i=2,3,4$ a.s. and $v^{1}\ge\widetilde{v}^{1}$ such that $v$ can be represented solely by transfers

$$\begin{aligned} \lambda_{t}^{1j}\ \mbox{with}\ \pi_{t}^{1j}< a\qquad \mbox{and}\qquad \lambda_{t}^{j1} \mbox{ with } \pi_{t}^{j1}< a. \end{aligned}$$

(4.4)

Indeed, purchasing an asset $i\in\{2,3,4\}$ at price $a=5$ or short-selling it at price $1/a=1/5$ (in terms of the asset 1) leads to a sure loss after liquidating this position afterwards. Hence we only need to consider $v=\xi_{0}+\xi _{1}+\xi_{2}+\xi_{3}\in\widetilde{\mathcal{A}}_{0}^{3}$, where

$$\begin{aligned} \xi_{0} &\in\mathrm{cone}(e^{2}-e^{1}), \\ \xi_{1} &\in L^{0}\big(\mathcal{F}_{1} ; \mathrm{cone}(e^{3}-e^{1},e^{4}-e^{1})\big),\\ \xi_{2} &\in L^{0}\big(\mathcal{F}_{2} ; \mathrm{cone}(e^{1}-\widetilde{\pi }^{3,1}_{2}e^{3}, e^{1}-\widetilde{\pi}^{4,1}_{2}e^{4})\big),\\ \xi_{3} &\in L^{0}\big(\mathcal{F}_{3} ; \mathrm{cone}(e^{1}-\widetilde{\pi }^{2,1}_{3} e^{2}, e^{1}-\widetilde{\pi}^{3,1}_{3} e^{3})\big), \end{aligned}$$

with the additional restrictions $\xi^{3}_{1}+\xi^{3}_{2}\geq0$ a.s. and $\xi^{4}_{1}+\xi^{4}_{2}=0$ a.s. Under the assumptions above, we get

$$\begin{aligned} 0&\leq v^{1}(n,m,i,j) \\ &\leq\xi_{0}^{2}(j+1/4)+i\bigg(\xi^{3}_{1}(n)-\frac{\xi_{1}^{4}(n)}{n}\bigg)+\big(\xi^{3}_{1}(n)+\xi^{3}_{2}(n,m,i)\big)\frac{-j}{m}(1+i) \end{aligned}$$

(4.5)

for each state $(n,m,i,j)\in\Omega$ with $\xi_{0}^{2}\geq0$, $\xi ^{3}_{1}(n)\geq0$, $\xi^{3}_{2}(n,m,i)\leq0$ and $\xi^{4}_{1}(n)\geq0$. Here the notation highlights the required measurability of the random variables; for instance, we write $n\mapsto\xi^{3}_{1}(n)$ since the value of the $\mathcal{F}_{1}$-measurable random-variable $\xi^{3}_{1}$ can only depend on $n$. We have $\xi^{3}_{1}(n)+\xi^{3}_{2}(n,m,i)\le\xi_{1}^{3}(n)$, i.e., the investment in asset 3 between $t=2$ and $t=3$ is bounded from above by the $\mathcal {F}_{1}$-measurable random variable $\xi_{1}^{3}$. Consequently, the third summand in (4.5) becomes arbitrarily small for large $m\in\mathbb{N}$. But this implies that the sum of the first two terms, i.e.,

$$\begin{aligned} \xi_{0}^{2}(j+1/4)+i\bigg(\xi^{3}_{1}(n)-\frac{\xi_{1}^{4}(n)}{n}\bigg), \end{aligned}$$

that does not depend on $m$, must be almost surely nonnegative, which is only possible if

$$\begin{aligned} \xi_{0}^{2}=0\qquad \mathrm{and} \qquad \xi_{1}^{3}(n)=\frac{\xi_{1}^{4}(n)}{n}\ \mathrm{for\ each}\ n\in\mathbb{N}. \end{aligned}$$

(4.6)

But then (4.5) reduces to

$$\begin{aligned} 0\leq v^{1}(n,m,i,j)\leq\big(\xi^{3}_{1}(n)+\xi^{3}_{2}(n,m,i)\big)\frac {-j}{m}(1+i). \end{aligned}$$

Taking $j=1/2$, this implies $\xi^{3}_{1}(n)=-\xi_{2}^{3}(n,m,i)$ and consequently $v^{1}\equiv0$. Hence $(\widetilde{\Pi}_{t})_{t=0}^{3}$ satisfies (NA).

Step 3. Let us now show $\mathcal{A}_{0}^{t}\cap-\widetilde {\mathcal{A}}_{t}^{T}\subseteq\widetilde{\mathcal{A}}_{t}^{T}$ for $t=1,2,3,4$ (for $t=0$, there is nothing to show). This is similar to the proof in Step 2. As in (4.4), we can restrict to portfolios which can be represented by transfers that do not trade at price $a=5$. Indeed, since we only consider positions that can be liquidated for sure, the cancellation of a transfer at price $a$ (with re-transfer at a later time to asset 1) would lead to a strict improvement and thus an arbitrage. Since this would contradict the property (NA) of $(\widetilde{\Pi }_{t})_{t=0}^{3}$ shown in Step 2, we can exclude such silly trades in the following considerations.

By the arguments leading to (4.6), it follows that $e^{2}-e^{1}\not\in-\widetilde{\mathcal{A}}_{1}^{3}$. Consequently, we have $\mathcal{A}_{0}^{1}\cap-\widetilde{\mathcal{A}}_{1}^{3}=\mathrm {cone}(e^{3}-e^{1},e^{4}-e^{1})+ L^{0}(\mathcal{F}_{1} ; \mathrm {cone}(e^{1}-e^{4}))\subseteq\widetilde{\mathcal{A}}_{1}^{3}$.

Now consider the case $t=2$. Let $w\in\mathcal{A}_{0}^{2}\cap- \widetilde{\mathcal{A}}_{2}^{3}$, which means that we may write $w=\xi_{0}+\xi_{1}+\xi_{2}= -\widetilde{\xi}_{2}-\widetilde{\xi}_{3}$ for $\xi_{0}\in\mathrm{cone}(e^{2}-e^{1},e^{3}-e^{1}, e^{4}-e^{1})$, $\xi_{1}\in L^{0}(\mathcal{F}_{1} ; \mathrm{cone}(e^{4}-e^{1}))$, $\xi _{2},\widetilde{\xi}_{2}\in L^{0}(\mathcal{F}_{2} ; \mathrm{cone}(e^{1}-\pi ^{31}_{2}e^{3}, e^{1}-\pi^{41}_{2}e^{4}))$ and $\widetilde{\xi}_{3}\in L^{0}(\mathcal{F}_{3} ; \mathrm{cone}(e^{1}-\pi ^{21}e^{2}, e^{1}-\pi^{31}e^{3}))$ with the restrictions $\xi _{0}^{3}+\xi_{2}^{3}+\widetilde{\xi}_{2}^{3}\geq0$, $\xi_{0}^{4}+\xi_{1}^{4}\geq0$ and $\xi_{0}^{4}+\xi_{1}^{4}+\xi_{2}^{4}+\widetilde {\xi}_{2}^{4}=0$. Indeed, this is a consequence of (NA) and the avoidance of silly trades. Now define $v:=w-w=\xi_{0}+\xi_{1}+\xi _{2}-(-\widetilde{\xi}_{2}-\widetilde{\xi}_{3})$. Note that we have $v^{i}=0$ for $i=2,3,4$, which uniquely determines $v^{1}$ as

$$\begin{aligned} v^{1}(n,m,i,j)& =\xi_{0}^{2}(j+1/4)+i\bigg(\xi^{3}_{0}-\frac{\xi_{0}^{4}+\xi _{1}^{4}(n)}{n}\bigg)\\ &\phantom{=:}+\bigg(\xi^{3}_{0}+\xi^{3}_{2}(n,m,i)+\widetilde{\xi }^{3}_{2}(n,m,i)\bigg)\frac{-j}{m}(1+i). \end{aligned}$$

On the other hand, we also have $v^{1}=0$. Since the first two terms do not depend on $m\in\mathbb{N}$, we must have that

$$\begin{aligned} \xi_{0}^{2}(j+1/4)+i\bigg(\xi^{3}_{0}-\frac{\xi_{0}^{4}+\xi_{1}^{4}(n)}{n}\bigg) = 0. \end{aligned}$$

Considering $j=-1/2$ and $i=\pm1/2$, $\xi^{2}_{0}\ge0$ implies that $\xi _{0}^{2}=0$ and

$$\begin{aligned} \xi_{0}^{3}-\left(\xi_{0}^{4}+\xi_{1}^{4}(n)\right)/n=0\qquad \mbox{for all}\ n\in\mathbb{N}. \end{aligned}$$

Hence $\xi_{0}^{4}=-\xi_{1}^{4}(n)$ for all $n\in\mathbb{N}$ and $\xi _{0}^{3}=0$. Consequently, we also have $\xi_{2}^{3}(n,m,i)=\widetilde{\xi }_{2}^{3}(n,m,i)=0$. But then we have shown $w=0$, which is tantamount to $\mathcal{A}_{0}^{2}\cap- \widetilde{\mathcal{A}}_{2}^{3}=\{0\}\subseteq \widetilde{\mathcal{A}}_{2}^{3}$.

The same arguments apply for $t=3$ and thus $\mathcal{A}_{0}^{3}\cap -\widetilde{\mathcal{A}}_{3}^{3}=\{0\}\subseteq\widetilde{\mathcal{A}}_{3}^{3}$.

Remark 4.4

Example 4.3 also allows us to discuss the following related question: Does the existence of a bid–ask process $(\widehat{\Pi}_{t})_{t=0}^{T}$ with $\widehat{\Pi}_{t}\leq\Pi _{t}$ a.s. for all $t=0,\ldots,T$ and such that $(\widehat{\Pi }_{t})_{t=0}^{T}$ satisfies (NA) and

$$\begin{aligned} &\sum_{t=0}^{T}\xi_{t}=0\ \mathrm{a.s.\ with}\ \xi_{t}\in L^{0}(\mathcal {F}_{t} ; -K_{t}) \\ &\Longrightarrow \quad \xi_{t}\in L^{0}(\mathcal{F}_{t} ; \widehat {K}^{0}_{t})\ \textrm{for\ all\ } t=0,\ldots,T \end{aligned}$$

(4.7)

already imply the absence of an approximate arbitrage, i.e., $\overline {\mathcal{A}_{0}^{T}}\cap L^{0}(\mathbb{R}^{d}_{+})=\{0\}$? Here (4.7) means that each transaction which is involved in a null-strategy in the original model is carried out at frictionless prices in the adjusted market.

It turns out that the answer to the above question is negative. Indeed, in the setting of Example 4.3, we define the adjusted bid–ask process $(\widehat{\Pi}_{t})_{t=0}^{3}$ by

$$\begin{aligned} \widehat{\Pi}_{0}= \begin{pmatrix} 1 & 1 & 1& 1\\ a & 1 & \cdot& \cdot\\ a & \cdot& 1& \cdot\\ 1 & \cdot& \cdot& 1 \end{pmatrix} , \qquad \widehat{\Pi}_{1}= \begin{pmatrix} 1 & a & a & 1\\ a & 1 & \cdot& \cdot\\ a & \cdot& 1& \cdot\\ 1 & \cdot& \cdot& 1 \end{pmatrix} , \end{aligned}$$

$\widehat{\Pi}_{2}=\Pi_{2}$ and $\widehat{\Pi}_{3}=\Pi_{3}$. Then we have $\widehat{\Pi}_{t}\leq\Pi_{t}$ a.s. for all $t=0,1,2,3$. In addition, the previously considered adjusted bid–ask process $(\widetilde{\Pi }_{t})_{t=0}^{3}$ satisfies (NA) and yields better terms of trade than $(\widehat{\Pi}_{t})_{t=0}^{3}$, i.e., $\widehat{\mathcal {A}}_{0}^{T}\subseteq\widetilde{\mathcal{A}}_{0}^{T}$. Consequently, $(\widehat{\Pi}_{t})_{t=0}^{3}$ inherits the property (NA). In addition, the only (up to multiplication with nonnegative scalars) null-strategy in the original market is $(\vartheta_{t}-\vartheta _{t-1})_{t=0}^{3}=(e^{4}-e^{1},e^{1}-e^{4},0,0)$. Thus (4.7) is satisfied, but as we have shown, $\overline{\mathcal{A}_{0}^{T}}\cap L^{0}(\mathbb{R}^{d}_{+})\supsetneq\{0\}$.

The key observation is that the bid–ask process $(\widehat{\Pi }_{t})_{t=0}^{3}$ satisfies (4.7), but not (3.1). This means that a transfer $\xi_{s}\in L^{0}(\mathcal{F}_{s} ; -K_{s})$, $s\in\{0,\ldots,3\}$, which can be extended to a null-strategy $(\xi_{0},\ldots,\xi_{3})$ in the original market $(\Pi_{t})_{t=0}^{3}$ is frictionless in the better market $(\widehat{\Pi}_{t})_{t=0}^{3}$, i.e., $\xi_{s}\in L^{0}(\mathcal{F}_{s} ; (-\widehat{K}_{s})\cap\widehat {K}_{s})$. On the other hand, by the extension of the market from $(\Pi_{t})_{t=0}^{3}$ to $(\widehat{\Pi }_{t})_{t=0}^{3}$, additional null-strategies occur, and their transfers need not be frictionless.

The bid–ask process $\widehat{\Pi}$ is obtained by adjusting the trading prices via

(4.8)

where $B^{ji}$ is given by

(4.9)

with the essential supremum with respect to the $\sigma$-algebra $\mathcal{F}_{t}$. This means that if the transfer , $B\in\mathcal{F}_{t}$, can be compensated by trades during $\{0,\dots,T\}$, the adjusted price $\widehat{\pi }^{ij}_{t}$ allows to compensate it by trading at time $t$ only. In our concrete example, one has , and for all other triples $(j,i,t)$.

The adjustment (4.8), (4.9) ensures that the null-strategies in the original market are frictionless in the extended market (see the arguments in Jacka et al. [9, pages 592 and 593]). But it was a finding by Jacka et al. [9] (see the paragraph before Definition 3.2 therein) that the latter is not sufficient to obtain closedness of the set $\widehat {\mathcal{A}}_{0}^{T}$ of attainable portfolio values in the extended market. Thus, they define their “adjusted trading prices” slightly differently from (4.8), (4.9) with $\mathcal{A}_{0}^{T}$ replaced by its closure in probability $\overline{\mathcal{A}_{0}^{T}}$. Example 4.3 shows that the price adjustment (4.8), (4.9) with $\mathcal{A}_{0}^{T}$ instead of $\overline{\mathcal{A}_{0}^{T}}$ does not imply that the set $\widehat{\mathcal{A}}_{0}^{T}$ of attainable portfolio values is closed. Thus the example justifies the approach by Jacka et al. [9].

On the other hand, in [9, Example 3.3] with $T=1$, the adjustment (4.8), (4.9) with $\mathcal{A}_{0}^{T}$ already yields that the set $\widehat{\mathcal{A}}_{0}^{T}$ of attainable portfolio values is closed. Indeed, in [9, Example 3.3], the price adjustment (4.8), (4.9) consists of changing $\pi ^{12}_{0}$ to $\widehat{\pi}^{12}_{0}=1=1/\pi^{21}_{0}$ and $\pi^{21}_{1}$ to $\widehat{\pi}^{21}_{1}=1=1/\pi^{12}_{1}$ on $\Omega$, which makes the null-strategy $(e^{1}-e^{2},e^{2}-e^{1})$ of the original market frictionless in the extended market. Considering the scenario $\omega=2$, it can easily be seen that

$$\widehat{\mathcal{A}}_{0}^{0}\cap(-\widehat{\mathcal{A}}_{1}^{1})= \mathrm {cone}(e^{1}-e^{2},e^{2}-e^{1},e^{3}-e^{4}), $$

which is contained in $\widehat{\mathcal{A}}_{1}^{1}$. From this, one can easily deduce that the extended market $\widehat{\Pi}$ satisfies (NA^ps). Consequently, $\widehat{\mathcal{A}}_{0}^{1}$ is closed by Theorem 2.6.