A survey of trajectory distance measures and performance evaluation

Abstract

The proliferation of trajectory data in various application domains has inspired tremendous research efforts to analyze large-scale trajectory data from a variety of aspects. A fundamental ingredient of these trajectory analysis tasks and applications is distance measures for effectively determining how similar two trajectories are. We conduct a comprehensive survey of the trajectory distance measures. The trajectory distance measures are classified into four categories according to the trajectory data type and whether the temporal information is measured. In addition, the effectiveness and complexity of each distance measure are studied. The experimental study is also conducted on their effectiveness in the six different trajectory transformations.

1 Introduction

Driven by major advances in sensor technology, GPS-enabled mobile devices, and wireless communication, large amounts of data describing the motion history of moving objects, known as trajectory, are currently generated and managed in scores of application domains, such as environmental information systems, meteorology, wireless technology, video tracking, and video motion capture. Typical examples include collecting GPS location histories of taxicabs for safety and management purpose, tracking animals for their migration patterns, gathering human motion data by tracking body joints, and tracing the evolution of migrating particles in biological sciences. This inspires a tremendous amount of research efforts in analyzing large-scale trajectory data from a variety of aspects in the last decade. Representative works include the design of effective trajectory indexing structures [7, 9, 15, 19, 27, 59, 90, 91], built to manage trajectories and support high-performance trajectory queries [15, 27, 98]. Data mining methods are applied to trajectories to detect points of interest (POI), find popular routes from a source to a destination, predict traffic conditions, discover significant patterns, and perform data compression [40, 41, 49, 52, 99, 100]. As a result, trajectories are used in many applications across different domains. For example, public transportation system may go back in time to any particular instant or period to analyze the pattern of traffic flow and the causes of traffic jams. Movements of animals may be analyzed in biological studies with consideration of road networks to reveal the impact of human activity on wild life; the urban planning authority of a city council may analyze the trajectories to predict the development of suburbs and provide support to decision making; other applications include path optimization of logistics companies, improvement in public security management, personalized location-based service, etc.

Despite various kinds of analysis tasks and applications of moving objects data, measuring the distance between the trajectories of moving objects is a common procedure of most tasks and applications. Thus, a fundamental ingredient of those trajectory analysis tasks and applications is distances that allow to effectively determine how similar two trajectories are. However, unlike other simple data types, such as ordinal variables or geometric points where the distance definition is straightforward, the distance between trajectories needs to be carefully defined in order to reflect the true underlying distance. This is due to the fact that trajectories are essentially high-dimensional data attached with both spatial and temporal attributes, which needs to be considered for distance measures. As such, there are dozens of distance measures for trajectory data in the literature. For example, there are distance measures measuring the sequence-only distance between trajectories, such as Euclidean distance and dynamic time wrapping distance (DTW); there are also trajectory distance measures measuring both spatial and temporal dimensions of two trajectories, such as spatiotemporal longest common subsequence (STLCSS) similarity and spatiotemporal locality in-between polyline (STLIP) distance. Many of these works, and some of their extensions, have been widely cited in the literature and used to facilitate query processing and mining of trajectory data.

Being faced with the multitude of competitive techniques, we need a systematic survey that studies the contribution of each individual research and explore the relations and differences among them. Gudmundsson et al. [33] and Toohey and Duckham [88] both review four basic trajectory distance measures, i.e., Euclidean distance, DTW, LCSS, and Fréchet distance. However, many other widely used or recent distance measures, e.g., EDR, ERP, MD, STLC, and EDwP, are not introduced in these two papers. In addition, comprehensive empirical evaluation and comparison of these measures are not sufficiently studied in previous work.

Motivated by these observations, we conduct a most comprehensive survey on the trajectory distance measures proposed in studies of referred conferences and journals. We studied all 15 distance measures in the following perspectives, namely: (1) the targeted trajectory data type, (2) considering temporal information or not, (3) properties of distance measure function, e.g., parameter free or not, metric or not, indexing, pruning, etc., and (4) time complexity of the distance measure. What’s more, as collected in the complex real-life environment, trajectory data usually have characteristics such as asynchronous observations, explicit temporal attribute, and some other quality issues (detailed in Sect. 2.2). We provide a benchmark to simulate these characteristics in a real setting by introducing six trajectory transformations of three different types, i.e., point shift, trajectory shift, and noise (see Sect. 5.3), on three real-life and synthetic datasets. We also extensively studied and compared the capability of handling the above-mentioned characteristics for all distance measures. The contributions of this article are as follows:

• We complete a comprehensive literature review on trajectory distance measures and classify these measures into four categories in terms of the trajectory data type and whether the temporal information is measured by the measure.

• We design three types of trajectory transformations and run extensive experiments based on large-scale real trajectory datasets to evaluate the capabilities of all the trajectory distance measures.

• We have a key observation that DTW, LCSS, ERP, MD, and STLC are distance measures with capabilities of handling at least four transformations. Among them, STLC is the best distance measures that can handle all the transformations.

• We have a key observation that the distance measures with low time costs have low effectiveness in handling all transformations.

The remainder of this paper is organized as follows. Section 2 introduces the preliminary concepts of trajectory and overviews the classification of trajectory distance measures. We introduce the trajectory distance measures in Sects. 3 and 4. The capability evaluation of distance measures is presented in Sect. 5. Section 6 concludes the survey and outlines the observations we make.

2 Overview

2.1 Preliminary concepts

In this subsection, we will introduce the preliminary concepts about trajectories and formalize the operations and notations that will be used frequently in the remainder of the paper. A trajectory is a sequence of time-stamped point records describing the motion history of any kind of moving objects, such as people, vehicles, animals, and natural phenomenon. Theoretically, a trajectory should be a continuous record, i.e., a continuous function of time mathematically, since the object movement is continuous in nature. In practice, however, the continuous location record for a moving object is usually not available since the positioning technology (e.g., GPS devices, roadside sensors) can only collect the current position of the moving object in a periodic manner. Due to the intrinsic limitations of data acquisition and storage devices, such inherently continuous phenomena are acquired and stored (thus, represented) in a discrete way. This subsection starts with approximations of object trajectories. Intuitively, the more the data about the whereabouts of a moving object are available, the more accurate its true trajectory can be determined. Still, to be consistent with existing works, we refer to such kind of discrete representation as the trajectory, despite the fact that it is just an approximation of the original trajectory of the moving object. Next, we formalize this kind of representation for a trajectory.

Definition 1

(Trajectory sample point) A trajectory sample point p is a location in d-dimensional space, and p.t is the time stamp when p is observed.

The location and time stamp pair ((116.364629, 39.940511), 3/1/2012 12:00:31 AM) is an example of a sample point, where ‘116.364629’ and ‘39.940511’ are longitude and latitude, respectively, and ‘3/1/2012 12:00:31 AM’ is the time stamp. In practice, a trajectory sample point p is usually two or three dimensional. Without loss of generality, we assume objects are moving in a two-dimensional space, i.e., p is a two-dimensional vector, and the time attribute is discrete. Therefore, the trajectory distance functions discussed in this paper are all defined in two-dimensional space.

Definition 2

(Trajectory) Trajectory is a sequence of trajectory sample points, ordered by time stamps t. Trajectory T is represented by a sequence of trajectory sample points. Therefore, $T = [{p_1}, {p_2}, \dots , {p_n}]$.

Definition 3

(Trajectory distance measure) A trajectory distance measure is a method that evaluates the distance between two trajectories. $d(T_1, T_2)$ denotes the distance between two trajectories $T_1$ and $T_2$. The larger the value is, the less similar the two trajectories are.

Definition 4

(Metric distance measure) A distance measure d is metric if for all $T_1$, $T_2$, and $T_3$ of a trajectory dataset the following conditions are satisfied:

• 1. Nonnegativity: $d(T_1, T_2) \ge 0$.

• 2. Identity of indiscernibles: $d(T_1, T_2) =0 \Leftrightarrow T_1=T_2$.

• 3. Symmetry: $d(T_1, T_2) =d(T_2, T_1)$.

• 4. Triangle inequality: $d(T_1, T_3)\le d(T_1, T_2) + d(T_2, T_3)$.

As we shall see in the rest of our paper, trajectory distance measures may or may not satisfy all the above conditions, which means not all of the proposed trajectory distance measures are metric. This will impact how the index structures and pruning strategies are designed and applied to query the trajectories as some index structures and pruning strategies only work properly in a metric space.

With the definition of trajectory, we define some operators on the sample point p and trajectory T that will be used throughout the remainder of this paper. Notations used in this paper are listed in Table 1.

• 1. ${{d(p_1,p_2)}}$: $d(p_1,p_2)$ stands for the distance between sample points $p_1$ and $p_2$. Without specifying, $d(p_1,p_2)$ is the Euclidean distance between $p_1$ and $p_2$.

• 2. ${{t(p_1,p_2)}}$: $t(p_1,p_2)$ stands for the time interval between sample points $p_1$ and $p_2$, i.e., $t(p_1,p_2) = p_2.t-p_1.t$.

• 3. Head(T): For trajectory $T = [p_1, p_2,\dots , p_n]$, $Head(T)$ is to get the first sample point of a trajectory, that is $Head(T) = p_1$.

• 4. Rest(T): For trajectory $T = [p_1, p_2,\dots , p_n]$, Rest(T) is to get the tail sample points of the trajectory except the first sample point. Therefore, $Rest(T) = [p_2, p_3,\dots ,p_n]$.

• 5. Length(T): Length(T) represents the absolute length of trajectory T = $[p_1, p_2,\dots , p_n]$ in space, i.e., $Length(T) = \sum \nolimits _{i = 1}^{n - 1} {d({p_i},{p_{i + 1}})}$. For example, the Length(T) for a trajectory $T=[((0,0),0), ((2,0),1), ((4,0),2), ((6,0),3)]$ is 6.

• 6. Size(T): Size(T) represents the number of trajectory sample points of T. For example, the Size(T) for a linear trajectory $T=[((0,0),0), ((2,0),1), ((4,0),2),((6,0),3)]$ is 4.

• 7. Time(T): Time(T) represents the absolute time interval of a trajectory $T = [p_1,\dots , p_n]$ travels, i.e., Time(T) = $\sum \nolimits _{i = 1}^{n - 1} {t({p_i},{p_{i + 1}})}$. For example, the Time(T) for a trajectory $T=[((0,0),0), ((2,0),1),((4,0),2),((6,0),3)]$ is 3.

Table 1 Notations used in the paper

2.2 Characteristics of trajectory data

Trajectories are usually treated as multidimensional (2D or 3D in most cases) time series data; hence, existing distance measures for 1D time series (e.g., stock market data) can be applied directly or with minor extension. Typical examples include the distance measures based on DTW, edit distance, and longest common subsequence (LCSS), which were originally designed for traditional time series but now have been extensively adopted for trajectories. However, with the more widely applicability and deeper understanding of trajectory data, it turns out that trajectories are not simply multidimensional extensions of time series, but have some unique characteristics to be taken into account during the design of effective distance measures. We summarize them below.

• Asynchronous observations Time series databases usually have a central and synchronized mechanism, by which all the data points can be observed and reported to the central repository simultaneously in a controlled manner. For example, in the stock market, the data of all stocks, such as trade price and amount, are reported every 5 s simultaneously. In this way, the data points of the stock time series are synchronized, which makes the comparison of two stock data relatively simple. It just needs to compare the pairs of values reported at the same time instant. However, in trajectory databases there is usually no such mechanism to control the timing of collecting location data. Moving objects, such as GPS-embedded vehicles, may have different strategies when they need to report their locations to a central repository, such as time-based, distance-based, and prediction-based strategies. Even worse, they might suspend the communication with a central server for a while and resume later. The overall result is that the lengths and time stamps of different trajectories are not the same.

• Explicit temporal attribute Although time series data always have the time attribute attached with each data point, in practice we do not explicitly use this information. In other words, time series are usually treated as sequences without temporal information. The reason for doing this is, as mentioned in the first property, all time series data in a system have the same time stamps; hence, explicitly maintaining the time attributes is not necessary. However, in trajectory databases, time stamps cannot be dropped because they are asynchronous among different trajectories. To make this point clear, we consider two moving objects which travel through the exactly same set of geographical locations, but take different time duration. Without looking at the temporal attribute, the two trajectories are identical, despite the fact that they have different time periods.

• More data quality issues Traditional time series databases are expected to contain high-quality data since they usually have stable and quality-guaranteed sources to collect the data. Financial data may be one of the most precise time series data and almost error free. In environmental monitoring applications, data readings from sensors also have little noise. In contrast, trajectory data are faced with more quality issues, since they are generated by individuals in a complex environment. First, GPS devices have measurement precision limits; in other words, what they report to the server might not be the true location of the moving object, but with a certain deviation. Even worse, a GPS device might report a completely wrong location when it cannot find enough satellites to calculate its coordinate. Second, when a device loses power or the moving object travels to a region without GPS signals, its position cannot be sent to the server, resulting in a period of “missing values” in its trajectory data.

2.3 Capabilities of trajectory distance measures

As introduced before, trajectory data have several significant characteristics. A trajectory distance measure needs the capability of handling a certain characteristic if their evaluation is not affected by the characteristic. Thus, we summarize the capabilities of handling trajectory distance measures as follows.

• Point shift A trajectory can be added/deleted from some sample points or even totally be sampled by different sampling strategies and different sampling rates, while its shape and trend are not modified. A distance measure with the capability of handling point shifting should keep the low distance values between a trajectory and its point shifted counterparts.

• Trajectory shift There are several kinds of trajectory shifts, e.g., time stretch shift and space scale suppress. A distance measure with the capability of handling time stretch can detect trajectories moving on the same path regardless of their speed. A distance measure with the capability of handling space suppress can identify two trajectories moving on the paths with similar shapes.

• Noise Since the trajectory data are generally of low quality, the collected sample points of a trajectory are often not accurate, or simply noisy points. A distance measure with the capability of handling noise can correctly measure the distance between trajectories even if the data quality of these trajectories is low.

2.4 Classification of trajectory similarity measures

In this survey, we study and compare 15 widely used trajectory distance measures in the literature. We systematically label these measures by two classification dimensions: (1) whether the measure considers the spatial attribute only, i.e., treating two compared trajectories as sequences, or consider both spatial and temporal information in the trajectory. Spatial information means the sequence order of trajectory. Temporal information is time-related information. For distance measures that only measure the spatial distance between trajectories, we name them sequence-only distance measures. For distance measures which measure both the spatial and temporal distance between trajectories, we name them spatiotemporal distance measures; (2) whether the measure is defined in a discrete or continuous way, i.e., considering the sample point only, or the sample point as well as the movement in-between. For distance measures of which distance values are only calculated on sample points, we name them discrete distance measures. For distance measures of which distance values are calculated on both sample points and movement in-between, we name them continuous distance measures. For distance measures within the same category, theoretically they have the same targeted trajectory data type (continuous or discrete) and the same requirement of information type (sequence-only or spatiotemporal). By this means, each trajectory distance measure can be put into one of the four classes, i.e., continuous sequence-only measures, discrete sequence-only measures, continuous spatiotemporal measures, and discrete spatiotemporal measures. Figure 1 shows this classification.

Fig. 1

Categorization of trajectory distance measures

It is worth noting that this classification is not unique, and there are many other aspects that can be used to connect and distinguish those distance measures. For instances, ED, DTW, PDTW, OWD, LIP, MD, STLC, Fréchet distance, STED, and SLIP are all derived by calculating the Euclidean distance between certain parts of the given two trajectories, while EDR, ERP, EDwP, LCSS, and STLCSS actually reflect the proportion of the two trajectories that are close to each other based on a distance function. From the perspective of distance function adoption, they can be grouped into Lp-norm family (ED, DTW, PDTW, OWD, LIP, MD, STLC, Fréchet distance, STED, and SLIP) and edit distance family (EDR, ERP, EDwP, LCSS, and STLCSS).

2.5 Trajectory indexing and pruning

Trajectory retrieval is arguably the most important application for trajectory distance measures, that is, given a target trajectory retrieving the most similar trajectories in terms of some distance/similarity measures to the inquired target. The most representative scenario is the K-nearest neighbor queries (KNN), which is to return top-k most similar trajectories by a given query trajectory. When extracting qualitative information by querying databases containing large numbers of trajectories, the performance crucially depends upon an efficient index of trajectories that can cluster close-by trajectories together and help pruning trajectories far apart as early as possible.

This survey focuses on studying the application of the distance measures in R-tree-based indexing and pruning methods, due to its popularity in academia and industry. In particular, KNN queries are used as the example. Some distance measures, such as EDwP, OWD, and STLCSS, have their specially designed indexing methods. Due to the limited application scope of these indexing methods, we briefly summarize them in Table 2 without giving details for the sake of space.

R-tree and its variations R-tree [35] is a height-balanced data structure. Each node in R-tree represents a region which is the minimum bounding rectangle (MBR) of all its children nodes. Each data entry in a node contains the information of the MBR associated with the referenced children node. R-tree is widely used in the processing of KNN queries for a given query trajectory. Because of its popularity, there are also many index structures that are variants of R-tree. Most of them can be divided into two types. The first type uses any multidimensional access method like R-tree indexes with augmentation in temporary dimensions such as 3D R-tree [68] and STR-tree [68]. The second type uses multiversion structures, such as MR-tree [94], HR-tree [58], HR+-tree [86], and MV3R-tree [87]. This approach builds a separate R-tree for each time stamp and shares common parts between two consecutive R-trees.

Query processing for KNN Since enumerating all trajectories and computing distances is expensive and impractical, the basic idea behind arguably all KNN query processing techniques in literal is to employ a filter-and-refine approach to aggressively pruning. Algorithm 1 shows the general framework of the filter-and-refine approach to the spatial query processing. Basically in a filter-and-refine scheme, the filtering step uses relatively low computation cost to find a set of candidate trajectories that are likely to be the results; the refining step then identifies the actual query result from the small set of candidates.

The overall performance of a spatial query processing algorithm heavily relies on the effectiveness of the filtering step, where distance measures are used for pruning the trajectories that are impossible to be returned. There are many filtering methods (pruning strategies), such as mean value Q-gram pruning strategy [15] and morphological pruning strategy [34]. Among them, the lower bounding pruning strategy and triangle inequality pruning strategy are the most commonly used in practice.

• Lower bounding pruning strategy In lower bounding pruning strategy, we start the search with an initial lower bound l. We randomly select k nearby trajectories and calculate the distances between the query trajectory Q and these k trajectories. The initial lower bound is set as the maximum distance among the k distances. During the search in the R-tree, we calculate the minimum distance $d_{\min }(Q, M)$ from the query trajectory Q and a MBR M. If $d_{\min }(Q, M)$ is greater than the current lower bound l, we can safely filter out all trajectories within the MBR; otherwise, we need to recursively check MBRs within the current MBR. The lower bound l can be adjusted and tightened during the search. The lower bounding pruning strategy can be used with most trajectory distance measures.

• Triangle inequality pruning strategy Triangle inequality pruning strategy is only applicable to distance measures that satisfy triangle inequality, such as ERP and STED. In triangle inequality pruning strategy, we usually pre-compute the pairwise distance for every two trajectories of a trajectory dataset. During the search, we record the true distances of a set of candidate trajectories $\{T_1, T_2, \dots , T_i, \dots , T_u\}$ and the queried trajectory Q, denoted by A. For a trajectory $T^*$ currently being evaluated, if this distance $d(Q, T_i) -d(T_i, T^*)$ is already worse than the current KNN distance stored in the result, then $T^*$ can be filtered out entirely. This is because the triangle inequality ensures that $d(Q, T^*) \ge d(Q, T_i) -d(T_i, T^*), \forall 1\le i \le u$. Otherwise, the true distance $d(Q, T^*)$ is computed, and A is updated to include $T^*$. As $d(T_i, T^*)$ is pre-computed, it is usually faster than the process of computing $d(Q, T_i)$ directly.

For brevity, in the following section, we simply mark whether a distance measure satisfies triangle inequality, and corresponding applicable pruning strategies as discussed above.

Fig. 2

Two matching methods used by discrete trajectory distance measures

3 Sequence-only distance measures

This section introduces the sequence-only distance measures, which measure the spatial distance of two trajectories without considering their temporal information. Existing works in this field usually consider a trajectory as a sequence of geo-spatial points, while ignoring the explicit time stamps associated with the points. Sequence-only distance measures are suitable for the cases where the shape is the only consideration in measuring the distance between two trajectories. For example, in the study of migrating animals, we may be only interested in the shape of the migration path; the sequence-only distance measures can be applied to this case.

3.1 Discrete sequence-only distance measures

In this subsection, we review six discrete sequence-only distance measures. Though these distance measures are different, they share similar steps in measuring distance. Firstly, these distance measures find all the sample point match pairs among the two compared trajectories $T_1$ and $T_2$. A sample point match pair, $pair(p_i, p_j)$, is formed by two sample points where $p_i \in T_1$ and $p_j \in T_2$. There are several sample point matching strategies such as minimal Euclidean distance or minimal transformation cost. Then, these distance measures accumulate the distance for matched pairs or count the number of match pairs to get the final distance results. Thus, the sample point matching strategy is the key for every discrete sequence-only distance measure. The sample point matching strategies can be divided into the following two types:

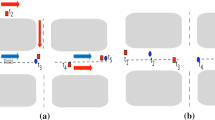
• Complete match For two compared trajectories $T_1$ and $T_2$, complete match strategy requires every sample points of $T_1$ and $T_2$ should be in a match pair, as shown in Fig. 2a. Thus, the match pair number of complete match is $\max (size(T_1), size(T_2))$.

• Partial match For two compared trajectories $T_1$ and $T_2$, partial match strategy does not require every sample points of $T_1$ and $T_2$ should be in a match pair, as shown in Fig. 2b. Thus, some sample points will not be matched to any sample points.

3.1.1 Complete match measures

Complete match measures require all sample points to have their match points (Fig. 2a). Since the size of two comparing trajectories may be different, some sample points have duplicate match points. In this case, trajectories need to be shifted, stretched, and/or squeezed to find best match pairs of sample points. Euclidean distance is a special case of complete match measures since it requires two comparing trajectories should be of the equal size. Among many complete match distance measures, dynamic time warping (DTW) is the most representative one. This subsection mainly introduces the Euclidean distance, DTW, and piecewise DTW (PDTW) (an extension of DTW).

Euclidean distance

The most commonly used equal-size discrete sequence-only distance measure is Lp-norm distance. It is a distance measure that pairwisely computes the distance between corresponding points of two trajectories. Among all other $L_p$-norms, $L_2$-norm, also known as Euclidean distance, is the most commonly adopted distance measures in the literature. Besides being relatively straightforward and intuitive, Euclidean distance and its variants have several other advantages. The complexity of evaluating these measures is linear; in addition, they are easy to implement, indexable with any access method, and parameter free. Euclidean distance was proposed as a distance measure between time series and was once considered as one of the most widely used distance functions since the 1960s [24, 45, 67, 70]. As trajectories are closely related to time series, Euclidean distance is also adopted in measuring trajectory distance [18, 42, 72, 77, 85].

For two trajectories $T_1$ and $T_2$ with the same size n, the Euclidean distance $d_{Euclidean}(T_1, T_2)$ is defined as follows:

$$\begin{aligned} d_{Euclidean}(T_1, T_2) = {{{ {\sum \nolimits _{i = 1}^n {d({p_{1,i}},{p_{2,i}})} } \over n}}} \end{aligned}$$

(1)

where $p_{1,i}$ and $p_{2,i}$ are the ith sample point of $T_1$ and $T_2$, respectively. The time complexity is O(n). Euclidean distance measure is straightforward; however, it requires the comparing trajectories to be the same size, which is not common in the actual situation; otherwise, it will fail to decide the match pairs of the trajectories to be compared. Hence, in reality, people always use a sliding widow of size n to measure the distance of $T_1$ and $T_2$, where $size(T_1) = n$, $size(T_2) = m$ and $n \le m$. Thus, the Euclidean distance with a sliding window can be defined as follows:

$$\begin{aligned} d_{Euclidean}(T_1, T_2) = \mathop {\min }\limits _{j = 1}^{m - n + 1} {\sum \nolimits _{i = 1}^n {d({p_{1,i}},{p_{2,j+i}})} \over n}. \end{aligned}$$

(2)

Thus, the time complexity of Euclidean distance with a sliding window is O(nm). It is parameter free. Since it is metric, it satisfies triangle inequality and can use R-tree as an index structure. The lower bounding pruning strategy and triangle inequality pruning strategy can be used to speed up the Euclidean-distance-based k-NN queries. However, it is sensitive to noisy data.

$$\begin{aligned} {d_{DTW}}(T{}_1,{T_2}) = \left\{ \begin{array}{ll} 0,&{}\quad {\mathrm{if}~n=0~\mathrm{and}~m=0}\\ \infty , &{}\quad {\mathrm{if}~n=0~\mathrm{or}~m=0}\\ d(Head(T{}_1),Head(T{}_2)) + \min \{ d_{DTW}(T_1,Rest(T_2)),\\ \quad d_{DTW}(Rest(T_1),T_2), \\ \quad d_{DTW}(Rest(T{}_1),Rest(T{}_2))\} &{}\quad {\mathrm{otherwise}}\\ \end{array}. \right. \end{aligned}$$

(3)

DTW distance

Dynamic time warping (DTW) is an algorithm for measuring the distance between two sequences. DTW has existed for over a hundred years. Initially, DTW was introduced to compute the distance of time series [30, 57]. In 1980s, [48, 56, 61, 69, 81] introduced DTW to measure trajectory distance. DTW has become one of the most popular trajectory distance measures since then. DTW distance is defined in a recursive manner and can be easily applied in dynamic programming. It searches through all possible points’ alignment between two trajectories for the one with minimal distance. Specifically, the DTW $d_{DTW}(T_1,T_2)$ between two trajectories $T_1$ and $T_2$ with lengths of n and m is defined as Eq. (3).

The time complexity of DTW is O(mn). Since DTW is one of the most widely used trajectory distance measures, people have brought up many pruning methods to accelerate the efficiency of DTW, such as preprocessing methods (e.g., FastMap algorithm and piecewise dynamic time warping) and lower bound methods [75, 96]. FastMap is an algorithm reducing the dimension of trajectory data while preserving the dissimilarities between trajectories. Piecewise dynamic time warping (PDTW) operates on higher-level abstraction of the data, namely piecewise aggregate approximation (PAA), which will be introduced in detail later.

Fig. 3

Match pairs of DTW and PDTW

Piecewise dynamic time warping (PDTW) [10, 29, 32, 45, 46, 76, 90] is a trajectory distance function that speeds up DTW by a large constant c, where c is data dependent. Same as DTW, PDTW was originally designed for time series. PDTW takes advantage of the fact that a piecewise aggregate approximation can approximate most trajectories. PDTW takes the following two steps to speed up DTW.

• Piecewise aggregate approximation (PAA) PAA cuts a trajectory T of size n into $N=n/c$ pieces, where $[p_{c\cdot (i-1)+1}, p_{c\cdot (i-1)+2}, \dots , p_{c\cdot i}]$ is the ith piece. For piece i, PAA computes ${\bar{p}}_i$ as a representative point, where ${\bar{p}}_i$ is defined as

  $$\begin{aligned} {{\bar{p}}_i} =\frac{ \sum _{j = c(i - 1) + 1}^{c*i} {{p_j}}}{c}. \end{aligned}$$

  (4)

  It transforms T into piecewise approximation ${\bar{T}}=[{\bar{p}}_1, {\bar{p}}_2, \dots , {\bar{p}}_N]$. For example, Fig. 3a demonstrates the two original trajectories denoted by thick lines and Fig. 3b demonstrates the two compared trajectories after PAA. The figure shows the trajectories after PAA can roughly keep the shape of the original trajectories. In other words, the distance between the trajectories after PAA is similar to that between the original trajectories.

• DTW For the compared two trajectories $T_1$ and $T_2$ with the size n and m, respectively, the algorithm then computes DTW distance on PAA trajectories $\bar{T}_1$ and ${\bar{T}}_2$. This DTW distance is used as an approximation of $d_{DTW}(T_1,T_2)$, that is $d_{DTW}(T_1,T_2) \cong d_{PDTW}(T_1,T_2) = d_{DTW}({\bar{T}}_1, {\bar{T}}_2)$. As shown in Fig. 3a, b, the number of match pairs reduces significantly from original trajectories to trajectories after PAA. Thus, it speeds up the DTW calculation.

The time complexity of PDTW is O(NM), where $N = n/c$ (n is the size of $T_1$) and $M = m/c$ (m is the size of $T_2$). Compared to the original DTW algorithm with the complexity of O(nm), PDTW speeds DTW up by a factor of $O(c^2)$. Overall, DTW distance is free of parameters. It is non-metric, since it does not satisfy the triangle inequality. It can use R-tree as an index structure. It mainly supports the lower bounding pruning strategy when answering k-NN queries. Similar to Euclidean distance, it is sensitive to noisy data.

$$\begin{aligned} s_{LCSS}(T_1, T_2) = {\left\{ \begin{array}{ll} \phi , &{}\quad \text {if }i = 0\text { or }j = 0\\ s_{LCSS}(Rest(T_1), Rest(T_2))+1, &{} \quad \text {if } d(Head(T_1),Head(T_2))\le \epsilon \\ \max {\{s_{LCSS}(T_1, Rest(T_2)), s_{LCSS}(Rest(T_1), T_2)\}}, &{}\quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(5)

3.1.2 Partial match measures

Partial match measures are distance measures which do not require all the sample points to be in match pairs (Fig. 2b). The existing partial match measures compare trajectories using some similar methods of compared strings. Longest common subsequence (LCSS) and edit distance-based distance measures are the mainly used distance metrics of partial match measures. LCSS is a traditional similarity metric for strings, which is to find the longest subsequence common to two compared strings. ED quantifies how dissimilar two strings are to one another by counting the minimum number of operations required to transform one string into the other. The following paragraph will introduce how LCSS measures the similarity between two trajectories, followed by the description of distance-based distance measures including ERP and EDR, and their usage in measuring trajectory distance.

LCSS distance

The value of LCSS similarity between sequences $S_1$ and $S_2$ stands for the size of the longest common subsequence of $S_1$ and $S_2$. Trajectory can be treated as a sequence of sample points, so [38, 44, 74] used LCSS to measure the similarity between trajectories. The value of LCSS similarity between trajectories $T_1$ and $T_2$ stands for the size of the longest common subsequence of $T_1$ and $T_2$. However, it can hardly find any two sample points with the exact same location information. Thus, in measuring the similarity of trajectories $T_1$ and $T_2$, LCSS treats $p_i$ ($p_i \in T_1$) and $p_j$ ($p_j \in T_2$) to be the same as long as the distance between $p_i$ and $p_j$, which is less than a threshold $\epsilon$. In other words, LCSS finds all match pairs $(p_i, p_j)$ where $d(p_i, p_j) \le \epsilon$. Thus, some sample points of $T_1$ and $T_2$ cannot be in any match pairs. Then, LCSS distance simply counts the number of match pairs between $T_1$ and $T_2$. Since the sample points far apart do not contribute to the value of LCSS distance, these sample points do not have match points. In contrast to Euclidean distance, LCSS is robust to noise. The algorithm of $s_{LCSS}(T_1, T_2)$ is given by Eq. (5).

LCSS measures the similarity of two trajectories. Using Eq. (6) [74], LCSS similarity can be transformed to LCSS distance. Hence, the LCSS distance between trajectories is defined as:

$$\begin{aligned} {d_{LCSS}}({T_1},{T_2}) ={ size({T_1})+size({T_2})-2\cdot s_{LCSS}({T_1},{T_2})} \nonumber \\ \end{aligned}$$

(6)

And the normalized LCSS distance is defined as:

$$\begin{aligned} {d_{LCSS}}({T_1},{T_2}) =1- \frac{s_{LCSS}({T_1},{T_2})}{ size({T_1})+size({T_2})-s_{LCSS}({T_1},{T_2})} \nonumber \\ \end{aligned}$$

(7)

The time complexity of LCSS is O(nm), where n and m are the size of the $T_1$ and $T_2$, respectively. LCSS works well with noisy trajectory data since noisy sample points will not affect the value of LCSS. The disadvantage of LCSS is that the value of LCSS highly relies on the size of compared trajectories. Therefore, when the sampling rates of comparing trajectories change, the result can be quite different. Moreover, LCSS value is not parameter free and its effectiveness highly relies on the value of $\epsilon$. And LCSS is not a metric distance measure. This is because it does not satisfy the identity of indiscernibles and the triangle inequality. It can use R-tree as an index structure and supports the mean value Q-gram pruning strategy, the near triangle inequality pruning strategy, and the histogram pruning strategy [15] when answering k-NN queries.

Similar to LCSS, edit distance is another string metric for measuring the amount of difference between two sequences. The edit distance between two strings is defined as the minimum number of edits needed to transform one string into the other, with the allowable edit operations including insertion, deletion, and substitution of a single character. Given two strings s = “ab” and r = “ac,” $s_1$ and $r_1$ are a match pair since they have the same character “a,” while $s_2$ and $r_2$ are not. Hence, the edit distance between s and r is 1 (one substitution). EDR and ERP are two distance measures based on edit distance, which will be introduced in the following subsection.

EDR distance

Edit distance on real sequence (EDR) [2, 12, 15, 21, 37, 49, 62, 80] is an ED-based trajectory distance measure. The EDR distance $d_{EDR}$$(T_1, T_2)$ between two trajectories $T_1$ and $T_2$ with lengths of n and m, respectively, is the number of edits (insertion, deletion, or substitutions) needed to change $T_1$ into $T_2$. Similar to LCSS, it can hardly find any two sample points with exactly the same location information. To measure the distance of trajectories $T_1$ and $T_2$, EDR treats $p_i$ ($p_i \in T_1$) and $p_j$ ($p_j \in T_2$) the same only if the locations of $p_i$ and $p_j$ are within a range $\epsilon$. EDR uses subcost($p_1, p_2$) (Eq. 8) to represent the contribution of $p_1, p_2$ to the value of EDR distance. The algorithm of $d_{EDR}(T_1, T_2)$ is defined as Eq. (9):

$$\begin{aligned} subcost({p_1},{p_2})= & {} \left\{ \begin{array}{l} 0~~,\begin{array}{*{20}{c}} &{}\quad {d(p_1, p_2)} \end{array}\le \varepsilon \\ 1,~~\begin{array}{*{20}{c}} &{}\quad {otherwise} \end{array} \end{array} \right. \end{aligned}$$

(8)

$$\begin{aligned} d_{EDR}(T_1,T_2)= & {} {\left\{ \begin{array}{ll} n, &{} \quad \text {if }\,m = 0\\ m, &{}\quad \text {if }\,n = 0\\ \min {\{ d_{EDR}(Rest(T_1),Rest(T_2))} {+ subcost(Head(T_1),Head(T_2)),}\\ \quad d_{EDR}(Rest(T_1),T_2) +1, d_{EDR}(T_1,Rest(T_2)) + 1\},&{}\quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(9)

Similar to LCSS, EDR is robust to noisy trajectory data. For example, there are four trajectories shown in Fig. 4a, $T_1 = [p_1, p_2, p_3, p_4]$, $T_2 = [p_5, p_6, p_7, p_8]$, $T_3 = [p_1, p_9, p_3, p_4]$, and $T_4 = [p_1, p_9, p_{10}, p_3, p_4]$. Assume that $T_1$ is the query trajectory, and $p_9$ and $p_{10}$ are noise points (they are significantly different from other points). The correct ranking in terms of similarity to $T_1$ is: $T_3$, $T_4$, and $T_2$. This is because, except noise, the rest of the elements of $T_3$ and $T_4$ match the elements of Q perfectly. Previous distance measures, i.e., Euclidean distance and DTW, rank $T_2$ as the most similar trajectory of $T_1$. However, even from general movement trends (subsequent values increase or decrease) of the two trajectories, it is obvious that $T_3$ is more similar to $T_1$ than $T_2$. Since the EDR distance is not affected by a noisy sample point, EDR ranks $T_3$ to the most similar trajectory of $T_1$.

The disadvantage of EDR is that the distance value of EDR heavily relies on the parameter $\epsilon$, which is not easy for users to adjust; a not well-adjusted $\epsilon$ may cause inaccuracy. For example, there are three trajectories shown in Fig. 4b, $T_5 = [p_1, p_2, p_3, p_4]$, $T_6 = [p_5, p_6, p_7, p_8]$, and $T_7 = [p_9, p_{10}, p_{11}, p_{12}]$. We set $\epsilon$ to be $d(p_1, p_9)$ (the distance between $p_1$ and $p_9$). According to this $\epsilon$, the $d_{EDR}(T_1,$$T_2)$ and $d_{EDR}(T_1,T_3)$ are both 0. EDR cannot tell that $T_6$ is obviously more likely near to $T_5$ than $T_7$.

The time complexity of EDR is O(mn). EDR is not parameter free. Not satisfying the identity of indiscernibles and the triangle inequality, EDR is not a metric distance measure. R-Tree can be used as its index structure. It supports the mean value Q-gram pruning strategy, the near triangle inequality pruning strategy, and the histogram pruning strategy when answering k-NN queries.

ERP distance

Edit distance with real penalty (ERP) [1, 14, 16, 47, 51, 55, 102] is a trajectory distance measure that combines Lp-norm and edit distance. As introduced above, Euclidean distance and DTW both use Lp-norm for measuring the distance between trajectories. However, they require every sample point to be in a match pair. ERP uses the edit-distance-like sample point matching method. In edit distance, there are three operations, i.e., addition, deletion, and substitution. Thus, when a substitution operation happens on a sample point $p_i$ from $T_1$ for transforming $T_1$ to $T_2$, there must be a counterpart $p_j$ from $T_2$ and ERP treats $p_i$ and $p_j$ as a match pair. When an addition operation happens, $p_j$ is added to $T_1$ for transforming $T_1$ to $T_2$. ERP treats $p_j$ to be matched to an empty point, namely gap. When a deletion operation happens, $p_i$ is deleted from $T_1$ for transforming $T_1$ to $T_2$, and ERP treats $p_i$ to be matched to a gap. [14] claims that for most applications, strict equality will not make sense. For instance, the distance $d(p_1, p_2)$ between sample points $p_1 = 1$ and $p_2 = 2$ should be less than the distance $d(p_1, p_3)$ between sample points $p_1 = 1$ and $p_3 = 10{,}000$. Thus, instead of using the number of edits which edit distance uses, ERP uses $L_1$-norm as the distance of match pairs.

Fig. 4

Example of EDR

Specifically, ERP uses edit distance to get match pairs. And then for every match pair $(p_1, p_2)$, ERP calculates the $L_1$-norm distance between $p_1$ and $p_2$; for every sample point $p_3$ that matches to a gap, ERP calculates the $L_1$-norm distance from $p_3$ to a constant. Formally, the distance metric between sample points used by ERP is as follows:

$$\begin{aligned} dist_{ERP}({p_1},{p_2}) = \left\{ \begin{array}{ll} |{p_1} - {p_2}|, &{}\quad {\mathrm{if}~{p_1},~{p_2}~\mathrm{not}~\mathrm{gaps}}\\ |{p_1} - g|,&{}\quad {\mathrm{if}~{p_2}~\mathrm{is}~\mathrm{a}~\mathrm{gap}}\\ |{p_2} - g|,&{}\quad {\mathrm{if}~{p_1}~\mathrm{is}~\mathrm{a}~\mathrm{gap}}\\ \end{array} \right. \end{aligned}$$

(10)

where g is a user-defined constant. Chen and Ng [14] suggest g should be chosen as 0.

$$\begin{aligned} d_{ERP}({T_1},{T_2}) = {\left\{ \begin{array}{ll} \sum \nolimits _{}^n{dist_{ERP}({p_{1,i}},g)}, &{} \text {if }m = 0\\ \sum \nolimits _1^m{dist_{ERP}({p_{2,i}},g)}, &{} \text {if }n = 0\\ \min {\{ d_{ERP}(Rest(T_1),Rest(T_2)) + dist_{ERP}(Head(T_1),Head(T_2)),} &{}\\ \quad d_{ERP}(Rest(T_1),T_2) + dist_{ERP}(Head(T_1),g),&{}\\ \quad d_{ERP}(T_1,Rest(T_2)) + dist_{ERP}(Head(T_2),g)\} &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(11)

The time complexity of ERP is O(mn). Introducing $L_1$-norm makes ERP a measure that satisfies the triangle inequality, which is a prominent advantage over edit distance and EDR. It allows efficient pruning by using triangle inequality. For example, there are three trajectories $T_1 = [((0,0), 1)]$, $T_2 = [((1,0), 1), ((2, 0), 2)]$, and $T_3 = [((2, 0), 1), ((3, 0), 2), ((3, 0), 3)]$. Let $\epsilon$ to be 1. Thus, the EDR distances between these trajectories are $d_{EDR}$$(T_1, T_2) = 1$, $d_{EDR}(T_2, T_3)$$=1$, and $d_{EDR}(T_1, T_3) =3$. This leads to $d_{EDR}$$(T_1, T_3) > d_{EDR}(T_1, T_2) + d_{EDR}(T_2, T_3)$, so that EDR does not satisfy the triangle inequality. The ERP distances between these trajectories are $d_{ERP}$$(T_1, T_2) = 3$, $d_{ERP}(T_2, T_3)=5$, and $d_{ERP}(T_1, T_3) =8$. And this leads to $d_{ERP}$$(T_1, T_3) \le d_{ERP}(T_1, T_2) + d_{ERP}(T_2, T_3)$, so that ERP satisfies the triangle inequality. However, ERP uses $L_1$-norm as the distance measure which is sensitive to outliers. In addition, ERP is not parameter free due to the involvement of parameter g.

3.2 Continuous sequence-only distance measures

This subsection will introduce four continuous sequence-only distance measures, i.e., EDwP, OWD, LIP, and MD. Continuous sequence-only distance measures view trajectories as continuous functions, i.e., interpolating the sequence of sample points into a sequence of line segments. Generally, they compare the shapes of the compared trajectories or the re-synchronized line segments instead of matching the trajectory sample points directly.

EDwP distance

Edit distance with projections (EDwP) [8, 25, 54, 71, 84, 93] uses dynamic interpolation to match sample points and calculates how far two trajectories are based on their edit distances, i.e., how many edit operations must be done to make the trajectories similar to each other. EDwP uses two edit operations, substitution and addition, in order to match the sampling point of the compared trajectories using dynamic interpolation. The idea is to compute the smallest sequence of edits that makes the compared trajectories $T_1$ and $T_2$ identical; edits are calculated by computing the cost of the projection of a sample point from $T_1$ onto $T_2$ in order to match them. Given two segments $e_1$ and $e_2$ from trajectories $T_1$ and $T_2$, respectively, the two edit operations, substitution and addition, performed by the EDwP are described as follows:

Addition The addition operation, denoted by $add(e_1, e_2)$, is the operation of inserting a point into $e_1$ in order to make it identical to $e_2$, thus splitting $e_1$ into two new segments. The operation inserts new points into the trajectories in order to allow a robust matching between the segments of $T_1$ and $T_2$. The point $p_{ins}$ to be inserted is in $e_1$ that is the closest to the end point of $e_2$, that is:

$$\begin{aligned} p_{ins} = \arg \min _{p \in e_1} d(p, e_2.p_2) \end{aligned}$$

Substitution The substitution operation $sub(e_1, e_2)$ represents the cost of matching $e_1$ with $e_2$, and it is defined as:

$$\begin{aligned} sub(e_1; e_2) = d(e_1.p_1, e_2.p_1) + d(e_1.p_2, e_2.p_2). \end{aligned}$$

Given the previously specified edit functions, the EDwP distance between two trajectories $T_1$ and $T_2$ is given by the recursive function as Eq. (12):

$$\begin{aligned} d_{EDwP}(T_1, T_2) = \left\{ \begin{array}{ll} 0,&{}\quad {\mathrm{if}~|T_1|= |T_2| = 0 }\\ \infty , &{}\quad {\mathrm{else}~ \mathrm{if}~ |T_1| = 0 ~\mathrm{or}~ |T_2| = 0}\\ \min \{d_{EDwP}(Rest(T_1), Rest(T_2))\\ \quad + (sub(T_1.e_1, T_2.e_1) \times Coverage(T_1.e_1, T_2.e_1)),\\ \quad d_{EDwP}(add(T_1, T_2), T_2), d_{EDwP}(T_1, add(T_2, T_1))\}&{}\quad \mathrm{otherwise}\\ \end{array} \right. \end{aligned}$$

(12)

where Coverage$(e_1, e_2) = length(e_1) + length(e_2)$. It means that segments with large length will add a higher cost to the edit function.

The time complexity of EDwP is $O((m+n)^2)$. EDwP is parameter free. It is not a metric distance measure since it does not satisfy the triangle inequality. EDwP can use an index structure called TrajTree [71] to answer k-NN queries efficiently on large trajectory databases. It supports the lower bounding pruning strategy when answering k-NN queries.

One-way distance

One-way distance (OWD) [17, 22, 28, 53, 64] is a typical continuous sequence-only distance measure. Instead of finding match pairs and using the distance of each match pair, OWD distance between trajectories $T_1$ and $T_2$ is the average minimal distance of $T_1$’s all sample points to the line approximated $T_2$. OWD is an asymmetric distance measure, i.e., the distance from $T_1$ to $T_2$ is not necessarily equal to that from $T_2$ to $T_1$.

Fig. 5

Linear representation OWD distance and grid representation OWD distance (colour figure online)

OWD approximates a trajectory using a sequence of line segments. A line segment is represented by a pair of trajectory sample points $(p_i, p_j)$, the length of which is defined as the Euclidean distance between $p_i$ and $p_j$. A linear trajectory is a sequence of points $(p_1,\dots ,p_n)$, where each adjacent pair of points $(p_i,p_{i+1})$$(1\le i\le n-1)$ is a line segment in the trajectory. The OWD distance measure is to find the average minimal distance of sampling points of a trajectory $T_1$ to another linearly represented trajectory $T_2$, as shown in Fig. 5a. The distance from a point p to a trajectory T is defined as:

$$\begin{aligned} d_{point}(p,T) = \min _{p'\in T}{d(p,p')}. \end{aligned}$$

(13)

With the definition of $d_{point}(p,T)$, the OWD distance from $T_1$ to $T_2$ is defined as:

$$\begin{aligned} d_{owd}(T_1\rightarrow T_2) = \frac{1}{Size(T_1)} \cdot \sum \limits _{p \in T_1}{d_{point}(p,T_2)}. \end{aligned}$$

(14)

Since OWD is asymmetric, the distance between two trajectories $T_1$ and $T_2$ is the average of their one-way distances:

$$\begin{aligned} d_{OWD}(T_1,T_2) = \frac{1}{2}(d_{owd}(T_1\rightarrow T_2) + d_{owd}(T_2\rightarrow T_1)).\nonumber \\ \end{aligned}$$

(15)

The time complexity of OWD is O(nm), hindering its scalability to trajectory data with a large number of sample points. In order to improve the performance, another representation method called grid representation is designed.

Grid representation is an approximation of OWD to reduce the computation cost. In a grid representation, the entire workspace is divided into equal-size grid cells, and each grid cell is labeled by its x, y coordinates. Trajectories $T_1$ and $T_2$ are approximated in grid representation as shown in Fig. 5b, denoted by red grids. Given a grid cell $g = (i,j)$, i is the x-label of g (i.e., g.x) and j is the y-label of g (i.e., g.y). The distance between two grid cells $g_1$ and $g_2$ is defined as:

$$\begin{aligned} {d_{grid}}({g_1},{g_2}) = \sqrt{({{({g_1}.x - {g_2}.x)}^2} + {{({g_1}.y - {g_2}.y)}^2})}.\nonumber \\ \end{aligned}$$

(16)

With grids, a trajectory can be represented as a grid sequence, that is, $T^g = (g_1,\dots ,g_n)$, so that for each $1 \le i < n$, $g_i$ and $g_{i+1}$ are adjacent. The number of grid cells, n, is called the length of $T^g$, denoted as $|T^g|$. The distance from a grid cell g to a grid trajectory $T^g$ is the shortest distance from g to $T^g$.

$$\begin{aligned} d_{point}^g(g,T^g) = \min _{g' \in {T^g}}{d_{grid}(g,g')}. \end{aligned}$$

(17)

The one-way distance from $T^g_1$ to $T^g_2$ in the grid representation is defined as the sum of the distance from all grid cells of $T^g_1$ to $T^g_2$ normalized by the length of $T^g_1$.

$$\begin{aligned} d_{owd}(T_1^g\rightarrow T_2^g) = \frac{1}{|T_1^g|}\sum _{p \in T_1^g}{d_{point}^g(p,T_2^g)}. \end{aligned}$$

(18)

The distance between two grid trajectories $T^g_1$ and $T^g_2$ is defined as the average of $d^g_{owd}(T^g_1\rightarrow T^g_2)$ and $d^g_{owd}(T^g_2\rightarrow T^g_1)$.

$$\begin{aligned} d^g(T^g_1,T^g_2)=\frac{1}{2}(d^g_{owd}(T^g_1\rightarrow T^g_2)+d^g_{owd}(T^g_2\rightarrow T^g_1)).\nonumber \\ \end{aligned}$$

(19)

The time complexity of grid-based OWD is O(MN), where M and N are the size of $T_1^g$ and $T_2^g$, respectively. If the average size of the original trajectory is c times of that of grid represented trajectory, the grid representation can speed up the calculation of OWD by a factor of $O(c^2)$. OWD is parameter free. It is not symmetry, hence non-metric. The index structure [75] composed of multiple granularity levels can be employed to improve the efficiency of k-NN search. And it supports the lower bounding pruning strategy.

Locality in-between polylines distance

More specific to a two-dimensional trajectory, Refs. [3, 4, 65, 73] suggest that it can be mapped to the two-dimensional geometry space. Figure 6 demonstrates how trajectories $T_1$ and $T_2$ can be mapped to a XY-plane. All the sample points of $T_1$ are mapped to XY-plane and connect the adjacent two sample points by a line, so do those of $T_2$. Then, the two start (end) points are connected using a line, and the intersection points of $T_1$ and $T_2$, e.g., $i_1$, $i_2$, etc., are marked. After the mapping, the distance between $T_1$ and $T_2$ can be easily transformed into a geometry problem according to [65].

Fig. 6

Mapping trajectories $T_1$ and $T_2$ to 2D the geometry space

With mapped trajectories, the locality in-between polylines (LIP) distance between two trajectories $T_1$ and $T_2$ can be defined as the area between two polylines $T_1$ and $T_2$. The LIP algorithm is shown as follows:

$$\begin{aligned} d_{LIP}(T_1,T_2) = \sum _{\forall polygon_i} {Are{a_i} * w_i}. \end{aligned}$$

(20)

In order to reduce data noise, LIP gives weight to each polygon area. Let $Length_T(i_k,i_{k+1})$ be the length of the portion of trajectory polyline T that participates in the contribution of $polygon_k$. The weight is defined as:

$$\begin{aligned} w_k = \frac{Length_{T_1}(i_k,i_{k + 1}) + Length_{T_2}({i_k},i_{k + 1})}{Length({T_1}) + Length({T_2})}. \end{aligned}$$

(21)

Regarding the complexity of $d_{LIP}(T_1,T_2)$ computation, let N denote the total size of the sample point, i.e., $N =$ Length($T_1$) $+$ Length($T_2$), and K denote the size of intersection points. Finding intersection points can be transformed into the red–blue intersection problem [11], which can be solved in $O(\,N\mathrm{log}N+K)$ [13]. Since the number of polygons defined over the K intersection points is K, O(K) time is required to calculate the areas of polygons. In total, the time complexity of LIP is $O(N\mathrm{log}N)$, assuming that K and N are of the same order. Using the shape information to compare the trajectories can avoid many problems in sampling-based trajectory distance measures such as different sampling rates. However, since this distance measure requires mapping the trajectory to the geometry space, it can only work well on trajectories whose spatial deployment follows, on the average, a stable trend without dramatic rotations; otherwise, it fails to measure the distance. If a trajectory T has the shape as shown in Fig. 7a, the distance from T to itself T may not be zero according to this method. Also, it will fail to measure the distance of two cycling moving objects’ trajectories shown in Fig. 7b. Overall, LIP is parameter free. It is non-metric for not satisfying the triangle inequality. Index structures and pruning strategies for LIP have not been studied yet.

Fig. 7

Two kinds of trajectory shapes LIP cannot handle

Fig. 8

Example of merge distance (colour figure online)

Merge distance

Merge distance (MD) [39, 50, 66, 78] is to find the shortest trajectory that is a super-trajectory of the two compared trajectories. As shown in Fig. 8a, $T_1$ and $T_2$ are two compared trajectories; MD is to find a shortest super-trajectory $T_{super}$ connecting all the sample points of $T_1$ and $T_2$, denoted by the green line. Intuitively, this length should be similar to the length of two compared trajectories when the two trajectories come from the same curve. For example, as shown in Fig. 8b, the two compared trajectories from the same curve are denoted by the red dotted line and the blue dotted line, respectively, and the shortest super-trajectory is denoted by the green solid line. Obviously, the length of the green line is almost equal to the lengths of the red line and the blue line.

The length of the shortest super-trajectory $T_{super}$ is denoted by $Length(T_{super})$. Let T(1, i) denote the subtrajectory $[p_1, p_2, \dots , p_i]$, and $Length(T_1(1, i), T_2(1, j))$ denote the length of the shortest super-trajectory that connects $T_1(1, i)$ and $T_2(1, j)$, so that its last point is the ith point of $T_1$, i.e., $T_{1,i}$. For two compared trajectories $T_1({Size}(T_1) =m)$ and $T_2 ({Size}(T_2) =n)$, $Length(T_{super})$ can be computed using Eq.  22:

$$\begin{aligned} \left\{ \begin{array}{ll} Length(T_1(1, i), T_2(1, j))= \min (Length(T_1(1, i-1), T_2(1, j))+d(T_{1,i-1}, T_{1,i}),\\ \quad Length(T_2(1, j),T_1(1, i-1))+d(T_{2,j}, T_{1,i})),&{}\quad \mathrm{if}~\le i \le m ~\mathrm{and}~ 1\le j \le n \\ Length( T_2(1, j),T_1(1, i))= \min (Length(T_1(1, i), T_2(1, j-1)) +d(T_{1,i}, T_{2,j}),\\ \quad Length(T_2(1, j-1),T_1(1, i))+d(T_{2,j-1}, T_{2,j})),&{}\quad \mathrm{if}~\le i \le m ~\mathrm{and}~ 2\le j \le n \\ Length(T_1(1, i), T_2(1, j))= \left( {\sum \limits _{k = 1}^{j - 1} {d(T_{2,k}, T_{2, k+1})} } \right) +d(T_{2,j},T_{1,1}),&{}\quad \mathrm{if}~i = 1\\ Length(T_1(1, i), T_2(1, j))= \left( {\sum \limits _{k = 1}^{i - 1} {d(T_{1,k}, T_{1, k+1})} } \right) +d(T_{1,i},T_{2,1}),&{}\quad \mathrm{if}~j = 1\\ Length(T_{super}) = \min \left( {Length(T_1(1, m), T_2(1, n)), Length( T_2(1, n),T_1(1, m))}\right) &{} \\ \end{array} \right. \nonumber \\ \end{aligned}$$

(22)

After computing the length of the shortest super-trajectory, $Length(T_{super})$, the merge distance can be obtained as:

$$\begin{aligned} d_{MD}(T_1, T_2)=\frac{{Length(T_{super})}}{{Length(T_1)+Length(T_2)}} -1. \end{aligned}$$

(23)

The time complexity of merge distance is O(mn). It is robust in detecting trajectories with different sampling rate, as GPS devices only provide sample points along the actual trajectory. MD is parameter free and non-metric since it does not satisfy the identity of indiscernibles. Index structures and pruning strategies for MD have not been studied yet.

4 Spatiotemporal distance measures

This section will introduce the spatiotemporal distance measures that measure the distance between two trajectories by both their spatial and temporal attributes. Sometimes, temporal information is a key feature to determining whether two trajectories are similar. For example, the moving paths of athletes on tracks are always the same while the difference in these trajectories is their moving speed. Thus, in this case, spatiotemporal distance measures are much more suitable. Also considering merely spatial information of trajectory may cause some inaccuracy when time interval of the trajectory sampling ranges a lot. For example, there are three trajectories $T_1=\{((1,0),1), ((2,0),2),((3,0),3)\}$, $T_2=\{((1,0),1), ((2,0),2), ((3,0),100)\}$, and $T_3=\{((1,0),1), ((2,0),2), ((2.9,0),3)\}$. If we only consider the spatial information, $T_2$ is more similar to $T_1$ than to $T_3$. But obviously, $T_1$ and $T_3$ are more alike. Spatiotemporal distance measures can be further classified into discrete spatiotemporal distance measures and continuous spatiotemporal distance measures.

4.1 Discrete spatiotemporal distance measures

The following subsection will introduce 2 discrete spatiotemporal distance measures, i.e., STLCSS and STLC.

Spatiotemporal LCSS

As mentioned in Sect. 3.1.2, LCSS was originally designed to measure the distance of strings, not considering temporal information. Several extensions to LCSS have been proposed in order to consider temporal information in measuring trajectory distance. In [90], Vlachos et al. introduced a time-sensitive LCSS distance measure, the spatiotemporal longest common subsequence STLCSS. Kahveci et al. [43], Vlachos et al. [89], and Patel et al. [63] also used STLCSS as trajectory distance measure. However, it can hardly find any two sample points with exactly the same location information and temporal information. Thus, in measuring the distance between two sample points $p_1$ and $p_2$, STLCSS involves two constants: one integer $\delta$ and one real number $\epsilon > 0$. The constant $\delta$ controls how far in time two trajectories can go in order to match a given point from one trajectory to a point in another trajectory; the constant $\epsilon$ is the matching threshold. STLCSS treats $p_1$ and $p_2$ to be spatially same only if the distance between $p_1$ and $p_2$ is less than the threshold $\epsilon$. In Fig. 9, the gray region is the matching region of a trajectory with $\delta$ and $\epsilon$.

Fig. 9

Matching region of a trajectory with $\delta$ and $\epsilon$

Consider two trajectories $T_1$ and $T_2$ with a size of n and m, respectively. The STLCSS similarity $s_{STLCSS}(T_1, T_2)$ with constants $\delta$ and $\epsilon$ is shown in Eq. (24):

$$\begin{aligned} s_{STLCSS}(T_1,T_2) = {\left\{ \begin{array}{ll} 0, &{} \text {if }T_1\text { or }T_2\text { is empty} \\ 1 + s_{STLCSS}(Rest(T_1),Rest(T_2)), &{} \text {if } |Head(T_1).x-Head(T_2).x|<\varepsilon \text { and } \\ &{} |Head(T_1).y- Head(T_2).y|<\varepsilon \text { and} \\ &{}|Head(T_1).t-Head(T_2).t|\le \delta \\ \max {(s_{STLCSS}(Rest(T_1),T_2)}, {s_{STLCSS}(T_1,Rest(T_2)))}, &{} \text {otherwise} \end{array}\right. }.\nonumber \\ \end{aligned}$$

(24)

The key idea of this extended LCSS is to allow stretching the restricted time ($\le \delta$). The STLCSS distance is defined as:

$$\begin{aligned} d_{STLCSS}(T_1,T_2) =1- \frac{s_{STLCSS}(T_1,T_2)}{\min (n,m)}. \end{aligned}$$

(25)

This measure tries to give more weight to the similar portions of the sequences.

The time complexity of STLCSS is O(mn). It is robust to noisy trajectory data. The drawback of STLCSS is that it involves two parameters $\delta$ and $\epsilon$, making the choice of parameters an important issue. Similar to LCSS, it violates identity of indiscernibles and triangle inequality, becoming a non-metric distance measure. A hierarchical tree introduced by [90] can be used as an index structure of STLCSS in order to efficiently answer k-NN queries in a dataset of trajectories. It supports the lower bounding pruning strategy when answering k-NN queries.

Spatiotemporal linear combine distance

STLCSS extends LCSS to consider temporal information using a string-based distance. Naturally, there is another way to define a distance measure by the Lp-norm. Shang et al. [79] proposed the spatiotemporal linear combine distance, STLC which linearly combines spatial distance and temporal distance between two compared trajectories. Shang et al. [79] uses $L_2$-norm to measure the spatial distance and $L_1$-norm to measure the temporal distance. Thus, given a sample point p and a trajectory T , the spatial distance $d_{spa}(p, T)$, and the temporal distance $d_{tem}(p, T)$ between p and T are defined as:

$$\begin{aligned} d_{spa}(p, T)= & {} \mathop {\min }\limits _{p' \in T}\{d(p, p')\}\\ d_{tem}(p, T)= & {} \mathop {\min }\limits _{p' \in T}\{|p.t - p'.t|\}. \end{aligned}$$

Given trajectories $T_1$ and $T_2$, their spatial and temporal similarities, $s_{spa}(T_1,T_2)$ and $s_{tem}(T_1, T_2)$, are defined as:

$$\begin{aligned} {s_{spa}}({T_1},{T_2}) = \frac{{\sum \nolimits _{p \in {T_1}} {{e^{ - {d_{spa}}(p,{T_2})}}} }}{{Size({T_1})}} + \frac{{\sum \nolimits _{p' \in {T_2}} {{e^{ - {d_{spa}}(p',{T_1})}}} }}{{Size({T_2})}}\nonumber \\ \end{aligned}$$

(26)

$$\begin{aligned} {s_{tem}}({T_1},{T_2}) = \frac{{\sum \nolimits _{p \in {T_1}} {{e^{ - {d_{tem}}(p,{T_2})}}} }}{{Size({T_1})}} + \frac{{\sum \nolimits _{p' \in {T_2}} {{e^{ - {d_{tem}}(p',{T_1})}}} }}{{Size({T_2})}}.\nonumber \\ \end{aligned}$$

(27)

The spatial and temporal similarities are in the range [0, 2]. Finally, a linear combination method is used to combine spatial and temporal similarities, and the spatiotemporal similarity is defined as:

$$\begin{aligned} s_{STLC}(T_1, T_2) = \lambda \cdot s_{spa}({T_1},{T_2}) +(1-\lambda )\cdot s_{tem}({T_1},{T_2}).\nonumber \\ \end{aligned}$$

(28)

Here, parameter $\lambda \in [0,1]$ controls the relative importance of the spatial and temporal similarities.

The time complexity of STLC is O(mn). It is not parameter free. Due to violating triangle inequality, STLC is non-metric. A hierarchical grid index introduced by [79] can be used as an index structure of STLC in order to efficiently answer k-NN queries in a dataset of trajectories. It mainly supports the lower bounding and upper bounding pruning strategies when answering k-NN queries.

4.2 Continuous spatiotemporal distance measures

This section will introduce three continuous spatiotemporal distance measures, i.e., Fréchet distance, STED, and STLIP. Generally, they compare the shapes of compared trajectories or the re-synchronized line segments, instead of matching the trajectory sample points directly.

Fréchet distance

The Fréchet distance [92] is a distance measure between curves in mathematics, which considers the location and order of the points along the curves. The Fréchet distance between two curves is defined as the minimum length of a leash required to connect two separate paths. The Fréchet distance and its variants find application in several problems, from morphing, handwriting recognition to protein structure alignment. Gasmelseed and Mahmood [30], Lin and Su [53], and Xie et al. [93] used the Fréchet distance as a time-sensitive trajectory distance measure.

Let $T_1$ and $T_2$ be two trajectories which can be represented as two continuous functions $f_1$ and $f_2$ over time t, where the stating time and end time of time period t are denoted by t.start and t.end, respectively. The Fréchet distance between $T_1$ and $T_2$ is defined as the infimum over all reparametrizations $f_1(t)$ and $f_2(t)$. Figure 10 shows the distance between trajectories $T_1$ and $T_2$. The Fréchet distance algorithm is shown as follows:

(29)

Fig. 10

Fréchet distance between trajectories $T_1$ and $T_2$

The time complexity of Fréchet distance is O(mn) [23]. Since its value is the longest distance between two trajectories at the same time, a noisy point is always far away from a trajectory, causing Fréchet distance to be very sensitive to noise. It is parameter free and metric and can use R-tree as an index structure. It supports the morphological characteristic pruning strategy and the ordered coverage judgment pruning strategy proposed by [34] when answering k-NN queries.

Spatiotemporal Euclidean distance

D’Auria et al. [20] proposed a spatiotemporal Euclidean distance measure (STED) to describe the distance of trajectories along time. More precisely, this distance measure only considers pairs of contemporary instantiations of objects; in other words, for each time instant it compares the object positions at that moment. This measure excludes subsequence matching, and shifting transformation that tries to align trajectories.

This distance measure assumes the object moves in a piecewise linear manner: It moves along a straight line at some constant speed and reports a sample point when it changes the direction and/or speed. Following the assumption, the moving object’s position function p(t) over time t can be generated. The distance function $d(T_1, T_2)$ between two trajectories $T_1$ and $T_2$ is the average distance between objects. Formally, let l be the temporal interval over which trajectories $T_1$ and $T_2$ exist. The distance is shown as:

$$\begin{aligned} d_{STED}({T_1},{T_2}) = \frac{\int {_ld({p_1}(t),{p_2}(t))\mathrm{d}t}}{|l|}. \end{aligned}$$

(30)

The time complexity of STED is O(mn) [5]. This Euclidean-distance-based spatiotemporal similarity measure is a natural extension of the Euclidean spatial distance. Similar to Euclidean distance, STED is parameter free. And it is metric, thus allowing the use of several indexing techniques such as R-tree to improve performances in k-NN queries. It supports the lower bounding pruning strategy and the triangle inequality pruning strategy when answering k-NN queries.

Spatiotemporal LIP

The sequence-only LIP distance introduced in Sect. 3.2 does not take temporal information into consideration. Pelekis et al. [64] proposed a spatiotemporal version locality in-between polylines distance STLIP which takes temporal information into consideration. The STLIP distance between two trajectories $T_1$ and $T_2$, as shown in Fig. 6, is defined as:

$$\begin{aligned} d_{STLIP}(T_1, T_2, k, \theta )=\sum \limits _{\forall polygon{_i}} {STLIP_i}, \end{aligned}$$

(31)

where $STLIP_i$ for $polygon_i$ is defined as:

$$\begin{aligned} STLI{P_i} = LI{P_i}*(1 + k*TLI{P_i}),~\mathrm{where} ~k\ge 0. \end{aligned}$$

(32)

As shown in Eq. (32), STLIP is defined as a multiple of LIP (by a factor greater than 1). Temporal LIP (TLIP) is a measure modeling the local temporal distance and participates in the STLIP measure by a penalty factor k which represents user-assigned importance to the time factor. In order to define the local temporal distance $TLIP_i$ and associate it with the corresponding $LIP_i$, which is implicitly introduced by the polygons, the time points when $T_1$ and $T_2$ cross each other need to be found. Let $T_1\_I_i$ be the time point when $T_1$ passes from intersection point $I_i$ and $T_1\_I_{i+1}$ be the time point when $T_1$ reaches the next intersection point $I_{i+1}$. Let $T_1\_p_i=[T_1\_I_i, T_1\_I_{i+1})$ be the time interval for trajectory $T_1$ moving from $I_i$ to $I_{i+1}$. Then, $TLIP_i$ is formulated in Eq. (33):

$$\begin{aligned} TLIP_i = \left\| 1 - \frac{2*\max \{T_1\_p_i,T_2\_p_i\}}{Duration_{T_1} + Duration_{T_2}} \right\| . \end{aligned}$$

(33)

The time complexity of STLIP is $O(n\log n)$. It can only be applied to trajectories with two-dimensional spatial data. In addition, it fails to measure the distance shown in Fig. 7a, b. Overall, STLIP is parameter free. It is a non-metric distance measure, since it violates the triangle inequality. Index structures and pruning strategies for STLIP have not been studied yet.

For each distance measure, we analyze five characteristics: (1) what is the time complexity, (2) whether it is parameter free, (3) whether it is a metric, (4) whether it supports indexing, and (5) whether it supports pruning. Table 2 summarizes all these aspects.

Table 2 Characteristics of distance measures

5 Capability evaluation

This section presents our objective experimental evaluation on the capability of different trajectory distance measures. To test the capability of these trajectory distance measures, we define three types of transformations on trajectory, as shown in Table 3, and find out which trajectory distance measures can identify the transformation. We firstly introduce the testing dataset and our capability evaluation framework of trajectory distance measures. Then, we present the result of our objective experiments. At last, we analyze the appropriate usage occasion of every trajectory distance function and their limitations.

Table 3 Trajectory transformations

5.1 Dataset

We employed three datasets for our experimental study, i.e., Geolife data [101], Planet.gpx data [60], and synthetic data. Both GeoLife data and Planet.gpx data are real-world and public data.

The Geolife data are created by 178 users in a period of over four years (from April 2007 to October 2011). This dataset contains 17,621 trajectories with a total distance of 1,251,654 km and a total duration of 48,203 h. These trajectories were recorded by different GPS loggers and GPS phones, with a variety of sampling rates. About 91% of the trajectories are logged in a dense representation, e.g., every 1–5 s or every 5–10 m per point.

Planet.gpx is a trajectory dataset uploaded by OpenStreet-Map users within 7.5 years. In this dataset, there are about 2.7 billion sample points and 11 million trajectories in total. The data only consist of spatial information, i.e., latitude and longitude. Thus, when using Planet.gpx data to test spatiotemporal distance measures, we artificially add temporal information to every sample point.

The synthetic data are artificially generated continuous trajectories. Adopting the methods provided by [6, 26, 95, 97], we build several trajectory generators to artificially generate continuous trajectories. Given any time stamp of a continuous trajectory, we can get its corresponding coordinate (latitude and longitude). Also, we conduct sampling on the continuous trajectory in order to get sample-based trajectories. It is similar to the real-world trajectory dataset.

5.2 Capability evaluation framework

Since the distance of two trajectories does not have a benchmark, it is hard to determine whether the value given by trajectory distance measures for measuring the distance of two trajectories is right or not. What’s more, different distance measures give varied values to measure the distance of two trajectories $T_1$ and $T_2$. It is meaningless to cross-check the distance value provided by different distance measures. And it is always no means to compare the values of a distance, since most distance measures are non-metric. For example, even given $d_{EDR}(T_1, T_2) < d_{EDR}(T_3, T_4)$, we cannot say $T_1$ and $T_2$ are more alike than $T_3$ and $T_4$.

Since the distance measures are always incomparable, we cannot simply tell which distance measure is the best. In this work, we tackle this problem from a novel aspect. As some distance measures are suitable for noisy data and some are suitable for different sampling, we conduct an objective experimental evaluation to check the capability of a distance measure has to handle certain problems of trajectory data. Our evaluation procedure is listed as follows.

• We construct a ground truth result set by computing the k-NN list for a randomly chosen query T from the original trajectories. The k-NN list is denoted as $list_T^{before}$.

• We perform three types (six operations) of transformations on the trajectory dataset in a controlled way (by using parameters), resulting in several sets of transformed trajectories.

• We re-compute the k-NN list for the same query trajectory T in each transformed dataset. The re-computed k-NN list is denoted as $list_T^{after}$.

• A distance measure with the capability of handling a certain transformation should produce an answer list $list_T^{after}$ that is close to the k-NN list on the original dataset $list_T^{before}$. Based on this hypotheses, we compute Spearman’s rank correlation coefficient [31] between the two k-NN lists. The closer the correlation is to 1, the better capability of handling the transformation a distance measure has.

• We conclude the distance measures that have the capability to handle certain transformations.

5.3 Transformations

Trajectory data usually have characteristics such as asynchronous observations, explicit temporal attribute, and some other quality issues. In order to benchmark the trajectory measures in a real setting, following similar methodology as in [71, 82, 83], we simulate these characteristics by introducing six trajectory transformations of three different types, i.e., point shift, trajectory shift, and noise, on trajectory datasets. These transformations are controlled by four parameters, ratio, sampling frequency, scale, and distance. The parameter ratio is used to specify the percentage of sample points to be changed in a trajectory. For instance, $ratio=15\%$ means that $15\%$ of the sample points need to be changed by the transformation function. The parameter sampling rate determines the sampling rate of the transformed trajectory. The parameter scale indicates the scale that the text trajectory should be stretched or suppressed to form the transformed trajectory. For instance, spatial scale = 2 indicates that a trajectory is generated by stretching aa original trajectory by two times in space. The parameter distance is a threshold on how far a sample point might be shifted with respect to the original trajectory. Table 3 summarizes all the transformations and their corresponding parameters.

Fig. 11

Trajectory sampling points of T

As the table demonstrates, there are three ways to re-sample a trajectory, i.e., adding sampling points, removing sampling points, and sampling a trajectory with different sampling rates. For the whole trajectory shifting, transformations are conducted on stretching or suppressing both spatial and temporal information. In terms of noise, we add some significant outliers to the original trajectory. The following subsection will detail the transformations.

5.3.1 Transformation of point shift

Point shift transformation is to modify the sample point sequence of a trajectory rather than the shape and trend. We know that the sample point sequences of a continuous trajectory can be quite different. For instance, both sampling point sequence $[p_1,p_3,p_5,p_7,p_8]$ and sampling point sequence $[p_1,p_2,p_4,p_6, p_8]$ can represent the trajectory T shown in Fig. 11.

However, adding or deleting some important sampling points may change the trajectory a lot. For example, $[p_1,p_3, p_5,p_7,p_8]$ represents the rough trend of T, while $[p_1,p_3,p_7, p_8]$ may not. In order to avoid significant changes in the original trajectory, we try to avoid adding or deleting some skeleton points to the original trajectory. The skeleton points are key turning sampling points that can largely change the trend of a trajectory, such as $[p_3,p_5,p_7]$ of T. We use Ramer–Douglas–Peucker (RDP) method [36] to get a trajectory’s skeleton points.

1. Transformation of adding sampling points

For the transformation of adding sampling points, two methods were used to transform the real-world trajectory data and the synthetic trajectory data, respectively. First, regarding the real-world trajectory data, we add a point ${\bar{p}}$ between two continuous sampling points $p_i$ and $p_{i+1}$ in the sampling point sequence, where the coordinate of ${\bar{p}}$ is the mean coordinate of $p_i$ and $p_{i+1}$ as well as the time. After adding ${\bar{p}}$, we will use RDP to test whether ${\bar{p}}$ is in skeleton point sequence; if not, ${\bar{p}}$ is a suitable adding point. The user-defined parameter of adding sampling points is ratior. Adding ratio r to a real-world trajectory T with a size of n is repeatedly adding the sample point method for $n \cdot r$ times. A real-world trajectory is shown in Fig. 12a where the blue dots represent its sample points. Figure 12b exemplifies the transformed trajectory after adding sample points with a ratio of 50%.

Fig. 12

Transformation example of adding sample points (colour figure online)

Second, regarding the synthetic trajectory, we collect the skeleton point sequence using RDF firstly. Then, the skeleton point sequence forms a representative trajectory ${\bar{T}}$ of the simulated continuous trajectory T. We use ${\bar{T}}$ as the original trajectory. Then, adding a point is just randomly adding a non-skeleton points to ${\bar{T}}$, as well as its time stamp. Adding ratio r sampling points to a ${\bar{T}}$, with a size of n, is adding $n\cdot r$ sample points to ${\bar{T}}$.

2. Transformation of deleting sampling points

Similar to transformation of adding sampling points transformation, two methods are also used for deleting sampling points transformation on real-world trajectory data and the synthetic trajectory data. 1). Regarding the real-world trajectory data, we use RDF to get the skeleton point sequence ${\mathbb {P}}$ of T. We delete a point $p_i \notin {\mathbb {P}}$ from the sampling point sequence of a trajectory. In this way, we keep the shape of the original trajectory. Deleting ratio r of sampling points to a real-world trajectory T with a size of n is repeatedly the method of deleting sample point for $n \cdot r$ times. Figure 13 exemplifies the transformed trajectory after deleting sample points with a ratio of 50%.

2). Regarding the synthetic trajectory, we use RDF to get the skeleton point ${\mathbb {P}}$ with a size of n. We form the original trajectory T by randomly adding 9n non-skeleton sampling points to the skeleton trajectory, where the size of T is 10n. Deleting a point from T is just randomly deleting a non-skeleton point from T. In the same way, deleting ratio r sampling points is deleting $10n \cdot r$ sampling points repeatedly.

3. Transformation of sampling with different rates

For a real-world trajectory $T =[p_1, p_2, \dots , p_n]$, we assume the moving object moves in a state of uniform motion between any two consecutive sample points $p_i$ and $p_{i+1}$. Thus, we can get a continuous trajectory. In the transformation of sampling with different rates, sampling rate sr is used to indicate every sr time interval a sample point is collected. For instance, when $\hbox {sr}=10s$, regardless of the original sampling rate, a transformed trajectory is obtained of which the time interval between two consecutive sample points is 10s. The time stamp of the k’s sample point of the re-sampled trajectory is $p_1.t + 10 \cdot (n -1)$.

Fig. 13

Transformed trajectory after deleting sample points

5.3.2 Transformation of trajectory shift

All the previous transformations focus on the partial shift of sample points of trajectories. This subsection will introduce two transformation methods that affect the whole sampling points. Trajectory ${\bar{T}}$ transformed by these transformation methods has the same length as the original trajectory T; but all sampling points of ${\bar{T}}$ are different from their corresponding sampling points of T. We divide the whole trajectory shift into two types, spatial stretch and suppression, and temporal stretch and suppression.

1. Transformation of spatial stretch and suppression

We implement the transformation of spatial stretch and suppression on the real-world trajectory data and the synthetic trajectory data. The phenomenon is commonly observed in real life that the trajectory lengths or radii of two moving objects are quite different but have many similar moving patterns after normalization, e.g., the moving trajectory of the Earth and Mars. A transformed trajectory ${\bar{T}}$ after spatial stretch and suppression has the same moving trend as the original trajectory ${\bar{T}}$, but the trajectory length or the moving radius is quite different. In transformation implementation, we use the parameter scale to measure the stretch or suppression scale of the spatial information (coordinate) of original trajectories. Figure 14 shows the original trajectory T and its transformed trajectory ${\bar{T}}$ with scale=2. In transformation of spatial stretch and suppression, we keep the temporal information unchanged.

Fig. 14

Transformed trajectory after spatial stretch and suppression

2. Transformation of temporal stretch and suppression

There are many objects moving along the same path but with different speeds. In this transformation, we use parameter scale to change the speed of a trajectory. For the original trajectory $T=[p_1,p_2,\dots ,p_n]$, we use $t_i$ to denote the time interval of $p_i$ and $p_{i+1}$. Then, the transformed trajectory ${\bar{T}}$ can be denoted as $[{\bar{p}}_1, {\bar{p}}_2,\dots ,{\bar{p}}_n]$, where the coordinate of ${\bar{p}}_i$ is the same as $p_i$, but the time interval between ${\bar{p}}_i$ and ${\bar{p}}_{i+1}$ is $t_i\cdot scale$.

5.3.3 Transformation of adding outlier

In real life, trajectory collectors may report some quite strange sampling points that are far away from real locations. There are many trajectory distance measures dealing with this problem such as LCSS, EDR, and ERP. Here, the method of the adding outlier transformation is used. It adds some significant outliers to the original trajectory $T = [p_1, p_2, \dots , p_n]$ to get the transformed trajectory ${\bar{T}}$. We use parameter ratio to control the number of outliers added to the original trajectory T, with a size of n. We use parameter distance to control how far away the outliers might be shifted. Figure 15 shows a transformed trajectory after adding noise with a $\hbox {ratio}=25\%$. The time stamp of a noisy point is a random time stamp between $p_1.t$ and $p_n.t$.

Fig. 15

Transformed trajectory after adding noise

Fig. 16

Transformation correlations of adding sample points

Fig. 17

Transformation correlations of deleting sample points

5.4 Capability of handling transformation of point shift

This part describes the test of the capabilities of these distance measures to handle point shift. As mentioned in Sect. 5.2, we use Spearman’s rank correlation between two k-NN lists $list_{T}^{before}$ and $list_{T}^{after}$ to check the capabilities of distance measures.

5.4.1 Capability of handling transformation of adding sample points

Specifically, for transformation of adding sample points, we test the correlation of every distance measure by tuning the parameter ratio. The parameter ratio decides the number of sampling points to be added to the original trajectory. We select a series of numbers as the parameter ratio, which are 25%, 50%, 100%, and 200%. For EDR, LCSS measures use another threshold $\epsilon$ to determine whether two sampling points can be regarded as the same. We fix $\epsilon$ to be a quarter of the maximum standard deviation of trajectories recommended by [15]. STLC uses $\lambda$ to combine spatial distance and temporal distance. Hence, we set $\lambda =0.5$ as the authors recommended. Frechet distance and STED require handling two trajectories with overlapping time intervals. Thus, in this survey, we extended Frechet distance and STED by comparing relative time instead of absolute time. Specifically, we align the start time of the two trajectories in comparison, and shift all time points in the trajectories accordingly. Figure 16 shows the correlations of discrete and continuous distance measures with respect to the transformation of adding sample points. Moreover, since the results on different datasets are similar, the figures in the experiments study are the average performance over three datasets.

From Fig. 16, we can see that the correlations of a certain distance measure do not vary a lot with the changing ratio. Among these measures, STLC has the best capability of handling the transformation of adding sample points, since its correlations remain over 0.9 for all values of ratio. DTW, ERP, LCSS, and MD are also insensitive algorithms under this transformation; their correlations are over 0.8 under all conditions. This is because the value of LCSS is affected by the number of match pairs, while the added sample points can hardly form new match pairs for two different trajectories. Since the added sample points do not change the shape of transformed trajectories, continuous distance measures MD is insensitive to the transformation of adding sample points.

According to the correlations of each distance measure, we find STLC, DTW, ERP, LCSS, and MD are not sensitive to the transformation of adding sample points. In other words, they have the capability of handling transformation of adding sample points.

5.4.2 Capability of handling transformation of deleting sample points

For transformation of deleting sample points, we test the Spearman’s rank correlation between two k-NN lists of every distance measure by tuning the parameter ratio. The parameter ratio decides the number of sampling points to be deleted from the original trajectory. We select a series of numbers as the parameter ratio, which are 10%, 20%, 40%, and 80%. The correlation values of every distance measure are shown in Fig. 17.

Just like the transformation of adding sample points, most distance measures share the same trend that correlations of distance measures do not vary a lot with the increasing ratio. STLC still has the highest correlation values, indicating the best capability of handling transformation of deleting sample points. DTW, ERP, LCSS, EDwP, and MD have high correlations over 0.8. According to the correlation values of each distance measure, we find DTW, ERP, LCSS, EDwP, MD, and STLC are not sensitive to the transformation of deleting sample points. Hence, they have the capability of handling the transformation of deleting sample points.

5.4.3 Capability of handling transformation of different sample rates

For the transformation of different sampling rates, we test the Spearman’s rank correlation of every distance measure by tuning the parameter’s sampling rate. The parameter’s sampling rate ranges from 20 to 80 s with a asymmetry step. Figure 18 shows correlation values for discrete and continuous distance measures.

Fig. 18

Transformation correlations of changing sampling rates

As Fig. 18 demonstrates, the correlations of all the distance measures change slightly with the increasing sampling rate. Generally, the discrete distance measures have higher correlations than continuous distance measures. DTW, ERP, LCSS, STLC, EDwP, and MD perform well under this transformation, and their correlations are over 0.8. Except for LCSS, all these distance measures use the Lp-norm distance metric to measure the distance between sample points or segments in-between. STLC is still the best distance measure of handling transformation of changing sampling rate, with correlations over 0.9. In contrast, EDR and OWD are the most sensitive distance measures with correlations less than 0.6.

5.5 Capability of handling transformation of trajectory shift

In this part, we evaluate how effective each trajectory distance measure to recognize the whole shift trajectories.

5.5.1 Capability of handling transformation of spatial stretch and suppression

Transformation of spatial stretch and suppression is simulating the similar moving patterns but with different moving lengths or radii in reality. We tune the parameter scale from 0.25 to 4.0 to find out the trajectory distance measures able to handle the transformation of spatial stretch and suppression. The correlations of all trajectory distance measures are shown in Fig. 19.

Fig. 19

Transformation correlations of spatial stretch and suppression

As Fig. 19 shows, the correlations of discrete distance measures are generally higher than those of continuous distance measures. Correlations of distance measures do not vary a lot with the increasing scale. DTW, ERP, LCSS, and STLC are not sensitive to the transformation of spatial stretch and suppression, and their correlations are over 0.8. STLC still has the highest correlations of over 0.9. Thus, DTW, ERP, LCSS, and STLC have the capability of handling the transformation of spatial stretch ad suppression. Among them, STLC has the best capability. In contrast, OWD again does not work well under this transformation.

5.5.2 Capability of handling transformation of temporal stretch and suppression

Transformation of temporal stretch and suppression is simulating objects moving in the same path but with different speeds. We tune the parameter scale from 0.25 to 2.0 to get the correlations for distance measures. Since temporal stretch does not affect the k-NN lists of sequence-only distance measures, we only demonstrate the correlations of spatiotemporal distance measures in Fig. 20.

As Fig. 20 shows, the correlations of different spatiotemporal distance measures do not change dramatically with the increasing scale. STLC has the highest correlations among all the spatiotemporal distance measures, with the correlation of more than 0.9. STLCSS and STLIP also have correlations over 0.8 with all scale values. According to the correlation values, we find STLCSS, STLIP, and STLC are not sensitive to the transformation of temporal stretch ad suppression; hence, they have the capability of handling transformation of temporal stretch ad suppression.

Fig. 20

Transformation correlations of temporal stretch and suppression

5.6 Capability of handling transformation of adding outliers

Regarding adding noise, here we just add some significant outliers to the original trajectory. For the transformation of adding outliers transformation, we tune the parameter ratio to be 1% and 5% and the parameter distance to be 0.02, 0.05, and 0.1. Hence, we get six parameter combinations. The correlations of all trajectory distance measures are shown in Fig. 21.

Fig. 21

Transformation correlations of adding outliers

Fig. 22

Correlations of mixed transformation

Figure 21 reveals the correlations of all distance measures increase with the growing ratio and distance. The correlations of EDR, ERP, LCSS, STLC, and MD are all over 0.8, indicating that they have the capability of handling transformation of adding outliers. EDR, ERP, and LCSS all use some string distance metric to measure the distance of trajectories making them robust to noise. OWD and Fréchet distance are the most sensitive to the transformation of adding noise. This is because a noisy sample point can largely change the maximum distance between sample points and the value of OWD, and Fréchet distance is determined by the maximum distance.

5.7 Capability of handling mixed transformations

We have studied the distance measures under each transformation individually. However, in practice trajectory data usually have multiple problems mixed at the same time. For example, a low-resolution GPS under poor network connection can cause noisy sample points as well as missing sample points. Therefore, this section studies the performance of different distance measures under a mixed transformations. We follow the same experiment setup (using k-NN) as in Sect. 5.2. Differently, in the second step we perform six operations of transformations on the trajectory dataset with random parameters.

As shown in Fig. 22, traditional distance measures that have been widely used, such as DTW, LCSS, and Euclidean distance, work well in handling mixed transformations. Some newly proposed distance measures, i.e., STLC, EDwP, and MD, also work well in handling mixed transformations. STLC, with the capability of all transformations, still has the highest correlation. It means STLC has the best capability of handling mixed transformations.

5.8 Performance evaluation

We also evaluate the time cost of each distance measure, which is especially important for online trajectory applications. The average time cost for measuring the distance between two trajectories is shown in Fig. 23. We observe that most distance measures can return the distance between two trajectories within tens of milliseconds. PDTW and LIP turn out to be the most efficient algorithms of which the time cost is 76 ms and 78 ms, respectively. Other distance measures share a similar time cost of around 90 ms.

5.9 Application scope

This subsection summarizes the application scope of the surveyed distance measures under real-life scenarios, as shown in Fig. 24.

Fig. 23

Time cost

Fig. 24

Application scope of different distance measures in terms of transformation types

Point shift Point shift is the most common type of trajectory transformations in practice. In this paper, we consider three concrete transformations in this type, that is, adding sample points, deleting sample points, and changing the sampling rate. They are usually applicable to the case where the trajectory data are unsynchronized sampled. In such applications, the sampling strategies used to collect trajectory data can vary significantly. First of all, there are different sampling methods, such as distance-based methods (e.g., reporting every 100 m), time-based methods (e.g., reporting every 30 s), or prediction-based methods (e.g., reporting when the actual location exceeds a certain distance from the predicted location). Secondly, even for the same sampling strategy, different parameters may be used. For example, although using the time-based sampling strategy, a geologist equipped with specialized GPS devices can report her locations with high frequency (say every 5 s), while a casual mobile phone user may only check in on a location-based web service every couple of hours or even days. As we can see from Fig. 24, DTW, LCSS, ERP, EDwP, MD, and STLC are capable to handle point shifts, and are good choices in the applications discussed above.

Trajectory shift Trajectory shift consists of two transformations: spatial stretch and suppression, temporal stretch and suppression.

DTW, LCSS, ERP, and STLC perform well in handling spatial stretch and suppression, indicating that they can detect the trajectories with similar shape and moving trends, modulo different moving radius and real geographical location. This capability is especially valuable in applications that care only the moving shape and the trend of trajectories, such as the movement of planets and animal migration.

STLCSS, STLC, and STLIP are not sensitive to the variation of moving speeds and thus have good performance in handling temporal stretch and suppression. These three measures are very useful in applications where only the spatial aspect of trajectories matters. In contrast, for applications where speed information is critical, for instance, analyzing the trajectory of an athlete, one should use speed-sensitive measures, such as Fréchet distance and STED.

Noise data Noise data are usually caused by low-resolution GPS equipments or obstacles during data collection. It is a popular problem in practice. For example, car trajectories collected in large cities, especially in CBD areas, are usually full of noises, due to the tall buildings around. LCSS, EDR, ERP, MD, and STLC have the strong denoise capability, and are good choices in such scenarios.

Summary Overall, DTW, LCSS, ERP, MD, and STLC are distance measures with capabilities of handling at least four transformations. Among them, STLC is the best distance measures that can handle all the six transformations. For every transformation, we can find at least three distance measures with the capability of handling it. In handling mixed transformations, DTW, LCSS, Euclidean distance, EDwP, MD, and STLC demonstrate their good capability. STLC again is the best distance measure of handling multiple transformations. The most efficient distance algorithms, i.e., ED and LIP, fail to handle most transformations. Therefore, under performance or latency critical circumstances, one has to consider the trade-off between efficiency and effectiveness when picking distance measure algorithms.

6 Conclusions

We classify trajectory distance measures into four categories, based on (1) whether the trajectory data are discrete or continuous and (2) whether the measure considers temporal information. Each distance measure has its pros and cons. For six trajectory transformations that are common in applications, we identify the most effective trajectory distance measures and experimentally verify the conclusion on large-scale trajectory data. We find that DTW, LCSS, ERP, MD, and STLC are able to handle at least four transformations. Among them, STLC is the best distance measure that can handle all the transformations. In addition, we make a key observation that the efficient distance measures have low effectiveness in handling all transformations.