Top-K structural diversity search in large networks

Abstract

Social contagion depicts a process of information (e.g., fads, opinions, news) diffusion in the online social networks. A recent study reports that in a social contagion process, the probability of contagion is tightly controlled by the number of connected components in an individual’s neighborhood. Such a number is termed structural diversity of an individual, and it is shown to be a key predictor in the social contagion process. Based on this, a fundamental issue in a social network is to find top-$k$ users with the highest structural diversities. In this paper, we, for the first time, study the top-$k$ structural diversity search problem in a large network. Specifically, we study two types of structural diversity measures, namely, component-based structural diversity measure and core-based structural diversity measure. For component-based structural diversity, we develop an effective upper bound of structural diversity for pruning the search space. The upper bound can be incrementally refined in the search process. Based on such upper bound, we propose an efficient framework for top-$k$ structural diversity search. To further speed up the structural diversity evaluation in the search process, several carefully devised search strategies are proposed. We also design efficient techniques to handle frequent updates in dynamic networks and maintain the top-$k$ results. We further show how the techniques proposed in component-based structural diversity measure can be extended to handle the core-based structural diversity measure. Extensive experimental studies are conducted in real-world large networks and synthetic graphs, and the results demonstrate the efficiency and effectiveness of the proposed methods.

1 Introduction

Recently, online social networks such as Facebook, Twitter, and LinkedIn have attracted growing attention in both industry and research communities. Online social networks are becoming more and more important media for users to communicate with each other and to spread information in the real world [17]. In an online social network, the phenomenon of information diffusion, such as diffusion of fads, political opinions, and the adoption of new techniques, has been termed social contagion [25], which is a similar process as epidemic diseases.

Traditionally, the models of social contagion are based on analogies with biological contagion, where the probability that a user is influenced by the contagion grows monotonically with the number of his or her friends who have been affected already [3, 10, 26]. However, such models have recently been challenged [22, 25], as the social contagion process is typically more complex and the social decision can depend more subtly on the network structure. Ugander et al. [25] study two social contagion processes in Facebook: the process that a user joins Facebook in response to an invitation email from an existing Facebook user (recruitment) and the process that a user becomes an engaged user after joining (engagement). They find that the probability of contagion is tightly controlled by the number of connected components in a user’s neighborhood, rather than by the number of friends in the neighborhood. A connected component represents a distinct social context of a user, and the multiplicity of social contexts is termed structural diversity. A user is much more likely to join Facebook if he or she has a larger structural diversity, i.e., a larger number of distinct social contexts. This finding reveals that the structural diversity of a user is an important factor in the social contagion process. As suggested in [25], the analysis of structural diversity in a social network can be beneficial to a wide range of application domains. For example, in a political campaign, to convince individuals to change their attitude, it is obviously more important that they receive messages from multiple directions than that they receive many endorsements [25]. In the promotion of health practices, we can find such top users with the highest structural diversity and inject vaccine for them for reducing their influenced probability. In the marketing, to promote a new product, we can find such top customers as the first priority.

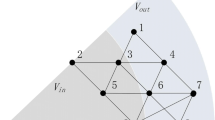
Among all of these applications, a fundamental problem is to find the individuals in a social network with high structural diversity [25]. Motivated by this, in this paper, we study a problem of finding top-$k$ individuals with the highest structural diversity in a social network. Following the definition in [25], the structural diversity of a node $u$ is the number of connected components in a subgraph induced by $u$’s immediate neighbors. Take the network in Fig. 1a as an example. The structural diversity of vertex $f$ is 2, as the induced subgraph by $f$’s neighbors shown in Fig. 1b has two connected components. This structural diversity definition has been shown to be a good predictor for the recruitment study on Facebook in [25]. However, it may fall short in some other scenarios. For example, in the engagement study, the friendship neighborhoods on Facebook are significantly larger than the email contact neighborhoods from the recruitment study. In such a situation, a large number of one-node components, or “singletons,” is not an accurate reflection of social context diversity.

Fig. 1

An example of component-based structural diversity. a A graph G, b f’s neighborhood subgraph

To address this problem, [25] proposed two distinct parametric generalizations of the component count. First, it measures diversity simply by counting only components over a certain size $t$. This is called component-based structural diversity. Second, it measures diversity by the component count of the $t$-core of the neighborhood graph, where a $t$-core is the subgraph formed by repeatedly deleting all vertices of degree less than $t$. This measure is called core-based structural diversity. We have studied the problem of top-$k$ component-based structural diversity search in our previous work [14]. To have a comprehensive investigation of the structural diversity search problem, we further extend our study by adopting the core-based structural diversity in this work. The core-based structural diversity measure has been proven effective through case studies in [25], as the $t$-core notion can exclude small and loose components more effectively.

To solve the top-$k$ structural diversity search problem, a naive method is to compute the structural diversity for all the vertices and then return the top-$k$ vertices. Clearly, such a naive method is too expensive. To efficiently find the top-$k$ vertices, the idea of traditional top-$k$ query processing techniques [15] can be used, which finds the top-$k$ answers according to some search order, and prunes the search space based on some upper-bound score. Following this framework, in our problem, we have to address two key issues: (1) how to develop an effective upper bound for the structural diversity of a vertex and (2) how to devise a good search order in the computation.

In this paper, we propose several efficient and effective techniques to address these issues. For the component-based structural diversity measure, we find that for two vertices connected by an edge, some structural information of them can be shared. For example, in Fig. 1b, vertex $e$ forms a component of size 1 in $f$’s neighborhood. From this fact, we can infer that vertex $f$ also forms a component of size 1 in $e$’s neighborhood. Based on this important observation, the structural diversity computation for different vertices can also be possibly shared. To achieve this, we design a $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$ data structure to keep track of the known structural information of a vertex so as to avoid the computation of structural diversity for every vertex. A novel upper bound of the structural diversity is developed for pruning unpromising vertices effectively. Interestingly, the upper bound can be incrementally refined in the search process to become increasingly tighter. Based on the upper bound and the $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$ data structure, we propose a novel $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework for top-$k$ structural diversity search.

Beyond this, we explore how to apply our $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework to support the core-based structural diversity measure. We find that this definition brings new structural properties, which are different from those of the component-based definition. Thus, our proposed $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$ data structure and upper bound are not applicable to the core-based structural diversity measure. We study new properties of this measure and leverage it to design a new upper bound. We also propose an efficient algorithm for computing the core-based structural diversity score and finally integrate these new techniques into our $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework. This study demonstrates that our $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework can be generalized to handle different instantiations of the structural diversity measure.

The main contributions of our study are summarized as follows.

• We study top-$k$ structural diversity search for the first time by adopting two measures, i.e., the component-based and core-based structural diversity. Structural diversity has been proven to be a positive predictor in social contagion [25]. We develop a novel $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework to efficiently identify the individuals that play a key role in social contagion.

• For the component-based structural diversity measure, we design a $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$ data structure to keep track of the known structural information during the computation and an effective upper bound for pruning. We devise a useful search order to traverse the components in a vertex’s neighborhood. According to this search order, we propose a novel $\mathsf {A^{*}}$ search-based algorithm to compute the structural diversity of a vertex.

• We also design efficient techniques to handle frequent updates in dynamic networks and maintain the top-$k$ results. We use the $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$ structure and a spanning tree structure to efficiently handle edge insertions and deletions, respectively.

• For the core-based structural diversity measure, a new upper bound and an efficient search algorithm are designed.

• We conduct extensive experimental studies on large real networks to show the efficiency of our proposed methods. We also conduct case studies on DBLP and a word association network, which show that structural diversity is useful for identifying ambiguous names in DBLP and finding words with diverse meanings in the word association network.

The rest of this paper is organized as follows. We formulate the top-$k$ structural diversity search problem in Sect. 2 and then discuss and compare the component-based and core-based structural diversity measures in Sect. 3. For the component-based measure, we first present a simple degree-based algorithm in Sect. 4 and then design a novel and efficient $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework in Sect. 5. We design two useful search strategies in Section 6 and discuss update in dynamic networks in Sect. 7. For the core-based measure, we design a new upper bound and an efficient search algorithm in Sect. 8. Extensive experimental results are reported in Sect. 9. We discuss related work in Sect. 10 and conclude this paper in Sect. 11.

2 Problem definition

Consider an undirected and unweighted graph $G=(V, E)$ with $n=|V|$ vertices and $m=|E|$ edges. Denote by $N(v)$ the set of neighbors of a vertex $v$, i.e., $N(v) = \{ u\in V: (v, u)\in E \}$, and by $d(v)=|N(v)|$ the degree of $v$. Let $d_\mathrm{max}$ be the maximum degree of the vertices in $G$. Given a subset of vertices $S\subseteq V$, the induced subgraph of $G$ by $S$ is defined as $G_{S} = (V_{S}, E_{S})$, where $V_{S} = S$ and $E_{S} = \{(v, u): v, u \in S, (v, u) \in E \}$. The neighborhood-induced subgraph is defined as follows.

Definition 1

(Neighborhood-induced subgraph) For a vertex $v \in V$, the neighborhood-induced subgraph of $v$, denoted by $G_{N(v)}$, is a subgraph of $G$ induced by the vertex set $N(v)$.

Consider the graph in Fig. 1a. For vertex $f$, the set of neighbors is $N(f) = \{a,e,g,i\}$. The neighborhood- induced subgraph of $f$ is $G_{N(f)}=(\{a, e, g, i\}, \{(a,g), (g, i)\})$, as shown in Fig. 1b. We define the structural diversity of a vertex as follows.

Definition 2

(Component-based structural diversity [25]) Given an integer $t$ where $1 \le t \le n$, the structural diversity of a vertex $v \in V$, denoted by $score(v)$, is the number of connected components in $G_{N(v)}$ whose size measured by the number of vertices is larger than or equal to $t$. $t$ is called the component size threshold.

$G_{N(f)}$ in Fig. 1b contains a size-1 connected component $\{e\}$ and a size-3 connected component $\{a, g, i\}$. If $t=1$, then $score(f)=2$. Alternatively, if $t=2$, $score(f) = 1$ as there is only one component $\{a, g, i\}$ whose size is no less than 2.

Ugander et al. [25] gave another definition of structural diversity based on the core subgraph concept [6]. Their study showed that the core subgraph-based definition suffices to provide a positive predictor of future long-term engagement in a social network.

A $t$-core of a graph is the largest subgraph in which every vertex is connected to at least $t$ vertices within the subgraph. Note that a $t$-core subgraph may be disconnected and have several components. For instance, consider a graph $G$ in Fig. 2a. The entire graph is a 2-core, and the subgraph inside the dashed circle is a 3-core. As another example, the neighborhood-induced subgraph $G_{N(e)}$ in Fig. 2b is a 1-core containing 2 connected components $\{a, b, c, d\}$ and $\{f, g, h\}$. Based on the $t$-core subgraph, we define the structural diversity of a vertex as follows.

Fig. 2

An example of core-based structural diversity. a G, b $G_{N(e)}$

Definition 3

(Core-based structural diversity [25]) Given an integer $t$ where $1 \le t \le n$, the structural diversity of vertex $v \in V$, denoted by $score^{*}(v)$, is measured by the number of connected components in the $t$-core of $G_{N(v)}$. $t$ is called the core value threshold.

Consider $G_{N(e)}$ in Fig. 2b. If $t=1$, there are two connected components $\{a, b, c, d\}$ and $\{f, g, h\}$ in the 1-core, so $score^{*}(e)=2$. But if $t=2$, there is only one component $\{a, b, c, d\}$ in the 2-core of $G_{N(e)}$, so $score^{*}(e)=1$ in this case.

Based on the two different structural diversity definitions above, we can formulate our top-$k$ component-based and core-based structural diversity search problems, which are, respectively, denoted as $\mathsf {CC}$-$\mathsf {TopK}$ and $\mathsf {Core}$-$\mathsf {TopK}$.

Problem 1 ( $\mathsf {CC}$-$\mathsf {TopK}$ ) Given a graph $G$ and two integers $k$ and $t$ where $1 \le k, t \le n$, top-$k$ structural diversity search is to find a set of $k$ vertices in $G$ with the highest structural diversity with respect to the component size threshold $t$.

Let us reconsider the example in Fig. 1 for $\mathsf {CC}$-$\mathsf {TopK}$. Suppose that $k=1$ and $t=1$. Then, $\{e\}$ is the answer, as $e$ is the vertex with the highest structural diversity ($score(e)=3$).

Problem 2 ( $\mathsf {Core}$-$\mathsf {TopK}$ ) Given a graph $G$ and two integers $k$ and $t$ where $1 \le k, t \le n$, top-$k$ structural diversity search is to find a set of $k$ vertices in $G$ with the highest core-based structural diversity with respect to the core value threshold $t$.

It is important to note that although we focus on the top-$k$ structural diversity search, the proposed techniques can also be easily extended to process the iceberg query, which finds all vertices whose structural diversity is greater than or equal to a pre-specified threshold. Unless otherwise specified, in the rest of this paper, we assume that a graph is stored in the adjacency list representation. Each vertex is assigned a unique ID. In addition, for convenience, we assume that $m \in \varOmega (n)$, which does not affect the complexity analysis of the proposed algorithms. Similar assumption has been made in [18].

3 Problem comparison

In this section, we discuss and compare the problems of $\mathsf {CC}$-$\mathsf {TopK}$ and $\mathsf {Core}$-$\mathsf {TopK}$ in terms of measure definition, computational cost, and result quality.

Measure definition For the core-based structural diversity, every component of a $t$-core subgraph has at least $t+1$ vertices, i.e., it forms a size-($t+1$) connected component. When $t=0$, the core-based structural diversity score is equivalent to the component-based structural diversity, which is simply the component count of the original graph; when $t=1$, the core-based structural diversity score is equivalent to the component-based structural diversity (with a component size of at least 2) in Definition 2; when $t>1$, a component in a $t$-core subgraph is more cohesive than a size-($t+1$) connected component in Definition 2, due to the $t$-core definition that every vertex is connected to at least $t$ vertices in the $t$-core. Thus, all tree-like components will be discarded, and the remaining components are counted for the core-based structural diversity score. On the other hand, the tree-shaped structure may exist and be counted for the component-based structural diversity for any $t$.

Fig. 3

Comparison of $\mathsf {Core}$-$\mathsf {TopK}$ and $\mathsf {CC}$-$\mathsf {TopK}$. a $G_{N(v)}$, b $G_{N(u)}$

Computational cost Compared with the component-based structural diversity, the core-based structural diversity additionally requires to compute the $t$-core and remove unqualified components. Thus, computing $\mathsf {Core}$-$\mathsf {TopK}$ is more costly than $\mathsf {CC}$-$\mathsf {TopK}$.

Result quality Compared with the component-based structural diversity which only imposes a constraint of connectivity, the core-based structural diversity considers both the size and cohesiveness of each component. Thus, the core-based definition can help identify densely connected and more meaningful and distinct social contexts among a user’s friends. For example, Fig. 3a shows the $G_{N(v)}$ of node $v$ containing 15 nodes, 11 of which are connected in one component. If we apply the component-based structural diversity on $G_{N(v)}$ with $t=3$, the component with the 11 nodes is counted. However, this large component is loosely connected through node $w$. But if we apply the core-based structural diversity on $G_{N(v)}$ with $t=3$, two components $A$ and $B$ in the 3-core of $G_{N(u)}$ can be discovered as shown in the shadow regions of Fig. 3a. Each node in $A$ and $B$ has at least three neighbors in the corresponding component, which are densely connected. Obviously, in such a case, the core-based structural diversity can capture the two dense social contexts $A$ and $B$ more precisely than the component-based structural diversity.

On the other hand, the component-based structural diversity is more suitable for analyzing the social context diversity for nodes whose neighbors are not densely connected, since very few results can be discovered by the core-based structural diversity in this case. For example, Fig. 3b shows the $G_{N(u)}$ of node $u$ containing 8 nodes. If we apply the component-based structural diversity with $t=2$, we can find three connected components of size no less than 2 in $G_{N(u)}$ as marked in the shadow regions. However, if we apply the core-based structural diversity with $t= 2$, no component can be found. Therefore, the component-based diversity is better than the core-based structural diversity in such a case.

In summary, $\mathsf {CC}$-$\mathsf {TopK}$ is simpler. However, it does not consider the closeness of members in each component. $\mathsf {Core}$-$\mathsf {TopK}$ has more constraints by considering both cohesiveness and size. However, it is more difficult to compute and may lose the information of vertices that do not participate in a cohesive subgraph. Therefore, both definitions have advantages and disadvantage, and they can be jointly used to discover more social context diversity information in a large network. More comparisons and meaningful results for both $\mathsf {CC}$-$\mathsf {TopK}$ and $\mathsf {Core}$-$\mathsf {TopK}$ using real-world networks can be found in the case studies in our experiments.

4 A simple degree-based approach for $\mathsf {CC}$-$\mathsf {TopK}$

In this section, we present a simple degree-based algorithm for top-$k$ component-based structural diversity search. To compute the structural diversity $score(v)$ for a vertex $v$, we can perform a breadth-first search in $G_{N(v)}$ to find connected components and return the number of components whose sizes are no less than $t$. We call this procedure $\mathsf {bfs}$-$\mathsf {search }$, the pseudocode of which is omitted for brevity.

Next we introduce a useful lemma, which leads to a pruning strategy in the degree-based algorithm.

Lemma 1

For any vertex $v$ in $G$, $score(v)\le \lfloor \frac{d(v)}{t} \rfloor$ holds.

We denote $\lfloor \frac{d(v)}{t} \rfloor$ by $\overline{bound}(v)$. Equipped with Lemma 1 and the $\mathsf {bfs}$-$\mathsf {search }$ procedure, we present the degree-based approach in Algorithm 1, which computes the structural diversity of the vertices in descending order of their degree. After initialization (lines 1–2), Algorithm 1 sorts the vertices in descending order of their degree (line 3). Then it iteratively finds the unvisited vertex $v^*$ with the maximum degree and calculates $\overline{bound}(v^*)$ (lines 5–6). If the answer set $\mathcal {S}$ has $k$ vertices and $\overline{bound}(v^*)\le \min _{v\in \mathcal {S}}score(v)$, the algorithm terminates (lines 7–8). The rationale is as follows. By Lemma 1, we have $score(v^*)\le \overline{bound}(v^*)\le \min _{v\in \mathcal {S}}score(v)$. For any vertex $w\in V$ with a smaller degree, we have $score(w)\le \overline{bound}(w)\le \overline{bound}(v^*)\le \min _{v\in \mathcal {S}}score(v)$. Therefore, we can safely prune the remaining vertices and terminate. On the other hand, if such conditions are not satisfied, then the algorithm computes $score(v^*)$ by invoking $\mathsf {bfs}$-$\mathsf {search }$ and checks whether $v^*$ should be added into the answer set $\mathcal {S}$ (lines 10–13). Finally, the algorithm outputs $\mathcal {S}$.

Fig. 4

Illustration of the $\mathsf {degree }$ algorithm

The following example illustrates the working of Algorithm 1.

Example 1

Consider the graph in Fig. 1a. Suppose that $k=1$ and $t=1$. The top-$k$ running process is illustrated in Fig. 4. The sorted vertex list is $c, a, b, f, h, i, d,$ $e,$ $g$ in descending order of their degree. The algorithm computes the structural diversity of these vertices in turn and terminates before computing $score(g)$. This is because we have $\min _{v\in \mathcal {S}}$ $score(v)=$ $score(e)=3$ and $\overline{bound}(g)=$ $3\le$ $\min _{v\in \mathcal {S}}$ $score(v)$. Therefore, Algorithm 1 can save one structural diversity computation.

Theorem 1

For $1 \le k \le n$ and $1 \le t \le n$, Algorithm 1 performs top-k structural diversity search in $O(\sum _{v \in V}(d(v))^2)$ time and $O(m)$ space.

Proof

The algorithm first sorts all vertices in $O(n)$ time using the bin-sort algorithm [9]. It has to calculate the structural diversity for every vertex to answer a top-$k$ query in the worst case. Consider a vertex $v$. When the algorithm computes $score(u)$ for each neighbor $u\in N(v)$, it has to scan the adjacency list of $v$ in $O(d(v))$ time. Since there are $|N(v)|=d(v)$ neighbors, the total cost for scanning $v$’s adjacency list is $O((d(v))^2)$. Thus, it takes $O(\sum _{v\in V}(d(v))^2)$ time to calculate the structural diversities for all vertices. In addition, one can maintain the top-$k$ results in $O(n)$ time and $O(n)$ space using a variant of bin-sort list. Thus, the time complexity of Algorithm 1 is $O(\sum _{v\in V}$ $(d(v))^2)$.

In terms of the space consumption, the graph storage takes $O(n+m)$ space, and $\mathcal {S}$ takes $O(n)$ space. Thus, the space complexity of Algorithm 1 is $O(n+m)$ $\subseteq$ $O(m)$.

Remark 1

The worst-case time complexity of Algorithm 1 is bounded by $O(\sum _{v \in V}d(v)\cdot d_\mathrm{max})=O(md_\mathrm{max})\subseteq O(mn)$.

5 A novel top-K search framework for $\mathsf {CC}$-$\mathsf {TopK}$

The $\mathsf {degree }$ algorithm is not very efficient for top-$k$ search because the degree-based upper bound in Lemma 1 is loose. To improve the efficiency, the key issue is to develop a tighter upper bound. To this end, in this section, we propose a novel framework with a tighter pruning bound and a new algorithm called $\mathsf {bound}$-$\mathsf {search }$ to compute the structural diversity score. Before introducing the framework, we present two structural properties in a graph, which are very useful for developing the new bound.

5.1 Two structural properties

Property 1

For any vertex $v\in V$, if a vertex $u\in N(v)$ and $u$ forms a size-1 component in $G_{N(v)}$, then $v$ also forms a size-1 component in $G_{N(u)}$.

As an example, in Fig. 1b, vertex $e$ forms a size-1 component in $G_{N(f)}$. Symmetrically, vertex $f$ also forms a size-1 component in $G_{N(e)}$.

Property 2

If three vertices $u, v, w$ form a triangle in $G$, then we have the sets $\{u, v\}$, $\{v, w\}$, and $\{u, w\}$ belong to the same component in $G_{N(w)}$, $G_{N(u)}$, and $G_{N(v)}$, respectively.

Proof

This property can be easily derived by definition; thus, we omit the proof for brevity.

For instance, in Fig. 1a, vertices $a, f, g$ form a triangle in $G$. We can observe that $\{a, g\}$ belong to a connected component in $G_{N(f)}$ in Fig. 1b. Similarly, $\{a, f\}$ ($\{f, g\}$) belong to a connected component in $G_{N(g)}$ ($G_{N(a)}$).

Remark 2

Property 2 is based on the structure of a triangle (a clique of 3 nodes). We can extend the property to $k$-cliques for any $k\ge 3$. The following property can be similarly obtained: “In a clique $C=\{v_1, \ldots , v_k\}$ of $k$ $(k\ge 3)$ nodes in $G$, for each node $v_i\in C$, all other nodes in $C\setminus \{v_i\}$ belong to the same component in $G_{N(v_i)}$.” Based on a $k$-clique with $k>3$, we can obtain more structural information than using a triangle. However, computing $k$-cliques is more costly than computing triangles. According to [7], the time complexity of listing all $k$-cliques for a constant $k$ is $O(k\rho ^{k-2} m)$, where $\rho$ is the arboricity of the graph $G$. Therefore, listing all $k$-cliques for a constant $k\ge 4$ is more costly than our proposed algorithm $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {search }$, whose time complexity is $O(\rho m)$.

Fig. 5

Disjoint-set forest data structure g[f]. a Make-Forest(f), b g[f].Union(a,g), c g[f].Isolate(e)

In addition, from [9, 18], we can obtain the lower bound for the time complexity of any $k$-clique listing algorithms as $\varTheta (m^{\frac{k}{2}})$. This is because for a constant $k\ge 3$, there can be $\varTheta (m^{\frac{k}{2}})$ $k$-cliques in a graph, since the graph may contain a clique of $\sqrt{m}$ vertices and thus contain $\left( \begin{array}{c} \sqrt{m}\\ k \end{array}\right)$ $= \varTheta (m^{\frac{k}{2}})$ $k$-cliques. Hence, even the lower bound for the time complexity of enumerating all 4-cliques as $\varTheta (m^{2})$ is higher than the time complexity of our algorithms shown in Remarks 3 and 4. Therefore, the extra cost taken by computing $k$-cliques is much larger than the cost saving obtained by using the new property based on $k$-cliques. Based on the above discussion, in this paper, we only make use of triangles other than larger cliques in order to guarantee the efficiency of our algorithms.

Based on these two properties, we can save a lot of computational costs in computing the structural diversity scores. For example, if we find that vertex $u$ forms a size-1 component in $G_{N(v)}$, then we know that $v$ also forms a size-1 component in $G_{N(u)}$ by Property 1. Thus, when we compute $score(u)$, we do not need to perform a breadth-first search from $v$, because we already know $v$ forms a size-1 component in $G_{N(u)}$. If we can efficiently record such structural information of $v$’s neighbors when we compute $score(v)$, we can save a lot of computational costs. More importantly, such structural information can help us to get a tighter upper bound of the structural diversity. In the following subsection, we shall introduce a modified disjoint-set forest data structure to maintain such structural information efficiently.

5.2 Disjoint-set forest data structure

Intuitively, for the vertices in the same component, we can simply regard them as elements in the same set, while for the vertices in different components, we can represent them as elements in different sets. Thus, we modify the classical disjoint-set forest data structure and the $\mathsf {Union}$-$\mathsf {Find }$ algorithm [9] to maintain the structural information for each vertex efficiently. The modified structure consists of four operations: $\mathsf {Make}$-$\mathsf {Forest}$, $\mathsf {Find\text {-}Set}$, $\mathsf {Union}$, and $\mathsf {Isolate}$. Compared with the classical disjoint-set forest data structure, the new structure includes an additional operation $\mathsf {Isolate}$ which is used to record the structural information described in Property 1, i.e., a vertex forms a size-1 component. Thus, the modified structure is called $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$. Algorithm 2 describes the four operations.

$\mathsf {Make}$-$\mathsf {Forest}$: For each vertex $v\in V$, we create a disjoint-set forest structure, denoted as $g[v]$, for its neighbors $N(v)$ using the $\mathsf {Make}$-$\mathsf {Forest}$ ($v$) procedure in Algorithm 2. Specifically, for each $u\in N(v)$, we build a single-node tree $T[u]$ with three fields: parent, rank and count. The parent is initialized to be $u$ itself, the rank is set to 0 and the count is set to 1, as there is only one vertex $u$ in the tree. In addition, we also create a virtual node $T[0]$ which is used to collect all size-1 components in $G_{N(v)}$. The parent of $T[0]$ is set to 0 and the count is set to 0 because there is no size-1 component identified yet. For convenience, we refer to the operation of creating a single-node tree (line 4) or a virtual node (line 5) as a $\mathsf {Make\text {-}Set}$ operation.

$\mathsf {Find\text {-}Set}$: The $\mathsf {Find\text {-}Set}$ $(x)$ procedure is to find the root of $T[x]$ using the path compression strategy. The path compression strategy is a way of flattening the structure of the tree $T[x]$ whenever $\mathsf {Find\text {-}Set}$ $(x)$ is used on it. Specifically, the idea is that each node visited on the path to a root node may as well be attached directly to the root node, because they are all in the same set and share the same representative. As a result, the obtained tree is much flatter, which can speed up future operations not only on these elements but on those referencing them, directly or indirectly.

$\mathsf {Union}$: The ${\mathsf {Union}} (x, y)$ procedure applies the union by rank strategy to union two trees $T[fx]$ and $T[fy]$ which $x$ and $y$ belong to, respectively. The union by rank strategy is to always attach the smaller tree to the root of the larger tree. For example, $fx$ and $fy$ are the roots of these two trees $T[fx]$ and $T[fy]$. If $fx$ and $fy$ have unequal rank, the one with a higher rank is set to be the parent of the other with a lower rank. Otherwise, we arbitrarily choose one of them as the parent and increase its rank by 1. For both cases, we update the $count$ of the root of the new tree.

$\mathsf {Isolate}$: Procedure ${\mathsf {Isolate}} (x)$ unions a size-1 tree $T[x]$ into the virtual tree $T[0]$. It sets $T[x].parent$ to 0 and increases $T[0].count$ by 1. ${\mathsf {Isolate}} (x)$ essentially labels $x$ as a size-1 component if we find $x$ is not connected with any other node in a neighborhood-induced subgraph.

We can apply the disjoint-set forest structure to maintain the connected components in $G_{N(v)}$. For any vertex $v\in V$, we create a rooted tree for every neighbor $u\in N(v)$ initially. If we find that $u$ and $w$ are connected in $G_{N(v)}$, we process it by $g[v].{\mathsf {Union}} (u,w)$. If we identify that $u$ forms a size-1 component in $G_{N(v)}$, we process it by $g[v].{\mathsf {Isolate}} (u)$. Take $G_{N(f)}$ in Fig. 1b as an example again. First, we create $g[f]$ by $\mathsf {Make}$-$\mathsf {Forest}$ $(f)$ as shown in Fig. 5a. Since vertices $a$ and $g$ are connected, we invoke $g[f].{\mathsf {Union}} (a,g)$ and the resulted structure is shown in Fig. 5b. The combined tree is rooted by $g$ and has 2 vertices. Vertex $e$ forms a size-1 component; thus, we invoke $g[f].{\mathsf {Isolate}} (e)$, and the result is shown in Fig. 5c.

The time complexity of the $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$ algorithm is analyzed in the following lemma.

Lemma 2

A sequence of $M$ $\mathsf {Make\text {-}Set}$, $\mathsf {Union}$, $\mathsf {Find\text {-}Set}$ and $\mathsf {Isolate}$ operations, $N$ of which are $\mathsf {Make\text {-}Set}$ operations, can be performed on a disjoint-set forest with “union by rank” and “path compression” strategies in worst-case time $O(M\alpha (N))$. $\alpha (N)$ is the inverse Ackermann function, which is incredibly slowly growing and at most 4 in any conceivable application. Thus, the time complexity of the $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$ algorithm can be regarded as $O(M)$.

Proof

The proof is similar to that in [9], thus is omitted.

In the following, for simplicity, we treat $\alpha (N)$ as a constant in the complexity analysis.

5.3 A tighter upper bound

With the disjoint-set forest data structure $g[v]$, we can keep track of the structural information of the connected components in $G_{N(v)}$ and derive a tighter upper bound of $score(v)$ than the degree-based bound in Lemma 1. Before introducing the upper bound, we give a definition of the identified size-1 set as follows.

Definition 4

(Identified size-1 set) In the disjoint-set forest structure $g[v]$, if $u\in N(v)$ and $T[u].parent = 0$, we denote $\mathbb {S}_u = \{u\}$ as an identified size-1 set, and $|\mathbb {S}_u| =1$. If $u\in N(v)$, $T[u].parent$ $=u$, we denote $\mathbb {S}_u = \{w\in N(v):{\mathsf {Find\text {-}Set}} (w)=u\}$ as an unidentified set, and $|\mathbb {S}_u| = T[u].count$.

By Definition 4, we know that each identified size-1 set is resulted from an $\mathsf {Isolate}$ operation, and the total number of the identified size-1 sets is $T[0].count$. According to Property 1, all these sets do not union with other sets. On the other hand, unidentified sets may further union with other sets or become an identified size-1 set. Consider the example in Fig. 5c. $\mathbb {S}_e =\{e\}$ is an identified size-1 set and $T[0].count = 1$. Both $\mathbb {S}_g=\{a, g\}$ and $\mathbb {S}_i=\{i\}$ are unidentified sets.

Let $\mathbb {S} = \{\mathbb {S}_u:u\in N(v), T[u].parent = u$ or $T[u].$ $parent$ $= 0\}$ denote all disjoint sets in $g[v]$, excluding the virtual set $T[0]$. After traversing all the vertices and edges in $G_{N(v)}$, $\mathbb {S}$ contains all actual sets corresponding to the connected components in $G_{N(v)}$, and we have $score(v)=|\{\mathbb {S}_u: \mathbb {S}_u\in \mathbb {S}, |\mathbb {S}_u|\ge t\}|$. However, before traversing the neighborhood-induced subgraph $G_{N(v)}$, $\mathbb {S}$ may not contain all the actual sets corresponding to the connected components, but includes some intermediate results. Even with such intermediate results maintained in $\mathbb {S}$, we can still use them to derive an upper bound. Specifically, we have the following lemma.

Lemma 3

Let $\mathbb {S} = \{\mathbb {S}_1, \ldots , \mathbb {S}_l\}$ be the disjoint sets of $g[v]$, $a$ be the number of identified size-1 sets, $b$ be the number of sets whose sizes are larger than or equal to $t$, and $c$ be the total size of these $b$ sets. Then, we have an upper bound of $score(v)$ as follows. If $t = 1$, $\overline{bound}(v) = b$; if $t > 1$, $\overline{bound}(v) = b+\lfloor \frac{d(v)-c-a}{t} \rfloor$.

Proof

First, it is important to note that the current disjoint sets in $\mathbb {S}$ are not final, if we have not traversed all vertices and edges of $G_{N(v)}$. That is, some of them may be further combined by the $\mathsf {Union}$ operation and the number of sets may be reduced.

Next, we consider the following two cases.

If $t=1$, we have $\overline{bound}(v) = b$, as the current number of sets whose sizes are greater than or equal to 1 is $b$ and this number can only be reduced with the $\mathsf {Union}$ operation.

If $t>1$, the current number of sets whose sizes are greater than or equal to $t$ is $b$ and this number can only be reduced with the $\mathsf {Union}$ operation. In addition, besides $a$ identified size-1 sets and $c$ vertices from the above $b$ sets, there are still $d(v)-c-a$ vertices which may form sets whose sizes are greater than or equal to $t$. The maximum number of such potential sets is $\lfloor \frac{d(v)-c-a}{t} \rfloor$. Thus, we have $\overline{bound}(v)= b+\lfloor \frac{d(v)-c-a}{t} \rfloor$.

For any vertex $v\in V$, at the initialization stage, each neighbor vertex $u\in N(v)$ forms a size-1 component. Thus, $\overline{bound}(v)=0+\lfloor \frac{d(v)-0-0}{t} \rfloor =\lfloor \frac{d(v)}{t} \rfloor$, the same as the bound in Lemma 1. As the disjoint sets are gradually combined, $\overline{bound}(v)$ is refined toward $score(v)$ and becomes tighter. For example, in Fig. 5c, suppose $t=2$, we obtain $\mathbb {S}=\{\mathbb {S}_e, \mathbb {S}_g, \mathbb {S}_i\}$ and the three parameters in Lemma 3 are $a=1$, $b=1$ and $c=2$. It follows that $\overline{bound}(f)=1+\lfloor \frac{4-2-1}{2} \rfloor = 1$, which is equal to $score(f) = 1$. This bound based on the disjoint-set forest is obviously tighter than the degree-based bound $\lfloor \frac{4}{2} \rfloor =2$ derived in Lemma 1.

5.4 Top-K search framework

Based on the disjoint-set forest data structure and the tighter upper bound, we propose an advanced search framework in Algorithm 3 for top-$k$ structural diversity search.

Advanced top-k framework For each vertex $v\in V$, the algorithm initializes the disjoint-set forest data structure $g[v]$ by invoking $\mathsf {Make}$-$\mathsf {Forest}$ (line 4). It also pushes each vertex $v$ with the initial bound $\lfloor \frac{d(v)}{t} \rfloor$ into $\mathcal {H}$, which is a variant of bin-sort list. Then the algorithm iteratively finds the top-$k$ results (lines 6–19). It first pops the vertex with the largest upper-bound value from $\mathcal {H}$. Such a vertex and its bound are denoted as $v^*$ and $topbound$, respectively (line 7). The algorithm re-evaluates $\overline{bound}(v^*)$ from $g[v^*]$ based on Lemma 3, as the component information in $g[v^*]$ may have been updated. And then, it compares the refined bound $\overline{bound}(v^*)$ with the old bound $topbound$.

In order to avoid frequently calculating the upper bounds and updating $\mathcal {H}$, we introduce a new parameter $\theta \ge 1$, and compare $\theta \cdot \overline{bound}(v^*)$ with $topbound$.

If $\theta \cdot \overline{bound}(v^*)<topbound$, it suggests that $\overline{bound}(v^*)$ is substantially smaller than $topbound$. That is, the old bound $topbound$ is too loose. Under this condition, if $|\mathcal {S}|<k$ or $\overline{bound}(v^*)$ $>$ $\min _{v\in \mathcal {S}}score(v)$, the algorithm pushes $v^*$ back to $\mathcal {H}$ with the refined bound $\overline{bound}(v^*)$ (lines 10–11). Otherwise, the algorithm can safely prune $v^*$. In both cases, the algorithm continues to pop the next vertex from $\mathcal {H}$ (lines 9–12).

If $\theta \cdot \overline{bound}(v^*)\ge topbound$, it means that $\overline{bound}(v^*)$ is not substantially smaller than $topbound$. In other words, the old bound is a relatively tight estimation. Then the algorithm moves to lines 13–14 to check the termination condition. If $|\mathcal {S}|=k$ and $topbound\le \min _{v\in \mathcal {S}}score(v)$, the algorithm can safely prune all the remaining vertices in $\mathcal {H}$ and terminate, because the upper bound of those vertices is smaller than $topbound$.

If the early termination condition is not satisfied, the algorithm invokes the $\mathsf {bound}$-$\mathsf {search }$ algorithm (line 15) to compute $score(v^*)$. $\mathsf {bound}$-$\mathsf {search }$ is shown in Algorithm 4 and will be described later. After computing $score(v^*)$, the algorithm uses the same process to update the set $\mathcal {S}$ by $v^*$ as the $\mathsf {degree }$ algorithm does (lines 16–19).

Bound-search Algorithm 4 shows the $\mathsf {bound}$-$\mathsf {search }$ procedure to compute $score(v)$. Based on the disjoint-set forest $g[v]$, we know that any vertex $u\in N(v)$ with $T[u].parent=0$ corresponds to an identified size-1 component resulted from an $\mathsf {Isolate}$ operation. So $\mathsf {bound}$-$\mathsf {search }$ does not need to search them again. It only adds the vertices whose $parent\ne 0$ into an unvisited vertex hashtable $R$ (lines 1–2). This is an improvement from $\mathsf {bfs}$-$\mathsf {search }$, as $\mathsf {bound}$-$\mathsf {search }$ avoids scanning the identified size-1 components. For each vertex $u\in R$, the algorithm invokes the procedure $\mathsf {bound}$-$\mathsf {bfs }$ (lines 5–18) to search $u$’s neighborhood in a breadth-first search manner. For $u$’s neighbor vertex $w$, if $w\in R$, i.e., $w\in N(v)$, the algorithm unions $u$ and $w$ into one set in $g[v]$. According to Property 2, we also union $v$ and $w$ into one set in $g[u]$, and union $v$ and $u$ into one set in $g[w]$ (lines 11–15). If $u$ does not union with any other vertex, the algorithm invokes an $\mathsf {Isolate}$ operation on $u$ to mark that $u$ forms a size-1 component in $g[v]$ (lines 16–18). Symmetrically, by Property 1, the algorithm invokes an $\mathsf {Isolate}$ operation on $v$ to mark that $v$ forms a size-1 component in $g[u]$ too. After the BFS search, the algorithm can compute $score(v)$ using the procedure $\mathsf {count}$-$\mathsf {components }$ (lines 19–25) to count the number of sets in $g[v]$ whose sizes are at least $t$. The following example illustrates how the $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework (Algorithm 3) works.

Fig. 6

Illustration of $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ with $\mathsf {bound}$-$\mathsf {search }$ running on the graph in Fig. 1a. $k = 1$, $t = 1$, and $\theta =1$. a Initialization, b compute score(c), and add c into S, c update $\overline{bound}(a)$ into H, d compute score(f), and update S by f, e Pop out h, i, d from H, f compute score(e), and update S by e

Example 2

Consider the graph shown in Fig. 1a. Suppose that $t=1$ and $k=1$. We apply the $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ algorithm with $\theta =1$ and the running steps are depicted in Fig. 6. For initialization, we push each vertex $v$ with the upper bound $\lfloor \frac{d(v)}{t}\rfloor$ into $\mathcal {H}$, as shown in Fig. 6a.

In the first iteration, as shown in Fig. 6b, we pop vertex $c$ from $\mathcal {H}$ with $topbound = 5$. We calculate $\overline{bound}(c)=5$ according to Lemma 3. Then, we compute $score(c)$ by $\mathsf {bound}$-$\mathsf {search }$. In $G_{N(c)}$, there is a single path connecting all vertices $a, b, d, h, i$ in $N(c)$, so $score(c)=1$. When the algorithm traverses the edge $(a, b)$, we perform two operations $g[a].$ $\mathsf {Union}$ $(c, b)$ and $g[b].$ $\mathsf {Union}$ $(c, a)$ in $g[a]$ and $g[b]$, respectively, according to Property 2. Then we push vertex $c$ into $\mathcal {S}$.

In the next iteration, as shown in Fig. 6c, we pop vertex $a$ from $\mathcal {H}$ which has $topbound=4$. Then we update $\overline{bound}(a)=3$ as we know that vertices $b$ and $c$ are in the same set in $g[a]$. Since $\theta \cdot \overline{bound}(a)<topbound$ and $\overline{bound}(a)>\min _{v\in \mathcal {S}}score(v)$, we push $(a,3)$ into $\mathcal {H}$ again.

When the algorithm goes to process vertex $f$ in Fig. 6d, we have $\theta \cdot \overline{bound}(f) = topbound = 4$ and $topbound> \min _{v\in \mathcal {S}}score(v)$. And then we compute $score(f)=2$ and replace vertex $c$ in $\mathcal {S}$ with $f$.

After that, we pop vertices $h, i, d$ from $\mathcal {H}$ in turn, as shown in Fig. 6e. One can easily check that none of them satisfies the condition in line 10 of Algorithm 3. Thus, we do not push $h, i, d$ back into $\mathcal {H}$ again.

Next we pop vertex $e$, compute $score(e) = 3$ and update $\mathcal {S}$ by $e$, as shown in Fig. 6f. Since $topbound$ in $\mathcal {H}$ is no greater than $score(e) = 3$, we can safely terminate. In this process, we only invoke $\mathsf {bound}$-$\mathsf {search }$ three times to calculate the structural diversity score, while the previous $\mathsf {degree }$ algorithm calculates the structural diversity score of eight vertices, which is clearly more expensive.

5.5 Complexity analysis

Lemma 4

The upper bound $\overline{bound}(v)$ defined in Lemma 3 for any vertex $v\in V$ can be updated in $O(1)$ time in Algorithm 3.

Proof

We need to maintain $a$, $b$ and $c$ in $g[v]$ to recompute $\overline{bound}(v)$. Obviously, $a=T[0].count$, and $b, c$ can be easily maintained in the ${\mathsf {Union}}$ operation of $g[v]$ without increasing the time complexity. Thus, $\overline{bound}(v)$ can be updated in $O(1)$ time.

Lemma 5

The total time to compute $\overline{bound}$ for all vertices in Algorithm 3 is $O(\frac{m}{t})$.

Proof

According to Lemma 4, $\overline{bound}(v)$ for a vertex $v$ can be computed in $O(1)$ time. The initial upper bound of $v$ is $\lfloor \frac{d(v)}{t} \rfloor$, and $\overline{bound}(v)$ is updated in non-increasing order. In line 9 of Algorithm 3, we compare $\theta \cdot \overline{bound}(v)$ and $topbound$ to check whether $v$ should be pushed into $\mathcal {H}$. Since $topbound\le \lfloor \frac{d(v)}{t} \rfloor$, $\overline{bound}(v)$ can be updated for at most $\lfloor \frac{d(v)}{t} \rfloor$ times. Thus, the total time cost is $O(\sum _{v\in V}\frac{d(v)}{t})$ $=O(\frac{m}{t})$.

Lemma 6

In $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$, $\mathcal {H}$ can be maintained in $O(\frac{m}{t}+n)$ time using $O(n)$ space.

Theorem 2

Algorithm 3 takes $O$ $(\sum _{v\in V}$ $(d(v))^2)$ time and $O(m)$ space.

Proof

Since the time to access the adjacency lists in $\mathsf {bound}$-$\mathsf {search }$ is $O(\sum _{v\in V}(d(v))^2)$, and all $\mathsf {Union}$ operations are in the loop of accessing adjacency lists (lines 13–15 of Algorithm 4), the number of $\mathsf {Union}$ operations is $O(\sum _{v\in V}(d(v))^2)$. The algorithm invokes $n$ $\mathsf {Make}$-$\mathsf {Forest}$ operations (line 4 of Algorithm 3), which includes $\sum _{v\in V} (d(v)+1)=2m+n$ $\mathsf {Make\text {-}Set}$ operations. Next, all $\mathsf {Isolate}$ operations are in the procedure $\mathsf {bound}$-$\mathsf {bfs }$ (lines 17–18 of Algorithm 4). The number is no greater than $\sum _{v\in V} 2d(v)=4m$. No $\mathsf {Find\text {-}Set}$ operation is directly invoked. Thus, $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$ includes $O(\sum _{v\in V} (d(v))^2)$ $\mathsf {Make\text {-}Set}$, $\mathsf {Union}$, $\mathsf {Find\text {-}Set}$, $\mathsf {Isolate}$ operations, $2m+n$ of which are $\mathsf {Make\text {-}Set}$. By Lemma 2, the time complexity of $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$ is $O(\sum _{v\in V} (d(v))^2)$.

By Lemma 6, $\mathcal {H}$ takes $O(\frac{m}{t}+n)$ time. $\mathcal {S}$ maintains the top-$k$ results using $O(n)$ time. By Lemma 5, updating the upper bounds for all vertices takes $O(\frac{m}{t})$ time. Therefore, the time complexity of Algorithm 3 is $O$ $(\sum _{v\in V}$ $(d(v))^2)$.

Next, we analyze the space complexity. For $v\in V$, $g[v]$ contains $d(v)+1$ initial disjoint singleton trees, in which each node takes constant space. Hence, the disjoint-set forest structure takes $O(m)$ space for all vertices. $\mathcal {S}$ and $\mathcal {H}$ both consume $O(n)$ space. In summary, the space complexity of Algorithm 3 is $O(m)$.

Hence, Theorem 2 is established.

6 Fast computation of component-based structural diversity score

In this section, on top of the $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework, we propose two methods for fast computing the structural diversity score for a vertex. The first method is $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {search }$, which improves $\mathsf {bound}$-$\mathsf {search }$ and achieves a better time complexity using the same space. The second is an $\mathsf {A^{*}}$ search method, which uses a new search order and a new termination condition.

6.1 Fast bound-search

We present $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {search }$ in Algorithm 5, which is built on $\mathsf {bound}$-$\mathsf {search }$. The major difference is in procedure $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {bfs }$ for traversing a connected component. When accessing the adjacency list of vertex $u$ having $d(u) > d(v)$, we will access the adjacency list of $v$ instead (lines 10–13), i.e., we always select the vertex with a smaller degree to access. Checking whether $(w, u) \in E$ in line 13 can be done efficiently by keeping all edges in a hashtable. Moreover, $R$ can also be implemented by a hashtable. Thus, line 13 can be done in expected constant time by hashing.

Fig. 7

$G_{N(r)}$ has two vertices $p$ and $q$ with degree 1 and 100

To show the effectiveness of this improvement, we consider an example $G_{N(r)}$ in Fig. 7. Suppose that $r$ has two neighbors $p$ and $q$ with degree 1 and 100, respectively. To compute $score(r)$, $\mathsf {bound}$-$\mathsf {search }$ needs to access the adjacency lists of $p$ and $q$ and check $|N(p)|+|N(q)|= 101$ vertices. In contrast, $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {search }$ accesses $N(r)$ instead of $N(q)$ because $d(q)>d(r)$; thus, the number of visited vertices is reduced to $|N(p)|+|N(r)|= 3$.

Complexity analysis Using $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {search }$ to compute structural diversity scores, we achieve a better time complexity of the $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework shown in the following theorem.

Theorem 3

The $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework using $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {search }$ takes $O(\sum _{(u,v)\in E}\min \{d(u),d(v)\})$ time and $O(m)$ space.

Proof

For a vertex $v$, the time cost of accessing the adjacency lists is $\sum _{u\in N(v)} \min \{d(u), d(v)\}$ for computing its score. To compute scores for all vertices, accessing the adjacency lists consumes $O($ $\sum _{v\in V}$ $\sum _{u\in N(v)}$ $\min \{d(u),$ $d(v)\})$ $=$ $O($ $\sum _{(u,v)\in E}$ $\min \{d(u),$ $d(v)\})$.

Since the number of $\mathsf {Union}$ operations is bounded by the number of accessing adjacency lists, the number of $\mathsf {Union}$ operations is $O(\sum _{(u,v)\in E}$ $\min \{d(u), d(v)\})$. Moreover, there are $2m+n$ $\mathsf {Make\text {-}Set}$ operations, $O(m)$ $\mathsf {Isolate}$ operations and no direct $\mathsf {Find\text {-}Set}$ operation invoked by the algorithm. By Lemma 2, $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$ takes $O($ $\sum _{(u,v)\in E}$ $\min$ $\{d(u),$ $d(v)\})$ time in total. The other steps in the loop of accessing adjacency list take constant time. Therefore, it takes $O(\sum _{(u,v)\in E}$ $\min \{d(u),$ $d(v)\})$ time to calculate all vertices’ structural diversity scores using the $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {search }$ algorithm.

By Lemma 5, the total time of estimating upper bound is $O(\frac{m}{t})\subseteq O(m)$, and by Lemma 6, the total time to maintain $\mathcal {H}$ is $O(\frac{m}{t}+n)\subseteq O(m)$.

The remaining steps in Algorithm 3 using $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {search }$ totally cost $O(m)$ time.

Compared with $\mathsf {bound}$-$\mathsf {search }$, $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {bfs }$ needs extra $O(m)$ space for storing the edge hashtable. Thus, the space consumption is still $O(m)$.

Hence, Theorem 3 is established.

Fig. 8

$G_{N(r)}$ containing two components $P$ and $Q$

Remark 3

According to [7], we have

$$\begin{aligned} O \left( \sum _{(u,v)\in E}\min \{d(u),d(v)\}\right) \subseteq O\left( \rho m \right) , \end{aligned}$$

where $\rho$ is the arboricity of a graph $G$ and $\rho$ $\le$ $\min$ $\{\lceil \sqrt{m}~ \rceil ,$ $d_\mathrm{max}\}$ for any graph $G$. Thus, the worst-case time complexity of the $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework using $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {search }$ is bounded by

$$\begin{aligned} O\left( \sum _{(u,v)\in E}\min \{d(u),d(v)\}\right) \subseteq O(\rho m)\subseteq O\left( m^{1.5}\right) . \end{aligned}$$

6.2 A*-based bound-search

In this subsection, we design a new search order and a new termination condition to compute the structural diversity score for a vertex.

Take Fig. 8 as an example which shows the neighborhood-induced subgraph of $r$. Suppose that before examining $G_{N(r)}$, the algorithm has computed the structural diversity scores for $r$’s neighbors $p_1,\ldots , p_4$. Then, by Property 2, the vertices $p_1,\ldots ,p_4$ are combined into one component $P$ in $G_{N(r)}$. There is another component $Q$ in $G_{N(r)}$ with only one vertex $q$. To compute $score(r)$, the algorithm needs to further check whether the components $P$ and $Q$ are connected or not. If the algorithm first checks vertex $q$ in the component $Q$, then it will go through $q$’s adjacency list $N(q)$ to verify whether $q$ connects with any vertices in $p_1,\ldots ,p_4$. If $q$ is not connected with any one of them, we can conclude that $Q$ forms a size-1 component and $P$ forms a size-4 component in $G_{N(r)}$. Thus, the algorithm does not need to traverse the adjacency lists of $p_1,\ldots , p_4$, and it can terminate early. In contrast, if the algorithm first checks the component $P$, then it needs to go through the adjacency lists of vertices $p_1,\ldots , p_4$ to verify whether they connect with $q$ or not. This is clearly more expensive than starting from the component $Q$. Motivated by this observation, we propose an $\mathsf {A^{*}}$ search strategy to efficiently compute the structural diversity in the neighborhood-induced subgraph of a vertex. Below, we first give the definition of component cost which is used as a cost function to determine the component visiting order in the $\mathsf {A^{*}}$ search process.

Definition 5

(Component cost) Given a component $S$ in a neighborhood-induced subgraph, the component cost of $S$ is the sum of degree of the unvisited vertices in $S$, denoted as $cost(S)=\sum _{{\textit{unvisited }}v\in S} d(v)$.

Suppose that in Fig. 8 all vertices in $N(r)$ are unvisited. The component costs are $cost(P)=16$ and $cost(Q)=1$. The component cost measures the cost of accessing the adjacency lists of a component. If we check the low-cost components first and the high-cost components later, we can potentially save more computation. Thus, in $\mathsf {A^{*}}$ search, we always pick a component $T[x]$ in $G_{N(v)}$ which has the least cost to traverse.

Fig. 9

$\mathsf {A^{*}}$-$\mathsf {bound}$-$\mathsf {search }$ example for computing $score(r)$. a $G_{N(r)}$, b Vertex degree and parent in T[.], c initialization, d step 1, estep 1 (termination)

To record the cost, we add the component cost as a field in the $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$ data structure. Specifically, for a vertex $u$, when we create a single-node component $T[u]$, we initialize $T[u].cost=d(u)$. When we union two components $T[u]$ and $T[v]$, we add up their costs, i.e., $T[u].cost+T[v].cost$.

The algorithm $\mathsf {A^{*}}$-$\mathsf {bound}$-$\mathsf {search }$ uses the component cost for determining a fast search order to traverse the components in $G_{N(v)}$ until there is only one unvisited component left. In traversing a component, the algorithm accesses the adjacency lists of the unvisited vertices in increasing order of their degrees until the component is connected with other components or traversed.

Algorithm 6 shows $\mathsf {A^{*}}$-$\mathsf {bound}$-$\mathsf {search }$. For a vertex $v$, the algorithm uses a minimum heap $\mathcal {TC}$ to maintain all the unidentified components in $G_{N(v)}$ ordered by their component costs. For a component rooted by a vertex $u$, the algorithm makes use of a minimum heap $\mathcal {C}[u]$ to maintain all vertices in this component ordered by their degree. Initially, for each vertex $u$ whose $parent$ is not 0, the algorithm pushes $u$ with cost $d(u)$ into the minimum heap $\mathcal {C}[T[u].parent]$ and adds $u$ into the hashtable $R$ which stores all the unvisited vertices (line 5). Moreover, if $u$ is the root of $T[u]$, the algorithm pushes the component of $u$ and its component cost $T[u].cost$ into the heap $\mathcal {TC}$ (lines 6–7).

Let us consider an example. Figure 9a shows the neighborhood-induced subgraph $G_{N(r)}$, and Fig. 9b shows the degree and the parent in $T[.]$ for each vertex in $N(r)$. We know that $p_1, p_2, p_3$ are in a component rooted by $p_1$, and $q_1, q_2$ are in a component rooted by $q_1$, and $s$ is in a component rooted by $s$ itself. After initialization, the minimum heaps $\mathcal {TC}$, $\mathcal {C}[s]$, $\mathcal {C}[p_1]$, $\mathcal {C}[q_1]$ and the hashtable $R$ are illustrated in Fig. 9c.

The algorithm iteratively pops a component with the minimum cost from $\mathcal {TC}$, denoted as $x$ with cost $tcost_x$ (line 9). If the component is rooted by vertex $x$ and $tcost_x$ $=T[x]$ $.cost$, the algorithm will examine the vertices in the component of $x$. Otherwise, if the component is no longer rooted by $x$ or $tcost_x\ne T[x].cost$, it means that the component of $x$ has been combined with another component in a previous iteration. Then, the algorithm pops the next component from $\mathcal {TC}$. If $|R|=|\mathcal {C}(x)|$ holds, then all the unvisited nodes in $R$ are from the same component rooted by $x$, and this component is the last to be traversed in $G_{N(v)}$ (line 13). By the early termination condition, the algorithm does not need to traverse this component and can directly go to count the number of components in $G_{N(v)}$ (line 33).

For a popped component rooted by $x$, the algorithm iteratively examines the vertices in the component in increasing order of their degree (lines 14–26). For such a vertex $u$, we will access its adjacency list $N(u)$ to find out those vertices denoted as $w$ that are also in $N(v)$. Then we will union the components which contain $u$ and $w$, respectively, into one. This process is very similar to the previous algorithms. So we omit the details for brevity.

Continuing with our example in Fig. 9, after initialization, we pop the first component $(s, 8)$ from $\mathcal {TC}$, as shown in step 1 (Fig. 9d). Then, we examine vertex $s$ in this component and find that it is not connected with other components in $G_{N(r)}$. Next, we move to step 2 (Fig. 9e) to pop the component $(p_1, 12)$. In this component, we first examine the adjacency list of $p_1$, i.e., $N(p_1)$. We find that $p_1$ is connected with $q_1$, so we union the components rooted by $p_1$ and $q_1$. Assume that the new component is rooted by $p_1$. Then we set $T[q_1].parent=p_1$ and merge $\mathcal {C}(q_1)$ into $\mathcal {C}(p_1)$. We push the new component $(p_1, 24)$ into $\mathcal {TC}$ again. In step 3 (Fig. 9f), we pop the component $(q_1, 15)$ and find that $T[q_1].parent\ne q_1$, as the component of $q_1$ has been combined with that of $p_1$ in step 2. In this step, there is only one component in $\mathcal {TC}$, which meets the early termination condition.

Complexity analysis In the component union process (line 22 of Algorithm 6), we need to merge two heaps $\mathcal {C}[fw]$ and $\mathcal {C}[fu]$ into one. We can implement $\mathcal {C}[.]$ by the mergeable heap such as leftist heap or binomial heap [9], which support the merge of two heaps in $O(\log n)$ time and a push/pop operation in $O(\log n)$ time for a heap with $n$ elements.

Lemma 7

In Algorithm 6, the operations for $\mathcal {TC}$ and all $\mathcal {C}[.]$ take $O(d(v)\log d(v))$ time and $O(d(v))$ space in total.

Proof

Since the number of components in $G_{N(v)}$ is no greater than $d(v)$, we perform at most $d(v)-1$ $\mathsf {Union}$ operations before termination. Hence, there are at most $d(v)-1$ new components to be pushed into $\mathcal {TC}$ (lines 12 and 28). In addition, for initialization $|\mathcal {TC}|\le d(v)$ holds, which indicates that $|\mathcal {TC}| \le 2d(v)$ always holds. As there are at most $2d(v)$ push and pop operations, respectively, and each operation takes $O(\log d(v))$ time, overall $\mathcal {TC}$ takes $O(d(v)\log d(v))$ time using $O(d(v))$ space.

For initialization, all $\mathcal {C}[.]$ heaps take $d(v)$ push operations in total (line 5), and the time cost of each operation is $O(\log d(v))$ as the size of the largest heap is smaller than $d(v)$. Hence, the initialization time is $O(d(v)\log d(v))$. As analyzed above, there are at most $d(v)-1$ heap merging operations and each operation costs $O(\log d(v))$, the total time cost in line 22 is $O(d(v)\log d(v))$. Moreover, there are at most $d(v)$ pop operations in line 15, the time cost of which is $O(d(v)\log d(v))$. All $\mathcal {C}[.]$ heaps contain at most $d(v)$ vertices totally costing $O(d(v))$ space. As a result, all $\mathcal {C}[.]$ heaps take $O(d(v)\log d(v))$ time and $O(d(v))$ space.

Theorem 4

The $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework using $\mathsf {A^{*}}$-$\mathsf {bound}$-$\mathsf {search }$ takes $O(\sum _{(u,v)\in E}(\min \{d(u),d(v)\}+(\log d(u) + \log d(v))))$ time and $O(m)$ space.

Remark 4

The worst-case time complexity of $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework using $\mathsf {A^{*}}$-$\mathsf {bound}$-$\mathsf {search }$ is bounded by

$$\begin{aligned}&O \left( \sum _{(u,v)\in E}( \min \{d(u),d(v)\}+(\log d(u)+\log d(v)))\right) \\&\quad \subseteq O((\rho +\log d_\mathrm{max})m)\\&\quad \subseteq O(m^{1.5}), \end{aligned}$$

where $\rho$ is the arboricity of the graph as mentioned in Remark 3.

6.3 Complexity comparison

We compare the time complexity of algorithms $\mathsf {degree }$ and $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$, to understand why the proposed $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework is more efficient.

According to Theorem 1, $\mathsf {degree }$ takes $O(\sum _{v \in V}(d(v))^2)$ time, which can be equivalently rewritten as

$$\begin{aligned}&O\left( \sum _{v \in V}(d(v))^2\right) \\&\quad = O\left( \sum _{v\in V}\sum _{u\in N(v)} d(u)\right) \\&\quad =O\left( \sum _{(u,v)\in E}(d(u)+d(v))\right) \\&\quad =O\left( \sum _{(u,v)\in E}(\max \{d(u), d(v)\}+\min \{d(u), d(v)\})\right) \\&\quad =O\left( \sum _{(u,v)\in E}\max \{d(u), d(v)\}\right) \end{aligned}$$

For $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ using $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {search }$, according to Theorem 3, it takes $O(\sum _{(u,v)\in E}$ $\min \{d(u),$ $d(v)\})$ time, obviously better than $O(\sum _{(u,v)\in E}$ $\max \{d(u), d(v)\})$, the time complexity of $\mathsf {degree }$. The two algorithms have the same complexity only if all vertices in the graph have the same degree. In a power-law graph such as a social network, the degrees of vertices have a large variance; thus, $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ using $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {search }$ is much better than $\mathsf {degree }$ in such networks. For example, on a star graph with $n$ nodes, $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ using $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {search }$ takes $O(n)$ time while $\mathsf {degree }$ takes $O(n^2)$ time.

Fig. 10

Illustration of updates in a dynamic graph. a G, b $G_{N(r)}$, c update $G_{N(r)}$ with edge insertion of $(r,q)$, d spanning tree of Component P in $G_{N(r)}$ as $T_{p}$, e update $G_{N(r)}$ with edge deletion of $(r,p_2)$, f update $T_{p}$ with edge deletion of $(r,p_2)$

For $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ using $\mathsf {A^{*}}$-$\mathsf {bound}$-$\mathsf {search }$, its time complexity, which is $O(\sum _{(u,v)\in E}$ $(\min \{d(u),d(v)\}+$ $(\log d(u)$ $+$ $d(v))))$, is also better than $O(\sum _{(u,v)\in E}$ $\max \{d(u),$ $d(v)\})$ of $\mathsf {degree }$. This is because the first part $O(\sum _{(u,v)\in E}$ $\min \{d(u),$ $d(v)\})$ is better for the same reason as stated above, and the second part $O(\sum _{(u,v)\in E}$ $(\log d(u)+\log d(v)))$ is also better since $O(\log d(u)+\log d(v))$ $\le$ $O(\max \{d(u),$ $d(v)\})$ holds.

7 Handling update for $\mathsf {CC}$-$\mathsf {TopK}$ in dynamic networks

Many real-world networks undergo frequent updates. When the network is updated, the top-$k$ structural diversity results also need to be updated. The challenge, however, is that inserting or deleting a single edge $(u, v)$ can trigger updates in a series of neighborhood induced subgraphs including $G_{N(u)}$, $G_{N(v)}$ and $G_{N(w)}$ where $w\in N(u)\cap N(v)$. This can be a costly operation because the corresponding structural diversity scores need to be recomputed, and the top-$k$ results need to be updated too.

In the following, we will show that our $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework can be easily extended to handle updates in dynamic graphs. We consider two types of updates: edge insertion and edge deletion. Vertex insertion/deletion can be regarded as a sequence of edge insertions/deletions preceded/ followed by the insertion/deletion of an isolated vertex, while it is trivial to handle the insertion/deletion of an isolated vertex.

7.1 Handling edge insertion

Consider the insertion of an edge $(u, v)$. Let $L = N(u)\cap N(v)$ denote the set of common neighbors of $u$ and $v$. The insertion of $(u,v)$ causes the insertions of vertex $v$ and a set of $|L|$ edges $\{(v,w)|w\in L\}$ into $u$’s neighborhood-induced subgraph $G_{N(u)}$. For each $w\in L$, we perform a $\mathsf {Union}$ operation $g[u].{\mathsf {Union}} (v,w)$ to update the components and $score(u)$. For vertex $v$, $G_{N(v)}$ is updated in a similar way.

The insertion of $(u,v)$ also affects $G_{N(w)}$ for each $w\in L$. We check the disjoint-set forest structure $g[w]$. If $u,v$ belong to the same connected component before the edge insertion, then all components remain unchanged and so does $score(w)$. If $u,v$ are in different components before the edge insertion, we merge the two components into one with a $\mathsf {Union}$ operation $g[w].{\mathsf {Union}} (u,v)$ and update $score(w)$ accordingly.

Consider the graph $G$ in Fig. 10a as an example. Suppose that $t=2$ and the inserted edge is $(r,q)$. $L= N(r)\cap N(q) = \{s, p_1\}$. Figure 10c shows the updated $G_{N(r)}$ with the edge insertion. $G_{N(r)}$ has two new edges $(p_1, q)$ and $(s, q)$, but $score(r) = 1$ remains unchanged. For vertex $s \in L$, vertices $r, q$ are now connected in the same component in $G_{N(s)}$ with the insertion of $(r,q)$, so we update $score(s)$ from 0 to 1.

7.2 Handling edge deletion

Consider the deletion of an edge $(u, v)$. To handle the edge deletion, we maintain a spanning tree for each connected component in the affected subgraphs $G_{N(u)}$, $G_{N(v)}$ and $G_{N(w)}$ where $w\in L$. For example, consider the component $P=\{p_1,\ldots ,p_5\}$ of $G_{N(r)}$ in Fig. 10b and the corresponding spanning tree $T_{P}$ in Fig. 10d. The edges in the spanning tree are called tree edges, and other edges in the component are called non-tree edges, e.g., $(p_1, p_2)$ is a tree edge and $(p_1, p_5)$ is a non-tree edge.

For each $w\in L$, we consider updating $G_{N(w)}$ with the deletion of $(u, v)$. We check whether $(u, v)$ is a tree edge in the spanning tree of the component. If $(u, v)$ is a non-tree edge, $score(w)$ remains unchanged because vertices $u, v$ are still in the same component connected by the corresponding spanning tree. Continuing with the example above, the deletion of the non-tree edge $(p_1, p_5)$ will not split the component $P$ in $G_{N(r)}$, and $p_1, p_5$ are still in the same component. If $(u, v)$ is a tree edge, then the deletion of $(u, v)$ splits the spanning tree into two trees denoted as $T_{u}$ and $T_{v}$. We will search for a replacement edge so as to reconnect $T_{u}$ and $T_{v}$. If a replacement edge $(u', v')$ exists, we insert $(u', v')$ to connect $T_{u}, T_{v}$ into a new spanning tree. Then the original component is still connected, and $score(w)$ remains unchanged. If the replacement edge does not exist, the deletion of $(u, v)$ splits the original connected component into two components, and the corresponding spanning trees are $T_{u}$ and $T_{v}$. So we update $score(w)$ accordingly. Maintaining the spanning tree can be implemented easily with the $\mathsf {Union}$ operation by keeping track of the bridge edge between two different components. In the example above, if a tree edge $(p_1, p_2)$ is deleted, we can find a replacement edge $(p_1, p_4)$ to reconnect the spanning tree in Fig. 10d.

The deletion of $(u, v)$ also affects $G_{N(u)}$ and $G_{N(v)}$. Consider $u$ as an example. For all $w \in L$, we remove those non-tree edges $(v, w)$ from $G_{N(u)}$ and remove those tree edges $(v, w)$ from the spanning tree which is then split into multiple trees. Then we search for replacement tree edges to reconnect the spanning tree. Finally, we remove $v$ from $G_{N(u)}$ and update $score(u)$. Figure 10e, f shows the updates of $G_{N(r)}$ and $T_{P}$ with the deletion of $(r, p_2)$.

The above techniques apply to updating both the actual score and the upper bound in our $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework given edge insertions/deletions. In updating an upper bound $\overline{bound}(v)$ for vertex $v$, given an edge deletion as a tree edge, we only split the original spanning tree into two, but do not have to search for the replacement edge. This will only relax $\overline{bound}(v)$ without affecting the result correctness. This strategy can avoid the cost of finding the replacement edge and achieve higher efficiency.

Summary Handling edge insertion is trivial using our disjoint-set forest structure, while handling deletion is more costly as it maintains the spanning tree. In the real-world networks, edge insertions are usually more frequent than deletions. Our update techniques do not increase the space complexity of $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$.

8 Top-K core-based structural diversity search

Ugander et al. [25] gave another definition of structural diversity based on the core subgraph concept [6]. Their study showed that, the core-based structural diversity suffices to provide a positive predictor of future long-term engagement in a social network. In this section, we further study top-$k$ structural diversity search using this definition.

Due to the different definition of structural diversity, the structural properties for the component-based measure (Definition 2) may not hold for the core-based measure. For example, in Fig. 2a, vertices $e$, $b$ and $d$ form a triangle, and $b, d$ belong to the same component in the 2-core of $G_{N(e)}$, as depicted in Fig. 2b. But vertices $e$ and $d$ do not belong to the same component in the 2-core of $G_{N(b)}$, neither do vertices $e$ and $b$ belong to the same component in the 2-core of $G_{N(d)}$. This shows that Property 2 does not hold for the core-based definition. In addition, the $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$ data structure is designed for keeping the information of components that vertices belong to; however, we can not know whether two vertices belong to the same component in a $t$-core beforehand. Hence, our proposed $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$ structure and the upper bound which leverage such property can not be directly applied to the top-$k$ core-based structural diversity search. In the following, we will derive a new upper bound and a new algorithm for computing the core-based structural diversity score.

8.1 Upper bound of core-based structural diversity

Similar to Lemma 1, a simple upper bound of the core-based structural diversity can be derived based on the vertex degree and the parameter $t$.

Lemma 8

For any vertex $v\in V$, $score^{*}(v)\le \lfloor \frac{d(v)}{t +1} \rfloor$ holds.

However, this upper bound can be too loose for efficient pruning. In the following, we introduce an important structural property, which is useful for designing a tighter upper bound. First we give a definition of core value.

Definition 6

(Core value) The core value of a vertex $v\in V$ in a graph $G$, denoted by $\varphi (v)$, is the maximum integer $t$ such that there exists a $t$-core subgraph of $G$ that contains $v$.

Continue with the above example. For the graph in Fig. 2a, vertex $f$ has a core value of 2, and the other vertices have a core value of 3. Based on the core value, we can derive a new structural property as follows.

Property 3

If a vertex $v\in V$ has $\varphi (v)\le t$, then for each vertex $u\in N(v)$, $v$ is not in the $t$-core of $G_{N(u)}$.

A tighter upper bound is derived in Lemma 9 based on Property 3.

Lemma 9

For any vertex $v\in V$, we have an upper bound of $score^{*}(v)$ as

$$\begin{aligned} \overline{bound}(v) = \left\lfloor \frac{d(v)-w(v)-q(v)}{t+1} \right\rfloor , \end{aligned}$$

where $w(v)$ and $q(v)$ are defined as follows:

$$\begin{aligned} w(v)&= |\{u: u\in N(v), \varphi (u)\le t\}|,\\ q(v)&= |\{u: u\in N(v), \varphi (u)>t, |N(v)\cap N(u)| < t\}|. \end{aligned}$$

Proof

First, according to Property 3, these $w(v)$ vertices with $\varphi (u)\le t$ is not in the $t$-core of $G_{N(v)}$.

Next, we prove that any vertex $u\in N(v)$ with $\varphi (u)> t$ and $|N(v)\cap N(u)|<t$ is not in the $t$-core of $G_{N(v)}$, because $u$ has less than $t$ neighbors in $G_{N(v)}$. Therefore, these $q(v)$ vertices are not in the $t$-core of $G_{N(v)}$.

Therefore, the maximum possible number of vertices in the $t$-core is $d(v)-w(v)-q(v)$. Similar to the proof of Lemma 8, we can derive $\overline{bound}(v)$ $= \lfloor \frac{d(v)-w(v)-q(v)}{t +1} \rfloor$ as an upper bound of $score^{*}(v)$.

For example, in Fig. 2b, let $t=2$. We have $w(e)=1$ because there is one vertex, $f$, with $\varphi (f)=2 \le t$. We also have $q(e)=1$ because there is one vertex, $h$, with $\varphi (h)=3 > t$ and $|N(e)\cap N(h)|=1<t$. It follows that $\overline{bound}(e)=\lfloor \frac{7-1-1}{2+1} \rfloor = 1$, which is equal to $score^{*}(e) = 1$. This bound is tighter than the degree-based bound $\lfloor \frac{7}{2+1} \rfloor =2$.

8.2 Core-based structural diversity computation

8.2.1 Top-K search framework

For top-$k$ core-based structural diversity search, we adopt the $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework in Sect. 5 with the new upper bound in Lemma 9. To assign an initial upper bound to every vertex, we apply core decomposition [4] on $G$ to compute the core value of every vertex in $G$. For the self-completeness of this paper, the core decomposition algorithm [4] is outlined in Algorithm 7. The algorithm first sorts the vertices in $G$ in ascending order of their degree. Then the algorithm iteratively removes from $G$ a vertex $v$ with the minimum degree, together with all the edges incident to it, and assigns $d$, the current minimum degree in $G$, as its core value $\varphi (v)$. Upon the removal of $v$, we also update the degree of the remaining vertices and reorder them according to their new degree. The algorithm terminates when all vertices are removed from $G$. In this way, we compute the core value of all vertices in $G$.

Next we initialize the upper bound of each vertex $v\in V$ as $\overline{bound}(v)$ $=\lfloor \frac{d(v)-w(v)}{t+1} \rfloor$ $= \lfloor \frac{|\{u: u\in N(v), \varphi (u)>t\}|}{t+1}\rfloor$ by Lemma 9, where we set the parameter $q(v)=0$ at this stage. Note that $\overline{bound}(v)$ can be incrementally refined during the top-$k$ search process, because the vertex $u\in N(v)$ with $\varphi (u)> t$ and $|N(v)\cap N(u)| < t$ can be identified when computing $score^{*}(u)$.

In summary, we make the following modifications in the $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework (Algorithm 3) to adapt it to the core-based structural diversity search.

• 1. For initialization, we compute the core value $\varphi (v)$ for every $v\in V$ using Algorithm 7.

• 2. We initialize the upper bound in line 5 using $\overline{bound}(v)=\lfloor \frac{d(v)-w(v)}{t+1} \rfloor$.

• 3. We compute $\overline{bound}(v^*)$ according to Lemma 9 in line 8.

• 4. In line 15, a new $\mathsf {A^{*}}$-$\mathsf {core}$-$\mathsf {search }$ algorithm is invoked, which will be introduced in details in Sect. 8.2.2.

8.2.2 A$^*$-based search algorithm

Next we propose an efficient method for computing the core-based structural diversity score for a vertex. This new method, called $\mathsf {A^{*}}$-$\mathsf {core}$-$\mathsf {search }$, is shown in Algorithm 8. It has two main steps: (1) for a vertex $v$, it first applies core decomposition on $G_{N(v)}$ and computes the $t$-core of $G_{N(v)}$; and (2) it then invokes $\mathsf {A^{*}}$-$\mathsf {bound}$-$\mathsf {search }$ (Algorithm 6) to efficiently compute the number of components in the $t$-core and returns $score^{*}(v)$.

In the first step for computing the $t$-core, a graph $H$ is initialized to be $G_{N(v)}$. Since any vertex $u\in N(v)$ with $\varphi (u)\le t$ is not in the $t$-core of $G_{N(v)}$ by Lemma 3, $u$ is removed from the graph $H$, together with all the incident edges (lines 1–3). Then, for each vertex $u$ in $H$, we compute the degree $d(u)$. If $d(u)<t$, the algorithm inserts $u$ into the queue $Q$, which keeps the candidate vertices for removal from $H$ and updates $\overline{bound}(u)$ according to Lemma 9 (lines 4–13). Next, it performs core decomposition by iteratively removing vertex $u$ in $Q$ from $H$, and inserting new vertices with degree less than $t$ into $Q$. This process terminates when $Q$ is empty (lines 14–21). The remaining graph $H$ is the $t$-core of $G_{N(v)}$.

In the second step, the algorithm applies the $\mathsf {A^{*}}$ strategies in Algorithm 6 for computing the number of connected components in the $t$-core of $H$ as $score^{*}(v)$ and returns it. Specifically, we modify Algorithm 6 by removing lines 25–26 (designed according to Property 2) and lines 29–32 (designed according to Property 1), since neither property is applicable for core-based structural diversity search. The other parts of Algorithm 6 remain unchanged.

8.2.3 Complexity analysis

We analyze the time and space complexity of the core-based $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework as follows.

Theorem 5

The core-based $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework using $\mathsf {A^{*}}$-$\mathsf {core}$-$\mathsf {search }$ takes $O(\sum _{(u,v)\in E}$ $(\min \{d(u),d(v)\}+$ $(\log$ $d(u)$ $+$ $\log d(v))$ $))$ time and $O(m)$ space.

Proof

First, in the initialization step, the algorithm applies core decomposition (Algorithm 7) on the whole graph $G$, which can be done in $O(m)$ time [4]. The total time cost of estimating the upper bound for all vertices is $O(m)$.

Second, for a vertex $v$, we consider the time cost of computing $score^{*}(v)$. Compared with $\mathsf {A^{*}}$-$\mathsf {bound}$-$\mathsf {search }$, it takes extra $O(\sum _{u\in N(v)} \min \{d(u),$ $d(v)\})$ time for computing the degree of vertices in $N(v)$. Moreover, performing core decomposition on $G_{N(v)}$(lines 14–21) also takes extra $O(\sum _{u\in N(v)}$ $\min \{$ $d(u),$ $d(v)\})$ time. Finally, it invokes Algorithm 6 for computing the number of components in the $t$-core of $G_{N(v)}$. By Theorem 4, the top-$k$ search process takes $O(\sum _{(u,v)\in E}$ $(\min \{d(u),$ $d(v)\}$ $+(\log d(u)+\log d(v))))$ time.

Compared with $\mathsf {A^{*}}$-$\mathsf {bound}$-$\mathsf {search }$, $\mathsf {A^{*}}$-$\mathsf {core}$-$\mathsf {search }$ needs extra $O(n)$ space for storing the core value for all vertices. Thus, the space complexity is still $O(m)$.

Hence, Theorem 5 is established.

8.3 Network structural properties analysis

In this subsection, we discuss the impact of real-world network properties on the performance of the proposed algorithms for $\mathsf {CC}$-$\mathsf {TopK}$ and $\mathsf {Core}$-$\mathsf {TopK}$. We consider three well-known structural properties, namely, power-law degree distribution, average path length, and clustering coefficient.

Power-law degree distribution Social networks usually follow a power-law degree distribution, that is, a small percentage of nodes are high-degree ones and the vast majority of nodes are low-degree ones. According to our upper-bound definition which depends on the node degree, those high-degree nodes will be examined first in the top-$k$ search framework. As the degree difference between the high-degree and low-degree nodes can be quite large, we can easily find that many low-degree nodes are impossible to be the top-$k$ answers simply based on their upper-bound estimate; thus, they can be pruned at an early stage. Therefore, our algorithms are expected to work more efficiently on graphs with power-law degree distribution than those with uniform degree distribution.

Average path length Social networks usually have a small average path length, that is, the small-world effect. For a node in such a network, the neighbors of the node are more likely to be closely connected, leading to few large components. As a result, the node tends to have a low structural diversity score. In contrast, for a node in a network with a large average path length, the neighbors of the node are loosely connected or even scattered far apart, leading to many components. Thus, the node tends to have a high structural diversity score. In the latter case, the upper-bound estimate of the nodes tends to be tighter and thus provides more effective pruning for top-$k$ search.

Clustering coefficient Social networks often have a high clustering coefficient, in which nodes tend to cluster together with high density of ties. Obviously, in a graph with a larger clustering coefficient, the probability of a triplet to form a triangle is higher. As a result, for the component-based structural diversity, Property 2 is easier to be satisfied and thus will be more frequently used for upper-bound refinement to reduce the overall computational cost. The clustering coefficient has no obvious impact on the algorithms for the core-based structural diversity since it does not make use of triangles for upper-bound refinement.

9 Experiments

We conduct extensive performance study to evaluate the algorithms proposed in this paper. All algorithms are implemented in C++, and all the experiments are conducted on the Linux operating system with 2.67 GHz six-core CPU and 50 GB main memory.

Evaluation metrics We use the running time and the number of vertices whose structural diversity scores are computed in the search process as two metrics. The latter evaluates the number of vertices that are pruned by the algorithm.

Datasets We use 13 real-world networks covering social, communication, collaboration, location-based networks, and webgraphs. The network statistics are shown in Table 1. Except for Epinions, Digg and KDDTrack1¹ which are from their respective websites, the other 10 networks are downloaded from the Stanford Network Analysis Project (snap.stanford.edu). We treat all the networks as undirected.

Table 1 Network statistics (K $=10^3$ and M $=10^6$)

Table 2 Comparison of running time (wall-clock time in seconds) and search space (the number of vertices whose structural diversity score are computed in search process) of different algorithms

9.1 Connected component-based structural diversity

Comparison methods To the best of our knowledge, we are the first to study top-$k$ structural diversity search. In the literature, no algorithms have been proposed to address this problem yet. Thus, we compare our algorithms with the degree-based approach (Algorithm 1) which serves as a baseline. Compared with the baseline method, our proposed algorithms produce exactly the same true top-$k$ results. We evaluate four algorithms.

• $\mathsf {Deg }$: The degree-based approach in Algorithm 1.

• $\mathsf {Bou }$: $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ equipped with $\mathsf {bound}$-$\mathsf {search }$ (Algorithm 4) and $\theta =1$.

• $\mathsf {FB }$: $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ equipped with $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {search }$ (Algorithm 5) and $\theta =(\frac{n}{t})^{\frac{1}{\sqrt{m}}}$.

• $\mathsf {A^{*}}$-$\mathsf {B }$: $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ equipped with $\mathsf {A^{*}}$-$\mathsf {bound}$-$\mathsf {search }$ (Algorithm 6) and $\theta = (\frac{n}{t})^{\frac{1}{\sqrt{m}}}$.

In our experiments, we find that $\theta =(\frac{n}{t})^{\frac{1}{\sqrt{m}}}$ which is close to 1 always yields a good performance in the $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework. For $\mathsf {FB }$ and $\mathsf {A^{*}}$-$\mathsf {B }$, their performances are not very sensitive to the value of $\theta$ as long as $\theta \in (1.001,1.05)$ on all datasets.

Fig. 11

Running time (in second) of different algorithms versus parameter $k$. a Digg, b WikiTalk, c AstroPh, d Gowalla, e NotreDame, f Flickr

Fig. 12

Number of vertices whose structural diversity scores are computed versus parameter $k$. a Digg, b WikiTalk, c AstroPh, d Gowalla, e NotreDame, f Flickr

Fig. 13

Running time (in second) of different algorithms versus parameter $t$. a Digg, b WikiTalk, c AstroPh, d Gowalla, e NotreDame, f Flickr

9.1.1 Efficiency comparison

In this experiment, we compare the efficiency of different methods over all networks. We set $k=100$ and $t=2$. Similar results can be observed for other $k$ and $t$ values. Table 2 reports the results. We can see that $\mathsf {A^{*}}$-$\mathsf {B }$ is the most efficient, followed by $\mathsf {FB }$, $\mathsf {Bou }$, and $\mathsf {Deg }$. Notice that the performance of $\mathsf {A^{*}}$-$\mathsf {B }$, $\mathsf {FB }$, and $\mathsf {Bou }$ which adopt the $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework is substantially better than that of the degree-based algorithm $\mathsf {Deg }$. The speedup ratio between $\mathsf {Deg }$ and $\mathsf {A^{*}}$-$\mathsf {B }$ defined as $R_{s} = t_{{\mathsf {Deg }}}/t_{\mathrm{A}^{\star }-\mathrm{B}}$ is between 2.1 and 69.1 (column 6 in Table 2). The result conforms with the complexity analysis in Sect. 6. In addition, we define the pruning ratio between $\mathsf {Deg }$ and $\mathsf {A^{*}}$-$\mathsf {B }$ as $R_{p}=S_{{\mathsf {Deg }}}/S_{\mathrm{A}^{\star }-\mathrm{B}}$, where $S_{{\mathsf {Deg }}}$ and $S_{\mathrm{A}^{\star }-\mathrm{B}}$ denote the number of vertices whose structural diversity scores are computed by the respective methods. The pruning ratio is between 2.1 and 11.1 over all networks (column 11 in Table 2). This result suggests that the upper bound derived in Lemma 3 is indeed tighter than the degree-based upper bound in Lemma 1.

When we compare $\mathsf {Bou }$ and $\mathsf {Deg }$, the reduction of running time and search space by $\mathsf {Bou }$ demonstrates the effectiveness of the tighter upper bound in Lemma 3 and the $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$ data structure. When we compare $\mathsf {Bou }$ and $\mathsf {FB }$, the reduction of running time by $\mathsf {FB }$ shows the effectiveness of the $\mathsf {fast}$-$\mathsf {bound}$-$\mathsf {search }$ method. Finally we observe that $\mathsf {A^{*}}$-$\mathsf {B }$ is more efficient than $\mathsf {FB }$, which proves the effectiveness of the $\mathsf {A^{*}}$ search order.

9.1.2 Performance evaluation by varying k

In this experiment, we evaluate the performance of all the methods by varying the parameter $k$. We set $t=2$ and focus on six networks Digg, WikiTalk, AstroPh, Gowalla, NotreDame and Flickr. Similar results can be observed for other $t$ values and on other networks. Figure 11a–f depicts the running time of different algorithms. Again, we can see that $\mathsf {A^{*}}$-$\mathsf {B }$ is the most efficient and $\mathsf {Deg }$ is the least efficient in most networks. The running time of $\mathsf {A^{*}}$-$\mathsf {B }$ is very stable as $k$ increases.

Fig. 14

Number of vertices whose structural diversity scores are computed versus parameter $t$. a Digg, b WikiTalk, c AstroPh, d Gowalla, e NotreDame, f Flickr

Figure 12a–f shows the number of vertices whose structural diversity scores are computed by different methods on the six networks. $\mathsf {A^{*}}$-$\mathsf {B }$ is the clear winner by pruning the largest number of vertices, and $\mathsf {Deg }$ performs worst. In addition, we find that $\mathsf {FB }$ and $\mathsf {Bou }$ achieve very similar performance in terms of the number of vertices that are pruned. This is because $\theta =(\frac{n}{t})^{\frac{1}{\sqrt{m}}}$ in $\mathsf {FB }$ is very close to 1 (as listed in the last column of Table 2), and $\theta$ in $\mathsf {Bou }$ is set to 1 in our experiment. Thus, the pruning condition in $\mathsf {FB }$ and $\mathsf {Bou }$ is very similar. But on the other hand, $\mathsf {FB }$ runs much faster than $\mathsf {Bou }$ as shown in Fig. 11, which conforms with the time complexity analysis in Theorems 2 and 3.

9.1.3 Performance evaluation by varying t

We evaluate the performance of all methods by varying the parameter $t$. In this experiment, we set $k=100$ and similar results can be observed for other $k$ values. Figure 13a–f shows the running time of different algorithms. Once again, $\mathsf {A^{*}}$-$\mathsf {B }$ is the most efficient algorithm, and $\mathsf {Deg }$ is the least efficient one. We also observe that in many cases, the running time of all methods increases with increasing $t$ at first, but it may drop slightly when $t$ further increases. A possible reason is that when $t$ is large, the number of the qualified components (i.e., the components whose sizes are no less than $t$) reduces. Thus, by the estimated upper bound, the search space can be quickly pruned.

Figure 14a–f shows the number of vertices whose structural diversity scores are computed in different networks by varying $t$. We observe that $\mathsf {A^{*}}$-$\mathsf {B }$ prunes the most number of vertices, and $\mathsf {Deg }$ prunes the least number of vertices.

9.1.4 Handling update in dynamic networks

In this experiment, we evaluate the time for incrementally maintaining the top-$k$ results when the input network is updated. For each network, we randomly insert/delete 1K edges and update the top-$k$ results after every edge insertion/deletion. The average update time per edge insertion/deletion is reported in Table 3. In addition, we report the batch update time for the 1K edge insertions/deletions. We repeat this experiment for 50 times and report the average performance. For comparison, we also report the time for computing the top-$k$ results from scratch when the network is updated with an edge insertion/deletion.

Fig. 15

Running time (in second) of different algorithms versus parameter $k$. a Digg, b WikiTalk, c AstroPh, d Gowalla, e NotreDame, f Flickr

Fig. 16

Number of vertices whose structural diversity scores are computed versus parameter $k$. a Digg, b WikiTalk, c AstroPh, d Gowalla, e NotreDame, f Flickr

Fig. 17

Running time (in second) of different algorithms versus parameter $t$. a Digg, b WikiTalk, c AstroPh, d Gowalla, e NotreDame, f Flickr

Fig. 18

Number of vertices whose structural diversity scores are computed versus parameter $t$. a Digg, b WikiTalk, c AstroPh, d Gowalla, e NotreDame, f Flickr

The result in Table 3 shows that handling edge insertions is highly efficient. The update time per edge insertion is 0.01 or 0.02 ms on most networks, and the batch update time for 1K edge insertions is within 10 ms on most networks. Handling edge deletions is more costly, because an edge deletion may trigger to check whether the two endpoints of the deleted edge are still in the same component or not in a number of neighborhood-induced subgraphs. The update time per edge deletion is within 1 ms on most networks, and the batch update time for 1K edge deletions is $<$1 s on most networks. Finally we can see the incremental update (per edge as well as batch update of 1K edges) is several orders of magnitude faster than recomputing the top-$k$ results from scratch.

9.2 Core-based structural diversity

Comparison methods In this experiment, we focus on evaluating the top-$k$ core-based structural diversity search, and compare two proposed algorithms.

• $\mathsf {Core}$-$\mathsf {Deg }$: a simple degree method with the degree-based upper bound in Lemma 8. Specifically, we adapt Algorithm 1 with the following changes: (1) in line 6, the upper bound is changed using the new upper bound in Lemma 8; and (2) in line 9, we compute the $t$-core of $G_{N(v^*)}$ and count the number of connected components in the $t$-core as $score^{*}(v^*)$.

• $\mathsf {Core}$-$\mathsf {A^{*} }$: the core-based $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework introduced in Sect. 8.2.1 equipped with $\mathsf {A^{*}}$-$\mathsf {core}$-$\mathsf {search }$ (Algorithm 8) and $\theta = (\frac{n}{t})^{\frac{1}{\sqrt{m}}}$.

Table 3 Update Time (wall-clock time in milliseconds)

Compared with the baseline $\mathsf {Core}$-$\mathsf {Deg }$, $\mathsf {Core}$-$\mathsf {A^{*} }$ produces exactly the same true top-$k$ results. For all datasets, we also find that $\theta =(\frac{n}{t})^{\frac{1}{\sqrt{m}}}$ which is close to 1 always yields a good performance in the core-based $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework. For $\mathsf {Core}$-$\mathsf {A^{*} }$, its performances is not very sensitive to the value of $\theta$ as long as $\theta \in (1.001,1.05)$.

9.2.1 Performance evaluation by varying k

In this experiment, we evaluate the performance of $\mathsf {Core}$-$\mathsf {Deg }$ and $\mathsf {Core}$-$\mathsf {A^{*} }$ by varying the parameter $k$. We set the parameter $t=2$ by default and test on six networks Digg, WikiTalk, AstroPh, Gowalla, NotreDame and Flickr. Similar results can be observed for other $t$ values and on other networks. Figure 15a–f shows the running time of different algorithms on the six networks. We can see that $\mathsf {Core}$-$\mathsf {A^{*} }$ is the clear winner by running much faster than $\mathsf {Core}$-$\mathsf {Deg }$ on all networks, which demonstrates the advantage of the core-based $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework and the $\mathsf {A^{*}}$-$\mathsf {core}$-$\mathsf {search }$ method.

Figure 16a–f shows the number of vertices whose structural diversity scores are computed by different methods on the six networks. $\mathsf {Core}$-$\mathsf {A^{*} }$ prunes many more vertices than $\mathsf {Core}$-$\mathsf {Deg }$. This result shows that the upper bound derived in Lemma 9 is indeed much tighter than the degree-based upper bound in Lemma 8.

9.2.2 Performance evaluation by varying t

In this experiment, we evaluate the performance of all methods by varying the core number $t$ on the six networks above. In this experiment, we set $k=100$ and similar results can be observed for other $k$ values. Figure 17a–f shows the running time of different algorithms. The running time of $\mathsf {Core}$-$\mathsf {A^{*} }$ is 2–4 times shorter than that of $\mathsf {Core}$-$\mathsf {Deg }$ on all networks. In addition, the performance of $\mathsf {Core}$-$\mathsf {A^{*} }$ remains very stable as $t$ increases.

Figure 18a–f shows the number of vertices whose structural diversity scores are computed in different networks by varying $t$. Again $\mathsf {Core}$-$\mathsf {A^{*} }$ prunes many more vertices than $\mathsf {Core}$-$\mathsf {Deg }$.

9.3 Case study

9.3.1 Identifying ambiguous names

Name ambiguity has long been viewed as a challenging problem in social network analysis. For example, when we search a person named “Wei Wang” from the DBLP website, there are at least 52 distinct persons with the same name. Our top-$k$ structural diversity search method provides a novel approach for identifying ambiguous names in a soci al network, which is the first and important step for name disambiguation. In this case study, we build a collaboration network from the DBLP dataset.² A vertex represents an author name and an edge is added between two authors if they have co-authored 3 times or more. The network contains 234,879 vertices and 541,814 edges.

We first apply the component-based structural diversity measure on the DBLP network for finding top-5 authors with the highest number of connected components of size over 2. The result is shown in Table 4. As we can see, these five names are indeed popular but ambiguous ones which can correspond to different distinct persons in the real world. For comparison, we select five famous authors who have a large degree, i.e., a large number of collaborators and report their structural diversity score. Despite the large degree, their structural diversity score is far smaller than that of the ambiguous names. Intuitively, we can imagine that an ambiguous name corresponds to different distinct persons, each of who has his/her own research communities. This leads to a large number of non-overlapping research communities associated with an ambiguous name. In addition, we also observe that many of such communities are tiny and loosely connected. This is because the component-based structural diversity does not enforce a cohesive structure in the components.

Table 4 Ambiguous names (Top-5 structural diversity result based on size-2 connected component) and selected famous authors in DBLP network

Table 5 Ambiguous names (Top-5 structural diversity result based on 2-core) and selected famous authors in DBLP network

Fig. 19

Top-1 structural diversity based on size-2 connected component in word association network. Here $\mathsf {``black}$ ” has the highest structural diversity score as 9

Fig. 20

Top-2 structural diversity based on 2-core in word association network. Here $\mathsf {``word}$ ” and $\mathsf {``Christmas}$,” respectively, has the top-2 highest structural diversity score as 4 and 3. a Word, b Christmas

We also apply the core-based structural diversity measure on the DBLP network for finding top-5 authors using 2-core subgraphs and report the result in Table 5. By definition, the 2-core-based measure discards all tree-shaped components and counts the remaining cohesive components into the score. As a result, the obtained scores in Table 5 are smaller than the component-based scores in Table 4. Moreover, we observe that the core-based top-5 ambiguous names are different from the component-based top-5 names in Table 4. This suggests that these two diversity measures can complement each other.

This case study shows that our top-$k$ structural diversity search provides an effective mechanism for finding ambiguous names in a social network.

9.3.2 Words with diverse meanings

In this case study, we apply the two structural diversity measures on a word association network.³ The expected result is to find words with the most diverse meanings, and to analyze and understand the different meanings of these words in different contexts. In this network, a vertex represents a word, and an edge between two words indicates that they are meaningfully related or strongly associated. The network contains 7,207 vertices and 31,784 edges.

We first query top-1 vertex in the word association network by counting the number of connected components of size over 2. The result is depicted in Fig. 19. The word $\mathsf {``black}$ ” has the highest structural diversity score as 9, indicating 9 distinct connected components in the neighborhood-induced subgraph of $\mathsf {``black}$,” and each distinct component represents a certain meaning of $\mathsf {``black}$.” The largest connected component (depicted in red) contains 22 words, and most of those words can be roughly summarized by three words as $\mathsf {``color}$,” $\mathsf {``race}$ ” and $\mathsf {``dark}$.” For example, $\mathsf {``black}$ ” is a $\mathsf {``color}$,” and $\mathsf {``black}$ ” is related to other colors such as $\mathsf {``white}$,” $\mathsf {``red}$,” $\mathsf {``blue}$,” and $\mathsf {``yellow}$.” For the other 8 connected components, each contains 2–3 words, and represents a distinct context of words associated with $\mathsf {``black}$,” such as, {$\mathsf {``penguin}$,” $\mathsf {``tuxedo}$ ”}, {$\mathsf {``panther}$,” $\mathsf {``cat}$ ”}, {$\mathsf {``death}$,” $\mathsf {``widow}$,” $\mathsf {``funeral}$ ”}, and so on.

Next, we query top-2 vertices in the word association network using 2-core subgraphs. Two words $\mathsf {``word}$ ” and $\mathsf {``Christmas}$ ” have the highest two structural diversity scores of 4 and 3, which are shown in Fig. 20. As we can see, each vertex in the 2-core component in Fig. 20 has at least two neighbor words. Specifically, the word $\mathsf {``word}$ ” in Fig. 20a has four distinct contexts of associated words with different meanings. For example, {$\mathsf {``swear}$,” $\mathsf {``oath}$,” $\mathsf {``promise}$ ”} represent the synonym of “words” as “promise,” and {$\mathsf {``verb}$,” $\mathsf {``noun}$,” $\mathsf {``pronoun}$ ”} are different types of “word.” The word $\mathsf {``Christmas}$ ” has three distinct contexts of associated words, as shown in Fig. 20b, {$\mathsf {``reindeer}$,” $\mathsf {``sleigh}$,” $\mathsf {``Santa}$ ”} describe the “Santa,” {$\mathsf {``present}$,” $\mathsf {``gift}$,” $\mathsf {``package}$ ”} represent the “Christmas gifts” and {$\mathsf {``tree}$,” $\mathsf {``ornament}$,” $\mathsf {``decoration}$ ”} are related to the “Christmas tree.”

When we compare Figs. 19 and 20, using the component-based structural diversity, we can find words with many different meanings. However, the terms in a certain context may be loosely related to each other (e.g., “hair” and “blue” in the same connected component in Fig. 19). On the other hand, using the core-based structural diversity, the terms in each component are highly related to each other. But the core-based measure may discard some loosely connected components, thus fail to extract the corresponding meanings of a word.

This case study shows that our top-$k$ structural diversity search can be applied for finding different meanings of a word, which is a fundamental problem in natural language understanding.

10 Related work

To the best of our knowledge, top-$k$ structural diversity search has not been studied before. In the following, we briefly review the existing work that are related to ours.

First, our work is closely related to the work on top-$k$ query processing. The goal of top-$k$ query processing is to find $k$ objects with the highest rank based on some pre-defined ranking function. A commonly used framework for this problem is to examine the candidates in a heuristic order and prune the search space using an upper bound. After the seminal work by Fagin et al. [12, 13], a large number of studies on top-$k$ query processing have been done for different application scenarios, such as processing distributed preference queries [5], keyword queries [20], set similarity join queries [27]. Recently, many studies take the diversity into consideration in top-$k$ query processing, in order to return diversified ranking results [1, 2, 19, 21, 28, 29]. A comprehensive survey of top-$k$ query processing can be found in [15].

Second, our proposed techniques are related to the algorithms for the triangle listing problem, which is to find all triangles in a graph. Itai and Rodeh [16] first proposed an $O(m^{1.5})$ algorithm for the triangle listing problem. Latapy [18] proved that the time complexity $O(m^{1.5})$ is optimal. Subsequently, Schank and Wagner [23, 24] proposed a simpler and particularly fast solution with the optimal complexity based on the vertex ordering and efficient lookup of the adjacency lists for neighborhood testing. Recently, Chu and Cheng [8] proposed an I/O-efficient algorithm for triangle listing in a massive graph, which cannot fit into the main memory. In this paper, we study the top-$k$ structural diversity search problem. The complexity of our algorithm is proved to be $O(m^{1.5})$.

11 Conclusions

In this paper, we study the top-$k$ structural diversity search problem motivated by a number of network analysis applications. We develop a novel $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework to tackle this issue. Specifically, we design a $\mathsf {Union}$-$\mathsf {Find}$-$\mathsf {Isolate }$ data structure to keep track of the known structural information of each vertex, and an effective upper bound for pruning. For further speeding up the structural diversity evaluation, several well-designed search strategies are proposed. Our $\mathsf {Top}$-$\mathsf {k}$-$\mathsf {search}$ framework can be generalized to handle both the connected component-based measure and the core-based measure for structural diversity search. We evaluate the proposed algorithms on real-world large networks and synthetic graphs, and the results demonstrate the effectiveness and efficiency of the proposed algorithms.