1 Introduction

Because of its versatility, dependability, and minimal space occupancy requirements, the integrated motor pump-jet thruster (IMP thruster) has gained increased interest in recent years. According to Wang et al. [1], the IMP thruster has progressed with the development of integrated electric power technology to further attain high power density, high efficiency, low noise, and high agility in electric propulsion. The low-order surface panel approach based on velocity potentials was applied to investigate a pump-jet propulsor [2], and the results demonstrate that adjusting the size of the duct gap had the opposite effect on overall and rotor efficiency. Increasing the duct camber enhances the pump-jet propulsor’s efficiency, improves the rotor blades’ cavitation resistance, optimizes the load distribution on the rotor, and mitigates the increase in duct resistance at high speeds. These improvements significantly enhance the performance and reliability of the propulsion system. Yu et al. [3] investigated the propulsion performance and unsteady forces of a pump-jet propulsor with varying pre-swirl stator parameters. The findings revealed that increasing the stator pre-whirl angle led to an augmentation in the circumferential velocity of the rotor inflow, resulting in higher overall thrust and improved propulsion efficiency of the pump-jet propulsor. Shirazi et al. [4] conducted a comprehensive study involving numerical simulations and experimental analysis of fluid flow in a full-scale pump-jet thruster. Comparing the results with conventional propellers, they observed significant reductions in hydrodynamic coefficients, especially the torque coefficient, as a function of advance coefficients. Zhu et al. [5] aimed to investigate and compare the hydrodynamic performance of the Supercavitating Propeller Tunnel (SPT) with that of a traditional mechanical pump-jet thruster (MPT) and the E779A propeller. The results indicated that the open-water efficiency of SPT reached 0.662, which was slightly lower than that of the conventional propeller. However, the high efficiency working range of SPT was notably broader than that of the propeller, implying that SPT could operate efficiently under a wider range of working conditions. Baltazar et al. [6] conducted a comparison between the results obtained from a panel code and a Reynolds-averaged Navier–Stokes (RANS) code. The objective was to gain a deeper understanding of the viscous effects on the ducted propeller and identify the limitations of the inviscid flow model. To accurately predict the loads on the propeller and duct, they found it necessary to incorporate an alignment model that aligned the wake shape with the local flow conditions. This alignment model proved crucial in achieving more reliable forecasts of the propeller and duct loads. Sikirica et al. [7] assessed the suitability of hexahedral block-structured grids for predicting marine propeller performance. The results indicated that hexa and hybrid grids yielded comparable results within a specific range of advanced ratios. However, for low and high ratios, structured grids used in conjunction with the Realizable model achieved more accurate results. This suggests that for certain operating conditions, the structured grids with the realizable model offer better predictive capabilities for marine propeller performance. Tu [8] conducted numerical simulations of propeller open-water characteristics using the RANSE method with a rotating reference frame approach. The study found that hexahedral meshes demonstrated a greater capacity to deliver high-quality results in the SST k-omega turbulence model compared to other case studies in their research. Liu and Vanierschot [9] conducted a comparison of the hydrodynamic performance between a ducted propeller (DP) and a rim-driven thruster (RDT) using computational fluid dynamics (CFD). The findings revealed that the gap flow present in the RDT significantly influenced its performance. Specifically, the RDT generated less thrust on both the propeller and the duct compared to the DP. In addition, due to the presence of the rim, the overall efficiency of the RDT was notably lower than that of the ducted propellers. Gaggero [10] performed a numerical design of a rim-driven thruster using a RANS-based optimization approach. The results of the optimizations demonstrated the flexibility and reliability of the SBDO (shape-based design optimization) framework in handling unconventional configurations. Zhou et al. [11] utilized both direct and inverse design methods to create a three-dimensional pump-jet model. The direct design process involved comparing the lifting and lifting-line design methods. Subsequently, the superior model underwent further geometric optimization. The findings indicated that the lifting method was better suited for low and medium speeds, while the lifting-line method demonstrated greater suitability for medium and high speeds. To gain a more comprehensive understanding of the performance of the rim-driven thruster, Zhu and Liu [12] conducted experimental investigations on the external characteristics and carried out numerical simulations to study the inner flow characteristics. The results revealed that as the flow rate decreased, large-scale backflows progressively emerged near the wall in front of the impeller inlet, the central area of the impeller outlet, and the two sides of the central low-pressure zone. These backflows caused significant flow losses and led to a head drop in the system.

According to the analysis of literature, most previous investigations have concentrated on optimizing the duct profile of the thruster and the propeller’s hydrodynamic characteristics. The IMP thruster is distinct from a conventional thruster in that the stator of the motor is relocated inside the duct. The motor’s rotor, however, is relocated to the blade’s tip rim. The blade is driven to rotate by the rotor and stator magnetization of the motor, a novel and unique drive method that brings advantages in terms of noise reduction and efficiency. However, its structure also generates problems different from those of conventional electric thrusters, the most important of which are the gap flow between the rim and the inner wall of the duct and the torque loss of the rim. Therefore, the influence of the thruster’s gap flow between the rotor and stator on its hydrodynamic performance cannot be ignored.

Cao et al. [13] utilized the RANS solver and angular momentum current analyzing method to investigate the impact of gap flow in a rim-driven thruster on the torque of the blades when the propeller was replaced by a rotating disk. They developed a new predictive method for calculating the torque of end faces by fitting the results obtained from computational fluid dynamics (CFD) simulations. To validate this method, experiments were conducted in the large cavitation tunnel of CSSRC. By varying the axial and radial clearance ratios, different clearance options were obtained, and the clearance flow with and without differential pressure was calculated. The study analyzed the effects of varying parameters, such as radial clearance ratio and axial clearance ratio, on the clearance flow and hydrodynamics. In addition, the variation law of friction torque was determined based on changes in the axial and radial clearance [14]. Liu and Vanierschot [9] used a moving reference frame (MRF) technique to investigate the hydrodynamic performance of both ducted propellers and rim-driven thrusters (RDT) with gap flow. The research revealed that the presence of the rim and the induced gap flow had predominantly negative effects on the hydrodynamic performance of the RDT. As a result, the RDT exhibited a significant reduction in efficiency when compared to the ducted propeller. Zhai et al. [15] performed an optimal design analysis of the duct for the rim-driven thruster (RDT) while considering the effect of the gap. They sought to optimize the duct’s design to enhance the hydrodynamic performance of the RDT. In addition, Jiang et al. [16] investigated the hydrodynamic characteristics of a counter rotating RDT, specifically considering the influence of the gap flow. They used the RANS (Reynolds-averaged Navier–Stokes) method for their analysis. Lin et al. [17] observed that when computing the torque with the inclusion of gap friction, the results deviated from empirical formulae by more than 10%. To understand the effects of the gap geometry on the performance of a classical hubless rim-driven thruster (RDT), they conducted a study by adjusting its axial passage length, as well as the inlet and outlet oblique angles. The investigation revealed that by shortening the axial passage length of the gap and simultaneously increasing the oblique angle with fixed inlet and outlet positions, the hydrodynamic efficiency of the RDT improved. However, moving the inlet and outlet to positions further upstream and downstream had negligible effects on the hydrodynamic efficiency and resulted in recirculating flow within the gap near its inlet. Weng et al. [18] aimed to improve the accuracy of predicting the hydrodynamic performance of a pump-jet propulsor by developing a suitable gap flow model. This model was constructed based on the existing tip leakage vortex model, but with additional considerations for the actual flow within the gap region of the pump-jet propulsor and the influence of fluid viscosity in that region. The introduction of this gap flow model had a significant impact, particularly on the duct of the pump-jet propulsor. As a result, the hydrodynamic performance and pressure distribution of the duct became more consistent with the trend of the calculation results for viscous flow. Ke and Ma [19] aimed to investigate the influence of the rotor’s speed and advance coefficient on the blade tip clearance flow and axial pressure of a rim-driven propulsor. To achieve this, they conducted computational fluid dynamics (CFD) calculations of the rim-driven propulsor using the FLUENT software under various working conditions. Bao et al. [20] examined the impact of various factors on the gap flow field of a 5.5 kW shaftless rim-driven thruster model. They investigated the effects of different gap ratios in both the radial and axial directions, as well as the influence of speed and pressure on the system. The results demonstrated that the friction torque increased with the gap size. In addition, they found that the friction torque in both the axial and radial directions had mutual effects on each other. Furthermore, the study revealed that the heat generated in the motor was efficiently dissipated in the gap flow. Donyavizadeh and Ghadimi [21] investigated on the hydrodynamic coefficients, such as thrust, torque, and efficiency, of a linear-jet propulsion system. They studied these coefficients at various advanced ratios to comprehensively analyze the performance of all components of the propulsion system. The research also involved computing the pressure distribution on the high- and low-pressure sides of the stator at different spans. This was achieved by considering various axial gap sizes between the stator and rotor, as well as the chord of the rotor in the propulsion system. The results of this pressure distribution analysis revealed different fluctuations caused by the interaction of the rotor and stator in the Linear-Jet propulsion system. Hu et al. [22] aimed to improve the accuracy of predicting the hydrodynamic performance of a pump-jet propulsor by considering the influence of fluid viscosity in the gap area. They proposed a gap flow model specifically designed for pump-jet propulsors. By analyzing the hydrodynamic performance of the pump-jet propulsor using the newly developed gap flow model, the researchers determined that the optimal gap height should be approximately 0.98 to 1.0 times the complete gap height. To study the gap flow characteristic and loss mechanism of shaftless pump-jet, Han et al. [23] calculated the hydrodynamic performance of the pump, and the results is evaluated by comparing with the experiments. On this basis, the vorticity transport equation in the cylindrical coordinate system and the entropy production are further used to analyze the clearance flow characteristics and energy loss mechanism of the propeller under different working conditions, the calculated results are in good agreement with the test. To study the influence of the structural characteristics of the rim gap of the shaftless pump-jet on the flow loss of the thruster, Ruan et al. [24] used the orthogonal test method to adjust and modify the rim gap, analyze the flow characteristics and loss around the propeller under different gap sizes, and then select the best matching scheme based on this. Based on the optimal gap matching program, the local structure of the gap area is adjusted to further improve the flow loss problem. To understand the hydrodynamic performance of IMP propulsor more accurately, Li [25] analyzed the influencing factors of wheel rim friction torque and determined the influence law of geometric parameters of different influencing factors on wheel rim friction torque, calculation results and empirical values good agreement.

There is no advancement regarding the IMP thruster in the current study for the gap flow, which is mainly concentrated on the RDT. Although the expected torque can be modified using empirical formulas, the impact of gap flow on the duct and propeller thrust is ignored. The RANS approach is used in this study to carry out a numerical investigation of the hydrodynamic performance of the IMP thruster taking gap flow into account. Based on gap flow cases such as channel and turbulent boundary layer [26,27,28,29] and rotating cylinders [30,31,32], and RDT flow [10, 33,34,35] it has been found that this approach is typically less expensive than advanced CFD methods like large eddy simulation.

2 Methodology

2.1 Geometric model

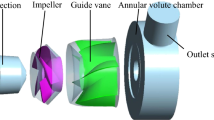
The IMP thruster was created using the 3D inverse design process, with the impeller airfoil being NACA4409 and the guide vane airfoil being 443. The design uses the No.19A duct to accommodate the motor installation. Figure 1 depicts the IMP thruster calculation model. In the design, there exist both axial and radial gaps between the motor rotor and the duct, as illustrated in Fig. 1. There are axial and radial gaps between the motor rotor and the duct, as shown in Fig. 1. The axial gap width at the inlet side is \(l_{{{\text{in}}}}\), the axial gap width at the outlet side is \(l_{{{\text{out}}}}\), the radial gap thickness is \(h\), the rotor blade radius is \(r\), the external diameter of the rim is 2 \(r_{1}\), and the diameter of the internal surface of the ducted stator is 2 \(r_{2}\). During the investigation of the radial gap, the diameter of the internal surface of the stator of the duct is kept fixed. However, the external diameter of the rim is varied to obtain different radial gap geometric parameters. Throughout this variation process, the axial gap is kept constant at 2 mm; to acquire different axial gap geometric parameters, when analyzing the axial gap, vary the distance between the gap’s inlet and outlet while maintaining the radial gap’s constant value of 3 mm. Table 1 summarizes the different gap geometric parameter cases in the present study. Gap-case 3 is the same as gap case 11, which is used as an object for gap flow calculation with/without the pressure difference.

Fig. 1
figure 1

IMP thruster calculation model

Full size image
Table 1 Varied radial and axial gap geometry (unit: mm)
Full size table

2.2 Basic governing equations and gap model

Considering that the IMP thruster inlet environment is a three-dimensional incompressible fluid, this paper proposes to use the method based on the Reynolds-averaged Navier–Stokes equations (RANS equations) for the computational domain to calculate the numerical simulation [36]. The governing equations are as follows:

The continuity equation:

$$\frac{\partial \rho }{{\partial t}} + \frac{{\partial \left( {\rho u_{i} } \right)}}{{\partial x_{i} }} = 0.$$
(1)

The momentum equation:

$$\frac{\partial }{\partial t}\left( {\rho u_{i} } \right) + \frac{{\partial \left( {\rho u_{i} u_{j} } \right)}}{{\partial x_{j} }} = - \frac{\partial p}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left[ {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \rho \overline{{u_{i}^{\prime } u_{j}^{\prime } }} } \right] + S_{j} ,$$
(2)

where \(u_{i}\) and \(u_{j}\) represent the mean velocity components (\(j\) = 1, 2, 3, standing for the component in the \(x,y,z\) direction), \(x_{i}\) and \(x_{j}\) represent the position vectors in tensor notation, \(\rho\) is the fluid density, \(t\) is the physical time, \(p\) is the time-averaged pressure, and \(S_{j}\) is the source term.

\(\rho \overline{{u_{i}^{\prime } u_{j}^{\prime } }}\) is found in the N–S equation after time-averaging, which is an additional unknown variable, In addition to the original 4 variables of \(u_{x} ,u_{y} ,u_{z} ,p\), etc., there are only 4 equations in the group of equations. Therefore, the equations are not enclosed, and new turbulence equations must be introduced to make the equations enclosed. In this paper, the SST \(k - \omega\) model is chosen, which combines the advantages of the standard \(k - \omega\) model, such as near-wall stability and external independence of the boundary layer, and will have better applicability in the calculation.

In the study by Bligen and Boulos [37] on the relationship between torque coefficients and torque in different turbulence models, empirical equations for frictional torque were proposed for three different types of cylinders: homoclinic cylinders, internally rotating cylinders, and externally stationary cylinders. The frictional torque coefficients for the turbulent state are divided into two parts based on the magnitude of the Reynolds number:

$$C_{{\text{M}}} = 1.03\left( {h/r_{1} } \right)^{0.3} {\text{Re}}^{ - 0.5} \left( {400\langle {\text{Re}} \langle 10000} \right),$$
(3)
$$C_{{\text{M}}} = 0.065\left( {h/r_{1} } \right)^{0.3} {\text{Re}}^{ - 0.2} \left( {{\text{Re}} \rangle 10000} \right),$$
(4)
$$C_{{\text{M}}} = {{\text{M}} \mathord{\left/ {\vphantom {{\text{M}} {0.5\pi \rho \omega^{2} }}} \right. \kern-0pt} {0.5\pi \rho \omega^{2} }}r_{1}^{4} h,$$
(5)

where \(h\),\(r_{1}\) as shown in Fig. 1, \({\text{Re}} = {{\rho \omega r_{1} h} \mathord{\left/ {\vphantom {{\rho \omega r_{1} h} \mu }} \right. \kern-0pt} \mu }\) is the radial gap Reynolds number, \(\mu\) is the dynamic viscosity, \(\rho\) is the fluid density, \(\omega\) is the angular acceleration, and \(M\) is the friction torque on the external surface of the inner rotating cylinder.

In order to further study the friction torque of homoclinic cylinders, internally rotating cylinders, and externally stationary cylinders, Daily and Nece [38] carried out a series of experiments to study how the torque varies with the axial gap ratio, and the results showed that the friction torque is only related to the gap ratio and the Reynolds numbers, and that the turbulence state can be classified into mixed laminar, separated laminar, and mixed turbulence and separated turbulence under a certain axial gap ratio. When the axial gap ratio is \(l/r_{1} \rangle 0.05\), the flow state in the gap is separated laminar or turbulent and when the axial gap ratio is \(0.01\langle l/r_{1} \langle 0.05\). The gap flow state is mixed turbulent, when the friction torque coefficient of the inlet and outlet end face is

$$C_{{\text{M}}} = 0.08\left( {l/r_{1} } \right)^{{ - {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0pt} 6}}} {\text{Re}}_{{\text{r}}}^{ - 0.25} ,$$
(6)
$$C_{{\text{M}}} = {{2M} \mathord{\left/ {\vphantom {{2M} {\rho \omega^{2} }}} \right. \kern-0pt} {\rho \omega^{2} }}r_{1}^{5} ,$$
(7)

where \(l/r_{1}\) is the axial gap ratio, \({\text{Re}}_{r} = {{r_{1} } \mathord{\left/ {\vphantom {{r_{1} } \mu }} \right. \kern-0pt} \mu }\) is the axial gap Reynolds number and \({\text{M}}\) is the friction torque of the end face.

3 Verification of simulation methods

3.1 Numerical method validation

To verify the correctness of the numerical calculation model as well as the computational mesh, the axial and radial gaps of 2 mm, respectively, are calculated first. According to the above gap models, it is found that the flow state within the gap of the studied parametric model is mixed turbulence, considering the realistic situation, it is necessary to refine the gap to ensure the correctness of the calculation results. There are three different \(y^{ + }\) of grids of 0.1, 1, and 30, which are generated according to the grid convergence principle. In general, for high Reynolds number models (e.g., k-Epsilon model, Reynolds stress model, etc.), \(y^{{ + }}\) is generally better to be close to 30, and for low Reynolds number models (e.g., \(k - \omega\) model, SA model, LES, etc.), it is better to be close to 1. Therefore, in the estimation of the first layer of the mesh, it is usually taken to be either 30 or 1, according to the turbulence model chosen to be used for the estimation. The circumferential velocity in the radial gap at the center of the rim is obtained in these three grids, as shown in Fig. 2, when\((r - r_{1} )/(r_{2} - r_{1} ) < 0.6\), the circumferential velocities in the radial gap at \(y^{ + }\) = 0.1 and\(y^{ + }\) = 1 are not much different, in addition to the flow model selected in this paper, so \(y^{ + }\) = 1 is selected as the grid for calculation.

Fig. 2
figure 2

Effect of grid on angular velocity in radial gap

Full size image

The circumferential velocity within the radial gap at the center of the rim when the axial gap is 3, 2, and 1 mm, respectively, for the radial gap fixed at 2 mm is also calculated, and these results are compared with Busse’s [39] empirical formulae as shown in Fig. 3, and it can be found that the calculated angular velocities match Busse’s empirical formulas better, which indicates that the numerical model in this paper is practicable. Many publications have demonstrated the benefits of using this turbulence model on propellers or pumps [2, 40,41,42].

Fig. 3
figure 3

Angular velocity distribution in radial gap

Full size image

3.2 Grid division

Based on the physical challenges investigated in this study, the computational domain is divided into three parts: the stator subsystem, the rotor system, and the external flow field. The rotor system is the rotating domain, while the stator system is the static domain. A flow field from the outside is incorporated in both systems. The interaction between the two regions is simulated using the slip grid technique. To improve the realism of the numerical computation, this study adopts a cylindrical region coaxial with the pump jet as the calculation domain, as illustrated in Fig. 4. The IMP thruster’s rotor has a maximum diameter of D. The computational domain of the external flow field has inlet and outlet boundaries that are 3D and 6D, respectively, from the rotor. The exterior flow field has a diameter of 6D.

Fig. 4
figure 4

Computational domain model

Full size image

The structure of the IMP thruster divides it into blocks, where a body-fitted grid meshes the impeller blade and guide vane. The structural grid divides the remaining sub-blocks, which are subsequently connected into the overall grid system [43]. It is vital to make sure that the mesh is continuous and smooth at the interface between the sub-blocks when the mesh is connected. Figure 5 displays the grid for each block, Fig. 6 displays the overall computing area grid, and the total number of grid nodes in the computing domain is 3,605,181.

Fig. 5
figure 5

Spatial blocking grid

Full size image
Fig. 6
figure 6

The overall grid of the calculation area

Full size image

When meshing, the axial and radial gaps of the IMP thruster must be considered. The structured grid, in which the initial layer of the air gap wall is 0.008 mm thick and there is a relative rise of 120% between succeeding layers of mesh, can be used to finish the grid processing of the air gap range (see Fig. 7). The pump spray wall’s maximum y+ value of 45.8 satisfies the relevant turbulence model parameters.

Fig. 7
figure 7

Rotor and air gap wall grid

Full size image

3.3 Grid independence verification

Verifying the mesh’s irrelevance is necessary to ensure the precision and correctness of the grid quality [41]. Five grid sets result from increasing the number of boundary layer nodes: 1.76 million, 3.6 million, 4.9 million, 6.5 million, and 8.9 million. The most appropriate number of estimated domain grids is determined by evaluating the thrust coefficient, torque coefficient, and propulsion efficiency of various numbers of grids under design parameters. To aid in the examination of the computation outcomes, the pertinent physical quantities are elucidated as follows: speed ratio \(J = {v \mathord{\left/ {\vphantom {v {(nD)}}} \right. \kern-0pt} {(nD)}},\) rotor thrust coefficient \({\rm K}_{T} = {T \mathord{\left/ {\vphantom {T {\left( {\rho n^{2} D^{4} } \right)}}} \right. \kern-0pt} {\left( {\rho n^{2} D^{4} } \right)}},\) rotor torque coefficient \({\rm K}_{{\text{Q}}} = {{\text{Q}} \mathord{\left/ {\vphantom {{\text{Q}} {\left( {\rho n^{2} D^{5} } \right)}}} \right. \kern-0pt} {\left( {\rho n^{2} D^{5} } \right)}}\) and propulsion efficiency \(\eta = \left( {{{{\rm K}_{{\text{T}}} } \mathord{\left/ {\vphantom {{{\rm K}_{{\text{T}}} } {{\rm K}_{{\text{Q}}} }}} \right. \kern-0pt} {{\rm K}_{{\text{Q}}} }}} \right) * \left( {{J \mathord{\left/ {\vphantom {J {2\pi }}} \right. \kern-0pt} {2\pi }}} \right)\). Among them \(v\) is the incoming flow velocity, \(n\) is the rotor rotating speed, D is the rotor diameter, \({\text{T}}\) is the rotor thrust and \({\text{Q}}\) is the rotor torque.

Table 2 shows that the propulsion efficiency changes very little and tends to remain constant as the number of grid nodes increases. Therefore, 3,605,181 grid nodes were chosen for the numerical analysis in this research based on the computational efficiency and resource usage.

Table 2 Grid independence verification
Full size table

3.4 Boundary conditions

Reasonable boundary conditions need to be established to generate numerical simulations of the gap flow performance of IMP thrusters. Among the boundary conditions are:

  • 1) Inlet: inlet with velocity.

  • 2) Outlet: operating pressure of 0 Pa for the pressure outlet.

  • 3) No slide wall: hub, duct, rotor, and stator blades are all subject to no slip wall requirements.

  • 4) Free slip wall: the wall is imposed at the cylindrical domain’s side surface.

ANSYS Fluent software is used to numerically simulate the IMP thruster. The three-dimensional flow field is solved using the RANS method, and the SST \(k - \omega\) turbulence model and Z-G-B cavitation model are integrated for closure. The finite-volume method (FVM) is used to discretize the system of equations. The basic idea is to create a grid within the calculation area and surround each grid point with a non-overlapping control volume. The control equations, or differential equations to be solved, are then integrated over each control volume to produce a set of discrete equations. The SIMPLEC algorithm is used to handle the coupling between speed and pressure. It is a pressure-based separation algorithm that can be applied to most flow issues and helps to increase the stability of the iterative process. Temporal discretization is used in first-order Eulerian post-interpolation format, while spatial discretization is performed in high-resolution hybrid differential format. To accelerate the numerical simulations, the computational model is first numerically simulated with steady flow non-cavitation. Then, the unsteady flow cavitation numerical simulations use the steady flow non-cavitation numerical calculations’ results as initial values.

4 Results and discussion

4.1 Pressure difference impact on the gap’s flow field

The gap variation cases listed in Table 1 were calculated with/without pressure difference, respectively, and the gap flow in the YOZ plane with/without pressure difference is shown in Figs. 8 and 9, respectively. In the case of no pressure difference, there is a stable gap flow in the radial gap. At axial gaps with more than 10 mm, there are Taylor vortices in the before and after axial gaps. In the case of no pressure difference, before and after the axial gap each forms an eddy, this is due to the rim surface boundary layer fluid by the centrifugal force flowing outward, the duct wall surface boundary layer of the fluid to the rim surface boundary layer compensation, thus forming a clear eddy, and this eddy “squeezes” the Taylor vortex in the radial gap.

Fig. 8
figure 8figure 8

Velocity (m/s) distribution in Case of 6–1 from top to bottom (left: non-pressure difference; right: pressure difference)

Full size image
Fig. 9
figure 9figure 9

Velocity (m/s) distribution in Case of 12–7 from top to bottom (left: non-pressure difference; right: pressure difference)

Full size image

In the case of the rotating blade, there is a pressure difference between the inlet and outlet ends of the axial gap due to the suction effect, and it can be observed that the flow direction in the gap is opposite to that of the inflow, forming an obvious flow from the outlet end to the inlet end, suppressing the Taylor vortex in the radial gap, and the vortex movement in the radial gap is weakened or even disappeared. This can be indicated as a higher pressure at the downstream gap opening than at the upstream gap opening because the main flow is pressurized by the rotating blades, as shown in Fig. 10. When the propeller is operating, the pressure difference between the two sides of the paddle disk surface causes the eddy flow region in the axial gap to become smaller for a time, but as the axial or radial gap increases, the eddy flow is still formed in the front and rear axial gaps, and the return flow region at the outlet end of the axial gap becomes larger as well.

Fig. 10
figure 10

The pressure distribution of the flow field in Case of 3/11

Full size image

4.2 Effect of gap geometry on rim torque in the presence of the pressure difference

In this paper, the effect of radial and axial gaps on the rim torque when they are varied individually is calculated in the case of pressure difference, and the radial and axial gap schemes are shown in Table 1. The effect of radial gap thickness and axial gap width on the torque of the external surface and front and rear end faces of the rim when they are changed separately is shown in Fig. 11. CM1 is the friction torque coefficient of the external surface of the rim, and CM2 is the friction torque coefficient of the front and rear end faces of the rim.

Fig. 11
figure 11

Torques of the rim varying with gap heights (left: radial gap; right: axial gap)

Full size image

Figure 11 shows that the friction torque coefficient on the external surface of the rim increases with the increase of the radial gap ratio, which agrees with the trend of the empirical equation of Bilgen and Boulos. The friction torque coefficient of the rim end face is almost unchanged with the increase of radial gap ratio, indicating that the change of radial gap ratio has almost no effect on the friction torque coefficient of the rim end face, which is inconsistent with the trend of the formula of the friction torque coefficient of the inner circular circle in the shell because the empirical formula does not take into account the pressure difference. The friction torque coefficient on the outer surface of the rim is maximum when the gap ratio increases to infinity. The torque coefficient of the outer surface of the rim is independent of the change in the axial gap, while the torque coefficient of the rim end face decreases with the increase in the axial gap. Therefore, in the case of the pressure difference, when the rim length is fixed, the torque coefficient of the rim can be reduced by decreasing the radial or increasing the axial gap ratio, or by increasing the Re and decreasing the flow in the gap.

4.3 Effect of gap geometry on hydrodynamics in the presence of the pressure difference

4.3.1 Variation of radial gap parameters

Figure 12 shows the hydrodynamic characteristics of the IMP thruster at different radial gap geometry, for presentation purpose, where the torque coefficient is shown in their absolute values, the rim thrust, and torque coefficients are relatively low and have been ignored. The \(\eta\) reduces then increases gradually as radial gap grows. When the radial gap size is 2 mm, the efficiency is at its minimum. The KT (thrust coefficient) of IMP thruster increases at the radial gap = 1.6 mm, but the KQ (torque coefficient) rises even more, which leads to a decrease in \(\eta\) instead. Through specifically examining the individual components of thrust and torque, as the radial gap grows, all of stator thrust coefficients (KTs), duct thrust coefficients (KTd), blade torque coefficients (KQb), and stator torque coefficients (KQs) do not show a significant variable trend.

Fig. 12
figure 12

Hydrodynamic characteristics of the IMP thruster at different radial gap geometry

Full size image

In Fig. 13, 3D pathlines in the gap are shown at different radial gap geometries. To simplify the presentation, only the pathlines passing through four feature points (I, II, III, and IV) are plotted. These four points are uniformly distributed at 90° intervals and are situated at the inlet of the gap, as depicted in Fig. 14. From Fig. 13, it is evident that the flow is influenced by the rotational motion of the rotor blade, resulting in an oblique angle of entry into the gap at the entrance. The flow within the gap is maintained in an inclined direction as it enters the gap due to the rotational motion of the rotor blade. It is known that fluid particles move a greater distance along a unidirectional pathline within the same time interval, it means they have a higher velocity. When the fluid particles are compared in Fig. 13a, b, and c, as the radial gap decreases, it is observed that the fluid particle leaves the gap earlier, and the relative angle between the gap outlet and the inlet is larger. This is because the reduced radial gap restricts the space for the fluid particles to flow, leading to a quicker exit from the gap region. This indicates that decreasing the radial gap reduces the decelerating effect of the gap corner on the particles. In other words, a smaller radial gap minimizes flow disturbances and promotes smoother flow development within the gap.

Fig. 13
figure 13

3D pathlines in the gap at different radial gap: a 2 mm, b 3 mm, c 5 mm (unit: m/s)

Full size image
Fig. 14
figure 14

Location of the 4 fluid particles

Full size image

To further observe the effect of the gap on the flow near the blade, three cross-sections, named sections A, B, and C, were cut at the inlet, middle, and outlet of the gap, as shown in Fig. 15. Figure 15 displays the axial velocities distribution in the three cross-sections at different radial gaps. Due to the rotation of the blades, there exists a certain phase difference in the flow field characteristics among the three cross-sections. The modification of the radial gap has an impact on the axial velocity distribution in sections A and C. However, the effect of the gap is less apparent in section B due to the dominant influence of the rotational motion of the blade. As the radial gap size increases, the axial flow velocity at the blade margin also increases, as evident in cross-section B. The shedding vortex was observed at the blade tip of the IMP thruster, as shown in cross-section C. Figure 16 depicts the distribution of gap vortices and axial vorticity in the wake field at various radial gaps. The vortex generated by the blade tip of the IMP thruster is clearly observed and validated in the results. In addition, the presence of gap vortices leaking out of the gap outlet can also be observed. Every condition evidently displays a tip vortex region, a blade shed vortex region, and a hub vortex region. Furthermore, it has been found that as the radial gap grows, the vortex strength decreases. At the tip vortex region, a shear layer flow emerges when the viscous fluid passes the surface of the duct, resulting in the shedding of several vortical structures from the trailing edge of the duct. In the tip region, vortical structures are deformed by the interaction between solid surfaces such as blades and duct. These vortex distributions are important to produce the thrust of the duct. This agrees with the trend of duct thrust coefficients (KTd) variation of the IMP thruster (see Fig. 12), indicating that the change of the radial gap on the gap vortex is one of the causes of the duct thrust. It is clearly seen that the vortical structures near the duct’s internal surface are more complicated at the low radial gap, under the opposite condition, the vortex deforms because of a stronger interaction between the propeller and duct surface, and therefore, the energy distribution is changed. The circumferential flow around the duct is intensified, and thus, propulsion efficiency is augmented, this agrees with the trend of efficiency variation of the IMP thruster (see Fig. 12).

Fig. 15
figure 15

The dimensionless axial velocity (m/s) contour distribution at different radial gap (from left to right: 2 mm, 3 mm, 5 mm; from top to bottom: cross-section A, B, C)

Full size image
Fig. 16
figure 16

Gap vortex distribution and axial vorticity visualized with an iso-surface of the instantaneous Q-criterion in the wake field with different radial gap. (From top to bottom: 2 mm, 3 mm, 5 mm; from left to right: gap vortex distribution Q = 0.11/s, axial vorticity)

Full size image

4.3.2 Variation of axial gap parameters

Figure 17 shows the hydrodynamic characteristics of the IMP thruster at different axial gap geometry, for presentation purpose, where the torque coefficient is shown in their absolute values, and the rim thrust, and torque coefficients are relatively low and have been ignored. The \(\eta\) reduces, then increases, and then reduces gradually as the axial gap grows. When the axial gap size is 2 mm, the efficiency is at its minimum. When the axial gap size is 4 mm, the efficiency is at its maximum. Through specifically examining the individual components of thrust and torque, it can be seen that as the axial gap grows, all of the blade thrust coefficients (KTb), and duct thrust coefficients (KTd) exhibit the same trend of change as \(\eta\).The blade torque coefficients (KQb) and stator torque coefficients (KQs) exhibit an opposite trend to \(\eta\).

Fig. 17
figure 17

Hydrodynamic characteristics of the IMP thruster at different axial gap geometry

Full size image

Figure 18 shows 3D pathlines in the gap at different axial gap geometry. When the fluid particles are compared in Fig. 18a, b, and c, as the axial gap decreases, the movement of fluid particles is the same as the situation of fluid particles under the radial gap.

Fig. 18
figure 18

3D pathlines in the gap at different axial gap: a 2 mm, b 6 mm, c 10 mm (unit: m/s)

Full size image

Figure 18 displays the axial velocities distribution in the three cross-sections at different axial gaps. As a result of the rotation of the blades, there is a certain phase difference in the flow field characteristics of the three cross-sections. It is found that the modification of the radial gap influences the axial velocity distribution in all sections. As the axial gap size increases, the axial flow velocity at the rim increases, as shown in cross-section C (see Fig. 19). The shedding vortex was observed at the blade tip of the IMP thruster, as shown in cross-section B and C. The vorticity distribution in the wake field at different axial gaps is illustrated in Fig. 20. The vortex generated by the blade tip of the IMP thruster is well observed and verified. The gap vortex leaking out of the gap outlet can be also observed. Every condition displays a tip vortex region, a blade shed vortex region, and a hub vortex region. Furthermore, it has been found that the axial gap of 6 mm results in the strongest vortex strength. This agrees with the trend of duct thrust coefficients (KTd) variation of the IMP thruster (see Fig. 17), indicating that the change of the axial gap on the gap vortex is one of the causes of the duct thrust. It is clearly seen that the vortical structures near the duct internal surface are least complicated with an axial gap of 6 mm, this is also in agreement with the trend of efficiency variation of the IMP thruster (see Fig. 17).

Fig. 19
figure 19

The dimensionless axial velocity (m/s) contour distribution at different axial gap (from left to right: 2 mm, 6 mm, 10 mm; from top to bottom: cross-section A, B, C)

Full size image
Fig. 20
figure 20

Gap vortex distribution and axial vorticity visualized with an iso-surface of the instantaneous Q-criterion in the wake field with different axial gap. (From top to bottom: 2 mm, 6 mm, 10 mm; from left to right: Gap vortex distribution Q = 0.11/s, axial vorticity)

Full size image

Subsequently, the impacts of different gap dimensions are compared by quantitatively analyzing the pressure and velocity variation at the gap inlet and outlet. The locations of the monitoring points (P1 ~ P10, corresponding to the angles, respectively: 0°, 10°, 20°, 30°, 40°, 50°, 60°, 70°, 80°, 90°) located at the quarter-gap inlet and outlet are displayed in Fig. 21. Figure 22 depicts the Cp of the gap inlet and outlet as well as the relative Cp of the two. At the gap inlet, the varying trends of Cp at different gaps are found to be consistent. Cp reaches a maximum at \(\varphi\) = 50° at different radial gaps and reaches a maximum (\(\varphi\) is equal to approximately 70°) at different axial gaps. At the gap outlet, the varying trends of Cp at different gaps are found to be consistent (beyond at axial gap = 2 mm). With increasing radial gaps dimensions beyond radial gap = 1.6 mm and axial gap = 2 mm, the Cpc increases at the gap outlet and inlet. This agrees with the trend of efficiency variation of the IMP thruster (see Figs. 8 and 13), indicating that the change of the gap dimensions on the pressure is one of the causes of the efficiency variation. Since the relative pressure coefficient is the difference between the inlet and outlet, the relative Cp is lowest at radial gap = 5 mm (axial gap = 4 mm) and largest at radial gap = 2 mm (axial gap = 3 mm). This suggests that reducing the relative Cp at the gap inlet and outlet is beneficial for improving the efficiency of the IMP thruster. Overall, the relative Cp for different axial gap dimensions is larger than the relative Cp for different radial gap dimensions, indicating a greater effect of the axial gap on the efficiency of the IMP thruster.

Fig. 21
figure 21

Positions of the monitoring points located at the quarter-gap inlet and outlet

Full size image
Fig. 22
figure 22

Pressure coefficient (Cp) curves at different monitoring points at different gaps (from top to bottom: Cp of the gap inlet, Cp of the gap outlet, relative Cp between the inlet and outlet of the gap; from left to right: at different radial gaps, at different axial gaps)

Full size image

Figure 23 demonstrates the flow velocities of different monitoring points at different radial gaps between the gap inlet and outlet. It is shown that the flow velocities at the gap outlet located in front of the blade are almost unaffected by the blade rotational flow, while the flow velocities at the gap inlet located behind the blade show a tendency to rise and then fall. The variation pattern of the UX at different radial gaps on cross-sections is proportional to that of KT, as shown in Fig. 12. When the radial gap is 5 mm, UX and KT is the largest. As a result, it is suggested that the UX be increased at the gap inlet to increase the IMP thruster’s thrust. The variation pattern of the combined velocity (\(U_{{{\text{YZ}}}} = \sqrt {U_{{\text{Y}}}^{2} + U_{{\text{Z}}}^{2} }\)) at different radial gaps on cross-sections is proportional to that of KQ, as shown in Fig. 12. When radial gap = 4 mm, UYZ is the largest and KQ is the largest. As a result, it is suggested that the UYZ be increased at the gap outlet to increase the IMP thruster’s torque.

Fig. 23
figure 23

Velocities of different monitoring points at different radial gaps (from top to bottom: UX, UYZ; from left to right: gap inlet, gap outlet)

Full size image

Figure 24 demonstrates the flow velocities of different monitoring points at different axial gaps between the gap inlet and outlet. The variation pattern of the UX at different axial gaps on cross-sections is proportional to that of KT, as shown in Fig. 13. When the axial gap is 6 mm, UX and KT is the largest. As a result, it is suggested that the UX be increased at the gap inlet to increase the IMP thruster’s thrust. The variation pattern of the combined velocity (\(U_{{{\text{YZ}}}} = \sqrt {U_{{\text{Y}}}^{{2}} + U_{{\text{Z}}}^{2} }\)) at different axial gaps on cross-sections is proportional to that of \(\eta\), as shown in Fig. 17. When the axial gap = 4 mm, UYZ is the largest and \(\eta\) is the largest. As a result, it is suggested that the UYZ be increased at the gap outlet to increase the IMP thruster’s \(\eta\).

Fig. 24
figure 24

Velocities of different monitoring points at different axial gaps (from top to bottom: UX, UYZ; from left to right: gap inlet, gap outlet)

Full size image

5 Conclusions

In this paper, the gap flow was decomposed into three regions, external, internal surfaces, and the front-rear end faces of the rim. Gap flow and friction torque assessment methods are reviewed, hydrodynamic performance for different gaps variation cases is calculated using numerical methods, Comparisons are made between the impacts on gap flow with and without the pressure difference, and the effects of changing parameter values, such as radial gap and axial gap, on hydrodynamic forces and friction torque are analyzed. The following are the conclusions generated from the numerical investigation:

  • (1) The pressure difference has a significant effect on the gap flow pattern and changes the flow direction of the gap flow. The fluid morphology and the formation of vortices in the axial and radial gaps are both affected differently during the presence or absence of the pressure difference. It is demonstrated that the impact of the pressure difference cannot be disregarded when studying the gap flow.

  • (2) In the case of the pressure difference, the friction torque coefficient of the outer surface of the rim increases with the increase of the radial gap ratio, and the torque coefficient of the end face decreases with the increase of the axial gap. When the length of the rim is fixed, reducing the radial gap ratio, increasing the axial gap ratio, or increasing Re, etc. can reduce the friction torque coefficient of the rim.

  • (3) Under the condition of different radial gaps, decreasing the radial gap is beneficial to the development of the gap flow. As the radial gap increases, the axial flow velocity at the blade margin increases. It is also observed that the vortex strength decreases with the increase of the radial gap. Indicating that the change of the radial gap on the gap vortex is one of the causes of the duct thrust and \(\eta\).

  • (4) When different axial gaps are carried out, the efficiency is lowest when the axial gap is 2 mm. The efficiency is greatest when the axial gap is 4 mm. It is also discovered that with an axial gap of 6 mm, the vortex strength is the greatest. This agrees with the trend of duct thrust coefficients (KTd) variation of the IMP thruster.

  • (5) Reducing the relative pressure at the gap inlet and outlet is beneficial for improving the efficiency of the IMP thruster. And the relative Cp for different axial gaps dimensions is larger than the relative Cp for different radial gap dimensions, indicating a greater effect of the axial gap on the efficiency of the IMP thruster. The change in pressure caused by varying gap dimensions is one of the factors that affect efficiency. The non-uniform flow velocity at the gap inlet and outlet is another factor contributing to the decreased efficiency.