Hydrodynamic optimization of ship’s hull-propeller system under multiple operating conditions using MOEA/D

Abstract

The aim of this paper is to develop a software, namely HPS-MOP, based on the multi-level and multi-point hydrodynamic optimization of hull-propeller systems during early-stage ship design. An efficient multi-objective evolutionary algorithm is used as the optimization technique to minimize the effective power and maximize the propulsive efficiency with considering some design constraints. Michell’s integral and lifting line theory are, respectively, employed for the hydrodynamic analysis of hulls and propellers in the first-level optimization. At the second level, the boundary element method is applied as a strong tool to predict the hydrodynamic performance of hulls and propellers. The ship added resistance in head waves is estimated using a fast and satisfactory semi-empirical formula. The effectiveness of the approach is illustrated by comparing the optimized results with initial ones in the optimization of series 60 hull form with DTMB P4118 single propeller and S175 hull form with KP505 twin-propeller as the original models.

1 Introduction

Minimizing effective power and maximizing propulsive efficiency of ships are caused a significant reduction in fuel consumption that is one of the main concerns of ship owners and designers. Therefore, the hydrodynamic optimization of ships’ hull-propeller system (HPS), in actual seas is the best way to increase powering performance and decrease operational costs in early-stage ship design. There exists two main factors in the hydrodynamic design optimization of marine systems. The first factor is simultaneously considering all components of the system influencing objective function(s) and the second one is selecting a less-time consuming solver with satisfactory accuracy. In the ship design process, these two factors must be taken for conducting a reasonable optimization into consideration. The well-known traditional way of ship design, called design spiral, is an iterative and sequential process in which the hull and propeller are designed separately. The design spiral does not take into account the interaction between the hull and propeller as iteration progress. Therefore, simultaneously optimizing the hull and propeller as an integrated system yields a more optimal result than the traditional one.

Often different methods can be used to evaluate the quality of a design. Robust and practical numerical methods have been employed as a replacement for the experimental tests. There is a trade-off between the computational time and the accuracy of numerical methods. In this point of view, a simple, fast technique is utilized in early stages of ship design and as the design progresses, a more accurate solver is used for solving the problem. Usually, the hydrodynamic optimization algorithm calls the numerical solver many times and that is why balancing between the computational time and solver accuracy. Among computational fluid dynamic (CFD) techniques for calculating ship resistance, Michell’s thin ship theory is a simple, fast technique and potential-based boundary element method (BEM) is a more accurate, yet more time consuming method than the former one. Michell’s integral and BEM can be, respectively, used in the conceptual and preliminary phases of ship design. The main advantage of BEM is its computational efficiency that decreases the dimensions of problems by one, i.e., only line integrals are required in 2D problems and surface integrals in 3D problems, from which a smaller system of equations will be generated. Moreover, this technique provides enough accurate solutions which make it a preferred computational approach for preliminary ship design.

Many researchers have studied on the optimization of ships’ hull or propeller among which Campana et al. [1] presented two different Simulation-Based Design, SBD, versions to optimize the total resistance of the model 5415 advancing in calm water. Several techniques were used in their study including Genetic Algorithm and a Derivative-based variable-fidelity approach as optimizer, NURBS and FFD tools as geometry modeler, RANS-based CFDSHIP-Iowa and MGShip codes as numerical analyzer. Zakerdoost et al. [2] presented a methodology for the optimization of Series 60 hull form in calm water from the total drag reduction point of view. The Michell’s theory was utilized to estimate wave drag and the evolution strategy to minimize the single objective function. Vernengo et al. [3] performed a hydrodynamic optimization of a Semi-SWATH ferry based on a 3D Rankine source panel method for analysis of steady wave resistance and seakeeping problem, and a multi-objective genetic algorithm as optimizer. Grigoropoulos et al. [4] applied potential flow and Reynolds-averaged Navier–Stokes equation solvers, global modification functions, control point-based methods, and parametric modelling, particle swarm optimization, sequential quadratic programming, genetic and evolutionary algorithms to optimize hull-form and propeller of the DTMB 5415 model for significant conditions, based on actual missions at sea. A methodology to optimize bow hull form of a bulk carrier in calm water and waves presented by Yu et al. [5]. They applied multi-objective optimization techniques to minimize the wave-making resistance in calm water and the added resistance in regular head waves. The Neumann–Michell theory was used to evaluate the wave resistance. In another study [6], hull-form stochastic optimization techniques were presented and evaluated for resistance reduction and operational efficiency, addressing stochastic sea state and operations. The computational cost analysis of the optimization procedure was carried out by comparison of four problems, from stochastic most general to deterministic least general and the results showed that the multi-objective deterministic optimization for resistance and motions was the most efficient problem. Regarding to the propeller optimization, there are many published articles for different ships. The propeller of a large container ship was optimized by Kuiper [7] to maximize propeller efficiency at a certain desired speed. Xie [8] implemented a multi-objective propeller optimization program to simultaneously maximize propeller efficiency and thrust coefficient at a single design speed. The well-known NSGA-II approach was used to approximate the Pareto solutions of the B-series propeller optimization. Mirjalili et al. [9] developed a multi-objective particle swarm optimization to maximize the efficiency and minimize the cavitation of marine propellers simultaneously. They employed the shape parameters and the number of propeller blades and operating conditions as design variables. Kamarlouei et al. [10] optimized marine propellers using evolution strategies based on minimizing cavitation, highest efficiency and acceptable blade strength. In the recent years, some researchers were dedicated to reducing the lifetime fuel consumption (LFC). The thin ship theory and regression relations were used by Nelson et al. [11] to minimize LFC of an HPS over its operational life. Ghassemi and Zakerdoost [12] applied blade element theory, Michell’s theory and NSGA-II algorithm to optimize an HPS based on LFC considering its mission profile.

The focus of this work is to generate a useful software based on the bi-stage multi-point optimization of HPSs using an efficient multi-objective evolutionary algorithm based on decomposition in early-stage ship design. The ultimate objective is to design an HPS with the minimum effective power and maximum propulsive efficiency and then, enhancing the conceptual/preliminary design process. The remainder of this paper is planned as follows: the forthcoming section discusses the numerical methods and the basic governing mathematical formulation for calculating hydrodynamic performances. Next, an explanation of the optimization technique and multi-level optimization procedure at two steps is given. The results and discussion are then presented. The last section concludes this research with the key findings.

2 Formulation of hydrodynamic analysis

Numerical methods for the hydrodynamic analysis of an HPS have different accuracy and time consumption. Michell’s theory and lifting line theory are two fast methods for calculating the ship wave-making resistance and the forces acting on propellers, respectively. These two theories are employed at the first level of the optimization algorithm as hydrodynamic solvers. BEM based on potential flow is another technique employed as a solver for the analysis of HPSs at the second level. Recently, potential-based BEM and its other versions have been widely used in various marine hydrodynamic problems [13, 14]. BEM has been more accurate, yet time consuming than the aforementioned theories. The ship added resistance is also estimated using an efficient and practical semi-empirical formula. Some mathematical relations of the formulas and the other three techniques are briefly presented.

2.1 Michell’s integral

The linearized thin ship theory of wave resistance was proposed by Michell [15]. This method represents the ship by a center-plane source distribution and develops an analytical solution for hull shapes based on the potential flow theory. The Michell’s thin ship theory is valid only under the condition that the slope of the hull surface relative to the center-plane is small (slender hull). Applying this approach to estimate the wave-making resistance shows a good agreement between predictions and experiments, especially at low Froude numbers [2]. Although the method overestimates the resistance and exaggerates humps and hollows in the wave-making resistance curve, their location is well predicted. Based on the energy flux far from the ship, the equation for the wave resistance is defined as follows:

$$R_{\text{W}} = \frac{\pi }{2}\rho U^{2} \int\limits_{ - \pi /2}^{\pi /2} {\left| {A\left( \theta \right)} \right|^{2} } \cos^{3} \left( \theta \right) {\text{d}}\theta ,$$

(1)

where $A\left( \theta \right)$ is the amplitude function of the wave component travelling at angle $\theta$. Working with the hull offsets $Y(x,z)$ is usually preferred over working with the slope of the offsets $Y_{x} (x,z)$; thus the amplitude function equation is integrated by parts including the transom stern:

$$\begin{aligned} A(\theta ) = - \frac{2i}{\pi }(k_{0} \sec^{2} \theta )^{2} \int_{ - \infty }^{0} {\int_{ - \infty }^{\infty } {Y(x,z)e^{{ik_{0} x\sec \theta }} e^{{k_{0} z\sec^{2} \theta }} {\text{d}}x{\text{d}}z} } \hfill \\ + \frac{2}{\pi }(k_{0} \sec^{3} \theta )\int_{ - \infty }^{0} {Y(x_{s} ,z)e^{{ik_{0} x_{s} \sec \theta }} e^{{k_{0} z\sec^{2} \theta }} {\text{d}}z} , \hfill \\ \end{aligned}$$

(2)

where $k_{0} = {g \mathord{\left/ {\vphantom {g {U^{2} }}} \right. \kern-0pt} {U^{2} }}$ is the wave number, g is the acceleration of gravity and $Y(x_{\text{s}} ,z)$ indicates the non-zero transom stern offsets. $A(\theta )$ is a property only of the body’s hull geometry (hull offsets).

2.2 Lifting line theory

The low-fidelity lifting line theory employed in this work for evaluating propeller performance was developed by Epps and Kimball [16]. This tool is valid for moderately loaded propellers and applies formulas developed in Wrench Jr [17]. In this technique, a lifting line is the representative of a propeller blade, with trailing vorticity aligned to the local flow velocity (i.e. the vector sum of free-stream plus induced velocity). The induced velocities are calculated by vortex lattice with helical trailing vortex filaments shed at discrete stations along the blade. The blade itself is modelled as discrete sections, having 2D section properties at each radius. Loads are estimated by integrating the 2D section loads over the blade span. The main limitation of the lifting line method is in the accuracy of the output blade geometry, so lifting surface geometry corrections were incorporated in the tool to account for finite-aspect-ratio effects. Figure 1 shows the velocities and forces on a 2D blade section [16]: $V_{\text{R}}$ is the total resultant inflow velocity as a result from the axial inflow $V_{\text{A}}$, and the induced axial and tangential velocities $u_{\text{a}}$ and $u_{t}$. $\phi$ and $\beta_{i}$ are the geometrical and hydrodynamical pitch angles, respectively.$\alpha$ is the angle of attack $\left( {\alpha = \phi \, - \beta_{i} } \right)$. $\omega$ is the angular velocity, $\varGamma$ is the circulation, $L = \rho V_{\text{R}} \varGamma$ is the inviscid lift force, and $D = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}\rho \left( {V_{\text{R}} } \right)^{2} C_{\text{D}} c$ is the viscous drag force, given the fluid density $\rho$, chord c, and drag coefficient C_D. A standard propeller vortex lattice model was used in this tool to compute the axial and tangential induced velocities. Assuming the Z blades are identical, then the thrust and torque are measured by

Fig. 1

Propeller velocity and force diagram

$$\begin{aligned} T = Z\int_{{R_{\text{h}} }}^{R} {\left[ {L\cos (\beta_{i} ) - D\sin (\beta_{i} )} \right]} {\kern 1pt} {\text{d}}r \hfill \\ Q = Z\int_{{R_{\text{h}} }}^{R} {\left[ {L\sin (\beta_{i} ) + D\cos (\beta_{i} )} \right]} {\kern 1pt} r{\text{d}}r, \hfill \\ \end{aligned}$$

(3)

where the integral domain R_h and R are the hub and tip radii, respectively. Finally, the propeller efficiency is defined as the ratio of the power consumed by the propeller to the useful power produced by the propeller:

$$\eta = \frac{{TV_{\text{A}} }}{Q\omega },$$

(4)

where $V_{\text{A}} = V_{\text{S}} (1 - w)$ is the advance velocity, $V_{\text{S}}$ is the ship speed and w is the wake factor. According to Eqs. 3 and 4 in the lifting line theory, we seek to develop a system of equations that directly results in the optimum circulation (loading) distribution and consequently efficiency. This solver applies the method of the Lagrange multiplier from variational calculus to solve the nonlinear system of equations iteratively.

2.3 Boundary element method (BEM)

The potential-based BEM technique is an efficient and applicable method for hydrodynamic analysis of hulls and propellers. The approach was validated by the second author in different literatures [18, 19]. Considering the Laplace equation, by means of which the flow around a body can be modelled, BEM is applied to estimate the velocity potential and then pressure,$P$, around HPSs. The wave-making resistance can then be obtained as:

$$R_{\text{W}} = \int_{{S_{\text{H}} }} {Pn_{x} {\text{d}}S} ,$$

(5)

where $S_{\text{H}}$ and $\vec{n}(n_{x} ,n_{y} ,n_{z} )$ are the hull wetted surface and the outward unit normal vector on $S_{\text{H}}$ respectively. Finally, the calm water resistance is defined as:

$$R_{\text{CW}} = (1 + k)R_{\text{F}} + R_{\text{W}} ,$$

(6)

where $R_{\text{F}}$ and k are the frictional resistance and form factor, respectively. Those parameters are determined by the ITTC’57 formulas and a fit of three data points taken from the research of Van Manen and Van Oossanen [20].

The total forces and moments acting on the propeller can be calculated by integrating the pressures over the all blades and hub surfaces, $S_{\text{P}}$. The total thrust and torque of propeller can be determined as

$$\begin{aligned} T = - Z\int_{{S_{\text{p}} }} {P\,} n_{x} {\text{d}}s - T_{\text{F}} \hfill \\ Q = - Z\int_{{S_{\text{p}} }} P \left( {n_{y} Z - n_{z} Y} \right){\text{d}}s + Q_{\text{F}} , \hfill \\ \end{aligned}$$

(7)

where $(X,Y,Z)$ is the coordinate of source point P and $Z$ is the number of propeller blades. To overcome the BEM’s shortcoming of not taking viscosity into account, the viscous elements, $T_{\text{F}}$ and $Q_{\text{F}}$, were calculated using the Prandtl–Schlichting law. Finally, the hydrodynamic coefficients of propellers (thrust and torque coefficients and efficiency) are defined as usual:

$$\begin{aligned} K_{\text{T}} = \frac{T}{{\rho N^{2} D^{4} }},\,\,\,\,K_{\text{Q}} = \frac{Q}{{\rho N^{2} D^{5} }}, \hfill \\ \eta_{\text{o}} = \frac{{K_{\text{T}} }}{{K_{\text{Q}} }}\frac{J}{2\pi },\,\,\,\,\,\,J = \frac{{V_{\text{A}} }}{ND} \hfill \\ \end{aligned}$$

(8)

Here, $J$ is the advance coefficient. $D$, $N$ and $\eta_{\text{o}}$ is the diameter, revolution rate and the open water efficiency of the propeller, respectively.

2.3.1 Cavitation

Cavitation phenomenon is one of the most important criteria in propeller design. Cavitation inception on each propeller panel can be determined by comparing the pressure coefficient and local cavitation number. Those parameters are defined as follows:

$$C_{\text{p}} (r) = \frac{{p(r) - \left( {p_{\text{a}} + \rho gh(r)} \right)}}{{0.5\rho \left( {V_{\text{R}} (r)} \right)^{2} }}$$

(9)

$$\sigma (r) = \frac{{p_{\text{a}} + \rho gh(r) - p_{\text{v}} }}{{0.5\rho \left( {V_{\text{R}} (r)} \right)^{2} }}$$

(10)

where $p_{\text{a}} = 101\;{\text{kPa}}$ is the atmospheric pressure, $V_{\text{R}} \left( { = \sqrt {(V_{\text{A}} + u_{\text{a}} )^{2} + (2\pi rn - u_{t} )^{2} } } \right)$ is the resultant velocity, h is the immersion depth on the propeller at radius r, and $p_{\text{v}} = 2500\;{\text{Pa}}$ is the vapour pressure. Comparing the definition of $\sigma$ and $C_{\text{p}}$, it is evident that if $\sigma \ge \left| {C_{\text{p}} } \right|$, then $p \ge p_{\text{v}}$ which means the pressure on the propeller surface is higher than the vapour pressure, so means that the cavitation is not occurred. If $\sigma < \left| {C_{\text{p}} } \right|$, the cavitation happens.

2.4 Added resistance in irregular head waves

The added resistance experienced by a ship under the influence of waves may be due to a number of causes. Two main parts of them considered here are: added resistance due to the motion of the ship, in particular heave and pitch motions and added resistance caused by the reflection or diffraction of the incident waves [21]. The former is usually dominated in the short wave region and the latter in the medium wave region.

Recently, Liu and Papanikolaou [22] developed a semi-empirical formula for predicting the added resistance of ships in regular head waves ($R_{\text{AW}}$). This practical approach has a good agreement with experimental results and is the most suitable method for optimization problems in which time is a valuable factor.

Considering the energy spectrum of the sea $S(w)\,$, mean added resistance $\bar{R}_{\text{AW}}$ of the ship, operating at a given speed in irregular head seas, $R_{\text{W}}$ can be predicted from the mean response curve $R(w) = {{R_{\text{AW}} } \mathord{\left/ {\vphantom {{R_{\text{AW}} } {\zeta_{\text{A}}^{2} }}} \right. \kern-0pt} {\zeta_{\text{A}}^{2} }}$, where $\zeta {}_{A}$ is the regular wave amplitude:

$$\bar{R}_{\text{AW}} = 2\int_{0}^{\infty } {R(w)S(w)\,{\text{d}}w} .$$

(11)

In this paper, $\bar{R}_{\text{AW}}$ is computed using ITTC spectrum for head sea.

2.5 Power and propulsive efficiency

After calculating the different components of ship resistance, the total resistance in waves may be expressed as follows:

$$R_{\text{T}} = R_{\text{CW}} + \bar{R}_{\text{AW}}$$

(12)

Then, the ship effective power at any operating condition can be determined as:

$$P_{\text{E}} = R_{\text{T}} V_{\text{S}}$$

(13)

The effective power is described as the power required to tow the ship through the water. In this study, one of the objective functions is defined based on the effective power. Another objective function in the optimization problem is a function of propulsive efficiency. The propulsive efficiency of the hull/propeller system performance forms an essential link between the effective power required to drive the vessel and the power delivered from the engine to the propeller:

$$\eta_{\text{P}} = \eta_{\text{H}} \eta_{\text{o}} \eta_{\text{R}} ,$$

(14)

where $\eta_{\text{H}}$ and $\eta_{\text{R}}$ are the hull efficiency and relative rotative efficiency, respectively. In this research, the relations for estimating the parameters including thrust deduction factor, wake fraction and thus the hull efficiency as well as the relative rotative efficiency are taken from the study of Carlton [23].

3 Optimization algorithm and design process

The methodology presented here is a kind of multi-level and multi-point optimization problems. Ship design is always a trade-off between different objectives and constraints, for example, in this work: minimize the effective power at any of its four operating conditions with keeping the displacement fixed and maximize the propulsive efficiency at any of those operating conditions with avoiding the cavitation phenomenon. Such design problems may be solved by an optimization algorithm that results in Pareto-optimal solutions among which the best design can be selected.

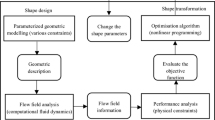
Generally speaking, the developed software consists of three main modules. The first module is related to the numerical methods for evaluating HPSs. The selection of the hydrodynamic solvers depends on the optimization level and whether it is the ship’s hull or propeller that is being evaluated. In the second module, MOEA/D-DRA is utilized as optimizer, which is briefly described in the next section. In the third module, the geometry modelling of ship hull and propeller shapes is based on Non-Uniform Rational B-Splines (NURBS) technique for allowing the variation of hull and propeller forms during the optimization process. The NURBS approach is a well-known model for geometric representations of 3D shapes due to its excellent properties, generality, and incorporation in international standards. Based on the selection of the hydrodynamic solvers, design variables and design constraints, the software procedure is divided into two levels.

3.1 Optimization technique

Evolutionary techniques for multi-objective optimization problems (MOPs) are currently gaining significant attention from researchers in various fields due to their effectiveness and robustness in searching for a set of trade-off solutions. There exist different strategies in traditional multi-objective optimization algorithms among which decomposition is a well-known one. However, the decomposition strategy was not widely used in MOPs until Zhang and Li [24] proposed the multi-objective evolutionary algorithm based on decomposition (MOEA/D). The new version of MOEA/D, i.e. MOEA/D with dynamical resource allocation (MOEA/D-DRA) [25], was developed and used to solve some benchmark functions with complicated Pareto set shapes. Moreover, in the unconstrained MOEA competition (CEC) 2009, MOEA/D-DRA ranked first on the list of 13 state-of-the-art MOEAs. MOEA/D-DRA is employed in this work to optimize and design HPSs which is an innovation in the application of this algorithm for hydrodynamic shape optimization. Besides, it is a population-based algorithm capable to escape from local optima. Other advantages of MOEA/D are simple to code, uniform distribution of final Pareto front and high computational efficiency [24, 26, 27]. MOEA/D combines an aggregation strategy, such as Tchebycheff approach, with MOEA to convert a MOP into N scalar optimization sub-problems and then each sub-problem in a collaborative manner. In this study, the parameter settings of the optimizer are presented in Table 1.

Table 1 Parameter settings of MOEA/D-DRA

It should be noted that, reproducibility of the results of an optimization algorithm is one of the main quality properties of an algorithm that have to be analysed before using in the field of applied sciences. Reproducibility is the capability of an algorithm to provide the same, or close to, solution by rerunning the algorithm with the same setup. The quality characteristics of the algorithm we have employed in our study have been analysed in the main reference [25].

3.2 Procedure of bi-level HPS optimization

The flowchart of the optimization procedure is demonstrated in Fig. 2. The first step is the definition of design variables and their bounds. The hull length to beam ratio (L/B), beam to draft ratio (B/d) and draft (d), propeller diameter (D), number of blades (Z) and pitch ratio (P/D) are considered as the design variables whose bounds are listed in Table 2. Latin Hypercube Sampling (LHS) technique is employed in the next step to create an initial population. After creating the initial population, the total resistance of the ships’ hull is evaluated at each iteration using coupled Michell’s theory and ITTC-57 correction line formula. The hydrodynamic performance of the ships’ propeller(s) is also calculated by utilizing lifting line theory. Moreover, the added resistance in head waves is estimated by using the efficient empirical formula, as described in Sect. 2.4. The operating propeller RPM at the design speed is obtained from the intersection point of the required thrust (obtained from the resistance of the hull) and generated thrust obtained by the propeller. The hydrodynamic characteristics of the propellers are calculated at this point. If the physical constraints are not satisfied, the objective functions are penalized by a penalty function. MOEA/D-DRA is then applied to optimize the objective functions, a linear combination of the effective power and propulsive efficiency at four operating conditions. These steps are repeated until a stopping condition is met. Formulation of MOP presented at this level is as follows:

Fig. 2

Flowchart of first-level optimization

Table 2 Limits of design variables for HPSs

Minimize:

$$H(X) = [F_{1} (X),F_{2} (X)]^{T} ,\;X \in R^{6}$$

(15)

where

$$F_{1} (X) = \frac{{w_{1} P_{{{\text{E}}\_1}} + w_{2} P_{{{\text{E}}\_2}} + w_{3} P_{{{\text{E}}\_3}} + w_{4} P_{{{\text{E}}\_4}} }}{{w_{1} P_{{{\text{E}}_{0} \_1}} + w_{2} P_{{{\text{E}}_{0} \_2}} + w_{3} P_{{{\text{E}}_{0} \_3}} + w_{4} P_{{{\text{E}}_{0} \_4}} }} = \frac{{f_{1} }}{{f_{{_{0} 1}} }}$$

$$F_{2} (X) = \frac{{w_{1} \frac{1}{{\eta_{{{\text{P}}\_1}} }} + w_{2} \frac{1}{{\eta_{{{\text{P}}\_2}} }} + w_{3} \frac{1}{{\eta_{{{\text{P}}\_3}} }} + w_{4} \frac{1}{{\eta_{{{\text{P}}\_4}} }}}}{{w_{1} \frac{1}{{\eta_{{{\text{P}}_{0} \_1}} }} + w_{2} \frac{1}{{\eta_{{{\text{P}}_{0} \_2}} }} + w_{3} \frac{1}{{\eta_{{{\text{P}}_{0} \_3}} }} + w_{4} \frac{1}{{\eta_{{{\text{P}}_{0} \_4}} }}}} = \frac{{f_{2} }}{{f_{{_{0} 2}} }}$$

(16)

subject to the physical constraints:

$$\begin{aligned} g_{1} \left( X \right) \equiv \left| {\frac{{\Delta - \Delta_{0} }}{{\Delta_{0} }}} \right| < 0.05 \hfill \\ g_{2} \left( X \right) \equiv 0.55 \le \frac{D}{d} \le 0.80, \hfill \\ \end{aligned}$$

(17)

where $\Delta$ and $\Delta_{0}$ are, respectively, the ship displacement of the current design during the optimization process and the initial design. The design variables vector, X, is defined as:

$$X = \left[ {\frac{L}{B},\frac{B}{d},d,Z,D,\frac{P}{D}} \right].$$

Based on the output of the first level optimization, the second level starts. In addition to the defined design variables, the propeller chord distribution (c/D) is also added at this level whose limits are $\pm 0.05$ of the initial one. Next, the medium-fidelity BEM is utilized as hydrodynamic solver for calculating both the hull wave-making resistance and the propeller hydrodynamic performance. The flexibility in the 3D geometric description, the high accuracy in predicting hydrodynamic forces and cavitation phenomenon as well as its acceptable computational time (a few minutes) are the main reasons for this choice. Like in the previous section, an empirical formula is applied to calculate the added resistance in head waves. The cavitation evaluated by using BEM is considered here as another design constraint. The prevention of the cavitation phenomenon in propellers plays a key role in ship design to mitigate the side effects, including induced pressure pulses, degradation of performance, radiated noise and erosive phenomena. Based on Eqs. 9 and 10, this constraint is defined as follows:

$$g_{3} \left( X \right) \equiv \frac{\sigma }{{\left| {C_{\text{p}} } \right|}} > 1.$$

(18)

Finally, the algorithm is repeated and once the algorithm reaches its maximum generation, the Pareto front is drawn and the solution that is as close as possible to the utopia point is selected as the final design. This type of solution is called compromise solution [12] and here denoted as CS which is chosen for comparison with the initial solution (IS) in the latter discussion. At the second level, the design variables vector is defined as:

$$X = \left[ {\frac{L}{B},\frac{B}{d},d,Z,D,\frac{P}{D},\frac{{c_{1} }}{D},\frac{{c_{2} }}{D}, \ldots ,\frac{{c_{11} }}{D}} \right]$$

where $\frac{{c_{i} }}{D},\;i = 1, \ldots ,11$ is the propeller chord distribution. Chord must be made large enough such that the minimum pressure coefficient satisfies Eq. (18).

4 Application

In this section, two different initial HPSs are optimized and then some numerical results are presented showing the robustness of the proposed integrated method outlined in the preceding section. The first case used in this study is a Series 60 hull form propelled by DTMB P4118 single-propeller (S60-P4118 HPS) and the second one is S175 container ship driven by her designed twin-propeller, KP505 propeller (S175-KP505 HPS). The weights (w) and operating conditions (OCs) of the two optimization cases are presented in Table 3.

Table 3 Characteristics of case studies

4.1 Case I

As it was already expressed in this case S60-P4118 HPS is chosen as the initial HPS. The optimized individuals in each generation, Pareto-optimal front and initial solution are denoted in Fig. 3. The Four HPSs (i.e. ID 301, ID 321, ID 302 and ID 316) are selected from the Pareto frontier for comparison with the initial HPS. The compromise solution (CS) of the multi-objective optimization problem which is the final HPS design corresponds to the fourth optimized solution ID 321. Figure 3 shows that MOEA/D-DRA can promote the spreading of the designs (individuals) along the Pareto front. This means that the diversity of the algorithm which is a main factor in the evolutionary optimization algorithms is appropriate. Horizontal and vertical axes are, respectively, indicated the first and second objective functions. The optimization algorithm we have used, may not be able to provide exactly the same Pareto front by rerunning the algorithm with the same setup (reproducibility property), but the algorithm obtained as close as possible solutions to real Pareto front in the cases of different mathematical functions, as mentioned in Sect. 3.1. Therefore, MOEA/D-DRA is an efficient and validated algorithm to apply in this study.

Fig. 3

Evolution of Pareto fronts during S60-P4118 HPS optimization (blue: feasible solution; red: optimal solution; black: initial solution) (color figure online)

The comparison of the initial design and the four optimal designs is listed in Table 4. The L/B and B/d ratios of the optimal designs are higher and lower than those of IS, respectively. The hull draft does not change significantly as well. These three parameters of CS have changed by + 4.13%, − 4.8% and − 1.3% in comparison with those of IS. Regarding to the propeller design variables, the blade number of the optimal designs is the same as the initial one. The propeller diameter has increased while the pitch ratio has approximately kept unchanged. The hull and propeller parameters have changed in such a way that the first objective function, i.e. effective power, has been decreased and the second objective function, i.e. propulsive efficiency, has been increased while the design constraints have been satisfied.

Table 4 Characteristics of IS and CS for S60-P4118 HPS optimization

The chord distribution of the optimal and initial designs is shown in Fig. 4. The figure demonstrates that the chord distribution of CS over all radii, r/R, is higher than that of IS which may lead to an improvement in the probability of occurrence of cavitation phenomena in the aft part of the vessel. Figure 5 depicts the geometrical body of the IS and CS’s hull and propeller. As can be calculated from Table 4, the CS’s hull is about 2.5 m longer and 1.0 m narrower than the IS design. A comparison between the hydrodynamic performance of the IS and CS designs is reported in Table 5 at the four operating conditions (OCs). The resistance in calm water and waves and thus the total resistance of the CS’s hull have been lowered compared to those of the IS’s hull as it was expected from the variation of the hull dimensions of CS. Comparing the added resistance to the calm water resistance ratio $({{R_{\text{AW}} } \mathord{\left/ {\vphantom {{R_{\text{AW}} } {R_{\text{CW}} }}} \right. \kern-0pt} {R_{\text{CW}} }})$ at three consecutive operating conditions, for example OC₂, OC₃ and OC₄, shows that: (a) the increase of the ship speed in a given sea state (SS) has a higher impact on the calm water resistance than the added resistance, (b) rougher weather will increase the added resistance more than the calm water resistance at a given Froude number. Moreover, Table 5 shows a reduction in the effective power and an increase in the propulsive efficiency of CSs relative to those of ISs. Figure 6 compares the hydrodynamic performance of the IS and CS’s propeller. The propeller efficiency of CS has been increased, especially at about J > 0.9. As Table 5 confirms the operating J values of CS has shifted towards the J value at which the maximum efficiency occurs. This is due to an increase in the propeller diameter and pitch ratio. Figure 7 shows the comparison between the hull total resistance of IS and CS at the operating sea states 4 and 5 over a wide range of Froude numbers. The total resistance of CS is lower than that of the IS at both the operating weather conditions and all speeds including the operating speeds.

Fig. 4

Chord distribution of optimal designs (Pareto front) for S60-P4118 HPS optimization

Fig. 5

Geometrical body of IS and CS’s HPS (up: IS, down: CS)

Table 5 Performance of IS and CS for S60-P4118 HPS optimization

Fig. 6

Hydrodynamic performance of IS and CS for S60-P4118 HPS optimization

Fig. 7

Hull resistance of IS and CS at the operating sea states 4 and 5 for S60-P4118 HPS optimization

It is worth nothing that as described in Sect. 3.2, the software used BEM in the second level of the optimization flowchart, so the final results are obtained using BEM.

4.2 Case II

The initial HPS in the second case includes S175-KP505 HPS. Figure 8 demonstrates the initial and compromise solutions as well as the optimized solutions obtained in each generation. The figure indicates that the solutions are well distributed over the Pareto front. We select the optimal designs ID 401, ID 413, ID 410 and ID 412 for later comparisons. The optimal design ID 410 is corresponding to CS as the final optimized design. Table 6 reveals the design variables of the initial and optimal designs during the optimization of S175-KP505 HPS using MOEA/D-DRA. The L/B and P/D values of CS have increased while the B/d and propeller diameter (D) parameters have decreased compared to those of IS. The number of blades has not changed. Figure 9 shows the comparison between the chord distribution of the initial and optimized designs. It is observed that the chord distribution of the CS’s propeller has relatively increased. This variation of the design variables of CS implies on the improvement of the objective functions. As can be seen from Table 6, F₁ and F₂ have been, respectively, improved by 8% and 6%.

Fig. 8

Evolution of Pareto fronts during S175-KP505 HPS optimization

Table 6 Characteristics of IS and CS for S175-KP505 HPS optimization

Fig. 9

Chord distribution of optimal designs for S175-KP505 HPS optimization

The geometrical body of the IS and CS’s HPS is shown in Fig. 10. The IS’s hull is about 4.0 m longer and 1.5 m wider than the CS’s hull. Table 7 compares the hydrodynamic performance of the hull-propeller system of IS and CS. The added resistance, calm water resistance and so the total resistance of the CS’s hull is lower than those of the IS’s hull at all the operating conditions. These results also imply that the weather conditions may influence on ${{R_{\text{AW}} } \mathord{\left/ {\vphantom {{R_{\text{AW}} } {R_{\text{CW}} }}} \right. \kern-0pt} {R_{\text{CW}} }}$ more than the ship speed. This table also shows a reduction in the effective power and an increase in the propulsive efficiency of CS compared to IS. It is obvious from the hydrodynamic point of view that even a one percent increase in propulsive efficiency may decrease fuel consumption and then total cost significantly. Unlike in the previous case study, the revolution rate of CS’s propeller is higher than that of IS which surely has an undesirable effect on the propeller induced hull-pressure fluctuations and vibrations. This effect should be taken for a comprehensive optimization into consideration and this is our goal for future works. The hydrodynamic performance of the IS and CS’s propeller is shown in Fig. 11. It can be seen from the figure that the propeller efficiency of CS increases as the J value increases, especially at J > 0.75 where the maximum efficiency is located for both IS and CS. The total resistance of IS and CS’s hull at two different operating sea states over a wide range of Froude numbers are shown in Fig. 12. As it was expected from the variation trend of the CS’s hull dimensions the total resistance has been decreased compared to that of IS over all speeds, including the two operating conditions.

Fig. 10

Geometrical body of IS and CS’s HPS (up: IS, down: CS)

Table 7 Performance of IS and CS for S175-KP505 HPS optimization

Fig. 11

Hydrodynamic performance of IS and CS for S175-KP505 HPS optimization

Fig. 12

Hull resistance of IS and CS at the operating sea states 4 and 5 for S175-KP505 HPS optimization

5 Conclusion

This paper presented an efficient and useful software (HPS-MOP) based on a multi-level and multi-point optimization of HPSs simultaneously. Two hydrodynamic solvers were used with different fidelities to minimize the effective power and maximize the propulsive efficiency. Based on the numerical results, the following conclusions can be drawn:

• The results showed that the employed optimization algorithm, MOEA/D-DRA, may efficiently distribute the designs over the Pareto front and is an efficient approach with a good diversity and convergence.

• The intersection point of the required and propeller thrust coefficient curves of CSs for the two MOPs was obtained near to the location of the maximum efficiency in comparison with that of ISs.

• The total resistance of the optimized hulls was reduced compared to that of the initial hulls over a wide range of ship speeds.

• The variation trend of the design variables illustrated an improvement in the hydrodynamic performance and so the objective functions, i.e. effective power and propulsive efficiency of the CS’s designs at all the operating conditions.

• Worsening the weather conditions can change the added resistance to calm water resistance ratio more than increasing the ship speed.

• The proposed software presented an efficient tool to integrate the conceptual and preliminary stages of ship’s hull-propeller systems into one stage and decrease the total design cost.