Introduction

The GUM (Guide to the expression of Uncertainty in Measurement) is widely applied for evaluating the quality of measurement in different areas. Recently, ISO published ISO/TS 20914:2019 [1] for estimating measurement uncertainty in medical laboratories. This guidance follows the general GUM framework but provides simple practical approach for calculation of measurement uncertainty using available information, so called “top-down” approach. ISO/TS 20914 considers two main uncertainty inputs. One relates to calibrators (which are used by the laboratory for “in-house” internal calibration of an analytical system) and corresponding information about assigned values and associated uncertainties should be provided by a manufacturer. The other relates to laboratory imprecision for a long-term period, which is evaluated using internal quality control data. Evaluation of the second input needs collecting, analyzing and processing a huge number of data to obtained pooled estimates of imprecision and then updating these estimates when new information becomes available. When combining these datasets, the question often arises about their homogeneity (or almost homogeneity, acceptable from a practical point of view).

The work considers the criteria for variance homogeneity and consists of two chapters. The first provides some critical values for certain variance homogeneity tests, obtained under assumption that the values of the samples has a symmetric two-side power (TSP) distribution [2]. Some comparative analysis of the tests power is provided as well. The approach applied in this section is similar to one used in [3,4,5].

The second section contains the similar results for some variance proximity tests, this can be useful when exact equality of variances is not required. We consider the case when the null hypothesis assumes a minor random scatter of the variance around some constant value.

TSP distribution

A pdf (probability density function) for a symmetric TSP distribution, having a unity variance, is given by the following expression:

$$\begin{aligned} f(x)= & {} \left\{ \begin{array}{cc} \frac{p}{2 x_0} \left( 1 + \frac{x}{x_0} \right) ^{p - 1}, \quad &{} -x_0< x< 0, \\ \frac{p}{2 x_0} \left( 1 - \frac{x}{x_0} \right) ^{p - 1}, \quad &{} 0 \le x < x_0, \\ 0, \quad &{} x = \pm x_0, \quad p > 1, \end{array}\right. \nonumber \\ \left. \right. \qquad x_0= & {} \sqrt{ \frac{(p + 1) (p + 2)}{2} }. \end{aligned}$$

Here p is the distribution power parameter (\(p = 1\) corresponds to a uniform distribution case, and \(p = 2\) corresponds to a triangular one). This family of distributions is quite wide and at the same time has an uncomplicated mathematical description that facilitates modeling.

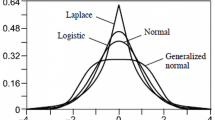
It is expected that the value of the parameter p for each specific application case can be estimated based on the information about the experimental data accumulated in laboratory (see [2]). The plots for some pdfs are given in Fig. 1 (the pdf for a normal distribution is also given for comparison).

Fig. 1
figure 1

TSP pdfs

Full size image

Variance homogeneity tests

Variance homogeneity tests for two samples

Let us have two data samples \(x_1, x_2\) from the same TSP(p) distribution, of length \(n_1\) and \(n_2\), correspondingly. The test hypothesis of the variance homogeneity (uniformity) is assumed to be the equality

$$\begin{aligned} H_0: \quad \sigma _1 = \sigma _2 \end{aligned}$$

(and the competing hypothesis \(H_1\) implies inequality of variances).

Consider two variance homogeneity tests. The first one is the Fisher test (of course, here we cannot say that it is exactly the classic Fisher test, since the distribution of sample values differs from normal); corresponding test statistic is given by

$$\begin{aligned} F = s_1^2 / s_2^2, \end{aligned}$$

where \(s_i^2\) are the sample variances for \(x_i\). The other is the Link test [6],

$$\begin{aligned} {\tilde{F}} = \omega _1 / \omega _2, \end{aligned}$$

where \(\omega _i\) are the sample ranges, \(\omega _i = x_{i, \max } - x_{i, \min }\).

Here we consider two-tailed test, and for given critical values \(c(n_1, n_2)\) the checks look like

$$\begin{aligned} \begin{array}{ccc} \left( c(n_2, n_1) \right) ^{-1} \le F, {\tilde{F}} \le c(n_1, n_2), &{} \quad \text {if} \quad F, {\tilde{F}} \ge 1, \\ \left( c(n_1, n_2) \right) ^{-1} \le F, {\tilde{F}} \le c(n_2, n_1), &{} \quad \text {otherwise}. \end{array} \end{aligned}$$

In case when \(n_1 = n_2 = n\) one can simply test if

$$\begin{aligned} c^{-1} \le F, {\tilde{F}} \le c, \quad c = c(n). \end{aligned}$$

Some critical values (obtained by the Monte Carlo method) corresponding to the probability level of \(P_0 = 0.95\) could be found in Table 1; some other (for unequal \(n_1\), \(n_2\)) could be found at [7, 8].

Table 1 Critical values, \(c = c(n)\)
Full size table

Comparing the test power

To estimate and compare the power of the tests let us consider the probability of rejecting the null hypothesis when the variance ratio is given (and differs from unity):

$$\begin{aligned} P = P(k) = P \left\{ H_0 \text { rejected } \mid \sigma _2 = k \sigma _1, \; k > 1 \right\} . \end{aligned}$$
(1)

Hereinafter, it is assumed that the samples are taken from the TSP distribution having the same value of the parameter p (i.e., (1) assumes the “scaling” of the distribution rather than varying the distribution law due to the change of TSP parameter, and P represents the probability of detecting such “scaling”).

The plots of P(k) (also obtained by the Monte Carlo method) are given in the below Figs. 2, 3. The case of normal distribution is considered for comparison.

Fig. 2
figure 2

P(k), fisher test

Full size image
Fig. 3
figure 3

P(k), link test

Full size image

It could be noted that the power of the Link test is higher when the TSP power parameter is less than two; otherwise the Fisher test is preferable. The case \(p = 3\) is closest to the case of normal distribution of all the considered above (but, of course, an even closer one can be found by varying the parameter p).

Variance homogeneity multi-sample tests

Let us have m data samples \(x_i\) of length n from the same TSP distribution. Here, the null hypothesis has the form

$$\begin{aligned} H_0: \quad \sigma _1 = \sigma _2 = \ldots = \sigma _m \end{aligned}$$

(the competing hypothesis \(H_1\) implies inequality of at least some pair of variances). Consider the following one-tailed variance homogeneity criteria:

Cochran test [9]:

$$\begin{aligned} C = \frac{\max _{1 \le i \le m} s_i^2}{\sum _{i = 1}^m s_i^2} \end{aligned}$$

Bliss-Cochran-Tukey (BCT) test [10]:

$$\begin{aligned} {\tilde{C}} = \frac{\max _{1 \le i \le m} \omega _i}{\sum _{i = 1}^m \omega _i} \end{aligned}$$

Some critical values (corresponding to a probability level of 95 %) for the tests are provided in Table 2.

Table 2 Critical values, Cochran and Bliss–Cochran–Tukey tests
Full size table

In case of multiple samples formula (1) does not provide estimation of the test power, as we can have an outlier of variance for more than one sample. Nevertheless, consider a particular trivial case of single outlier (here, again, the parameter p is assumed to be immutable):

$$\begin{aligned} P = P(k) = P \left\{ H_0 \text { rejected } \mid \sigma _2 = \ldots = \sigma _m,\; \sigma _1 = k \sigma _2, \; k > 1 \right\} . \end{aligned}$$

Consider an example, \(m = 3\), \(n = 5\). A comparison of power for the Cochran and the Cochran-Bliss-Tukey tests is presented in the corresponding Fig. 4.

Fig. 4
figure 4

P(k), single outlier, \(m = 3\), \(n = 5\)

Full size image

It can be noted again that the first or the second test may be preferred (as more powerful) depending on parameter p value (again, roughly, \(p = 2\) is some “equilibrium” point).

Variance proximity tests: random scatter of the variances

If a homogeneity test passes, the pooled estimate of imprecision is calculated. In practice, quite often the pooled estimate is calculated when the critical values of the criteria are slightly exceeded, but the variances of the series differ insignificantly. So, let us test a null hypothesis which allows a small variability in the series variances.

Consider the following trivial case. Let the variance of the distribution varies in a random way between the subsequent samples, i.e.,

$$\begin{aligned} \sigma _1 = k_1 \sigma _0, \quad \sigma _2 = k_2 \sigma _0, \quad k_{1, 2} \sim U(1 - d, 1 + d), \end{aligned}$$
(2)

here U is for a uniform distribution, and d is a minor positive deviation (below we will consider d from a range [0.05, 0.20], i.e., \(\sigma \) deviation is \(\pm 5\, \%...20\,\%\) of \(\sigma _0\)). Again, we consider the TSP parameter p to be immutable, i.e., these changes of the deviation are not due to fluctuations in the form of the distribution law (this special case can be considered separately).

This model, on the one hand, is in good agreement with practical needs, and, on the other hand, is well suited for the Monte Carlo method (it allows simple randomization of samples, followed by obtaining the test statistics and, after some averaging, the corresponding critical values). Of course, this trivial model allows the further modification (another distributions for d, systematic effects, etc.).

The acceptance of the variance homogeneity hypothesis when the random effect is neglected

As a starting point, let us estimate the probability of acceptance of the “strict” null hypothesis neglecting the random effect

$$\begin{aligned} {\tilde{H}}_0: \quad \sigma _1 = \sigma _2 \end{aligned}$$

when in fact it is present according to (2):

$$\begin{aligned} {\tilde{P}} = P \left\{ {\tilde{H}}_0 \text { accepted } \mid (2) \right\} \end{aligned}$$

Some corresponding probability values when using the Fisher test are given in the below Table 3.

Table 3 Some values for \({\tilde{P}}\), Fisher test
Full size table

It could be noted that for relatively low values of n and d the probability do not differ significantly from \(P_0 = 0.95\). i.e., someone using the Fisher test (being unaware of the random effect (2)) hardly notice the difference for relatively small values of d (0.05) and n (5..20). However, while increasing d and n, this effect becomes more and more significant, requiring the calculation of the correct critical values (which is done below).

For the other tests the situation is the same.

Two-sample tests: critical values and power of the tests

Some critical values c(d, n) for \(n_1 = n_2 = n\) for the Fisher and Link tests are given in the following Table 4. The case of normal distribution is also considered.

Table 4 Critical values, Fisher and Link tests
Full size table

Note that in the range of relatively small values of d the critical values for the criteria also vary insignificantly. For example, the following Fig. 5 contains plots of the ratio c(d, n) /c(0, n) for the Fisher and Link tests as a function of the parameter d, when \(n = 10\). It can be seen that for almost all cases here the increment of c does not exceed 5 %, when \(d \in (0, 0.1]\) (and even for larger d sometimes).

Fig. 5
figure 5

c(d, n) /c(0, n), \(n = 10\)

Full size image

The plots of P(k) for \(n_1 = n_2 = 10\), \(d = 0.1\) (see (1)) are given in the below Figs. 6 and 7. As it can be seen, the values of P do not differ sufficiently from the case when the random scatter of the standard deviation is absent (but the test power is expectedly lower as compared with the case of zero d).

Fig. 6
figure 6

P(k), fisher test, \(n = 10\), \(d = 0.1\)

Full size image
Fig. 7
figure 7

P(k), link test, \(n = 10\), \(d = 0.1\)

Full size image

Multi-sample tests

Let us restrict ourselves here to providing of some critical values for the Cochran and Cochran–Bliss–Tukey criteria. The values are given in Table 5.

Table 5 Critical values, Cochran and Bliss–Cochran–Tukey tests
Full size table

Conclusion

Long-term imprecision variance is used by analytical, testing, medical and other laboratories in their internal quality control procedures. This information is also very valuable for uncertainty calculation in “top-down” approach. So, a laboratory should obtain and update the variance estimates of precision which are used in their internal quality control. The widely used ANOVA and corresponding software should be accompanied by analysis of homogeneity of imprecision variance. The relating criteria are available but the critical intervals are based on the assumption of normality. In this paper we investigated the performance of the well-known criteria for TSP family distribution and discussed their properties and limitations of usage.

The work allows an expansion in the direction of considering other various criteria for the variance homogeneity (see, e.g., [3, 4]). Some further generalizations of the random model (2) could be considered as well. For example, [11] contains critical values for some variance proximity tests when the sample values are normally distributed, and the scatter of standard deviation has a TSP distribution.