1 Introduction

Gradient coils play a determinant role in implementing spatial encoding in magnetic resonance imaging (MRI) for achieving high quality. Low-field MRI systems with permanent magnets present specific problems: the lack of free space between the poles of the permanent magnet, the existence of eddy currents (EC), the relatively high contribution of concomitant gradient inductances and warming a patient, which are critical factors to take into consideration [1].

In modern low-field MRI systems, a prevalent solution involves planar gradient coils positioned at the magnet poles to generate the three gradients of the magnetic field (Gx, Gy, Gz). This configuration partially preserves free space within the magnet. However, it introduces challenges related to induced EC, and attempts to mitigate their impact may compromise the gradient coil efficiency and linearity [1, 2]. Fortunately, there are also known approaches that propose the design of gradient systems of arbitrary, including cylindrical, geometry, allowing coils to be located near the area of interest [3]. These coils could reduce EC preserving a good efficiency. However, the dense conductor arrangement and complex geometry in such systems result in increased mutual inductance. Finally, classical gradient field formation, using Maxwell coils, requires additional optimization for characteristics such as linearity and gradient intensity within the area of interest while maintaining good efficiency [4, 5].

Knowing the restrictions of planar coils for low-field MRI systems with permanent magnets, this work presents an alternative possible coil configuration for low-field MRI systems. In our specific case, a permanent magnet is “C”-configuration with a magnetic field intensity equal to 69 mT. The calculations carried out do not take into consideration, for the moment, the influence of the magnetic material on the parameters of the coils or other collateral effects related to the interaction of the magnetic field pulses.

2 Material and Methods

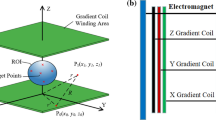
In this study, the specific requirements and initial parameters took into account the configuration of our magnet. Aiming at the development of a compact MRI for a human head, these dimensions encompass 0.27 m distance between poles and 0.78 m width. The proposed configuration has non-local coils for gradient field along the Y axis and two local cylindrical coils for gradient fields along the X and Z axes of the chosen coordinate system. The Y gradient coil is represented as two pairs of Maxwell’s rings with symmetry axis along the Y direction. The first (inner) pair of Maxwell’s rings is located inside near the edges of the magnet. The second (outer) pair of Maxwell’s rings make possible solving the problem of the inner radius requirements. The outer pair is located on the side of the magnet with a bigger radius, as illustrated in Fig. 1, where the Y coil is schematically depicted by yellow color. Local coils have a cylindrical symmetry with the axis along the Y direction. Therefore, local coils have the same wire configuration for X and Z coils, nevertheless rotated one with respect to the other 90° along Y axis. The diameter of the Tx/Rx RF coil is 25.8 cm and the shield around the RF coil is about 0.5 mm thick, increasing the diameter to 25.9 cm. Thus, local gradient coils are placed in the free space (1 cm) between the RF shield and the magnet poles. The general view of the gradient coil configuration together with a permanent magnet is shown in Fig. 1A.

Fig. 1
figure 1

Main view of the proposed configuration: positioning of the patient inside the MRI system, where 1—magnet, 2—local coil, 3—non-local coils (A); magnet dimensions (B)

Full size image

The magnet, whose dimensions are shown in Fig. 1B, has little free space between the poles. The proposed system provides more free space inside the magnet because of relocating the Y gradient coil. It may also potentially reduce the EC, heating effects, and mutual inductance.

2.1 Non-local Coils

The dimensions (diameter of the each pair and distance between them) as well as currents in the each pair of non-local coils were optimized using the target function method. In different mathematical programming problems [6], the target function method is widely used. To optimize our system of non-local coils, an iteratively derived target function was used:

$$\begin{aligned}\text{Target function }Q &={\omega }_{1}\frac{{V}^{2}}{2{\mu }_{0}} \sum\nolimits_{i=1}^{n}{({G}_{i}-{G}_{0}{|}_{z=0})}^{2}+{\omega }_{2}\frac{1}{2} \sum\nolimits_{i=1}^{n}{L}_{i}{I}_{i}^{2} \\ & \quad +{\omega }_{3}\tau \sum\nolimits_{i}^{n}{R}_{i}{I}_{i}^{2}-{\omega }_{4}\left|\frac{{V}^{2}}{2{\mu }_{0}}{\sum }_{i}^{n}{\left(\frac{d{B}_{i}}{dy}\right)}^{2}\right|. \end{aligned}$$
(1)

\({\omega }_{i}\)—the weight coefficients chosen so that different components of the target function contribute equally to the optimization of the characteristics, V = ROI, \({L}_{i}\)—self-inductance of the coil, \({I}_{i}\)—current of the coil, \({G}_{i}\)—the value of the gradient field intensity at some point, \({G}_{0}\)—the value of the gradient field intensity at the isocenter, \({B}_{i}\)—magnetic field at the point “i” in space, \({R}_{i}\)—coil resistance, \(\tau \)—gradient pulse duration, \({\mu }_{0}\)—vacuum magnetic permeability, \(n\)—number of points selected in ROI space.

Each term of the proposed function contains wi—weight coefficients, which are selected so that all summands should contribute equally. The first is responsible for linearity, the second for minimizing inductance, the third for minimizing resistance, and the last for increasing gradient efficiency. Spatial constraints were taken into account, which allowed the output of the script to obtain dimensions in accordance with the specified dimensions of the magnet and other coils.

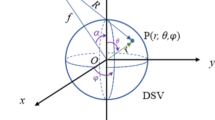
To perform optimization of the non-local coils, it was necessary to calculate the gradient field of one coil pair in the region of interest (ROI) of a sphere with a radius of 20 cm. It can be described by equation [7]:

$$\begin{aligned}{G}_{i} & =N\cdot I\cdot \frac{{\mu }_{0}}{4\pi }\cdot \frac{\partial k}{\partial z}\cdot \frac{1}{r\cdot \sqrt{ar}} \\ & \quad \cdot \left(r\cdot K\left(\frac{\pi }{2},k\right)+r\cdot k\cdot \frac{\partial K\left(\frac{\pi }{2},k\right)}{\partial k}+E\left(\frac{\pi }{2},k\right)\cdot \frac{\partial P}{\partial k}+P\cdot \frac{\partial E\left(\frac{\pi }{2},k\right)}{dk}\right),\end{aligned}$$
(2)

where

$$P=\frac{{k}^{3}\cdot a+k\cdot r\cdot r\left({k}^{2}-2\right)}{2(1-{k}^{2})} ; \; k=\frac{\sqrt{4ar}}{\sqrt{{\left(z-{z}_{0}\right)}^{2}+{\left(a+r\right)}^{2}}}.$$

\({G}_{i}\)—gradient field of one coil at the point “i” in space; I—coil’s currents, r—distance in the cylindrical coordinate system, a—radius of the ring, z—coordinate on the OZ axis in the cylindrical coordinate system, \({z}_{0}\)—coordinate of a point in the cylindrical coordinate system on the OZ axis, E—elliptic integral of the second kind, K—elliptic integral of the first kind, \(N\)—number of turns per coil.

The optimization algorithm was selected among several candidates that could handle this task: BFGS [8], TNC [9] and JADE [10]. To optimize the geometric parameters (radius of rings and distance between pairs of rings) as well as currents and inductances, the Python script was used. Then optimization was performed using each of the algorithms. As a result, it can be noted that the BFGS and TNC algorithms fall into the local minimum of target function. The local minimum was found by changing the optimization input values and obtaining different optimization parameters under the same boundary conditions. The JADE algorithm showed stability with respect to the change of the initial optimization point and produced the point of global minimum of the target function.

The program code consisted of several stages. At the beginning, parameters of optimization (currents, radius and distances between rings) were defined according to limitations with magnet dimensions. In the ROI, a set of points was generated. The target function was calculated at these points and optimized. As a result, the optimized data were obtained. The CST Studio 2022 software (Dassault Systems) was used for magnetostatic numerical simulations. Based on the data obtained, it is possible to estimate the efficiency and linearity of the gradient.

2.2 Local Coils

In general, the process of designing gradient coils could be divided into the optimization stage and the post-processing stage. Local coils were designed using an algorithm based on the boundary element method (BEM) [11]. Together with the target field method, it is used for wire geometry creation which is required for magnetic field gradient formation in ROI. The current density or its scalar flux function (SF) satisfying optimization conditions is calculated. Subsequently, the total current density of the entire coil is obtained by the individual contribution of each of the turns.

Numerical calculations were carried out in Matlab 2022b (The MathWorks) using an open-source code—CoilGen [12]. Based on the results of constructing an array of conductor points for a given cylindrical configuration, magnetostatic numerical simulations were performed using CST Studio. The points were combined into a single current path. As a result of the simulation, magnetic field values were obtained, as well as efficiency and linearity of the gradient.

3 Result and Discussion

Due to the initial calculations performed for local coils (X coil and Z coil), the height of the cylinder must be greater than the radius to ensure target gradient field linearity. The efficiency of the gradient coils depends on the number of turns of the wire, and consequently the length of the conductor, as well as the total inductance and resistance. The values of the resistance, inductance, coil efficiency and linearity for the planar configuration described in the literature [1, 2] were taken as reference values for inductance and resistance. The cross section of the conductor was also taken into account to maintain the reference resistance value.

As a result of the calculations carried out, a cylindrical configuration with a diameter of 0.26 m and a height of 0.35 m was obtained. The total length and wire cross section was 26 m and 7 mm2, respectively; thus each of the coil has 15 turns. The inductance was 132 μH and the resistance 60 mΩ. The general view of the Z gradient coil is shown in Fig. 2A. The configuration for the X gradient is obtained by slightly improving the radius of the Z coil and rotating it by 90° along the symmetry axis. The distribution of the Z coil magnetic field along the Z axis is shown in Fig. 2B.

Fig. 2
figure 2

Local Z gradient coil: a coil geometry with a diameter of 0.26 m and a cylinder height of 0.35 m (A) and a distribution of the magnetic field in ROI along the Z axis normalized to 1 A of the coil current (B)

Full size image

The radius of the inner Maxwell’s pair of non-local coils was limited by distance between magnet poles and distance between outer Maxwell`s pair was limited by the magnet width. In [5], the best linearity and good efficiency are obtained when the ratio of the currents between the inner and outer pairs equal to \(\frac{1}{8}\). This current ratio was obtained due to the difference in resistance of the coils, by varying the winding cross section. In the proposed configuration, the ratio is equal to \(\frac{1}{8}\). In the outer coils, the current was 80 and the wire cross section 7 mm2; in the inner pair it was 10 A and wire cross section 0.7 mm2.

The general view and dimensions of the Y gradient coil is shown in Fig. 3A. The distribution of magnetic field along the Y axis is shown in Fig. 3B. As a result of optimization, the distance between the Maxwell’s rings of the inner pair was 0.26 m and of the outer pair was 0.78 m. The radius of pairs was 0.128 m and 0.25 m, respectively. The outer pair of rings reduces the total inductance of the setup to 148 μH, and total resistance of setup is 36 mΩ. In the next step, the number of turns for each ring and the ratio between the inner and outer pair was found. The same number of turns, equal to 10, was obtained for each ring.

Fig. 3
figure 3

Non-local coil: a coil geometry with dimensions of \({a}_{1}=0.128 \text{m}, {a}_{2}=0.25 \text{m}\) (radius of inner/ outer coils) \({d}_{1}=0.26 \text{m} , {d}_{2}=0.78 \text{m}\) (distance between coils) (A) and distribution of B-field along the Y axis for input currents of \({I}_{1}=80 \text{A}, {I}_{2}=10 \text{A}\) (B)

Full size image

Results of numerical calculations for the obtained configuration were compared with reference results for planar coils. As a result, at lower currents, less heat is generated inside the system. Moving the Y coil outside the magnet allows to reduce EC, as well as the influence of mutual inductance. All the optimization results for local and non-local coils are summarized in Table 1.

Table 1 Calculated characteristics of the proposed gradient coil configuration
Full size table

4 Conclusion

An alternative design of coil configuration for the generation of the gradient of the magnetic field in low-field MRI with permanent magnets is presented. The obtained inductance and resistance of coils as well as the linearity of the gradient field and coil efficiency make them a competitive option compared to classical solutions. The proposed configuration could potentially mitigate some demands and difficulties associated with planar coils. The calculations carried out do not take into account, for the moment, the influence of the magnetic material on the parameters of the coils or other collateral effects related to the interaction of the magnetic field pulses. As well, the calculations are surely also valid for “C”-configurations of permanent magnets in the range of hundreds to a few tens of mT. It is expected that by increasing the distance of the non-local coils from the center of the magnet and those being orthogonal to their poles, the EC and heat generated will be relative smaller in the ROI. These approximations will be the subject of future work.