1 Introduction

The correspondence between the Heisenberg equation \(\dot{\hat{\vec{\mu }}} = - i/\hbar \left[ {\hat{\vec{\mu }},\hat{\mathcal{H}}} \right]\) for the operator \(\hat{\vec{\mu }}\) of the magnetic moment in an external field \(\vec{H}\) (the Hamiltonian is \(\hat{\mathcal{H}} = - \hat{\vec{\mu }}\vec{H}\)) and classical equation of motion \(\frac{{d\vec{\mu }}}{dt} = \gamma \vec{\mu } \times \vec{H}\) (\(\gamma\) is the gyromagnetic ratio) is obvious when individual magnetic moments \(\vec{\mu }_{k}\) do not interact with each other. But it can be shown [1] that the equations for \(\vec{\mu }_{k}\) and \(\hat{\vec{\mu }}_{k}\) are identical in form even when magnetic moments interact by dipole or exchange forces.

Within the framework of the quantum mechanical description consider a spin system described by the Hamiltonian consisting of Zeeman and dipole parts:

$$ \hat{\mathcal{H}} = \hat{\mathcal{H}}_{Z} + \hat{\mathcal{H}}_{dd} = - \hbar \sum\limits_{k} {\gamma_{k} H^{\alpha } \hat{S}_{k}^{\alpha } } + \frac{{\hbar^{2} }}{2}\gamma_{l} \gamma_{k} \sum\limits_{l > k} {D_{lk}^{\alpha \beta } } \hat{S}_{l}^{\alpha } \hat{S}_{k}^{\beta } $$
(1)

where \(D_{lk}^{\alpha \beta } = \frac{1}{{r_{lk}^{3} }}\delta_{\alpha \beta } - \frac{3}{{r_{lk}^{5} }}r_{lk}^{\alpha } r_{lk}^{\beta }\). Latin letters represent particle numbers and Greek letters correspond to spatial dimensions (a summation over repeating Greek superscripts is implied). The external field, \(H^{\alpha }\), can depend on spin location and time.

For operators \(\hat{\vec{\mu }}_{l} = \gamma_{l} \hbar \hat{\vec{S}}_{l}\), equation \(\dot{\hat{\vec{\mu }}} = - i/\hbar \left[ {\hat{\vec{\mu }},\hat{\mathcal{H}}} \right]\) gives

$$ \dot{\hat{\mu }}_{l}^{\delta } = \gamma_{l} \sum\limits_{k} {e_{\delta \alpha \sigma } \left( {\hat{\mu }_{l}^{\alpha } H^{\sigma } + D_{lk}^{\alpha \beta } \hat{\mu }_{k}^{\beta } \hat{\mu }_{l}^{\sigma } } \right)} $$
(2)

Within a classical description, the dynamics of vector \(\vec{\mu }_{l}\) is given by equation

$$ \dot{\vec{\mu }}_{l} = \gamma_{l} \vec{\mu }_{l} \times (\vec{H} + \vec{H}_{l} ) $$
(3)

where \(\vec{H}\) is an external field, \(\vec{H}_{l}\) is the magnetic (dipole) field at the coordinate of the \(l\)-th magnetic moment. This field can be calculated as

$$ H_{l}^{\alpha } = - \partial E_{dd} /\partial \mu_{l}^{\alpha } $$
(4)

where \(E_{dd} = \frac{1}{2}\sum\limits_{l > k} {D_{lk}^{\alpha \beta } } \mu_{l}^{\alpha } \mu_{k}^{\beta }\) is the dipole energy of a system of classical magnetic moments. As the result, Eq. (3) becomes

$$ \dot{\mu }_{l}^{\delta } = \gamma_{l} e_{\alpha \sigma \delta } \left( {H^{\alpha } + H_{l}^{\alpha } } \right)\mu_{l}^{\sigma } = \gamma_{l} \sum\limits_{k} {e_{\delta \alpha \sigma } \left( {\mu_{l}^{\alpha } H^{\sigma } + D_{lk}^{\alpha \beta } \mu_{k}^{\beta } \mu_{l}^{\sigma } } \right)} $$
(5)

The exchange interactions, potentially important for electron spin systems, can be taken into account by adding to the Hamiltonian the exchange term

$$ \hat{\mathcal{H}}_{J} = \frac{1}{2}\sum\limits_{l > k} {J_{lk} } \hat{\vec{S}}_{l} \hat{\vec{S}}_{k} $$
(6)

Because \(\hat{\mathcal{H}}_{J}\) has the same spin structure as \(\hat{\mathcal{H}}_{dd}\), the exchange coefficients \(J_{lk}\) can be placed in both Eqs. (2) and (5) instead of tensors \(D_{lk}^{\alpha \beta }\).

Equations (2) and (5) give the correspondence between the classical and quantum pictures for interacting magnetic moments: the Heisenberg equation for operators \(\hat{\vec{\mu }}_{l}\) and classical equation for vectors \(\vec{\mu }_{l}\) result in equations identical in form.

Clearly, the formal similarity does not mean that simulations with classical and quantum equations (if the quantum Hamiltonian would be feasible to diagonalize) should necessarily lead to identical results, the reason is that the assumption \(\left\langle {\hat{\vec{\mu }}_{k} \hat{\vec{\mu }}_{l} } \right\rangle \approx \left\langle {\hat{\vec{\mu }}_{k} } \right\rangle \left\langle {\hat{\vec{\mu }}_{l} } \right\rangle\) is the simplest form of the mean field approximation. Another reason for disagreement is that the value of spin in classical calculations can be taken into account only trivially through the magnitude of a magnetic moment \(\mu\).

Note, that even though the correspondence seems to be intuitively expected, it is not obvious in advance. Moreover, despite being valid for spin components \(\hat{\vec{S}}_{k}\) and \(\vec{S}_{k}\) (as well as for components of the total spin \(\sum\nolimits_{k} {\hat{\vec{S}}_{k} }\) and \(\sum\nolimits_{k} {\vec{S}_{k} }\)) it is not valid for some other observables, such as the magnitude of the total spin. Another situation when the gyration equation does not formally follow from the Heisenberg equation occurs if the tensor \(J_{lk}\) in the exchange interactions (6) is not symmetrical– in this case, the classical equation \(\frac{{d\vec{\mu }_{k} }}{dt} = \gamma_{k} \vec{\mu }_{k} \times \vec{H}\) for individual magnetic moments \(\vec{\mu }_{k}\) is unrelated with the equation \(\dot{\hat{\vec{\mu }}}_{k} = - i/\hbar \left[ {\hat{\vec{\mu }}_{k} ,\hat{\mathcal{H}}} \right]\) (thus we cannot say any longer that it is based on this equation) and can be only postulated by the analogy with the gyration equation for the total magnetic moment.

The same form of Eqs. (2) and (5) presents one of the unique cases when a general Ehrenfest’s theorem, which states that the Hamilton equations of classical mechanics hold for operators’ expectation values, result in the practical tool.

The validity of such correspondence gives some arguments toward modeling of the dynamics of the expectation values of quantum observables with classical spins. Anyway, the classical spin systems are often used for evaluating the macroscopic quantities characterizing the spin system, see, for instance, discussion in works [2,3,4,5,6,7,8,9]. The quantum calculations are currently limited to systems with simple Hamiltonians [10], or hybrid quantum–classical simulations in situations when each spin has a small effective number of interacting neighbors [11].

2 Classical Spins Simulation: Free Induction Decay

Let us write the classical Eq. (5) for the magnetic moment \(\vec{\mu }_{l}\) of the \(l\)-th particle in the form (in the following calculations we consider magnetic moments with equal \(\gamma\)):

$$ \frac{d}{dt}\vec{\mu }_{l} = |\gamma |\vec{\mu }_{l} \times \left( {\vec{H}_{0} + \vec{H}_{l} } \right) $$
(7)

Here \(\vec{H}_{0} = \left( {0,0,H_{0} } \right)\) is an external longitudinal field and \(\vec{\rm H}_{l} = \left( {H_{l}^{x} ,H_{l}^{y} ,H_{l}^{z} } \right)\) is the dipole field at the location of the \(l\)-th spin, determined by Eq. (4). Let us introduce the frequencies:

$$ \omega_{0} = |\gamma |H_{0} ,\omega_{d} = |\gamma |H_{d} $$
(8)

Here \(H_{d} = \mu /a^{3}\) with \(a\) being the mean distance between adjacent voxels (in simulations it is the lattice parameter of the unit cell). Notice, that \(\omega_{d}\) is just a characteristic of the mean value of the local dipole field (\(\omega_{d}\) is \(\omega_{loc}\)), the actual dipole fields at the locations of each spin are calculated by Eq. (4). Then in simulations, we use the parameter \(p_{d} = \omega_{d} /\omega_{0}\). It is convenient to use unit vectors of magnetic moments \(\vec{e}_{l} = \vec{\mu }_{l} /\mu\) for the l-th spin and the dimensionless time \(\tilde{t} = \omega_{{0 }} t\).

Let us consider the free-induction decay (FID) of the transverse magnetization in a dipolar-coupled rigid lattice—a fundamental magnetic resonance problem. For the first time, a similar simulation of FID for classical spins was performed by Jensen and Platz [2] for each spin interacting with 26 neighbors.

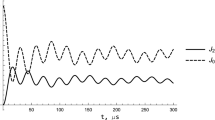
The time evolution of the NMR signal is obtained by numerically integrating the system of 3 N Eq. (7). Some details about the numerical approach can be found in work [7]. Figure 1 presents the results of simulations for cubic sample \(N_{x} = N_{y} = N_{z} = 7\) spins (the periodic boundary conditions are imposed) all coupled by dipolar interactions. Panel (a) demonstrates the transverse polarization, \(e^{x} (t) = (1/N)\sum\nolimits_{l} {e_{l}^{x} } (t)\). The dimensionless time in all Figs. 1, 2, 3,4 is \(\tilde{t} = \omega_{{0 }} t\).

Fig. 1
figure 1

Free precession signal \(G(t)\) and dipolar shape function \(f(\omega )\). a graph of \(e^{x} (t)\) for \(e^{x} (0) = 0.95\), \(p_{d} = 0.0025\); b shape function \(f(\omega )\) (high frequencies are removed); frequency is in \(\omega /\omega_{0}\) units, amplitude is in arbitrary units. c \(e^{x} (t)\) and Abragam’s trial function \(f(t)\) with parameters \(a = 0.0021\), \(b = 0.011\)

Full size image
Fig. 2
figure 2

Free precession signal \(e^{x} (t)\) for \(e^{x} (0) = 0.95\), \(p_{d} = 0.0025\). a Nx = 3, Ny = 3, Nz = 3 b Nx = 5, Ny = 5, Nz = 5

Full size image
Fig. 3
figure 3

Results of simulations of FID with 12 quantum spins. Left panel \(S^{x} (t)\) (normalized by unity), right panel—its Fourier transform, \(S^{x} (\omega )\)

Full size image
Fig. 4
figure 4

Time evolution of total magnetization and individual magnetic moment. In panel a: solid line \(S^{x} (t)\), dashed line \(S_{k}^{x} (t) = \Psi^{*} (t)\hat{S}_{k}^{x} \Psi (t)\); in panel (b) solid show the total magnetic moment \(e^{x} (t) = (1/N)\sum\nolimits_{l} {e_{l}^{x} } (t)\), dashed line—individual magnetic moment \(e_{k}^{x} (t)\)

Full size image

Simulations for different initial values of \(e^{x} (0)\) show that the regime of FID is almost independent of the initial polarization and just to specify, simulations below were performed for \(e^{x} (0) = 0.95\). After an initial steady part, the polarization suddenly decreases and vanishes. A very remarkable feature of the decay curves is their oscillatory behavior with the characteristic time of about \(1/\omega_{d}\).

Function \(e^{x} (t)\) is proportional to the amplitude of the free precession signal, \(G(t)\), its Fourier transform is the shape function \(f(\omega )\) [12], meaning that experimental observations of \(G(t)\) and \(f(\omega )\) are complementary. The Fourier transform (FT) of \(e^{x} (t)\) is shown in Fig. 1b. The spectrum centered at \(\omega_{0}\) (in dimensionless units \(\tilde{\omega } = \omega /\omega_{0}\) it is \(\tilde{\omega }_{0} = 1\)) has a width (the broadening) determined by the mean value of the dipole field, \(H_{d}\), which in dimensionless units is given by parameter \(p_{d}\). The two peak structure in Fig. 1b is the manifestation of the Pake doublet [12]. Panel (c) shows that Abragam’s trial function [13]\(f(t) = 0.95e^{{ - \frac{{a^{2} t^{2} }}{2}}} \frac{\sin bt}{{bt}}\) fits \(e^{x} (t)\) pretty well. The ratio \(b/a\) is close to the ratio of the moments \(M_{4} /M_{2}^{2}\) [14], which in turn, is close to the experimental FID observed in a \({\text{CaF}}_{2}\) single crystal. It should be noticed, that good agreement of classical calculations with experiment can be credited only for the description of dephasing in the spin system, i.e. a signal shape. The time scale, for instance, the location of the first zero of \(e^{x} (t)\), is determined by the value of the parameter \(p_{d}\)—the relaxation speed is nearly proportional to \(p_{d}\). As we already mentioned, this parameter only formally contains spin length, therefore the time scale in classical calculations trivially depends on spin value.

The results for \(N = 10^{3}\) spins are very similar to those for \(N = 7^{3}\), thus several hundreds of classical spins are sufficient for reliable simulations.

How adequately do classical spin simulations describe macroscopic phenomena, like FID, if the number of spins is substantially smaller? For several tens of spins, the collective decay already appears. Figure 2 demonstrates that the first stage, the collective decay of the polarization, looks rather similar for 27 and 125 spins. For the number of spins more than 100, the decay time practically does not change with increasing of \(N\), but in order for the oscillation amplitude to vanish at long times \(t > > 1/\omega_{d}\), several hundred spins, like in Fig. 1, are needed.

3 Quantum Spins

In this section, we briefly describe the results of simulations of FID with quantum spins 1/2. The procedure that we take is exact and straightforward. First, we find the eigenvalues and the eigenvectors of the Hamiltonian (1) and construct the general solution of the Schrödinger equation as the superposition of the time-dependent eigenfunctions of the Hamiltonian:

$$ \Psi (t) = \sum\limits_{k = 1}^{{2^{N} }} {C_{k} \Psi_{k} (t) \, } . $$
(9)

If in the beginning all \(N\) spins were directed along the x axis, the initial wave function \(\Psi_{0} = \Psi (0)\) is determined by the equation

$$ S^{x} \Psi_{0} = \frac{N}{2}\Psi_{0} $$
(10)

where \(S^{x} = \sum\nolimits_{i}^{N} {S_{i}^{x} }\) with \(S_{i}^{x} = I \otimes \ldots \otimes I \otimes S^{x} \otimes I \otimes \ldots \otimes I\); matrix \(S^{x} = \frac{1}{2}\left( {\begin{array}{*{20}c} 0 & 1 \\ 1 & 0 \\ \end{array} } \right)\) is placed in the i -th position, and \(I = \left( {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right)\).

That allows to find coefficients \(C_{i}\) in (9) and then we can find the expectation value of \(S^{x} (t)\):

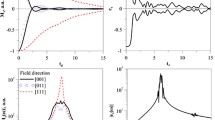
$$ S^{x} (t) = \left\langle {\Psi (t),\hat{S}^{x} \Psi (t)} \right\rangle = \Psi^{*} (t)\hat{S}^{x} \Psi (t) $$
(11)

Function \(S^{x} (t)\) for 12 spins and its Fourier transform are shown in Fig. 3. Note, that for a relatively small number of spins the results are sensitive to spin arrangement. The simulation in Fig. 3 was made for an incomplete cubic lattice: 8 spins arranged in the vertices of a unitary cube with the coordinates (0,0,0), (0,0,1), …, (1,1,0), (1,1,1), and additional four spins, (0,0,− 1), (0, − 1,0), (− 1,0,0), (− 1,0, − 1), arranged around the (0,0,0) point. In such a configuration more spins, like spin (0,0,0), interact with nearest neighbors and some of those spins interact with at least 5–6 nearest neighbors. Different configurations, such as a vertical stack of three horizontal unit squares, where spins do not have as many nearest neighbors, do not lead to complete decay of FID oscillations and do not exhibit a clear two-peak structure, the Pake doublet, which is seen in Fig. 3b with the frequency spread of several \(p_{d} \omega_{0}\) (the value of parameter \(p_{d} = 0.0025\)).

It is interesting to compare the results of quantum and classical calculations. Figure 4 presents the results of quantum (left panel) and classical (right panel) simulations for \(N = 12\) and the same value of constant \(p_{d} = 0.0025\). All magnetic moments are initially directed along the x-axis. Solid lines represent total magnetizations, dashed lines show the evolution of one spin (magnetic moment) located at \((0,0,0)\).

One can notice a qualitative similarity between these two pictures and significant differences. First, the value of parameter \(p_{d}\) should be different in these pictures to have close values of the relaxation time. The quantitative coincidence can be improved when the classical simulations are carried out with the parameter \(p_{d}\) two times larger than that in the quantum simulations. Also notice that the classical simulations of individual magnetic moments,\(\mu_{i} (t)\), do not show similarity with their quantum counterparts. This is not surprising because a quantum spin can quantum-entangle with the others (be a member of a mixed state), contrary to a classical spin. Let us emphasize that the quantum simulations demonstrate the large-time decay of the transverse magnetization rather well even with a relatively small number of spins (\(N = 12\)), while the classical simulations reveal that effect only with several hundreds of spins.

4 Conclusion

The fact that in systems of interacting spins the Heisenberg equations for spin operators \(\hat{\vec{\mu }}_{l}\) have the same form as the equations for classical magnetic moments \(\vec{\mu }_{l}\), partially supports often used modeling of spin system dynamics with classical spins.

The FID gives a good example of a relation between classical and quantum dynamics. The numerical simulations of a classical spin system and the direct solution of the Schrödinger equation for a finite system of spins reveal a qualitative similarity between these two pictures. At the same time, a detailed comparison of results obtained by two different approaches demonstrates some significant differences. Despite the qualitative pictures of ‘beating’ and decay of oscillations being similar, a quantitative coincidence of the classical simulation results with the exact quantum results needs a certain renormalization of parameter \(p_{d}\). Recall that in classical picture spin has an infinite length and the magnitude of a magnetic moment in simulations is just an arbitrary parameter (as well as the value of the parameter \(p_{d}\)). Besides that, the behavior of individual magnetic moments in classical and quantum pictures is very different.

In conclusion, let us mention one more essential difference between quantum and classical spin dynamics. The quantum problem is linear, and its solution is given by formula (9). Therefore, the temporal spectrum of oscillations of any matrix element is finite (though large) and discrete, and it consists just of differences between Hamiltonian eigenvalues. The classical problem is nonlinear, and the spectrum of any observable quantity is typically either discrete with an infinite number of frequencies (quasiperiodic motion) or continuous (chaotic motion), depending on the initial condition. Therefore, one cannot expect that the results of quantum and classical simulations will match each other at any time. Still, it is remarkable that the description of essential physical effects that take place during the initial stage of the process, with all the reservations discussed above, is similar in both cases.

Calculations with a bigger number of quantum spins for different geometries are in progress.