1 Introduction

Hydrides of Group IV elements are a major subject of concern and have been investigated extensively from the theoretical as well as from the experimental point of view. Silicon dihydride SiH2 is one of the simplest Si-containing compounds and is known to be a reactive intermediate species in chemical-vapor deposition process in the silicon semiconductor manufacturing process. SiH2 appears as an important intermediate during decomposition reactions of silane, which have attracted much attention because of their importance in manufacturing amorphous silicon. SiH2 can undergo further dissociation SiH + H or Si + H2. The dissociation processes of the low-lying electronic states of SiH2 have been studied experimentally and theoretically [1–7].

The spectra in the SiH2 stretching region have already been reported [8, 9]. In this work, considered the electron correlation which requires basis sets of much larger size than necessary for Hartree–Fock calculations and is rather expensive when a large number of geometries have to be, we calculated the interaction potential covering a large range in the distance R between the two subsystems. As far as we know, all the PESs calculated before for this title system are either semiempirical or obtained by fitting preexisting but old ab initio calculations. In the present work, we decide to improve previous theoretical results using more accurate basis sets to gain an accurate ab initio PES for the SiH2 complex. In the following section, we present the results of the CCSD (T) interaction energy calculations and the corresponding fits to analytical functions. Section 3 deals with the evaluation, results, and the scattering calculations; then in the last section, we give our conclusion.

2 Computational Details

2.1 Ab Initio Calculations

We all know that the accuracy of the calculation depends on both the selection of the basis set and the choice of the approximation method. In the recent years, the coupled cluster singles-and-doubles method [10] with noniterative inclusion of connected triples [11] [CCSD (T)] has been shown to yield results close to full-configuration-interaction (FCI) for a given basis set [12]. Therefore, in our calculations, we will use the CCSD (T) method.

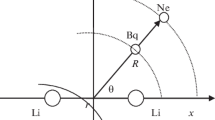
We performed a quantum vibration calculation based on the discrete variable representations [13–15]. The geometries are specified in the conventional Jacobi coordinate system (r,R,θ), as shown in Fig. 1. Here R is the length of the vector connecting the H–H center of mass and the Si atom, θ is the angle between this vector and the H–H bond, and r is the distance of H–H. The bond functions (bf) are centered at the midpoint of R, as a circle shown in Fig. 1.

Fig. 1
figure 1

Coordinates for Si–H2 complex. Bq indicates the position of the bond functions

Full size image

For a given value of R, the angle \(\theta\) changes from 0° to 90° in steps of 10°. The experimentally determined equilibrium value of r e  = 2.19a 0, the interaction energy is calculated for 198 geometries.

  1. 1.

    In the short range \(\left( {1a_{0} \le R \le 2a_{0} } \right)\), we use equally spaced grids with \(\Delta R = 0. 1a_{ 0} ;\)

  2. 2.

    In the well range θ = 87.9° \(\left( { 2a_{ 0} \le R \le 3a_{ 0} } \right)\), we use \(\Delta R = 0. 0 5a_{ 0} ;\)

  3. 3.

    In the long range \(\left( { 4a_{ 0} \le R \le 2 0a_{ 0} } \right)\), with \(\Delta R = 1a_{ 0} .\)

To elect an appropriate basis sets in our computations, we choose different basis sets to perform a series of “test” calculations at geometry of (r e ,θ = 90°). Figure 2 shows how interaction energy of the Si–H2 complex varies with different basis sets for the different R configuration. We can know from the “test” results, for different basis sets, the change of potential energy is basically the same, but it is obvious difference near the potential well. For aug-cc-pCVTZ basis set on Si, the average absolute error is 0.0142605 in the potential well range. Therefore, we use aug-cc-pCVTZ basis sets on Si and aug-cc-pVTZ basis sets on H. We treated electron correlation by using the CCSD (T) method as implemented in G09 for our basis set test calculations.

Fig. 2
figure 2

Energy for the different basis sets for Si at geometry of (r e ,θ = 90°)

Full size image

The potential energy V for a complex AB can be found from the three ab initio total energies of monomer A, monomer B, and dimer AB as \(V = E_{AB} - (E_{A} + E_{B} )\), in the limit of a complete basis set on each atom. We cannot use complete basis sets, and in an incomplete basis set, because of computational limits, an artificial lowering of the potential energy occurs. We use the conventional way to correct it based on the Boys–Bernardi counterpoise method [16].

The expression is as follows:

$$V(R,\theta ) = E_{{{\text{Si}}{-}{\text{H}}_{2} }} \left[ {\chi_{\text{Si}} + \chi_{{{\text{H}}{-}{\text{H}}}} } \right] - E_{\text{Si}} \left[ {\chi_{\text{Si}} + \chi_{{{\text{H}}{-}{\text{H}}}} } \right] - E_{{{\text{H}}_{2} }} \left[ {\chi_{\text{Si}} + \chi_{{{\text{H}}{-}{\text{H}}}} } \right],$$
(1)

where \(E_{{{\text{Si}}{-}{\text{H}}_{ 2} }} \left[ {\chi_{\text{Si}} + \chi_{{{\text{H}}{-}{\text{H}}}} } \right]\) is the energy of the complex, \(E_{\text{Si}} \left[ {\chi_{\text{Si}} + \chi_{{{\text{H}}{-}{\text{H}}}} } \right]\) and \(E_{{{\text{H}}_{ 2} }} \left[ {\chi_{\text{Si}} + \chi_{{{\text{H}}{-}{\text{H}}}} } \right]\) are the energies of monomers Si and H2, respectively.

2.2 Analytical Representation of the PES

We fit the interaction potential to an empirical function in the following form [17]:

$$V\left( {q,R,q} \right) = V_{\text{as}} \left( {q,R,q} \right) + V_{\text{sh}} \left( {q,R,q} \right),$$
(2)

where the \(V_{\text{as}} \left( {q,R,\theta } \right)\) denotes asymptotic interaction energy components, and \(V_{\text{sh}} \left( {q,R,\theta } \right)\) denotes a short range. We define q by q = r i  − r e , where r e denotes a certain value of the H–H bond length which is used as a reference value. In the present case, we use r e  = 1.095\(a_{0}\). The asymptotic term \(V_{\text{as}} \left( {q,R,\theta } \right)\) is of the form:

$$V_{\text{as}} \left( {q,R,\theta } \right) = \frac{{f_{6} \left[ {B(q,\theta )R} \right]}}{{R^{6} }}\left[ {C_{6}^{0} (q) + C_{6}^{2} (q)P_{2} (\cos \theta )} \right],$$
(3)

where the term \(f_{6} (x)\) is the Tang and Toennies damping function [18] defined by

$$f_{6} (x) = 1 - e^{ - x} \sum\limits_{k = 0}^{6} {\frac{{x^{k} }}{k!}} .$$
(4)

The functional form of the short-range part of \(V\left( {q,R,\theta } \right)\) is as below:

$$V_{\text{sh}} \left( {q,R,\theta } \right) = G\left( {q,R,\theta } \right)e^{{\left[ {D(q,\theta )\; - \;B(q,\theta )R} \right]}} ,$$
(5)

where \(D(q,\theta )\), \(B(q,\theta )\), and \(G(q,R,\theta )\) all denote expansions in Legendre polynomials:

$$D\left( {q,\theta } \right) = \sum\limits_{l = 0}^{{L_{1} }} {d^{l} \left( q \right)P_{l} \left( {\cos \theta } \right)} ,$$
(6)
$$B\left( {q,\theta } \right) = \sum\limits_{l = 0}^{{L_{2} }} {b^{l} \left( q \right)P_{l} \left( {\cos \theta } \right)} ,$$
(7)
$$G\left( {q,R,\theta } \right) = \sum\limits_{l = 0}^{{L_{2} }} {\left[ {g_{0}^{l} \left( q \right) + g_{1}^{l} \left( q \right)R + g_{2}^{l} \left( q \right)R^{2} + g_{3}^{l} \left( q \right)R^{3} } \right]P_{l} \left( {\cos \theta } \right)} ,$$
(8)

\(P_{l} \left( {\cos \theta } \right)\) in Eqs. 6, 7, and 8 represents a Legendre polynomial of order l. By considering of the symmetry only, even orders are allowed with L 1 = 8, L 2 = 8.

All adjustable parameters in Eqs. 4, 5, 6, 7, and 8 are further expressed in the form of \(y\left( q \right) = y_{0} + y_{1} q + y_{2} q^{2},\) where y denotes one of the following: \(d^{l} ,b^{l} ,g_{n}^{l}\) or \(C_{6}^{l}\). There are 96 parameters in the fitting. In Table 1, we present all the fitted results of the parameters, the 198 ab initio points on the PES are fitted to a 96-parameter algebraic. In order to test the accuracy, we compare the interaction energies predicted by our three-dimensional PES with the ab initio values calculated at the location of the potential well. The theoretical results in this work with an average absolute error of 0.3425 % and a maximum error less than 4.0072 % are compared with the ab initio values calculated.

Table 1 Fitted parameters of the potential energy surface
Full size table

3 Potential Energy Surface and Computational Method

In Fig. 3, from ten different anglers, we show the behavior of the potential as a function of the Si–H2 separation for a number of relative orientations for H2 fixed at equilibrium distance. We can see that in the long range for all angles, the interaction energy almost converges to the same asymptotic value.

Fig. 3
figure 3

Orientation features of the potential energy surface of Si–H2

Full size image

When R < 4a 0, as the R increasing induces the potential energy reducing, the potential is mainly of repulsion, while for the R > 4a 0, potential energy surface change leveled off. We can clearly see that the well is at θ = 87.9° which is the same as the experimental data θ = 92.1°, at R = 2.86a 0. The depth is 0.12339 cm−1. The results fit well with the experiment results. We put the results listed in Table 2.

Table 2 Comparison of the experimental data
Full size table

In Fig. 4, we show the contour plots of the new PES for the Si–H2 complex. There is a single global minimum located in a nearly T-shaped geometry. The potential is rather flat, making possible large amplitude motions. The figure shows that the PES presents mainly isotropic interactions and weak anisotropy. The depth is shallower than the others; the reason may be the lack of a proper correction for BSSE and the smaller basis sets used in their calculations.

Fig. 4
figure 4

Contour plots of the potential for Si–H2 complex at r = r e . Contours are labeled in eV

Full size image

In Fig. 5, the potential energy surface shows a mostly shallow attractive van der Waals minimum, which is due to electron correlation effects, resulting in dispersion forces that cannot be examined at the Hartree–Fock level. In the intermediate region, Hartree–Fock repulsion and dispersion attraction are of about the same magnitude but opposite in sign.

Fig. 5
figure 5

3D view of the interaction potential for Si–H2 complex at r = r e

Full size image

In order to get more detailed study of the potential energy surface, we draw the close shot in Fig. 6. One can easily see the mainly isotropic interaction and the well-defined molecular core identified by the repulsive regions which show vanishing angular dependence for this very weakly bound van der Waals complex. The interaction energy potential well position is clearly displayed.

Fig. 6
figure 6

Close shot for the three-dimensional potential energy surface

Full size image

4 Concluding Remarks

The first three-dimensional PES for the interaction of rigid H2 with Si has been calculated using CCSD (T) theory, with full counterpoise corrections and a large basis set including bond functions. The 198 ab initio points on the PES are fitted to a 96-parameter algebraic form with an average absolute error of 0.3425 % and a maximum error less than 4.0072 %.

A comparison of the characteristics of our fitted CCSD (T) surface with previous ones indicates that it seems to satisfy the criteria believed [21] necessary to obtain agreement with a wide variety of experimental data pertaining to beam scattering, transport phenomena, and relaxation phenomena. Extensive tests will be required to determine whether this is so. We think that our CCSD (T) surface is unlikely to differ from the true PES by more than 10 % over the range of intermolecular distances (2a 0–6a 0) sampled in this work. Unlike the older surfaces, our PES has the anisotropy thought to be required for a proper description of experimental data. We invite further work to test this assertion; therefore, this work should provide useful information for further experimental and theoretical studies.