Privatization in the presence of patent licensing

Abstract

This paper analyzes the licensing policy for a cost-reduction technology of a foreign R&D institution when it is faced with a domestic monopoly manufacturer. It is found that, due to objective differences, a public domestic manufacturer will be charged higher than a private domestic manufacturer for a certain licensed technology. Accordingly, to save on the licensing payment made to the foreign R&D institution, the domestic government is recommended to (partly) privatize the public manufacturer.

1 Introduction

Technology is an important factor in the process of economic development. For firms in developing countries, one way of acquiring or improving their technologies is to get it from firms in developed countries that have been involved in generating state-of-the-art know-how (Marjit and Mukherjee 1990). Meanwhile, technology firms in developed countries are increasingly using licensing to exploit knowledge-based assets in global markets (Aulakh et al. 2010). According to Arora and Gambardella (2010), the international flow of royalty payments and receipts increased at $9.8$ and $5.6\,{\%}$, respectively, in 1990–2003. Another fact is that, public or partly public enterprises constitute a significant part of the economy of a developing country. For example, as of 1996, public and collective-owned sectors in China accounted for about half of the gross industrial output value (Chao and Yu 2006). Even in some OECD countries, public firms can represent up to 40 % of value added and 10 % of employment (Van Long and Stähler 2009). Against this background, this paper analyzes the licensing policy of a foreign R&D institution when it is faced with a (partly) public domestic manufacturer.

In addition to the empirical reasons, the topic of this paper also deserves attention for the theoretical interest. In economics, it is often assumed that a (private) firm pursues the maximization of its own profit. In contrast, a public or state-owned firm is usually considered to be a welfare-maximizer (see, for example, De Fraja and Delbono 1987; Bös and Peters 1988; Cremer et al. 1989; Fjell and Pal 1996; Pal and White 1998; Anderson et al. 1997; Matsumura 1998). The existence of public enterprises and their unique objectives encourage researchers to reevaluate some classic conclusions drawn under the private enterprises framework, such as the analysis of the continental common market comprised of national firms (Corneo and Jeanne 1992), the relative dominance of the price and quantity strategies (Ghosh and Mitra 2010; Matsumura and Ogawa 2012), the endogenous timing of movement (Pal 1998; Matsumura 2003; Amir and De Feo 2013), the free entry issues (Sertel 1988; Matsumura and Kanda 2005), the capacity choice (Willner 1994; Lu and Poddar 2005), and the foreign direct investment decisions (Mukherjee and Suetrong 2009; Naya 2010), just to name a few. As a natural continuation of this line of thought, patent licensing in the presence of a public rather than private licensee is discussed in this paper.

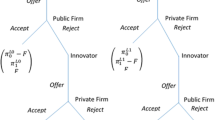
Consider a simple model with a foreign non-producing R&D institution and a domestic manufacturer. The domestic manufacturer is a monopoly in the domestic market and it can be fully public, fully private, or jointly owned by public and private sectors. The foreign R&D institution owns a cost-reduction technology and considers making a take-it-or-leave-it licensing offer to the domestic manufacturer. The ownership structure of the manufacturer, which is assumed to be determined by the domestic government, will influence the licensing policy of the foreign R&D institution and then the domestic welfare.

Suppose that initially the domestic manufacturer is fully public owned; then, in the presence of inward international licensing, the domestic government may have incentives to privatize the manufacturer. The main reason is that privatization helps to save on the licensing payment made to the foreign R&D institution (the pros of privatization). Generally speaking, application of the new technology raises the surplus of both manufacturer and consumers. The public owners of the manufacturer takes total surplus into consideration when making the evaluation of the new technology, whereas the private owners cares only about the manufacturer surplus. As a standard method to resolve the conflict between the two interest groups, the manufacturer as a whole is supposed to maximize the weighted sum of manufacturer and total surplus. Presumably, the weight placed on the manufacturer surplus will increase when the proportion of shares the private sectors hold increases. Given this, it can be anticipated that the manufacturer’s willingness to pay for the licensed technology will decrease when it is further privatized. Under licensing, a licensee with a lower willingness to pay for the new technology will be charged lower in equilibrium.

Privatization, however, is not without cost. Unless the manufacturer is fully public owned, due to monopoly pricing (i.e., excessive price-cost margins), there exists a deadweight loss in the domestic market. And, the deadweight loss will increase when the proportion of shares the private sectors hold increases. That is the cons of privatization.

The domestic government weighs the pros and the cons to determine the optimal level of privatization. It is proved that some degree of privatization is always conducive to enhancing domestic welfare. Put differently, a fully public ownership is never the best choice in the presence of international licensing. Furthermore, intuition indicates that the optimal privatization level should increase when the foreign technology becomes more significant in cost reduction (hence the saving in licensing fees associated with privatization increases) or the market demand becomes more elastic (hence the increase in the deadweight loss associated with privatization is alleviated).

The remainder of this paper is organized as follows. Related literature is reviewed in Sect. 2. Section 3.1 lists the basic model setup and introduces a four-stage game. The analysis of the game is conducted in Sect. 3.2. Section 3.3 is a comparative static analysis of the equilibrium level of privatization. By introducing the break-even constraint for the domestic manufacturer, Sect. 4 discusses the robustness of the conclusions derived in the paper. Section 5 summarizes the main results.

2 Related literature

Most previous studies on patent licensing are confined to the setting that the prospective licensees are all profit-maximizers. For instance, Kamien and Tauman (1986) explored how much profit an external owner of a cost-reduction innovation can realize by licensing it to a private oligopoly by means of fixed fees or per-unit royalties. Licensing by means of an auction was analyzed in Katz and Shapiro (1985). Katz and Shapiro (1985) analyzed the licensing policy when the patentee existed as an internal competitor of the prospective licensees. Later researchers extended the early studies in different ways. Representative contributions include Rockett (1990), Marjit (1990), Wang (1998), Kabiraj and Mukherjee (2000), Mukherjee and Balasubramanian (2001), Faulí-Oller and Sandonís (2002), Poddar and Sinha (2004), Sen (2005), Saracho (2005), Sen and Tauman (2007), Tauman and Weng (2012), to name but a few.

Although the vast majority of the licensing literature took the private ownership as a default assumption, a few noticed that the ownership structure of the prospective licensees might have a bearing on a patentee’s licensing strategy. As mentioned in the preceding paragraph, per-unit royalty and fixed fee are two common licensing payment collection mechanisms. Under the private oligopoly framework, it is usually the case that fixed-fee payment is superior to per-unit royalty payment when the patentee exists as an external licensee and the relationship is reversed when the patentee is an internal licensee. In contrast to this, Lu et al. (2009) explored a foreign patentee’s optimal licensing strategy when faced with a publicly owned domestic monopoly enterprise (the external case) and demonstrated that the two payment collection mechanisms are equally profitable. Through a model with a less-efficient foreign private firm and a more-efficient domestic public firm competing in the domestic market (the internal case), Ye (2012) demonstrated that it is always optimal for the public firm to license to the foreign competitor and licensing by a fixed fee is superior to licensing by a royalty. As an extension to Ye (2012), Mukherjee and Sinha (2014) and Chen et al. (2014) explored internal licensing between private and public firms under the assumption that the private firm enjoyed a technological superiority.

This paper is similar in many respects with Lu et al. (2009), but with significant differences. First, the analysis in this paper is conducted under a general demand setting rather than linear demand. Second, in this paper the domestic manufacturer can be fully public, fully private, or jointly owned by public and private sectors, whereas in Lu et al. (2009) it is either fully private or fully public and the issue of partial privatization is not addressed. Third, the analysis in Lu et al. (2009) critically depends on the assumption that the public manufacturer must at least break even, whereas this paper also covers the case when the break-even constraint is relaxed. Sometimes, it is reasonable to relax the break-even constraint because the government may provide extra financial assistance for technological upgrading of domestic firms.¹ Lastly, this paper makes clear the pros and cons associated with privatization in the presence of international licensing, which are not stated explicitly in Lu et al. (2009).

3 The model

3.1 Setup

Consider a case with one manufacturing firm and one R&D institution. The R&D institution is located abroad and it does not produce in or export to the domestic market. The manufacturer is a domestic firm and it is jointly owned by public and private sectors. The private owners’ interest is to maximize the manufacturer’s profits, whereas the public owners’ interest is to maximize domestic welfare (the sum of consumer surplus and profits by the manufacturer). As a compromise between the two interest groups, the manufacturer as a whole is assumed to maximize the weighted average of domestic welfare and its own profits, i.e.,

$$\begin{aligned} (1-\theta ) \times [\text{ Domestic } \text{ Welfare }]+ \theta \times [\text{ Profits }], \end{aligned}$$

(1)

where $\theta \in [0,1]$ is the proportion of the manufacturer’s shares held by private sectors.

The inverse demand function is given by $p(q)$, where $p$ and $q$ respectively denote the manufacturer’s price and quantity. Suppose that the manufacturer has a constant marginal cost of production, $c$, and there is no fixed costs or capacity limits; then, the objective function of the manufacturer can be expressed as

$$\begin{aligned} R(q)=(1-\theta )\left[ \int _{0}^{q} p(t) dt - c q\right] +\theta [p(q)q-cq]. \end{aligned}$$

(2)

The R&D institution has a new technology, which can decrease the marginal production cost of the manufacturer by $x$, where $x \in (0,c]$. The R&D institution considers selling the new technology to the manufacturer via two-part tariff licensing. Under two-part tariff licensing, the licensing revenues are collected according to

$$\begin{aligned} r q+F, \end{aligned}$$

(3)

where $(r \ge 0)$ is the per-unit royalty rate, $q$ is the manufacturer’s output, and $(F \ge 0)$ is the fixed fee. If licensing occurs, the objective function of the manufacturer will be expressed as

$$\begin{aligned} \hat{R}(q)=(1-\theta )\left[ \int _{0}^{q} p(t) dt - (c-x) q-r q-F\right] +\theta [p(q)q-(c-x)q-r q-F]. \end{aligned}$$

(4)

Given the above setup, a four-stage game is considered. The timing of it is as follows. In the first stage, the domestic government selects the level of privatization, $\theta$. In the second stage, the R&D institution makes a take-it-or-leave-it licensing offer (which specifies $r$ and $F$) to the manufacturer. In the third stage, the manufacturer decides to accept or reject the offer. In the forth stage, the manufacturer decides on the level of output.

Before solving the game, the following assumptions are made on the inverse demand function:

Assumption 1

$p(0)>c$ and $\lim \limits _{q \rightarrow \infty } p(q) =0$;

Assumption 2

$p(q)$ is twice continuously differentiable and decreasing as long as $q \ge 0$;

Assumption 3

$2 p^{\prime }(q)+ p^{\prime \prime }(q) q <0 \quad {\text { for all}}\, q \in [0,\infty )$.

The last assumption implies that the marginal revenue for a monopoly manufacturer is decreasing in the output. These assumptions are standard in the literature and their roles will become obvious in due course.

3.2 Equilibrium

The backward induction approach is used to solve for the subgame perfect Nash equilibrium of the four-stage game.

3.2.1 The forth stage

Without licensing, in the forth stage of the game, the manufacturer will select $q$ to maximize $R(q)$. And, the optimal output level, denoted by $q^*$, is determined according to the following first-order condition²

$$\begin{aligned} p(q)+\theta p^{\prime }(q)q-c=0. \end{aligned}$$

(5)

If licensing occurs, however, the manufacturer will select $q$ to maximize $\hat{R}(q)$. In this case, the optimal output level, denoted by $q^{**}$, is determined as follows³

$$\begin{aligned} p(q)+\theta p^{\prime }(q)q-(c-x)-r=0. \end{aligned}$$

(6)

Before turning to the analysis of the third stage of the game, it is useful to know that both the manufacturer’s equilibrium payoff without licensing and the equilibrium output with licensing are decreasing functions with respect to $\theta$.

Lemma 1

$\partial R(q^*) / \partial \theta <0\quad {\text {and}}\, \partial q^{**} / \partial \theta <0$.

Proof

Given 2 and 5, it can be proved that $\partial R(q^*) / \partial \theta =[p(q^*)+\theta p^{\prime }(q^*)q^*-c][\partial q^* / \partial \theta ] -[\int _{0}^{q^*} p(t) dt - c q^*] +[p(q^*)q^*-cq^*]=- \int _{0}^{q^*} p(t) dt+p(q^*)q^*<0$. Totally differentiating both sides of 6 with respect to $\theta$, the following result can be derived, $\partial q^{**} / \partial \theta = - p^{\prime }(q^*)q^* / [(1+\theta )p^{\prime }(q^*)+\theta p^{\prime \prime }(q^*) q^*]$. According to Assumption 2 and 3, $(1+\theta )p^{\prime }(q^*)+\theta p^{\prime \prime }(q^*) q^*=(1-\theta )p^{\prime }(q^*)+\theta [2 p^{\prime }(q^*)+ p^{\prime \prime }(q^*) q^*]<0$; then, $\partial q^{**} / \partial \theta <0$. $\square$

3.2.2 The third stage

In the third stage of the game, the manufacturer decides whether or not to accept the licensing offer. As a common practice, it is assumed that the manufacturer will accept the offer if it is indifferent between acceptance and rejection. Then, the licensing offer will be accepted only if $\hat{R}(q^{**}) \ge R(q^*)$ (the participation constraint).

3.2.3 The second stage

In the second stage of the game, the R&D institution selects $r$ and $F$ to maximize the licensing revenue. The decision-making process can be modelled as follows

$$\begin{aligned} \max _{r,F} \, r q^{**}+F \quad \text{ s.t. } \, \hat{R}(q^{**}) \ge R(q^*). \end{aligned}$$

(7)

The solutions to 7 are denoted by $r^*$ and $F^*$, respectively.

From 4 and 7, it is straightforward to infer that, when taking the optimal licensing contract terms, the manufacturer’s participation constraint must be binding, i.e.,

$$\begin{aligned} \hat{R}(q^{**})|_{r=r^*,F=F^*}=R(q^*). \end{aligned}$$

(8)

Given this, the optimization problem specified by 7 can be rewritten as

$$\begin{aligned} \max _{r} \, (1-\theta ) \int _{0}^{q^{**}} p(t) dt +\theta p(q^{**})q^{**}-(c-x)q^{**}-R(q^*). \end{aligned}$$

(9)

It can be proved that the corresponding optimal royalty rate is zero.⁴ In other words, $r^*=0$. Then, the optimal fixed fee can be expressed as $F^*=[(1-\theta ) \int _{0}^{q^{**}} p(t) dt +\theta p(q^{**})q^{**}-(c-x)q^{**}]|_{r=0}-R(q^*)$.

For convenience of illustration, the equilibrium of the second stage of the game and a comparative static analysis on the license revenue are summarized below.

Lemma 2

Fixed fee licensing occurs in equilibrium and the equilibrium fixed fee is a decreasing function of $\theta$, i.e., $r^*=0$ and $\partial F^* / \partial \theta <0$.

Proof

Let $M=(1-\theta ) \int _{0}^{q^{**}} p(t) dt +\theta p(q^{**})q^{**}-(c-x)q^{**}-R(q^*)$; then, $\partial M / \partial r =[p(q^{**}) +\theta p^{\prime }(q^{**})q^{**}-(c-x)][\partial q^{**} / \partial r ]$. From 6, it is known that $p(q^{**}) +\theta p^{\prime }(q^{**})q^{**}-(c-x)=r$. From Lemma 1, it is known that $\partial q^{**} / \partial r<0$. Accordingly, to maximize $M$, the optimal royalty rate should be zero, i.e., $r^*=0$. Given that $r^*=0$, the optimal fixed fee would be $F^*=[(1-\theta ) \int _{0}^{q^{**}} p(t) dt +\theta p(q^{**})q^{**}-(c-x)q^{**}]|_{r=0}-R(q^*)$. Accordingly, $\partial F^* / \partial \theta = [q^{**} +\theta p^{\prime }(q^{**})q^{**}-(c-x)]|_{r=0}[\partial q^{**} / \partial \theta ]- [\int _{0}^{q^{**}} p(t) dt-p(q^{**})q^{**}]|_{r=0}-[\partial R(q^*) / \partial \theta ]$. According to 6, $q^{**} +\theta p^{\prime }(q^{**})q^{**}-(c-x)=0$ if $r=0$. From the proof of Lemma 1, it is known that $\partial R(q^*) / \partial \theta =- \int _{0}^{q^*} p(t) dt+p(q^*)q^*$. Then, $\partial F^* / \partial \theta =[\int _{0}^{q^*} p(t) dt-p(q^*)q^*]- [\int _{0}^{q^{**}} p(t) dt-p(q^{**})q^{**}]|_{r=0}$. The comparison of 5 and 6 indicates that $q^{**}>q^*$ if $x>0$ and $r=0$. It can also be proved that $\partial [\int _{0}^{q} p(t) dt-p(q)q] / \partial q= -p^{\prime }(q)q >0$ for $q>0$, which means $[\int _{0}^{q^{**}} p(t) dt-p(q^{**})q^{**}]|_{r=0}>\int _{0}^{q^*} p(t) dt-p(q^*)q^*$. Accordingly, $\partial F^* / \partial \theta <0$. $\square$

It can be seen that fixed fee is the most profitable payment collection mechanism for an external licensor, which is a standard conclusion in the licensing literature. More importantly, Lemma 2 implies that the licensing revenue decreases along with the deepening of privatization. The intuition behind the latter conclusion is explained below.

In general, application of a new cost-reduction technology benefits both manufacturer and consumers. Due to objective differences, when making the evaluation of a new technology, only the public manufacturer takes the consumer benefit into consideration.⁵ Consequently, a public manufacturer has a higher willingness to pay for a certain licensed technology than a private manufacturer. Accordingly, the licensing revenue when the R&D institution is faced with a private manufacturer should be lower than that when it is faced with a public manufacturer. As a continuous version of this story, $F^*$ is proved to be a decreasing function of $\theta$.

3.2.4 The first stage

In the first stage of the game, the domestic government selects the level of privatization to maximize domestic welfare. Combined with the above analysis, the optimal level of privatization, denoted by $\theta ^*$, will be specified by the following optimization problem

$$\begin{aligned} \max _{\theta } \, W=\int _{0}^{q} p(t) dt -(c-x)q-F^*, \end{aligned}$$

(10)

with $q=q^{**}|_{r=0}$.

Differentiating the objective function of 10 with respect to $\theta$, the following result can be derived

$$\begin{aligned} \frac{\partial W}{\partial \theta }=\underbrace{[p(q)-(c-x)] \frac{\partial q}{\partial \theta }}_{\text{ negative }} +\overbrace{\left[ -\frac{\partial F^*}{\partial \theta }\right] }^{\text{ positive }}. \end{aligned}$$

(11)

It can be seen that increasing the level of privatization has two opposing effects on domestic welfare, which are captured by the right hand side of 11. On the one hand, as $\theta$ increases, the licensing payment made to the foreign R&D institution will dicrease, represented by $- \partial F^* / \partial \theta >0$. On the other hand, an increase in $\theta$ will raise the monopolistic deadweight loss in the final product market, represented by $[p(q)-(c-x)] ( \partial q / \partial \theta )< 0$.⁶

To sum up, the benefit of privatization is that it decreases the licensing payment for a certain foreign technology and the downside of privatization is that it increases the deadweight loss in the domestic final product market. To determine the optimal level of privatization, the domestic government needs to strike a balance between the tradeoffs.

Proposition 1

In the presence of international licensing, the domestic government will always have an incentive to privatize (probably partly) a fully public manufacturer, i.e., $\theta ^*>0$ as long as $x>0$.

Proof

According to 6 and the fact $r=0$, $p(q)-(c-x)=-\theta p^{\prime }(q)q$. That means that, at $\theta =0$, $\partial W / \partial \theta =- \partial F^* / \partial \theta$. From the proof of Lemma 2, it is known that $\partial F^* / \partial \theta <0$ if $x>0$. Hence, in the presence of licensing, the optimal level of privatization should be positive, i.e., $\theta ^*>0$ if $x>0$. $\square$

In the literature on mixed oligopolies, privatization of public firms can be warranted for several reasons (refer to Heywood and Ye 2010 for a brief summary). A representative argument can be found in Matsumura (1998): a welfare-maximizing public firm tends to produce more than a profit-maximizing private firm generating a cost inefficiency when there is an increasing marginal cost.

By adopting a setting with a constant marginal cost, this paper assumes away the improvement in production efficiency associated with privatization.⁷ In stead, it argues that the domestic government has an incentive to privatize the public firm because doing that helps to save on the licensing payment made to the foreign licensor. That constitutes a new explanation for the privatization waves in developing regions.

3.3 An example

In the above analysis, it is shown that the introduction of international licensing provides a justification for domestic privatization. This subsection performs a comparative static analysis of the optimal privatization level.

For tractability, it is assumed that the domestic manufacturer is faced with a constant elasticity demand function, $p(q)=q^{-1/\eta }$ with $\eta >1$. If other settings remain unchanged, the optimal level of privatization would be⁸

$$\begin{aligned} \theta ^*=\frac{\eta [1-(1-x/c)^{\eta -1}]}{\eta -(1-x/c)^{\eta -1}}. \end{aligned}$$

(12)

Given this, the following conclusion can be derived.

Proposition 2

The domestic government will deepen privatization when the foreign technology becomes more significant or the elasticity of the demand increases, i.e., $\partial \theta ^* / \partial x >0$ and $\partial \theta ^* / \partial \eta >0$.

The intuition behind Proposition 2 is as follows. It is already known that privatization decreases the licensing payment made to the foreign R&D institution (pros of privatization) and increases the deadweight loss in the domestic final product market (cons of privatization). When the foreign technology becomes more significant ($x$ increases), the licensing payment savings become larger, which strengthens the pros of privatization. When the demand becomes more elastic ($\eta$ increases), the monopoly power of a private manufacturer (and then the associated deadweight loss in the domestic final product market) decreases, which weakens the cons of privatization. As a result, $\theta ^*$ will increase when $x$ or $\eta$ increases.

4 Discussion

It should be pointed out that, in the above analysis, when licensing occurs the domestic manufacturer may earn negative profits. As an extreme example, suppose that the manufacturer is fully public, i.e., $\theta =0$; then, according to 6, its profits under licensing would be $-F$, which is negative. With negative profits, it is difficult to explain how the manufacturer raises funds to purchase the licensed technology. Mukherjee and Sinha (2014) suggested that the government could raise the money to finance the fee for the licensed technology by imposing a tax on the consumers.

However, it is well known that distortionary taxation induces a deadweight loss. Taking this into account, Capuano and De Feo (2010) incorporated the shadow price of public funds into the objective function of the public firm. Suppose that the shadow cost is sufficiently large. It follows that the public firm should not expect money transfer from the government and should assume sole responsibility for its profits. Accordingly, in the mixed oligopoly literature, it is usually recommended to impose a break-even constraint on the (partly) public firm (see, for example, Cremer et al. 1989; Estrin and De Meza 1995).

Ignoring the break-even constraint, it is known from 5 that the manufacturer’s equilibrium profit without licensing can be expressed as $-\theta p^{\prime }(q^*){q^*}^2$, which is non-negative. That means introducing the break-even constraint will make no difference and the manufacturer’s equilibrium profit without licensing would remain $R(q^*)$.

In the forth stage of the game, if licensing occurs, the output decision with the break-even constraint will be made according to the following optimization problem,

$$\begin{aligned} \max _{q} \, \hat{R}(q) \quad \text{ s.t. } \, p(q)q-(c-x)q-r q-F \ge 0. \end{aligned}$$

(13)

When $q$ takes the optimal solution, there are two possibilities: the break-even constraint is either binding or not binding. The case when the constraint is not binding is already covered by the above analysis. The following analysis focuses on the case when the break-even constraint is binding, i.e.,

$$\begin{aligned} p(q)q-(c-x)q-r q-F=0. \end{aligned}$$

(14)

From 4 and 14, it is known that the manufacturer’s equilibrium payoff under licensing can be expressed as

$$\begin{aligned} \hat{R}(q)=(1-\theta )\left[ \int _{0}^{q} p(t) dt -p(q)q \right] . \end{aligned}$$

(15)

Then, in the third stage of the game, the manufacturer will accept the licensing offer only if $\hat{R}(q) \ge R(q^*)$ (the participation constraint).

In the second stage of the game, the R&D institution selects the licensing contract terms to maximize $r q+F$ given the manufacturer’s participation constraint, i.e.,

$$\begin{aligned} \max _{r,F} \, r q+F \quad \text{ s.t. } \, \hat{R}(q) \ge R(q^*). \end{aligned}$$

(16)

Given 14 and 15, 16 can be equivalently restated as follows

$$\begin{aligned} \max _{q} \, p(q)q-(c-x)q \quad \text{ s.t. } \, (1-\theta )\left[ \int _{0}^{q} p(t) dt -p(q)q\right] \ge R(q^*). \end{aligned}$$

(17)

Then, the following conclusions can be derived.

Lemma 3

In the case when the break-even constraint is binding, the foreign R&D institution’s licensing revenue will remain unchanged or decrease when the domestic manufacturer is further privatized and the equilibrium output of the domestic manufacturer under licensing will remain unchanged or increase when it is further privatized.

Proof

From 2, it is known that $R(q^*)=(1-\theta )[\int _{0}^{q^*} p(t) dt - c q^*] +\theta [p(q^*)q^*-cq^*]=(1-\theta )[\int _{0}^{q^*} p(t) dt -p(q^*)q^*]+[p(q^*)q^*-cq^*]$. Then, the constraint of the optimization problem specified by 17 can be rewritten as $[\int _{0}^{q} p(t) dt -p(q)q]-[\int _{0}^{q^*} p(t) dt-p(q^*)q^*] \ge \theta [p(q^*)q^*-cq^*] / (1-\theta )$. From 5, it is known that $p(q^*)q^*-cq^*=-\theta p^{\prime }(q^*){q^*}^2>0$ for $\theta >0$. Accordingly, $[\int _{0}^{q} p(t) dt -p(q)q]-[\int _{0}^{q^*} p(t) dt-p(q^*)q^*]>0$. From the proof of Lemma 1, it is known that $\partial R(q^*) / \partial \theta =- \int _{0}^{q^*} p(t) dt+p(q^*)q^*$. Let $N=(1-\theta )[\int _{0}^{q} p(t) dt -p(q)q] - R(q^*)$; then, it can be proved that $\partial N / \partial \theta =[\int _{0}^{q^*} p(t) dt-p(q^*)q^*]-[\int _{0}^{q} p(t) dt -p(q)q]<0$ and $\partial N / \partial q=-(1-\theta )p^{\prime }(q)q>0$ for $\theta <1$. Suppose the solution to $N=0$ is $\bar{q}(\theta )$; then, the constraint $N \ge 0$ will be equivalent to the constraint $q \ge \bar{q}(\theta )$. Furthermore, it can be proved that $\bar{q}^{\prime }(\theta )>0$. To sum up, increasing $\theta$ will decrease the admissible outputs specified by the constraint of 17. As the objective function of 17 is independent of $\theta$, a higher $\theta$ will possibly lead to a lower licensing benefit. As the constraint of the optimization problem is $q \ge \bar{q}(\theta )$ and $\bar{q}^{\prime }(\theta )>0$, it is straightforward to conclude that the optimal output under a higher $\theta$ should be equal to or higher than the optimal output under a lower $\theta$. $\square$

It can be seen that privatizing the domestic manufacturer may increase the output in the final product market and may also reduce the payment for a certain licensed foreign technology. Both effects tend to increase domestic welfare.⁹ That means that, in the case when the break-even constraint is binding, the domestic government would have an even stronger incentive to privatize the manufacturer. That confirms the robustness of the conclusions of this paper.

To end the analysis in this section, how the presence or absence of the break-even constraint will influence the licensing policy of the foreign R&D institution is briefly presented below.¹⁰

Lemma 4

When the break-even constraint is binding, the maximum licensing revenue is independent of the licensing contract terms and fixed fee licensing, royalty licensing, and two-part tariff licensing can be equally profitable.

Strictly speaking, suppose that the solution to 17 is $\tilde{q}$; then, the maximum licensing revenue can be achieved under any combination of $r$ and $F$ that satisfies the equation, $p(\tilde{q})\tilde{q}-(c-x)\tilde{q}-r \tilde{q}-F = 0$. Relaxing the break-even constraint, however, fixed fee licensing would be the most profitable licensing mechanism (see Lemma 2).

5 Conclusion

It is already known that the government can strategically manipulate the objective function of the domestic firm in order to maximize domestic welfare (see, for example, De Fraja and Delbono 1989). The present paper provides another example of such theoretical result in the context of international technology licensing. In particular, this paper analyzes the licensing policy for a cost-reduction technology of a foreign R&D institution when it is faced with a domestic public manufacturer. It is shown that, due to objective differences, a public manufacturer will be charged higher than a private manufacturer. Accordingly, to save on the licensing fees, the domestic government is recommended to (partly) privatize the public manufacturer. This conclusion provides a new explanation for the privatization waves in developing regions.