Numerical study of refill friction stir spot welding of dissimilar metallic materials using smoothed particle hydrodynamics (SPH)

Abstract

Refill friction stir spot welding (RFSSW) has found several industrial applications, especially in the transportation and automotive sectors. However, modeling the RFSSW process has been tackled mainly with empirical approaches. At the same time, the key physical phenomena involved have been explained and predicted by a few numerical studies in the literature. This study uses a fully Lagrangian method, smoothed particle hydrodynamics (SPH), for the simulation of RFSSW. The Lagrangian particle method simulates materials undergoing large deformation, interface dynamic changes, void formations, material temperature, and strain evolution without using complex tracking schemes often required by traditional grid-based methods. As a relevant example, magnesium-to-steel welding simulation is presented by accounting for all the main thermo-mechanical phenomena involved. Temperature, stress, and strain field histories as well as material flow taking place during the process, are determined as characteristic aspects for qualification of RFSSW; the proposed computational approach is validated by comparing the predicted and experimentally measured welding temperature. The results obtained demonstrate that SPH is a reliable tool for welding design and process optimization and provides the information related to the involved physics needed to precisely evaluate the quality, the mechanical characteristics, and the material flow of the joined region.

1 Introduction

Many applications require joining metals having different compositions. Similarly, in weight reduction problems, high-temperature or extreme condition applications, various parts having different properties are often used in the same weldment.

Consequently, the requirement to join dissimilar metals arises. Welding dissimilar metals must guarantee the mechanical characteristics to be at least as those of the weakest among the two metals being joined; in other words, welding must have sufficient tensile strength and ductility to ensure reliability and safety during the entire service life of the structural component. Multiple materials joints are obtained by using a variety of different metals welded together by a number of welding processes.

The low density, high strength, and sound-dampening properties of magnesium alloys make them competitive materials for the automotive industry [1]; despite the above-mentioned advantages, steel remains the dominant structural material owing to its excellent ductility, strength, and low fabrication costs [2]. As far as real applications are concerned, magnesium alloys and steels represent a fascinating combination of materials whose properties can be suitably exploited especially in the transportation sector [3]. Due to the huge differences in their physical properties, such as melting points and thermal expansion coefficients, joining such materials is challenging, and the use of conventional fusion welding is not a reliable solution. Welding defects, such as solidification cracks, liquation cracks, and porosity, often originate because of the differences in physical properties. Moreover, the formation of brittle intermetallic compounds (IMCs) at the interface between different metals, such as Mg and steel, is another detrimental effect hindering the effectiveness of welding different metals.

Existing studies dealing with the interfacial microstructure arising in friction stir spot welding process used for Mg/steel joining have demonstrated that Mg₂Zn₁₁, Mg₇Zn₃, and Mg₂Sn are formed as a result of metallurgical reactions between Mg and Zn or Sn coatings on the steel surface [4, 5]. The presence of the IMC layer causes the weld to lose mechanical properties. It is possible to reduce this detrimental effect on the quality of the joints by limiting the thickness of IMCs at the Mg/steel interface. It is therefore necessary to employ low-heat-input welding techniques in dissimilar Mg/steel welding to obtain defect-free joints.

Refill friction stir spot welding (RFSSW, patented by Helmholtz-Zentrum Hereon [6]) has been developed to produce high-quality Mg/steel spot welding. As one of the most significant variants of friction stir spot welding (FSSW), RFSSW offers a more effective joining process with respect to traditional methods, such as resistant spot welding and riveting.

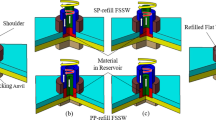
It involves the use of a non-consumable tool composed of two rotating components, namely a probe and a shoulder. In Fig. 1, a schematic representation of the process is shown; the clamping ring is fixed to the upper sheet’s top surface, and both the shoulder and the probe rotate and rub against the sheet in order to soften the material, facilitating a smoother penetration. Subsequently, the shoulder moves downwards and the probe moves upward. As the shoulder moves, it displaces the plasticized material, which is then squeezed into the cylindrical cavity formed by the upward motion of the probe. Once the tool reaches a predetermined plunge depth and remains fixed at a given position for a specific duration called dwelling time, the direction of movement for both the shoulder and the probe is reversed; as a result of the reversed movement, the plasticized material in the cylindrical cavity is squeezed back by the shoulder, effectively refilling the previously created cylindrical cavity.

Fig. 1

The RFSSW process components and sequence: a Plunging, b Dwelling, c Refilling

The refill FSSW process provides several advantages over conventional spot joining methods. Due to the solid-state nature of the process, issues commonly encountered in traditional fusion welding, such as porosity and liquation cracking, can be avoided. In addition, beyond avoiding common issues in traditional fusion welding, the RFSSW process also offers significant benefits over the basic FSSW process. Keyhole-free welds, which are highly desirable in certain applications, can be achieved through the RFSSW process. This has been successfully demonstrated in high-performance welding of similar materials such as Al/Al [7, 8] and Mg/Mg [9].

Furthermore, the RFSSW process provides significant advantages for welding dissimilar material combinations, including Al/Cu [10], Al/Mg [11], Al/steel [12,13,14,15], Al/Ti [16], and even metal to composite materials [17]. Experimental investigations on RFSSW of Mg/steel joints have also been published in the literature [3, 9, 18].

Intense deformation, frictional contact, and elevated temperatures are all involved in the RFSSW process. To produce high-strength welds and optimize the process parameters and welding tool design, it is essential to comprehend the physical phenomena involved in the RFSSW process and their interplay. To date, studies on RFSSW have primarily relied on experimental investigations; however, such studies cannot provide a complete understanding of the temperature distribution, plastic strains, strain rates, and material flow that take place during the process.

Consequently, coupled thermo-mechanical simulations of the RFSSW process are essential for predicting the temperature profile and material flow pattern. Modeling the thermo-mechanical and large deformations involved in RFSSW enables one to consider the simultaneous effects of heat flow, temperature distribution, severe plastic mixing, and visco-plastic flow behavior of the deformed material. Several studies have been conducted on the thermomechanical modeling of RFSSW.

For example, Muci-Küchler et al. [19] developed a fully coupled thermo-mechanical finite element (FE) model by using ABAQUS-Explicit to predict temperature and material flow during the plunging stage of the probe plunging variant of the process. In addition, Ji et al. [20, 21] used Ansys-Fluent to simulate material flow in RFSSW, with a particular focus on material flow occurring at various rotating speeds and plunging depths. Kubit et al. [22] created an axisymmetric thermo-mechanical FE model of the RFSSW process; in their study, they used a temperature-dependent shear friction coefficient to account for incipient melting and tool slippage during the process. Similarly, Zhang et al. [23] developed a numerical model of RFSSW using a Coupled Eulerian–Lagrangian (CEL) formulation implemented in ABAQUS.

Within the Lagrangian framework, a suitable computational tool for modeling RFSSW is represented by the SPH approach. Although the SPH approach is computationally burdensome in simulating welding processes, the method can be easily adapted to exploit parallel computing, nowadays easily enabled by graphics processing units (GPUs) or central processing units (CPUs), with a significant computational time reduction [24]. SPH is a Lagrangian particle method that allows tracking each node representing a small region of material belonging to the process domain over time. Compared with traditional grid-based methods, SPH can simulate interface dynamics, handle large material deformations, and provide the material’s strain and temperature history without requiring complex tracking schemes [25].

It is worth noticing that a fully Lagrangian approach, such as the SPH method, offers several advantages over CEL-based approaches typically used for simulating this class of problems. With SPH, tracking the material path in substantial deformation problems is straightforward and does not require following any material interface as usually done in the Eulerian FE framework, which requires the prior definition of an Eulerian meshed region where material flow is supposed to take place during the evolution of the involved problem’s phenomena. Moreover, history-dependent material properties as well as nonzero Dirichelet boundary conditions, can hardly be modeled within a CEL approach. SPH provides a fully physical description of the problem being modeled and closely resembles the real phenomena in multiphysics cases where material flow and mixing occur.

While SPH has been used by some researchers in simulating various welding techniques such as friction stir welding (FSW) [26,27,28,29,30,31], there is a notable lack of literature on the numerical modeling of RFSSW using this Lagrangian particle-based method. RFSSW differs significantly from conventional FSW in terms of process steps and objectives. As a result, the simulation methodology for RFSSW needs to be tailored to address these unique differences. To date, the SPH method has not been applied to simulate the entire RFSSW process of similar or dissimilar materials. A preliminary study was reported by Yang et al. [32] who used SPH to investigate the material flow in the plunge stage of RFSSW of aluminum alloys. Despite its straightforward and physically accurate nature, the SPH model is capable of accurately replicating temperature changes, stress distributions, and strain profiles that take place in the real RFSSW process. In this study, the RFSSW is modeled by adopting the SPH approach, and its effectiveness is demonstrated by simulating the RFSSW of AZ31 Mg alloy and galvanized DP600 steel. The Johnson–Cook material model with a full iterative visco-plasticity method is employed to implement the SPH model in the ABAQUS software for RFSSW numerical modeling. The SPH method in ABAQUS indeed has limitations in handling explicit dynamic temperature displacements. However, due to the short duration of the RFSSW process, heat dissipation has a minimal impact on temperature curves and can be neglected. This assumption is based on the rapid nature of the welding process, where the primary thermal effects occur faster than significant heat dissipation. Several studies that have demonstrated the capability of ABAQUS SPH modeling to accurately simulate thermo-mechanical processes, yielding results comparable to experimental data [33, 34].

The adopted computational approach allows for the simulation of the process evolution in time. It provides a large amount of information related to the RFSSW process, such as the temperature field, the stress and strain states, and, most importantly, the material flow taking place in the joining process. The proposed approach introduces a novel and advantageous method that tackles the inherent complexity of the process. With its ability to capture the intricate material flow and temperature distribution dynamics, the SPH simulation provides a sophisticated tool for accurately adjusting welding parameters. This level of precision is crucial for optimizing the welding process and ensuring reliable weld quality in highly demanding applications.

2 Model description

In the RFSSW process, very large strains occur, so its simulation with finite element analysis (FEA) suffers from an excessive mesh distortion. Early Lagrangian models relying on mesh-based numerical methods were also limited by the issue of mesh distortion. To overcome this drawback, the present study utilizes an advanced mesh-free SPH model. In SPH simulations, the material elements of the discretized domain are not connected to each other (i.e., it is a meshfree method), enabling the workpiece to withstand significant displacements and deformations. Due to the physical-based representation of the involved quantities, the SPH Lagrangian method enables all the output fields to be determined easily over time. In the SPH method, ‘numerical’ nodes used to convert the continuous model into a discrete one are spread over the problem domain. In this way, each node moves and accelerates depending on the effective forces (arising from the acting stress or hydrostatic pressure) it feels. The mechanical effect of each node on its neighbors is calculated using kernel functions, leading to a very effective method for assessing stress, force, and strain distributions.

In this study, the SPH model is employed to simulate the relevant example of the RFSSW process of AZ31 magnesium alloy to galvanized DP600 steel. The model is implemented in ABAQUS software in EXPLICIT mode. To validate the proposed computational approach, experimental results from the work by Fu et al. [18] are used. By comparing the simulated results with the experimental data, the accuracy and reliability of the SPH simulation in predicting key welding outputs are evaluated. The agreement between the simulated and experimental results provides confidence in the fidelity of the SPH model for simulating the RFSSW process.

2.1 Governing equations

The RFSSW process is modeled using momentum and energy equations whose parameters represent temperature-dependent material properties. In addition, the Navier–Stokes equations [35] are used to model the mass, momentum, and energy conservation of the material considered as a non-Newtonian incompressible fluid during the RFSSW process:

$$\frac{\partial \rho }{\partial t}=-\rho \nabla \cdot {\varvec{V}}$$

(1)

$$\frac{\partial {\varvec{V}}}{\partial t}=-\frac{\nabla p}{\rho }+\frac{\nabla \cdot{\varvec{\sigma}}}{\rho }$$

(2)

$${C}_{p}\frac{\partial T}{\partial t}=-\frac{1}{\rho }\nabla \left(K \nabla T\right)+\frac{1}{\rho }\left({\varvec{\sigma}}:\nabla {\varvec{V}}\right)-I$$

(3)

In the above equations, $\rho ,$ ${\varvec{V}},$ $p,$ ${\varvec{\sigma}}$, $T$, ${C}_{p}$, $K$, and I represent the material fluid density, flow velocity, pressure, deviatoric stress tensor, temperature, specific heat, thermal conductivity, and sink term that describes the loss of heat from the problem’s domain to the surrounding environment, respectively.

2.2 The SPH method

The SPH mesh-free method is a computational technique that can be used in FE computational frameworks for simulating fluids and solid mechanics problems. Its primary advantage is the ability to trace failure events physically, and it does not suffer from severe domain shape and size changes. Compared to traditional Lagrangian grid-based methods, the SPH’s particle-like nature allows for more accurate handling of problems with large displacements and distortions. As such, it has been demonstrated to be useful for analyzing shock, impact, damage, and fracture problems [31].

SPH can be integrated into FE software, such as ABAQUS, as an extension of the explicit method used to solve dynamic problems by integrating the equations of motion in the time domain. Beyond the lack of elements’ connectivity, the primary difference between the SPH approach and the standard FE method is the way the forces acting on particles are determined. In contrast to the common FE approach – which calculates nodal displacements using residual forces evaluated by element volume integration – in SPH the forces acting on particles are determined differently, as described as follows.

To obtain the problem’s variable fields, such as density, velocity, deformation, and stresses, SPH employs weighted average values of node quantities over neighboring nodes. An interpolation function, known as the kernel, is used to accomplish the weighted average evaluation [36]. The model can, therefore, simulate large deformations and problems involving inhomogeneous node distributions. In addition, it is easy to track all field variables in time since the approach is fully Lagrangian. Depending on the physics involved in the problem, interpolation smoothing kernel functions can be selected to model large deformations. A finite number of neighbors associated with the central node in a two-dimensional or three-dimensional model is usually suggested to be 27 or 56 elements, respectively [31].

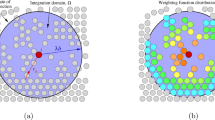
The calculation time and accuracy of a solution can be modified by adjusting the so-called scaling factor (λ) typically used in meshfree computational methods. By increasing or decreasing λ, the number of neighboring elements considered in the calculation can be adjusted accordingly. A large value of λ entails a greater number of neighboring elements to be taken into account, resulting in higher accuracy but longer computational time. Conversely, a small value of λ makes fewer neighboring elements to be considered, resulting in lower accuracy but shorter computational time. In real simulations, it is important to find an appropriate value of λ that balances the trade-off between accuracy and computational time. In this study, physical particles are represented by discrete points, and the interpolation kernel function used to define their behavior is the cubic spline function. This kernel function is commonly used as the default in the ABAQUS software package, and it is effective for interpolating the behavior of physical particles representing discrete points of the model. Figure 2 illustrates the typical bell-shaped weighting function $W$ whose kernel’s length is $\lambda h$. The weighting kernel function type and its length determine how many particles among all the particles of the model are taken into account, i.e., those having a distance $r$ from the particle of interest not greater than $\lambda h$. For the purpose of SPH interpolation, particles within the range distance $h$ from the particle of interest are considered using the continuous first derivative.

Fig. 2

Schematic of the kernel function used in the SPH interpolation

From Fig. 2, it is evident that spatial integration is performed directly at the particle sites. Therefore, the value of the field variable can be calculated at the $i-th$ node by taking into account the weighted sum evaluated over the $j-th$ neighboring nodes falling within its effective domain [37]. The discretized field variable ($f$) at the $i-th$ material node placed at the spatial location ${{\varvec{r}}}_{i}^{\alpha }$ is approximately evaluated as follows:

$$f\left({r}_{i}^{\alpha }\right)=\sum_{J=1}^{{N}_{i}}\frac{{M}_{j}}{{\rho }_{j}}f\left({{\varvec{r}}}_{j}^{\alpha }\right) W\left(r,h\right)$$

(4)

where ${M}_{j}$ and ${\rho }_{j}$ are the density and the elements mass, respectively, while $W\left(r,h\right)$ is the interpolation kernel function, being $r=\left|{{\varvec{r}}}_{i}^{\alpha }-{{\varvec{r}}}_{j}^{\alpha }\right|$. The evaluation of the gradient and of the divergence vector is performed as described as follows:

$$\nabla {f}_{i}=\sum_{J=1}^{{N}_{i}}\frac{{M}_{j}}{{\rho }_{j}}{f}_{i} \cdot {\nabla }_{i}W({r}_{i}-{r}_{j},h)$$

(5a)

$$\nabla \cdot {f}_{i}^{\alpha }=\sum_{J=1}^{{N}_{i}}\frac{{M}_{j}}{{\rho }_{j}}{f}_{j}^{\alpha }\cdot {\nabla }_{i}W({r}_{i}-{r}_{j},h)$$

(5b)

In the above equations, $\sum_{J=1}^{{N}_{i}}(\dots )$ indicates the sum over all the ${N}_{i}$ particles included within the support region of the particle of interest $i$; the smoothing length $h$ defines the number of particles (resolution) which directly affects the properties of particle $i$ itself. Numerical simulations can be tuned, and the solution procedure becomes more efficient by selecting $h$ in accordance with the local particle density [38]. Further, in SPH, the mass of particle $i$ is assumed to be constant and proportional to ${\rho }_{i}{{h}_{i}}^{3}$. Thus, ${h}_{i}$ can be calculated as follows [39]:

$$\frac{\partial {h}_{i}}{\partial t}=-\left(\frac{{h}_{i}}{3{\rho }_{i}}\right)\frac{\partial {\rho }_{i}}{\partial t}$$

(6)

The set of differential Eqs. (1)-(3) can be rewritten to solve the SPH model by using the above-defined approximations and operators (3)–(6) [38]. A key distinction between SPH and traditional grid-based finite element analysis (FEA) is related to the approach used in solving field value differential equations. While grid-based FEA uses a point-wise discretization of space–time to represent the volume domain, SPH instead employs particles to discretize the domain. The particle-based approach allows for a different way of solving differential equations, which can provide certain advantages over traditional grid-based methods [40]. In SPH, the traditional Lagrangian explicit technique based on Newton’s second law of motion is augmented with the use of conservation equations for mass, momentum, and energy to determine the response of particles.

On the other hand, using a Lagrangian-based formulation, such as the SPH method, ensures that the conservation equations are satisfied for each particle at every time step. This means that the updated field values for each particle are carried forward to the next time step, allowing for a more accurate and efficient simulation. The following equations represent the mass conservation, material momentum, and energy conservation written in the SPH framework:

$$\frac{\partial {\rho }_{i}}{\partial t}={\rho }_{i}\sum_{J=1}^{{N}_{i}}\frac{{M}_{j}}{{\rho }_{j}}{V}_{ij}\cdot {\nabla }_{i}W({{\varvec{r}}}_{i}-{{\varvec{r}}}_{j},h)$$

(7)

$$\frac{\partial {V}_{i}}{\partial t}=-\sum_{J=1}^{{N}_{i}}{M}_{j}\left(\frac{{p}_{i}+{p}_{j}}{{\rho }_{i}{\rho }_{j}}+{\Pi }_{ij}\right){\nabla }_{i}W\left({{\varvec{r}}}_{i}-{{\varvec{r}}}_{j},h\right)+{F}_{i}$$

(8)

$$\begin{aligned}\frac{\partial {T}_{i}}{\partial t}&=-\frac{1}{{\rho }_{i}{C}_{p,i}}\left[\sum_{J=1}^{{N}_{i}}\frac{{M}_{j}}{{\rho }_{j}}\frac{4{K}_{i}{K}_{j}}{{K}_{i}+{K}_{j}}\frac{\left({T}_{i}-{T}_{j}\right)}{{\left|{r}_{ij}\right|}^{2}}{r}_{ij}. {\nabla }_{i}W\left({{\varvec{r}}}_{i}-{{\varvec{r}}}_{j},h\right)\right.\\& \quad \left. -\frac{1}{2}\sum_{J=1}^{{N}_{i}}{M}_{j}{\Pi }_{ij}{V}_{ij}\cdot {\nabla }_{i}W\left({{\varvec{r}}}_{i}-{{\varvec{r}}}_{j},h\right)-R{T}_{i}{\delta }_{i}\right]\end{aligned}$$

(9)

where ${F}_{i}$, ${\Pi }_{ij}$, ${V}_{ij}$, ${p}_{i}$, $K$, and $R$ are boundary force, viscous term, the velocity of particle $i$, the fluid pressure at the position ${{\varvec{r}}}_{i}$, the heat conductivity, and the heat transfer coefficient, respectively. For particles at the boundary and outside the domain, ${\delta }_{i}$ is set to one and zero, respectively.

The continuity equation, also known as the conservation of mass, is the first equation that must be satisfied in SPH simulations. This equation is used to calculate the density of each particle, which is necessary to satisfy the other two conservation equations. Specifically, as shown in Eq. (7) the continuity equation provides the time rate of the mass density when evaluating the interaction between a pair of particles.

The conservation of momentum, expressed by Eq. (8), is evaluated once the mass conservation equation has been satisfied. Finally, the conservation of energy is provided by the energy Eq. (9). It is worth recalling that in SPH, several energy equations have been proposed; however, in some cases, the energy conservation equation could provide non-realistic physical solutions, such as meaningless negative internal energy. To address this issue, a predictor–corrector approach is often used; according to this approach, the governing conservation equations are used to predict the field variables using the chosen kernel (the predictor phase). However, to correct any unbalanced energy solutions, a local restoration of the energy conservation equation is performed (the corrector phase). Once the corrector phase is complete, the field values are adjusted to provide the updated particle state. This approach is applied at every time step of the analysis, with a sufficiently small time increment assumed to minimize the impact of numerical adjustments made on the accuracy of the solution during the predictor–corrector phase. As a result, the predictor–corrector approach can be used to improve the accuracy and the stability of the simulation without significantly increasing the computational cost [41].

Suitable boundary forces are applied particles situated near the boundary region to enforce a zero velocity for workpiece. These forces act between the tool boundary particles and the workpiece particles located in the vicinity of the boundary [42]. The appropriate boundary force and viscosity are determined by using specific equations as follows:

$${\Pi }_{ij}=-16\frac{b{V}_{ij}.{r}_{ij}}{\left|{r}_{ij}\right|}\frac{{\mu }_{i}{\mu }_{j}}{\left({\mu }_{i}+{\mu }_{j}\right)h{\rho }_{i}{\rho }_{j}}$$

(10)

$${F}_{i}=\sum_{J=1}^{{N}_{i}}{{V}_{MAX}}^{2}\left(\frac{2{M}_{j}}{{M}_{i}{+M}_{j}}\right){W}^{b}\left(\frac{\left|{r}_{ij}\right|}{h}\right)\frac{{r}_{ij}}{\left|{r}_{ij}\right|}\left(\frac{1}{\left|{r}_{ij}\right|-\Delta {p}_{b}}\right)$$

(11)

where ${\mu }_{i}$ is the fluid viscosity, while ${W}^{b}\left(\frac{\left|{r}_{ij}\right|}{h}\right)$, ${V}_{MAX}$, and $\Delta {p}_{b}$ are a Wendland 1D cubic kernel, the maximum absolute value of ${V}_{ij}$, and the boundary particle spacing, respectively. During the process, the deviatoric stress needed for plastic deformation calculation is determined as follows [43]:

$${\sigma }_{e}=3{\mu }_{e} {\dot{\varepsilon }}_{e}$$

(12)

where ${\dot{\varepsilon }}_{e}$ is the effective strain rate defined as: ${\dot{\varepsilon }}_{e}=\sqrt{\frac{2}{3}{\dot{\varepsilon }}^{kl}{\dot{\varepsilon }}^{lk}}$, being ${\dot{\varepsilon }}^{kl}$ and ${\dot{\varepsilon }}^{lk}$ the strain rate tensor components, with ${\dot{\varepsilon }}^{kl}=\frac{1}{2}\left(\frac{\partial {V}^{k}}{\partial {x}^{l}}+\frac{\partial {V}^{l}}{\partial {x}^{k}}\right)$; for a symmetric velocity tensor, $l$ and $k$ are equal to 1, 2, and 3, respectively.

2.3 Material constitutive modeling

In RFSSW, the deformation of the material involves large strains, high strain rates, and high-temperature effects, which can be effectively captured using a constitutive model known as the Johnson–Cook model. This model provides a mathematical expression that relates the material’s stress to strain, strain rate, and temperature, allowing for an accurate prediction of the material’s behavior under these extreme conditions [31]:

$${\sigma }_{JC}=\left[A+B{\varepsilon }^{n}\right]\left[1+C\mathit{ln}\left(\frac{\dot{\varepsilon }}{{\dot{\varepsilon }}_{o}}\right)\right] \left[1-\frac{T-{T}_{r}}{{T}_{m}-{T}_{r}}m\right]$$

(13)

In the above equation ε is the equivalent plastic strain, $\dot{\varepsilon }$ is the equivalent plastic strain rate, $T$ is the current process temperature, $A, B, n, m, {\dot{\varepsilon }}_{o}$ and $C$ are material parameters related to a temperature equal or less than the melting temperature of the material ${T}_{m}$, while ${T}_{r}$ is the room temperature. The above-mentioned material parameters, available in the literature for the materials considered in the following examples, are listed in Table 1. The remaining material properties required in the computational model are shown in Table 2.

Table 1 Johnson–cook constitutive model parameters for the used materials [44, 45]

Table 2 AZ31 Mg alloy and DP600 steel properties

2.4 Contact modeling

The contact conditions between the tool parts and the workpiece during RFSSW can have a significant impact on the resulting properties of the process, such as the stress and strain distributions within the material. This is due to the high level of plastic deformation occurring during the process, which can further exacerbate the effects of the contact conditions. As a result, precisely modeling these contact conditions is crucial for obtaining accurate simulations of the RFSSW process. Research on traditional FSW has shown that using the Coulomb friction model provides results that are accurate and closer to real conditions [46]. Thus, a modified Coulomb friction law is used in this study. This modified model takes into account the partial-slip boundary condition, which allows for a more realistic representation of the contact conditions observed during the process:

$${\tau }_{friction}={\tau }_{shear}=\left\{\begin{array}{c}{\mu }_{f}p, \quad for\;\; {\mu }_{f}p<{\tau }_{max}\\ \frac{{\sigma }_{s}}{\sqrt{3}}, \quad for \;\;{\mu }_{f}p>{\tau }_{max}\end{array}\right.$$

(14)

where ${\tau }_{friction}$, ${\tau }_{shear}$, ${\mu }_{f}$, p, and ${\sigma }_{s}$ are the friction shear stress, flow shear stress, friction co-efficient, contact pressure and equivalent flow stress, respectively. During the plunging and refilling stages of the process, the material can adhere to the shoulder and to the probe, resulting in a stick–slip condition. In such situations, the yield shear stress is equal to the critical frictional stress which is used to identify the onset of the stick–slip condition. Furthermore, as the FSW process progresses, the frictional stress between the tool and workpiece increases until it reaches a critical value, after which it remains constant. This means that the frictional stress is no longer equivalent to the contact pressure between the tool and workpiece. According to the fulfillment of the critical bound provided by Eq. (17) [47], in this study, a maximum frictional stress equal to $\frac{{\sigma }_{s}}{\sqrt{3}}$ is used. Accordingly, the friction coefficient of the modified model is set to a constant value equal to 0.3; based on previous studies on Mg plastic deformation [48, 49], it has been observed that the friction coefficient for this particular material shows minimal variation with respect to temperature. As a result, it is commonly regarded as a fixed value of 0.3. Additionally, in order to simplify the calculations, it is common practice to use an average value for the friction coefficient in simulations, even when the actual value is obtained through experiments at various temperature values [50]. This approach, which is important for accurately modeling the behavior of the material during the process, enables the determination of the tangential forces existing between the tool components and the workpiece. The normal contact force, denoted as ${F}_{N}$, is computed at the contact interface between the SPH and rigid elements; the penalty approach pushes the $i-th$ material point out of the $j-th$ rigid element along its normal vector $\widehat{{\varvec{n}}}$:

$${F}_{N}=\left({K}_{ij}\varrho -{\zeta }_{Contact} \dot{\varrho }\right) {\widehat{n}}_{j}$$

(15)

where, $\varrho$, $\dot{\varrho }$, ${K}_{ij}$, and ${\zeta }_{Contact}$ are the penetration depth, the penetration rate, the contact stiffness, and the damping, respectively; ${K}_{ij}$ and ${\zeta }_{Contact}$ are calculated as follows:

$${K}_{ij}=\frac{{E}_{i}{E}_{j} \Delta s}{{E}_{i}+{E}_{j}} ,\quad {\zeta }_{Contact}=0.2({m}_{i}+{m}_{j})\sqrt{{K}_{ij} \frac{{m}_{i}+{m}_{j}}{{m}_{i}{m}_{j}}}$$

(16)

where $E$ and $m$ are the modulus of elasticity and the material point mass, respectively. Moreover, the frictional force acting tangentially to the $i-th$ material point is expressed as follows:

$${F}_{T}=\left\{\begin{array}{c}-\mu {F}_{N}{\widehat{n}}_{Ti} \quad if \mu {F}_{N}<\frac{{\sigma }_{s}}{\sqrt{3}}{A}_{c} \\ -\frac{{\sigma }_{s}}{\sqrt{3}}{A}_{c}{\widehat{n}}_{Ti} \quad otherwise\end{array}\right.$$

(17)

where $\mu$, ${\widehat{{\varvec{n}}}}_{T}$, and ${A}_{c}$ are the coefficient of friction, the tangential unit vector, and the contact area, respectively. To determine the tangential unit vector ${\widehat{{\varvec{n}}}}_{T}$, the relative velocity of the $i-th$ material point at the $j-th$ contact element point is normalized while taking into account the plane that passes through the element nodes.

2.5 Constructing the SPH model from FEM

The SPH model is created based on the FEM model by converting the finite elements’ nodes into discrete particle elements; these elements are also called SPH elements. Figure 3a illustrates the process of converting FE nodes into SPH elements (see also Fig. 3b). The SPH elements are constituted by particles which do not possess any actual volume nor have any connectivity. The distance between two particles, denoted by $l$, is known as the feature length which serves as the smoothing length used in the SPH Kernel function to model the continuum domain through the use particles. In SPH, the feature length corresponds to the mesh size in the FEM. Continuum particle elements are useful for simulations involving material undergoing extremely large deformation, such as in open-surface fluid flow or obliteration/fragmentation of solid structures.

Fig. 3

a FEM element transformed into SPH particles, b Schematic of the transformation of a meshed workpiece into SPH particles adopted in the present study

The FE framework employs an all-pairs search algorithm to track all particles throughout the analysis [51]. To identify neighboring particles in the simulation, the FE framework analyzes all particles within the domain and verifies their inter-particle distances. Implementing this approach requires a calculation time that increases quadratically with the number of particles involved in the simulation, i.e., it is of the order of ${N}^{2}$, where $N$ is the total number of particles in the system [52]. In SPH user-defined elements in 3D problems, each node that represents a continuum particle possesses six degrees of freedom, including three translational and three rotational degrees of freedom. The element centered at each node (particle) receives contributions from all particles that fall within its sphere of influence. This sphere of influence has a radius known as the smoothing length, $h$, and determines the range of neighboring particles that can provide forces to the element under consideration. The flow chart of the SPH method implemented in the ABAQUS FE package is illustrated in Fig. 4.

Fig. 4

Flow chart of the SPH method implemented in a FE framework

2.6 Simulation controls

To obtain the temperature field, a dynamic explicit step type with adiabatic definition is employed. This approach is used to accurately model the thermal effects that occurring during the process. The simulation assumes an initial room temperature of 27 °C, equal to the temperature of the material before the welding process begins.

An automatic time increment procedure with a time scaling factor equal to 1 is chosen during the simulation. By using an automatic time increment, the FEM software starts incrementing the time by using the value entered for the initial increment size. The amplitude of subsequent time increments is adjusted based on the rate of convergence of the solution. This approach, based on adapting the time increment size to the rate of change in the solution, ensures that the simulation is stable and accurate. To ensure both model convergence and calculation efficiency, in this study the mass scaling factor is set to ${10}^{4}$ [53]. Mass scaling is a technique frequently employed in ABAQUS/Explicit to enhance computational efficiency in quasi-static and in certain dynamic analyses (particularly when small elements are present), which control the time increment ensuring stability of the numerical solution. By adjusting the mass of the particles in the simulation, mass scaling can stabilize the time increment, leading to a more efficient prediction of the behavior of the materials during the process without compromising accuracy. However, applying mass scaling to the elements in the simulation leads to an artificial increase in the material density. This density increase has the effect of slowing down the wave propagation speed within the material. This, in turn, affects the contact conditions and the dynamic behavior of the material flow. While applying mass scaling can affect the dynamic behavior of the material flow during the process, it has no significant effect on the strain and stress generated during the process through plastic deformation and friction phenomena. This is because the kinetic energy stored in the system is not significant compared to the total energy involved in the process. Therefore, the effects of mass scaling on the mechanical behavior of the material are negligible.

2.7 Computational strategies

For dynamic analyses of problems that involve a large number of degrees of freedom, explicit time integration schemes are often preferred. However, in an explicit analysis the time increment must be less than the central-difference operator’s stability limit. As a matter of fact, an unstable solution will result if a not properly small time increment is used. The time increment size during the analysis can be kept fixed or it can be automatically adapted; this feature is offered, for instance by the ABAQUS/Explicit package.

By adopting a fixed time increment, the initial element-by-element stability estimate of the time step (or a time increment supplied directly by the user), defines the fixed time increment size. When a more precise representation of the problem’s response accounting for higher modes is desired, a fixed time increment may be advantageous. A time increment size smaller than the element-by-element estimations may be employed in this situation.

The use of a Lagrangian formulation, such as SPH, allows for the calculation of individual stable time increments for different parts of the discretized problem. This is because the time increment ensuring solution stability is defined by the elastic wave speed, which should not travel a distance greater than the minimum length of the element within a single time step. The maximum time increment fulfilling the requirement of stability of the solution is defined as follows:

$$\Delta {t}_{max}=\frac{{L}_{small}}{{C}_{d}}$$

(18)

where the ${L}_{small}$ and ${C}_{d}$ are the smallest characteristic element length and dilatational wave speed of the material, respectively being ${C}_{d}$ provided by:

$${C}_{d}=\sqrt{\frac{E}{\rho }}$$

(19)

where the $E$ and $\rho$ are Elastic modulus and the material density, respectively. In the current model, $E$ and $\rho$ are selected equal to 45 GPa and 1730 kg/m³, respectively. Therefore, ${C}_{d}$ results to be 5100 m/s. In addition, the smallest element size for the workpiece is assumed to be $5\cdot {10}^{-4}\text{ m}$; therefore, the stable time increment must not exceed $\Delta {t}_{max}= 9\cdot {10}^{-8}$ s.

The use of a fixed time increment does not guarantee that the computed solution is stable during all the integration steps; in these cases, the user should carefully examine the energy history and other response parameters to check if a reliable solution is obtained. It must be considered that during the solution process, the nonlinearities arising because of the large deformations and/or nonlinear material behavior influence the highest frequency of the system that constantly changes; it is thus necessary to adjust the time size required for the time integration stability. The automatic increment feature is used in all the presented numerical examples to avoid the possibility of inducing numerical instability.

When using automatic time increment, the stability limit is calculated using both global and element-by-element estimates. The element-by-element estimate approach must be performed at the beginning of a study, even if the global estimation method may be used in some cases. Evaluating the actual dilatational wave speed enables a global time step estimate based on the maximum frequency assessment of the entire model during the analysis. This approach is based on a continuous estimate of the highest frequency of the mechanical system. It is worth recalling that time increments greater than the element-by-element estimated values are usually acceptable also for the global estimator.

The use of small time increments can greatly increase the computational cost in terms of CPU time. To improve the efficiency of the solution, mass scaling is employed for the elements. While this technique leads to an artificial increase in material density and a reduction of the wave propagation rate, it has no significant effect on strain and stress calculation. The plastic deformation and friction mechanisms that occur during the process mostly affect the stress and deformation state of the material. Moreover, the kinetic energy stored in the system is not significant compared to the total energy of the system. Therefore, the use of mass scaling is an effective way to reduce the CPU time without compromising the accuracy of the simulation.

3 Results

3.1 FEM validation and verification

For the validation of the developed model, experimentally measured temperatures from Fu et al. [18] are used. During the process, temperature measurements were done by K-type thermocouples embedded in the steel sheets placed at a depth of 0.1 mm away from the Mg/steel interface, at the weld centerline and 6 mm far from the weld centerline, respectively. It should be noted that computational errors can occur during numerical modeling for a variety of reasons, including modeling the tool’s components with discrete rigid elements that disregard their thermal properties, modeling the contact condition using a constant coefficient of friction, adiabatic heat effect assumptions, temperature-independent properties of the workpiece, and because of the simplified boundary conditions adopted to reduce the simulation CPU costs. Besides the computational errors, experimental errors such as the general error of temperature measurement technique could affect the results comparison. In the developed model, the maximum relative error was less than 10%, indicating that the numerical model results are close to the experimental ones.

3.2 Geometrical conditions and mesh generation

The numerical set-up adopted consists of 2 mm thick sheets of commercial AZ31B Mg alloy and 1.5 mm thick hot-dip galvanized DP600 steel samples as parent materials [18]. The used tools consist of a clamped ring (14.5 mm in diameter), a shoulder (9 mm in diameter), and a probe (6 mm in diameter); these parts are assumed to be rigid and described through Lagrangian elements. The sheets were then assembled in a lap joint configuration with a 25.4 mm overlap. The simulation of the RFSSW process in this study utilized the shoulder plunge variant and a backing plate made of steel, which was modeled using shell elements. The simulation setup consisted of workpieces, rigid tools, and the backing plate, as illustrated in Fig. 5.

Fig. 5

Modeling setup: a Front view, b Isometric view, c Discretized workpiece

The workpieces undergo large deformations during processing, so SPH elements are suitable to model the real deformability of the involved materials. Material flow and plastic deformation primarily occur in the weld region and its surrounding area during the process. In the present numerical model, the workpieces were limited in length and width, hence, the computing time was reduced without compromising the accuracy of the results.

The RFSSW process parameters include rotation speed (RS), plunge depth (PD), plunge (PT), dwell time (DT), and refilling time (RT). To simulate the process accurately, two different parameter combinations were selected based on experimental investigations presented in the reference article. In the first combination, which is defined as high-speed weld in the following, the rotational speed, plunge time, dwelling time, and refilling time were set to 2000 rpm, 3s, 2s, and 2s, respectively. The plunge depth was set at 1.9 mm in this case. In the second combination, which is defined as low-speed weld, the rotational speed, plunge time, and refilling time were considered to be 1200 rpm, 2s, and 1s, respectively. The dwelling time was removed from the second set of process parameters, and the plunge depth was set to 1.6 mm in this case.

Based on experimental parameters, the RFSSW model conditions are considered in terms of rotational speed, plunge time, dwelling time, refilling time, and plunge depth. During the process, the probe and shoulder rotate with a certain speed around their local axis. The plunge stage is continued until the shoulder reaches a predefined depth. To generate auxiliary frictional heat in high-speed welding, the tool is kept in contact with the workpiece for a specific amount of time. To prevent material movement at the bottom and sides of the workpiece during the process, an interface is defined between the backing-plate surface and the bottom and side nodes. Velocity boundary conditions are also assigned to the workpiece bottom and side nodes. As the plate is less deformable than the materials being joined, constraints on the backing plate are assigned based on the assumption of a reference point. The body’s global size is approximately equal to 1 mm, and the domain is meshed by three-dimensional quadrilateral rigid elements. Furthermore, the shoulder, probe, and clamping ring in the experimental setup are hardened to stir into the workpiece material during the RFSSW process. To accurately model these tools, a discrete Lagrangian body formulation with the same geometry and details as the experimental setup is utilized. This approach enables a convenient and precise representation of the tools used in the experimental study. The element size for the shoulder, probe, and clamping ring was roughly 1 mm, while the domains is meshed through 600, 700, and 560 3D rigid beam elements, respectively. The workpiece is discretized through 19.845 elastic–plastic SPH elements characterized by eight-node three-dimensional degree of freedom. Furthermore, reduced integration was used in this study for the workpiece elements.

In Fig. 6, the predicted temperature evolution in time is compared with the experimental values for the two considered welding conditions [18]. In this figure, different welding phases are shown with vertical dashed lines. In both cases, the numerical estimations agree well with the experimental results. In the weld centerline of the high-speed weld, the results indicate that the temperature increased rapidly during the plunge stage until reaching 430 °C, which is slightly higher than the melting point of pure Zn. After getting that value, the temperature drops with a very gentle slope. The temperature remains almost stationary during the dwelling and refilling stages, with very few fluctuations. At the 6 mm position far from the weld centerline, a similar temperature variation is observed, with a temperature increase up to 315 °C at first, which subsequently remains at that value during the following stages. In the second case, temperature changes are examined at two positions. After an initial increase in the plunging stage, in the center of the low-speed weld the temperature stabilizes at 310 °C. At 6 mm from the weld centerline, the maximum temperature is much lower than 210 °C. A general comparison of temperature diagrams in high-speed and low-speed welds shows the relevant effect of the rotational speed on the amount of heat produced during the process.

Fig. 6

Temperature evolution in time obtained from experimental results [18] and simulation. a High-speed weld, b Low-speed weld

3.3 Temperature, stress and strain analysis

Figure 7 shows the temporal and spatial evolution of the main field variables, namely the temperature, strain, and stress fields at three different time instants of the process in the high-speed weld situation. First, the relative movement of the shoulder and probe starts and continues for 3s. During this stage, the shoulder moves down with a certain rotational speed and the probe rises at the same time as it rotates. The result of this relative movement is the upward movement of the material under the probe. This situation is similar to the material movement taking place in conventional indirect extrusion. As soon as the time instant $t=$ 3s is reached, the relative movement is stopped and the probe and shoulder remain in a fixed position for two more seconds. Then the reverse relative movement of the probe and shoulder starts for 2 s. At this stage, the probe moves down and the extruded material in the shoulder is pushed back toward the workpiece.

Fig. 7

Simulation results: a temperature, b stress fields in high-speed weld, c plastic strain

Figure 7a shows the temperature distribution at different stages of the process. In the RFSSW process the temperature is strongly correlated to the amount of generated heat, which in turn affects the stirring and softening of the material. There are three main sources of heat generation during the RFSSW process: (a) frictional heat generated by partial stick–slip at the sleeve/probe-workpiece interface, (b) plastic dissipation of the material, and (c) viscous dissipation from the plastic material’s stored deformation energy. Investigations have shown that higher temperatures are observed when all three components are simultaneously involved in heat production. For example, during the plunging and dwelling stage, when the probe moves up and the material flows into the shoulder, the heat produced in the weld center—where most of the plastic deformation occurs—is much higher than in its surroundings under the shoulder. Beneath the shoulder, the material experiences far less plastic deformation, resulting in heat production mainly due to friction. During retraction, i.e., when the probe and shoulder return, all three sources contribute again to the amount of heat produced. Hence, a larger volume of material experiences higher temperatures.

Further, it is worth noticing that the spatial temperature distribution is axisymmetric during the process with respect to the weld center. It is shown that the maximum temperature during the process reaches 530 °C at the shoulder periphery. This temperature is about 90% of the Mg melting temperature (${T}_{m}$), which is required to trigger dynamic recrystallization.

As shown in Fig. 7b, the symmetrical stress distribution is observed during the process of high-speed welding. The metal undergoes a high thermal cycle through direct tangential friction between the stirring tool and the center metal. This causes the plastic flow to release stress, creating a low stressed region at the center of the weld zone during the plunging and the dwelling stage. As a result of the temperature difference between the metal in the weld zone and the surrounding cold metal, in these two stages, the metal under the shoulder is more heavily restrained, which in turn results in a high stress concentration. In the next step of the process, with the movement of the probe and shoulder for refilling, the stress in the center is reduced. The highest stress takes place around the outer edge of the shoulder. At this time instant, the high temperature reached in the central region causes high fluidity of the plastic metal, resulting in a high amount of thermal stress release.

Figure 7c presents the distribution of plastic strain at different stages of the RFSSW process. The plastic strain obtained from the simulation is consistent with the microstructural analysis presented in the literature, and is symmetrical about the welding center. During the plunging stage, large plastic strains are mainly observed around the inner diameter of the shoulder. No significant change in strain is observed during the dwelling stage. In the refilling stage, the strain increases underneath the probe as it pushes the material into the weld. The region near the shoulder experiences the highest amount of deformation due to the shoulder-plunging variant. The strain contour obtained from the simulation is comparable with the characteristic zones observed in the experimental investigations [18].

Low-speed welding is performed in two steps: in this case, the second stage of the welding process, the dwelling stage, is removed. The results obtained through the simulations show that the two weld conditions provide similar results. A preliminary comparison of the results obtained in low-speed weld conditions and their comparison with the previous weld shows that they are apparently similar, but the weld area is wider in the former case. The reason for this can be the higher temperature due to the higher rotational speed and the longer process time in high-speed welding. The strain field of low-speed weld is shown in Fig. 8.

Fig. 8

Simulation results: a temperature, b stress fields in low-speed weld, c plastic strain

Similar to what has been observed in the high-speed weld condition, in the early stages of deformation, strain localization occurs only in regions close to the inner diameter of the shoulder. In addition, the comparison of the strain distribution at high- and low-speed welds in the refilling stage shows that the strain in the low-speed weld region is higher than in the high-speed weld case. Experimental studies have shown that this increase in strain causes a decrease in bond strength [18].

3.4 Material flow

Understanding material flow behavior during RFSSW process is of practical importance for optimizing the tool shape and obtaining welds with high structural properties. Material flow is usually determined experimentally using the tracker technique which uses markers inserted in the forming processes. The markers are inserted into the workpiece material and their final positions are determined by metallography or X-ray radiography techniques. However, this experimental method is very time-consuming and costly. It is thus quite desirable to track the material flow through numerical simulations which operate by tracking some specified points during the process evolution. In this case, a series of points belonging to an initial straight line lying on the workpiece surface is tracked during the simulation. This method has already been used by Lee et al. [54] for the friction stir extrusion process and its reliability have been validated with experimental data. Figure 9 shows the initial position of the points being analyzed and their subsequent movement path at different time instants. The simulation results show that the material particles flow similarly in high-speed and low-speed welding. Thus, only high-speed welding has been examined further in this section.

Fig. 9

Material flow during different time frames of RFSSW process

In the plunge stage of the RFSSW process, the material inside the shoulder inner diameter region moves upwards toward the reservoir created by the moving probe. As a result, a plasticized rod grows upwards, with a flow pattern resembling a screw shape. The material adjacent to the shoulder edges is squeezed inwards and sheared outwards. However, outside the outer periphery of the shoulder, material movement is negligible. During plunging, the observed material flows in directions that are consistent with both experimental results and with other numerical studies reported in the literature [55, 56].

In the dwelling stage (corresponding to the time interval ranging from 3 to 5s), the probe and shoulder remain fixed at their positions while rotating. During this time interval, the rotation of the material inside the extruded rod in the plunging stage can be clearly seen, while the material in the outer areas of the shoulder does not move.

As the refilling stage starts, the probe moves downward, and the shoulder retreats. By rotating the probe, the material in the reservoir is refilled in the weld region. Plunging causes the material accumulated in the reservoir to be pushed downward by the probe, which is sheared into the keyhole left by the shoulder, rising upward. As the shoulder moves upward, the material outside the outer periphery of the shoulder slightly moves inward. The material inside the reservoir is slightly sheared outwards due to the action of the rotating probe. As shown in Fig. 9, a flat weld is produced after the filling stage. Overall, the reservoir material is pushed back into the weld during refilling. Throughout the entire process, the material outside the shoulder periphery remains unaffected by the process. Material movement mostly occurs in the center of the weld within the shoulder periphery region.

4 Discussion

In this section, the results obtained by Zhang et al. [23] are compared with those obtained by the SPH simulations of the present study. In [23], the Authors used the coupled Eulerian–Lagrangian (CEL) formulation to analyze the thermal history and plastic deformation mechanisms of an AZ91D magnesium arising during the RFSSW joint processing.

Figure 10 compares the temperature distribution during welding at two specific time instants: 0.5 s and 5 s. Examining the temperature field at 0.5 s, it is evident that the results obtained from both simulations exhibit a similar pattern, albeit with some differences. In both cases, the temperature decreases by increasing the distance from the inner edge of the sleeve. In the cross-sectional view of the joint depicted in Fig. 10a (present study), due to the upward movement of the probe, it can be observed that friction heat is primarily generated near the bottom and inner surface of the sleeve during the plunging stage. On the other hand, the CEL results in Fig. 10b indicate that the temperature gradually decreases within the sheet thickness, resulting in a U-shaped distribution of temperature isotherms. As shown in both Fig. 10a and b, at the welding time of 5 s, an increase in the temperature is observed; in both cases, the maximum temperature value occurs inside the tool. Additionally, Fig. 10b exhibits a heterogeneous stratification gradient in the temperature distribution across the thickness direction.

Fig. 10

Temperature distribution at the welding times 0.5 and 5 s: a present SPH approach, b CEL approach [23]

The material velocity profile on the cross section of the weld at two time instants, namely 1.65 s and 5 s, is depicted in Fig. 11a-d for both simulation results. The material velocity field represents the motion and flow of material particles taking place within the simulation domain. It is a key parameter—influenced by various boundary conditions, including initial particle velocities and wall constraints—that characterizes the dynamic behavior of the welding process and determines the flow patterns during welding. From the comparison of results, it can be observed that the primary characteristic of material flow is the rotational and symmetrical motion relative to the center of the weld. At the welding time of 1.65 s, the material from the bottom of the sleeve flows into the reservoir left by the probe in a steady laminar flow. At the welding time 5 s, corresponding to the refill stage, the material is extruded by the probe and exhibits a downward flow. This downward flow is responsible for the incongruence and inhomogeneity in the direction of the flow velocity.

Fig. 11

Material flow velocity at the welding times 1.65 and 5 s: a, c present SPH approach, b, d CEL approach [23]

5 Conclusions

In this study, the SPH formulation implemented within a standard FE code for modeling the joining of dissimilar materials through RFSSW welding has been presented. It has the advantage of enabling multiple physics to be modeled (thermal, mechanical, material flow, etc.) and does not suffer from drawbacks usually observed in FEM analyses where large mesh distortion takes place due to the above-mentioned mechanisms. The SPH approach in modeling RFSSW has been validated using data from experimental tests by Fu et al. [18] on RFSSW of Mg to steel.

Although the model has been developed specifically to simulate the RFSSW of Mg to steel, it can be straightforwardly extended to combinations of other materials. A mass scaling method has been used to enhance the convergence, allowing for a CPU time reduction. As it has been presented, considering a 10,000 × mass scaling factor resulted in being reliable in modeling the process efficiently. The SPH results include temperature, stress, and stress fields, as well as material flow during the process, which has been simulated in two welding conditions, namely high- and low-speed. According to the performed simulations, experimental and numerical results have been observed to be in close agreement. The numerical results showed that the joint formation procedures using the RFSSW of Mg/galvanized steel in high-speed and low-speed welding conditions are characterized by various phenomena. The amount and distribution of temperature, stress, and strain are different under different welding conditions.

The temperature evolution during RFSSW shows a rapid increase during the plunge stage, followed by a gradual decrease during dwelling and refilling. The rotational speed of the process significantly affects heat generation. The spatial distribution of the temperature is axisymmetric, with the maximum values attained at the shoulder periphery. The stress distribution in high-speed welding is symmetrical, with low stress values at the center and high stress at the outer edge of the shoulder. Finally, plastic strain distribution is symmetrical, with large strain values taking place during plunging and increased strain underneath the probe during refilling. Low-speed welding produces similar results but within a narrower welded region.

The analysis of material flow reveals valuable insights; during plunging, the material inside the shoulder moves upwards, forming a screw-shaped flow pattern. In the dwelling stage, material rotation occurs within the extruded rod, while material outside the shoulder remains approximately located in that region. Refilling involves the downward movement of the probe and shoulder, leading to material refilling in the weld region and creating a flat weld. Material movement primarily occurs in the weld center and at the shoulder periphery.

Simulation of RFSSW through the SPH approach provides a precise landscape of all the main variables involved. The SPH computational method represents a reliable computational tool for simulating complex welding procedures that are usually designed and optimized through experimental trial-and-error studies. The fully Lagrangian SPH approach provides straightforwardly all the fields involved in the various physics of the problem, namely the temperature, the mechanical deformation and stress state, the velocity and displacement fields, as well as the volume fraction composition of the welded region when different materials are joined together. The above-mentioned features are not readily available with other numerical techniques such as CEL. Since the mechanical properties of the obtained welded parts strongly depend on the RFSSW process parameters, an efficient simulation tool is required to fully control the characteristics of the final material.