Flow characteristics at the interface during droplet formation in a flow-focusing microfluidic channel—numerical analysis of dripping and jetting regimes

Abstract

This work has the purpose to elucidate in deeper detail the conjugated physical phenomena at the interface between two immiscible fluids in microfluidic devices. The two typical regimes—dripping and jetting—emerging in flow-focusing devices are considered for the analysis. Dynamic (time-dependent analysis of fixed or Lagrangian-tracked points) and local (lines along the interface, at a fixed time instance) analyses have been conducted from a parallel numerical simulation on a fine numerical grid. The results comprise various pressures and tangential stresses and their balance during the droplet formation process with special attention paid to the moments and locations of the droplet release. It was found that the dripping regime is characterized by the local balance of the pressure drop due to surface tension ${ {\Delta p}}_{\upsigma } \text{and}$ the Laplace pressure ${ {\Delta p}}_{\text{Lapl}}$ across the interface. Only at the last moments before the droplet pinch-off does the former pressure dominate. In contrast, in the jetting regime, there is a clear domination of the pressure due to tension during the whole process of droplet formation. Shear stresses, presented by the von Mises criterion, are several times (jetting regime) or even an order of magnitude (dripping regime) lower than the surface tension pressure and the Laplace pressure. In both regimes, when the interface curvature κ changes locally its sign, the pressure at the centerline axis shows a clear local maximum. For the jetting regime, the downstream derivative of this centerline pressure is the first parameter that changes along the jet axis—thus indicating the onset of instabilities for this regime—and it is then followed by a wavelike change of the radius of the jet.

1 Introduction

In recent years, microfluidics developed as a novel approach for solving numerous questions arising from the realization of different biological, chemical and medical processes [1]. Having fluidic channels with dimensions smaller than a millimeter, i.e., microscale, microfluidic devices significantly reduce reaction times and energy consumption for a given process [2]. The low Reynolds number values result in strictly laminar flow conditions in the channels, thus providing an absolute control over fluidic flows supply in different chip regions [3]. One of the key areas, where this technique is utilized as a precise and reliable tool for the automation of different assays, is droplet-based microfluidics. These small microreactors provide a cheap and easily implementable method for a broad range of processes including cell lysis [4], antibiotics susceptibility screening [5] and digital polymerase chain reaction (PCR) [6]. The massive number of possible independent reactions in the individual droplets also adds a high parallelization factor into the conducted experiments.

Various theoretical, experimental and numerical descriptions of the hydrodynamical phenomena triggering droplet formation in microchannels have been produced in the last years and will be summarized below. The reviewed works focus mostly on the influence of individual global parameters on the droplet generation. However, to understand the physical phenomena in microfluidic systems in greater detail, local and/or time-resolved distribution of variables that impact the processes is required. This is especially crucial when considering the distinct flow regimes and their inherent disparities.

In one of the first works to address droplet formation in microchannels, Cramer et al. [7] introduced the idea of dispersion of a fluid in a microcapillary inserted into a rectangular microfluidic device (co-flow geometry). The authors separated the observed flow into the dripping regime, characterized by big droplets with a pinch-off near the tube’s tip, and jetting in which smaller droplets pinch-off from a long-suspended column of the dispersed fluid downstream the tube, due to the so-called Rayleigh–Plateau instability [8]. Flow rate and flow rate ratio as well as viscosity and interfacial tension were identified as the main parameters causing the above-mentioned differences between the two regimes, as shown by Costa et al. [9]. Specifically, a higher viscosity contrast between the two phases and/or lower interfacial tension resulted in smaller droplet diameters. These differences were also evident in the mechanisms responsible for droplet detachment in both regimes, as described by Cordero et al. [10], emphasizing the distinctive characteristics of absolutely unstable flows (for dripping) and convectively unstable flows (for jetting). Within this context, Kovalchuk et al. [11] conducted experimental research to investigate the transition between these regimes using a flow-focusing microfluidic device, employing different combinations of viscosity ratios for the continuous and dispersed phases. The transition from dripping to jetting was effectively characterized by the capillary number (Ca), defined as Ca = (u·μ) / σ, where “u” and “μ” represent the velocity and dynamic viscosity of the respective phase and “σ” signifies the surface tension between the two liquids. For moderate and large values of Ca for the continuous phase, the transition from dripping to jetting was well predicted by comparing the characteristic timescales for drop pinch-off and jet growth, as proposed in earlier works [12] and [13].

The aforementioned studies dig into the distinctions between the two regimes, revealing their distinct characteristics by drawing from integral parameters gathered through experimental observations, such as generation frequency, droplet size and volume. In recent years, a multitude of works have presented analytical derivations, aiming to estimate the behavior of these droplet-based microfluidic systems across various geometric configurations. While some of these efforts focus specially on the dripping regime [14–16], others endeavor to encompass both dripping and jetting phenomena [17, 18]. In general, these theoretical models consider the balance of forces, including interfacial tension, pressure forces and shear stress forces. These forces are primarily integrated over an idealized spherical droplet shape, while considering the influences of viscosity changes and flow rates in both phases. When compared against experimental data and/or numerical simulations, they exhibit a relatively good agreement of approximately ± 10% for the dripping regime and ± 20% for the jetting regime when predicting droplet size. The primary limitation of such studies lies in the idealization of the droplet shape and the inherent simplifications that might not fully capture the complexities of real-world microfluidic systems.

Numerical analysis, on the other hand, allow a more detailed presentation of the hydrodynamic parameters in the channel. As a rule, they contain all the velocity components, the pressure and the exact position/shape of the interface between the two fluids. This enables the possibility of studying the influence of various parameters, without the need for expensive experimental setups.

In their numerical work, Nekouei et al. [19] utilized the volume of fluid (VOF) method to perform simulations of the droplet formation in a T-junction microfluidic device. The authors determined the droplet size as a function of system parameters such as viscosity ratio λ (µ_d/μ_c) between the dispersed and the continuous phase in the dripping regime. The results showed that for λ < 1, the reduction in the droplet size is stronger than for λ > 1, for increasing continuous phase velocity. The authors developed an analytical model for predicting the droplet size which included viscosity-dependent breakup time for the dispersed phase. The model successfully predicted the effects of the viscosity ratio observed in simulations.

Comparable insights into three-dimensional models were garnered in the studies conducted by Sontti et al. [20], Han et al. [21] and Grigorov et al. [22]. These investigations involved the analysis of integral parameters such as droplet size, velocity and volume. The assessment of droplet behavior encompassed factors like surface tension, flow rates and the viscosity of the dispersed phase. In summary, increased flow rates of the dispersed phase were correlated with larger emulsions and reduced generation frequencies, while an increase in the viscosity of the continuous phase corresponded to smaller droplet sizes. Notably, the findings in [22] underscored that the transition point between the two regimes depended not only on the capillary number (Ca) of the continuous phase but was also influenced, to some extent, by the physical properties of the dispersed fluid.

Rahimi et al. [23] conducted both numerical and experimental investigations into the influence of local geometries on droplet generation in a flow-focusing system with circular channel cross sections. Their study highlighted the significant impact of continuous phase flow rates and the dimensions of dispensing nozzles and flow-focusing orifices on droplet size. Additionally, smaller nozzle radii produced smaller droplets, and the radius of the flow-focusing orifice played a crucial role in determining droplet size. The influence of the geometric configurations in the droplet formation process was also studied in [24]. The findings demonstrated that even a small geometrical modification of the junction of the channel enhanced the presence of the dripping regime compared to non-modified designs.

The above overview shows that detailed, conjugated data at the interface of the two fluids, or within the individual droplets during the process of droplet formation are quite limited. Understandably, experimental methods could obtain such conjugate data only with considerable effort. While measuring pressures within the channels is technically possible [25], it is not straightforward. The reason is the high requirements for the pressure sensors, which should be capable of capturing any small changes so rapidly and accurately, keeping at the same time the spatial restrictions. At high generation frequencies (which is often the case in these type of systems), it becomes nearly impossible to describe the unsteady three-dimensional velocity field, responsible for the droplet formation. To the best knowledge of the authors, there are also no numerical studies showing the mutual interplay of the variables at the interface of the two fluids during droplet formation—although such studies usually contain all the hydrodynamic parameters as well as the proper geometry of the interface between the two fluids.

The present work aims to fill this gap by presenting mutually correlated results from relatively fine-resolved time-dependent three-dimensional numerical results for a typical dripping and a typical jetting regime. Local parameters like pressure drop, surface tension (pressure), Laplace pressure and shear stresses along the lines of the interface between the two fluids are presented at fixed time instances. Additionally, these parameters are traced also in time and presented graphically at certain characteristic spatial points of interest, like the neck of the forming droplet, or the location where the curvature of the interface surface changes its sign. This approach allows to reveal the differences in droplet formation mechanisms for the two considered flow regimes.

2 Model and methodology

In this chapter, both the model and the methodology (mathematical description, numerical method, geometrical setup and boundary conditions) as well as the parameters for the evaluation of the results (in terms of distributed forces—pressures and stresses) are described.

2.1 System of equations for the volume of fluid method

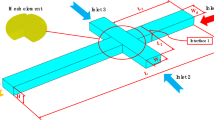
In the present study, three-dimensional simulations of droplet formation in a flow-focusing geometry as shown in Fig. 1 are carried out. The two immiscible fluids, water and oil as well as their interface, are modeled by the volume of fluid (VOF) method. In this method, following the Eulerian principle, the fluid flow is treated as a continuum. A phase fraction parameter (α) is utilized to indicate the presence of each phase at every location of the domain. Fluid properties such as viscosity and density are linearly interpolated between the two fluids, and the surface tension force is distributed near the interface as a body force in the Navier–Stokes equations.

Fig. 1

Representation of the dripping regime (on the left), the geometry of the investigated setup (in the middle) and representation of the jetting regime (on the right). All dimensions are given in µm

The system of coupled partial differential equations consists of the continuity equation (Eq. 1), the momentum balance equation (Eq. 2) and the phase fraction equation for α (Eq. 3). In the present work, bearing in mind that the density ($\uprho$) and the viscosity μ are not constant in the domain and that the flow is laminar, the equations are [26]:

$$\frac{\partial\uprho }{\partial \text{t}}+ \nabla \cdot \left(\uprho \mathbf{U}\right)=0$$

(1)

$$\frac{\partial (\uprho \mathbf{U})}{\partial \text{t}}+\nabla .\left(\uprho \mathbf{U}\mathbf{U}\right)=-\nabla \text{p}+\nabla \cdot (\upmu [ \nabla \mathbf{U}+{\nabla \mathbf{U}}^{\text{T}}])+{\mathbf{F}}_{\mathbf{s}}$$

(2)

$$\frac{\partial ({\rho \alpha })}{\partial \text{t}}+\nabla \cdot \left({\rho \alpha }\mathbf{U}\right)=0$$

(3)

In the above equations, U is the velocity vector, p—the pressure and t—the time. F_S represents the term with the surface tension force [N/m³] and is defined as shown in Eq. 4:

$${\mathbf{F}}_{\mathbf{s} }={ \sigma \kappa }(\nabla {\alpha })$$

(4)

where κ is the local curvature of the phase fraction α:

$$\upkappa = \nabla \cdot ( \nabla {\alpha }/\left|\nabla {\alpha }\right|)$$

(5)

and $\upsigma$ is the surface tension [N/m].

Although a mixture of two different immiscible fluids is considered, only one transport equation (Eq. 3) needs to be solved for the phase fraction α since the volume fraction of the other phase can be inferred from the constraint:

$${{\alpha }}_{c}+ {{\alpha }}_{d}=1$$

(6)

where the index “c” stands for the continuous and “d”—for the dispersed phase. In the following, the indexes are omitted and α denotes the phase fraction of the dispersed phase.

The viscosity μ and the density ρ are based on the weighted average of the phase fraction:

$$\upmu ={\alpha }\cdot {\upmu }_{c}+(1-{\alpha })\cdot {\upmu }_{d}$$

(7)

$$\uprho ={\alpha }\cdot {\uprho }_{c}+(1-{\alpha })\cdot {\uprho }_{d}$$

(8)

In the present work, the continuous phase (water + 40% glycerol) is introduced through the two side channels and the dispersed phase (oil:octane + 2.5% SPAN 80) is entered from the main (central) channel as shown in Fig. 1. Table 1 summarizes the physical properties of the two oil–water systems considered for the verification of the model and the later calculations in our work. The physical properties of the two fluids are obtained from the experimental results of Yao et al. [27] considered at atmospheric pressure conditions and room temperature (25 ± 1.5 °C). The surface tension $\upsigma$ at the interface of the two fluids has the value of 0.00504 [N/m].

Table 1 Physical properties of continuous and dispersed Phases

2.2 Geometry, boundary and initial conditions

A scheme of the investigated flow-focusing setup together with the surfaces where the fluids enter and leave the computational domain is given in Fig. 1.

The length of the channel is 9.1 mm, and its width W and height H are both 0.6 mm. The other dimensions can be seen in Fig. 1 (middle). For both dripping (Fig. 1 left) and jetting regimes (Fig. 1 right), this allows for the development of several droplets before the dispersed phase reaches the outflow plane. The first and the second droplets formed have a different size and formation frequency than the droplets formed later. Therefore, in the consequent analysis, the fourth droplet for the dripping regime and the sixth droplet for the jetting regime are considered.

A finite volume method-based CFD solver from ANSYS Fluent 21 with the implemented volume of fluid technique is used to solve the system of time-dependent partial differential equations. For the boundary conditions, a constant velocity profile was utilized for both continuous and dispersed phase inlets. Pressure outlet boundary condition with p = 0 Pa is prescribed at the channel exit. A value of α = 1 is set at the inlet of the dispersed phase and α = 0 at the inlet of the continuous phase. The walls of the channels were considered as fully wetted by the continuous phase. No-slip boundary conditions are applied at the walls. The inlet velocity of the dispersed phase (oil) was kept constant at u_d = 0.0185 m/s for all simulated cases. For the dripping regime, u_c is chosen to be also equal to u_c = 0.00925 m/s. The jetting regime conditions have a higher inlet velocity of the flow in the side channels which is set to u_c = 0.074 m/s. The chosen setup is geometrically close to that of [20] but larger in the x-direction; the original channel in [20] was 6 mm long. A verification of the present methodology with the numerical results of Sontti et al. [20] and the experiments of Wu et al. [28] has been completed in a previous work [22].

The resulting capillary number, defined with the viscosity and the velocity of the continuous phase, is Ca_drip = 0.0061 for the dripping regime and Ca_jet = 0.0487 for the jetting regime. Based on a previous study by the authors [22], the regime change of the described fluids occurs at the critical value Ca_crit = 0.0131. Therefore, the parameters chosen in the current study are typical for the two flow regimes and the inlet velocities differ from those in [20]. Both simulations were initialized with the continuous fluid (α = 0) at time t = 0 s.

2.3 The numerical grid and details of the parallel simulations

The flow in the microfluidic channel is laminar (Re = 52 based on the viscosity of the continuous fluid in the jetting regime) which does not lead to steep gradients at the walls that are characteristic at turbulent conditions. Together with the fact that the droplet formation (at least for the jetting regime) appears away from the walls of the channel and that the interface constantly changes its position and shape, the use of an equidistant numerical grid is adopted for the present study. This allows to adequately resolve the small curvatures of droplets formed in the middle of the channels in case of the jetting regime and resembles the widely adopted approach used in setups with constantly changing flame position as in [29].

A cubical (equidistant) hexahedral mesh with a spatial resolution of 10 μm is utilized. Thus, the total number of control volumes is 5 581 500. The physical time simulated for the dripping regime was 0.30 s, while for the jetting regime it was 0.19 s, due to the higher generation frequencies. The Courant–Friedrichs–Lewy number was CFL = 0.25 which resulted in typical time steps Δt = 3.1E-5 for the dripping and Δt = 5.1E-6 for the jetting regimes. Both parallel computations (one for the dripping and one for the jetting regime) had a wall clock time of 72 h for both parallel simulations utilizing 160 cores on the “bwUniCluster 2.0” at Karlsruhe Institute of Technology.

2.4 Definition and numerical calculation of flow parameters

Parameters of main interest in the present work are hydrodynamic pressures and stresses which have a dimension of Pascals, or forces per unit area [Pa] = [N/m²]. Besides this, there are also forces acting on the molecules of the two fluids at their interface. They are introduced through the surface tension $\upsigma$ which has a dimension [N/m], see [27, 28]. To be able to quantitatively compare the effect of the surface tension with the usual hydrodynamic pressures, the surface tension pressure ${ {\Delta p}}_{\upsigma }$ is defined in the following. It has the dimension [Pa] and is calculated from Eq. (9):

$${ {\Delta p}}_{\upsigma }=-\upsigma \cdot \kappa $$

(9)

Please note that in Eq. 9 the curvature $\kappa$ is a geometrical parameter and the surface tension $\upsigma$ is a constant. Therefore, the value of surface tension pressure ${ {\Delta p}}_{\upsigma }$ turns out to be a result of a purely geometric quantity—the curvature $\kappa$. The curvature $\kappa$ is computed—during the postprocessing stage—in the whole three-dimensional domain from the gradient of phase fraction α (Eq. 5). After this, $\kappa$ and ${ {\Delta p}}_{\upsigma }$ are interpolated at the isosurface with α = 0.5.

The static pressure difference through (normal to) the curved interface between the two fluids is called Laplace pressure, ${ {\Delta p}}_{\text{Lapl}}$, and is defined as:

$${ {\Delta p}}_{\text{Lapl}}={\text{p}}_{\text{i}}-{\text{p}}_{\text{o}}$$

(10)

In the above equation, ${\text{p}}_{\text{i}}$ is the pressure inside the disperse phase and ${\text{p}}_{\text{o}}$—in the continuous phase. When the two fluids are at rest and for perfect geometries of the interface (sphere or cylinder), it can be shown [30, 31] that the surface tension pressure ${ {\Delta p}}_{\upsigma }$ is equal to the Laplace pressure ${ {\Delta p}}_{\text{Lapl}}$.

Numerically, the pressures inside and outside the forming droplet—p_i and p_o—are evaluated at the isosurfaces α_i = 0.98 (inner side of the droplet) and α_o = 0.02 (outer side of the droplet), as shown in Fig. 2. The quantities in the brackets in Fig. 2 show the typical variables which are presented on the corresponding isosurface, e.g., the outer pressure p_o is presented (per definition) on the surface α = 0.02 (or α = 2%), etc. Table 2 illustrates the sensibility of the Laplace pressure in terms of the chosen α-values where the pressure differences are evaluated. In theory, the ideal case would be to evaluate the pressures at α_o = 0.0 and α_i = 1,0 which is not possible in this microfluidic channel. For the droplet in Fig. 2, the choice for α_i = 0.98 (together with α_o = 0.02) is compared to the choice α_i = 0.95 (together with α_o = 0.05). The resulting relative error is 3.80% which could be acceptable; however, in this work the choice closer to the theoretical one, namely α_o = 0.02 and α_i = 0.98, is accepted.

Fig. 2

Surfaces of different phase fractions α near the interface of the two fluids

Table 2 Sensitivity of the Laplace pressure with respect to the chosen values for α

The static pressure changes due to fluid motion. In that case, the surface tension pressure and the Laplace pressure are no more in balance. With the fluids set in motion, it is reasonable to account for forces acting in the tangential direction of a fluid element. For isotropic Newtonian fluids, the viscous stress tensor is used; it has six values at each point of the domain. To reduce the amount of information, it seems appropriate to use only one representative value for the stress tensor at each point. The value utilized in the present work is the von Mises criterion ${\sigma }_{v}$, defined as:

$${\sigma }_{v}=\sqrt{\frac{1}{2}{{\cdot ((\sigma }_{xx }{- \sigma }_{yy })}^{2}+{{(\sigma }_{yy }{- \sigma }_{zz })}^{2}+{{(\sigma }_{zz }{- \sigma }_{xx })}^{2}+6\cdot {({\sigma }_{xy}}^{2}{{+ \sigma }_{yz}}^{2}{{+ \sigma }_{xz}}^{2}))}$$

(11)

The components from Eq. (11) represent the shearing and the normal stresses and are calculated in the postprocessing stage as follows:

$${\sigma }_{{x}_{i}{x}_{j}}=\mu \cdot \left(\frac{\partial {u}_{i}}{\partial {x}_{j}}+\frac{\partial {u}_{j}}{\partial {x}_{i}}\right) \quad \text{if i}\ne \text{j and}$$

(12a)

$${\sigma }_{{x}_{i}{x}_{j}}=-p+2\mu \cdot \frac{\partial {u}_{i}}{\partial {x}_{j}} \quad \text{ if i}=\text{j}$$

(12b)

In the above equations, u_i is the velocity component along the axis x_i. When substituted in Eq. 11, the pressure from Eq. 12b cancels. Therefore, Eq. 11 reflects the integral action of the viscous forces. The viscosity μ is computed for each grid point according to the VOF method (Eq. 7).

All parameters described in this subsection are computed after the simulations have been completed, i.e., during the postprocessing stage of the results.

3 Results

In this section, the temporal and spatial distribution of the interface between the two fluids, along with the relevant parameters within the domain affecting this interaction, is showcased. The evolution of the interface's geometry at various time intervals is initially presented to provide an overall understanding of the droplet formation process. Subsequently, attention is directed toward the tracking of specific points, such as the neck of the droplet, the maximum diameter of the forming droplet and the inflection point where the curvature changes sign. The latter point is of particular interest due to its correlation with changes in static pressure during the jetting regime. Moving forward, the dynamic analysis examines the parameters at these characteristic points over time. Of particular significance is the phase during which the droplet approaches the pinch-off state, driven by the steadily increasing curvature at its neck. The focus here is on the presentation and discussion of the spatial distribution of parameters along the interface, emphasizing local analysis.

The results depicted in the figures encompass regions well upstream of the impending droplet detachment, allowing for the inclusion of areas where initial instabilities, especially in the jetting regime, originate. Additionally, the incorporation of spatial and temporal derivatives of pressure and curvature enhances the pinpointing of key turning points in droplet development.

3.1 Droplet formation and detachment in the dripping regime

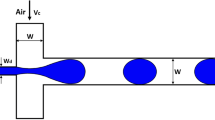
In the first part of this section, the so-called dripping regime is discussed. It is characterized by bigger emulsions and relatively low detachment frequencies [20]; the process is shown in Fig. 1. The first characteristic parameter that describes the process of droplet break-off is the point at which the lateral size of the droplet (along the y-axis) has its extremum. In other words, this is the point where the droplet diameter has its maximum (during the stage of droplet penetration in the side channels when it increases its lateral size) or it has its minimum (during the stage of droplet squeezing when it already entered the central channel). From now on, we will refer to this characteristic point as the max–min point. Figure 3 illustrates the time development of the interface and indicates the location of the min–max point on it by the black arrows.

Fig. 3

Development of the neck of the forming droplet in the dripping regime

3.1.1 Dynamic analysis

The normalized diameter (D_max-min/W) of the advancing max–min point of the interface is shown in Fig. 4a. Following [15], there are 2 stages called “filling” and “squeezing” which are also shown in the figure as well as in Fig. 3 and are separated by a dashed line in Fig. 4a. During the filling stage, for a duration of time t_fill, the dispersed phase enters the cross section. The diameter of the forming droplet grows, becoming larger than the width of the channel, W. At the beginning of this filling stage, the dispersed fluid slowly blocks the flow in the side channels, causing the upstream pressure there to increase, as shown by the green squares in Fig. 4b, a phenomenon which is described also qualitatively in [32]. The green and the red squares in Fig. 4b represent the pressure signals in the side and the main channels (points A and B from Fig. 3d), which, in Fig. 4b, are compared to the two parts of the Laplace pressure.

Fig. 4

Parameters of the dripping regime: a time development of the lateral droplet size D in the max–min point; b various pressures explained in the text

In the squeezing stage, also known as the necking stage, the neck of the droplet begins to shrink, becoming smaller than the width of the channel, as shown for time t = 0.2570 s in Fig. 3c.

As the D_max-min decreases, the continuous phase remains obstructed by the advancing oil front, causing pressure values to rise further in the side channel(s). Figure 4b illustrates that the pressure in the side channel fluctuates by more than 13 Pa over time, while the central left channel experiences fluctuations of only around 8 Pa. Interestingly, these pressure variations also affect the interface between the two fluids as time progresses. In this context, the inner part of the Laplace pressure (α = 98%) aligns with the pressure changes in the entry channel, while the pressure at α = 2% closely mirrors the pressure in the side channels. This pattern holds during most of the droplet formation process. However, as the pinch-off approaches (indicated by the green arrow in Fig. 4a), the four pressure signals in Fig. 4b begin to deviate from each other, no longer following the same trend.

Figure 5a shows the time development of the three parameters defined in Sect. 2.4 (pressures and shear stress) tracked at the max–min point. Initially, during the filling stage, there is a slight domination of the surface tension pressure Δp_σ over the Laplace pressure Δp_Lapl. For a certain period (t = 0.2504 s to t = 0.2754 s), the curvature of the oil front (Δp_σ), strictly follows the change of Δp_Lapl,, signifying a local equilibrium. Up to this time, the process of pressure change is slow enough, and as a result, droplet generation proceeds through a series of equilibrium states. However, after t = 0.2755s Δp_σ starts increasing faster than Δp_Lapl (Fig. 5a) so that an imbalance between the two values occurs; the time for this imbalance is in tune with the diverging pressures from Fig. 4b. At this point, the droplet's diameter begins to decrease more rapidly (refer to Fig. 4a) and processes at the interface and neck accelerate. While surface tension pressure promptly responds to changes in the now rapidly evolving interface curvature, Laplace pressure, linked to the static pressure field, lags in its response. It should be noted that the magnitude of the von Mises stress is more than one order lower than the one of Δp_σ and Δp_Lapl during the whole droplet formation process.

Fig. 5

Parameters of the dripping regime: a time development of the pressures and von Mises criterion in the neck (max–min point); b area-averaged downstream velocity u inside the neck of the droplet during the formation process; c velocity profiles (z = 0.3 mm) for four different time instances inside the neck of the forming droplet; d time development of the volume flow rate Q through the cross section of the max–min point

The area-averaged downstream velocity component inside the neck of the droplet is shown in Fig. 5b. Except for the first point, the average u velocity in the neck constantly accelerates until droplet pinch-off. This is also visible from the velocity profile inside the cross section of the max–min area (mid-height z = 0.3 mm) for the four time instances, denoted in Fig. 5c.

The volume flow rate Q, however, behaves differently as it is influenced by changes in both average velocity and cross-sectional area. As depicted in Fig. 5d, it initially increases until the static pressure in the side channels reaches its maximum (cf. Figure 4b). Consequently, this elevated static pressure, acting on the entire outer surface of the forming droplet, hinders further growth of diameter of the propagating oil front. At t = 0.2794s, another factor contributes to the flow rate decrease, originating from inside the droplet. The increasing static pressure at the centerline, just upstream of the smallest neck diameter, restricts the inflow of oil into the droplet. This pressure increase will be discussed in the following subsection.

3.1.2 Local analysis

As previously mentioned, the final phase of the detachment process, as illustrated in Figs. 4 and 5, is characterized by the dominance of surface tension pressure. The analysis associated with these figures focuses on the interface between the two fluids. However, for a broader perspective, Fig. 6 provides insights into the evolution of static pressure along the central channel axis at various stages of droplet formation. In Fig. 6, two black dashed lines mark specific points on the interface (α = 0.5): one where the curvature changes from convex to concave, referred to as the inflection point (left black dashed line “a”) and the other at the neck of the droplet (right dashed line “b”). Subsequent analysis explores the relationship between these characteristic interface points and the pressure along the dashed centerline.

Fig. 6

Pressure development along the middle (symmetry) line inside the neck of the forming droplet for different time instances together with the corresponding shape of the interface

Figure 6a and b presents moments when the droplet's neck is still relatively large, and the surface tension pressure remains in equilibrium with the Laplace pressure (cf. Figure 5). During these instances, a gradual and consistent decrease in static pressure along the entire red dashed line presented in Fig. 6a and b can be observed. As time progresses, the neck of the droplet becomes thinner, leading to an increased pressure difference between points “a” and “b” as evident in Fig. 6c and d. In these later stages, pressure variations are no longer monotonic. Instead, a pressure peak forms at point “a,” corresponding to the location where the curvature of the interface changes its sign along the x-axis. Over time, the distance between points “a” and “b” diminishes. In the final moments before droplet detachment (t = 0.2794 s), a substantial pressure difference of approximately 35 Pa is observed. Figure 6c and d clarifies that this pressure peak, which obstructs fluid flow from the left to feed the droplet, occurs not at point “b,” representing the narrowest part of the forming droplet's neck, but rather at point “a,” which corresponds to the upstream inflection point of the interface.

Figure 7 provides a local distribution of the parameters mentioned in subSect. 2.4 on the surface of the emerging droplet at the time instance t = 0.2794 s. In Fig. 7 a, the distribution of Δp_σ at α = 0.5 can be seen, while in b both the pressures inside (α = 0.98) and outside (α = 0.02) of the droplet are displayed. Across the entire surface, there is a clear dominance of Δp_σ over Δp_Lapl. The points where both parameters reach their highest values correspond to the inflection point of the surface labeled as “a” in Fig. 6c. Interestingly, despite point “b” being characterized by the narrowest neck and, consequently, the smallest diameter, it experiences a decrease in both surface tension pressure and Laplace pressure. This decrease in surface tension pressure at location “b” results from the overall curvature, which is influenced by two opposing components. The first component's center of curvature is within the oil phase, contributing to an increase in Δp_σ. In contrast, the other component lies outside the droplet and leads to a decrease in Δp_σ. In the current time instance, the latter component prevails at point “b” causing a reduction in surface tension pressure. Notably, the von Mises criterion, σ_v, shown in Fig. 7c, attains its maximum value at the smallest diameter, specifically at point “b.” All of the above-mentioned effects are shown quantitatively in Fig. 7d for the line one oil surface defined by the x–y plane at z = 0 m (symmetry plane) for the same time instance.

Fig. 7

Pressures and stresses for the dripping regime at t = 0.2794 s: a spatial distribution of the surface tension pressure Δp_σ for α = 0.5; b pressures inside (α = 0.98) and outside (α = 0.02) the droplet; c von Mises criterion σ_v on the surface of the droplet; d static analysis of pressures and stresses on the line, defined by the cross section of the oil front surface and the xy symmetry plane (z = 0 m)

3.2 Droplet formation and detachment in the jetting regime

In this second part of “Results” section, an analysis of the jetting regime is conducted. To design a flow setup for this regime, the boundary condition for the inflow velocity of the continuous phase has been increased from 0.00925 m/s to 0.0740 m/s. This has two major consequences for the resulting flow. First, the larger momentum of the continuous phase that enters through the side channels retards the spreading of the dispersed phase and does not allow it to grow toward the side channels [32]. The dispersed phase is constantly narrowed and displaced once it leaves its part of the main (entry) channel. This is well seen in the insert of Fig. 8a where a cone-like shape, filled by the disperse phase, is formed. Therefore, the droplets cannot be built inside, or near the place, where the main and the side channels meet. Hence, the location where the formation of droplets occurs is now moved downstream.

Fig. 8

Development of the neck of the forming droplet in the jetting regime at different time instances. The walls of the channels are presented also for orientation

The second consequence when the continuous phase velocity is increased is that a long-suspended column of the dispersed fluid flows into the central channel. A perturbation on this long thread that has a cylindrical shape triggers interface fluctuations known as the Rayleigh–Plateau instability [8]. As a result, droplets with smaller sizes and higher generation frequencies than those for the dripping regime are released from the central column. Often this column of dispersed fluid is referred to as “jet” [8].

The two regimes result in quite different frequencies of the generated droplets. Table 3 reveals that, for the boundary conditions studied, the jetting regime generates approx. 20 times more droplets. Because the flow rate of the oil droplets remains the same in both regimes, the volume of the droplets for the jetting regime will also be approx. 20 times smaller. The Strouhal number is calculated with the width of the channel side and the average velocity in the main channel.

Table 3 Frequency of the generated droplets for the two regimes

3.2.1 Dynamic analysis

In contrast to the dripping regime, the generation process in the jetting regime consists of only the necking stage [31]. Due to the lack of a pronounced maximum diameter of the neck during the formation process, we will refer to the characteristic point, described in Sect. 3.1, as the min point (D_min). The tracking process is depicted in Fig. 8. The value for the non-dimensional diameter of the neck—as tracked in time—is presented in Fig. 9a. The analysis in the figure was conducted for the sixth generated droplet. The decrease of D_min is nearly linear. At t = 0.1277s the process finishes with droplet pinch-off (marked by the green arrow). Due to the far distance of droplet detachment from the junction region and the relatively thin thread, the front of the dispersed phase does not enter (does not block) the fluid from the side channels. Therefore, the pressure in the side channels does not affect the droplet detachment and vice versa. As shown in Fig. 9b, both the pressure in the side channel and the pressure in the entry channel change within 1% during the whole process of droplet formation.

Fig. 9

Parameters of the jetting regime: a diameter of the neck of the forming droplet (min point); b corresponding pressure signals in the channels (for the location of pressure points, see Fig. 3)

As a next step of the analysis, the development of the parameters defined in subSect. 2.4 is tracked in time at the neck of the forming droplet. Clear domination of the surface tension pressure Δp_σ over Δp_Lapl is noticeable during the whole process (Fig. 10a). The disbalance between Δp_Lapl and Δp_σ becomes larger with decreasing neck diameter. Figure 10b presents the components of the Laplace pressure (isosurfaces α = 0.02 and α = 0.98). All above-described pressures, as well as the velocity inside the neck (Fig. 10c), change their behavior at time t = 0.1259 s. This time instant is marked by the red arrow in Fig. 9a. At the same point in time, the von Mises criterion ${\sigma }_{v}$ and the area-averaged velocity (Fig. 10c) in the neck reach their maximum. The area-averaged velocity outside the jet remains nearly constant in time and is around 0.08 m/s. This is more than two times slower than the values inside the jet presented in Fig. 10c and e.

Fig. 10

Parameters of the jetting regime: a surface tension pressure, Laplace pressure and von Mises stress at the neck of the forming droplet; b components of the Laplace pressure; c area-averaged downstream velocity u inside the neck of the droplet; d volume flow rate Q through the cross-sectional area of the neck; e velocity profiles (z = 0.3mm) for four different time instances inside the neck

In contrast to the dripping regime, here the flow rate through the neck of the forming droplet decreases constantly, as shown in Fig. 10d. Similar to the dripping regime, a pressure jump just before the neck of the droplet (discussed in the section below) restricts and therefore reduces the entering volume flow rate. In the jetting regime, the decrease in the neck diameter is so rapid that the initial velocity increase shown in Fig. 10c is not sufficient to compensate for the reduced cross-sectional area of the neck. This leads to a constant reduction in the volume flow rate that enters the droplet as shown in Fig. 10d and is qualitatively different from the dripping regime. The reduction in the volume flow rate could be inferred also by the u velocity profiles presented in Fig. 10e.

The clear domination of the surface tension pressure over the Laplace pressure at all time instances from Fig. 10a is in contrast to the dripping regime where the two pressures are in balance—at least for time instances not very close to pinch-off, cf. Figure 5a. As we will see later (Fig. 13a), the local analysis along the jet surface also shows that for a long distance downstream of the jet body, there is a persistent difference between the two pressures in the jetting regime. This local disbalance occurs as a major difference between the jetting and the dripping regimes. The effect of the shear stresses, summarized with the von Mises criterion, becomes also more noticeable, compared to the dripping regime. However, Fig. 10a shows that its values are still several times lower than the two pressures, in contrast to the results discussed in [15].

3.2.2 Local analysis

When discussing the mechanisms behind droplet detachment, the pressures inside the jet must be considered. Figure 11 shows the static pressure along the middle line (red dashed line) of the jet for three different stages of droplet formation denoted in the figure. Similarly, to Fig. 6 two dashed lines mark the locations on the interface of the inflection point (left dashed line “a”) and the neck itself (right dashed line “b”). Additionally, two arrows denote other characteristic points (“c” and “d” in Fig. 11c), which mark the locations of the next (second) forming droplet. They will be discussed in detail further down in this section.

Fig. 11

Static pressure along the dashed middle line of the jet at the area of the forming droplet: a t = 0.1246 s; b t = 0.1259 s; c t = 0.1273 s

Similar to the dripping regime in Fig. 6, at the beginning of the droplet formation, the highest pressure occurs upstream in the inflection point marked by the left black line (“a”). This is the point, at which the surface changes from convex to concave and where the new tip of the jet will appear after droplet pinch-off. It is worth noticing that the pressure peak at the upstream inflection point “a” and the pressure drop between point “a” and the narrowest neck point “b” are quite pronounced and that both are present for all time steps shown in Fig. 11. This pressure difference increases with the time from 21 Pa at t = 0.1246 s (Fig. 11a) to around 40 Pa at t = 0.1259 s (Fig. 11b). Please note that the peak prevents the upstream fluid from entering the forming droplet.

When examining the local distribution of parameters defined in subSect. 2.4 for a fixed time step just before droplet pinch-off (t = 0.1273 s), we observe similar patterns as in the dripping regime (c.f. Figure 7). The surface tension pressure (Δp_σ) dominates over the Laplace pressure (Δp_Lapl) across the entire surface of the jet. The most significant difference between these two pressures occurs at the inflection point (“a” in Fig. 11c), represented by the red ring in Fig. 12a. It is noteworthy that the minima of Δp_σ and Δp_Lapl correspond to the two narrowest sections of the jet, marked as arrows “b” and “d” in Fig. 11c. These sections exhibit a saddle shape of the interface, resulting in curvature from two sources, similar to the dripping regime. This dual curvature is particularly pronounced at locations “b” and “d,” leading to a local minima in surface tension pressure. In contrast, locations “a” and “c” in Fig. 11c feature a conical shape of the interface, meaning there is no second radius of curvature beyond the surface. Consequently, both Δp_σ and Δp_Lapl, as well as the static pressure along the middle line of the jet, exhibit local maxima in these regions. At locations where Δp_σ and Δp_Lapl have local minima, the von Mises criterion σ_v reaches its maximum, as shown in Fig. 12c. The above-mentioned effects are summarized quantitatively in Fig. 12d for the line one jet surface defined by the x–y plane at z = 0 m (symmetry plane).

Fig. 12

Pressures and stresses for the jetting regime at t = 0.1273 s: a spatial distribution of the surface tension pressure Δp_σ for α = 0.5; b pressures inside α = 0.98 and outside α = 0.02 the droplet; c von Mises criterion σ_v on the surface of the droplet for α = 0.5; d static analysis of pressures and stresses on the line, defined by the cross section of the oil jet and the xy symmetry plane (z = 0 m)

Figure 13a illustrates the static pressure development along the midline (y = 0 m, z = 0.0003m) for the dispersed phase and at the line (y = 0.000145 m, z = 0.0003 m) for the continuous phase. The latter is located in the middle between the channel wall and the jet surface (green line) for the same time instance at t = 0.1273s. For comparison, the static pressure development along the centerline of the dispersed phase within the jet (from Fig. 12c) is presented here again (red line). Initially, both pressures exhibit a similar decay until a certain point (x ≈ 0.0053 m), after which the pressure of the fluid inside the jet no longer decreases linearly. This phenomenon is more pronounced in the pressure gradient shown in Fig. 13b (insert with zoomed view). Thereafter, a visible oscillation of both pressures inside and outside the jet is observed. These gradients (which are an expression of the instability of Rayleigh–Plateau [33, 34]) grow and eventually lead to the situation shown in Fig. 11c, where a significant pressure jump occurs between the inflection point “a” and the narrowest neck of the jet at “b,” finally leading to the droplet formation.

Fig. 13

Pressures and the gradient of pressures at t = 0.1273 s: a static pressure along the symmetry line inside the jet (red) and along the middle line between the channel wall and the jet (green); b pressure gradients along the lines from “a” and a zoomed view of the first visible pressure fluctuation

4 Conclusion

In the presented study, the process of droplet formation in the flow-focusing microfluidic device is numerically analyzed. A gap in the literature is filled by the presentation of the exact values of the parameters at the interface between the two immiscible fluids. This quantification has been carried out in two ways. The first method, called “dynamic analysis,” defines different parameters at precise spatial points, but with changing time. Some of those points have fixed coordinates while others are tracked in a Lagrangian manner, such as the neck of the forming droplet. The note tracking is performed during the postprocessing of the results. The second method for results assessment is performed at fixed time instances, and it follows the distribution of parameters along/downstream the phase interface, referred to as “local analysis.” The main quantities that are compared and presented are defined in §2.4. Typically for similar fluid mechanics problems, these quantities are all presented in terms of pressures (Laplace pressure, showing the pressure difference inside and outside the fluids’ interface as well as surface tension pressure which is the result of the local curvature of this interface) and stresses (viscous shear stresses and von Mises stress).

The two regimes considered have capillary number values (Ca_drip = 0.0061 and Ca_jet = 0.0487) far away from the critical Ca number (Ca_crit = 0.0131), and therefore, they present typical characteristics for each flow regime. The regime change was achieved by increasing 8 times the inflow velocity of the continuous phase (water and glycerol) through the side channels while the inflow velocity of the dispersed phase (oil) remained unchanged.

The discussed parameters were obtained through simulations utilizing the “volume of fluid” method on a uniform numerical grid with a fine spatial resolution of 10 μm and a total number of 5 581 500 control volumes. Those simulations were carried out on a parallel supercomputer for a total time of 11 520 CPU hours (sum over all processors).

It was found that in the dripping regime, the process of droplet formation is characterized by the balance (equality) of surface tension pressure and Laplace pressure. The Laplace pressure typically exhibits values around 20 Pa. This is comparable to the static pressure differences between the middle (entry) and side inflow channels. The balance between the Laplace and the surface tension pressures deteriorates only when the droplet approaches pinch-off. Immediately before pinch-off, when the neck of the droplet starts to decrease its size more quickly, surface tension pressure immediately reflects these changes in the curvature and starts dominating over the Laplace pressure which, being based on the static pressure field, needs a longer time to react.

Other interesting observations for the dripping regime could be summarized as follows:

• The droplet first grows in diameter (filling stage) and starts blocking the fluid from the side channels. This, in turn, leads to an increase in the static pressure in these channels causing the droplet—which at that time already enters the large outflow channel—to decrease its diameter (squeezing stage).

• The process of rapid decreasing of the droplet size when approaching pinch-off is featured by the formation and emergence of a peak of static pressure at the centerline axis. At this stage, this peak prevents the upstream fluid from entering the droplet and the volume flow rate entering the droplet also starts decreasing more rapidly. However, the volume flow rate is not compensated by the observed constant increase in the velocity in the neck of the droplet, as at the same time the area of the neck decreases more rapidly.

• The above-mentioned static pressure peak at the centerline axis occurs not in the neck of the droplet, but a bit upstream. The peak location is connected with the position, where the interface between the two fluids has an inflection point, i.e., where the interface changes its curvature sign in the x–y plane.

In contrast to the dripping regime, in the jetting regime, the surface tension pressure constantly dominates over the Laplace pressure. One explanation for this is again the more rapidly occurring changes in the geometry of the interface: The droplet formation in the jetting regime is more than 20 times quicker than in the dripping regime.

Our main observations for the jetting regime were:

• In the jetting regime, the pressure in the side channels does not play a role in the formation of the droplet neck, and vice versa—neck formation does not affect the pressure in the side and entry channels.

• Similar to the dripping regime, when the interface curvature locally changes its sign, the pressure at the centerline axis shows a clear local maximum. The downstream derivative of this centerline pressure is the first parameter that changes along the jet axis—thus indicating the onset of the Rayleigh–Plateau instabilities for this regime.

• The average velocities of the dispersed phase inside the jet are more than two times higher than those around the jet.

• The averaged u velocity within the neck of the droplet initially increases and subsequently decreases. There is a constant reduction in the volume flow rate that enters the droplet.

• Due to the higher flow rate, the pressure level and the pressure gradients are generally higher than in the dripping regime.

Finally, the observed viscous stresses, as determined by the von Mises criterion, were approximately an order of magnitude lower than the surface tension pressure and Laplace pressure, regardless of the regime—dripping or jetting.