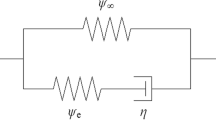
Abstract
The 3D creep and dynamic displacements and stresses of the suddenly pressurized “finite-length” thick visco-hyperelastic cylinders with fixed ends are investigated here for the first time, employing a hybrid semi-analytical approach. By incorporating the incompressibility condition of the material and the hierarchical Prony-series-type Mooney–Rivlin constitutive model, the dynamic 3D visco-hyperelasticity equations of the vessel are interpreted in terms of the instantaneous axial and radial time variations of the radii. The heredity integral is written in terms of the time-derivative of the relaxation kernel rather than the time derivatives of the stresses, for the first time. The resulting nonlinear integrodifferential governing equations whose number of terms grows with time are solved by an iterative solution that uses a point-collocation technique, the time-domain trapezoidal technique, and the Runge–Kutta time-marching method. Comprehensive parametric studies are performed to evaluate the effects of various geometric, hyperelastic, and viscous/creep material properties on the creep and dynamic/vibration responses of the structure. Results show that (1) in comparison with the traditional structures, the effects of the superimposed higher vibration modes and damping are much more notable in visco-hyperelastic structures, (2) the displacement and stress components are affected by not only radial inflation but also the time-dependent magnitude and sign of the bending-inspired curvatures, (3) the largest hoop and axial stresses occur in regions located about the mid-length section and in the vicinity of the fixed ends, respectively, and (4) the displacements and stresses increase but the thickness reduction decreases by increasing the cylinder length. The creep results show while the slopes of the creep curves are larger for longer cylinders, the shorter cylinder reaches the steady state earlier.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Hyperelastic materials are among the most common synthetic or living constituent materials of natural and industrial/medical substances or structures. As their name implies, they are generally soft and can exhibit very/extremely large recoverable deformations, and due to their compliance, they feature apparent material flow and viscosity and structural damping. Therefore, this special category of materials may show exaggerated deformations and energy dissipation. In addition to kinematic nonlinearity that may be observed in the traditional elastic structures [1], these nonlinear elastic/viscoelastic materials feature constitutive nonlinearities as well. Recently, Dal et al. [2] reviewed the challenges made for proposing 44 hyperelastic constitutive models for rubber-like elastomers and assessed their strengths and weaknesses under uniaxial, pure shear, and equal-biaxial deformations. To date, numerous constitutive models have been proposed to capture the hyperelastic behavior, and few of these models are extended to model the more actual visco-hyperelasticity nature of these materials [3,4,5].
Some researchers have focused on behavior analysis of the hyperelastic cylinders and spheres. Batra et al. [6] investigated radial deformations and stress components of a cylinder composed of an inhomogeneous Mooney–Rivlin material whose material parameters varied continuously through the thickness. Shariyat et al. [7] investigated the stress and displacement distributions for pressurized thick hyperelastic cylindrical pressure vessels/tubes analytically, experimentally, and numerically. Furthermore, they used different hyperelasticity constitutive models to generalize their comparisons. Yazdani et al. [8] presented a semi-analytical solution for large deformation and stress analyses of pressurized finite-length thick-walled incompressible hyperelastic cylinders. Static loads were imposed, and no viscoelasticity was considered for the constituent material.
There are mainly two common approaches for creep analysis of structures under static loads. The majority of the works on creep behavior analysis of the structures were performed by using plasticity-type flow rules in conjunction with the power-law-type definition of the effective stress and successive approximations. For polymeric and rubber-like components and reinforced plastics, the viscoelasticity-based models were much more successful in the reproduction of the experimental results. Vanin and Duc [9] studied the creep behavior of pressure vessels with spherical inclusions or pores under hydrostatic pressures, using Volterra’s integral and Rabotnov's theory of viscoelasticity. Later, Duc [10] extended the two-phase model for shear creep and relaxation investigation of the orthogonally reinforced sphero-fibrous composite and glass-reinforced plastics with hollow fibers. Vanin and Duc [11] used Rabomov's creep model for 3D stress field analysis of the orthogonally reinforced sphero-fibrous composites. Duc et al. [12] analyzed the bending and creep of a three-phase composite plate reinforced by glass fibers and titanium oxide particles in the presence of shear stress.
The formulation development of the hyperelastic/visco-hyperelastic structure usually commences by defining an adequate strain energy function. The nonlinear shear vibrations of pre-compressed multilayer plates with stiff and damping visco-hyperelastic layers were studied by Gacem et al. [8]. A Gent-Thomas energy density function that multiplies the individual coefficient of the hyperelastic material by exponential relaxation functions was used. Sahoo et al. [9] proposed and implemented a visco-hyperelastic model for the brain, considering fractional anisotropy and axonal fiber orientation. In this regard, three strain energy density functions that included the matrix and fiber distortional strain energies and the rate effects were taken into account through an exponential relaxation function. Within the context of visco-hyperelasticity, Pascon [10] extended used similar neo-Hookean energy density functions for the two branches of the Zener rheological model and summing up the energies, employing a rate equation for the viscous branch. He used the simple Voigt’s relation of the elastic mixtures for the functionally graded material. Zhao et al. [11] investigated the nonlinear limit cycles and chaos behaviors of the visco-hyperelastic spherical shells, using Gent’s strain energy function of the Zener-type visco-hyperelastic materials. Wu et al. [12] extended the Mooney–Rivlin hyperelastic constitutive model by multiplying it by a time-dependent function that uses an exponential relaxation function to simulate the behavior of the soft materials. Numerous complicated but less applicable models have also been proposed so far. By using a Zener model for the visco-hyperelastic constitutive model, Dal et al. [13] extended the well-known eight-chain model for the creep and relaxation behavior modeling of rubber-like materials.
Some studies of the visco-hyperelastic vessels were performed by utilizing the stress-based elasticity theory. For this reason, they started by defining the visco-hyperelastic constitutive model rather than the definition of explicit strain energy density functions. Yang and Shim [14] focused on the constitutive modeling of finite deformation of incompressible elastomeric foams, using a polynomial series that involves a four-parameter Maxwell relaxation model with exponential relaxation functions for the strain energy, due to the sensitivity to strain rate. López-Campos and Segade [15] extended the Mooney–Rivlin hyperelastic model by adding a nonlinear viscous part including strain and time dependencies and developed a genetic algorithm for optimizing the model parameters. Based on the tube theory of polymer dynamics, Xiang et al. [16] developed a physically based viscoelastic constitutive model according to a microscopic picture at the molecular chain scale and decomposed the stress into a hyperelastic part, which comes from the elastic crosslinked and entanglement network, and a viscose part, which is originated from free chains. Exponential disentanglement and contour length relaxation functions were used. Dadgar-Rad and Firouzi [17] studied the large creep deformations of the visco-hyperelastic beams and frames. They started with a compressible neo-Hookean model and extended its constitutive law to a visco-hyperelastic one by utilizing an exponential relaxation kernel. Recently, the authors [18] have published an article on 1D dynamic response analysis of infinitely long visco-hyperelastic cylinders.
To date, no research has been published even on static creep behavior analysis of pressurized visco-hyperelastic cylinders. Therefore, deformation and stress analyses of pressurized visco-hyperelastic vessels under dynamic and shock loads have never been accomplished. It is intended to undertake these tasks in the current research. In this regard, the governing equations are derived based on the three-dimensional theory of elasticity and rewritten in terms of the displacements by using a hierarchical incompressible Zener–Mooney–Rivlin visco-hyperelastic constitutive model. These equations are solved by novel semi-analytical solutions that are accompanied by the point-collocation spatial and Runge–Kutta time discretization procedures. Some of the points/novelties that distinguish the present research from the previous ones are:
-
It is the first time that dynamic stresses and deformations are reported for internally pressurized finite-length hyperelastic and visco-hyperelastic cylinders.
-
The incompressibility inspired main formulation of the present research has been developed by an exact analytical procedure (rather than an approximate approach such as the finite element method).
-
The present study considers the thickness reductions that vary in the longitudinal direction of the cylinder.
-
It is the first time that the creep redistribution of the deformation and stresses has been reported for neither the finite-length nor infinite-length visco-hyperelastic cylindrical pressurized cylinder.
-
Not only the quasi-static creep phenomenon but also the dynamic vibration dissipation phenomenon is investigated in the present research.
-
In the available articles, displacement-based boundary conditions were imposed. The incorporation of the pressure boundary conditions requires a more sophisticated technique, especially for time-varying pressures.
-
A solution algorithm is proposed for the resulting integrodifferential governing equations whose number of terms grows with time.
-
To extract a more accurate and efficient formulation, the heredity integral is written in terms of the time-derivative of the relaxation kernel rather than the time derivatives of the stresses, for the first time.
-
The results comprise distributions/redistributions of the resulting three-dimensional stress field.
-
Effects of the cylinder length on the creep and dynamic behaviors of the cylinder are investigated for the first time.
-
The type of the reported results and conclusions is quite new; so, similar types of results have never been reported so far.
2 The 3D governing equations
Consider the vibrating finite-length visco-hyperelastic cylinder shown in Fig. 1 which is subjected to dynamic pressures. In Fig. 1, the \(L\), \({R}_{\mathrm{in}}\), and \({R}_{\mathrm{out}}\) symbols stand for the length and initial inner and outer radii of the cylinder, respectively.
Let us denote the original and instantaneous coordinates of each material particle of the cylinder by \(\boldsymbol{\Psi }(R,\Theta ,Z)\) and \({\varvec{\psi}}\left(r,\theta ,z\right)\), respectively, wherein the first, second, and third coordinates of each set are measured, respectively, in the radial, circumferential, and longitudinal directions. When both ends of the pressurized cylinder are fixed, as shown in Fig. 1, one may use the \(\theta =\Theta , z=Z\) identities. Therefore, the deformation gradient (\({\varvec{F}}\)) and left Cauchy–Green (\({\varvec{B}}\)) tensors may be defined as [7]:
On the other hand, the invariants of the left Cauchy–Green tensor may be written as follows:
where following a tensor analysis rule, the repeated indices indicate summations. It is assumed that the cylinder is fabricated from an incompressible (e.g., a rubber-like) material. Hence,
Therefore, Eqs. (2) and (4) lead to the following conclusion:
Indeed, since no displacement occurs in the \(z\) direction, a material ring of an initial radius \(R\) and thickness \(\mathrm{d}R\) transforms to a material ring of radius \(r\) and thickness \(\mathrm{d}r\), so that the incompressibility condition leads to:
The first identity of Eq. (6) confirms that for a positive magnitude of \(\mathrm{d}R\), \(\mathrm{d}r\) is positive as well, so that either \(\frac{\mathrm{d}r}{\mathrm{d}R}\) or \(\frac{\partial r}{\partial R}\) is a positive-definite quantity. Substitution of Eq. (5) into Eqs. (2) and (3) gives:
To achieve higher accuracies, the Mooney–Rivlin rather than the simpler neo-Hookean strain energy density function is employed to model the hyperelastic behavior. For incompressible materials, the appearance of this function becomes:
For a given strain energy density function (\(W\)), the constitutive law may be obtained from [19]:
where \({\mathcalligra{p}}\equiv {\mathcalligra{p}}(R,Z)\) is the hydrostatic pressure arising from the incompressibility constraint and \({\varvec{I}}\) is the identity matrix. According to Eqs. (2) and (5), one may write:
Therefore, according to Eqs. (2), (9), (10), and (11), the following explicit stress expressions are obtained:
Choosing a Prony series arrangement with nonlinear hyperelastic stiffness elements, the visco-hyperelasticity constitutive equation may be obtained by using the following Volterra-type convolution heredity integral [18]:
where \({{\varvec{\sigma}}}_{HE}\left({\varvec{B}}\right)\) is the nonlinear hyperelastic stress tensor:
The time-dependent function \(\mathcal{G}\left(t\right)\) is the Prony series relaxation moduli and may be introduced as [18]:
where \({\mathcal{G}}_{i}\) and \({\theta }_{i}\) are material constants. Therefore, the generalization of the hyperelastic constitutive law to the visco-hyperelastic one may be achieved through the following Volterra-type convolution integral:
Since the stress tensor is itself unknown, the derivative expression that appeared in the integrand of Eq. (19) is inadequate from the numerical accuracy point of view. This integrand may be replaced by a numerically more accurate form using the integration by-parts technique:
where \(\mathfrak{L}\) is a time-dependent mathematical operator:
The dynamic three-dimensional visco-hyperelasticity equations have the following form in the absence of the body forces [20]:
Equation (23) is automatically satisfied in the present problem. By using the following rule for an arbitrary function \(f\), one has based on Eq. (6):
Because the instantaneous axial orientation of each longitudinal section is a fixed value that is equal to that of the original/initial configuration, therefore Eqs. (22) and (24) may be rewritten as:
Therefore,
Because the boundary conditions of the cylinder are:
Moreover, according to Eq. (31), one has:
According to Eq. (12), the following identity exists for a hyperelastic cylinder:
Therefore, by imposing the mathematical operator defined in Eq. (21), the visco-hyperelastic (VHE) hydrostatic pressure may be written as:
So, according to Eq. (31):
Substituting Eq. (36) into Eqs. (17) and (20):
Since \({p}_{o}\) varies with time only and does depend on \(r\) or \(z\), the displacement-based governing equations of motion/vibration of the cylinder may be obtained based on Eqs. (26), (27), and (37) as:
Equations (38) and (39) may be assembled to constitute a single system that governs the two-dimensional spatial and time variations of the radii of the cylinder:
This system of equations has to be augmented by the incorporation of the boundary conditions that appeared in Eqs. (32) and (33), to form a system with the following compact form:
When this solution is obtained, the stress components may directly be computed from Eq. (37).
3 The second-order spatial point-collocation and time-marching solution procedures
The time-dependence of Eq. (41) may be treated by using the second-order Runge–Kutta that relates the instantaneous acceleration and velocity of the end of the \(n\)-th time step to its instantaneous radius as follows [21,22,23,24]:
The initial acceleration of the suddenly loaded cylinder may not be zero. Therefore, based on Eq. (41), when the analysis begins from a stress-free condition, the general forms of the initial conditions become:
After the substitution of Eq. (42) into Eq. (41), a nonlinear system of time-accumulated (due to the presence of time integral of the \(\mathfrak{L}\) operator) is obtained.
By choosing the trapezoidal rule, one may write the following identity based on Eq. (21):
\(\mathfrak{D}\) contains terms that belong to the previous time steps and thus is a known expression at each time step:
Utilizing the concepts introduced in Eqs. (42) and (44) reduces Eq. (41) to a partial differential differentiation equation in terms of \(R\) and \(Z\), with an accumulation term whose magnitude and number of terms grow with time (i.e., grow as \(n\) grows):
The spatial discretization of the solution domain is accomplished by a mesh containing \(M\) and \(N\) grid points in the radial and axial directions, respectively. Therefore, for a mesh whose grids are uniformly distributed in each of the radial and axial directions, the radial and axial coordinates of a grid point that is located at the \(m\)-th and \(n\)-th radial and axial locations, respectively, become:
Using second-order approximations that are equivalent to using second-order Taylor’s expansions implies that the approximation error reduces to one-fourth when the distances between the nodal points are been halved. The following finite difference expressions are valid for the interior grid points (\(2\le m\le M-1, 2\le n\le N-1\)) only:
For the grid points that are located at the lower (\(m=1\vee n=1\)) or upper (\(m=M\vee n=N\)) layers, forward and backward finite difference expressions have to be used, e.g.,
Since the radial (natural) boundary conditions are already incorporated in Eq. (41), the following axial boundary conditions have to be added to the augmented discretized system of equations:
Eventually, the resulting discretized augmented system of nonlinear integrodifferential governing and boundary equations of the entire cylinder takes the following compact form:
The steps of the solution procedure of the nonlinear integrodifferential augmented system of the governing and boundary conditions of the cylinder may be summarized as:
-
1.
The cylinder is discretized spatially by a mesh that is composed of \(M\) and \(N\) grid points in the radial and axial directions, respectively.
-
2.
The initial conditions are defined.
-
3.
The time-domain solution begins by computing the required finite difference expressions of the partial derivatives of the displacement and stress components. At the first stage, the instantaneous magnitudes of the radii are set equal to those of the initial configuration for all grid points of the 2D radial section of the cylinder.
-
4.
The discretized form of the governing and boundary conditions is established.
-
5.
The second-order Runge–Kutta discretization of the time domain is accomplished [25,26,27,28,29].
-
6.
The portions of the trapezoidal form of the Volterra/convolution-type integrals that are associated with the accumulated terms of the previous time steps must be updated by adding the term that corresponds to the previous time step.
-
7.
The resulting discretized nonlinear system of equations, i.e., Eq. (55), is solved:
$${\varvec{r}}\left(n.\Delta t\right)={\mathcal{K}}^{-1}\left(n.\Delta t\right)\mathcal{F}\left(n.\Delta t\right)$$(56)\(\mathcal{F}\) contains the accumulated heredity viscoelasticity term, the previous displacements, velocities, and accelerations of the grid points, and the expressions containing the pressure values.
-
8.
The convergence of the responses of the nonlinear augmented integrodifferential system of equations has to be checked using the following criterion:
$$\mathop {\max }\limits_{{\forall \left( {m,n} \right)}} \frac{{\left| {r_{m,n}^{\left( s \right)} - r_{m,n}^{{\left( {s - 1} \right)}} } \right|}}{{\left| {r_{m,n}^{\left( s \right)} } \right|}} \le 0.0001$$(57)where \(s\) is the iteration counter. In case of convergence occurrence, the solution procedure is continued by following the steps from step 10.
-
9.
Since the formulations contain nonlinear expressions (e.g., expressions comprising \(r\) in the denominator or include powers of \(r\) or its polynomials) and the initial finite difference expressions were constructed based on initial approximate or non-convergent magnitudes of the radial displacements and stresses, they are updated based on the values obtained according to step 7 and steps 4 to 8 are repeated.
-
10.
The relevant stress components are computed based on Eq. (37), performing the required spatial discretizations and time-integral evaluations (using the trapezoidal numerical integration technique).
-
11.
The resulting velocities and accelerations are computed based on Eq. (42).
-
12.
Steps 4 to 11 are repeated for the next time steps until the final analysis time is reached.
4 Numerical results and discussions
4.1 The employed geometric, loading, and visco-hyperelastic material parameters
The present section contains (1) verification of the results by comparing them with the results of the Abaqus finite element analysis code, (2) evaluation of the effects of the viscoelasticity on the dynamic displacement and stress responses of the visco-hyperelastic cylindrical vessel, (3) sensitivity analyses for the examination of the influences of the magnitude of the finite length and parameters of the relaxation kernel of the visco-hyperelastic material on the resulting radial and longitudinal distributions of the radial displacement and hoop, axial, and transverse shear stresses of the cylinder, and (4) sensitivity analyses for evaluation of the relaxation parameters of the visco-hyperelastic material on the creep responses of the cylinder, for various finite lengths.
Unless otherwise stated, the magnitudes of the geometric and load parameters of the cylinder are as follows:
\(H\left(t\right)\) is Heaviside’s step function. In other words, the pressure is applied suddenly.
The employed properties of the visco-Mooney–Rivlin visco-hyperelastic material are taken from Ref. [18] and listed in Table 1. These properties are extracted by Ref. [18] based on experimental results reported for an isoprene rubber.
4.2 Verification of the results
4.2.1 Verification with Abaqus results
Since no visco-hyperelastic results have been reported so far for finite-length cylinders and the only available results of the finite-length cylinders were published recently by the same authors, the verification of the present results is accomplished by comparing our results with those of Abaqus finite element analysis computer code. It is evident that the Abaqus uses traditional quite different formulations and solution techniques. For example, while the present research has exactly/analytically incorporated the incompressibility condition, analytically ascertained the space and time variations of the hydrostatic pressure, and analytically incorporated the boundary conditions of a cylinder with time-varying visco-hyperelastic material properties in addition to proposing a more accurate processing of the relaxation kernel, the general-purpose Abaqus software has used approximated indirect and less efficient/accurate approaches to achieve these tasks.
Due to symmetry, the Abaqus finite element model was constructed from a one-degree segment of the 3D cylindrical model. The top and side views of the resulting 3D finite element model are shown in Fig. 2. The model consists of 2000 8-node linear brick, reduced integration (C3D8R) elements with hourglass control, and while the symmetry condition was imposed on the circumferential faces/boundaries of the model, the internal/radial boundary was exposed to a specified pressure.
Figure 3 illustrates the radial deformations and the relevant radial and axial distributions of the radial displacement predicted by Abaqus for the finite-length visco-hyperelastic vibrating cylinder at some distinct time instants.
The time variations of the radial displacements and hoop stresses of the inner and outer boundaries of the visco-hyperelastic cylinder that are predicted by the present formulation and Abaqus are compared in Fig. 4 for the mid-length section of the cylinder. This figure reveals that although a good concordance may be noted between the time histories of the radial displacement, the discrepancies between the time histories of the hoop stress are more remarkable. Due to the sudden imposing the internal pressure and dependence of the stiffness of the cylinder on both the hyperelastic and viscoelastic characteristics of the material, a lag may be noted in the formation of the largest peak of the vibration and stress time variations of the visco-hyperelastic cylinder. In other words, the largest peak appears after a few oscillations. Moreover, Fig. 4 indicates that the effect of the superimposed higher vibration modes on the time variations of the responses is significant, so this effect has even governed the time instants of the formations of the local and global extrema (peaks and valleys). However, the oscillations generally exhibit dissipation with time, so the responses eventually tend to the steady-state condition. Since the inner boundary is affected directly by the imposed pressure, its response magnitudes, oscillations, and steady-state values are higher than those of the outer boundary.
4.2.2 Verification with experimental results of the authors
Although a relatively good concordance was noted between our results and the results of Abaqus in Sec. 4.2.1, our formulation is built on some exact formulations and the following hints that not only increase the accuracy but also drastically decrease the solution time:
-
The formulation used in Abaqus is displacement-based and requires defining two displacement components and one rotation to obtain the deformed shape, whereas our formulation uses a single variable, i.e., the instantaneous radius.
-
The spatial integrals are determined by an approximate/numerical method in Abaqus. The integrals are exactly/analytically computed in our formulations.
-
Some of the partial differentiation terms are replaced by exact expressions in the present research.
-
The heredity/Volterra-type time integrals are computed by an exact procedure in our research in contrast to that of Abaqus software.
-
The finite element technique is an integral-based, i.e., domain-averaging method and thus can only trace the averaged domain-based variations in contrast to our second-order point-collocation method that can trace the local variations.
-
The incompressibility condition is imposed exactly, and the hydrostatic pressure is determined in all longitudinal sections of the cylinder. In Abaqus, the incompressibility condition can be imposed by choosing either an arbitrary high bulk modulus or an arbitrary but not zero D1 parameter; hence, this condition is imposed approximately in Abaqus.
The above-mentioned facts lead to mathematically higher accuracy in our formulation and results in comparison with Abaqus. Furthermore, our run times are less than one-tenth (1/10) of that of Abaqus, for the presented verification example. Moreover, the above-mentioned hints clarify why Abaqus cannot be regarded as a professional or even economic tool for the design and analysis of the arbitrary-length thick or thin cylindrical pressure vessels and piping in comparison with our more configuration-consistent specialized semi-analytical approach.
Now another verification example is presented. Any advantageous and relevant verification example should at least include the following characteristics:
-
1.
Hyperelastic (but not necessarily visco-hyperelastic) cylinder,
-
2.
Finite-length cylinder (present results cannot be verified by those of an infinite-length cylinder),
-
3.
Uniform thickness,
-
4.
Moony–Rivlin or Neo-Hookean constitutive models,
-
5.
Uniform internal pressure,
-
6.
Load-induced axial stress (rather than imposing a fixed external axial extension either by a hanging weight or artificially)
After exhaustive searches, no works with these specifications were found in the literature (even for static loading and non-viscoelastic cylinders). For this reason, present results are now verified by results of experiments that are conducted by the present authors for a finite-length internally-pressurized hyperelastic cylinder/pipe, as a second verification tool. The adopted cylinder/pipe is a traditional flexible clear water hose pipe/tube that is fabricated from a material composition including the thermoplastic PVC (polyvinyl chloride), NBR (acrylonitrile butadiene rubber), and mineral fillers as constituent materials. The Moony–Rivlin hyperelastic material properties of this material were already published by the presented authors as:
The geometric specifications of the specimen are:
A metallic box with two internal opposite short protruding supporting copper tubes is used to provide the required fixed supports for the pressurized PVC pipe. The PVC pipe is secured by gas hose clamps to the protruding copper tubes (one of these tubes was a dead end), so that the effective length of the specimen is 30 mm. During the test, the box was closed for defense/safety purposes, but the inflation measurement was enabled via a dial gauge with an accuracy of 0.01 mm through crossed the box through a hole in the walls of the metallic box. Therefore, the test rig had a very simple and preliminary structure. The air pressure was supplied by a DPI 610 Pneumatic Calibrator/Hand-Pump. Pictures of the employed dial gauge and the Calibrator/Hand-Pump may be found in a previously published article by the authors [6]. The maximum radial displacement of the outer surface of the pipe (that occurs at the middle section of pipes) that is predicted by the present research is compared with the experimental one in Table 2, for various internal pressures. As may be seen, there is a good agreement between the two types of results. Although our results are negligibly larger.
4.3 A comparison between the responses of the hyperelastic and visco-hyperelastic cylinders
To assess the influence of the damping/viscoelastic nature of the material on the resulting distributions and time variations of the displacement and hoop stress, cylinders with and without viscoelasticity are considered. Figure 5 compares the time histories of the radial displacements and hoop stresses of the inner and outer boundaries of the mid-length section of the visco-hyper and hyperelastic cylinders. In contrast to the visco-hyperelastic cylinder whose responses generally decay with time, due to the stretch-dependent behavior of the hyperelastic materials, the responses of the hyperelastic cylinder are composed of blocks of time history (whose time length is about 0.72 s, here) that are repeated with time without any decay. However, due to the apparent influence of the higher vibration modes, the repetitions do not take form in identical shapes of the history segments. Figures 4 and 5 confirm that the influence of the higher vibration modes is especially remarkable when the amplitude of the fundamental vibration mode decays, i.e. when time elapses. Due to the lower stiffness of the hyperelastic materials in comparison with other categories of materials such as metals, ceramics, and composites, the oscillation times of these materials are much larger, so the influence of higher vibration modes on the vibration history is much more remarkable. It is worth mentioning that due to the finite length of the cylinder and the clamped ends of the cylinder, the global vibration of the cylinder is composed of not only radial (breathing) but also bending vibration modes. In other words, while a specific radial section of the cylinder experiences expansion some other radial sections of the cylinder length may feature contraction. Therefore, the origin of some higher vibration modes may be attributed to the longitudinal bending of the inner and outer surfaces of the cylinder. On the other hand, due to the energy-dissipation-inspired higher apparent stiffness of the visco-hyperelastic material in comparison with the hyperelastic material, both the displacements and stresses of the visco-hyperelastic cylinder are smaller. Moreover, the oscillation times of this cylinder are larger, due to the resulting relaxations.
4.4 Additional characteristic of the behaviors of the visco-hyperelastic cylinder
Some of the important characteristics of the responses of the visco-hyperelastic cylinder are discussed in the verification section as well as during the comparison of the responses of the viscoelastic and non-viscoelastic hyperelastic cylinders. The time histories of the radial deformations and thickness variations of the inner and outer boundaries of the mid-length section of the visco-hyperelastic cylinder are plotted in Fig. 6. As stated before, the general patterns of the time variations are dissipative. Figure 6b shows that due to the abrupt imposing of the internal pressure, the cylinder experiences large deformations (up to about 1.8 mm reduction in the 5 mm thickness). Therefore, the hyperelastic nature of the material has surely engaged. However, as time elapses, both radial deformations and thickness reduction quantities approach the steady-state magnitudes that are equal to those of a hyperelastic cylinder under static loads. Moreover, the effects of the superimposed higher vibration modes can readily be noted in Fig. 6.
Time variations of the hoop and longitudinal stresses of the inner and outer boundaries of the mid-length section of the cylinder are depicted in Fig. 7. Since the global vibration of the finite-length cylinder is composed of not only radial but also bending modes, the longitudinal stress has become negative in some time instants. In other words, as in other sections, the direction of the curvature of the mid-length section of the cylinder varies with time, so negative bending stresses may be superimposed on the tensile hoop/axial stresses at some time instants. In addition to demonstrating the dissipative nature of the responses, Fig. 7 reflects the influence of the higher vibration modes, especially as time elapses. The presented discussion reveals that due to the induced bending, the steady-state stresses are affected by the induced both static inflation and bending.
The bending of the cylinder may be confirmed by investigation of the longitudinal distribution of the inner and outer boundaries. Figure 8 illustrates the longitudinal distribution of the radial displacement of the inner boundary for distinct time instants. From this figure, one may deduce that while the global distribution resembles a trapezoid, it is altered by local bendings whose direction and location of extremum occurrence vary with time. The 3D plot that is presented in Fig. 9 for the time of occurrence of maximum deflection of the inner boundary of the mid-length section (i.e., corresponds to \(t=0.190605 \mathrm{s}\), according to Fig. 6a) gives the simultaneous radial and axial distributions of the radial displacement of the whole thickness at that time instant.
The longitudinal distributions of the hoop, longitudinal, and transverse shear stresses of the inner boundary are shown in Fig. 10, for various time instants. These distributions clearly show the effects of the local bending of the inner surface of the cylinder. Figure 10a shows that except for the bending-dominant stresses of sections that are located near the two ends of the cylinder, the longitudinal distribution of the hoop stress resembles that of the radial displacement (Fig. 8). From Fig. 10b, one may infer that while the largest hoop stresses are induced in regions located about the mid-length section, the largest longitudinal stresses that are bending stresses happen in the vicinity of the fixed ends. The signs of the transverse shear stresses of the two ends of the cylinder are in agreement with the stress sign convention. Moreover, due to the longitudinal symmetry, the magnitude of the transverse shear stress is zero at the mid-length section.
The effects of the changes in the curvatures of the cylinder may be traced in the curves of the radial distributions of the radial displacement and hoop and axial stresses. As may be seen in Fig. 11, the radial distribution curves of each quantity have not remained parallel and their slopes have changed with time. Comparing all the stress results, including the relevant longitudinal and radial distributions of the stress components, leads to the practically important conclusion that although all the stress components are affected by the bending and inflation of the cylinder, the hoop stresses of the mid-length section are the largest stresses of the cylinder.
The key numerical quantities of the instantaneous radial distributions of the radial displacement, hoop stress, and axial stress are depicted in Fig. 11 and are given in Table 3 to serve as future benchmarks.
4.5 Sensitivity analyses
4.5.1 The length effects
Effects of the length of the cylinder on the resulting radial displacements of the inner and outer boundaries of the mid-length section may be sought in Fig. 12. Due to the resulting higher compliance and capability of free expansion, the radial displacements of this section increase with the cylinder length. As mentioned before, due to the relaxation and damping of the material, the largest displacements occur later in the longer cylinders. However, the dissipative nature of the responses may easily be detected. Moreover, due to the resulting decreases in the radial and bending stiffnesses at higher length-to-thickness ratios, the effects of the higher vibration modes are suppressed in the longer cylinder. It is worth reminding that the formation of the bending radial displacements is affected by the reflection of the deformation waves from the fixed ends as well. Moreover, comparing Fig. 12a, b indicates that while the radial displacements are larger for longer cylinders, the resulting thickness reduction is slightly smaller. In other words, the bending and curvature changes are larger, but the local thickness reductions are smaller in the longer cylinders. This reason is behind neglecting the thickness reduction (or equivalently, neglecting the transverse normal strain) in the classical thin-shell (whose arc length is much larger than the thickness) theory.
The influence of the length to thickness of the cylinder on the resulting hoop and axial stresses of the mid-length section of the cylinder can be explored in Figs. 13 and 14, respectively. These figures reveal that while the hoop stresses grow with the radial displacements of the longer cylinder, the effects of the supports, i.e., the axial stress, diminish by increasing the cylinder length. Indeed, the movability of the cylinder wall increases in the interior regions when a longer cylinder is utilized. Thus, the resulting radial displacements and hoop stresses become larger. Moreover, due to the resulting higher transverse and bending compliances, the mean oscillation frequency becomes smaller and the effects of the superimposed higher vibration modes on the resulting response diminish.
4.5.2 Sensitivity against the viscoelastic parameters
According to either of Eqs. (19) or (20), while increasing the relaxation time coefficients (\({\theta }_{j}\); j = 1,2,3) leads to larger visco-hyperelastic stress for fixed hyperelastic stress, increasing the normalized relaxation moduli (\({g}_{j};j=\mathrm{1,2},3\)) that is multiplied by a negative-definite parenthesis contributes to decreasing the resulting displacements and stresses. On the other hand, the radial stresses are dependent on the imposed pressure and thus mainly governed by the equilibrium requirements rather than the constitutive law. Therefore, for a fixed internal pressure, the resulting stresses and displacements become larger for larger \({\theta }_{j}\) and smaller \({g}_{j}\) parameters. Moreover, the roles of these two parameters and their influences on the cylinder stiffness and vibration manner are quite different. The effects of each of these parameters are investigated by comparing the original results with results obtained by using one-half or twice the initial values of \({\theta }_{j}\) and \({g}_{j}\) that are introduced in Table 1.
Figures 15, 16, and 17 show the influence of the magnitude of the exponent of the relaxation kernel (\({\theta }_{j};j=\mathrm{1,2},3\)) on the time histories of the induced displacements and stresses and the vibration decay of inner and outer boundaries of the mid-length section of the cylinder. It may readily be noted that while this exponent exhibits a small effect on the oscillation frequency, it alters the contribution and shape of the superimposed responses of the higher vibration modes. In addition, the magnitudes of the resulting radial displacements, and hoop and axial stresses increase by increasing \({\theta }_{j}\).
Figures 18, 19, and 20 are devoted to the effects evaluation of the normalized relaxation moduli of the Prony series elements (\({g}_{j};j=\mathrm{1,2},3\)). As may be deduced from Eq. (19), these parameters directly affect the stiffness of the visco-hyperelastic cylinder. Figures 18, 19, and 20 present the effects of these parameters on the time variations of the radial displacements/vibration, hoop stresses, and axial stresses. From these figures, one may conclude that larger values of \({g}_{j}\) lead to higher displacement and stress dissipation. Comparing Figs. 15, 16, and 17 with Figs. 18, 19, and 20 confirms the fact that in comparison with the relaxation time coefficients, the normalized relaxation moduli play a stronger role in the suppression of the responses. Furthermore, the magnitude of the \({g}_{j}\) parameters significantly affects the shapes of the superimposed higher vibration modes and their contribution degree. Figures 18, 19, and 20 emphasize the fact that in contrast to the relaxation kernel exponent, \({g}_{j}\) notably changes the mean oscillation frequency of the displacement and stress responses.
4.6 Creep behavior sensitivity analysis
Now the long-term creep behavior of the finite-length visco-hyperelastic cylinder that is initially exposed to a sudden internal pressure is studied. It is proven in Sec. 4.4. that the largest deformations and stresses appear in the mid-length section of the cylinder. For this reason, it is focused here on the creep behaviors of the inner and outer layers of this section. Figures 21, 22, and 23 show the long-term time variations/creep of the radial displacement, hoop stresses, and axial stresses of the inner and outer layers of the visco-hyperelastic cylinder for three distinct lengths, i.e., \(L=50, 100, 200\,\, \mathrm{mm}\). The local peaks of the beginnings of the time histories are associated with the early overshoots of the short-term/vibration portions of the time histories. These figures indicate that the rates of displacement and stress relaxations are affected by the cylinder length, and while the slopes of the curves are larger for longer cylinders, the shorter cylinder reaches the steady state earlier. Moreover, the resulting displacements are quite large and slightly exceed the thickness of the thick-walled cylinder. In other words, not only the hyperelasticity nature of the material is invoked but also the resulting stresses are large enough to lead to pronounced creep effects. Depending on the cylinder length, the steady state begins at about 500 s. In other words, due to the mentioned severe conditions of the visco-hyperelastic material, this time is much less than that of the metallic counterpart components.
Some of the numerical values of the creep time histories of the radial displacements and hoop stresses that are plotted in Figs. 21, 22, and 23 are given in Table 4, to enable a quantitative tracking of the creep events.
5 Conclusions
In this research, novel modeling, formulation, and solution techniques are proposed to study the short-term (vibration) and long-term (creep) responses of the abruptly loaded finite-length visco-hyperelastic thick-walled cylindrical pressure vessels. In addition, verification and sensitivity results are presented. The sensitivity analyses have investigated the effects of the viscoelasticity, length, and relaxation parameters on both the vibration and creep responses. Some of the resulting practical conclusions are:
-
Due to the hyperelastic and viscoelastic characteristics of the material, the largest peak may not be the first one, so that a lag may be noted in the formation of the largest peaks of the time histories of the displacements and stresses.
-
The influence of the higher vibration modes becomes remarkable as time elapses.
-
As time elapses, the magnitudes of the deformations and stresses approach those of a hyperelastic cylinder under static inflation and bending.
-
The stress components are affected by not only radial inflation but also bending-inspired curvatures whose magnitudes and signs vary with time.
-
The largest hoop stresses occur in regions located about the mid-length section but the largest longitudinal stresses happen in the vicinity of the fixed ends and are bending stresses.
-
The displacements and stresses increase but the thickness reduction decreases by increasing the cylinder length.
-
The larger length postpones the appearance of the largest history peaks.
-
The effects of the higher vibration modes are smaller in the longer cylinder.
-
For a fixed internal pressure, the resulting stresses and displacements are larger for larger relaxation time coefficients and smaller normalized relaxation moduli.
-
In comparison with the relaxation time coefficients, the normalized relaxation moduli play a stronger role in the suppression of the responses.
-
The creep results show that the rates of displacement and stress relaxations are affected by the cylinder length, and while the slopes of the creep curves are larger for longer cylinders, the shorter cylinder reaches the steady state earlier.
Although other creep analysis approaches may be found in the literature [30,31,32,33,34], the majority of these approaches have been proposed based on relatively old flow-rule-based formulations that were combined with empirical 1D creep models such as Norton’s law. These types of creep formulations are mainly limited to static loading and materials with very small strains (such as metals) where the superposition of the strains may hold. For materials with extremely large deformations (e.g., polymeric and rubber-like hyperelastic materials) that especially exhibit dissipative and incompressibility natures, utilizing such models may lead to inaccurate or even erroneous results. Utilizing the viscoelastic models may resolve these shortcomings. The multi-branch visco-hyperelastic constitutive model that is proposed in the current research may be regarded as the most general constitutive model in this regard. However, some researchers [35,36,37] have suggested using fractional-order viscoelastic models instead of the traditional integer-order ones. Therefore, the results of the current creep model may be re-extracted based on those models as well in future works, but the known fractional-order viscoelasticity models have been built on simple models (such as the Voigt-Kelvin-type or Zener-type models) and thus are not well-developed yet.
References
Duc, N.D.: Nonlinear Static and Dynamic Stability of Functionally Graded Plates and Shells. Vietnam National University Press, Hanoi (2014)
Dal, H., Açıkgöz, K., Badienia, Y.: On the performance of isotropic hyperelastic constitutive models for rubber-like materials: a state of the art review. Appl. Mech. Rev. 73(2), 020802 (2021)
Chaimoon, K., Chindaprasirt, P.: An anisotropic hyperelastic model with an application to soft tissues. Eur. J. Mech. A Solids 78, 103845 (2019)
Kumar, A., Khurana, A., Sharma, A.K., Joglekar, M.M.: Dynamics of pneumatically coupled visco-hyperelastic dielectric elastomer actuators: theoretical modeling and experimental investigation. Eur. J. Mech. A Solids 95, 104636 (2022)
Narayanan, P., Pramanik, R., Arockiarajan, A.: A hyperelastic viscoplastic damage model for large deformation mechanics of rate-dependent soft materials. Eur. J. Mech. A Solids 98, 104874 (2023)
Batra, R.C., Bahrami, A.: Inflation and eversion of functionally graded non-linear elastic incompressible circular cylinders. Int. J. Non-Linear Mech. 44, 311–323 (2009)
Shariyat, M., Yazdani Ariatapeh, M., Khosravi, M., Najafipour, M.: Nonlinear stress and deformation analysis of pressurized thick-walled hyperelastic cylinders with experimental verifications and material identifications. Int. J. Press. Vessels Pip. 188, 104211 (2020)
Yazdani Ariatapeh, M., Shariyat, M., Khosravi, M.: Semi-analytical large deformation and three-dimensional stress analyses of pressurized finite-length thick-walled incompressible hyperelastic cylinders and tubes. Int. J. Appl. Mech. 15, 2250100 (2023)
Vanin, G.A., Duc, N.D.: Creep of plastics with spherical inclusions. Mech. Compos. Mater. 32(5), 467–472 (1996)
Duc, N.D.: Shear creep of orthogonally reinforced spherofibrous composites. Mech. Compos. Mater. 32(6), 532–538 (1996)
Vanin, G.A., Duc, N.D.: Creep of orthogonally reinforced spherofibrous composites. Mech. Compos. Mater. 32(6), 539–543 (1996)
Duc, N.D., Minh, D.K., Thu, P.V.: The bending analysis of three phase polymer composite plate reinforced by glass fiber and titanium oxide particles including creep effect. Int. J. Aeronaut. Space Sci. 11(4), 360–365 (2010)
Gacem, H., Chevalier, Y., Dion, J.L., Soula, M., Rezgui, B.: Nonlinear dynamic behaviour of a preloaded thin sandwich plate incorporating visco-hyperelastic layers. J. Sound Vib. 322(4–5), 941–953 (2009)
Sahoo, D., Deck, C., Willinger, R.: Development and validation of an advanced anisotropic visco-hyperelastic human brain FE model. J. Mech. Behav. Biomed. Mater. 33, 24–42 (2014)
Pascon, J.P.: Large deformation analysis of functionally graded visco-hyperelastic materials. Comput. Struct. 206, 90–108 (2018)
Zhao, Z., Niu, D., Zhang, H., Yuan, X.: Nonlinear dynamics of loaded visco-hyperelastic spherical shells. Nonlinear Dyn. 101(2), 911–933 (2020)
Wu, S.W., Jiang, C., Jiang, C., Liu, G.R.: A selective smoothed finite element method with visco-hyperelastic constitutive model for analysis of biomechanical responses of brain tissues. Int. J. Numer. Methods Eng. 121(22), 5123–5149 (2020)
Dal, H., Gültekin, O., Açıkgöz, K.: An extended eight-chain model for hyperelastic and finite viscoelastic response of rubberlike materials: theory, experiments and numerical aspects. J. Mech. Phys. Solids 145, 104159 (2020)
Yang, L.M., Shim, V.P.: A visco-hyperelastic constitutive description of elastomeric foam. Int. J. Impact Eng. 30(8–9), 1099–1110 (2004)
López-Campos, J.A., Segade, A., Fernández, J.R., Casarejos, E., Vilán, J.A.: Behavior characterization of visco-hyperelastic models for rubber-like materials using genetic algorithms. Appl. Math. Model. 66, 241–255 (2019)
Xiang, Y., Zhong, D., Wang, P., Yin, T., Zhou, H., Yu, H., Baliga, C., Qu, S., Yang, W.: A physically based visco-hyperelastic constitutive model for soft materials. J. Mech. Phys. Solids 128, 208–218 (2019)
Dadgar-Rad, F., Firouzi, N.: Large deformation analysis of two-dimensional visco-hyperelastic beams and frames. Arch. Appl. Mech. 91(10), 4279–4301 (2021)
Yazdani Ariatapeh, M., Shariyat, M., Khosravi, M.: Analytical-based exact-kernel vibration and long-term creep stress and large deformation redistributions of the suddenly pressurized incompressible viscohyperelastic thick cylinders. Int. J. Non-Linear Mech. 151, 104383 (2023)
Bower, A.F.: Applied Mechanics of Solids. CRC Press (2009)
Eslami, M.R., Hetnarski, R.B., Ignaczak, J., Noda, N., Sumi, N., Tanigawa, Y.: Theory of Elasticity and Thermal Stresses. Springer, Dordrecht (2013)
Javani, M., Kiani, Y., Eslami, M.: Nonlinear axisymmetric response of temperature-dependent FGM conical shells under rapid heating. Acta Mech. 230, 3019–3039 (2019)
Shariyat, M., Jahanshahi, S., Rahimi, H.: Nonlinear Hermitian generalized hygrothermoelastic stress and wave propagation analyses of thick FGM spheres exhibiting temperature, moisture, and strain-rate material dependencies. Compos. Struct. 229, 111364 (2019)
Shariyat, M., Jahangiri, M.: Nonlinear impact and damping investigations of viscoporoelastic functionally graded plates with in-plane diffusion and partial supports. Compos. Struct. 245, 112345 (2020)
Shariyat, M., Hosseini, S.H.: 3D layerwise impact investigation of sandwich plates with multi-directional phase transformation SMA face sheets and nearly incompressible compliant hyperelastic cores. Acta Mech. 233, 4385–4406 (2022)
Eslami, M.R., Shariyat, M.: A technique to distinguish the primary and secondary stresses. Trans. ASME J. Pressure Vessel Technol. 117(3), 197–203 (1995)
Shariyat, M., Eslami, M.R.: Isoparametric finite-element thermoelasto-plastic creep analysis of shells of revolution. Int. J. Press. Vessels Pip. 68(3), 249–259 (1996)
Mahbadi, H., Eslami, M.R.: Cyclic loading behaviour of thick cylindrical vessels under creep deformation. J. Strain Anal. Eng. Des. 46(8), 727–739 (2011)
Mahbadi, H., Eslami, M.R.: Effect of creep on thermal cyclic loading of thick cylindrical vessels based on the kinematical hardening models. Encyclop. Therm. Stress. 3, 1130–1140 (2014)
Shariyat, M., Ghafourinam, M.: Hygrothermomechanical creep and stress redistribution analysis of thick-walled FGM spheres with temperature and moisture dependent material properties and inelastic radius changes. Int. J. Press. Vessels Pip. 169, 94–114 (2019)
Shariyat, M., Mohammadjani, R.: Three-dimensional dynamic stress and vibration analyses of thick singular-kernel fractional-order viscoelastic annular rotating discs under nonuniform loads. Int. J. Struct. Stab. Dyn. 20, 2050007 (2020)
Shariyat, M., Mohammadjani, R.: 3D nonlinear variable strain-rate-dependent-order fractional thermoviscoelastic dynamic stress investigation and vibration of thick transversely graded rotating annular plates/discs. Appl. Math. Model. 84, 287–323 (2020)
Mohammadjani, R., Shariyat, M.: Nonlinear thermomechanical vibration mitigation analysis in rotating fractional-order viscoelastic bidirectional FG annular disks under nonuniform shocks. J. Therm. Stress. 43, 829–873 (2020)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Shariyat, M., Yazdani Ariatapeh, M. 3D hybrid semi-analytical creep, dissipation, and dynamic stress analyses of abruptly pressurized finite-length thick visco-hyperelastic cylinders. Acta Mech 234, 6451–6480 (2023). https://doi.org/10.1007/s00707-023-03717-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-023-03717-w