1 Introduction

Fibrous and laminated composites made of magnetoelectroelastic materials exhibit magnetoelectric effect that is not present in single-phase piezoelectric or piezomagnetic materials, and have found increasingly wide engineering applications. On the other hand, the magnetoelectroelastic materials are very susceptible to fracture because of their brittleness. Owing to various causes, cracks or flaws are inevitably present in such magnetoelectroelastic materials and magnetoelectroelastic field concentration occurs near their tips, which can cause crack advance, and finally leads to serious degradation of the performance of magnetoelectroelastic materials.

Much attention was devoted to the investigations of cracks in magnetoelectroelastic materials. Between the publications on this subject an exact treatment on the problem of an elliptic hole or a crack in a magnetoelectroelastic solid subject to the far field loadings was carried out in [1]. The solutions of a limited-permeable crack or two collinear limited-permeable cracks in piezoelectric/piezomagnetic materials subjected to a uniform tension loading were investigated in Ref. [2]. Applicability of the crack-face electromagnetic boundary conditions for fracture of magnetoelectroelastic materials was discussed in [3]. The periodic set of collinear electromagnetically permeable crack problem in infinite magnetoelectroelastic solids was studied in [4]. The case of limited permeable cracks for the same problem was investigated in [5] and additional accounting of electrically and magnetically induced Maxwell stresses was carried out in Ref. [6].

The cracks between two different magnetoelectroelastic materials are even more dangerous than internal cracks; therefore, essential attention was devoted to their investigations. The problem of electrically permeable interfacial crack in magnetoelectroelastic solid loaded by remote uniform loads, by a generalized line force or/and by a generalized line dislocation was studied in [7] and also a uniform heat flow was taken into account in [8]. The interface crack problem of dissimilar piezoelectromagneto-elastic anisotropic bimaterials under in-plane deformation was investigated in [9] taking the electric–magnetic field inside the interface crack into account. The singular characteristics of stress, electric displacement and magnetic induction fields near the tip of impermeable interfacial cracks in two-dimensional magnetoelectroelastic bimaterials were studied in [10] using the generalized Stroh formalism. An interface crack with a contact zone at the right crack tip between two semi-infinite piezoelectric/piezomagnetic spaces under the action of a remote mechanical loading, magnetic and electric fluxes was studied in [11]. The cases of electro-magnetically permeable crack, and also electrically permeable and magnetically impermeable one were considered. A magnetoelectrically permeable interface crack with a contact zone between two semi-infinite magnetoelectroelastic planes under the action of a heat flow and remote magnetoelectromechanical loadings was considered in [12]. The paper [13] analyzed the contact zone model for an interface crack between two dissimilar magnetoelectroelastic materials under the action of remote mechanical, electrical and magnetic loads, assuming that the open part of the crack is electrically impermeable and magnetically permeable. A magnetically impermeable and electrically permeable interface crack with a contact zone in a magnetoelectroelastic bimaterial under concentrated magnetoelectromechanical loads on the crack faces was studied in [14]. An electrically impermeable and magnetically permeable interface crack with a contact zone in magnetoelectroelastic bimaterials under a thermal flux and magnetoelectromechanical loads was studied in [15] and pre-fracture zone model on electrically impermeable and magnetically permeable interface crack between two dissimilar magnetoelectroelastic materials was developed in [16]. Electrically conductive interface crack with a contact zone in a magnetoelectroelastic bimaterial was studied in [17]. Pre-fracture zone model for a limited permeable crack in an adhesive thin interlayer between two semi-infinite electro-magneto-elastic spaces was considered in [18]. Electrically and magnetically charged interface crack in a piezoelectric/piezomagnetic bimaterial were studied in [19] under the assumption that the crack faces are covered with electrodes.

Single interface cracks in magnetoelectroelastic solids were considered in [20, 21] and [22] for antiplane case. Also similar problems, but for two interface cracks were studied in [23, 24] and [25], and periodic set of mode III interface cracks under magnetic or electric field in multilayered piezomagnetic/piezoelectric composite was considered in [26]. Planar interface cracks in three-dimensional magnetoelectroelastic bimaterials were considered in papers [27, 28]. Green’s functions and extended displacement discontinuity method were used to analyze interfacial cracks in three-dimensional transversely isotropic magnetoelectroelastic bimaterials in [29, 30]. Fundamental solutions and numerical modeling were considered in the paper [31] for the analysis of an elliptical crack with polarization saturation in a transversely isotropic piezoelectric medium.

The problem of multiple interface cracks in magnetoelectroelastic materials is insufficiently studied till now. Only plane problem for magnetoelectroelastic layers with interfacial cracks under magnetoelectromechanical loads was studied in [32] for the magnetoelectrically impermeable model of crack faces, and also multiple cracks on the arc-shaped interface in a magneto-electro-elastic composite was analyzed in [33] for antiplane deformation. Thus, the problem of arbitrary number of collinear electrically conducting interface cracks of arbitrary length and location in magnetoelectroelastic bimaterial has never been considered earlier. Namely this problem investigation is the main purpose of this paper.

2 Formulation of the problem

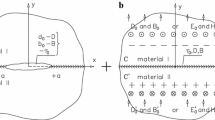
Consider a set of \(n\) cracks \(a_{1} \le x_{1} \le b_{1}\), \(a_{2} \le x_{1} \le b_{2}\),…,\(a_{n} \le x_{1} \le b_{n}\) having an arbitrary length and location on the interface between two semi-infinite magnetoelectroelastic spaces \(x_{3} > 0\) and \(x_{3} < 0\) (Fig. 1). It is assumed that \(c_{ijks}^{\left( m \right)}\), \(e_{iks}^{\left( m \right)}\), \(h_{iks}^{\left( m \right)}\), \(\mu_{is}^{\left( m \right)}\) are the elastic, piezoelectric, piezomagnetic, and electromagnetic constants, respectively, \(\alpha_{is}^{\left( m \right)}\), \(\gamma_{is}^{\left( m \right)}\) are the dielectric permittivities and magnetic permeabilities; \(i\), \(j\), \(k\), \(s\) range in {1, 2, 3} and the repeated indexes imply summation; \(m = 1\) for the upper and \(m = 2\) for lower materials and both materials have the symmetry class of 6 mm with the poling direction \(x_{3}\).

Fig. 1
figure 1

A finite set of cracks \(a_{1} \le x_{1} \le b_{1} ,\;a_{2} \le x_{1} \le b_{2} , \ldots ,a_{n} \le x_{1} \le b_{n}\) at the interface \(x_{3} = 0\) between two magnetoelectroelastic materials

Full size image

Let’s denote by \(L^{\prime } = \bigcup\limits_{k = 1}^{n} {\left( {a_{k} ,b_{k} } \right)}\) the set of the crack regions and \(L^{\prime \prime } = ( - \infty ,\;\infty )\backslash L^{\prime }\).

The loading at infinity is given by

$$\sigma_{33}^{\left( m \right)} = \sigma^{\infty } ,\;\sigma_{13}^{\left( m \right)} = \tau^{\infty } ,\;E_{1}^{\left( m \right)} = E^{\infty } ,\;H_{1}^{\left( m \right)} = H^{\infty } ,\;\sigma_{11}^{(m)} = \sigma_{xxm}^{\infty } ,\;D_{1}^{\left( m \right)} = D_{xm}^{\infty } ,\;B_{1}^{\left( m \right)} = B_{xm}^{\infty } ,$$
(1)

(\(m = 1\) stands for the upper domain, and \(m = 2\) for the lower one).

It is assumed that due to \(\sigma_{11}^{\left( m \right)}\), \(D_{1}^{\left( m \right)}\) and \(B_{1}^{\left( m \right)}\) this loading produces stresses and displacements which satisfy continuity conditions at the remote part of the interface. Because the load does not depend on the coordinate \(x_{2}\), the plane strain problem in the \(\left( {x_{1} ,x_{3} } \right)\) plane depicted in Fig. 1 can be considered. We assume that the crack is completely open, and its faces are free of prescribed mechanical loading, electric and magnetic charges.

The cracks are assumed electrically conducting and having a uniform distribution of magnetic potential along the electrodes, i.e., electric and magnetic fields on its faces are the following

$$E_{1}^{(1)} (x_{1} ,0) = E_{1}^{(2)} (x_{1} ,0) = 0\;\;{\text{and}}\;\;H_{1}^{(1)} (x_{1} ,0) = H_{1}^{(2)} (x_{1} ,0) = 0\;{\text{for}}\;x_{1} \in L^{\prime }$$
(2)

In addition, it is assumed that the total electric charge \(D_{0k}\) is prescribed on the \(k\)-th crack. In a particular case of a grounded electrode the corresponding values \(D_{0k}\) must be taken to be zero.

In addition to (2), the remaining conditions on the interface take the form:

$$\sigma_{i3}^{(1)} (x_{1} ,0) = \sigma_{i3}^{(2)} (x_{1} ,0),\;E_{1}^{(1)} (x_{1} ,0) = E_{1}^{(2)} (x_{1} ,0),\;H_{1}^{(1)} (x_{1} ,0) = H_{1}^{(2)} (x_{1} ,0)\;for\;x_{1} \in L^{\prime \prime } ,$$
(3)
$$D_{3}^{(1)} (x_{1} ,0) = D_{3}^{(2)} (x_{1} ,0),\;u_{i}^{\prime (1)} (x_{1} ,0) = u_{i}^{\prime (2)} (x_{1} ,0),\;B_{3}^{(1)} (x_{1} ,0) = B_{3}^{(2)} (x_{1} ,0)\;for\;x_{1} \in L^{\prime \prime } ,$$
(4)
$$\sigma_{i3}^{(1)} (x_{1} ,0) = 0\;{\text{for}}\;x_{1} \in L^{\prime } ,$$
(5)

where \(m = 1,2\), \(i = 1,3\).

The following presentations were obtained in the paper [19]

$$ir_{j1} \sigma_{13}^{\left( 1 \right)} \left( {x_{1} ,0} \right) + r_{j3} \sigma_{33}^{\left( 1 \right)} \left( {x_{1} ,0} \right) + ir_{j4} E_{1}^{\left( 1 \right)} \left( {x_{1} ,0} \right) + ir_{j5} H_{1}^{\left( 1 \right)} \left( {x_{1} ,0} \right) = F_{j}^{ + } \left( {x_{1} } \right) + \gamma_{j} F_{j}^{ - } \left( {x_{1} } \right),$$
(6)
$$t_{j1} \left\langle {u^{\prime}_{1} \left( {x_{1} } \right)} \right\rangle + it_{j3} \left\langle {u^{\prime}_{3} \left( {x_{1} } \right)} \right\rangle + t_{j4} \left\langle {D_{3} \left( {x_{1} } \right)} \right\rangle + t_{j5} \left\langle {B_{3} \left( {x_{1} } \right)} \right\rangle = F_{j}^{ + } \left( {x_{1} } \right) - F_{j}^{ - } \left( {x_{1} } \right),$$
(7)

where \(r_{ij}\) and \(t_{ij}\) \(\left( {i,j = 1,3,4,5} \right)\) are the components of known real matrices and \(\gamma_{j}\) are the constants determined by the physical characteristics of materials, \(r_{13} = r_{33} = r_{44} = r_{55} = 1\) and \(r_{43} = r_{45} = r_{53} = r_{54} = 0\).

Using the boundary conditions at infinity (1) and using (6), it is possible to write:

$$\left. {F_{j} \left( z \right)} \right|_{z \to \infty } = \tilde{\sigma }_{j} - i\tilde{\tau }_{j} ,$$
(8)

where

$$\tilde{\sigma }_{j} = \frac{{r_{j3} \sigma^{\infty } }}{{\vartheta_{j} }},\;\tilde{\tau }_{j} = - \frac{1}{{\vartheta_{j} }}\left( {r_{j1} \tau^{\infty } + r_{j4} e^{\infty } + r_{j5} h^{\infty } } \right),\;\left( {j = 1,3,4,5} \right),\;\vartheta_{k} = 1 + \gamma_{k} ,\;\left( {k = 1,3} \right),\;\vartheta_{4} = \vartheta_{5} = 2.$$

Satisfying the boundary conditions (2) and (5) with the use of Eqs. (6) we get the following problems of linear relationship:

$$F_{j}^{ + } \left( {x_{1} } \right) + \gamma_{j} F_{j}^{ - } \left( {x_{1} } \right) = 0,\;{\text{for}}\;x_{1} \in L^{\prime } .$$
(9)

Here and afterward \(j = 1,\,3,\,4,\,5\).

According to Muskhelishvili [34] the solution of Eq. (9) can be presented in the form:

$$F_{j} \left( z \right) = X_{j} \left( z \right)P_{{n{\kern 1pt} j}} \left( z \right),$$
(10)

where

$$X_{j} \left( z \right) = \prod\limits_{k = 1}^{n} {\left( {z - a_{k} } \right)^{{ - \frac{1}{2} + i\varepsilon_{j} }} \cdot \left( {z - b_{k} } \right)^{{ - \frac{1}{2} - i\varepsilon_{j} }} } ,\;\varepsilon_{j} = \frac{{\ln \gamma_{j} }}{2\pi },$$
(11)
$$P_{nj} \left( z \right) = C_{0j} z^{n} + C_{1j} z^{n - 1} + \ldots + C_{nj} ,$$
(12)

where \(C_{kj}\) \((k = 0,1,...n)\) are arbitrary complex coefficients.

From Eq. (8) one has

$$C_{0j} = \tilde{\sigma }_{j} - i\tilde{\tau }_{j} .$$
(13)

For the determination of the remaining coefficients in (12) the conditions of the single validness of the displacements

$$\int\limits_{{a_{k} }}^{{b_{k} }} {\left\langle {u_{1}^{\prime } (x_{1} )} \right\rangle {\text{d}}x_{1} = 0} ,\;\int\limits_{{a_{k} }}^{{b_{k} }} {\left\langle {u_{3}^{\prime } (x_{1} )} \right\rangle {\text{d}}x_{1} = 0} \;k = 1,2,...n,$$
(14)

and the total values of electric and magnetic induction jumps [35]

$$\int\limits_{{a_{k} }}^{{b_{k} }} {\left\langle {D_{3} (x_{1} )} \right\rangle {\text{d}}x_{1} = D_{0k} } ,\;\int\limits_{{a_{k} }}^{{b_{k} }} {\left\langle {B_{3} (x_{1} )} \right\rangle {\text{d}}x_{1} = 0} ,\;k = 1,2,...n$$
(15)

are used.

Performing the integration of (7) on each crack and taking into account (14) and (15) we arrive to the equations:

$$\int\limits_{{a_{{_{k} }} }}^{{b_{k} }} {\{ F_{j}^{ + } (x_{1} ) - F_{j}^{ - } (x_{1} )\} {\text{d}}x_{1} = t_{j4} D_{0k} } ,j = 1,3,4,5;\;k = 1,2,...n,$$
(16)

Taking into account (9) the Eqs. (16) can be written in the form

$$\frac{{\gamma_{j} + 1}}{{\gamma_{j} }}\int\limits_{{a_{{_{k} }} }}^{{b_{k} }} {F_{j}^{ + } (x_{1} ){\text{d}}x_{1} = t_{j4} D_{0k} } ,\;j = 1,3,4,5;\;k = 1,2,...n$$
$$or \int\limits_{{a_{m} }}^{{b_{m} }} {P_{nj} \left( t \right)X_{j} \left( t \right){\text{d}}t} = \tilde{t}_{j4} D_{0m} ,\;m = 1,2, \ldots ,n;\;j = 1,3,4,5,$$
(17)

where \(\tilde{t}_{j4} = \frac{{\gamma_{j} \,t_{j4} }}{{\gamma_{j} + 1}}\),and rewritten in an expanded form as follows:

$$\int\limits_{{a_{m} }}^{{b_{m} }} {\frac{{C_{0j} t^{n} + C_{1j} t^{n - 1} + \ldots + C_{nj} }}{{\prod\limits_{k = 1}^{n} {\left( {t - a_{k} } \right)^{{\frac{1}{2} - i\varepsilon_{j} }} \cdot \left( {t - b_{k} } \right)^{{\frac{1}{2} + i\varepsilon_{j} }} } }}} {\text{d}}t = \tilde{t}_{j4} D_{0m} ,\;m = 1,2, \ldots ,n;\;j = 1,3,4,5.$$
(18)

Further we designate:

$$I_{msj} = \int\limits_{{a_{m} }}^{{b_{m} }} {\frac{{t^{s} }}{{\prod\limits_{k = 1}^{n} {\left( {t - a_{k} } \right)^{{\frac{1}{2} - i\varepsilon_{j} }} \cdot \left( {t - b_{k} } \right)^{{\frac{1}{2} + i\varepsilon_{j} }} } }}} {\text{d}}t;\;m,s = 1,2, \ldots ,n;\;j = 1,3,4,5.$$
(19)

Then, the systems (18) can be presented in the form

$$C_{1j} \hat{a}_{m1j} + \ldots + C_{nj} \hat{a}_{mnj} = \hat{b}_{mj} ,$$
(20)

where

$$\hat{a}_{m\alpha j} = I_{m,n - \alpha ,j} ,\;\hat{b}_{mj} = - I_{mnj} C_{0j} + \tilde{t}_{j4} D_{0m} ;\;m,\;\alpha = 1,2, \ldots ,n;\;j = 1,3,4,5.$$
(21)

Thus, we arrived to the systems of linear algebraical equations

$$\sum\limits_{\alpha = 1}^{n} {\hat{a}_{m\alpha j} C_{\alpha j} } = \hat{b}_{mj} ,\;m = 1,2, \ldots ,n;\;j = 1,3,4,5.$$
(22)

with respect to \(C_{\alpha j}\).

The exact analytical solution of these systems can be done for any \(n\) by Cramer or Gauss methods.

3 Electro-magneto-mechanical components on different parts of the material interfaces

Substituting (10) into the conjugated equation of (6) and taking into account that \(F_{j}^{ + } \left( {x_{1} } \right) = F_{j}^{ - } \left( {x_{1} } \right) = F_{j} \left( {x_{1} } \right)\) for \(x_{1} \in L^{\prime \prime }\), one can writes:

$$r_{j3} \sigma_{33}^{\left( 1 \right)} \left( {x_{1} ,0} \right) - i\left[ {r_{j1} \sigma_{13}^{\left( 1 \right)} \left( {x_{1} ,0} \right) + r_{j4} E_{1}^{\left( 1 \right)} \left( {x_{1} ,0} \right) + r_{j5} H_{1}^{\left( 1 \right)} \left( {x_{1} ,0} \right)} \right] = \Gamma_{j} \left( {x_{1} } \right),$$
(23)

where

$$\Gamma_{j} \left( {x_{1} } \right) = \left( {1 + \gamma_{j} } \right)\overline{{F_{j} \left( {x_{1} } \right)}} ,\;j = 1,\,3,\,4,\,5.$$
(25)

Due to \(r_{13} = 1\) we get from Eq. (2) for \(j = 1\):

$$\sigma_{33}^{\left( 1 \right)} \left( {x_{1} ,0} \right) = {\text{Re}} \left\{ {\Gamma_{1} \left( {x_{1} } \right)} \right\},\;x_{1} \in L^{\prime \prime } .$$
(23)

To find the expressions for \(\sigma_{13}^{\left( 1 \right)} \left( {x_{1} ,0} \right),E_{1}^{\left( 1 \right)} \left( {x_{1} ,0} \right),H_{1}^{\left( 1 \right)} \left( {x_{1} ,0} \right)\) for \(x_{1} \in L^{\prime \prime }\) we can consider the system, which follow from the imaginary part of (23):

$$r_{j1} \sigma_{13}^{\left( 1 \right)} \left( {x_{1} ,0} \right) + r_{j4} E_{1}^{\left( 1 \right)} \left( {x_{1} ,0} \right) + r_{j5} H_{1}^{\left( 1 \right)} \left( {x_{1} ,0} \right) = - {\text{Im}} \left[ {\Gamma_{j} \left( {x_{1} } \right)} \right] \;{\text{for}}\;j = 1,\,4,\,5\;{\text{and}}\;x_{1} \in L^{\prime \prime } .$$
(26)

The solution of the system (26) can be easily found by the Cramer formula and it is given in Appendix 1.

Substituting further (10) into Eq. (7) and taking into account that \(F_{j}^{ - } \left( {x_{1} } \right) = - \frac{1}{{\gamma_{j} }}F_{j}^{ + } \left( {x_{1} } \right)\) for \(x_{1} \in L^{\prime }\), we can write:

$$t_{j1} \left\langle {u_{1}^{\prime } \left( {x_{1} } \right)} \right\rangle + it_{j3} \left\langle {u_{3}^{\prime } \left( {x_{1} } \right)} \right\rangle + t_{j4} \left\langle {D_{3} \left( {x_{1} } \right)} \right\rangle + t_{j5} \left\langle {B_{3} \left( {x_{1} } \right)} \right\rangle = \theta_{j} \left( {x_{1} } \right)\;on\;L^{\prime } ,$$
(27)

where \(\theta_{j} \left( {x_{1} } \right) = \frac{{\gamma_{j} + 1}}{{\gamma_{j} }}F_{j}^{ + } \left( {x_{1} } \right)\).

One can get from Eq. (27) for \(j = 1\):

$$\left\langle {u^{\prime}_{3} \left( {x_{1} } \right)} \right\rangle = \frac{1}{{t_{13} }}{\text{Im}} \left[ {\theta_{1} \left( {x_{1} } \right)} \right] \;{\text{for}}\;x_{1} \in L^{\prime } .$$
(28)

Considering further the real part of Eq. (27) one can write

$$t_{j1} \left\langle {u_{1}^{\prime } \left( {x_{1} } \right)} \right\rangle + t_{j4} \left\langle {D_{3} \left( {x_{1} } \right)} \right\rangle + t_{j5} \left\langle {B_{3} \left( {x_{1} } \right)} \right\rangle = {\text{Re}} \left[ {\theta_{j} \left( {x_{1} } \right)} \right] \;{\text{for}}\;j = 1,\,4,\,5\;{\text{and}}\;x_{1} \in L^{\prime } .$$
(29)

The last relations are the system of three equations with respect to \(\left\langle {u_{1}^{\prime } \left( {x_{1} } \right)} \right\rangle ,\,\left\langle {D_{3} \left( {x_{1} } \right)} \right\rangle ,\,\left\langle {B_{3} \left( {x_{1} } \right)} \right\rangle\). The solution of this system was also found by the Cramer formula and the results are given in Appendix 1.

4 Asymptotic behaviors of electro-magneto mechanical components on different parts of the material interface

In many cases, the knowledge of the asymptotic expressions for the electromechanical components are important. According to the formulas (16, 17 and 26) the asymptotic presentations for \(\Gamma_{j} \left( {x_{1} } \right)\) at \(x_{1} \to b_{k} + 0\) can be written in the form:

$$\Gamma_{1} \left( {x_{1} } \right)|_{{x_{1} \to b_{k} + 0}} = \overline{R}_{1k} \left( {x_{1} - b_{k} } \right)^{{ - 0.5 + i\varepsilon_{1} }} ,$$
(30)

where

$$\overline{R}_{1k} = \left( {1 + \gamma_{1} } \right)\overline{P}_{n1} \left( {b_{k} } \right)\left( {b_{k} - a_{k} } \right)^{{ - 0.5 - i\varepsilon_{1} }} \prod\limits_{j = 1,j \ne k}^{n} {\left( {b_{k} - a_{j} } \right)^{{ - 0.5 - i\varepsilon_{1} }} \left( {b_{k} - b_{j} } \right)^{{ - 0.5 + i\varepsilon_{1} }} } ,$$
(31)

and

$$\Gamma_{s} \left( {x_{1} } \right)|_{{x_{1} \to b_{k} + 0}} = \overline{R}_{sk} /\sqrt {x_{1} - b_{k} } ,\;s = 4,5,$$
(32)

where

$$\overline{R}_{sk} = 2\overline{P}_{ns} \left( {b_{k} } \right)\frac{1}{{\sqrt {b_{k} - a_{k} } }}\prod\limits_{j = 1,j \ne k}^{n} {\frac{1}{{\sqrt {\left( {b_{k} - a_{j} } \right)\left( {b_{k} - b_{j} } \right)} }}} {\text{are pure imaginer}}.$$
(33)

For the determination of \(\varphi^{(1)} \left( {x_{1} ,0} \right)\) and \(\psi^{(1)} \left( {x_{1} ,0} \right)\) the integrals from (30) and (32) are required. We denote them:

$$\hat{\Gamma }_{j} \left( {x_{1} } \right) = \int {\Gamma_{j} \left( {x_{1} } \right)} dx_{1} \;(j = 1,\,4,\,5)$$
(34)

and their asymptotic expressions are the following:

$$\hat{\Gamma }_{1} \left( {x_{1} } \right)|_{{x_{1} \to b_{k} + 0}} = \frac{{\overline{R}_{1k} }}{{0.5 + i\varepsilon_{1} }}\left( {x_{1} - b_{k} } \right)^{{0.5 + i\varepsilon_{1} }} ,\;\hat{\Gamma }_{s} \left( {x_{1} } \right)|_{{x_{1} \to b_{k} + 0}} = 2\overline{R}_{4s} \sqrt {x_{1} - b_{k} } ,\;s = 4,5.$$
(35)

According to the formulas (10), (11) and (27) the asymptotic presentations for \(\theta_{j} \left( {x_{1} } \right)\) at \(x_{1} \to b_{k} - 0\) can be given as follows:

$$\theta_{1} \left( {x_{1} } \right)|_{{x_{1} \to b_{k} - 0}} = L_{1k} \left( {b_{k} - x_{1} } \right)^{{ - 0.5 - i\varepsilon_{1} }} ,$$
(36)

where

$$L_{1k} = - \frac{{i\left( {1 + \gamma_{1} } \right)}}{{\sqrt {\gamma_{1} } }}P_{n1} \left( {b_{k} } \right)\left( {b_{k} - a_{k} } \right)^{{ - 0.5 + i\varepsilon_{1} }} \prod\limits_{j = 1,j \ne k}^{n} {\left( {b_{k} - a_{j} } \right)^{{ - 0.5 + i\varepsilon_{1} }} \left( {b_{k} - b_{j} } \right)^{{ - 0.5 - i\varepsilon_{1} }} }$$
(37)

and

$$\theta_{s} \left( {x_{1} } \right)|_{{x_{1} \to b_{k} - 0}} = L_{sk} /\sqrt {b_{k} - x_{1} } ,\;s = 4,5,$$
(38)

where

$$L_{sk} = - 2iP_{ns} \left( {b_{k} } \right)\frac{1}{{\sqrt {b_{k} - a_{k} } }}\prod\limits_{j = 1,j \ne k}^{n} {\frac{1}{{\sqrt {\left( {b_{k} - a_{j} } \right)\left( {b_{k} - b_{j} } \right)} }}} ,\;(s = 4,5)\;{\text{are pure imaginer}}.$$
(39)

For the determination of \(\left\langle {u_{1} \left( {x_{1} } \right)} \right\rangle\) and \(\left\langle {u_{3} \left( {x_{1} } \right)} \right\rangle\) the integrals from (36) and (37) are required. We denote them:

$$\hat{\theta }_{j} \left( {x_{1} } \right) = \int {\theta_{j} \left( {x_{1} } \right)} {\text{d}}x_{1} \;\;(j = 1,\,4,\,5)$$
(40)

and they are the following:

$$\hat{\theta }_{1} \left( {x_{1} } \right)|_{{x_{1} \to b_{k} - 0}} = \frac{{L_{1k} }}{{i\varepsilon_{1} - 0.5}}\left( {b_{k} - x_{1} } \right)^{{0.5 - i\varepsilon_{1} }} ,\;\hat{\theta }_{s} \left( {x_{1} } \right)|_{{x_{1} \to b_{k} - 0}} = - 2L_{sk} \sqrt {b_{k} - x_{1} } ,\;s = 4,5.$$
(41)

5 The energy release rate (ERR)

According to crack closure integral Rybicki and Kanninen [36], the energy release rate (ERR) at a crack tip \(b_{k}\) can be presented in the form:

$$\begin{aligned} G_{{b_{k} }} = & \mathop {\lim }\limits_{\Delta l \to 0} \frac{1}{2\Delta l}\left\{ {\int\limits_{{b_{k} }}^{{b_{k} + \Delta l}} {\left[ {\sigma_{33}^{\left( 1 \right)} \left( {x_{1} ,0} \right)\left\langle {u_{3} \left( {x_{1} - \Delta l} \right)} \right\rangle + \sigma_{13}^{\left( 1 \right)} \left( {x_{1} ,0} \right)\left\langle {u_{1} \left( {x_{1} - \Delta l} \right)} \right\rangle } \right.} } \right. \\ & \quad \left. {\left. { - \varphi^{(1)} (x_{1} ,0)\left\langle {D_{3} \left( {x_{1} - \Delta l,0} \right)} \right\rangle - \psi^{(1)} (x_{1} ,0)\left\langle {B_{3} \left( {x_{1} - \Delta l,0} \right)} \right\rangle } \right]{\text{d}}x_{1} } \right\} \\ \end{aligned}$$
(42)

Performing further the integrations on parts to the last two terms in the integrand, one arrives at the formula:

$$G_{{b_{k} }} = \mathop {\lim }\limits_{\Delta l \to 0} \tilde{G}_{{b_{k} }} \left( {\Delta l} \right),$$
(43)

where

$$\tilde{G}_{{b_{k} }} \left( {\Delta l} \right) = \frac{1}{2\Delta l}\int\limits_{{b_{k} }}^{{b_{k} + \Delta l}} {g\left( {x_{1} ,\Delta l} \right)\,} dx_{1} ,$$
(44)
$$\begin{aligned} g\left( {x_{1} ,\Delta l} \right) = & \sigma_{33}^{\left( 1 \right)} \left( {x_{1} ,0} \right)\left\langle {u_{3} \left( {x_{1} - \Delta l} \right)} \right\rangle + \sigma_{13}^{\left( 1 \right)} \left( {x_{1} ,0} \right)\left\langle {u_{1} \left( {x_{1} - \Delta l} \right)} \right\rangle \\ & \quad - E_{1}^{\left( 1 \right)} \left( {x_{1} ,0} \right)\left\langle {\hat{D}_{3} \left( {x_{1} - \Delta l} \right)} \right\rangle - H_{1}^{\left( 1 \right)} \left( {x_{1} ,0} \right)\left\langle {\hat{B}_{3} \left( {x_{1} - \Delta l} \right)} \right\rangle \\ \left\langle {\hat{D}_{3} \left( {x_{1} ,0} \right)} \right\rangle = & \int {\left\langle {D_{3} \left( {x_{1} ,0} \right)} \right\rangle } dx_{1} ,\;\left\langle {\hat{B}_{3} \left( {x_{1} ,0} \right)} \right\rangle = \int {\left\langle {B_{3} \left( {x_{1} ,0} \right)} \right\rangle } {\text{d}}x_{1} . \\ \end{aligned}$$
(45)

Further we use formula (25) and the solution of the system (26) given by formulas (A2). Substituting in these formulas the asymptotic presentations (30) and (32) we arrive to the following formulas:

$$\begin{aligned} \sigma_{33}^{\left( 1 \right)} \left( {x_{1} ,0} \right)|_{{x_{1} \to b_{k} + 0}} = & \left( {x_{1} - b_{k} } \right)^{ - 0.5} \left[ {q_{1k} \cos \varphi_{1k} \left( {x_{1} } \right) - q_{2k} \sin \varphi_{1k} \left( {x_{1} } \right)} \right] \\ \sigma_{13}^{\left( 1 \right)} \left( {x_{1} ,0} \right)|_{{x_{1} \to b_{k} + 0}} = & \rho_{\sigma 1} \Lambda_{k} \left( {x_{1} } \right) + \rho_{\sigma 45} /\sqrt {x_{1} - b_{k} } , \\ E_{1}^{\left( 1 \right)} \left( {x_{1} ,0} \right)|_{{x_{1} \to b_{k} + 0}} = & \rho_{E1} \Lambda_{k} \left( {x_{1} } \right) + \rho_{E45} /\sqrt {x_{1} - b_{k} } , \\ H_{1}^{\left( 1 \right)} \left( {x_{1} ,0} \right)|_{{x_{1} \to b_{k} + 0}} = & \rho_{H1} \Lambda_{k} \left( {x_{1} } \right) + \rho_{H45} /\sqrt {x_{1} - b_{k} } , \\ \end{aligned}$$
(46)

where

$$\Lambda_{k} \left( {x_{1} } \right) = \left( {x_{1} - b_{k} } \right)^{ - 0.5} \left[ {q_{2k} \cos \varphi_{1k} \left( {x_{1} } \right) + q_{1k} \sin \varphi_{1k} \left( {x_{1} } \right)} \right],$$
$$q_{1k} = {\text{Re}} \left( {\overline{R}_{1k} } \right),\;q_{2k} = {\text{Im}} \left( {\overline{R}_{1k} } \right),\;\varphi_{1k} \left( {x_{1} } \right) = \varepsilon_{1} \log \left( {x_{1} - b_{k} } \right),$$
$$\rho_{\sigma 45} = \rho_{\sigma 4} {\text{Im}} \left( {\overline{R}_{4k} } \right) + \rho_{\sigma 5} {\text{Im}} \left( {\overline{R}_{5k} } \right),\;\rho_{E45} = \rho_{E4} {\text{Im}} \left( {\overline{R}_{4k} } \right) + \rho_{E5} {\text{Im}} \left( {\overline{R}_{5k} } \right),$$
$$\rho_{H45} = \rho_{H4} {\text{Im}} \left( {\overline{R}_{4k} } \right) + \rho_{H5} {\text{Im}} \left( {\overline{R}_{5k} } \right).$$

In a similar way we use formula (28) and the solution of the system (29) given by formulas (53). Substituting in these formulas the asymptotic presentations (41) we arrive to the following formulas:

$$\begin{aligned} \left\langle {u_{3} \left( {x_{1} } \right)} \right\rangle |_{{x_{1} \to b_{k} - 0}} = & \left( {b_{k} - x_{1} } \right)^{0.5} \left[ {p_{2k} \cos \varphi_{2k} \left( {x_{1} } \right) - p_{1k} \sin \varphi_{2k} \left( {x_{1} } \right)} \right]/t_{13} , \\ \left\langle {u_{1} \left( {x_{1} } \right)} \right\rangle |_{{x_{1} \to b_{k} - 0}} = & \eta_{u1} \Theta_{k} \left( {x_{1} } \right) + \eta_{u45} \left( {b_{k} - x_{1} } \right)^{0.5} , \\ \left\langle {\hat{D}_{3} \left( {x_{1} } \right)} \right\rangle |_{{x_{1} \to b_{k} - 0}} = & \eta_{D1} \Theta_{k} \left( {x_{1} } \right) + \eta_{D45} \left( {b_{k} - x_{1} } \right)^{0.5} , \\ \left\langle {\hat{B}_{3} \left( {x_{1} } \right)} \right\rangle |_{{x_{1} \to b_{k} - 0}} = & \eta_{B1} \Theta_{k} \left( {x_{1} } \right) + \eta_{B45} \left( {b_{k} - x_{1} } \right)^{0.5} , \\ \end{aligned}$$
(47)

where

$$\begin{aligned} p_{1k} = & {\text{Re}} \left[ {L_{1k} /\left( {i\varepsilon_{1} - 0.5} \right)} \right],\;p_{2k} = {\text{Im}} \left[ {L_{1k} /\left( {i\varepsilon_{1} - 0.5} \right)} \right],\;\varphi_{2k} \left( {x_{1} } \right) = \varepsilon_{1} \log \left( {b_{k} - x_{1} } \right), \\ \eta_{u45} = & - 2\left[ {\eta_{u4} {\text{Re}} \left( {L_{4k} } \right) + \eta_{u5} {\text{Re}} \left( {L_{5k} } \right)} \right],\;\eta_{D45} = - 2\left[ {\eta_{D4} {\text{Re}} \left( {L_{4k} } \right) + \eta_{D5} {\text{Re}} \left( {L_{5k} } \right)} \right], \\ \eta_{B45} = & - 2\left[ {\eta_{B4} {\text{Re}} \left( {L_{4k} } \right) + \eta_{B5} {\text{Re}} \left( {L_{5k} } \right)} \right]. \\ \end{aligned}$$

The expressions for \(\rho_{\sigma j}\), \(\rho_{Ej}\), \(\rho_{Hj}\), \(\eta_{uj}\), \(\eta_{Dj}\) and \(\eta_{Bj}\) for \(j = 1,4,5\) are given in Appendix 1.

Substituting the formulas (46) and (47) into (43)–(45) and performing the integration we arrive to the following formula:

$$G_{{b_{k} }} = \frac{\pi }{8}\left( {t_{13}^{ - 1} + h_{3} } \right)\;\frac{{h_{1k} + 2\varepsilon_{1} h_{2k} }}{{\cosh \left( {\pi \varepsilon_{1} } \right)}} + \frac{\pi }{4}h_{4k} ,$$
(48)

where

$$\begin{gathered} h_{1k} = q_{1k} p_{2k} + q_{2k} p_{1k} ,\;\,h_{2k} = q_{2k} p_{2k} - q_{1k} p_{1k} ,\;h_{3} = \rho_{\sigma 1} \eta_{u1} - \rho_{E1} \eta_{D1} - \rho_{H1} \eta_{B1} \hfill \\ h_{4k} = \rho_{\sigma 45} \eta_{u45} - \rho_{E45} \eta_{D45} - \rho_{H45} \eta_{B45} . \hfill \\ \end{gathered}$$

In a similar way, the ERR at the left tip of the \(k\)-th crack can be found and presented in the form

$$G_{{a_{k} }} = \frac{\pi }{8}\left( {t_{13}^{ - 1} + h_{3} } \right)\;\frac{{h_{1k}^{a} + 2\varepsilon_{1} h_{2k}^{a} }}{{\cosh \left( {\pi \varepsilon_{1} } \right)}} + \frac{\pi }{4}h_{4k}^{a} ,$$
(49)

where the expressions for \(h_{1k}^{a}\), \(h_{2k}^{a}\) and \(h_{4k}^{a}\) are given in Appendix 2.

6 Numerical results and discussion

Consider for the numerical illustration the bimaterial composed of BaTiO3–CoFe2O4 composite with volume fractions of BaTiO3 \(V_{{\text{f}}} = 0.5\) (upper half pane) and \(V_{{\text{f}}} = 0.1\) (lower one). The characteristics of these materials are given in Appendix 3. For the presentation of the results in the dimensionless form, we introduce the following dimensionless values:

$$\begin{aligned} & \hat{a}_{i} = \frac{{a_{i} }}{l},\;\hat{b}_{i} = \frac{{b_{i} }}{l},\;\hat{u}_{3} (x_{1} ) = \left\langle {u_{3} (x_{1} )} \right\rangle /l,\;\hat{\sigma }_{33} (x_{1} ) = \frac{{\sigma_{33}^{(1)} (x_{1} ,0)}}{{\sigma^{\infty } }}, \\ & \hat{D}_{02} = \frac{{D_{02} c_{11}^{0} }}{{\sigma^{\infty } D_{02}^{0} }},\;\hat{H}^{\infty } = \frac{{H^{\infty } c_{11}^{0} }}{{\sigma^{\infty } H_{0}^{\infty } }}, \\ \end{aligned}$$

where \(l = \left( {b_{2} - a_{2} } \right)/2\), \(c_{11}^{0} = 274\,{\text{GPa}}\), \(D_{02}^{0} = 5 \times 10^{ - 4} \;{\text{C/m}}\), \(H_{0}^{\infty } = 10^{5} \;{\text{A/m}}\). In all following calculations \(\sigma^{\infty } = 10\;{\text{MPa}}\) and \(b_{2} = - a_{2} = 0.01\,{\text{m}}\) were chosen.

The results for the case of 3 cracks having their normalized tip coordinates \(\hat{a}_{1} = - 4\), \(\hat{b}_{1} = - 2\), \(\hat{a}_{2} = - 1\), \(\hat{b}_{2} = 1\), \(\hat{a}_{3} = 1.2\), \(\hat{b}_{3} = 3.2\) are shown in Fig. 2. The external shear stress was chosen to be \(\tau^{\infty } = 0\) and the electric and magnetic fluxes \(E^{\infty } = 0\), \(H^{\infty } = 0\). The electric net charges of the left and right cracks were absent (\(D_{01} = 0\), \(D_{03} = 0\)) and several magnitudes of this value were considered for the middle crack. Solid lines illustrate the normalized crack openings \(\hat{u}_{3} (x_{1} )\) and the dashed lines show the variations of the normalized normal stress \(\hat{\sigma }_{33}^{{}} \left( {x_{1} ,0} \right)\) outside of cracks. Lines I, III correspond to \(D_{02} = 0\) and II, IV are related to \(\hat{D}_{02} = 2.74 \times 10^{4}\). It can be seen from Fig. 2 that rapprochement of cracks leads to the minor growing of the crack opening; the electric net charge applied to a certain crack essentially influences the crack opening of this crack and very slightly of the opening of other cracks as well as the normal stress outside cracks.

Fig. 2
figure 2

Variation of the crack openings (solid lines) and the normal stress outside the cracks (dashed lines) for different values of the normalized electric net charge \(\hat{D}_{02}\)

Full size image

The influence of magnetic flux and also electric net charge is illustrated in Fig. 3 for the cracks location and remote mechanical and electric loadings the same as in Fig. 2 and \(D_{01} = 0\), \(D_{03} = 0\). The lines I are drawn for \(H^{\infty } = 0\), \(D_{02} = 0\), II—for \(H^{\infty } = 0\), \(\hat{D}_{02} = 1.96 \times 10^{4}\), III—for \(\hat{H}^{\infty } = 1.37 \times 10^{5}\), \(D_{02} = 0\) and IV—for \(\hat{H}^{\infty } = 1.37 \times 10^{5}\), \(\hat{D}_{02} = 1.96 \times 10^{4}\). It follows from these graphs that the magnetic flux influences the crack opening, but this influence becomes appreciable only for rather large its value. The electric net charge of the middle crack tangible influences its opening and very insignificantly the opening of the left and right cracks.

Fig. 3
figure 3

Influence of magnetic flux and electric net charge to the crack openings for the case of three cracks

Full size image

The variation of the normalized magnetic flux \(\hat{H}_{1} \left( {x_{1} } \right) = H_{1}^{(1)} \left( {x_{1} ,0} \right)c_{11}^{0} /\left( {\sigma^{\infty } H_{0}^{\infty } } \right)\) on the interval \(( {\hat{b}_{2} ,\,\hat{a}_{3} } )\) for the system of three cracks defined by \(\hat{a}_{1} = - 4\), \(\hat{b}_{1} = - 2\), \(\hat{a}_{2} = - 1\), \(\hat{b}_{2} = 1\), \(\hat{a}_{3} = 2\), \(\hat{b}_{3} = 4\), \(\tau^{\infty } = E^{\infty } = 0\), \(D_{01} = 0\), \(D_{02} = 0\), \(D_{03} = 0\) and different \(H^{\infty }\) are shown in Fig. 4. Lines I, II, III, IV and V corresponds to \(\hat{H}^{\infty } = 0,\;2.74 \times 10^{3} ,\;6.85 \times 10^{3} ,\;1.37 \times 10^{4} ,\;2.74 \times 10^{4}\), respectively. It can be seen from Fig. 4 that the magnetic flux on the interface is very small for only mechanical loading, but its value increases accordingly to the applied external magnetic influence.

Fig. 4
figure 4

Variation of the normalized magnetic flux along the interface between the middle and right cracks for \(\tau^{\infty } = E^{\infty } = 0\) and different values of \(H^{\infty }\)

Full size image

The variation of the normalized electric flux \(\hat{E}_{1} \left( {x_{1} } \right) = E_{1}^{(1)} \left( {x_{1} ,0} \right)c_{11}^{0} /\left( {\sigma^{\infty } E_{0} } \right)\) (\(E_{0} = 10^{5} \;{\text{V/m}}\)) between the middle and right cracks for the same cracks locations as in Fig. 4, \(\tau^{\infty } = E^{\infty } = 0\), \(D_{01} = 0\), \(D_{02} = 0\), \(D_{03} = 0\) and \(\hat{H}^{\infty } = 0\) (line I), \(1.37 \times 10^{4}\) (II) and \(2.74 \times 10^{4}\) (III) are presented in Fig. 5. As it can be seen the influence of the magnetic flux to the electric flux is rather small and on the main part of Fig. 5 it is almost invisible. Only zoom of some part of the graph permitted to demonstrate the difference between the curves obtained for different \(H^{\infty }\).

Fig. 5
figure 5

Variation of the normalized electric flux in the same region and under the same external influences as in Fig. 4

Full size image

The variation of the ERR with respect to the location of the cracks on the interface between \(V_{{\text{f}}} = 0.5\) (upper) and \(V_{{\text{f}}} = 0.1\) (lower) materials, the value of mechanical, electric and magnetic loading are demonstrated in Tables 1, 2, 3 and 4 with special attention to the magnetic flux and the cracks electric charge influence.

Table 1 Comparison of the normalized ERRs of the crack in magnetoelectroelastic bimaterial and in piezoelectric one for \(D_{0k} = 0\) (\(k = 1,2,3\))
Full size table
Table 2 Comparison of the ERRs of the crack in magnetoelectroelastic bimaterial and in piezoelectric one for \(\hat{D}_{02} = 1.10 \times 10^{4}\) and \(\hat{D}_{0k} = 0\) (\(k = 1,3\))
Full size table
Table 3 ERRs variation of the middle crack for different values of the magnetic flux
Full size table
Table 4 ERRs variation of all cracks for different values of the total electric charge of the middle crack
Full size table

In Table 1 the variation of the normalized ERRs \(\hat{G}_{2a} = 10^{5} G_{2a} /\left( {\sigma^{\infty } l} \right)\) and \(\hat{G}_{2b} = 10^{5} G_{2b} /\left( {\sigma^{\infty } l} \right)\) of the middle crack \(\hat{a}_{2} = - 1\), \(\hat{b}_{2} = 1\) is demonstrated for \(\tau^{\infty } = E^{\infty } = H^{\infty } = 0\) and zero electric charges on all cracks. The position of the left crack \(\hat{a}_{1} = - 10\), \(\hat{b}_{1} = - 8\) is fixed and the right crack \(\left( {\hat{a}_{3} ,\hat{b}_{3} } \right)\) changes its location. The upper lines of each cell are related to the above mentioned magnetoelectroelastic material. For the comparison the ERRs for piezoelectric bimaterial with the same elastic, piezoelectric and dielectric constants as in \(V_{{\text{f}}} = 0.5/V_{{\text{f}}} = 0.1\) bimaterial, calculated according to the approach [37], are given in the lower lines of the cells related to \(H^{\infty } = 0\).

Similar results as in Table 1, but for the electrically charged middle crack are given in Table 2.

It follows from the results of these tables that:

  • Both total electric charge of the middle crack and the external magnetic field perceptibly influence the energy release rates at both crack tips;

  • The convergence of the middle and right cracks lead to essential grow of the ERRs especially on the neighboring crack tips;

  • The good agreement of the results obtained for magnetoelectroelastic and the corresponding piezoelectric materials is observed for \(H^{\infty } = 0\).

The special analysis of the magnetic flux influence to the ERR of the middle crack with the same location as for Table 1 and \(\hat{a}_{1} = - 10\), \(\hat{b}_{1} = - 8\), \(\hat{a}_{3} = 1.5\), \(\hat{b}_{3} = 3.5\) are illustrated in Table 3. The external influence was chosen to be \(\tau^{\infty } = E^{\infty } = D_{0k} = 0\) (\(k = 1,2,3\)) and different values of the magnetic flux were considered. It can be seen from this table that for large values of the electric flux the ERR increases almost proportionally to its square. Besides it is observed that \(G_{2b} /G_{2a}\) coefficient remains almost invariable for different magnitudes of \(H^{\infty }\).

The ERRs variation of all cracks for the same their locations as in Table 3, but for \(\tau^{\infty } = E^{\infty } = H^{\infty } = D_{01} = D_{03} = 0\) are given in Table 4 for different values of \(\hat{D}_{02}\). It can be seen that \(\hat{D}_{02}\) variation very slightly influences the ERRs at the left crack tips because this crack is situated rather far from the middle crack. This influence is more significant at the tips of the right crack because it is located nearer to the middle crack. The most tangible influence is observed concerning the middle crack tips because the electric charge variation is connected directly with this crack.

The influence of the crack locations to their opening and to the ERRs is demonstrated in Fig. 6 and in Table 5. At the beginning, the geometry is symmetric and then the right crack is approaching the central one. It is assumed that \(\tau^{\infty } = E^{\infty } = H^{\infty } = D_{02} = 0\) and \(\hat{D}_{01} = \hat{D}_{03} = 5.48 \times 10^{3}\). The left and middle cracks have fixed locations with \(\hat{a}_{1} = - 5\), \(\hat{b}_{1} = - 3\), \(\hat{a}_{2} = - 1\), \(\hat{b}_{2} = 1\) and the right crack has normalized length equal to 2. Lines I in Fig. 6 correspond to the symmetric case with \(\hat{a}_{3} = 3\), lines II are drawn for \(\hat{a}_{3} = 2\) and lines III—for \(\hat{a}_{3} = 1.1\)

Fig. 6
figure 6

Variations of the crack openings caused by approaching of the right crack to the central one

Full size image
Table 5 ERRs variation of the central crack and the crack openings at their middle points for different distances between central and right cracks
Full size table

The values of the ERRs of the central crack corresponding to the cases shown in Fig. 6 are presented in the first two lines of Table 5. In the last lines of this Table the crack openings at the middle points of the left (\(\hat{u}_{3m}^{(1)}\)), central (\(\hat{u}_{3m}^{(2)}\)) and right (\(\hat{u}_{3m}^{(3)}\)) cracks are given. It can be seen from the obtained results that the crack openings of the left and right cracks for the symmetrical case are identical, but their values are smaller than the value for the central crack because of the electric charges. Approaching the right crack to the middle one leads to the moderate growth of their openings and to the significant increase in the ERRs, especially for the nearest crack tips.

7 Conclusion

A finite set of cracks between dissimilar magnetoelectroelastic materials under the action of tension and shear mechanical loading, electric and magnetic fields parallel to the crack faces is considered. The set is not periodic, i.e., the cracks can have arbitrary lengths and distances between their centers. The materials are polarized in the direction orthogonal to the crack faces. It is assumed that the crack faces are covered with mechanically soft electrodes of ferroelectric material having a prescribed electric charge and zero magnetic induction and all electromechanical fields are independent on the coordinate parallel to the crack front. The open crack model is adopted.

By using the submissions of mechanical, electric and magnetic components via sectionally analytic functions, the Riemann-Hilbert problem of linear relationship is formulated and solved in an analytical form. The arbitrary constants are found from the conditions at infinity, single-valued ness of the displacements, prescribed net electric charge and magnetic induction for each crack. These give the system of linear algebraic equations of dimension equal to the number of cracks. All required mechanical, electric and magnetic components along the interface are presented in the closed form.

It is shown that all fields have an oscillating singularity at the crack tips. It means that the concept of the stress intensity factor is not convenient for the fracture process description. Therefore, close attention was paid to ERR determination. On this reason, the asymptotic presentations of mechanical, electric and magnetic fields at the crack tips were derived and the crack closure integral were applied. Carried out the careful analysis, the formulas (48) and (49) for the ERRs at the right and left tips of any crack has been obtained.

By visualization of the obtained analytical formulas, the dimensionless graphs of the crack faces displacement jumps, stresses, electric and magnetic fields along the interface are given for certain magnetoelectroelastic bimaterial. The ERRs are also shown in Table form for different crack tips, loading, crack lengths and locations. The obtained analytical and numerical results permit to derive the following valuable conclusions:

  • good agreement of the results obtained for magnetoelectroelastic and piezoelectric bimaterial having the same elastic, piezoelectric and dielectric constants is observed for zero external magnetic field, but increase in this field leads to the violation of this agreement;

  • the analysis of cracks interaction demonstrates that the cracks rapprochement leads to a significant increase in the associated energy ERR. However, the ERR increase for the near crack tips is more noticeably than for remote crack tips;

  • the decrease in the distance between cracks leads to the very intensive growth of the ERR for the neighboring crack tips and to more moderate variation of the cracks openings;

  • the variation of the external magnetic field causes the similar variation of the magnetic field on the bonded parts of the material interface; however, the influence of this variation upon the mechanical and electric components is very small;

  • the net electric charge of a crack essentially influences the ERRs of this crack; however, it influences also the ERRs of the neighboring cracks, but with less intensities.