Micromechanical modeling for the thermo-elasto-plastic behavior of functionally graded composites

Abstract

By gradually changing the compositions, functionally graded materials (FGMs) are constructed and possess comprehensive performance. In this paper, based on the micromechanics, the thermo-elasto-plastic behaviors of FGMs are studied with consideration of the pairwise particle interaction, where the graded microstructures of the FGMs are represented by employing a particular representative volume element (RVE). Based on the assumption that the matrix dominates the plastic behavior of the FGMs while the particles stay in their linearly elastic state, the von-Mises yield function is extended to solve FGMs problems. By employing the backward Euler’s method, the overall effective thermo-elasto-plastic behavior of FGMs can be numerically obtained. When eliminating the plastic or thermal effect, the proposed model can be downgraded to the thermoelastic model or the elastoplastic model of the FGMs, respectively. In addition, the proposed model is validated with available experimental results. Finally, the effects of temperature changes, particle distributions, volume fractions, and material properties on the effective thermo-elasto-plastic properties of FGMs are studied.

1 Introduction

In 1972, the initial concept of a microstructural gradient in composites and polymeric materials [3] was presented to build the connection between the microscale and the macroscale of the materials. After that, the functionally graded materials (FGMs) were first named in 1984 in the aerospace engineering field and then were applied in many industrial areas [11, 25, 32, 41, 45]. The capital concept of FGMs is to construct composite materials by varying the constituents continuously on the microscale, which enables the overall properties of the composites to possess the devisable comprehensive performance on the macroscale. For example, by gradually changing the compositions to withstand extreme temperatures [36], FGMs were designed to improve thermal resistance and mechanical properties. Due to their superior material properties, FGMs have been fabricated and applied for various multifunctional tasks. Recently, a two-phase FGMs panel has been integrated into the building-integrated photovoltaic-thermal (BIPVT) roofing system (as shown in Fig. 1), where its devisable thermal properties are utilized to enhance the conversion efficiency of the solar energy [52].

Fig. 1

BIPVT roofing panels containing a two-phase FGMs layer

Specifically, in this BIPVT panel, the FGMs layer is gradually composed of aluminum phase (Al phase) and high-density polyethylene phase (HDPE phase), where the Al-rich domain can transfer the heat to the water tube immediately to cool down the temperature of the solar cells, and the HDPE-rich domain can resistant the heat transfer into the indoor space to keep the thermal comfort. This FGMs layer can also prolong the lifespan of the solar panels and improve energy conversion efficiency by refrigerating the solar cells. During the actual application of BIPVT, the top surface of the FGMs layer (Al-rich domain) will be heated up under the sunlight. Due to the different thermal properties of the Al phase and the HDPE phase, thermo-elasto-plastic behavior will be generated. Particularly, in the application of the aerospace field, the temperature difference of the FGMs usually comes to thousands of degrees, where the thermal-induced deformation will extremely threaten the security of the structures. Therefore, it is very important to investigate the thermo-elasto-plastic behavior of the FGMs.

To study the thermo-elasto-plastic behavior of the FGMs, micromechanics is employed, which have been proven and widely used in the application of elastic problems, elasto-plastic problems, thermal-elastic problems of FGMs, and so on. Since Eshelby [12, 13] first proposed the equivalent inclusion method (EIM) and used it to solve the isotropic materials containing a single ellipsoid inclusion, the research on particle mixed composites has attracted more and more researchers’ attention. Many theoretical models [5, 10, 16, 17, 30, 31] have been created to study the effective properties of the composites with considering the particle distribution and microstructure. However, the above methods do not directly analyze the interaction between particles and the continuous properties of gradient materials at the microscopic scale. To obtain higher levels of accuracy, models that directly consider the pairwise particle interaction are conducted. Chen and Acrivos [8] first construct the solution to analyze the interaction between two particles. Based on this solution, the contribution of all particles on the effective properties was integrated by utilizing Legendre’s Series [9]. By considering the pairwise interaction between a particle and its neighboring particles, Ju and Chen [20] obtained the effective properties of the composite with the same size particles randomly distributed in the matrix. Yin et al. [50] extended this pairwise interaction concept to predict the elastic behavior of FGMs. Considering the particle interaction and the possibility of debonding, Paulino et al. [34] built a micromechanical damage model. During the last decades, the micromechanics-based numerical algorithms [4, 33, 46, 48] had been widely developed, which make micromechanics a powerful tool to analyze the overall material behaviors of FGMs.

Due to the wide application of FGMs in high-temperature scenarios, the investigation of their thermal properties has attracted many researchers’ attention. Kesler et al. [23], Ishibashi et al. [18], Khor and Gu [24] obtained thermal stress and the effective coefficients of thermal expansion (CTE) distribution of FGMs along the gradation direction by different methods. Ji et al. [19] analyzed the effect of substrate conditions on the thermal shocking properties of FGMs by the finite element method. Reiter et al. [37], Vel and Batra [44] studies the effective moduli and CTEs of FGMs by self-consistent models [17] and the Mori–Tanaka [31] models. Yin et al. [49] studied the thermoelastic behavior of FGMs with a micromechanical approach and predicted the effective CTE for FGMs. Aboudi et al. [1] built a higher-order model for FGMs, which captured the interaction between the microscale and global scale in the effective thermomechanical behavior. Lin et al. [26] developed an axisymmetric refined plate theory for a circular FGMs panel subjected to externally applied thermomechanical loading.

As for the elastoplastic behavior of composites, Ju and Chen [20] micromechanically derived the so-called effective yield criterion to estimate the effective elastoplastic properties of uniform metallic composites. After that, Ju and Tseng [22] extended the above method to investigate the ductile matrix composites, where the effective yield functions were obtained with considering two non-equivalent formulations and implemented it by conducting a strain-driven three-dimensional local return mapping algorithm [21]. When it comes to FGMs, Gasik [14] reviewed the existed micromechanical models and developed an explicit Gasik-Ueda model to simulate the elastoplastic behavior of FGMs. However, under high particle volume fraction, their model failed because their model did not include the particle interaction. Based on Yin’s work [50] on the elastic analysis of FGMs, Lin et al. [27] micromechanically derived the elastoplastic model with directly containing the effect of particle interaction. Zhang et al. [52] implemented it by using the backward Euler’s method and validated it with experimental data, where the image processing method was utilized to capture the particle distribution.

Based on the micromechanics, the studies of thermo-elasto-plastic behavior of FGMs had attracted many researchers’ attention. Gasik and Lilius [15] built a micromechanical model to evaluate the mechanical and thermal properties of two-phase FGMs, and discussed the application of this model by comparing with other approaches [14]. After that, Ueda and Gasik [42] discussed the thermo-elasto-plastic behavior of FGMs under uniform heat flow. Shabana and Noda [38,39,40] studied the thermo-elasto-plastic behavior of partial particle-reinforced FGMs under thermal loading and calculated the thermo-elasto-plastic stresses. Pitakthapanaphhong and Busso [35] established a self-consistent constitutive framework to study the behavior of FGMs which subjected to thermal transients loading, and obtained the analytical and semi-analytical solutions to describe the thermo-elasto-plastic behavior. Besides, other theoretical model [29] and numerical algorithm [43] have been applied to study the FGMs structures. However, the particle interaction within the FGMs is not directly analyzed among the above methods. Thus, a new micromechanical-based thermo-elasto-plastic model with considering the pairwise interaction between particles is necessary.

The purpose of this paper is to study the effective thermo-elasto-plastic behavior of FGMs, where the particle interaction at the microscale is calculated micromechanically and the particle distributions are considered by introducing a particle probability density function. The organization of this paper is as follows. In Sect. 2, we briefly review the Eshelby’s EIM and pairwise interaction in the infinite domain, and then apply it to construct the micromechanical-based thermo-elasto-plastic model. The verifications of model are discussed in Sect. 3, where we verified the proposed model with elastoplastic model, the thermoelastic model and the corresponding experiments. In Sect. 4, the influences of different factors such as temperature and material parameters on FGMs are studied. Finally, conclusions are provided in Sect. 5.

2 Micromechanical analysis of FGMs

As shown in Fig. 1, FGMs consist of two phases with isotropic elastic tensors ${\mathbf{C}}^{1}$ and ${\mathbf{C}}^{0}$. The isotropic coefficients of thermal expansions (CTEs) are ${\upalpha }^{1}$ and ${\upalpha }^{0}$, respectively. The thickness of the FGMs along the gradation direction is $t$. The global coordinate system can be represented as $\left( {X_{1} , X_{2} , X_{3} } \right)$, where $X_{3}$ is gradation direction. To study the microstructure of FGMs, the graded representative volume element (RVE) is introduced, where the particle phase with volume fraction $\phi$ and matrix phase with volume fraction $1 - \phi$ are included in the RVE. At an arbitrary point $X^{0}$ in the composites, the local Cartesian coordinate system ($x_{1}$, $x_{2}$, $x_{3}$) is employed in the RVE as shown in the right hand of Fig. 1. To start the derivation, all particles (black points) in the RVE are assumed to possess the same radius $a\left( {a \ll t} \right)$, where $t$ is the thickness of the FGMs. ${\mathbf{D}}$ denotes the overall RVE domain, ${\varvec{\varOmega}}_{{\varvec{i}}}$ denotes the i-th particle’s domain $\left( {i = 1, 2, 3, \ldots , \infty } \right)$.

To understand the thermo-elasto-plastic behavior of FGMs, the effective yield criterion should be constructed first. In this paper, following the same assumption that the particle phase always stays in its elastic stage while the matrix phase could go to the plastic stage [20, 22, 52], the effective yield function based on von Mises yield rule with isotropic hardening [52] is applied as

$$F\left( {{{\varvec{\upsigma}}},e^{p} } \right) = \sqrt {\left\langle H \right\rangle } - \sqrt{\frac{2}{3}} \left( {\sigma_{Y} + h\left( {e^{p} } \right)^{q} } \right),$$

(1)

where $\sigma_{Y}$ is the yield stress of matrix, $e^{p}$ is the effective plastic strain, $h$ and $q$ are the hardening factors, and $\left\langle H \right\rangle$ represents the extended ensemble average stress norm driven by the coupling fields at the macroscale. Based on the assumption that the plastic hardening only occurs in the matrix rather than particle phase, $\sqrt {\left\langle H \right\rangle }$ is defined as

$$\sqrt {\left\langle H \right\rangle } = \left( {1 - \phi } \right)\sqrt {\left\langle H \right\rangle_{{\text{m}}} } ,$$

(2)

where $\left\langle H \right\rangle_{{\text{m}}}$ denotes the stress norm of the matrix phase and $\phi$ is the particle volume fraction. By substituting Eq. (2) into Eq. (1), the overall effective yield function for two-phase thermo-elasto-plastic FGMs can be rewritten as

$$F\left( {{{\varvec{\upsigma}}},e^{p} } \right) = \left( {1 - \phi } \right)\sqrt {\left\langle H \right\rangle_{{\text{m}}} } - \sqrt{\frac{2}{3}} \left( {\sigma_{Y} + h\left( {e^{p} } \right)^{q} } \right).$$

(3)

In FGMs, the particles affect the plastic behavior of the matrix. Assuming that the particle distribution follows the probability density function $P\left( {{\mathbf{x}}{|}{\mathbf{x}}_{1} } \right)$, which can be expressed as

$$P\left( {{\mathbf{x}}{|}{\mathbf{x}}_{1} } \right) = \frac{3g\left( x \right)}{{4\pi a^{3} }}\left[ {\phi \left( {X_{3}^{1} } \right) + e^{{-\frac{{\mathbf{x}}}{\delta }}} \phi_{,3} \left( {X_{3}^{1} } \right)x_{3} } \right],$$

(4)

$P\left( {{\mathbf{x}}{|}{\mathbf{x}}_{1} } \right)$ is used to locate a particle centered at ${\mathbf{x}}$ when the first particle is located at ${\mathbf{x}}_{1}$ [49]. And g(x) is the Percu–Yevick radial distribution function, which is set as g(x = 1 to insure the density of local field is unchanged in this paper; $X_{3}^{1}$ denotes the gradation direction at ${\mathbf{x}}_{1}$; $\phi \left( {X_{3}^{1} } \right)$ is the average volume fraction of particle at $X_{3}$; $\delta = \frac{e}{{\phi_{,3} \left( {X_{3}^{1} } \right)}}{\text{min}}\left( {\phi ,\phi^{c} - \phi } \right)$ denotes the attenuating rate of the gradation of the particle volume fraction in the far field; and $\phi^{c}$ represents the maximum volume fraction of particles.

The stress norm of the matrix phase $\left\langle H \right\rangle_{{\text{m}}}$ can be obtained by combining the current stress norm at the macroscopic $H^{0} = {{\varvec{\upsigma}}}^{0} :{\mathbf{I}}_{d} :{{\varvec{\upsigma}}}^{0}$ and the integration of the disturbances from all particles over the RVE at the microscale. Thus, $\left\langle H \right\rangle_{{\text{m}}}$ can be derived as

$$\left\langle H \right\rangle_{{\text{m}}} \left( {\mathbf{x}} \right) = H^{0} + \mathop \int \limits_{{\left| {{\varvec{x}} - {\varvec{x}}_{1} } \right| > a}}^{{}} \left\{ {H\left( {{\mathbf{x}}{|}{\mathbf{x}}_{1} } \right) - H^{0} } \right\}P\left( {{\mathbf{x}}{|}{\mathbf{x}}_{1} } \right)d{\mathbf{x}}_{1} ,$$

(5)

where $H\left( {{\mathbf{x}}{|}{\mathbf{x}}_{1} } \right) = {{\varvec{\upsigma}}}:{\mathbf{I}}_{d} :{{\varvec{\upsigma}}}$ is the stress norm of matrix when there are two particles in infinite matrix, and ${{\varvec{\upsigma}}}$ is the combination of far-field stress ${{\varvec{\upsigma}}}^{0}$ and disturbed stress ${\varvec{\upsigma}}^{\prime}$, which has similar format to the strain (Eq. (32)) in the Appendix. Then, Eq. (5) is further derived as

$$\left\langle H \right\rangle_{{\text{m}}} \left( {\mathbf{x}} \right) = {{\varvec{\upsigma}}}^{0} :{\mathbf{I}}_{d} :{{\varvec{\upsigma}}}^{0} + \mathop \int \limits_{{\left| {{\varvec{x}} - {\varvec{x}}_{1} } \right| > a}}^{{}} \left\{ {{\varvec{\upsigma}}^{\prime}:{\mathbf{I}}_{d} :{\varvec{\upsigma}}^{\prime} + {{\varvec{\upsigma}}}^{0} :{\mathbf{I}}_{{\text{d}}} :{\varvec{\upsigma}}^{\prime} + {\varvec{\upsigma}}^{\prime}:{\mathbf{I}}_{{\text{d}}} :{{\varvec{\upsigma}}}^{0} } \right\}P\left( {{\mathbf{x}}_{1} } \right)d{\mathbf{x}}_{1} ,$$

(6)

where the disturbed stress ${\varvec{\upsigma}}^{\prime}$ is calculated as

$${\varvec{\upsigma}}^{\prime} = {\mathbf{C}}_{0} :{\varvec{\upvarepsilon}}^{\prime} = {\mathbf{B}}:\left( {{{\varvec{\upsigma}}}^{0} - {{\varvec{\upsigma}}}_{{{\text{eff}}}}^{{\text{T}}} } \right),$$

(7)

${\varvec{\upvarepsilon}}^{\prime}$ represents disturbed strain caused by material mismatch between particle and matrix (see the Appendix for the expression and derivation process of ${\varvec{\upvarepsilon}}^{\prime}$), and ${\mathbf{B}} = {\mathbf{C}}_{0} \cdot {\mathbf{A}} \cdot {\mathbf{C}}_{0}^{ - 1}$, ${\mathbf{A}} = - {\mathbf{D}}^{{\Omega }} :\left( {{\mathbf{D}}^{{\Omega }} - {\Delta }{\mathbf{C}}^{ - 1} } \right)^{ - 1}$. ${{\varvec{\upsigma}}}_{{{\text{eff}}}}^{{\text{T}}} = {\mathbf{C}}_{0} \cdot \left( {{\mathbf{I}} + {\Delta }{\mathbf{C}}^{ - 1} \cdot {\mathbf{C}}_{0} } \right):{{\varvec{\upvarepsilon}}}^{{\text{T}}}$ is the effective thermal stress.

Substituting Eq. (7) into Eq. (6), we can find that the third and fourth terms vanish and $\left\langle H \right\rangle_{{\text{m}}} \left( {\mathbf{x}} \right)$ becomes

$$\begin{aligned} \left\langle H \right\rangle_{{\text{m}}} \left( {\mathbf{x}} \right) & = {{\varvec{\upsigma}}}^{0} :{\mathbf{I}}_{d} :{{\varvec{\upsigma}}}^{0} + \left( {{{\varvec{\upsigma}}}^{0} - {{\varvec{\upsigma}}}_{{{\text{eff}}}}^{{\text{T}}} } \right):\left[ {\mathop \int \limits_{{\left| {{\varvec{x}} - {\varvec{x}}_{1} } \right| > a}}^{{}} \left( {{\mathbf{B^{\prime}}}:{\mathbf{I}}_{d} :{\mathbf{B}}} \right)P\left( {{\mathbf{x}}_{1} } \right)d{\mathbf{x}}_{1} } \right]:\left( {{{\varvec{\upsigma}}}^{0} - {{\varvec{\upsigma}}}_{{{\text{eff}}}}^{{\text{T}}} } \right) \\ & = {{\varvec{\upsigma}}}^{0} :{\mathbf{T}}^{0} :{{\varvec{\upsigma}}}^{0} - {{\varvec{\upsigma}}}^{0} :\left( {{\mathbf{T}}^{0} - {\mathbf{I}}_{d} } \right):{{\varvec{\upsigma}}}_{{{\text{eff}}}}^{{\text{T}}} - {{\varvec{\upsigma}}}_{{{\text{eff}}}}^{{\text{T}}} :\left( {{\mathbf{T}}^{0} - {\mathbf{I}}_{d} } \right):{{\varvec{\upsigma}}}^{0} + {{\varvec{\upsigma}}}_{{{\text{eff}}}}^{{\text{T}}} :\left( {{\mathbf{T}}^{0} - {\mathbf{I}}_{d} } \right):{{\varvec{\upsigma}}}_{{{\text{eff}}}}^{{\text{T}}} , \\ \end{aligned}$$

(8)

where ${\mathbf{B^{\prime}}} = - {\mathbf{C}}_{0} \cdot \left( {{\mathbf{D}}^{{\Omega }} - {\Delta }{\mathbf{C}}^{ - 1} } \right)^{ - 1} :{\varvec{D}}\left( {\mathbf{x}} \right) \cdot {\mathbf{C}}_{0}^{ - 1}$, ${\mathbf{I}}_{d}$ is the fourth rank deviatoric identity tensor $I_{dijkl} = \frac{1}{2}\left( {\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk} } \right) - \frac{1}{3}\delta_{ij} \delta_{kl}$. The first term of Eq. (8) denotes the pure elastoplastic effect, the second and third terms denote a coupling effect between mechanical and thermal loading, and the last term represents a pure thermal effect. The fourth-order tensor ${\mathbf{T}}^{0}$ is derived as

$$T_{ijkl}^{0} = T_{1}^{0} \delta_{ij} \delta_{kl} + T_{2}^{0} \left( {\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk} } \right),$$

(9)

where

$$T_{1}^{0} = - \frac{1}{3} + \frac{{\phi \beta \left[ {75\left( {1 - 2v_{0} } \right)^{2} \alpha + 2\left( {2 - 50v_{0} + 65v_{0}^{2} } \right)\beta } \right]}}{{2025\left( {1 - v_{0} } \right)^{2} \mu_{0}^{2} }},$$

(10)

$$T_{2}^{0} = \frac{1}{2} + \frac{{\phi \left( {23 - 50v_{0} + 35v_{0}^{2} } \right)\beta^{2} }}{{675\left( {1 - v_{0} } \right)^{2} \mu_{0}^{2} }},$$

(11)

$$\alpha = - \frac{{\lambda_{1} - \lambda_{0} }}{{2\left( {\mu_{1} - \mu_{0} } \right)\left[ {3\left( {\lambda_{1} - \lambda_{0} } \right) + 2\left( {\mu_{1} - \mu_{0} } \right)} \right]}} - \frac{1}{{30\mu_{0} \left( {1 - v_{0} } \right)}},$$

(12)

$$\beta = \frac{1}{{4\left( {\mu_{1} - \mu_{0} } \right)}} + \frac{{4 - 5v_{0} }}{{30\mu_{0} \left( {1 - v_{0} } \right)}},$$

(13)

$\mu_{0}$ and $\mu_{1}$ are the shear moduli of the matrix and the particle, respectively; $v_{0}$ and $v_{1}$ are the Poisson ratios of the matrix and the particle, respectively; $\lambda_{0}$ and $\lambda_{1}$ are the Lame constants of the matrix and the particle, respectively. When the volume fraction is high, the pairwise particle interaction should be considered. Based on the thermo-elastic analysis in the Appendix, the relationship between ${{\varvec{\upsigma}}}^{0}$ and $\left\langle {{\varvec{\upsigma}}} \right\rangle$ is

$${\varvec{\sigma}}^{0} = {\mathbf{P}}:\left\langle {{\varvec{\upsigma}}} \right\rangle + {\mathbf{M}},$$

(14)

where ${\mathbf{P}}$ is an fourth rank tensor $P_{ijkl} = P_{1} \delta_{ij} \delta_{kl} + P_{2} \left( {\delta_{il} \delta_{jk} + \delta_{ik} \delta_{jl} } \right)$ and ${\mathbf{M}}$ is a second rank tensor. Due to the existence of far field strain $\varepsilon_{,3}^{0}$, we cannot obtain the explicit form of ${\mathbf{P}}$ and ${\mathbf{M}}$. However, since Eq. (14) holds for each $i{\text{th}}$ layer $\left( {{{\varvec{\upsigma}}}^{0} } \right)^{i} = {\mathbf{P}}^{i} :\left\langle {{\varvec{\upsigma}}} \right\rangle^{i} + {\mathbf{M}}^{i}$. By applying the backward Euler’s method, we can numerically calculate the ${\mathbf{P}}^{i}$ and ${\mathbf{M}}^{i}$ in each individual layer. Then we have

$$\left\langle {{\varvec{\upsigma}}} \right\rangle^{i} = {\mathbf{H}}^{i} :\left( {{{\varvec{\upsigma}}}^{0} } \right)^{i} + {\mathbf{Q}}^{i} :\left( {{{\varvec{\upsigma}}}^{0} } \right)^{i - 1} + {\mathbf{S}}^{i} ,$$

(15)

where $i$ represents the $i{\text{th}}$ layer, and

$${\mathbf{H}}^{i} = \phi {\mathbf{C}}_{1} \cdot \left[ {\left( {{\mathbf{I}} - {\mathbf{D}}^{{\Omega }} \cdot {\Delta }{\mathbf{C}}} \right)^{ - 1} + \phi {\Delta }{\mathbf{C}}^{ - 1} \cdot {\mathbf{\mathcal{D}}} + \frac{N}{t}\phi_{,3} \Delta {\mathbf{C}}^{ - 1} {\mathbf{\mathcal{F}}}} \right] \cdot {\mathbf{C}}_{0}^{ - 1} + \left( {1 - \phi } \right){\mathbf{I}},$$

(16)

$${\mathbf{Q}}^{i} = - \frac{N}{t}\phi_{,3} \phi {\mathbf{C}}_{1} \cdot {\Delta }{\mathbf{C}}^{ - 1} \cdot {\mathbf{\mathcal{F}}} \cdot {\mathbf{C}}_{0}^{ - 1} ,$$

(17)

$${\mathbf{S}}^{i} = - \phi {\mathbf{C}}_{1} \left[ {\left( {{\mathbf{I}} - {\mathbf{D}}^{{\Omega }} \cdot {\Delta }{\mathbf{C}}} \right)^{ - 1} \left( {{\mathbf{D}}^{{\Omega }} {\mathbf{C}}_{0} + {\mathbf{I}}} \right) + \phi {\Delta }{\mathbf{C}}^{ - 1} \cdot {\mathbf{\mathcal{D}}}\left( {{\mathbf{I}} + {\Delta }{\mathbf{CC}}_{0} } \right)} \right]:{{\varvec{\upvarepsilon}}}^{{\text{T}}} ,$$

(18)

in which $N$ is the number of discrete layers and $t$ denotes the thickness of the FGMs. Thus, we have

$${\mathbf{P}}^{i} = \left( {{\mathbf{H}}^{i} } \right)^{ - 1} \left( {{\mathbf{I}} - {\mathbf{Q}}^{i} {\mathbf{P}}^{i - 1} } \right),$$

(19)

$${\mathbf{M}}^{i} = - \left( {{\mathbf{H}}^{i} } \right)^{ - 1} \left( {{\mathbf{Q}}^{i} {\mathbf{M}}^{i - 1} + {\mathbf{S}}^{i} } \right).$$

(20)

If the first layer of FGMs, i.e., $i = 0$, is 100% the matrix material, then ${\mathbf{P}}^{0}$ and ${\mathbf{M}}^{0}$ can be calculated explicitly. While the volume fraction of particle does not start from 0%, we can drop the ${\mathbf{Q}}{ }$ term in Eq. (15) to formulate the boundary condition, which means that the first layer ignores the gradation effect. Then the stress norm of matrix in the $i$th layer becomes

$$\left\langle {\mathbf{H}} \right\rangle_{{\text{m}}}^{i} \left( {\mathbf{x}} \right) = \left\langle {{\varvec{\upsigma}}} \right\rangle^{i} :{\overline{\mathbf{T}}}_{1}^{i} :\left\langle {{\varvec{\upsigma}}} \right\rangle^{i} + \left\langle {{\varvec{\upsigma}}} \right\rangle^{i} :{\overline{\mathbf{T}}}_{2}^{i} + {\overline{\mathbf{T}}}_{3}^{i} :\left\langle {{\varvec{\upsigma}}} \right\rangle^{i} + {\overline{\mathbf{T}}}_{4}^{i} ,$$

(21)

where ${\overline{\mathbf{T}}}_{1}^{i}$ represents the effect resulting from pure mechanical loading with

$${\overline{\mathbf{T}}}_{1}^{i} = {\mathbf{P}}^{i} \cdot \left( {{\mathbf{T}}^{0} } \right)^{i} \cdot {\mathbf{P}}^{i} ,$$

(22)

${\overline{\mathbf{T}}}_{2}^{i}$ and ${\overline{\mathbf{T}}}_{3}^{i}$ represent the coupling effect of the mechanical and thermal loading with

$${\overline{\mathbf{T}}}_{2}^{i} = {\mathbf{P}}^{i} \cdot \left( {{\mathbf{T}}^{0} } \right)^{i} :{\mathbf{M}}^{i} - {\mathbf{P}}^{i} \cdot \left( {\left( {{\mathbf{T}}^{0} } \right)^{i} - {\mathbf{I}}_{{\text{d}}} } \right):{{\varvec{\upsigma}}}_{{{\text{eff}}}}^{{\text{T}}} ,$$

(23)

$${\overline{\mathbf{T}}}_{3}^{i} = {\mathbf{M}}^{i} :\left( {{\mathbf{T}}^{0} } \right)^{i} \cdot {\mathbf{P}}^{i} - {{\varvec{\upsigma}}}_{{{\text{eff}}}}^{{\text{T}}} :\left( {\left( {{\mathbf{T}}^{0} } \right)^{i} - {\mathbf{I}}_{{\text{d}}} } \right) \cdot {\mathbf{P}}^{i} ,$$

(24)

${\overline{\mathbf{T}}}_{4}^{i}$ represents the effect of the pure thermal loading with

$$\begin{aligned} {\overline{\mathbf{T}}}_{4}^{i} & = {\mathbf{M}}^{i} :\left( {{\mathbf{T}}^{0} } \right)^{i} :{\mathbf{M}}^{i} + {{\varvec{\upsigma}}}_{{{\text{eff}}}}^{{\text{T}}} :\left( {\left( {{\mathbf{T}}^{0} } \right)^{i} - {\mathbf{I}}_{{\text{d}}} } \right):{{\varvec{\upsigma}}}_{{{\text{eff}}}}^{{\text{T}}} \\ & \quad - {\mathbf{M}}^{i} :\left( {\left( {{\mathbf{T}}^{0} } \right)^{i} - {\mathbf{I}}_{{\text{d}}} } \right):{{\varvec{\upsigma}}}_{{{\text{eff}}}}^{{\text{T}}} - {{\varvec{\upsigma}}}_{{{\text{eff}}}}^{{\text{T}}} :\left( {\left( {{\mathbf{T}}^{0} } \right)^{i} - {\mathbf{I}}_{{\text{d}}} } \right):{\mathbf{M}}^{i} . \\ \end{aligned}$$

(25)

Therefore, the yield function for FGMs can be expressed as

$$\overline{F}^{i} \left[ {\left\langle {{\varvec{\upsigma}}} \right\rangle^{i} ,\left( {e{_{{\text{m}}}^{p} }} \right)^{i} } \right] = \left( {1 - \phi } \right)\sqrt {\left\langle {\mathbf{H}} \right\rangle_{{\text{m}}}^{i} \left( {\mathbf{x}} \right)} - \sqrt{\frac{2}{3}} \left[ {\sigma_{{\text{Y}}} + h\left( {e_{{\text{m}}}^{ {\text{p}}^{i} } } \right)^{q} } \right].$$

(26)

Then, the plastic strain ${\dot{\overline{\varvec{\upvarepsilon}}}}^{p}$ and the effective plastic strain $\dot{e}^{p}$ in each individual layer at the macroscale can be obtained according to the associative flow rule, such as

$${\dot{\overline{\varvec{\upvarepsilon}}}}^{p} = \dot{\lambda }\frac{{\partial \overline{F}}}{{\partial {{\varvec{\upsigma}}}}} = \dot{\lambda }\left( {1 - \phi } \right)\frac{{{\overline{\mathbf{T}}}_{1} :\left\langle {{\varvec{\upsigma}}} \right\rangle + \frac{1}{2}\left( {{\overline{\mathbf{T}}}_{2} + {\overline{\mathbf{T}}}_{3} } \right)}}{{\sqrt {\left\langle {\mathbf{H}} \right\rangle_{{\text{m}}} \left( {\mathbf{x}} \right)} }}.$$

(27)

$$\dot{e}^{p} = \sqrt {\frac{2}{3}{\dot{\overline{\varvec{\upvarepsilon}}}}^{{\text{p}}} :{\dot{\overline{\varvec{\upvarepsilon}}}}^{{\text{p}}} } = \dot{\lambda }\left( {1 - \phi } \right)\sqrt {\frac{2}{3}\frac{{\left( {{\overline{\mathbf{T}}}_{1} :\left\langle {{\varvec{\upsigma}}} \right\rangle + \frac{1}{2}\left( {{\overline{\mathbf{T}}}_{2} + {\overline{\mathbf{T}}}_{3} } \right)} \right)}}{{\left\langle {\mathbf{H}} \right\rangle_{{\text{m}}} \left( {\mathbf{x}} \right)}}} .$$

(28)

The effective plastic strain of the matrix phase is

$$\dot{e}_{m}^{p} = \frac{{\dot{e}^{p} }}{1 - \phi } = \dot{\lambda }\sqrt {\frac{2}{3}\frac{{\left( {{\overline{\mathbf{T}}}_{1} :\left\langle {{\varvec{\upsigma}}} \right\rangle + \frac{1}{2}\left( {{\overline{\mathbf{T}}}_{2} + {\overline{\mathbf{T}}}_{3} } \right)} \right)}}{{\left\langle {\mathbf{H}} \right\rangle_{{\text{m}}} \left( {\mathbf{x}} \right)}}} .$$

(29)

The macroscopic total strain can be expressed with the particle strain and the matrix strain as

$${{\varvec{\upvarepsilon}}} = \left( {1 - \phi } \right){{\varvec{\upvarepsilon}}}_{m} + \phi {{\varvec{\upvarepsilon}}}_{p} ,$$

(30)

where the matrix strain ${{\varvec{\upvarepsilon}}}^{0}$ includes the elastic strain and the plastic strain with ${{\varvec{\upvarepsilon}}}_{m} = {{\varvec{\upvarepsilon}}}_{m}^{e} + {{\varvec{\upvarepsilon}}}_{m}^{p}$; the particle strain ${{\varvec{\upvarepsilon}}}^{1}$ only includes its elastic part based on the assumption that ${{\varvec{\upvarepsilon}}}_{p} = {{\varvec{\upvarepsilon}}}_{p}^{e}$, which is stated before.

In the algorithm, we know the macroscopic overall stress $\langle{{\varvec{\upsigma}}}\rangle$, and the process of solving the strain $\langle{{\varvec{\upvarepsilon}}}\rangle$ is divided into two parts, the first part obtains the elastic strain ${{\varvec{\upvarepsilon}}}^{e}$, the second part determines whether plastic strain ${{\varvec{\upvarepsilon}}}^{p}$ occurs and calculates the plastic strain when it occurs. After $\langle{{\varvec{\upsigma}}}\rangle$ is known, we can calculate the matrix elastic strain $\langle{{\varvec{\upvarepsilon}}}\rangle^{0}$ from Eqs. (42), (45), (47), (48). After that, the elastic strain ${{\varvec{\upvarepsilon}}}^{e}$ can be obtained from Eqs. (42), (46).

As for the second part, if the macroscopic stress $\langle{{\varvec{\upsigma}}}\rangle$ is known, the stress norm of matrix $H_{{\text{m}}}$ can be calculated by Eq. (21). Thus, the plastic strain can be computed when the yield function Eq. (26) is larger than zero as

$$\overline{F}^{i} \left[ {\left\langle {{\varvec{\upsigma}}} \right\rangle^{i} ,\left( {e_{{\text{m}}}^{{\text{p}}} } \right)^{i} } \right] = \left( {1 - \phi } \right)\sqrt {\left\langle {\mathbf{H}} \right\rangle_{{\text{m}}}^{i} \left( {\mathbf{x}} \right)} - \sqrt{\frac{2}{3}} \left[ {\sigma_{{\text{Y}}} + h\left( {e{_{{\text{m}}}^{{\text{p}}}}^{i} } \right)^{q} } \right] > 0.$$

(31)

Then, the material parameters are updated, and the corresponding plastic strain ${\dot{\overline{\varvec{\upvarepsilon}}}}^{p}$ and the effective plastic strain of the matrix phase $\dot{e}_{m}^{p}$. By substituting the updated parameters into the yield function in each loading step, the thermo-elasto-plastic behavior of FGMs can be numerically predicted. To descript the algorithm clearly, the numerical steps are shown in Fig. 2.

Fig. 2

Diagram illustrating the different steps of the numerical algorithm

3 Model validation

To demonstrate the capability of the proposed model, comparison to the existed methodology and the experiments are necessary. Due to its complex and coupling effects, there is neither available theoretical model nor the experiment data of thermo-elasto-plastic behavior of FGMs published in the literature. Thus, we applied four cases to validate our proposed model. Firstly, we compare the proposed model with elastoplastic theory for uniform composites and FGMs by ignoring the thermal term. Secondly, the thermoelastic behavior of FGMs is compared with the existed classical theoretical model and the corresponding experiments. Thirdly, our derived model with temperature changes is compared with the experiments for pure HDPE. Finally, we validate the present model with experimental data for FGMs samples.

3.1 Verification with elastoplastic model

When ignoring the thermal effect and particle gradient, our derived model can be degraded to the elastoplastic model for uniform composites. In this subsection, we use the existed theories of elastoplastic model for uniform composites [20], elastoplastic model for FGMs [52], and the proposed thermo-elasto-plastic model for FGMs, to predict the elastoplastic behavior of particle-reinforced metal matrix composites (PRMMC) and then compare those results with the experiment data [47].

In the experiment of reference [47], PRMMC is composed of SiC particles and Al/4Mg matrix, where the material properties of SiC and Al/4Mg are: $E_{{{\text{Al}}/4{\text{Mg}}}} = 75\,{\text{GPa}}$,$v_{{{\text{Al}}/4{\text{Mg}}}} = 0.33$; $E_{{{\text{SiC}}}} = 420\,{\text{GPa}}$; $v_{{{\text{SiC}}}} = 0.17$; $\sigma_{{\text{Y}}} = 46\,{\text{MPa}}$; $h = 320\,{\text{MPa}}$ and $q = 0.265$. The volume fraction of SiC is set as $\phi = 0{\text{\% }},{ }17{\text{\% }},{ }30{\text{\% }},{ }$ and 48%, respectively. Figure 3 shows the comparisons of the experimental results [47] and theoretical predictions of elastoplastic model for uniform composites [20], FGMs [52] and the present method. The solid line is the theoretical prediction based on thermo-elasto-plastic model of FGMs, the green circle represents the result of elastoplastic model of uniform composites, the red asterisk represents the result of elastoplastic model of FGMs, and the blue stars are the experimental results from Yang’s experiment. Figure 2 suggests that our proposed model is consistent with the former models [20, 52] and the available experimental data [47]. In addition, a minor deviation between experiments and theoretical predictions appears at φ = 30%, probably because of the imperfect particle bonding or the influence of residual stresses.

Fig. 3

Theoretical prediction and experimental data of plastic deformation of uniaxial compression. (EP: elastoplastic; TEP: thermo-elasto-plastic (present model))

3.2 Verification with thermo-elastic model

In the previous subsection, the present model is verified with the elastoplastic model. In this subsection, we compare the present model with eliminating the plastic effect of FGMs [49] with the corresponding experiment results [18].

In the experimental study, FGMs were consisted of Mo particles and continuous SiO₂ matrix. The material properties are followed the reference [18]. For matrix phase: $E_{{{\text{SiO}}_{2} }} = 80.4\,{\text{GPa}};\;v_{{{\text{SiO}}_{2} }} = 0.18; \;\alpha_{{{\text{SiO}}_{2} }} = 0.54 \times 10^{ - 6} \,{\text{C}}^{ - 1}$; for particle phase:$E_{{{\text{Mo}}}} = 324\,{\text{GPa}};\;v_{{{\text{Mo}}}} = 0.31$; $\alpha_{{{\text{Mo}}}} = 5.1 \times 10^{ - 6} {\text{C}}^{ - 1}$. The graded distribution of Mo particles is approximated to $\phi \left( {X_{3} } \right) = 0.2 \left( {e^{{ - 28\left( {X_{3} - 0.085} \right)^{2} }} - 0.1X_{3} + 0.1} \right).$ Fig. 4a shows the comparisons of the predicted CTE distribution along the gradation direction with theoretical prediction and the experimental data. The solid line is the effective CTE distribution prediction based on thermo-elasto-plastic model of FGMs, the red circle represents the prediction of thermoelastic model of FGMs [49], the blue star represents experimental results [18]. The effective CTE varies with particle volume fraction, and increases to the peak point at $X_{3} \approx 0.085$, then convergent to a constant value. The proposed model provides a very good agreement with the Yin’s theoretical model. However, both the two theoretical models underestimate the experimental results at large volume fractions (small values of $X_{3}$). This is mainly caused by the truth that Mo particles are not perfectly spherical with identical size.

Fig. 4

Comparison with the existed model and experimental data: a effective CTE of Mo/SiO₂ FGMs; b normalized effective CTE affected by different CTE ratio. (TEP: thermo-elasto-plastic; TE: thermo-elastic)

Figure 4b compares the proposed model with Yin’s model for the effect of the phase material properties on the effective CTE for FGMs. To simplify the model, we assume a linear volume fraction distribution $\phi \left( {X_{3} } \right) = X_{3} /t$, $v_{1} = v_{0} = 0.3$, $E_{1} /E_{0} = 10$, where $t$ is the thickness of the FGMs along the gradation direction. The theoretical prediction of present theory is shown as the solid line, the circle represents the result from Yin’s model. The proposed model fits well with the Yin’s model. When $\alpha_{1} /\alpha_{0} = 1$, the effective CTE is a constant and no thermal stress is induced. When $\alpha_{1} /\alpha_{0} = 10$, the effective CTE will increase as volume fraction increases and vice versa.

3.3 Validation with pure HDPE experiments

In Sects. 3.1 and 3.2, we compared the present model with the existed elastoplastic model, thermoelastic model and the corresponding experiments, which showed out very good agreement. In this subsection, we consider the effect of temperature changes. However, due to the limitation of the experimental results for the thermo-elasto-plastic behavior of FGMs, only that for the pure HDPE is considered.

Figure 5 illustrates theoretical prediction and experimental data of the thermo-elasto-plastic behavior for pure HDPE under different temperature conditions, where the experimental data in Fig. 5a, b are from different literatures published in studies [2, 28], respectively. In Fig. 5a, the initial parameters are selected when the temperature is 20 °C, where the Young’s modulus of the experimental specimen is 504.7 MPa, the yield stress is 6.6 MPa, the CTE is $70 \times 10^{ - 6}$/°C, $h = 35.5$, and $q = 0.48$. When the temperature changes at 20 °C, 60 °C and 100 °C, the thermo-elasto-plastic behavior of HDPE was exhibited. Similarly, Fig. 5b shows the thermo-elasto-plastic behavior curves of HDPE at 25 °C, 53 °C, and 82 °C, where the initial parameters (25 °C) of the specimen are as follows: the Young’s modulus is 722.4 MPa, the yield stress is 8.2 MPa, the thermal expansion coefficient is $70 \times 10^{ - 6}$/°C, $h = 34.0$, and $q = 0.36$. It can be seen that our proposed model can predict both of the experimental data very well, which proves that our present model can simulate the thermo-elasto-plastic behavior of materials at different temperatures.

Fig. 5

Comparisons of theoretical prediction and experimental results of pure HDPE under different temperature conditions a experiment data from Mahl et al. [28]; b experiment data from Amjadi and Fatemi [2]

3.4 Validation with FGMs experiments

The validation is performed with experiments in recent researches [6, 7, 51], which develop a BIPVT roofing panel with FGMs as an essential component. Vibration methods were used to make the FGMs from aluminum powder and HDPE. It is desired that the aluminum volume fraction is 0% to 50% along the thickness of the FGMs. In experiment, the volume ratio of Al to HDPE is 1:3, which the details are presented in reference [6]. As shown in Fig. 6 we compare this model with the experimental data of uniaxial compression tests of FGMs specimens, where the particle volume fraction is 23.42%, and the particle distribution form is $\phi \left( {X_{3} } \right) = - 0.5169\left( {X_{3} /t} \right)^{2} + 0.813\left( {X_{3} /t} \right)$ [52]. Since the temperature condition of experiment is not clear in reference [52], in order to clarify the thermal effect, different temperature changes as ${\text{d}}T = 0,{ }5,{ }10$ °C, are used during the comparison. It is worth noting that when ${\text{d}}T = 5$ °C, the prediction fits the experimental results very well.

Fig. 6

Comparison of theoretical prediction with experimental results of FGMs samples [52] under different temperature conditions

4 Parameter sensitivity analysis

4.1 Effect of particle distribution under temperature changes

Temperature is an important factor affecting the thermo-elasto-plastic behavior of FGMs. In this case, the overall particle volume fraction is set as 23.42%, which is identical to that in Sect. 3.4. However, different particle distribution functions (i.e., uniform, linear, quadratic and sigmoid) are applied. It is worth mentioning that the sigmoid distribution function can simulate the phenomenon of particle deposition. The initial (room temperature) material parameters and loading condition are as follows: for matrix phase: $E_{0} = 550\,{\text{MPa}}$, $v_{0} = 0.3$, $\alpha_{0} = 180 \times 10^{ - 6}$/°C; particle phase:${ }E_{1} = 70\,{\text{GPa}}$, $v_{1} = 0.33$, $\alpha_{1} = 24 \times 10^{ - 6}$/°C; and the hardening parameters for the matrix phase are $\sigma_{{\text{Y}}} = 17.6\,{\text{MPa}}$, $h = 67.5\,{\text{MPa}}$ and $q = 0.5444$.

To investigate the influence of different particle distribution on the overall effective thermo-elasto-plastic behavior of FGMs under different temperature changes, Fig. 7 illustrates the stress–strain curves of FGMs assuming the particle distributions are: (a) linear and sigmoid, (b) uniform and quadratic; the distribution schematic diagrams are displayed in Fig. 8. We can see that under the same temperature changes and particle distributions, the mechanical behaviors at elastic stage are almost the same, while those at plastic stage are different, especially for the uniform distributed composites. When the temperature changes, the overall effective behavior is affected evidently throughout both the elastic and plastic stage. Specifically, the detailed comparison of the offset yield stress $\sigma_{0.2}$, the overall effective Young’s modulus $E_{{{\text{overall}}}}$, and the corresponding total strain $\varepsilon_{0.2}$ with different particle distributions are given in Table 1. It is seen that the overall mechanical behaviors are strongly affected by the temperature changes, indicating that the temperature condition has a strong effect to the mechanical behavior of the FGMs. The maximum difference is larger than 77% for $E_{{{\text{overall}}}}$ and about 300% for $\varepsilon_{0.2}$ when the ${\text{d}}T = 30$, and those will increase with the increasing of the temperature changes. In addition, under the same temperature condition, the overall effective mechanical behavior is slightly affected by the particle distribution. The maximum difference is less than 6% for $E_{{{\text{overall}}}}$ and about 30% for $\varepsilon_{0.2}$ when the distributions are uniform and sigmoid, respectively. It is concluded that the temperature changes will produce big effect on mechanical behaviors of FGMs, even under the same particle distribution.

Fig. 7

Stress–strain curves of different particle distribution under different temperature changes: a linear and simoid; b uniform and quadratic

Fig. 8

The schematic diagram of particle distribution. a Uniform; b linear; c quadratic; d sigmoid; e particle distribution function

Table 1 Comparison of $E_{{{\text{overall}}}}$, $\sigma_{0.2}$, and $\varepsilon_{0.2}$ under different particle distribution, such as uniform, linear, quadratic and sigmoid, at different temperature conditions (take the corresponding ${\text{d}}T = 0$ as reference)

4.2 Effect of volume fraction under temperature changes

In a general way, volume fraction is one of the main factors that effects the FGMs overall properties. In this case, we study the overall mechanical behavior of FGMs with different volume fraction under different temperature conditions. For convenience, the material parameters and loading condition are same as those used in Sect. 4.1. The overall mechanical behavior of FGMs with linear distribution and sigmoid distribution are shown in Figs. 9 and 10, respectively, where the volume fractions are selected as 5%, 10% and 25%, and the temperature changes ${\text{d}}T = 0, 5, 10, 20$. It is seen that under the same temperature condition, as the volume fraction increasing, the overall effective Young’s modulus goes larger, and the plastic strain comes out earlier. Specifically, the detailed comparison of the offset yield stress $\sigma_{0.2}$, the overall effective Young’s modulus $E_{{{\text{overall}}}}$, and the corresponding total strain $\varepsilon_{0.2}$ with different volume fractions are given in Table 2. We can see that under the same volume fraction, temperature changes strongly affect the maximum difference of $E_{{{\text{overall}}}}$ and $\varepsilon_{0.2}$. Specifically, $E_{{{\text{overall}}}}$ and $\varepsilon_{0.2}$ will decline about 3.5% and 10% for each degree rise in temperature, respectively. In addition, under the same temperature condition, the higher the volume fraction is, the larger the $E_{{{\text{overall}}}}$ is. The offset yield stress $\sigma_{0.2}$ does not change obviously with the volume fraction and temperature changes, indicating that $\sigma_{0.2}$ is independent to the overall particle volume fraction and temperature changes. It is also worth noting that, as shown in Fig. 10b, when the volume fraction is larger than 15%, it can be found that the overall mechanical behavior of the FGMs exhibit similar performance (red and blue solid line). This phenomenon indicating that for a delaminated composite, under some fixed temperature condition, when the volume fractions is large enough, it will not generate big difference in the mechanical behavior.

Fig. 9

Stress–strain curves of FGMs of different linear distribution functions with different temperature changes: a dT = 0 °C, 10 °C; b dT = 5 °C, 20 °C

Fig. 10

Stress–strain curves of FGMs of different sigmoid distribution functions with different temperature changes: a dT = 5 °C, 20 °C; b dT = 0 °C, 10 °C

Table 2 Comparison of $E_{{{\text{overall}}}}$, $\sigma_{0.2}$, and $\varepsilon_{0.2}$ under different volume fraction with linear distribution at different temperature conditions (take the corresponding ${\text{d}}T = 0$ as reference)

4.3 Effect of material properties under temperature changes

In this subsection, the effect of material properties on the overall effective mechanical behavior of FGMs are investigated. we firstly studied the effect of CTE on the overall mechanical behavior of FGMs. After that, the offset yield stress $\sigma_{0.2}$, the overall effective Young’s modulus $E_{{{\text{overall}}}}$, and the corresponding total strain $\varepsilon_{0.2}$ vary with temperature changes are studied with considering the different volume fractions and particle distributions, respectively.

In Fig. 11, the effect of CTE ratio on the overall mechanical behavior of FGMs is illustrated. The material parameters and loading condition are same as those used in Sect. 4.1, except the CTE of the matrix are set as $\alpha_{0} = 180 \times 10^{ - 6}$ °C⁻¹, and the CTEs of particles $\alpha_{1}$ are 1, 5 and 10 times of $\alpha_{0}$, respectively. In this case, we employ the quadratic particle distribution for numerical simulation. When ${\text{d}}T = 0$ °C, the ratio of CTE has no effect on the elastoplastic behavior of FGMs model in Fig. 11a. The increase of CTE ratio and temperature changes will lead to the decrease of elastic modulus. Meanwhile, it is worth noting that similar overall effective mechanical behavior of FGMs can be achieved by adjusting the CTE ratio and temperature condition, as shown by the blue solid line and the black dash dot line in Fig. 11b.

Fig. 11

Stress–strain curves of FGMs considering CTE contrast ratio of two phases with different temperature changes: a dT = 0 °C, 10 °C; b dT = 5 °C, 20 °C

4.4 Effect of particles interaction

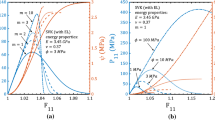
As shown in Fig. 12, we studied the influence of particles interaction and volume fraction on the stress–strain curve of FGMs, where the particles are linearly distributed in the matrix. It is worth noting that the interaction between particles has strongly affect the mechanical behavior of FGMs, especially the plastic behavior. This phenomenon is particularly pronounced when the volume fraction is increased. When the volume fraction is low (such as 5%), the distance between two particles is far enough, so that the interaction between particles can be ignored. When the volume fraction is high (such as 25%), the distance between particles is shortened, where the particle interaction strongly affects the plastic behavior.

Fig. 12

Stress–strain curves of FGMs considering the effect of particle interaction at different volume fractions

5 Conclusions

In this paper, the micromechanics-based modeling is exhibited to predict the effective thermo-elasto-plastic behavior of FGMs with considering the pairwise interaction between particles. At the microscopic scale, the graded microstructures of the FGMs are represented by employing a special representative volume element. By considering the coupling effect of the far field stress and the overall disturbances from all particles over the RVE, the effective stress norm of the matrix phase is constructed and then applied to the yield function of the FGMs to predict the overall thermo-elasto-plastic behavior of FGMs. Then, the proposed model is compared with the existed theoretical models and experimental data and show out great agreements. Finally, the effect of particle distributions, volume fraction, and material properties combined with temperature changes on the overall effective thermo-elasto-plastic behavior of FMGs are studied. To sum up, some significant conclusions are listed as:

• 1. The temperature changes dominate the overall effective thermo-elasto-plastic behavior of the FGMs, compared with the particle volume fraction and the particle distribution.

• 2. Under the same temperature condition, particle volume fraction strongly affects the overall effective mechanical behavior of FGMs compared with the particle distribution.

• 3. For FGMs with different particle distributions, when the volume fraction is beyond 15%, the sigmoid distributable FGMs are insensitive to the volume fraction while other distributable FGMs keep sensitive.

• 4. Similar overall effective mechanical behavior of FGMs can be achieved by adjusting the parameters like material properties, volume fraction and temperature condition.

To sum up, this paper micromechanically constructs a thermo-elasto-plastic model of FGMs and discusses the effect of the temperature changes, particle distribution, volume fractions and material parameters on the effective properties of FGMs. All the particles are assumed as the sphere and with the same size; however, it is also important to further study the local behavior of particles with arbitrary shape, which is more likely happened in the industrial application.

Appendix

Due to the existed of the particles (which is also called inhomogeneities), the local strain field ${{\varvec{\upvarepsilon}}}$ is equal to the superposition of the far field strain ${{\varvec{\upvarepsilon}}}^{0}$ and the disturbed strain ${\varvec{\upvarepsilon}}^{\prime}$, which is given as

$${{\varvec{\upvarepsilon}}} = {{\varvec{\upvarepsilon}}}^{0} + {\varvec{\upvarepsilon}}^{\prime},$$

(32)

where the far field strain ${{\varvec{\upvarepsilon}}}^{0} = \left( {{\mathbf{C}}_{0} } \right)^{ - 1} :{{\varvec{\upsigma}}}^{0} + \alpha_{0} T{{\varvec{\updelta}}}$ is caused by the external far field stress ${{\varvec{\upsigma}}}^{0}$ and the temperature change $T$. In Eq. (42), ${\mathbf{C}}_{0}$ is the elastic material coefficients tensor of the matrix; $\alpha_{0}$ is the CTE of the matrix; ${{\varvec{\updelta}}}$ is the Kronecker Delta tensor. The disturbed strain ${\varvec{\upvarepsilon}}^{\prime}$ is caused by the material mismatch. Using the Green’s function technique, the disturbed strain ${\varvec{\upvarepsilon}}^{\prime}$ is given as

$${\varvec{\upvarepsilon}}^{\prime} = - \mathop \int \limits_{{{\varvec{\Omega}}}}^{{}} {\mathbf{G}}\left( {{\mathbf{x}},{\mathbf{x^{\prime}}}} \right) \cdot {\mathbf{C}}_{0} :\left[ {{{\varvec{\upvarepsilon}}}^{*} \left( {{\mathbf{x^{\prime}}}} \right) + {{\varvec{\upvarepsilon}}}^{{\text{T}}} } \right]{\mathbf{dx^{\prime}}} = - {\mathbf{D}}^{{\Omega }} :{\mathbf{C}}_{0} :\left[ {{{\varvec{\upvarepsilon}}}^{*} \left( {{\mathbf{x^{\prime}}}} \right) + {{\varvec{\upvarepsilon}}}^{{\text{T}}} } \right],$$

(33)

where “$\cdot$” means the tensor contraction between two fourth-rank tensors, “$:$” represents the tensor contraction between fourth-rank and second rank tensors; ${{\varvec{\upvarepsilon}}}^{*}$ is the induced virtual elastic eigenstrain to refer the material mismatch of the elastic field; ${{\varvec{\upvarepsilon}}}^{{\text{T}}} = \left( {\alpha_{1} - \alpha_{0} } \right)T{{\varvec{\updelta}}}$ is the thermal eigenstrain caused by the thermal properties mismatch, where $\alpha_{1}$ is the CTE of the particle; ${\mathbf{G}}\left( {{\mathbf{x}},{\mathbf{x}}^{\prime}} \right)$ is the modified Green’s function; ${{\varvec{\Omega}}}$ accounts for the certain particle domain; the fourth rank tensor ${\mathbf{D}}^{{{\varvec{\Omega}}}}$ which is the integral of ${\mathbf{G}}\left( {{\mathbf{x}},{\mathbf{x}}^{\prime}} \right)$ over the spherical particle domain, which can be found in Yin’s work (2007). According to EIM and equivalent condition in particle domain ${{\varvec{\Omega}}}$, the following equation is obtained as

$${\mathbf{C}}_{1} :\left[ {{{\varvec{\upvarepsilon}}}^{0} + {\varvec{\upvarepsilon}}^{\prime} - \alpha_{1} T{{\varvec{\updelta}}}} \right] = {\mathbf{C}}_{0} :\left[ {{{\varvec{\upvarepsilon}}}^{0} + {\varvec{\upvarepsilon}}^{\prime} - \alpha_{1} T{{\varvec{\updelta}}} - {{\varvec{\upvarepsilon}}}^{*} } \right],$$

(34)

where ${\mathbf{C}}_{1}$ is the elastic material coefficients tensor of the particle. Substituting Eq. (33) into Eq. (34), the eigenstrain ${{\varvec{\upvarepsilon}}}^{*}$ is derived as

$${{\varvec{\upvarepsilon}}}^{*} = {\mathbf{C}}_{0}^{ - 1} \cdot \left( {{\mathbf{D}}^{{\Omega }} - {\Delta }{\mathbf{C}}^{ - 1} } \right)^{ - 1} :\left( {{{\varvec{\upvarepsilon}}}^{0} - \alpha_{1} T{{\varvec{\updelta}}} - {\mathbf{D}}^{{\Omega }} \cdot {\mathbf{C}}_{0} :{{\varvec{\upvarepsilon}}}^{{\text{T}}} } \right),$$

(35)

where ${\Delta }{\mathbf{C}} = {\mathbf{C}}_{1} - {\mathbf{C}}_{0}$ is the stiffness difference.

By substituting the disturbed strain ${\varvec{\upvarepsilon}}^{\prime}$ and eigenstrain ${{\varvec{\upvarepsilon}}}^{*}$ in Eq. (33) and Eq. (35) into Eq. (32), the strain field in the particle domain induced by a single particle can be obtained as

$${\overline{\varvec{\upvarepsilon}}} = \alpha_{1} T{{\varvec{\updelta}}} + \left( {{\mathbf{I}} - {\mathbf{D}}^{{\Omega }} \cdot {\Delta }{\mathbf{C}}} \right)^{ - 1} :\left( {{{\varvec{\upvarepsilon}}}^{0} - \alpha_{1} T{{\varvec{\updelta}}} - {\mathbf{D}}^{{\Omega }} \cdot {\mathbf{C}}_{0} :{{\varvec{\upvarepsilon}}}^{{\text{T}}} } \right),$$

(36)

where ${\mathbf{I}}$ is the standard fourth rank unit tensor, the overbar of ${\overline{\varvec{\upvarepsilon}}}$ represents the presence of only one particle in the infinite matrix domain. To conduct the pairwise interaction, Yin et al. [49] obtained the averaged strain field induced by two particles as

$$\begin{aligned} \overline{\overline{{{\varvec{\upvarepsilon}}}}} & = \alpha_{1} T{{\varvec{\updelta}}} + \left\{ {{\mathbf{I}} - \left[ {{\mathbf{D}}^{{\Omega }} + {\mathbf{D}}\left( {{\mathbf{x}}_{1} } \right)} \right] \cdot {\Delta }{\mathbf{C}}} \right\}^{ - 1} \\ & \quad :\left\{ {{{\varvec{\upvarepsilon}}}^{0} - \alpha_{1} T{{\varvec{\updelta}}} - \left[ {{\mathbf{D}}^{{\Omega }} + {\mathbf{D}}\left( {{\mathbf{x}}_{1} } \right)} \right] \cdot {\mathbf{C}}_{0} :{{\varvec{\upvarepsilon}}}^{{\text{T}}} } \right\} + O\left( {\rho^{8} } \right). \\ \end{aligned}$$

(37)

The double overbar indicates the presence of two particles in the infinite matrix domain, $\overline{\overline{{{\varvec{\upvarepsilon}}}}}$ is uniform strain inside the particle domain considering the interaction of the other particles. Subtracting Eq. (36) from Eq. (37), the average interaction between two particles is

$${\mathbf{d}}\left( {0,{\mathbf{x}}_{1} } \right) = \overline{\overline{{{\varvec{\upvarepsilon}}}}} - {\overline{\varvec{\upvarepsilon}}} = {\Delta }{\mathbf{C}}^{ - 1} \cdot {\mathbf{L}}\left( {0,{\mathbf{x}}_{1} } \right):\left( {{{\varvec{\upvarepsilon}}}^{0} - \alpha_{1} T{{\varvec{\updelta}}} - {\Delta }{\mathbf{C}}^{ - 1} \cdot {\mathbf{C}}_{0} :{{\varvec{\upvarepsilon}}}^{{\text{T}}} } \right) + O\left( {\rho^{8} } \right),$$

(38)

where ${\mathbf{L}}\left( {0,{\mathbf{x}}_{1} } \right)$ is the particle pairwise interaction tensor as

$${\mathbf{L}}\left( {0,{\mathbf{x}}_{1} } \right) = \left[ {\Delta {\mathbf{C}}^{ - 1} - {\mathbf{D}}^{{\Omega }} - {\mathbf{D}}\left( {{\mathbf{x}}_{1} } \right)} \right]^{ - 1} - \left( {\Delta {\mathbf{C}}^{ - 1} - {\mathbf{D}}^{{\Omega }} } \right)^{ - 1} .$$

(39)

When there are multiple particles $P_{i} { }\left( {i = 2,3, \ldots } \right)$, each of them will generate an additional interaction on the central particle ${\Omega }_{0}$ as Eq. (38) dominated. Thus, the average strain of the central particle considering pairwise particle interaction is

$$\left\langle {{\varvec{\upvarepsilon}}} \right\rangle^{1} \left( 0 \right) = \alpha_{1} T{{\varvec{\updelta}}} + \left( {{\mathbf{I}} - {\mathbf{D}}^{{\Omega }} \cdot {\Delta }{\mathbf{C}}} \right)^{ - 1} :\left[ {\left\langle {{\varvec{\upvarepsilon}}} \right\rangle^{0} \left( 0 \right) - \alpha_{1} T{{\varvec{\updelta}}} - {\mathbf{D}}^{{\Omega }} \cdot {\mathbf{C}}_{0} :{{\varvec{\upvarepsilon}}}^{{\text{T}}} } \right] + \mathop \sum \limits_{i = 1}^{\infty } {\mathbf{d}}\left( {0,{\mathbf{x}}_{i} } \right),$$

(40)

where $\left\langle {*} \right\rangle$ denotes the volume average over the material phase. By integrating pairwise interaction over all particles, the total particle interaction is obtained as

$$\begin{aligned} \left\langle {\mathbf{d}} \right\rangle \left( 0 \right) & = \mathop \sum \limits_{i = 1}^{\infty } {\Delta }{\mathbf{C}}^{ - 1} \cdot {\mathbf{L}}\left( {0,{\mathbf{x}}_{i} } \right):\left[ {\left\langle {{\varvec{\upvarepsilon}}} \right\rangle^{0} \left( {x_{3}^{i} } \right) - \alpha_{1} T{{\varvec{\updelta}}} - {\Delta }{\mathbf{C}}^{ - 1} \cdot {\mathbf{C}}_{0} :{{\varvec{\upvarepsilon}}}^{{\text{T}}} } \right] \\ & = \mathop \int \limits_{D}^{{}} P\left( {{\mathbf{x}}{|}0} \right){\Delta }{\mathbf{C}}^{ - 1} \cdot {\mathbf{L}}\left( {0,{\mathbf{x}}} \right):\left[ {\left\langle {{\varvec{\upvarepsilon}}} \right\rangle^{0} \left( 0 \right) + \left\langle {{\varvec{\upvarepsilon}}} \right\rangle_{,3}^{0} \left( 0 \right)x_{3} - \alpha_{1} T{{\varvec{\updelta}}} - {\Delta }{\mathbf{C}}^{ - 1} \cdot {\mathbf{C}}_{0} :{{\varvec{\upvarepsilon}}}^{{\text{T}}} } \right]d{\mathbf{x}}, \\ \end{aligned}$$

(41)

where $\left\langle {{\varvec{\upvarepsilon}}} \right\rangle^{0} \left( {x_{3}^{i} } \right) = \left\langle {{\varvec{\upvarepsilon}}} \right\rangle^{0} \left( 0 \right) + \left\langle {{\varvec{\upvarepsilon}}} \right\rangle_{,3}^{0} \left( 0 \right)x_{3}$. And $P\left( {{\mathbf{x}}{|}0} \right) = \frac{3g\left( x \right)}{{4\pi a^{3} }}\left[ {\phi \left( {X_{3} } \right) + e^{{ - \frac{{\mathbf{x}}}{\delta }}} \phi_{,3} \left( {X_{3} } \right)x_{3} } \right]$ is the particle number density function, where g(x) = 1 to insure the density of local field is unchanged [49], the $X_{3}$ denotes the gradation direction, $\phi \left( {X_{3} } \right)$ is the average volume fraction of particle at $X_{3}$, $\delta = \frac{e}{{\phi_{,3} \left( {X_{3}^{0} } \right)}}{\text{min}}\left( {\phi ,\phi^{c} - \phi } \right)$ denotes the attenuating rate of the gradation of the particle volume fraction in the far field, and $\phi^{c}$ represents the maximum volume fraction of particles. Thus, the effect of particle distribution at the microscale can be integrated to reflect the effective material properties at the macroscale. Specifically, by plugging Eq. (41) into Eq. (40), the average particle strain considering pairwise interaction at $X_{1} - X_{2}$ layer along the graded direction is obtained as

$$\begin{aligned} \left\langle {\upvarepsilon } \right\rangle^{1} \left( {{\text{X}}_{3} } \right) & = {\upalpha }_{1} {\text{T}}\updelta + \left( {{\text{I}} - {\text{D}}^{{\Omega }} \cdot \Delta {\text{C}}} \right)^{ - 1} :\left[ {\left\langle {\upvarepsilon } \right\rangle^{0} \left( {{\text{X}}_{3} } \right) - {\upalpha }_{1} {\text{T}}\updelta - {\text{D}}^{{\Omega }} \cdot {\text{C}}_{0} :{\upvarepsilon }^{{\text{T}}} } \right] \\ & \quad + \phi \Delta {\text{C}}^{ - 1} \cdot {\mathbf{\mathcal{D}}}:\left[ {\left\langle {\upvarepsilon } \right\rangle^{0} \left( {{\text{X}}_{3} } \right) - {\upalpha }_{1} {\text{T}}\updelta - \Delta {\text{C}}^{ - 1} \cdot {\text{C}}_{0} :{\upvarepsilon }^{{\text{T}}} } \right] \\ & \quad + \phi_{,3} \Delta {\text{C}}^{ - 1} \cdot {\mathbf{\mathcal{F}}}:\left\langle {\upvarepsilon } \right\rangle_{,3}^{0} \left( {{\text{X}}_{3} } \right), \\ \end{aligned}$$

(42)

where tensor ${\mathbf{\mathcal{D}}}$ represents the pairwise interaction, and tensor ${\mathbf{\mathcal{F}}}$ addresses the coupling effect of layers along the $X_{3}$ direction [49].

$${\mathbf{\mathcal{D}}} = \mathop \int \limits_{D}^{{}} \frac{3}{{4\pi a^{3} }}{\mathbf{L}}\left( {0,{\mathbf{x}}} \right)d{\mathbf{x}},$$

(43)

$${\mathbf{\mathcal{F}}} = \mathop \int \limits_{D}^{{}} e^{{ - \frac{{\mathbf{x}}}{\delta }}} \frac{3}{{4\pi a^{3} }}{\mathbf{L}}\left( {0,{\mathbf{x}}} \right)x_{3}^{2} d{\mathbf{x}}.$$

(44)

Thus, at a certain $X_{1} - X_{2}$ layer, the overall averaged stress and strain are expressed as

$$\langle{{\varvec{\upsigma}}}\left\rangle( {X_{3} } \right) = \phi \left( {X_{3} } \right)\langle{{\varvec{\upsigma}}}\rangle^{1} \left( {X_{3} } \right) + \left[ {1 - \phi \left( {X_{3} } \right)} \right]\langle{{\varvec{\upsigma}}}\rangle^{0} \left( {X_{3} } \right),$$

(45)

$$\langle{{\varvec{\upvarepsilon}}}\left\rangle( {X_{3} } \right) = \phi \left( {X_{3} } \right)\langle{{\varvec{\upvarepsilon}}}\rangle^{1} \left( {X_{3} } \right) + \left[ {1 - \phi \left( {X_{3} } \right)} \right]\langle{{\varvec{\upvarepsilon}}}\rangle^{0} \left( {X_{3} } \right),$$

(46)

where the averaged stress $\langle{{\varvec{\upsigma}}}\rangle^{1}$ and $\langle{{\varvec{\upsigma}}}\rangle^{0}$ for particle and matrix are

$$\langle{{\varvec{\upsigma}}}\rangle^{1} \left( {X_{3} } \right) = {\mathbf{C}}_{1} :\left[ \langle{{{\varvec{\upvarepsilon}}}\rangle^{1} \left( {X_{3} } \right) - \alpha_{1} T{{\varvec{\updelta}}}} \right],$$

(47)

$$\langle{{\varvec{\upsigma}}}\rangle^{0} \left( {X_{3} } \right) = {\mathbf{C}}_{0} :\left[ \langle{{{\varvec{\upvarepsilon}}}\rangle^{0} \left( {X_{3} } \right) - \alpha_{0} T{{\varvec{\updelta}}}} \right].$$

(48)