Frictional moving contact problem between a functionally graded monoclinic layer and a rigid punch of an arbitrary profile

Abstract

In this study, the moving contact problem of a rigid flat and cylindrical punch on a graded monoclinic layer is considered based on the linear elasticity theory. The punch is subjected to concentrated normal and tangential forces and moves steadily with a constant velocity on the boundary. The material properties of the graded layer are assumed to vary exponentially through the thickness direction. The friction between the layer and the punch is considered. Using the integral transform technique and boundary conditions of the problem, a second kind singular integral equation is obtained and solved numerically using the Gauss–Jacobi integration formulas. The effect of the moving velocity, the fiber angle, the material inhomogeneity, the friction coefficient, the punch radius and length, and the external load on the contact stress and in-plane stress is investigated.

1 Introduction

Many situations in engineering applications require basic load transfer between two solids, generally in the presence of friction. Thus, contact mechanics has an important place in solid mechanics. The contact type and the distribution of contact stresses play a fundamental role in engineering applications such as braking systems, coupling devices, clutches, pavements in roads and runways, railway ballast, and foundations.

Recently, studies on the contact problems have focused on functionally graded materials (FGMs). FGMs are a new kind of inhomogeneous composites with continuously varying volume fractions in any desired direction. The axisymmetric contact problem of FGMs was studied by Giannakopoulos and Suresh [1], Liu et al. [2], and Vasiliev et al. [3] using Hankel integral transform technique. The Young’s modulus is assumed to vary in depth direction either as a simple power law or exponentially [1]. Liu et al. [2] divided FGMs into a series of sub-layers with shear modulus varying linearly in each sub-layer. Plane contact problem of an FGM half plane is examined by Giannakopoulos and Palliot [4] and Chen et al. [5]. Plane sliding contact problem between a flat punch and an FGM layer bonded to the rigid substrate is investigated by Choi [6]. FGM coatings can improve mechanical and thermal properties such as stiffness, strength, fatigue life and resistance against wear. Plane frictional contact problem of an FGM-coated half plane is examined by Güler and Erdogan [7], Güler and Erdogan [8], Ke and Wang [9], and Chen and Chen [10] using Fourier integral transform technique. Plane frictionless and frictional contact problems of a coating structure consisting of a homogeneous coating, an FGM layer and a half plane indented by a rigid cylindrical punch are investigated by Yang and Ke [11] and Chidlow and Teodorescu [12], respectively. Interface behavior of a thin-film bonded to an FG layer-coated elastic half plane or finite thickness substrate is studied by Chen et al. [13] and Chen et al. [14].

When the layer resting on a substrate without bond, separation occurs between the contacting components and the contact boundaries decrease at the interface after the load is applied. In addition, if the body forces are neglected, the separation becomes infinite and this type of contact is referred as receding. The axisymmetric receding contact problem between FGM half plane and homogeneous half plane is studied by Rhimi et al. [15]. Plane frictional receding contact problems of FGMs are studied by El-Borgi et al. [16], El-Borgi and Çömez [17], Yilmaz et al. [18], and Çömez et al. [19, 41] using Fourier integral transform technique. Adiyaman et al. [20] examined the frictionless receding contact problem between an FGM layer and two quarter planes using Mellin transform technique. Frictionless receding contact problem of multilayered elastic structures is studied by and Yan and Mi [21] and Yan et al. [22]. Cao and Mi [23] investigated the frictionless receding contact problem between an FGM layer and an elastic layer indented by a flat-ended rigid punch. Yaylaci et al. [24] examined the receding contact problem between two layers resting on a Winkler foundation using both analytical method, finite element method (FEM), and multilayer perceptron.

In the studies mentioned so far, the material has been considered isotropic. Due to the increasing use of unconventional materials such as metal/polymer and polymer/polymer anisotropic materials have gained an increasing importance in recent years. Different from conventional isotropic materials, anisotropic material properties are directionally dependent. Thus, the contact mechanic of anisotropic materials is more complicated. Transversely isotropic materials have the same material properties in one plane and different properties in the direction normal to this plane. Axisymmetric contact problem between a rigid punch and a transversely isotropic layer fully bonded to the rigid substrate was studied by Ning et al. [25], Patra et al. [26], and Patra et al. [27]. Kuo and Keer [28] and Liu and Pan [29] investigated the contact problem of a transversely isotropic layered half plane indented by a rigid spherical and a flat-ended cylinder, respectively. Hou et al. [30] and Hou et al. [31] examined the three-dimensional contact problem of transversely isotropic-coated structure under the tilted circular flat punch and spherical punch, respectively. Piezoelectric materials such as barium titanate (BaTiO₃), silicon dioxide (SiO₂), PZT-5H, PZT4, and PZT5-A exhibits transversely isotropic characteristic. Due to their coupling effects between mechanical and electric field, piezoelectric materials are widely used in smart structures such as actuators and sensors. The contact problem of piezoelectric materials was studied by Giannakopoulos and Suresh [32], Ke et al. [33], Liu and Yang [34], Rodríguez-Tembleque et al. [35], Elloumi et al. [36], Patra et al. [37], Su et al. [38], Chen et al. [39], Chen et al. [40], and [19, 41].

Orthotropic materials are a subset of anisotropic materials that have three orthogonal planes of microstructural symmetry. Küçüksucu et al. [42] and Güler et al. [43] investigated the contact mechanics of FGM orthotropic half plane using Fourier transform and finite element method. Alinia and Güler [44] studied the partial slip contact problem of an orthotropic half plane. Frictionless contact problem of an orthotropic layer indented by a rigid punch was examined by Erbas et al. [45]. Frictional contact problem of an FGM- or homogeneous-coated half plane is examined by Arslan and Dag [46], Alinia et al. [47] and Yilmaz et al. [48, 50]. The other subset of anisotropic materials is monoclinic material (arbitrary oriented orthotropic materials) that have one symmetry plane. Çömez and Yilmaz [49] investigated the frictional contact problem of monoclinic layer indented by a rigid cylindrical punch both with analytical method and finite element method. The frictional contact problem of a monoclinic-coated isotropic half plane indented by rigid cylindrical, flat, and parabolic punch was examined by Yilmaz et al. [48, 50]. The contact problem of monoclinic layered half plane indented by a rigid parabolic punch was studied in the absence and presence of friction by Binienda and Pindera [51] and Yilmaz et al. [52]. The frictional contact problem of FGM monoclinic layer indented by a rigid cylindrical punch was examined by Çömez [53]. The receding contact problem of anisotropic materials was studied by Chaudhuri and Ray [54], Kahya et al. [55], Yildirim et al. [56], and Cao et al. [57].

In the studies listed above, the contact problems were studied under static loading. However, if the speed of one contacting component relative to other is quite large, the dynamic effect of the problem should be considered [58]. The frictional moving contact problem of an isotropic homogeneous or FG materials was studied by Çömez [59], Balci and Dag [60] and Balci and Dag [61]. The moving contact problem of orthotropic materials was investigated by Georgiadis [62], De and Patra [63], Zhou et al. [64], and Çömez and Güler [65]. The moving contact problem of piezoelectric/ magneto-electro-elastic materials was studied by Zhou and Lee [66], Zhou and Kim [67], Çömez [68], and Çömez [69].

Although there are many studies about the anisotropic materials, the studies generally focused on the static contact problems and moving contact problem of an FGM monoclinic material has not been investigated yet. To fill this gup in the literature, the author investigates in this paper frictional moving contact problem of an FGM monoclinic layer fully bonded to the rigid substrate. The layer is indented by moving rigid cylindrical or flat punches on the surface. The material properties of graded layer are assumed to vary exponentially through the thickness direction. Using the Fourier transforms and boundary conditions of the problem, a singular integral equation is obtained, and it is solved numerically applying the Gauss–Jacobi integration formulas.

2 Formulation of the problem

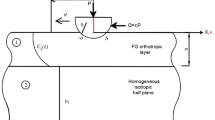
The geometry of the plane strain moving contact problem of an FG monoclinic layer is shown in Fig. 1. A rigid punch moves on the layer with constant velocity, $V$, and transmits a concentrated normal and tangential forces. The layer with the height $h$ is perfectly bonded to the rigid substrate.

Fig. 1

Geometry of the moving contact problem

The equations of motion can be written as

$$\frac{{\partial {\sigma _x}}}{{\partial {x_1}}} + \frac{{\partial {\tau _{xy}}}}{{\partial {z_1}}} = \rho \frac{{{\partial ^2}u}}{{\partial {t^2}}},$$

(1a)

$$\frac{{\partial {\tau _{yx}}}}{{\partial {x_1}}} + \frac{{\partial {\tau _{yz}}}}{{\partial {z_1}}} = \rho \frac{{{\partial ^2}v}}{{\partial {t^2}}},$$

(1b)

$$\frac{{\partial {\tau _{xz}}}}{{\partial {x_1}}} + \frac{{\partial {\sigma _z}}}{{\partial {z_1}}} = \rho \frac{{{\partial ^2}w}}{{\partial {t^2}}},$$

(1c)

where $u$, $v$, and $w$ are the $x_{1}$-, $y_{1}$-, and $z_{1}$-components of the displacement vector.

For the FG monoclinic layer, the constitutive equations under generalized plane strain state can be expressed as follows [70]:

$$ \sigma_{x} = \overline{C}_{11} (z)\frac{\partial u}{{\partial x_{1} }} + \overline{C}_{13} (z)\frac{\partial w}{{\partial z_{1} }} + \overline{C}_{16} (z)\frac{\partial v}{{\partial x_{1} }},\quad \tau_{yz} = \overline{C}_{44} (z)\frac{\partial v}{{\partial z_{1} }} + \overline{C}_{45} (z)\left( {\frac{\partial u}{{\partial z_{1} }} + \frac{\partial w}{{\partial x_{1} }}} \right), $$

(2a)

$$ \sigma_{y} = \overline{C}_{12} (z)\frac{\partial u}{{\partial x_{1} }} + \overline{C}_{23} (z)\frac{\partial w}{{\partial z_{1} }} + \overline{C}_{26} (z)\frac{\partial v}{{\partial x_{1} }},\quad \tau_{xz} = \overline{C}_{55} (z)\left( {\frac{\partial u}{{\partial z_{1} }} + \frac{\partial w}{{\partial x_{1} }}} \right) + \overline{C}_{45} (z)\frac{\partial v}{{\partial z_{1} }}, $$

(2b)

$$ \sigma_{z} = \overline{C}_{13} (z)\frac{\partial u}{{\partial x_{1} }} + \overline{C}_{33} (z)\frac{\partial w}{{\partial z_{1} }} + \overline{C}_{36} (z)\frac{\partial v}{{\partial x_{1} }},\quad \tau_{xy} = \overline{C}_{16} (z)\frac{\partial u}{{\partial x_{1} }} + \overline{C}_{36} (z)\frac{\partial w}{{\partial z_{1} }} + \overline{C}_{66} (z)\frac{\partial v}{{\partial x_{1} }}, $$

(2c)

where $\overline{C}_{ij} (z)$ are the transformed elastic stiffness constants that vary exponentially through the thickness of the layer as follows:

$$ \overline{C}_{ij} (z) = \overline{C}_{ij}^{0} e^{\gamma z} ,\quad \gamma h = - {\text{Log}}(\chi ),\quad \chi = \overline{C}_{ij}^{h} /\overline{C}_{ij}^{0}, $$

(3)

where $\gamma$ is the inhomogeneity parameter, $\overline{C}_{ij}^{0}$ and $\overline{C}_{ij}^{h}$ are the transformed material constants on the top and the bottom surfaces of the FG layer, respectively. The transformed stiffness coefficients $\overline{C}_{ij}^{0}$ can be written depending on the fiber angle $\theta$ (see the Appendix).

Due to constant speed, it is tractable to use the Galilei transformation [58] as follows:

$$ x = x_{1} + Vt,\quad y = y_{1} ,\quad z = z_{1} . $$

(4)

Substituting Eq. (2) into (1) and considering (4), the following partial differential equation system can be obtained:

$$ (\overline{C}_{11}^{0} - E_{xx} c^{2} )\frac{{\partial^{2} u}}{{\partial x^{2} }} + \overline{C}_{55}^{0} \frac{{\partial^{2} u}}{{\partial z^{2} }} + \overline{C}_{16}^{0} \frac{{\partial^{2} v}}{{\partial x^{2} }} + \overline{C}_{45}^{0} \frac{{\partial^{2} v}}{{\partial z^{2} }} + (\overline{C}_{13}^{0} + \overline{C}_{55}^{0} )\frac{{\partial^{2} w}}{\partial x\partial z} + \gamma \left( {\overline{C}_{55}^{0} \frac{\partial u}{{\partial z}} + \overline{C}_{45}^{0} \frac{\partial v}{{\partial z}} + \overline{C}_{55}^{0} \frac{\partial w}{{\partial x}}} \right) = 0, $$

(5a)

$$ \overline{C}_{16}^{0} \frac{{\partial^{2} u}}{{\partial x^{2} }} + \overline{C}_{45}^{0} \frac{{\partial^{2} u}}{{\partial z^{2} }} + (\overline{C}_{66}^{0} - E_{xx} c^{2} )\frac{{\partial^{2} v}}{{\partial x^{2} }} + \overline{C}_{44}^{0} \frac{{\partial^{2} v}}{{\partial z^{2} }} + (\overline{C}_{36}^{0} + \overline{C}_{45}^{0} )\frac{{\partial^{2} w}}{\partial x\partial z} + \gamma \left( {\overline{C}_{45}^{0} \frac{\partial u}{{\partial z}} + \overline{C}_{44}^{0} \frac{\partial v}{{\partial z}} + \overline{C}_{45}^{0} \frac{\partial w}{{\partial x}}} \right) = 0, $$

(5b)

$$ (\overline{C}_{13}^{0} + \overline{C}_{55}^{0} )\frac{{\partial^{2} u}}{\partial x\partial z} + (\overline{C}_{36}^{0} + \overline{C}_{45}^{0} )\frac{{\partial^{2} v}}{\partial x\partial z} + (\overline{C}_{55}^{0} - E_{xx} c^{2} )\frac{{\partial^{2} w}}{{\partial x^{2} }} + \overline{C}_{33}^{0} \frac{{\partial^{2} w}}{{\partial z^{2} }} + \gamma \left( {\overline{C}_{13}^{0} \frac{\partial u}{{\partial x}} + \overline{C}_{36}^{0} \frac{\partial v}{{\partial x}} + \overline{C}_{33}^{0} \frac{\partial w}{{\partial z}}} \right) = 0, $$

(5c)

where $c^{2} = V^{2} \rho_{0} /E_{xx}$.

To apply the integral transform technique, the following transformations are defined:

$$ \{ u(x,z),v(x,z),w(x,z)\} = \int\limits_{ - \infty }^{\infty } {\{ \tilde{u}(\xi ,z),\tilde{v}(\xi ,z),\tilde{w}(\xi ,z)\} } e^{ - I\xi x} {\text{d}}\xi, $$

(6)

where $\tilde{u}(\xi ,z),\,\tilde{v}(\xi ,z),\,\tilde{w}(\xi ,z)\;$ are the Fourier transforms of the $u(x,z),\,v(x,z),\,w(x,z)\;$, respectively, $\xi$ is the transform variable and $I = \sqrt { - 1}$. Substituting Eqs. (6) into (5), the following ordinary differential equation system can be obtained:

$$ - (\overline{C}_{11}^{0} + E_{xx} c^{2} )\xi^{2} \tilde{u} - \overline{C}_{16}^{0} \xi^{2} \tilde{v} - I\xi (\overline{C}_{13}^{0} + \overline{C}_{55}^{0} )\frac{{{\text{d}}\tilde{w}}}{{{\text{d}}z}} + \overline{C}_{55}^{0} \frac{{{\text{d}}^{2} \tilde{u}}}{{{\text{d}}z^{2} }} + \overline{C}_{45}^{0} \frac{{{\text{d}}^{2} \tilde{v}}}{{{\text{d}}z^{2} }} - \gamma \left( {\overline{C}_{55}^{0} \frac{{{\text{d}}\tilde{u}}}{{{\text{d}}z}} + \overline{C}_{45}^{0} \frac{{{\text{d}}\tilde{v}}}{{{\text{d}}z}} - I\xi \overline{C}_{55}^{0} \tilde{w}} \right) = 0, $$

(7a)

$$ - \overline{C}_{16}^{0} \alpha^{2} \tilde{u} + ( - \overline{C}_{66}^{0} + E_{xx} c^{2} )\alpha^{2} \tilde{v} - I\alpha (\overline{C}_{36}^{0} + \overline{C}_{45}^{0} )\frac{{{\text{d}}\tilde{w}}}{{{\text{d}}z}} + \overline{C}_{45}^{0} \frac{{{\text{d}}^{2} \tilde{u}}}{{{\text{d}}z^{2} }} + \overline{C}_{44}^{0} \frac{{{\text{d}}^{2} \tilde{v}}}{{{\text{d}}z^{2} }} - \gamma \left( {\overline{C}_{45}^{0} \frac{{{\text{d}}\tilde{u}}}{{{\text{d}}z}} + \overline{C}_{44}^{0} \frac{{{\text{d}}\tilde{v}}}{{{\text{d}}z}} - I\xi \overline{C}_{45}^{0} \tilde{w}} \right) = 0, $$

(7b)

$$ - (\overline{C}_{55}^{0} - E_{xx} c^{2} )\xi^{2} \tilde{w} - I\xi (\overline{C}_{13}^{0} + \overline{C}_{55}^{0} )\frac{{{\text{d}}\tilde{u}}}{{{\text{d}}z}} - I\xi (\overline{C}_{36}^{0} + \overline{C}_{45}^{0} )\frac{{{\text{d}}\tilde{v}}}{{{\text{d}}z}} - \overline{C}_{33}^{0} \frac{{{\text{d}}^{2} \tilde{w}}}{{{\text{d}}z^{2} }} + \gamma \left( {\xi \overline{C}_{13}^{0} \tilde{u} + \xi \overline{C}_{36}^{0} \tilde{v} + I\overline{C}_{33}^{0} \frac{{{\text{d}}\tilde{w}}}{{{\text{d}}z}}} \right) = 0. $$

(7c)

The solutions of Eq. (7) can be assumed as

$$ \tilde{u} = \sum\limits_{j = 1}^{6} {A_{j} } e^{{n_{j} \xi z}} ,\quad \tilde{v} = \sum\limits_{j = 1}^{6} {k_{j} A_{j} } e^{{n_{j} \xi z}} ,\quad \tilde{w} = \sum\limits_{j = 1}^{6} {m_{j} A_{j} } e^{{n_{j} \xi z}} . $$

(8)

Substituting (8) into (7) and applying some manipulations, the following characteristic equation can be obtained:

$$ \left| {\begin{array}{*{20}c} {( - \overline{C}_{11}^{0} + E_{xx} c^{2} )\xi^{2} + \overline{C}_{55}^{0} n(n + \gamma )} & { - \overline{C}_{16}^{0} \xi^{2} + \overline{C}_{45}^{0} n(n + \gamma )} & { - I\xi (\overline{C}_{13}^{0} n + \overline{C}_{55}^{0} (n + \gamma ))} \\ { - \overline{C}_{16}^{0} \xi^{2} + \overline{C}_{45}^{0} n(n + \gamma )} & { - \overline{C}_{66}^{0} \xi^{2} + E_{xx} c^{2} \xi^{2} + \overline{C}_{44}^{0} n(n + \gamma )} & { - I\xi (\overline{C}_{36}^{0} n + \overline{C}_{45}^{0} (n + \gamma ))} \\ {\xi (\overline{C}_{55}^{0} n + \overline{C}_{13}^{0} (n + \gamma ))} & {\xi (\overline{C}_{45}^{0} n + \overline{C}_{36}^{0} (n + \gamma ))} & { - I(( - \overline{C}_{55}^{0} + E_{xx} c^{2} )\xi^{2} + \overline{C}_{33}^{0} n(n + \gamma ))} \\ \end{array} } \right| = 0, $$

(9)

where $n_{j}$ $(j = 1,2,....6)$ are the roots of the characteristic equation (9). The functions $k_{j}$ and $m_{j}$ can be defined as

$$ \left[ {\begin{array}{*{20}c} k \\ m \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \overline{C}_{66}^{0} \xi^{2} + E_{xx} c^{2} \xi^{2} + \overline{C}_{44}^{0} n(n + \gamma )} & { - I\xi (\overline{C}_{36}^{0} n + \overline{C}_{45}^{0} (n + \gamma ))} \\ {\xi (\overline{C}_{45}^{0} n + \overline{C}_{36}^{0} (n + \gamma ))} & { - I(( - \overline{C}_{55}^{0} + E_{xx} c^{2} )\xi^{2} + \overline{C}_{33}^{0} n(n + \gamma ))} \\ \end{array} } \right]^{ - 1} \left[ {\begin{array}{*{20}c} {\overline{C}_{16}^{0} \xi^{2} - \overline{C}_{45}^{0} n(n + \gamma )} \\ { - \xi (\overline{C}_{55}^{0} n + \overline{C}_{13}^{0} (n + \gamma ))} \\ \end{array} } \right]. $$

(10)

Substituting Eqs. (8) into (2), the stress components for the FG monoclinic layer can be obtained as

$$ \sigma_{x} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ {e^{\gamma z} \sum\limits_{j = 1}^{6} {A_{j} } (\overline{C}_{13}^{0} m_{j} n_{j} - I\xi (\overline{C}_{11}^{0} + \overline{C}_{16}^{0} k_{j} ))\,e^{{n_{j} {\kern 1pt} \xi z}} } \right]} \,e^{{ - I{\kern 1pt} \xi {\kern 1pt} x}} {\text{d}}\xi, $$

(11a)

$$ \sigma_{y} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ {e^{\gamma z} \sum\limits_{j = 1}^{6} {A_{j} } (\overline{C}_{23}^{0} m_{j} n_{j} - I\xi (\overline{C}_{12}^{0} + \overline{C}_{26}^{0} k_{j} ))\,e^{{n_{j} {\kern 1pt} \xi z}} } \right]} \,e^{{ - I{\kern 1pt} \xi {\kern 1pt} x}} {\text{d}}\xi, $$

(11b)

$$ \sigma_{z} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ {e^{\gamma z} \sum\limits_{j = 1}^{6} {A_{j} } (\overline{C}_{33}^{0} m_{j} n_{j} - I\xi (\overline{C}_{13}^{0} + \overline{C}_{36}^{0} k_{j} ))\,e^{{n_{j} {\kern 1pt} \xi z}} } \right]} \,e^{{ - I{\kern 1pt} \xi {\kern 1pt} x}} {\text{d}}\xi, $$

(11c)

$$ \tau_{yz} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ {e^{\gamma z} \sum\limits_{j = 1}^{6} {A_{j} } (\overline{C}_{44}^{0} k_{j} n_{j} + \overline{C}_{45}^{0} (n_{j} - I\xi m_{j} ))\,e^{{n_{j} {\kern 1pt} \xi z}} } \right]} \,e^{{ - I{\kern 1pt} \xi {\kern 1pt} x}} {\text{d}}\xi, $$

(11d)

$$ \tau_{xz} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ {e^{\gamma z} \sum\limits_{j = 1}^{6} {A_{j} } (\overline{C}_{45}^{0} k_{j} n_{j} + \overline{C}_{55}^{0} (n_{j} - I\xi m_{j} ))\,e^{{n_{j} {\kern 1pt} \xi z}} } \right]} \,e^{{ - I{\kern 1pt} \xi {\kern 1pt} x}} {\text{d}}\xi, $$

(11e)

$$ \tau_{xy} (x,z) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ {e^{\gamma z} \sum\limits_{j = 1}^{6} {A_{j} } (\overline{C}_{36}^{0} m_{j} n_{j} - I\xi (\overline{C}_{16}^{0} + \overline{C}_{66}^{0} k_{j} ))\,e^{{n_{j} {\kern 1pt} \xi z}} } \right]} \,e^{{ - I{\kern 1pt} \xi {\kern 1pt} x}} {\text{d}}\xi, $$

(11f)

where $A_{j}$ $(j = 1,2,...6)$ are the unknowns which are obtained from the boundary conditions of the problem.

3 The boundary conditions and the singular integral equation

The boundary conditions of the given contact problem can be written as follows:

$$ \sigma_{z} (x,0) = \left\{ {\begin{array}{*{20}c} { - p(x)} & { - a < x < b}, \\ 0 & {x \le - a,\;x \ge b}, \\ \end{array} } \right.$$

(12a)

$$ \tau_{xz} (x,0) = \left\{ {\begin{array}{*{20}c} { - \eta {\kern 1pt} p(x)} & { - a < x < b}, \\ 0 & {x \le - a,\;x \ge b}, \\ \end{array} } \right.$$

(12b)

$$ \tau_{yz} (x,0) = 0, $$

(12c)

$$ u(x, - h) = 0, $$

(12d)

$$ v(x, - h) = 0, $$

(12e)

$$ w(x, - h) = 0, $$

(12f)

where $\eta$ is the friction coefficient and $p(x)$ is the contact stress on the interval $[ - a,b]$.

Using the boundary conditions given by (12), six unknowns which are $A_{j}$ $(j = 1,2,...6)$ can be determined depending on the contact stress $p(x)$. To obtain the contact stress $p(x),$ the following mixed condition should be considered:

$$ \frac{\partial w(x,0)}{{\partial x}} = f(x), $$

(13)

where $f(x)$ is the derivative of the punch profile. Substituting the unknowns $A_{j}$ into (13), the following second kind singular integral equation can be obtained:

$$ \eta \varphi_{2} p(x) + \frac{1}{\pi }\int\limits_{ - a}^{b} {p(t){\text{d}}t} \left[ {\frac{{\varphi_{1} }}{t - x} + K_{1} (x,t) + \eta \,K_{2} (x,t)} \right] = f(x)\quad \left( { - a < x < b} \right), $$

(14)

where $K_{1} (x,t)$ and $K_{2} (x,t)$ are the kernels of integral equation and $\varphi_{1}$ and $\varphi_{2}$ are the singular terms.

For a complete solution of the problem, the contact stress must satisfy the following equilibrium condition:

$$ \int\limits_{ - \infty }^{\infty } {\sigma_{z} (x,0){\text{d}}x} = - \int\limits_{ - a}^{b} {p(t){\text{d}}t} = - P. $$

(15)

4 Numerical solution of the singular integral equation

Using the following transformation:

$$ t = \frac{a + b}{2}r + \frac{b - a}{2},\quad x = \frac{a + b}{2}s + \frac{b - a}{2}, $$

(16)

the integral equation (14) and the equilibrium condition (15) may be written in normalized form as follows:

$$ \eta \varphi_{2} \,p(s) + \frac{1}{\pi }\int\limits_{ - 1}^{1} {p(r){\text{d}}r} \left[ {\frac{{\varphi_{1} }}{r - s} + K_{1}^{*} (s,r) + \eta \,K_{2}^{*} (s,r)} \right] = f(s), $$

(17)

$$ \frac{a + b}{2}\int\limits_{ - 1}^{1} {p(r){\text{d}}r} = P, $$

(18)

where

$$ K_{1}^{*} (s,r) = \frac{a + b}{2}K_{1} (x,t),\quad K_{2}^{*} (s,r) = \frac{a + b}{2}K_{2} (x,t). $$

(19)

The solution of the singular integral equation (21) can be assumed as

$$ p(r) = g(r)(1 - r)^{\alpha } (1 + r)^{\beta }, $$

(20)

where

$$ \alpha = \frac{1}{2\pi \,I}\ln \left[ {\left( {\eta \frac{{\varphi_{2} }}{{\varphi_{1} }} - I} \right)/\left( {\eta \frac{{\varphi_{2} }}{{\varphi_{1} }} + I} \right)} \right] + N_{0}, $$

(21a)

$$ \beta = - \frac{1}{2\pi \,I}\ln \left[ {\left( {\eta \frac{{\varphi_{2} }}{{\varphi_{1} }} - I} \right)/\left( {\eta \frac{{\varphi_{2} }}{{\varphi_{1} }} + I} \right)} \right] + M_{0}, $$

(21b)

where $N_{0}$ and $M_{0}$ are arbitrary (positive, zero, or negative) integers and can be determined depending on the physics of the problem.

Applying the Gauss–Jacobi formulation presented in [71, 72], the integral equation (17) can be reduced to the following algebraic equations:

$$ \sum\limits_{i = 1}^{N} {W_{i}^{N} } g(r_{i} )\left[ {\frac{1}{{r_{i} - s_{k} }} + K_{1}^{*} (s_{k} ,r_{i} ) + \eta \,K_{2}^{*} (s_{k} ,r_{i} )} \right] = f(s_{k} )\quad k = 1,2 \ldots N - \chi . $$

(22)

Similarly, the equilibrium condition (18) becomes

$$ \frac{b + a}{2}\sum\limits_{i = 1}^{N} {W_{i}^{N} } g(r_{i} ) = \frac{P}{\pi }, $$

(23)

where $r_{i}$ and $s_{k}$ are the roots of the following Jacobi polynomials, $W_{i}^{N}$ is the weighting constant and $\chi$ is the index of the integral equation:

$$ P_{N}^{(\alpha ,\beta )} (r_{i} ) = 0\quad i = 1,2, \ldots ,N, $$

(24a)

$$ P_{N - \chi }^{( - \alpha , - \beta )} (s_{k} ) = 0\quad k = 1,2, \ldots ,N - \chi, $$

(24b)

$$ W_{i}^{N} = - \frac{1}{\pi }\frac{2N + \alpha + \beta }{{(N + 1)!}}\frac{\Gamma (N + \alpha + 1)\Gamma (N + \alpha + 1)}{{\Gamma (N + \alpha + \beta + 1)}}\frac{{2^{(\alpha + \beta )} }}{{P_{N}^{{(\alpha ,\beta )^{^{\prime}} }} (r_{i} )P_{N + 1}^{(\alpha ,\beta )} (r_{i} )}}, $$

(24c)

$$ \chi = - (\alpha + \beta ). $$

(24d)

4.1 Cylindrical punch case

For the cylindrical punch case, derivative of the punch profile can be written as follows:

$$ f(x) = \frac{x}{R}\quad {\text{and}}\quad f(s_{k} ) = \frac{1}{R}\left( {\frac{a + b}{2}s_{k} + \frac{b - a}{2}} \right). $$

(25)

Since the contact stress between the cylindrical punch and FG orthotropic layer goes to zero at the end points, the index of the integral equations (22) is $\chi = - (\alpha + \beta ) = - 1$ [71].

Equations (22) and (23) provide $N + 2$ algebraic equations to find the $N + 2$ unknowns which are the contact widths $a$, $b$ and $g(r_{i} )$ $(i = 1,....,N)$. Note that, there is one more equation to determine the $N$ unknowns $g(r_{i} )$ in Eq. (22). The additional equation should be extracted from Eq. (22) and used as a control equation to determine the contact widths $a$, $b$ with the equilibrium condition (23). The system of equations is linear in $g(r_{i} )$, but highly nonlinear in $a$ and $b$. Thus, suitable iterative technique should be used.

4.2 Flat punch case

For the flat punch case, derivative of the punch profile can be written as follows:

$$ f(x) = 0\quad {\text{and}}\quad f(s_{k} ) = 0. $$

(26)

Note that, for the flat punch case the contact widths are known priory and $a = b$. Since, there is a sharp edge at the ends of the rigid flat punch, the index of the integral equation (22) is $\chi = - (\alpha + \beta ) = + 1$.

Equations (22) and (23) provide $N$ algebraic equations to find the $N$ unknowns which are $g(r_{i} )$ $(i = 1,....,N)$. After solving for the contact stress and contact widths, the in-plane stress at the surface of the FG monoclinic layer can be determined as

$$ \sigma_{x} (x,0) = \left\{ {\begin{array}{*{20}c} {\varphi_{3} p(x) + H(x),} & { - a < x < b} \\ {H(x),} & {x \le - a,\,x \ge b} \\ \end{array} } \right\} $$

(27)

where

$$ H(x) = \frac{1}{\pi }\int\limits_{ - a}^{b} {p(t)} \left[ {\varphi_{4} \frac{\eta }{t - x} + K_{3} (x,t) + \eta \,K_{4} (x,t)} \right]{\text{d}}t $$

(28)

where $K_{3} (x,t)$ and $K_{4} (x,t)$ are the kernels and $\varphi_{3}$ and $\varphi_{4}$ are the singular terms.

5 Results and discussion

This section presents the numerical results of the problem described in Fig. 1 where the FG monoclinic layer is indented by a moving rigid cylindrical and flat punch, respectively. The FG monoclinic layer is assumed to be glass/epoxy (Gl/Ep) whose material properties are listed in Table 1.

Table 1 Material properties of glass/epoxy [51]

First, in order to verify this solution a comparison study is performed. For this purpose, numerical results of a special case obtained from the presented solution, are compared to results by Çömez and Yilmaz [49], where an orthotropic and homogeneous layer was considered (Fig. 2). This validation is made possible by reducing the FGM monoclinic material properties to the homogenous orthotropic case by choosing the fiber angle $\theta = 0$ and the inhomogeneity parameter $\chi = 1$. It shows a good agreement between the present results and Çömez and Yilmaz [49].

Fig. 2

Comparison of the contact stress $p(x)$ and in-plane stress $\sigma_{x} (x,0)$ for various values of moving velocity $V^{*} = V^{2} \rho /C_{55}$ (Note that, solid lines represent the results from this study, symbols represent the results from [49]$(\theta = 0,\chi = 1,R/h = 10,\;C_{66} /(P/h) = 100,\eta = 0.4,Gl/Ep)$

5.1 Results of cylindrical punch

Figure 3 shows the nine stiffness elements $\overline{C}_{ij}^{0}$ as a function of the fiber/rotation angle.

Fig. 3

Variations of the elastic constants of $Gl/Ep$ with fiber angle $\theta$

Note that $\overline{C}_{16}^{0} = \overline{C}_{36}^{0} = \overline{C}_{45}^{0} = 0$ for $\theta = 0^{\circ}$ and the monoclinic layer turns orthotropic. When the stiffness element is compared, it can be seen that $\overline{C}_{11}^{\circ}$ is affected significantly by the fiber angle $\theta$, and it decreases with increasing fiber angle between $\theta = 0^{\circ}$ and $\theta = 90^{\circ}$. Thus, the layer becomes flexible, and as a result the contact width increases when the fiber angle increases between $\theta = 0^{\circ}$ and $\theta = 90^{\circ}$(Fig. 4). When the contact area increases, the contact stress is distributed to a larger area, and the peak values of contact stress are bigger for the $0^{\circ}$ layer and smallest for the $90^{\circ}$ layer. The in-plane stress $\sigma_{x} (x,0)$ may cause the surface damage or crack initiation/propagation when it becomes tensile at the surface. Note that the tensile peak occurring at the trailing edge decreases with increasing fiber angle between $\theta = 0^{\circ}$ and $\theta = 90^{\circ}$, and possible surface damage and crack initiation/propagation can be prevented.

Fig. 4

Effect of fiber angle $\theta$ on contact stress $p(x)$ and in-plane stress $\sigma_{x} (x,0)$ $(c^{2} = 0.05,\chi = 2,\eta = 0.4,R/h = 100,P/(E_{xx} h) = 0.00234)$

The effect of the moving velocity $c^{2} = V^{2} \rho /E_{xx}$ on the contact stress and in-plane stress are shown in Fig. 5. When punch moves faster the contact width increases and as a result the peak values of contact stress decrease. However, the reverse relation is observed for the in-plane tensile stress, that is, tensile stress increases when the punch moves faster. To prevent the surface damage and crack initiation/propagation low speed should be preferred.

Fig. 5

Effect of moving velocity $c$ on contact stress $p(x)$ and in-plane stress $\sigma_{x} (x,0)$ $(\theta = 30^{\circ} ,\chi = 2,\eta = 0.4,R/h = 100,P/(E_{xx} h) = 0.00234)$

Figure 6 illustrates the effect of inhomogeneity parameter $\chi = \overline{C}_{ij}^{h} /\overline{C}_{ij}^{\circ}$ on the contact stress and in-plane stress. To investigate the effect of material inhomogeneity, three different cases $(\chi = 0.2,1,5)$ are selected which correspond to $(\gamma h = 1.6094,0, - 1.6094)$. Note that the layer becomes stiffer as $\chi$ increases. The contact width decreases when the layer becomes stiffer and as a result the peak values of contact stress increases. However, the tensile peak is almost insensitive to the change of material inhomogeneity $\chi$.

Fig. 6

Effect of inhomogeneity $\chi$ on contact stress $p(x)$ and in-plane stress $\sigma_{x} (x,0)$ $(c^{2} = 0.05,\theta = 30^{\circ} ,\eta = 0.4,R/h = 100,P/(E_{xx} h) = 0.00234)$

The effect of friction coefficient $\eta$ on the contact stress and in-plane stress is presented in Fig. 7. The stress distributions are symmetrical with respect to the $x = 0$ plane in the frictionless case. The effect of the friction coefficient is not distinct on the contact stress, but its effect on the in-plane stress is very significant. It can be concluded from Fig. 7 that, with the increasing values of the friction coefficient higher tensile peak occurs at the trailing edge that can be lead possible crack initiation near the trailing edge. Therefore, small friction coefficient should be chosen to prevent such contact damages.

Fig. 7

Effect of friction coefficient $\eta$ on contact stress $p(x)$ and in-plane stress $\sigma_{x} (x,0)$ $(c^{2} = 0.05,\theta = 30^{\circ} ,\chi = 2,R/h = 100,P/(E_{xx} h) = 0.00234)$

Figure 8 shows the effect of punch radius on the contact stress and in-plane stress. Note that, when punch radius increases the contact stress is distributed to a larger area, and the peak values of contact stress are bigger for the $R/h = 50$ and smallest for the $R/h = 200$. The same is valid for the tensile peaks, that is, the tensile peaks increase as the punch radius decreases.

Fig. 8

Effect of punch radius $R$ on contact stress $p(x)$ and in-plane stress $\sigma_{x} (x,0)$ $(c^{2} = 0.05,\theta = 30^{\circ} ,\chi = 2,\eta = 0.4,P/(E_{xx} h) = 0.00234)$

The effect of indentation load $P$ on the contact stress and in-plane stress is shown in Fig. 9. Differ from other parameters both the contact width and the contact stress increase with the increasing values of the indentation load. The tensile peaks can be reduced with small indentation load which can avoid the crack formation.

Fig. 9

Effect of indentation load $P^{*} = P/(E_{xx} h)$ on contact stress $p(x)$ and in-plane stress $\sigma_{x} (x,0)$ $(c^{2} = 0.05,\theta = 30^{\circ} ,\chi = 2,\eta = 0.4,R/h = 100)$

5.2 Results of flat punch

Referring to Figs. 10, 11, 12, 13, 14 and 15, it can be observed that the contact stress is singular at both edges $x = \pm a$. This is the expected result since the flat punch has sharp corners at the end points. It is well known that, in frictional contact problem, the in-plane stress behind the trailing edge $(x = + a)$ is more likely to be tensile whereas it is compressive in front of the leading edge $(x = - a)$.

Fig. 10

Effect of fiber angle $\theta$ on contact stress $p(x)$ and in-plane stress $\sigma_{x} (x,0)$ $(c^{2} = 0.05,\chi = 2,\eta = 0.4,a/h = 0.8,P/(E_{xx} h) = 0.00234)$

Fig. 11

Effect of moving velocity $c$ on contact stress $p(x)$ and in-plane stress $\sigma_{x} (x,0)$ $(\theta = 30^{\circ} ,\chi = 2,\eta = 0.4,a/h = 0.8,P/(E_{xx} h) = 0.00234)$

Fig. 12

Effect of inhomogeneity $\chi$ on contact stress $p(x)$ and in-plane stress $\sigma_{x} (x,0)$ $(c^{2} = 0.05,\theta = 30^{\circ} ,\eta = 0.4,a/h = 0.8,P/(E_{xx} h) = 0.00234)$

Fig. 13

Effect of friction coefficient $\eta$ on contact stress $p(x)$ and in-plane stress $\sigma_{x} (x,0)$ $(c^{2} = 0.05,\theta = 30^{\circ} ,\chi = 2,a/h = 0.8,P/(E_{xx} h) = 0.00234)$

Fig. 14

Effect of punch radius $R$ on contact stress $p(x)$ and in-plane stress $\sigma_{x} (x,0)$ $(c^{2} = 0.05,\theta = 30^{\circ} ,\chi = 2,\eta = 0.4,P/(E_{xx} h) = 0.00234)$

Fig. 15

Effect of indentation load $P^{*} = P/(E_{xx} h)$ on contact stress $p(x)$ and in-plane stress $\sigma_{x} (x,0)$ $(c^{2} = 0.05,\theta = 30^{\circ} ,\chi = 2,\eta = 0.4,a/h = 0.8)$

The influence of the fiber angle $\theta$ on the contact stress and in-plane stress is examined in Fig. 10. The contact stress in the middle of the contact zone increases as the fiber angle increases $\theta = 0^{\circ}$ to $\theta = 90^{\circ}$. However, the tensile peak at the trailing end of the contact decreases as the fiber angle increases $\theta = 0^{\circ}$ to $\theta = 90^{\circ}$.

Figure 11 shows the effect of moving velocity $c^{2} = V^{2} \rho /E_{xx}$. The contact stress away from the end points increases as punch moves faster. Also, the tensile peak at the trailing end of the contact increases with increasing values of velocity.

The effect of the inhomogeneity parameter $\chi = \overline{C}_{ij}^{h} /\overline{C}_{ij}^{\circ}$ on the contact stress and in-plane stress is illustrated in Fig. 12. The contact stress away from the end points increases as the layer becomes stiff. The peak value of tensile stress is bigger for the $\chi = 0.2$ and smallest for the $\chi = 5$.

Figure 13 shows the effect of friction coefficient $\eta$ on the contact stress and in-plane stress. To investigate the effect of friction, three different cases $(\eta = 0,0.4,0.8)$ are selected. For $\eta = 0$ the problem is reduced to the frictionless case and the stress distributions become symmetric. It is seen that contact stress is not affected by friction coefficient. However, the tensile peaks increase significantly as the friction coefficient increases. From the fretting mechanics position, surface cracking caused by friction will inevitably lead to fretting fatigue and small friction coefficient has less possibility for crack initiation and propagation.

Figures 14 and 15 present the effect of the punch length $a$ and indentation load $P$ on the contact stress and in-plane stress, respectively. As expected, both the contact stress and tensile peak increase when the punch length decreases and indentation load increases.

6 Conclusion

In this study, frictional moving contact problem of a graded monoclinic layer indented by a rigid cylindrical or flat punch is considered based on the linear elasticity theory and integral transform technique. Applying the boundary conditions, the contact problem is converted to the second kind singular integral equation, and it is solved numerically using the Gauss–Jacobi integration formula. Important conclusions are outlined below.

• The layer becomes softer when the fiber angle increases between $0^{\circ}$ and $90^{\circ}$. As a result, the contact width increases, and the peak values of contact stress decrease for the cylindrical punch case. Also, tensile peaks are minimum at the orthotropic case $({0^\circ } )$ for both cylindrical and flat punch cases.

• Faster punch leads to the increase in contact width and as a result the peak values of contact stress decreases for the cylindrical punch case. However, when the cylindrical punch moves faster, the tensile peak increases.

• When the inhomogeneity parameter increases, the layer becomes stiffer and the contact stress increases significantly, but the tensile peaks almost become same for the cylindrical punch case.

• Contact stress is almost insensitive to the change of the friction coefficient for both cylindrical and flat punch cases. However, the tensile peaks increase with the increasing friction coefficient and the possible surface damage and crack initiation near the trailing edge can be prevented by choosing small friction coefficient.

• All the results should be helpful for the design of a system with a graded monoclinic layer and for engineers to choose a proper fiber angle in real applications.

Appendices

Appendix A

The material constants $\overline{C}_{ij}^{0}$ can be expressed as follows [73]

$$ \overline{C}_{11}^{0} = C_{11} \cos^{4} \theta + 2(C_{12} + 2C_{66} )\cos^{2} \theta \sin^{2} \theta + C_{22} \sin^{4} \theta, $$

(29)

$$ \overline{C}_{12}^{0} = (C_{11} + C_{22} - 4C_{66} )\cos^{2} \theta \sin^{2} \theta + C_{12} (\cos^{4} \theta + \sin^{4} \theta ), $$

(30)

$$ \overline{C}_{13}^{0} = C_{13} \cos^{2} \theta + C_{23} \sin^{2} \theta, $$

(31)

$$ \overline{C}_{16}^{0} = \cos \theta \sin \theta (\cos^{2} \theta (C_{11} - C_{12} - 2C_{66} ) + \sin^{2} \theta (C_{12} - C_{22} + 2C_{66} )), $$

(32)

$$ \overline{C}_{22}^{0} = C_{11} \sin^{4} \theta + 2(C_{12} + 2C_{66} )\cos^{2} \theta \sin^{2} \theta + C_{22} \cos^{4} \theta, $$

(33)

$$ \overline{C}_{23}^{0} = C_{23} \cos^{2} \theta + C_{13} \sin^{2} \theta, $$

(34)

$$ \overline{C}_{33}^{0} = C_{33}, $$

(35)

$$ \overline{C}_{36}^{0} = (C_{13} - C_{23} )\cos \theta \sin \theta, $$

(36)

$$ \overline{C}_{44}^{0} = C_{44} \cos^{2} \theta + C_{55} \sin^{2} \theta, $$

(37)

$$ \overline{C}_{45}^{0} = (C_{55} - C_{44} )\cos \theta \sin \theta, $$

(38)

$$ \overline{C}_{55}^{0} = C_{55} \cos^{2} \theta + C_{44} \sin^{2} \theta, $$

(39)

$$ \overline{C}_{66}^{0} = (C_{11} - 2C_{12} - 2C_{22} )\cos^{2} \theta \sin^{2} \theta + C_{66} (\sin^{2} \theta - \cos^{2} \theta )^{2}, $$

(40)

where $C_{ij}$ are the stiffness coefficient of the layer in the directions parallel and perpendicular to the fiber.

Appendix B: Cylindrical punch figures

See Figs. 4, 5, 6, 7, 8 and 9.

Appendix C: Flat punch figures

See Figs. 10, 11, 12, 13, 14 and 15.