Numerical and experimental verification of a method of identification of localized damages in a rod by natural frequencies of longitudinal vibration

Abstract

A method for identification of multiple transverse cracks and other localized defects in a rod by means of two spectra of longitudinal vibrations that correspond to free–free and fixed–free end conditions is presented. A numerical algorithm is developed that implements the method. The algorithm was tested on experimental data obtained on a cylindrical sample of aluminum alloy D16 with the created localized damages. The experiments were carried out on a rod with free ends. The created damages were ring grooves symmetrically located relative to the middle of the rod. With the help of such experiments, natural frequencies were obtained that correspond to two types of boundary conditions for a half-length rod. The experimental data were processed using the developed algorithm. The results showed that the model on which the developed algorithm is based describes well the longitudinal vibrations of the rod with localized damages in a fairly wide frequency range, and the algorithm enables to reconstruct multiple damages accurately enough.

1 Introduction

We consider a problem of identification of multiple transverse cracks or crack-like damages in a rod by natural frequencies of longitudinal vibration. In most of publications, the problem is considered in the frame of a model where the cracks are simulated by massless translational springs [1,2,3,4,5,6,7,8]. Using this model, the problem of identification of small cracks was considered in [2, 4,5,6,7]. The problem of identification of a single crack of an arbitrary size was solved in [8]. The most general result was obtained in [9]. It was proved that an arbitrary number of cracks is determined uniquely by two spectra corresponding to two types of the conditions at the ends of the rod: free–free and fixed–free. The extension of this result to the case of a rod of variable cross section is presented in [10]. A stable numerical algorithm for reconstruction of damages corresponding to the cracks was developed in [11]. The algorithm uses a slightly modified formulation of the problem. In a modified formulation, the partition of the rod into elements is considered. It is assumed that the presence of a crack in the element reduces its rigidity, but does not affect the mass.

According to the results of [9], in order to identify crack-like defects, it is necessary to know two spectra. Of course, in practice it is impossible to have an infinite number of natural frequencies, and for the implementation of the algorithm [11] it is required, although finite, but a sufficiently large number of natural frequencies. Previously, basically developed methods for identifying one or two cracks did not require knowledge of a large number of natural frequencies. In this connection, the question arises whether it is possible to use the considered model of a rod with crack-like defects in a fairly wide frequency range for reconstruction of damages. Thus, the aim of the paper is to refine algorithm [11], for better localization of crack-like defects, and also experimental verification of its efficiency.

The paper is organized as follows. In Sect. 2, we recall the initial mathematical formulation of the problem. The modified formulation of the problem and numerical algorithm are presented in Sect. 3. A description of the experiments is given in Sect. 4. The results of experiments and results of the damage reconstruction using experimental data are presented in Sect. 5. Conclusions are presented in Sect. 6.

2 Initial mathematical formulation of the problem

We consider a rod of length $l$ and cross section of constant area $A$. Assume that the rod occupies an interval $0 < x < l$ and the translational springs, which simulate the localized damages, are located at points $x_{1} ,x_{2} , \ldots ,x_{n}$ such that $0 = x_{0} < x_{1} < x_{2} < \cdots < x_{n} < x_{n + 1} = l$. Denote by $u_{j} \left( x \right)$ the amplitudes of longitudinal displacements under time-harmonic vibration on the interval $x_{j - 1} < x < x_{j}$, where $j = 1,2, \ldots ,n + 1$. The equation of harmonic longitudinal oscillations has the following form:

$$u_{j}^{{\prime \prime }} \left( x \right) + \lambda u_{j} \left( x \right) = 0,\quad j = 1,2, \ldots ,n + 1,\quad x_{j - 1} < x < x_{j}$$

(1)

where $\lambda = \frac{{\rho \omega^{2} }}{E}$, $E$ is Young’s modulus, $\rho$ is the material density and $\omega$ is a circular frequency.

The conjugation conditions at the locations of springs are of the form, see [3]

$$u_{j}^{\prime } \left( {x_{j} } \right) = u_{j + 1}^{{^{\prime } }} \left( {x_{j} } \right),\quad u_{j + 1} \left( {x_{j} } \right) - u_{j} \left( {x_{j} } \right) = \Delta_{j} = {\text{EA}}\,c_{j} u_{j}^{\prime } \left( {x_{j} } \right),\quad j = 1,2, \ldots ,n$$

(2)

where $c_{j}$ is the flexibility of the $j$th translational spring.

Consider two types of end conditions. The free–free condition has the form

$$u_{1}^{{\prime }} \left( 0 \right) = 0,\quad u_{n + 1}^{{\prime }} \left( l \right) = 0$$

(3)

The fixed–free end condition has the form

$$u_{1} \left( 0 \right) = 0,\quad u_{n + 1}^{{\prime }} \left( l \right) = 0.$$

(4)

Let us denote the eigenvalues of the problem (1), (2), (3) (except $\lambda = 0$) by $\lambda_{1} ,\lambda_{2} ,\lambda_{3} , \ldots$ and the eigenvalues of the problem (1), (2), (4) by $\mu_{1} ,\mu_{2} ,\mu_{3} , \ldots$. The problem is to reconstruct the number $n$ of the translational springs, their locations $x_{j}$ and flexibilities $c_{j}$, $j = 1,2, \ldots ,n$, using the eigenvalues $\lambda_{i}$ and $\mu_{i}$, $i = 1,2, \ldots$.

It was proved in [9] that an arbitrary finite number of springs simulating cracks can be uniquely determined using these two spectra. In addition, a constructive algorithm for the reconstruction of springs was presented in [9]. Unfortunately, this algorithm is unstable. In this context, another algorithm based on slightly changed formulation of the problem was developed in [11]. In the next Section, the modified formulation of the problem is presented. In this Section, we also briefly recall the algorithm developed in [11] and present some improvement.

3 Numerical algorithm

The substitution of the cracks by massless springs denotes that the cracks reduce local rigidity of the rod and do not influence its density. So, instead of Eqs. (1), (2) we can consider an equation of longitudinal vibrations of a rod with variable Young’s modulus,

$$\left( {E^{*} \left( x \right)u^{\prime } \left( x \right)} \right)^{\prime } + \rho \omega^{2} u\left( x \right) = 0,\quad 0 < x < l.$$

(5)

Here $E^{*} \left( x \right)$ is the desired dependence of Young’s modulus on the coordinate.

Equation (5) can be written in a weak form for both types of the end conditions (3) and (4),

$$K\left( {u,v} \right) - \lambda M\left( {u,v} \right) = 0.$$

(6)

Here $K\left( {u,v} \right) = \int\limits_{0}^{l} {p\left( x \right)} u^{{\prime }} \left( x \right)v^{{\prime }} \left( x \right){\text{d}}x$, $M\left( {u,v} \right) = \int\limits_{0}^{l} {u\left( x \right)v} \left( x \right){\text{d}}x$, and $p(x) = E^{*} \left( x \right)/E$.

The boundary conditions (3) and (4) are taken into account in (6) only in the classes of functions to which $u\left( x \right)$ and $v\left( x \right)$ must belong. We approximate the function $p\left( x \right)$ by a piecewise constant function,

$$p\left( x \right) = p_{i} ,\quad z_{i} < x < z_{i + 1} ,\quad i = 1,2, \ldots ,P,\quad z_{i} = (i - 1) \cdot l/P.$$

(7)

Note that the following inequalities are valid: $0 < p_{i} \le 1$. The case $p_{i} = 1$ corresponds to an intact element. In the case $p_{i} = 0$, the element is completely destroyed. For the prescribed values of $p_{i}$ we solve Eq. (6) by the finite element method. Thus, Eq. (6) is reduced to the matrix equation

$$\left( {{\mathbf{K}}_{q} - \lambda^{\left( q \right)} {\mathbf{M}}} \right){\mathbf{d}}_{q} = 0,\quad q = 1,2.$$

(8)

Here ${\mathbf{K}}_{q}$ is the stiffness matrix, ${\mathbf{M}}$ is the mass matrix, ${\mathbf{d}}_{q}$ is the eigenvector, $q = 1$ corresponds to the boundary conditions (3) and $q = 2$—to the conditions (4). So, according to the notation introduced above, $\lambda_{k}^{\left( 1 \right)} = \lambda_{k}$ and $\lambda_{k}^{\left( 2 \right)} = \mu_{k}$. The eigenvalues $\lambda_{k}$ and $\mu_{k}$ are functions of the vector of parameters ${\mathbf{p}} = \left( {p_{1} , \ldots ,p_{P} } \right)$.

Let us suppose that as a result of experiment the eigenvalues $\lambda_{k}^{*}$ and $\mu_{k}^{*}$, $k = 1, \ldots ,N$ are determined. The problem is to determine the values of parameters $p_{i}$, $i = 1, \ldots ,P$, using the known eigenvalues. If as a result of solving the problem it turns out that the value of some $p_{i}$ is less than 1, this will mean that the element located in the interval $z_{i} < x < z_{i + 1}$ is damaged.

To solve the problem, we construct an objective function

$$F_{N} \left( {\mathbf{p}} \right) = \sum\limits_{k = 1}^{N} {\left[ {\left( {\frac{{\lambda_{k} \left( {\mathbf{p}} \right) - \lambda_{k}^{*} }}{{\lambda_{k}^{*} }}} \right)^{2} + \left( {\frac{{\mu_{k} \left( {\mathbf{p}} \right) - \mu_{k}^{*} }}{{\mu_{k}^{*} }}} \right)^{2} } \right]}.$$

(9)

The determination of the values of the parameters $p_{i}$ is carried out by minimizing the function $F_{N} \left( {\mathbf{p}} \right)$. According to Eq. (9), minimization of the function $F_{N} \left( {\mathbf{p}} \right)$ is a nonlinear least square problem. To solve such problems, the Levenberg–Marquardt algorithm [12] is very effective. To apply the Levenberg–Marquardt algorithm, we need to set the initial approximation for the parameters ${\mathbf{p}}$ and, in the process of implementing the algorithm, calculate the derivatives of the eigenvalues $\partial \lambda_{k}^{\left( q \right)} \left( {\mathbf{p}} \right)/\partial p_{j}$. In the calculations below, ${\mathbf{p}}^{0} = \left( {1, \ldots ,1} \right)$ is taken as the initial approximation. Such a choice corresponds to an intact beam. Due to symmetry of the matrices in Eq. (8), the derivatives of the eigenvalues are expressed in terms of the eigenvectors and derivatives of the stiffness matrix [13] ,

$$\frac{{\partial \lambda_{k}^{\left( q \right)} \left( {\mathbf{p}} \right)}}{{\partial p_{j} }} = \left( {\frac{{\partial {\mathbf{K}}_{q} \left( {\mathbf{p}} \right)}}{{\partial {\mathbf{p}}_{j} }}{\mathbf{d}}_{k}^{\left( q \right)} \left( {\mathbf{p}} \right),{\mathbf{d}}_{k}^{\left( q \right)} \left( {\mathbf{p}} \right)} \right).$$

(10)

Here we assume that the eigenvectors are normalized $\left( {{\mathbf{Md}}_{k}^{\left( q \right)} \left( {\mathbf{p}} \right),{\mathbf{d}}_{m}^{\left( q \right)} \left( {\mathbf{p}} \right)} \right) = \delta_{km}$. As we noted above, the solution of the minimization problem should satisfy the following constraints: $0 < p_{i} \le 1$. Since the range of admissible values of the parameters ${\mathbf{p}}$ has a simple shape, these constraints can be taken into account in the algorithm in a fairly simple way. The Levenberg–Marquardt algorithm is an iterative algorithm. If at the step $k$ we obtain the values of some parameters that do not satisfy the constraints $(p_{i}^{k} > 1)$, then these values are replaced by $p_{i}^{k} = 1$. The used method of taking into account constraints is close to the projected Levenberg–Marquardt method [14].

The developed numerical algorithm is applied to a sequence of objective functions $F_{N} \left( {\mathbf{p}} \right)$, $N = 1, \ldots ,N^{*}$. Calculations are performed until the results are stabilized. As a result of solving a sequence of optimization problems, we determine the intervals in which crack-like defects are located. According to (7), the length of each interval is $h = l/P$. Since it is impossible to determine too many natural frequencies from the experiment, the number of intervals $P$ cannot be very large, as a result of which the cracks are not well localized. For better localization of crack-like defects, we made the algorithm a two-stage one. Note that partition (7) not necessarily coincides with the finite element partition. Each element of the partition (7) can contain several finite elements. After solving the minimization problem and determining the damaged elements from the partition (7), the number of intervals $P$ is doubled. Each interval $\left( {z_{i} ,z_{i + 1} } \right)$ is divided into two equal intervals, the relative rigidity of which is denoted by $p_{i1}$ and $p_{i2}$. If in the first stage the part of the beam located in the interval $\left( {z_{i} ,z_{i + 1} } \right)$ we determined as undamaged ($p_{i} = 1$), then we assume $p_{i1} = 1$ and $p_{i2} = 1$. The values $p_{i1}$ and $p_{i2}$ we consider as unknowns only if $p_{i} < 1$. At the same time, the finite element partitioning of the rod remains unchanged. After determining all the unknowns $p_{i1}$, $p_{i2}$ by the minimizing algorithm, the procedure described is repeated. For example, in the examples considered below, the rod was divided into 80 finite elements, the initial partition (7) consisted of 10 elements, and then, it was doubled three times.

In conclusion of this Section, we note that in many publications the problem of detecting crack-like defects was solved by minimizing the objective function characterizing the deviation of certain calculated values from the measured ones. Links to some of these publications can be found in our previous paper [11], which outlines the main ideas of the presented method. The peculiarity of our approach is as follows. (i) The objective functions we use take into account the deviations of the calculated natural frequencies from those measured for two types of boundary conditions. (ii) Objective functions are generated by overdetermined systems of equations. (iii) A sequence of minimization problems is considered. (iv) The rigorously proved statement about the uniqueness of reconstruction of any number of cracks from two spectra [9] gives reason to hope that as the minimum values of the objective functions tend to zero, the obtained solutions tend to inhomogeneity of the rod determined by the cracks. For a fixed partition (7) determined by the number of intervals $P$, we denote ${\mathbf{p}}\left( {N,{\mathbf{p}}} \right) = \arg \hbox{min} F_{N} \left( {\mathbf{p}} \right)$. Theoretically, the proposed numerical procedure consists of two passages to the limit that determine the inhomogeneity of a cracked rod, $\lim_{P \to \infty } \left( {\lim_{N \to \infty } {\mathbf{p}}\left( {N,P} \right)} \right)$.

4 Description of the experiment

As a sample for the study, a rectilinear round cross-sectional rod of aluminum alloy D16 with a length of 2006 mm and a diameter of 24.8 mm was chosen, a sketch of which is shown in Fig. 1 (on the left). The dashed lines on it show the locations of artificial defects—annular grooves of small width (0.6 mm) and different depths—from 1 to 1.5 mm. A photograph of one of these grooves is shown in Fig. 1 (right).

Fig. 1

Test sample. A sketch of the sample with dimensions in mm and marked locations of defects in the form of annular grooves (left). Photo of a fragment of a sample with one of the defects (right)

Carrying out experiments on longitudinal vibrations of a rod with free ends is simpler than experiments with a rod, one end of which is fixed. The aim of the work is to verify the adequacy of the model we used in a fairly wide range of frequencies and the effectiveness of the developed identification method. In this regard, we limited ourselves to simpler experiments with a rod with free ends and pairs of defects symmetrically located relative to the middle of the rod. This arrangement of defects made it possible to obtain the natural frequencies for a half-length rod with free–free and fixed–free ends from the spectrum of natural frequencies of a whole rod with free ends. For such a rod, the natural frequencies corresponding to the mode shapes symmetrical with respect to the middle of the axis of the initial rod are equal to the natural frequencies of the half of the rod with free ends. The natural frequencies of the antisymmetric vibrations correspond to the natural frequencies of the fixed–free half-length rod. During the experiments, the vibration spectrum of a defect-free rod was first measured, then grooves were performed, and the vibration spectrum of the rod with defects was measured.

To excite freely damped longitudinal vibrations of the rod after impact and to register their spectrum, an experimental setup was assembled, the scheme of which is shown in Fig. 2.

Fig. 2

Scheme of the setup

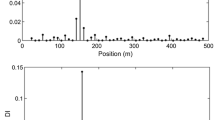
The oscillations were created by a single impact by a ball of hardened steel along one of the ends of the rod. The oscillations were recorded using a directional microphone of the BSWA MA231 type, which has a uniform frequency response in the sound frequency range and sufficient axial sensitivity to isolate the discrete components of the signal in the range up to 50 kHz. The microphone was installed near the opposite end of the rod. The signal from the microphone was transmitted to a ZETLab A19-U2 spectrum analyzer and then to a computer, where it was processed using the ZETLab software package [15]. Figure 3a shows a fragment of 0.4 s of a microphone recording of the multi-frequency signal of sound emission from the rod before and after the impact, and Fig. 3b shows the spectrum of this signal in Hz (the amplitudes along the ordinates are plotted in mV transmitted from the microphone and the spectrum analyzer to the computer).

Fig. 3

Microphone recording duration 0.4 s (a), spectrum of the signal in Hz (b)

From Fig. 3b, it can be seen that the distance between the peaks in the spectrum of the vibrational frequencies of the rod is practically the same, which is typical for a uniform spectrum of free longitudinal vibrations of the rod. However, despite the peaks in the spectrum being distinguished, in the automatic determination of frequencies using a spectrum analyzer, phantom frequencies were sometimes determined near the fundamental frequency.

The appearance of phantom frequencies is explained by the appearance of additional peaks in the vicinity of the main maximum, caused by the “blurring effect” of the spectrum, due to the fact that the fast Fourier transform used in the spectrum analyzer is applied to a limited interval of the amplitude–time dependence of the initial signal. As an illustration, Fig. 4 shows the vicinity of the second natural frequency. To increase the accuracy of determining the natural frequencies of the longitudinal vibrations of the rod from the amplitude–frequency dependence, the standard program used in the spectrum analyzer was supplemented by determination of the absolute maximum amplitude in the frequency interval that includes only one natural frequency, by means of the parabolic interpolation, close to the technique [16]. Such procedure in the vicinity of the considered frequency ensures the determination of the natural frequency with accuracy $\pm \,0.03$ Hz.

Fig. 4

Neighborhood of the second natural frequency

From the obtained amplitude–frequency dependences, up to 28 natural frequencies of the longitudinal vibrations of the test rod were determined. First, the natural frequencies of an intact rod were determined. The obtained values of natural frequencies $f_{i} = \omega_{i} /\left( {2\pi } \right)$ are presented in Table 1.

Table 1 Natural frequencies of an intact rod

Then, using the value $f_{2}$ the velocity of longitudinal wave propagation was determined. It turned out that this velocity is equal to $c = 5207.52$ m/s. The velocity is needed for calculation of the eigenvalues $\lambda_{i}$ and $\mu_{i}$ from the $f_{i}$.

5 Experimental data and results of their use for the defects reconstruction

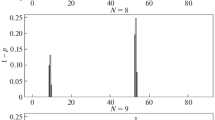
First, using the developed algorithm and the data presented in Table 1, we reconstructed the damages in the half-length intact rod. The natural frequencies from Table 1 with the even indexes are natural frequencies for a half-length rod with free ends. The natural frequencies with the odd indexes correspond to the natural frequencies of the half-length rod with the fixed–free end conditions. Initially, the half-length rod was divided into 10 parts $\left( {P = 10} \right)$. Then, according to our algorithm, the number of elements was doubled. This procedure was performed three times. As a result, the number of elements was brought to 80. The results of the search for defects when dividing half the rod into 80 elements are shown in Fig. 5. Here, the numbers of elements are indicated on the x-axis. Elements are numbered from left to right. Point 0 on the x axis corresponds to the middle of the original rod and the last element to its right end. The y-axis represents the values $1 - p_{k}$ that correspond to the flexibilities of the elements. The values of the flexibilities of the elements are shown by black columns. The height of the column corresponds to the value of flexibility.

Fig. 5

Result of identification damages in an intact rod

As shown in Fig. 5, a spurious damage is detected at the free end of the half-length rod. This is probably a consequence of the fact that according to the data presented in Table 1 the ratio $f_{n} /\left( {nf_{1} } \right)$ slowly decreases, although in accordance with the model used it should be equal to one. In the rest of the rod, as expected, the algorithm did not detect any damages. Graphically, the difference between the experimentally determined natural frequencies from the theoretical ones is shown in Fig. 6a. The x-axis shows the ordinal numbers of the natural vibration frequencies of the rod with free ends. The y-axis shows the values $\frac{{\lambda_{k}^{*} - \lambda_{k} \left( {\mathbf{p}} \right)}}{{\lambda_{k}^{*} }}$, where the values $\lambda_{k} \left( {\mathbf{p}} \right)$ and $\lambda_{k}^{*}$ were determined in Eq. (9). For the curve marked with $\times$, the values $\lambda_{k} \left( {\mathbf{p}} \right)$ correspond to the theoretical values for an intact rod. For the curve marked with $\bullet$, the values $\lambda_{k} \left( {\mathbf{p}} \right)$ are obtained after the damage reconstruction procedure.

Fig. 6

Deviation of experimental natural frequencies from calculated ones for an undamaged and a damaged rod

The dependence of the objective function on the number of iterations is presented in Fig. 7a.

Fig. 7

Dependence of the objective function on the number of iterations

The jumps in the function graph shown in Fig. 7a correspond to doubling the number P of intervals in the partition (7). Doubling the number of intervals in the partition (7) leads to a decrease in the objective function in the case of an intact rod due to the appearance of a spurious damage.

In the next step, a pair of ring grooves 0.6 mm width and 1 mm deep were made on the sample. The grooves are located symmetrically with respect to the middle of the rod at the distances of 500 mm from the ends of the original rod. Such location of a pair of grooves corresponds to one groove in a half-length rod. The natural frequencies of the original rod with a pair of grooves are presented in Table 2.

Table 2 Natural frequencies of the rod with a pair of symmetrical ring grooves

Graphically, the difference between the experimentally determined natural frequencies from the theoretical ones is shown in Fig. 6b. Dependence of the objective function on the number of iterations is presented in Fig. 7b. In Fig. 8, the results of the reconstruction of the defect in a half-length rod are shown for the cases when the half-length rod is divided into 20, 40 and, 80 elements.

Fig. 8

Identification of a single defect in a half-length rod

As can be seen from the Figure, the defect located approximately in the middle of the half rod is clearly determined for any of the presented partitions. Besides, similar to the case of an intact rod, a spurious damage is detected near the free end of the rod. We note that the flexibility of an element containing a defect increases with decreasing element length. The exact form of the dependence is given in [11].

At the next step, we added to the first pair of grooves a second pair of grooves of 0.6 mm width and 1 mm deep located at the distances 100 mm from the ends of the original rod. So in this experiment we have two defects on each half of the rod. The experimentally obtained values of natural frequencies of longitudinal vibration of a rod with two pairs of grooves are presented in Table 3. The difference between the experimentally determined natural frequencies from the theoretical ones is shown in Fig. 6c.

Table 3 Natural frequencies of the rod with two pairs of symmetrical ring grooves

The use of experimentally obtained natural frequencies for an original rod led to the result of defect reconstruction in a half of the rod that is presented in Fig. 9. In Fig. 9, only results corresponding to the partition into 80 elements are presented since the character of the change in the results when divided into 20, 40, and 80 elements approximately corresponds to the change in the results that are presented in Fig. 8.

Fig. 9

Identification of two defects in a half-length rod

As shown in Fig. 9, despite the fact that the second defect is near the spurious damage, the location of both defects is established with sufficiently high accuracy. At the same time, it can be noted that there is some difference in the values of flexibilities of damaged elements, although the depths of the grooves made are the same, and therefore, theoretically the flexibilities of damaged elements should also be equal.

The next experiment was performed with three pairs of ring grooves. The third pair of grooves was created at the distances 900 mm from the ends of the original rod. The width and the depth of these grooves are the same as those of the first and the second pairs of grooves. The corresponding values of natural frequencies are presented in Table 4. The difference between experimental and theoretical values of natural frequencies is shown in Fig. 6d. Processing of experimental data led to the results presented in Fig. 10.

Table 4 Natural frequencies of the rod with three pairs of symmetrical ring grooves

Fig. 10

Identification of three defects in a half-length rod

Figure 10 shows that the location of all three defects was established with fairly high accuracy. When determining the flexibility of damaged elements, there is some error, since the flexibility of elements is somewhat different, despite the same depth of grooves.

In the last experiment, we deepened the first pair of ring grooves to 1.5 mm. The corresponding values of natural frequencies are presented in Table 5. The results of processing of the experimental data are presented in Fig. 11.

Table 5 Natural frequencies of the rod with three pairs of symmetrical ring grooves of different depths

Fig. 11

Identification of three defects of different depth in a half-length rod

It can be noted here that in comparison with Fig. 10 the ratio of column heights that indicate the degree of the flexibility of the elements has changed. The column height corresponding to the central defect, after its deepening, became maximum. Thus, using the developed algorithm, it is possible not only to accurately determine the position of the defects, but also to approximately estimate their severity.

6 Conclusions

The algorithm for identifying multiple localized defects in the rod by two spectra of longitudinal vibrations is improved. Processing of experimental data showed that the model on which the algorithm is based describes rather well longitudinal vibrations of a rod with localized damage in a fairly wide frequency range. Using the developed algorithm, it is possible to detect and very accurately localize existing defects even of a relatively small size. The decrease in stiffness of the element containing the damage is determined with small errors. Processing of all experiments revealed spurious damage near the free end of the rod. This is probably due to small deviations of the experimentally measured natural frequencies from theoretical ones in an intact rod. In the experiments performed, two types of boundary conditions were modeled by a rod of double length with free ends. For the practical application of the developed method of defects identification, it is necessary to develop a method for high-precision measurement of the natural frequencies of longitudinal vibrations of a rod with fixed–free ends. It is known that if to excite a rod from one end and to measure the response at the same end, then it is possible to determine the natural frequencies for both types of the boundary conditions by means of determining poles and zeros of the frequency response function [4, 17]. In this paper, we did not use this measurement method, since one of the purposes of the paper is the study of the correctness of the used mathematical model of a rod with localized damages in a wide frequency range. Another purpose of the paper is clarification of the capabilities of the developed algorithm for determination of crack-like defects not only of large, but also of relatively small sizes. Experimental errors in the approach based on the frequency response function are larger than the in method used in this paper. For example, the added mass 4 g of the accelerometer used in [4] introduces errors into the values of natural frequencies for the rod considered in our paper that are much larger than the perturbations determined by the cracks under consideration.