1 Introduction

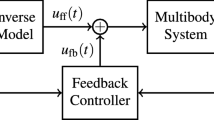
Trajectory tracking for underactuated manipulators is an important problem in control engineering. Some benefits are related to the ability to control lightweight flexible multibody systems that could result in real advances for industries and human–machine interactions. In industrial applications, this could increase productivity and decrease the electrical power demand of the actuators. Therefore, those manipulators could be well suited for the next-generation industry. In order to establish an efficient control design, a realistic mechanical model should be considered with an accurate description of elastic deformations. In addition, the elastic deformation of the joints/bodies should be controlled during the motion, e.g. by an effective feedforward control design for underactuated manipulators. Thus, this system could realize the same task as a rigid manipulator with a lighter design.

Trajectory tracking problems for systems with unstable internal dynamics, such as underactuated manipulators, can be successfully solved by the stable inversion method. This method involves the solution of a boundary value problem, see [8, 12, 22]. However, it is also known that robust direct methods in optimal control are well suited to solve problems with nonlinearities and instabilities. The direct transcription (DT) method [6] was successfully used for the inverse dynamics of underactuated multibody systems, see [2, 3, 18]. The direct multiple shooting (DMS) method [7] is proposed here for the feedforward control design of underactuated manipulators in trajectory tracking problems. This method is more difficult to implement, but possesses the advantage to permit a finer discretization and lends itself to parallel computation [17]. Therefore, DMS would be an ideal candidate to nonlinear model predictive control, see [13].

The main contributions of this work are: (i) the development of an alternative formulation for the trajectory tracking problem of underactuated manipulators; (ii) a parallel computation strategy for the inverse dynamics of underactuated manipulators, where, in consequence, large problems can be considered, e.g. related to the time interval; (iii) a comparison/validation with the direct transcription method and the stable inversion method.

A systematic numerical mechanical modelling approach is used based on the geometrically exact finite element method, as in [15]. In this case, the equation of motion of a multibody systems is composed of a dynamic equation and kinematic constraints, leading to an index-3 differential-algebraic equation (DAE). A trajectory constraint is then added to the equation of motion in order to establish the trajectory tracking problem. The generalized-\(\alpha \) time integration method [11] is considered for the dynamic analysis of constrained multibody systems, see [1]. This method is second-order accurate in the general case and unconditionally stable in the linear case. An analytical sensitivity analysis, as in [9], is considered for the optimization process. The method is illustrated by a planar underactuated manipulator with one passive joint.

2 Formulation of the optimization problem

For multibody systems, e.g. manipulators, the feedforward control design can be based on the inverse dynamics. In this context, the inverse dynamics of an underactuated manipulator can be formulated as an optimal control problem, which is summarized as follows. The equations of motion of the multibody system, including the kinematic constraints,

$$\begin{aligned} {\mathbf {M}}({\mathbf {q}}){\ddot{\mathbf{q}}} + {\mathbf {g}}({\mathbf {q}},{\dot{\mathbf{q}}}, t) + {\mathbf {B}}^T({\mathbf {q}})\varvec{\lambda } - {\mathbf {A}}{\mathbf {u}}= & {} {\mathbf {0}}, \end{aligned}$$
(1)
$$\begin{aligned} \varvec{\varPhi }({\mathbf {q}})= & {} {\mathbf {0}}, \end{aligned}$$
(2)

should be satisfied at any time. Here, \({\mathbf {q}}\) is the vector of r absolute coordinates, \({\mathbf {M}}\) is the mass matrix, \({\mathbf {g}}\) is the vector of internal and complementary inertia forces, \(\varvec{\varPhi }\) is the vector of m kinematic constraints, \(\varvec{\lambda }\) is the vector of m Lagrange multipliers, and \({\mathbf {B}} = {\partial \varvec{\varPhi }({\mathbf {q}}) / \partial {\mathbf {q}}}\) is the matrix of constraint gradients. The input matrix \({\mathbf {A}}\) distributes the s control inputs \({\mathbf {u}}\) onto the directions of the system coordinates, whereby \({\mathbf {A}}\) is often a constant matrix. We assume that \({\mathbf {M}}\) is non-singular and that the matrix \([{\mathbf {B}}^T \quad {\mathbf {A}}]\) is full rank. This equation of motion is then an index-3 DAE, since holonomic constraints on the position coordinates are present. The system is underactuated if \(r-m-s > 0\). The s trajectory constraints (servo-constraints) should also be fulfilled at any time:

$$\begin{aligned} {\mathbf {y}}({\mathbf {q}}) - {\mathbf {y}}_d(t) = {\mathbf {0}} , \end{aligned}$$
(3)

where the operator \({\mathbf {y}}({\mathbf {q}})\) computes the outputs of the dynamic system and the function \({\mathbf {y}}_d(t)\) represents the prescribed trajectory. However, for underactuated systems these constraints can be non-collocated with the actuators, and the internal dynamics might therefore become unstable. In order to find a bounded solution for the cases of non-minimum phase systems, a non-causal analysis can be considered. To achieve this aim, pre-/post-actuation phases should be considered. During these phases, the output is fixed, but the actuators can be active.

The relative degree of a system is defined as the number of differentiations of the output which are needed so that the input appears in the equations. In the present cases, the relative degree is assumed to be two for each output.

The main objective in the control design is to find the control inputs \({\mathbf {u}}\) in order to minimize the internal dynamics motion. Thus, the position of the end effector and the deformation of passive joint or flexible links must be controlled. To achieve this aim, the general index of performance, which should be minimized under the constraints that Eqs. (1–3) are satisfied for all time in \(t_0 \le t \le t_f\), is established as

$$\begin{aligned} J = \int _{t_0}^{t_f} L({\mathbf {q}}(t), {\dot{\mathbf{q}}}(t), {\mathbf {u}}(t))\, dt + E({\mathbf {q}}(t_f), {\dot{\mathbf{q}}}(t_f)). \end{aligned}$$
(4)

Theoretically, when the pre-/post-actuation phases tend to infinity, the solution of this optimization problem tends to the solution of the stable inverse method; otherwise, an approximation is obtained. In practice, increasing the pre-/post-actuation phases length tends to improve the results, at the interval extremities essentially, see [3].

3 Direct multiple shooting method

The multiple shooting strategy is based on multiple initial value problems (IVPs) to be solved within the optimization process. The initial values of position and velocity variables at each phase compose the optimization variables. Defects are established at the end of each phase after the forward integration, between final values at phase k and initial values at phase \(k+1\). Those defects are then treated as equality constraints of the optimization problem. Figure 1 illustrates the principle of the multiple shooting method, where we can see the initial guess of the optimization variables, the N solution of the IVPs, the defects and the optimal trajectory that represents the solution.

The problem is discretized into N phases or shooting subintervals \([t^{(k)}, t^{(k+1)}]\). The equations of motion (1–2) are then solved independently on each interval by forward time integration using approximated initial values \({\mathbf {q}}^{(k)}_0\), \({\dot{\mathbf{q}}}^{(k)}_0\) and a control input function \({\mathbf {u}}(t)\) defined by interpolation. In this work, a linear interpolation between the initial value \({\mathbf {u}}^{(k)}_0\) and the final value \({\mathbf {u}}^{(k+1)}_0\) is used, but other interpolation methods could also be considered.

Fig. 1
figure 1

Scheme—direct multiple shooting

Full size image

The numerical integration algorithm provides a solution of Eqs. (1–2) on the time interval \([t^{(k)}, t^{(k+1)}]\) which depends on \({\mathbf {q}}^{(k)}_0\), \({\dot{\mathbf{q}}}^{(k)}_0\), \({\mathbf {u}}^{(k)}_0\) and \({\mathbf {u}}^{(k+1)}_0\), i.e,

$$\begin{aligned}&{\mathbf {q}}^{(k)}(t^{(k+1)};{\mathbf {q}}_0^{(k)},{\dot{\mathbf{q}}}_0^{(k)}, {\mathbf {u}}^{(k)}_0,{\mathbf {u}}^{(k+1)}_0), \end{aligned}$$
(5)
$$\begin{aligned}&{\dot{\mathbf{q}}}^{(k)}(t^{(k+1)};{\mathbf {q}}_0^{(k)},{\dot{\mathbf{q}}}_0^{(k)}, {\mathbf {u}}^{(k)}_0,{\mathbf {u}}^{(k+1)}_0). \end{aligned}$$
(6)

Continuity conditions are imposed on the defect between two successive subintervals and at the final time interval \(t^{(N+1)}\):

$$\begin{aligned} {\mathbf {q}}^{(k)} (t;{\mathbf {q}}_0^{(k)},{\dot{\mathbf{q}}}_0^{(k)}, {\mathbf {u}}^{(k)}_0,{\mathbf {u}}^{(k+1)}_0)= & {} {\mathbf {q}}_0^{(k+1)}, \end{aligned}$$
(7)
$$\begin{aligned} {\dot{\mathbf{q}}}^{(k)} (t;{\mathbf {q}}_0^{(k)},{\dot{\mathbf{q}}}_0^{(k)}, {\mathbf {u}}^{(k)}_0,{\mathbf {u}}^{(k+1)}_0)= & {} {\dot{\mathbf{q}}}_0^{(k+1)}. \end{aligned}$$
(8)

It is known that trajectory tracking problems of underactuated multibody systems can hardly be solved by forward integration if the system is non-minimum phase, due to the instability of the internal dynamics, see [8, 12]. For that reason, the trajectory constraints, Eq. (3), are not added to the equation of motion (Eqs. (1–2)) in forward integration; for example, the dynamics is integrated forward in time based on the value of control inputs given by interpolation. For this reason, the servo-constraint, Eq. (3), is solely imposed as a constraint for the optimization problem at every time \(t^{(k)}, k=1,2,\ldots ,N\).

The optimization problem is then formulated in terms of the set of design variables which include the displacements \({\mathbf {q}}\), the velocities \({\dot{\mathbf{q}}}\) and the control inputs \({\mathbf {u}}\) of the system at the initial time of each shooting phase. The shooting step is defined as the length of the phase \(h_s^{(k)} = t^{(k+1)} - t^{(k)}\). Here, only constant shooting steps are used \(h_s = h_s^{(k)}\). For convenience, let us introduce a subset of the design variables which are related to the shooting time (k), with \(k=1,\ldots ,N+1\), as

$$\begin{aligned} {\mathbf {x}}^{(k)}=({\mathbf {q}}_0^{(k)};{\dot{\mathbf{q}}}_0^{(k)}; {\mathbf {u}}^{(k)}_0). \end{aligned}$$
(9)

Therefore, the set of design variables is written as

$$\begin{aligned} {\mathbf {x}} = ({\mathbf {x}}^{(1)}; \ldots ; {\mathbf {x}}^{(k)}; \ldots ;{\mathbf {x}}^{(N+1)}). \end{aligned}$$
(10)

The dimension of \({\mathbf {x}}\) is \(n = (N+1)(2r+s)\), which is generally large in practical applications. The design domain is defined as \(D \subset {\mathbb {R}}^n\).

The optimization problem takes the form

$$\begin{aligned} \begin{array}{c} \displaystyle \min _{\mathbf {x}} J^d({\mathbf {x}}) \\ \quad \text{ s.t } \mathbf {c^d}({\mathbf {x}}) = {\mathbf {0}} \end{array} \end{aligned}$$
(11)

where \( J^d \ : \! D \subset {\mathbb {R}}^n \! \longrightarrow \! {\mathbb {R}} \) is the discretized objective function and \( \mathbf {c}^\mathbf{d} \ : \! D \subset {\mathbb {R}}^n \! \longrightarrow \! {\mathbb {R}}^{n_{ec}} \) is the vector of \(n_{ec}\) discrete equality constraints, which includes the following contributions.

Continuity constraints have to be imposed at the end of each shooting step \( k = 1, \ldots ,N\),

$$\begin{aligned} {\mathbf {c}}^{(k)}_{\mathbf {cont}}({\mathbf {x}}^{(k)},{\mathbf {x}}^{(k+1)}) = \left( \begin{array}{c} {\mathbf {q}}^{(k)}(t^{(k+1)};{\mathbf {x}}^{(k)},{\mathbf {x}}^{(k+1)})-{\mathbf {q}}_0^{(k+1)}\\ {\dot{\mathbf{q}}}^{(k)}(t^{(k+1)};{\mathbf {x}}^{(k)},{\mathbf {x}}^{(k+1)})-{\dot{\mathbf{q}}}_0^{(k+1)} \end{array} \right) = {\mathbf {0}}, \end{aligned}$$
(12)

where \({\mathbf {q}}^{(k)}(t^{(k+1)};{\mathbf {x}}^{(k)},{\mathbf {x}}^{(k+1)})\) and \({\dot{\mathbf{q}}}^{(k)}(t^{(k+1)};{\mathbf {x}}^{(k)},{\mathbf {x}}^{(k+1)})\) represent the dynamic response at the end of the shooting interval and thus depend on a subset of design variables \({\mathbf {x}}^{(k)}\). These continuity constraints are treated in the optimization process and are crucial in multiple shooting methods to ensure an acceptable solution.

The solution should be such that \({\mathbf {q}}_0^{(k)}\) and \({\dot{\mathbf{q}}}_0^{(k)}\), with \(k=1,\ldots ,N+1\), satisfy the kinematic constraints at position level, see Eq. (2), and also at velocity level. In this work, the time integration is performed using an index-3 DAE solver without index reduction. This method guarantees that \({\mathbf {q}}^{(k)}(t^{(k+1)}\)) and \({\dot{\mathbf{q}}}^{(k)}(t^{(k+1)})\), with \(k=1,\ldots ,N\), satisfy the kinematic constraints at position level exactly (more precisely, up to the tolerance imposed for the constraints) and the kinematic constraints at velocity level approximately. If the continuity constraints are satisfied, the kinematic constraints will also be satisfied for the variables \({\mathbf {q}}_0^{(k)}\) (exactly) and \({\dot{\mathbf{q}}}_0^{(k)}\) (approximately), with \(k=2,\ldots ,N+1\). Therefore, to avoid a violation of the constraints at the initial time (there are no continuity constraints for \({\mathbf {q}}_0^{(1)}\) and \({\dot{\mathbf{q}}}_0^{(1)}\)), the following kinematic constraints need to be explicitly imposed:

$$\begin{aligned} {\mathbf {c}}_{\mathbf {kin}}({\mathbf {x}}^{(1)}) = \left( \begin{array}{c} \varvec{\varPhi }({\mathbf {q}}_0^{(1)}) \\ {\mathbf {B}}({\mathbf {q}}_0^{(1)})\;{\dot{\mathbf{q}}}_0^{(1)} \end{array} \right) = {\mathbf {0}}. \end{aligned}$$
(13)

The trajectory constraints in Eq. (3) are imposed as optimization constraints at each shooting time \(t^{(k)}\), \(k = 1,\ldots ,N+1\) to track the desired trajectory for the output of the system:

$$\begin{aligned} {\mathbf {c}}^{(k)}_{{{\mathbf {t}}}{{\mathbf {r}}}}({\mathbf {x}}^{(k)}) = {\mathbf {y}}({\mathbf {q}}^{(k)}_0) - \mathbf {y_{d}}(t^{(k)}) = {\mathbf {0}}. \end{aligned}$$
(14)

The vector of equality constraints then comprises each component of those constraints at each time step:

$$\begin{aligned} \mathbf {c}^\mathbf{d}({\mathbf {x}}) = ({\mathbf {c}}_{\mathbf {kin}};{\mathbf {c}}^{(1)}_{{{\mathbf {t}}}{{\mathbf {r}}}}; {\mathbf {c}}^{(1)}_{\mathbf {cont}}; \ldots ;{\mathbf {c}}^{(N)}_{{{\mathbf {t}}}{{\mathbf {r}}}}; {\mathbf {c}}^{(N)}_{\mathbf {cont}}; {\mathbf {c}}^{(N+1)}_{{{\mathbf {t}}}{{\mathbf {r}}}}) = {\mathbf {0}}. \end{aligned}$$
(15)

Each component of the constraint in Eq. (15) only depends on a few components of the large vector \({\mathbf {x}}\) given by Eq. (10), and then, the resulting NLP problem has a sparse structure.

The objective function in Eq. (4) can be discretized as

$$\begin{aligned} J^d = \sum _{k = 1}^{N} L({\mathbf {q}}^{(k)}, {\dot{\mathbf{q}}}^{(k)}, {\mathbf {u}}^{(k)})\, h_s + E({\mathbf {q}}^{(N+1)}, {\dot{\mathbf{q}}}^{(N+1)}), \end{aligned}$$
(16)

where \(h_s\) is the shooting step. In order to increase the accuracy, a higher-order discretization could be used or the objective function could be evaluated using the time integrator in each shooting phase. This might be mandatory if \(h_s\) is not sufficiently small for the problem under study.

The optimal solution satisfies the Karush–Kuhn–Tucker necessary conditions of optimality. Standard NLP solvers can be used to solve such problems efficiently, see [5]. In this work, the fmincon function of the MATLAB\(\copyright \) is used. The selected optimization algorithm is the interior point method, see [20], which is well suited for direct optimal control problems. Indeed, the interior point is a large-scale algorithm and can estimate the Hessian using a limited-memory through a quasi-Newton method.

4 Multiple forward integration

At each iteration of the optimization process and for each shooting subinterval \(k=1,\ldots ,N\), the equality constraint \({\mathbf {c}}^{(k)}_{\mathbf {cont}}({\mathbf {x}}^{(k)},{\mathbf {x}}^{(k+1)})\) is evaluated. This evaluation requires the solution of the following initial value problem over the time interval \([t^{(k)}, t^{(k+1)}]\)

$$\begin{aligned} {\mathbf {M}}({\mathbf {q}}){\ddot{\mathbf{q}}} + {\mathbf {g}}({\mathbf {q}},{\dot{\mathbf{q}}}, t) + {\mathbf {B}}^T({\mathbf {q}})\varvec{\lambda } - {\mathbf {A}}{\mathbf {u}}({\mathbf {u}}_0^{(k)},{\mathbf {u}}_0^{(k+1)}, t)= & {} {\mathbf {0}} , \end{aligned}$$
(17)
$$\begin{aligned} \varvec{\varPhi }({\mathbf {q}})= & {} {\mathbf {0}}, \end{aligned}$$
(18)

with the initial values \({\mathbf {q}}(t^{(k)})={\mathbf {q}}_0^{(k)}\), \({\dot{\mathbf{q}}}(t^{(k)})={\dot{\mathbf{q}}}_0^{(k)}\) obtained from the subset of design variables \({\mathbf {x}}^{(k)}\). The control inputs over each shooting subinterval are defined by linear interpolation between the extremities of each shooting step

$$\begin{aligned} {\mathbf {u}}({\mathbf {u}}_0^{(k)},{\mathbf {u}}_0^{(k+1)},t) = \frac{t^{(k+1)}-t}{t^{(k+1)}-t^{(k)}} {\mathbf {u}}_0^{(k)}+\frac{t-t^{(k)}}{t^{(k+1)}-t^{(k)}}{\mathbf {u}}_0^{(k+1)}. \end{aligned}$$
(19)

As already mentioned, Eq. (3) is not considered within the forward integration so that the dynamic system to be integrated is stable, even if it is non-minimum phase. Therefore, the trajectory constraints are considered after the simulation, see Eq. (14), together with the continuity constraints, see Eq. (12). This hybrid strategy combines multiple forward time integrations with an optimization approach for the analysis of the inverse dynamics of non-minimum phase systems.

For the index-3 DAE, Eqs. (17–18), the initial value problem is well-posed if the initial values satisfy the kinematic constraints at both position and velocity levels:

$$\begin{aligned} \varvec{\varPhi }({\mathbf {q}}^{(k)}_0)= & {} {\mathbf {0}} , \end{aligned}$$
(20)
$$\begin{aligned} {\mathbf {B}}({\mathbf {q}}^{(k)}_0)\,{\dot{\mathbf{q}}}^{(k)}_0= & {} {\mathbf {0}} . \end{aligned}$$
(21)

However, in the multiple shooting technique, the initial values are extracted from the vector of design variables, which is automatically updated by the optimization algorithm, regardless of the above conditions. Therefore, during the optimization process, the initial values may not be consistent with the constraints. In order to avoid numerical problems, a classical projection algorithm, see, for example, the mass orthogonal projection proposed, see [4, 21], can be used to project the initial value on the constraint manifold before starting the forward time integration process. Such a projection leads to a more robust and stable numerical integration of the equations of motion.

In practice, our experience is that such a projection step is not really mandatory if the initial guess of the design variable \({\mathbf {x}}\) is such that the initial values for each shooting subinterval \({\mathbf {q}}^{(k)}_0\) and \({\dot{\mathbf{q}}}^{(k)}_0\) satisfy the constraints at both position and velocity levels. Indeed, in this case, the initial values also stay in close neighbourhood of the constraints during the optimization process. Therefore, this projection can often be skipped in practice.

The generalized-\(\alpha \) method [1, 11] that is based on the Newmark formulae [19] is used to solve the index-3 DAE (Eqs. (17–18)). A constant step-size h is considered which is related to the length of the shooting subintervals \(h_s\) by a relation

$$\begin{aligned} h_s=M\, h, \end{aligned}$$
(22)

where \(M\ge 1\) is an integer. In our notations, the superscript [j], with \(j=1,\ldots ,M+1\), denotes the time step and it should not be confused with the superscript (k) which denotes the shooting step. For example, we have \(t^{[1]}=t^{(k)}\) and \(t^{[M+1]}=t^{(k+1)}\). The integration formulae are

$$\begin{aligned} {\dot{\mathbf{q}}}^{[j+1]}= & {} {\dot{\mathbf{q}}}^{[j]} + (1 - \gamma )h{\mathbf {a}}^{[j]} + \gamma h{\mathbf {a}}^{[j+1]} , \end{aligned}$$
(23)
$$\begin{aligned} {\mathbf {q}}^{[j+1]}= & {} {\mathbf {q}}^{[j]} + h{\dot{\mathbf{q}}}^{[j]} + (\frac{1}{2} - \beta )h^2{\mathbf {a}}^{[j]} + \beta h^2{\mathbf {a}}^{[j+1]}, \end{aligned}$$
(24)

with an additional acceleration update formula

$$\begin{aligned} {\mathbf {a}}^{[j+1]} = \frac{1}{(1-\alpha _m)} [-\alpha _m{\mathbf {a}}^{[j]} + (1-\alpha _f){\ddot{\mathbf{q}}}^{[j+1]}+\alpha _f{\ddot{\mathbf{q}}}^{[j]}],\quad {\mathbf {a}}^{[1]} ={\ddot{\mathbf{q}}}^{[1]} , \end{aligned}$$
(25)

where \(\gamma \), \(\beta \), \(\alpha _m\) and \(\alpha _f\) are numerical parameters which can be chosen to combine unconditional stability and second-order accuracy. The numerical damping can be adjusted to obtain a given spectral radius at infinite frequencies \(\rho _{\infty }\), see [11].

5 Initial guess

The convergence of gradient-based optimization algorithms is quite sensitive to the initial guess of the design variable \({\mathbf {x}}\). This initial guess should be carefully selected in order to guarantee the convergence of the optimization process. Therefore, for underactuated manipulators the desired output motion without elastic deformation of the passive elements is considered. The initial guess is defined as follows.

Let us assume that, for every time t, the system has an equilibrium point \({\mathbf {q}}_e(t)\) which is a solution of the algebraic system

$$\begin{aligned} {\mathbf {g}}({\mathbf {q}}_e,{\mathbf {0}}, t) + {\mathbf {B}}^T({\mathbf {q}}_e)\varvec{\lambda } - {\mathbf {A}}{\mathbf {u}}= & {} {\mathbf {0}}, \end{aligned}$$
(26a)
$$\begin{aligned} \varvec{\varPhi }({\mathbf {q}}_e)= & {} {\mathbf {0}}, \end{aligned}$$
(26b)
$$\begin{aligned} {\mathbf {y}}({\mathbf {q}}_e) - \mathbf {y}_\mathbf{d}(t)= & {} {\mathbf {0}}, \end{aligned}$$
(26c)

and assume that the matrix

$$\begin{aligned} \left[ \begin{array}{ccc} {\mathbf {K}}_t&{}\quad {\mathbf {B}}^T &{}\quad -{\mathbf {A}}\\ {\mathbf {B}}&{}\quad {\mathbf {0}}&{}\quad {\mathbf {0}}\\ {\mathbf {D}}&{}\quad {\mathbf {0}}&{}\quad {\mathbf {0}} \end{array}\right] \end{aligned}$$
(27)

is non-singular, where \({\mathbf {K}}_t = \partial ({\mathbf {g}}+{\mathbf {B}}^T\varvec{\lambda } - {\mathbf {A}}{\mathbf {u}})/\partial {\mathbf {q}}\) is the tangent stiffness matrix of the system and \({\mathbf {D}}=\partial {\mathbf {y}}/\partial {\mathbf {q}}\).

The initial guess is then defined as

$$\begin{aligned} {\mathbf {q}}^{(k)}_0= & {} {\mathbf {q}}_e(t^{(k)}) ,\end{aligned}$$
(28)
$$\begin{aligned} {\dot{\mathbf{q}}}^{(k)}_0= & {} \frac{\mathrm{d}{\mathbf {q}}_e}{\mathrm{d} t}(t^{(k)}). \end{aligned}$$
(29)

The equilibrium configuration \({\mathbf {q}}_e(t^{(k)})\) is found by solving the equilibrium condition at time \(t^{(k)}\) defined by Eq. (26). This is again a nonlinear problem which is solved using a Newton iterative procedure, and the value at the previous interval \({\mathbf {q}}^{(k-1)}_{0}\) is used as initial guess. The time derivative of \({\mathbf {q}}_e\) is found by solving the time-differentiated form of the equilibrium condition (26) as

$$\begin{aligned} {\mathbf {K}}_{t}\frac{\mathrm{d}{\mathbf {q}}_e}{\mathrm{d} t}+{\mathbf {g}}_t + {\mathbf {B}}^T({\mathbf {q}}_e)\frac{\mathrm{d}\varvec{ \lambda }}{\mathrm{d}t} - {\mathbf {A}}\frac{\mathrm{d}{\mathbf {u}}}{\mathrm{d}t}= & {} {\mathbf {0}}, \end{aligned}$$
(30)
$$\begin{aligned} {\mathbf {B}}\frac{\mathrm{d}{\mathbf {q}}_e}{\mathrm{d} t}= & {} {\mathbf {0}}, \end{aligned}$$
(31)
$$\begin{aligned} {\mathbf {D}}\frac{\mathrm{d}{\mathbf {q}}_e}{\mathrm{d} t} - {\dot{\mathbf{y}}_d}(t)= & {} {\mathbf {0}}. \end{aligned}$$
(32)

In this way, the initial guess is such that the initial conditions satisfy the kinematic constraints and the trajectory constraints at both position and velocity levels. As in the direct transcription method for underactuated multibody systems [2], the initial velocities could alternatively be set to zero. Our experience is that the direct multiple shooting also converges in this case, but a couple of additional iterations are required.

6 Sensitivity analysis

Analytical methods are used to compute the sensitivities of the design functions \(J^d\) and \(\mathbf {c}^\mathbf{d}\) with respect to the design variables \({\mathbf {x}}\). Analytical methods lead to an accurate estimation of the gradients which improves the convergence speed of the optimization algorithm and they naturally exploit the sparse structure of the NLP problem, which contributes to reduce the computational cost.

For the objective function discretized in Eq. (16), the Jacobian matrix has the form \( {\partial J^d \over \partial {\mathbf {x}}} \).

The gradient of the equality constraints is based on the gradient of the continuity constraints in Eq. (12),

$$\begin{aligned} { \partial {\mathbf {c}}^{(k)}_{\mathbf {cont}} \over \partial {\mathbf {x}}^{(k)} }= & {} \left( \begin{array}{ccc} \displaystyle { \partial {\mathbf {q}}^{(k)}_f \over \partial {\mathbf {q}}^{(k)}_0 } &{} \displaystyle { \partial {\mathbf {q}}^{(k)}_f \over \partial {\dot{\mathbf{q}}}^{(k)}_0 } &{} \displaystyle { \partial {\mathbf {q}}^{(k)}_f \over \partial {\mathbf {u}}^{(k)} } \\ \displaystyle { \partial {\dot{\mathbf{q}}}^{(k)}_f \over \partial {\mathbf {q}}^{(k)}_0 } &{} \displaystyle { \partial {\dot{\mathbf{q}}}^{(k)}_f \over \partial {\dot{\mathbf{q}}}^{(k)}_0 } &{} \displaystyle {\partial {\dot{\mathbf{q}}}^{(k)}_f \over \partial {\mathbf {u}}^{(k)} } \end{array} \right) , \end{aligned}$$
(33)
$$\begin{aligned} {\partial {\mathbf {c}}^{(k)}_{\mathbf {cont}} \over \partial {\mathbf {x}}^{(k+1)}}= & {} \left( \begin{array}{cccc} {\mathbf {I}} &{}\quad {\mathbf {0}} &{}\quad \displaystyle { \partial {\mathbf {q}}^{(k)}_f \over \partial {\mathbf {u}}^{(k+1)} } \\ {\mathbf {0}} &{}\quad {\mathbf {I}} &{}\quad \displaystyle { \partial {\dot{\mathbf{q}}}^{(k)}_f \over \partial {\mathbf {u}}^{(k+1)} } \end{array} \right) , \end{aligned}$$
(34)

on the gradient of the kinematic constraint, see Eq. (13),

$$\begin{aligned} {\partial {\mathbf {c}}_{\mathbf {kin}} \over \partial {\mathbf {x}}^{(1)}} = \left( \begin{array}{ccc} {\mathbf {B}}({\mathbf {q}}_0^{(1)}) &{}\quad {\mathbf {0}} &{}\quad {\mathbf {0}}\\ \displaystyle \frac{\partial \left( {\mathbf {B}}({\mathbf {q}}_0^{(1)})\;{\dot{\mathbf{q}}}_0^{(1)}\right) }{ \partial {\mathbf {q}}_0^{(1)}} &{} {\mathbf {B}}({\mathbf {q}}_0^{(1)}) &{}{\mathbf {0}} \end{array} \right) , \end{aligned}$$
(35)

and on the gradient of the trajectory constraint in Eq. (14),

$$\begin{aligned} {\partial {\mathbf {c}}^{(k)}_{{{\mathbf {t}}}{{\mathbf {r}}}} \over \partial {\mathbf {x}}^{k}} = \left( \begin{array}{ccccc} \displaystyle { {\mathbf {D}}}&\quad {\mathbf {0}}&\quad {\mathbf {0}} \end{array} \right) . \end{aligned}$$
(36)

With these contributions, the Jacobian matrix of the constraints in Eq. (15) is written as

$$\begin{aligned} {\partial \mathbf {c}^\mathbf{d} \over \partial {\mathbf {x}}} = \left( \begin{array}{c|c|c|c|c|c} \displaystyle {\partial {\mathbf {c}}_{\mathbf {kin}} \over \partial {\mathbf {x}}^{(1)}} &{}\quad &{}\quad &{} \quad &{}\quad &{}\quad \\ \hline \displaystyle {\partial {\mathbf {c}}^{(1)}_{{{\mathbf {t}}}{{\mathbf {r}}}} \over \partial {\mathbf {x}}^{(1)}} &{}\quad &{}\quad &{}\quad &{} \quad &{} \quad \\ \hline \displaystyle {\partial {\mathbf {c}}^{(1)}_{\mathbf {cont}} \over \partial {\mathbf {x}}^{(1)}} &{}\quad \displaystyle {\partial {\mathbf {c}}^{(1)}_{\mathbf {cont}} \over \partial {\mathbf {x}}^{(2)}} &{} \quad &{} \quad &{}\quad \\ \hline &{} \quad &{}\quad \ddots &{} \quad &{}\quad \\ \hline &{} \quad &{} \quad &{}\quad \displaystyle {\partial {\mathbf {c}}^{(N-1)}_{{{\mathbf {t}}}{{\mathbf {r}}}} \over \partial {\mathbf {x}}^{(N-1)}} &{} \quad \\ \hline &{} \quad &{} \quad &{} \quad \displaystyle {\partial {\mathbf {c}}^{(N-1)}_{\mathbf {cont}} \over \partial {\mathbf {x}}^{(N-1)}} &{} \quad \displaystyle {\partial {\mathbf {c}}^{(N-1)}_{\mathbf {cont}} \over \partial {\mathbf {x}}^{(N)}} &{} \quad \\ \hline &{} \quad &{} \quad &{} \quad &{}\quad \displaystyle {\partial {\mathbf {c}}^{(N)}_{{{\mathbf {t}}}{{\mathbf {r}}}} \over \partial {\mathbf {x}}^{(N)}} &{} \quad \\ \hline &{} \quad &{} \quad &{}\quad &{}\quad \displaystyle {\partial {\mathbf {c}}^{(N)}_{\mathbf {cont}} \over \partial {\mathbf {x}}^{(N)}} &{} \displaystyle {\partial {\mathbf {c}}^{(N)}_{\mathbf {cont}} \over \partial {\mathbf {x}}^{(N+1)}} \\ \hline &{} \quad &{} \quad &{}\quad &{}\quad &{}\quad \displaystyle { \partial {\mathbf {c}}^{(N+1)}_{{{\mathbf {t}}}{{\mathbf {r}}}} \over \partial {\mathbf {x}}^{(N+1)} } \end{array} \right) . \end{aligned}$$

As usual in direct optimal control methods, the Jacobian matrix is large, but it exhibits a sparse block diagonal structure. The size of the design variables and of the Jacobian matrix of the constraints and objective function depends on the number of shooting phases, but it is independent of the number of time steps in each shooting phase.

The gradient of the continuity constraint is evaluated from a direct differentiation of the time integration algorithm, see, for example, [9, 10]. Let us introduce the notations for the gradient of the constraint \({\mathbf {c}}^{(k)}_{\mathbf {cont}}\)

$$\begin{aligned}&{\mathbf {Q}}_1(t) =\frac{\partial {\mathbf {q}}(t)}{\partial \mathbf {q}_0^{(k)}},\; {\mathbf {Q}}_2(t) =\frac{\partial {\mathbf {q}}(t)}{\partial {\dot{\mathbf{q}}}_0^{(k)}},\; {\mathbf {Q}}_3(t) =\frac{\partial {\mathbf {q}}(t)}{\partial \mathbf {u}_0^{(k)}},\; {\mathbf {Q}}_4(t) =\frac{\partial {\mathbf {q}}(t)}{\partial \mathbf {u}_0^{(k+1)}}, \\&\varvec{\Lambda }_1(t) =\frac{\partial \varvec{\lambda }(t)}{\partial {\mathbf {q}}_0^{(k)}},\; \varvec{\Lambda }_2(t) =\frac{\partial \varvec{\lambda }(t)}{\partial {\dot{\mathbf{q}}}_0^{(k)}},\; \varvec{\Lambda }_3(t) =\frac{\partial \varvec{\lambda }(t)}{\partial {\mathbf {u}}_0^{(k)}},\; \varvec{\Lambda }_4(t) =\frac{\partial \varvec{\lambda }(t)}{\partial {\mathbf {u}}_0^{(k+1)}}. \end{aligned}$$

According to the direct differentiation method, the sensitivities are obtained by solving the differentiated form of Eqs. (17–18) with respect to \({\mathbf {q}}_0^{(k)}\), \({\dot{\mathbf{q}}}_0^{(k)}\), \({\mathbf {u}}_0^{(k)}\) and \({\mathbf {u}}_0^{(k+1)}\)

$$\begin{aligned} {\mathbf {M}}{{\ddot{\mathbf{Q}}}}_1+{\mathbf {C}}_t{\dot{\mathbf{Q}}}_1+{\mathbf {K}}_t{\mathbf {Q}}_1+{\mathbf {B}}^T\varvec{\Lambda }_1= & {} {\mathbf {0}}, \\ {\mathbf {B}}{\mathbf {Q}}_1= & {} {\mathbf {0}}, \\ {\mathbf {M}}{{\ddot{\mathbf{Q}}}}_2+{\mathbf {C}}_t\dot{\mathbf{Q}}_2+{\mathbf {K}}_t{\mathbf {Q}}_2+{\mathbf {B}}^T\varvec{\Lambda }_2= & {} {\mathbf {0}}, \\ {\mathbf {B}}{\mathbf {Q}}_2= & {} {\mathbf {0}}, \\ {\mathbf {M}}{{\ddot{\mathbf{Q}}}}_3+{\mathbf {C}}_t\dot{\mathbf{Q}}_3+{\mathbf {K}}_t{\mathbf {Q}}_3+{\mathbf {B}}^T\varvec{\Lambda }_3 -{\mathbf {A}}\left( \frac{t_f-t}{t_f-t_0}\right)= & {} {\mathbf {0}}, \\ {\mathbf {B}}{\mathbf {Q}}_3= & {} {\mathbf {0}}, \\ {\mathbf {M}}{{\ddot{\mathbf{Q}}}}_4+{\mathbf {C}}_t\dot{\mathbf{Q}}_4+{\mathbf {K}}_t{\mathbf {Q}}_4+{\mathbf {B}}^T\varvec{\Lambda }_4-{\mathbf {A}}\left( \frac{t-t_0}{t_f-t_0}\right)= & {} {\mathbf {0}}, \\ {\mathbf {B}}{\mathbf {Q}}_4= & {} {\mathbf {0}}, \end{aligned}$$

with the initial conditions

$$\begin{aligned}&{\mathbf {Q}}_1(0)={\mathbf {I}},\; {\mathbf {Q}}_2(0)={\mathbf {0}},\;{\mathbf {Q}}_3(0)={\mathbf {0}},\;{\mathbf {Q}}_4(0)={\mathbf {0}}, \\&\dot{\mathbf{Q}}_1(0)={\mathbf {0}},\; \dot{\mathbf{Q}}_2(0)={\mathbf {I}},\; \dot{\mathbf{Q}}_3(0)={\mathbf {0}},\; \dot{\mathbf{Q}}_4(0)={\mathbf {0}}. \end{aligned}$$

Even though the dynamic equilibrium is nonlinear with respect to \({\mathbf {q}}\), \({\dot{\mathbf{q}}}\), \({\ddot{\mathbf{q}}}\) and \(\varvec{\lambda }\), one observes that the sensitivity equations are linear with respect to \({\mathbf {Q}}_i\), \(\dot{\mathbf{Q}}_i\), \({{\ddot{\mathbf{Q}}}}_i\) and \(\varvec{\varLambda }_i\), \(i=1,2,3,4\). The sensitivities can be computed by time integration using the same algorithm as for the dynamic response. In our case, the generalized-\(\alpha \) method is thus used for that purpose. However, at a given time step [j], a single Newton iteration is sufficient to get the solution for the sensitivity. Moreover, the iteration matrix which defines the linear problem to be solved at each time step for the sensitivity is the same as the iteration matrix of the nominal problem. Therefore, this matrix has to be computed and factorized only once for the sensitivity analysis at time step \(n+1\). Taking advantage of these considerations, the evaluation of the gradient of continuity constraint can be achieved with a quite low computation cost compared to a finite difference approach.

7 Parallel computation

Direct multiple shooting is a numerical scheme for the solution of optimal control problems with potential to be explored for parallel computation, because the multiple initial value problems are independent from each other, see Fig. 1. Therefore, such IVPs a can be solved independently in different processing cores, using a multicore computer, in a cluster, or in a cloud. The parallel computation allows significant improvements in terms of computational time. The number of processing cores to obtain a required computing time is an important question for an online analysis. Considering a nonlinear model predictive control, this is a critical point, since the computing time of each optimization problem should be sufficiently small to meet the real-time constraint. For an offline analysis, fast test/simulation is important, but not mandatory in general. In this analysis, the potential and relevance of the parallel computation will be shown in comparison with other methods. For the application, time reduction is obtained for the multiple integrations of the index-3 DAE. Similarly, in [17], an effective heuristic load balancing strategy was used in order to enhance the efficiency of the parallel computation. In this case, the computing time related to DAE integrators tends to differ greatly on the multiple shooting intervals. Also, an estimation of the relative computational costs for all integration tasks was analysed.

In this work, the parallel matlab toolbox is considered. If the DMS method is written in a code with serial structure, one should first transform it into a parallel structure in order to benefit from MATLAB for parallel computation, e.g. based on the parfor structure, which generalizes the for structure.

Nowadays, graphics processing units (GPUs) are used for efficient computer graphics tasks and image processing thanks to their parallel architecture. They can be used for vectorized algorithms too, where the computation is done in parallel. However, GPUs are not used in this application, because their benefits are not directly related to the structure of the direct multiple shooting method for the solution of optimal control problems.

8 Application

This section shall demonstrate the ability of the alternative (proposed) formulation to compute the inverse dynamics of underactuated manipulators, defined in an index-3 DAE form. The mechanical model is obtained numerically using a nonlinear finite element method, as in [15], which is a general framework for the modelling of systems with rigid bodies, flexible bodies and kinematic joints.

Fig. 2
figure 2

Underactuated manipulator with one passive joint

Full size image

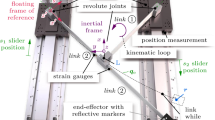
A planar manipulator with one passive joint (spring–damper element) and serial kinematic topology is considered as shown in Fig. 2a. Figure 2b shows the representation of the system using the finite element method (FEM) in absolute coordinates, as in [15]. The vector of the absolute coordinates for this system is defined as

$$\begin{aligned} {\mathbf {q}} = (x_1, x_2, y_2, \theta _2, x_3, y_3, x_5, y_5, \theta _5, x_6, y_6, x_8, y_8, \theta _8, x_9, y_9)^T, \end{aligned}$$
(37)

where \(x_i\) and \(y_i\) are the absolute translations of the node i along the axes \(e_1\) and \(e_2\), respectively, and \(\theta _i\) is the absolute orientation angle of node i. Those \(r=16\) absolute coordinates are not independent, but they have to satisfy \(m=12\) kinematic constraints, see Eq. (2). One observes that a formulation based on relative coordinates can also be used so that the dimension of the equation of motion would be reduced; however, the resultant equations are more nonlinear and complex to solve. Thus, a system formulated in FEM offers some advantages for the control of a complex system.

This system consists of a cart on which a chain of three arms is mounted. The \(s = 3\) outputs are

$$\begin{aligned} {\mathbf {y}} = \left( x, EF_x, EF_y \right) ^T, \end{aligned}$$
(38)

where the linear horizontal cart motion is represented by x and the end effector denoted by \({{\mathbf {E}}}{{\mathbf {F}}}\) should follow a semi-circular planar trajectory. This system is related to a non-minimum phase system, since the poles of the linearized zero dynamics values around the initial point are \(-24.79 \hbox {rad/s}\) and \(28.30 \hbox {rad/s}\). As one pole has a positive real part, the zero and the inverse dynamics are unstable and the time response would naturally diverge if a forward time integration were used. The time interval related to this motion is \(t_f-t_0=2.0s\), where the pre-actuation phase is \(t_1-t_0=0.2s\) and the post-actuation phase is \(t_f-t_2=0.3s\). Thus, we have output motion in \(t_2 - t_1 = 1.5s\). That machine possesses \(r-m = 4\) degrees of freedom \( (x, \alpha _1, \alpha _2, \beta ) \) which should be controlled by only \(s=3\) input controls

$$\begin{aligned} {\mathbf {u}} = (F, T_1, T_2)^T, \end{aligned}$$
(39)

where F is a translational force and \((T_1, T_2)\) are the joint torques. That system is underactuated, since it has one unactuated degree of freedom \(r-m-s=1\). The spring–damper element is the unactuated joint, represented by the angle \(\beta \). This example is taken from [22]. If an internal dynamics vector \(\varvec{\gamma }\) is defined to represent all non-actuated degree of freedom of an underactuated system, we have for the present case \(\varvec{\gamma } = [\beta ].\) A more complete description of that manipulator with the parameter values used can be found in [2, 22].

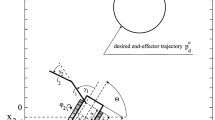
The initial guess of the design variables is considered for the motion without deformation of the passive joint, e.g. a rigid motion, as mentioned in Sect. 5. The solution should include some elastic deformations, since an underactuated system is considered and the stiffness of the passive joint is finite. Figure 3 shows the initial configuration at \(t = t_0\), both rigid and elastic motion of the underactuated manipulator and the desired trajectory for the output \({\mathbf {y}}(t)\), with \(t_0 \le t \le t_f\).

Fig. 3
figure 3

Motion of the underactuated manipulator

Full size image

The motion of the internal dynamics is defined by (\(\beta (t)\), \({\dot{\beta }}(t)\)), where the initial and final conditions, at the position level \(\beta (t_0) = \beta (t_f) = 0.0\) and velocity level \({\dot{\beta }}(t_0) = {\dot{\beta }}(t_f) = 0.0\), should define a boundary condition for the system. Thus, a bounded internal dynamic motion could be performed.

In the proposed approach, the problem is based on the definition of an index of performance to be minimized, where it can be defined as

$$\begin{aligned} J = \int _{t_0}^{t_f} ( \beta ^2 ) \, \mathrm{d}t. \end{aligned}$$
(40)

Alternatively, the integrand in Eq. (40) could be chosen as \(({\dot{\beta }}^2)\) or \(({\mathbf {u}}^T{\mathbf {u}}) \), but these cases are not considered in the following.

Fig. 4
figure 4

Inverse dynamics results for the underactuated manipulator (\(N = 80\) shooting phases, \(M = 5\) time steps and \(\rho _{\infty }=0.8\))

Full size image

The results using the proposed DMS method for the inverse dynamics of the underactuated manipulators are shown in Figs. 4 and 5. In Fig. 4a, the output error is about \(1\times 10^{-14}\) m at the extremities of the shooting phases, and one can observe that the constraints are not satisfied with such a high tolerance for the intermediate time steps inside a shooting phase, but the error is still very acceptable around \(1\times 10^{-5}\) m. This could be expected since the algorithm does not enforce the constraints at these intermediate points. Therefore, the accuracy of the trajectory mostly depends on the number of shooting phases, which should be high enough. In addition, at the beginning and at the end of the trajectory large residual errors are observed in comparison with the intermediate points since a finite pre-/post-actuation is considered. We checked that, for fixed time interval \(t_2 - t_1 = 1.5\) s and fixed time step values of h and \(h_s\), increasing the pre- and post-actuation intervals induces a reduction in the extremity of the output error. Figure 4b shows the phase diagram that represents the internal dynamics motion related to the \(r-m-s=1\) passive joint. Figure 4c shows the feedforward control that should be applied to obtain the desired trajectory for the system output. A zoom of the output error for \(N=40\) and \(N=80\) is shown in Figs. 5a, b. One observes that the results are similar, but the amplitude of the output errors is significantly reduced for \(N=80\).

Fig. 5
figure 5

Zoom: influence of the number of shooting phases, comparison of the output errors for \(N=40\) and \(N=80\) shooting phases (\(M = 5\) time steps and \(\rho _{\infty }=0.8\) in each case)

Full size image

Figure 6 shows a validation of the DMS approach using the stable inversion method as reference, see [8], for \(N = 120\). It includes an analysis of the angle of the passive joint \(\beta \), its time derivative \(\mathrm{d}\beta /\mathrm{d}t\) and the input torque \(T_1\). For all cases, the errors are rather small, but larger values are observed near the time \(t = 1.0 s\), when the motion is changing, see Fig. 3.

One could have considered the ACADO toolkit, see [16], which is a well-developed software for automatic control and dynamic optimization that is probably the state-of-the-art of the DMS to solve optimal control problems. However, some developments must be added for a due comparison; for example, the time integration method should be defined as the generalized-\(\alpha \) method, which is suited for structural dynamics and multibody systems. Moreover, ACADO considers the so-called condensing approach and our code does not. Thus, our contribution is more related to the application and specific considerations to solve inverse dynamics of underactuated manipulators.

Fig. 6
figure 6

Approach validation: direct multiple shooting method \(\times \) stable inversion method (reference)

Full size image

Figure 7 shows the evolution of the integrand of the objective function during the optimization process. One observes that the approximate solution is found using three iterations. The initial guess is related to a rigid motion, that is, \(\beta (t^{(k)}) = 0\), for \(k = 1,2,\ldots ,N\). The stopping criterion of the optimization process is the tolerance of the equality constraints, with value \(10^{-6}\). Figure 8 shows a convergence time analysis with respect to the number of shooting phases (N). As expected, the convergence time grows with N. This analysis was made considering three values of time steps per shooting phase \((M = 3, 5\) and 10). An ideal value for this application/problem is \(M = 3\), since for \(M = 1\) the convergence is not reached and for \(M = 2\) four iterations are required to satisfy the stopping criterion. Other values of M used in this analysis lead to only three iterations for the convergence.

Fig. 7
figure 7

Integrand \(\beta ^2\) evolution of the objective function at the optimization process

Full size image
Fig. 8
figure 8

Serial DMS: convergence time with respect to the number of shooting phases (N)

Full size image

Considering parallel computation, a computer with 10 processing cores was used. Figure 9 shows the convergence time versus the number of shooting phases, for the 10 processing cores. One can observe the potential of this method to deal with higher values of shooting phases allowing a higher time interval for the dynamic analysis in comparison with the serial DMS and the DT. Another analysis of the parallel computation is related to the number of processing cores/workers used, considering different shooting phases and observing convergence time, see Fig. 10. One can observe a reduction in the convergence time when the number of workers increases. A reduction in the speed-up rate is observed for the number of processing cores between 5 and 10, where a saturation can be observed. For a large manipulator in 3D, for example, the convergence time may saturate at a higher value.

Fig. 9
figure 9

Parallel DMS: convergence time with respect to number of shooting phases (N)

Full size image
Fig. 10
figure 10

Parallel DMS: influence of the number of processing cores (workers) on the convergence time

Full size image

9 Comparison of DMS and DT methods

This section establishes a comparison between the direct multiple shooting and the direct transcription methods, for the solution of the inverse dynamics problem. The inverse dynamics for underactuated manipulators considering direct transcription (DT) was treated in [2]. For the DT method, a constraint elimination method as made in [14] was used as a technique to reduce the number of design variables and constraints in the optimization problem. This constraint elimination method consists in partitioning the vector of the design variables into dependent and independent design variables and then only optimize the independent design variables. For the DMS method, a similar condensing approach is available in the literature, see [7]. However, this technique was not considered here.

Let us discuss the number of shooting phases in direct multiple shooting (DMS), and \(N = 1\) represents a particular case, named direct single shooting. In order to represent the time evolution of the control inputs \({\mathbf {u}}\) with sufficient accuracy, a minimal value of N is required. In the present application/problem, this minimum value appears to be \(N = N_\mathrm{{min}} = 29\). The maximum number of iterations was fixed to be 4. A comparison using the interior point and active-set algorithms was made. The interior point algorithm gives better results, while the computational time is around 3.5 times higher for the DT and \(12\%\) higher for the DMS in comparison with the active-set algorithm.

Fig. 11
figure 11

Convergence time comparison between the DT, DMS using serial computation and DMS using parallel computation

Full size image

Figure 11 shows a comparison between the DT, DMS using serial computation and DMS using parallel computation. The value of N for DT was obtained considering the same time step h for both methods. Therefore, since \(M = 3\), the time grid for \(N = 30\) shooting phases is equivalent to 90 phases in DT. One can observe the potential of DMS-parallel considering the computational time, as it grows very slowly with the number of shooting phases. In sequence, DT seems to be a second option, but for a number of collocation points smaller than \(N = 125\), after this value DMS-serial becomes the second option. Ten processing cores were used for the parallel computation.

Fig. 12
figure 12

Phase diagram: sensitivity to the spectral radius at infinite frequencies \(\rho _{\infty }\), DMS\(\times \)DT. The small circles at the DMS curve are related to the bound of the shooting phases

Full size image
Fig. 13
figure 13

Control torque \(T_1\): sensitivity to the spectral radius at infinite frequencies \(\rho _{\infty }\), DMS\(\times \)DT. The small circles at the DMS curve are related to the bound of the shooting phases

Full size image

It is known that direct methods in optimal control follow the principle first discretize and then optimize. In DMS, the forward integrations are solved within the optimization process. In DT, the forward integration is considered as equality constraints of the optimization process. The essential parameter for the generalized\(-\alpha \) formula is the spectral radius \(\rho _{\infty }\), see Eqs. (23–25), used to adjust the numerical damping of the generalized\(-\alpha \) method. The maximum damping is obtained with \(\rho _{\infty } = 0.0\), and the minimum damping is obtained with \(\rho _{\infty } = 1.0\). Figures 12 and 13 establish a comparison between the solution of the direct methods for the inverse dynamics of the underactuated manipulator. The same time step is considered for both \(N=40\) shooting phases, and \(M=3\), for the DMS, and 120 phases for the DT. A solution of reference is considered based on a stable inversion method as in [8] considering \(N = 120\). Figures 12a, b show the phase diagrams considering two values of the \(\rho _{\infty }\) for the direct methods. We can observe some discrepancies for DMS when \(\rho _{\infty } = 0.0\), where some artificial discontinuities are present. For DT, the choice \(\rho _{\infty } = 0.0\) is less penalizing than for DMS; this could be expected since the DMS is an hybrid method (time integration formulae are not considered as equality constraints). For the more realistic case \(\rho _{\infty } = 0.8\), the solution of the DMS was improved; this was observed for the DT too. Comparing these figures and Fig. 6, we observe that a smaller time step is required for DMS; thus, this is an advantage for the DT method. Figures 13a, b show the influence of \(\rho _{\infty }\) on the input torque \(T_1\). The same analysis can be performed, where DT shows better results than DMS for \(\rho _{\infty } = 0.0\). However, DT shows some artificial oscillations for \(\rho _{\infty } = 0.8\), essentially at the end of the trajectory. Clearly, more numerical damping is required and an ideal value for the DT should be around \(\rho _{\infty } = 0.5\). In contrast, DMS shows better results for the input control \(T_1\) for \(\rho _{\infty } = 0.8\) in comparison with the results of the DT.

10 Conclusion

The control of the elastic deformation (internal dynamics motion) for underactuated manipulators is important in various fields of engineering. This work was related to the inverse dynamics of this class of manipulators. A formulation using the direct multiple shooting method was proposed for the feedforward control design of underactuated manipulators in trajectory tracking problems. Based on the proposed formulation, a bounded solution of the inverse dynamics can be achieved. The main contributions of this work were: (i) the development of an alternative formulation for the trajectory tracking problem of underactuated manipulators; (ii) a parallel computation method for the inverse dynamics of underactuated manipulators; (iii) a comparison/validation with the direct transcription method and the stable inversion method. The proposed methodology is general and could be applied to more complex systems in the future, such as manipulators with flexible bodies, with parallel kinematics, and in 3D.