1 Introduction

Within the domain of hydrological research, the precise determination of crop evapotranspiration (ET) emerges as a crucial variable with far-reaching implications for water resource management, agricultural productivity, and environmental sustainability (Sagar et al. 2022; Raza et al. 2022; Mirzania et al. 2023). Mounting global population, escalating food requirements, and the spectre of climate change exert additional strain on already scarce water resources (Kumar et al. 2022b). Forecasts indicate a looming decline in crop productivity in the foreseeable future (Anapalli et al. 2016), underscoring the urgency of implementing water-conservation strategies and optimized irrigation schedules. Accurate evapotranspiration (ET) estimation provides valuable insights into the water lost through evaporation and transpiration processes, playing a pivotal role in ascertaining crop water requirements (Vishwakarma et al. 2022; Elbeltagi et al. 2023a). Studies suggest that a staggering 90% of agricultural water is lost through crop evapotranspiration in crop systems (Rana and Katerji 2000). Direct measurement of ET demands sophisticated and expensive instrumentation, including lysimeter systems, eddy covariance towers, evaporation pans, Bowen ratio stations, and scintillometer systems (Sagar et al. 2022). Given the cost, complexity, and inconvenience associated with direct measurements (Bachour et al. 2014; Jiang et al. 2016), various empirical equations, such as the Priestley-Taylor, Penman-Montieth, and Food and Agriculture Organization (FAO) crop coefficient methods, have been introduced over time. However, the accuracy of these methods hinges on the precise estimation of crop coefficients (Kc) (Kumar et al. 2021; Elbeltagi et al. 2023b). To address this challenge, the application of machine learning techniques for ET estimation has gained prominence.

The landscape of forecasting models has undergone significant evolution and refinement over time. Initially, the creation of an evapotranspiration (ET) forecast model relied on the simplicity of a stepwise multiple linear regression (SMLR) model, facilitating the identification of optimal predictors from a pool of variables within the model. However, the progression of time witnessed the displacement of these straightforward models by more sophisticated penalized regression techniques, including ridge regression, the least absolute shrinkage selection operator (LASSO), and elastic net (ELNET). In penalized regression models, the inclusion of variables is constrained or reduced to zero through penalization. Advancing beyond these methodologies, the subsequent development of diverse models saw the integration of machine learning (ML) algorithms, drawing inspiration from the intricacies of biological neuron processing (Khaniya et al. 2020; Karunanayake et al. 2020; Ekanayake et al. 2021; Tulla et al. 2024; Heddam et al. 2024).

In recent years, numerous researchers have endeavoured to develop machine learning algorithms for the estimation of crop evapotranspiration (ET) across various crops and regions (Elbeltagi et al. 2022; Mirzania et al. 2023; Vishwakarma et al. 2024). Abyaneh et al. (2011) employed artificial neural networks (ANN) and adaptive neuro-fuzzy inference system (ANFIS) to ascertain the ET requirements of garlic crops. Similarly, Aghajanloo et al. (2013) and Tabari et al. (2013) utilized a suite of approaches, including ANN, ANFIS, neural network-generic algorithm (NNGA), multivariate non-linear regression (MNLR), support vector machine (SVM), k-nearest neighbors (KNN), and AdaBoost, to estimate the evapotranspiration of potato crops. The estimation of Kc and ET values for maize and wheat crops involved the application of various models, such as Generalized Neural Regression (GRNN), fuzzy-genetic (FG), random forest (RF), deep neural network (DNN) and temporal-convolution neural network (CNN) (Feng et al. 2017; Chen et al. 2020; Saggi and Jain 2020). Notably, these studies grapple with the challenge of limited weather data availability for modelling ET values. Thus, there is a pressing need for ET estimation approaches that can effectively operate with a restricted set of weather data.

This research focuses on modelling the crop evapotranspiration process, specifically utilizing sugarcane as the target crop, given its year-round growth across all seasons. Notably, there is a dearth of studies employing machine learning for ET estimation in the Udham Singh Nagar district of Uttarakhand state. Uttarakhand, characterized by 86% hilly terrain and a mere 14% plains, faces topographical constraints, limiting cultivable land to only 14% of the total area. Moreover, 61% of the state is covered by forests (State profile, Government of Uttarakhand). Among the thirteen districts, Haridwar and Udham Singh Nagar stand out as the primary contributors to the plains. Udham Singh Nagar, chosen deliberately for this study, boasts the highest agricultural crop area in Uttarakhand (Directorate of Economics and Statistics). Situated in the Tarai belt at the foothills of the Shivalik range, approximately 80% of the crop area in Udham Singh Nagar is under irrigation (Krishi Vigyan Kendra, Udham Singh Nagar). This emphasis on irrigated land underscores the significance of studying evapotranspiration in this district for improved irrigation and water management practices.

This study introduces novel approaches and contributions to accurately estimate crop evapotranspiration (ET) for sugarcane in the Udham Singh Nagar district. The research encompasses a comprehensive set of models, including one statistical, three penalized regression and four machine learning models. To address limited weather variable availability, the study explores three scenarios: first using Net radiation (Rn) as the sole input, second excluding Rn while including all other weather variables and third incorporating all available weather variables. A thorough comparison of these models across different datasets is conducted to identify the most suitable model for ET estimation under varying data availability scenarios, aiming to enhance prediction accuracy.

2 Site description and data used

2.1 Study area

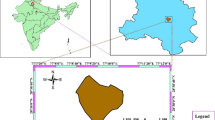
The research focuses on Udham Singh Nagar district in Uttarakhand, India, situated in the Tarai belt at the foothills of the Shivalik range of the Himalayas within the Kumaon division. The district spans from 28°53′ to 29°23′ N latitude and 78°45′ to 80°08′ E longitude, with an altitude of 214 m (Fig. 1). Known as the food bowl of Uttarakhand State, the district covers a geographical area of 3055 km2, with approximately 5% of the land under forest. Agriculture serves as the primary occupation for the majority. The district experiences two major cropping seasons, Kharif and Rabi, with prominent crops including rice, wheat, sugarcane, and mustard.

Fig. 1
figure 1

Location of the Bowen ratio tower over the study area

Full size image

2.2 Data collection

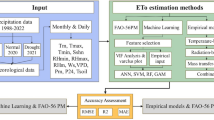
In the formulation of these models, a substantial volume of datasets was indispensable, encompassing both dependent and independent variables. The actual crop ET data based on the Bowen ratio, recorded at one-hour intervals (comprising 12 values per day), was computed from the flux tower situated at the research farm of GBPUAT Pantnagar. Concurrently, weather data, encompassing parameters such as temperature, relative humidity, net solar radiation, wind speed, and surface pressure, was gathered from the same farm utilizing a micro-meteorological flux tower. Of the overall datasets, 80% of the data was utilized for training the models, with the remaining 20% earmarked for model testing. The flowchart detailing the development of various models for ET estimation is delineated in Fig. 2.

Fig. 2
figure 2

Flowchart of different model development for ET estimation

Full size image

The descriptive statistics of the input data for the study area are reported in Table 1.

Table 1 Data statistics of hourly weather parameters at study stations
Full size table

3 Methodology

3.1 Calculation of ET with Bowen ratio

To employ the Bowen ratio method for calculating evapotranspiration (ET), it is essential to measure temperature and humidity at two different heights (Malek and Bingham 1993; Peacock and Hess 2004; Buttar et al. 2018). In this study, data on temperature and humidity were gathered at 2 m and 4 m above the surface, alongside measurements of net radiation (Rn), wind speed, wind direction, and surface pressure. Net radiation (Rn) was quantified using a Net radiometer positioned on the Bowen ratio tower. The ground heat flux (G) in this investigation was considered to be 10% of the Net radiation (Kato and Yamaguchi 2007; Teixeira et al. 2009). The Bowen ratio, representing the ratio of sensible heat flux to latent heat flux, can be expressed using the formula outlined by Buttar et al. (2018).

$${\text{ET}}=\frac{{{\text{R}}}_{{\text{n}}}-{\text{G}}}{(1+\upbeta )}$$
(1)

In the context of this study, denoting evapotranspiration as ET, net radiation as Rn, soil heat flux as G, and Bowen ratio as β, the calculation of β within the specified surface layers between two levels can be determined using the formula established by Verma et al. (1978):

$$\upbeta =\upgamma \frac{\Delta {\text{T}}}{\Delta {\text{e}}}$$
(2)

In the given context, where ∆T and ∆e represents the temperature and vapor pressure gradient between the two measured heights, and γ denotes the psychrometric constant, the computation of saturation vapor pressure values was conducted using the formula outlined by Allen et al. (1998):

$${\text{e}}=0.6108\mathrm{\;exp}\left(\frac{17.27+{\text{T}}}{{\text{T}}+237.3}\right)$$
(3)

The psychrometric constant, denoted as γ, establishes the connection between the partial pressure of water in the air and the air temperature. The formula for calculating the psychrometric constant (γ) is provided by Allen et al. (1998):

$$\upgamma =\frac{{{\text{C}}}_{{\text{p}}}{\text{P}}}{\mathrm{\varepsilon \lambda }}$$
(4)

In this context, where \({C}_{p}\) represents the specific heat at constant pressure, P is the atmospheric pressure, ε denotes the ratio of the molecular weight of water vapor to dry air, and λ stands for the latent heat of vaporization, the values of ET obtained at hourly intervals were employed for training and testing statistical and machine learning models.

3.2 Development of statistical, machine and deep learning models for ET estimation

Over the course of time, there has been a significant evolution in forecasting models. Initially, the creation of an ET forecast model involved employing a stepwise multiple linear regression (SMLR) model, facilitating the identification of optimal predictors from a pool of variables in model development. However, these rudimentary models were gradually supplanted by penalized regression models, including ridge regression, least absolute shrinkage selection operator (LASSO), and elastic net (ELNET). In these penalized regression models, the number of variables is constrained through the imposition of penalties or zero constraints. As the development of various models progressed, a diverse array of machine learning (ML) algorithms, inspired by the processing of biological neurons, made their entrance. An illustrative model in this regard is the artificial neural network (ANN), now extensively utilized across different disciplines. The ANN has proven instrumental in solving a myriad of problems across various fields (Ghiassi et al. 2005; Shukla et al. 2021; Elbeltagi et al. 2022; Saroughi et al. 2023; Mirzania et al. 2023). The neural network model exhibits intelligent learning capabilities during its training process. However, it is imperative to acknowledge certain drawbacks associated with ANN, including its intricate design, potential for offering ambiguous solutions, absence of explicit rules for network structure determination, and reliance solely on numeric information (Azzam et al. 2022). To address these challenges, numerous alternative machine learning models, such as support vector machine (SVM), random forest (RF), and sophisticated deep learning models like convolutional neural network (CNN) and deep neural network (DNN), were developed.

3.3 Model description

In the present study multiple models were developed based on three distinct sets of meteorological datasets. The first scenario involved utilizing only Rn as an input variable, as it exhibited the highest correlation coefficient when compared to other input variables. In the second scenario, all variables except Rn were employed as input variables as the net radiometer instrument is not available in all the weather observatories. Hence, to find good models which can predict ET values without data of Rn can be very useful. The third scenario incorporated all variables, including Rn, for model development. The specifics of each model are elaborated upon in the subsequent discussion:

3.3.1 Multiple linear regression (MLR)

The Multiple Linear Regression (MLR) stands as a traditional forecasting method, where regression equations are formulated using independent variables. In the context of this study, the MLR approach was compared with other advanced methods. One of the strengths of MLR lies in its capability to assist in the selection of optimal predictor variables from a vast array of candidates, as highlighted in previous works (Singh et al. 2014; Vishwakarma et al. 2018; Das et al. 2018). Notably, a significance level of 0.05 was adopted for p-values during the development of the MLR model.

3.3.2 Ridge regression

Ridge regression introduces a slight bias to predictor variables, mitigating the risk of overfitting in datasets (Li et al. 2010; Pavlou et al. 2016). Its primary objective is to enhance outcomes compared to traditional models by minimizing overfitting. This method affords researchers the capability to estimate coefficients, even in the presence of substantial correlations among predictor variables (Hilt and Seegrist 1977). The ridge regression may exhibit modest performance during training, its overall effectiveness tends to be consistently superior. The loss in ridge regression can be quantified as follows:

$${L}_{ridge}(\widehat{\beta })=\sum\limits_{i=1}^{n}{\left({y}_{i}-{x}_{i}^{\mathrm{^{\prime}}}\widehat{\beta }\right)}^{2}+\lambda \sum\limits_{j=1}^{m}{\beta }_{j}^{2}={\Vert y-X\widehat{\beta }\Vert }^{2}+\lambda {\Vert \widehat{\beta }\Vert }^{2}$$
(5)

where x and y represent the input and output vectors, respectively. The training dataset comprises n samples, while β denotes the regression coefficient, and λ serves as the penalty parameter.

3.3.3 Least absolute shrinkage selection operator (LASSO)

LASSO, a form of penalized regression model, functions by shrinking coefficients that exhibit correlation toward zero. Positioned as a data-driven model, LASSO is designed to counteract overfitting and promote the generalization of the model. The minimization of the objective function, as articulated by Hilt and Seegrist (1977), is expressed as:

$${L}_{lasso}(\widehat{\beta })=\sum\limits_{i=1}^{n}{({y}_{i}-{x}_{i}^{\mathrm{^{\prime}}}\widehat{\beta })}^{2}+\lambda \sum\limits_{j=1}^{m}\left|{\widehat{\beta }}_{j}\right|$$
(6)

The LASSO model incorporates a regression coefficient, denoted as β, which is linked to the input parameters. Here, x and y signify the input and output vectors, respectively. The training dataset comprises n samples, and the penalty parameter λ functions as a hyperparameter in the model.

3.3.4 Elastic Net (ELNET)

The penalty of both ridge regression and LASSO gets combined in the ELNET model (Abbas et al. 2020). In LASSO regression, a penalty in the form of the "absolute value of magnitude" is incorporated, while in ridge regression, a penalty is imposed in the form of the "squared magnitude of the coefficient." ELNET integrates both regularization techniques, and the loss can be defined as per the formulation by Zou and Hastie (2005):

$${L}_{enet}(\widehat{\beta })=\frac{\sum\limits_{i=1}^{n}{\left({y}_{i}-{x}_{i}^{\mathrm{^{\prime}}}\widehat{\beta }\right)}^{2}}{2n}+\lambda \left(\frac{1-\alpha }{2}\sum\limits_{j=1}^{m}{\widehat{\beta }}^{2}+\alpha \sum\limits_{j=1}^{m}\left|{\widehat{\beta }}_{j}\right|\right)$$
(7)

where x and y represent the input and output vectors, respectively. The training dataset consists of n samples, and the model parameters include β, the regression coefficient, λ, the penalty parameter, and α, which serves as the mixing parameter between ridge (α = 0) and LASSO (α = 1).

3.3.5 Artificial neural network (ANN)

The Artificial Neural Network (ANN) model, inspired by biological neurons akin to the human brain (Kaur and Sharma 2019; Shukla et al. 2021), is characterized by three layers: the input layer, hidden layer, and output layer. The hidden neurons incorporate an activation function, which transforms the activation level of a unit neuron into an output signal. The pivotal functions are performed within the hidden layer, and the outcomes are subsequently transmitted to the output layer. The determination of the number of nodes in the input layer is contingent upon the count of independent predictors. The expression for the output (hi) of neuron i in the hidden layer is articulated by Wang (2003):

$${h}_{i}=\sigma \left(\sum\limits_{j=1}^{N}{V}_{ij}{x}_{j}+{T}_{i}^{hid}\right)$$
(8)

here, \(\sigma\) is activation function, N is the number of input neurons, Vij is the weights, xj is the input to the neurons and Tihid is the threshold terms of the hidden neurons.

3.3.6 Support vector machine (SVM)

SVM, a machine learning algorithm primarily designed for classification and introduced by Vapnik (1998), extends its utility beyond classification to encompass tasks like time series estimation and regression analysis (Thissen et al. 2003). Its versatility extends to various applications, including hydrology, ecology, climatology, among others (Kushwaha et al. 2021; Kumar et al. 2022a; Singh et al. 2022a, b; Achite et al. 2023). SVM exhibits favourable performance in handling high-dimensional data, as noted by Azzam et al. (2022), although its efficacy diminishes in the presence of noisy and overlapped data. For a comprehensive understanding of the SVM model, interested readers can refer to the details provided by Fan et al. (2018).

3.3.7 K-nearest Neighbour (KNN) regression

The KNN, a non-parametric machine learning algorithm suitable for both classification and regression tasks, operates by assigning the value of an object in regression scenarios as the average of its K nearest neighbours, aligning with its name. KNN boasts advantages in terms of straightforward implementation and rapid real-time response. Nevertheless, its effectiveness diminishes when dealing with high-dimensional datasets and those containing noisy or missing values. For an in-depth understanding of KNN, interested readers can explore the detailed description provided by Kramer (2013).

3.3.8 Random forest (RF)

Random Forest, introduced by Breiman (2001) and investigated by Biau et al. (2008), represents a machine learning approach that integrates multiple decision trees. Each decision tree is generated independently, relying on a random vector sampled from the input data, while maintaining a consistent distribution across all trees (Azzam et al. 2022). The outcome is determined by selecting the most voted estimator among these classifications. Random Forest exhibits robust performance for both small and high-dimensional datasets. However, the model's complexity and training time requirements are notable disadvantages. For a comprehensive understanding of the RF algorithm, the mechanism of the RF model is elucidated in detail in references (Liu et al. 2012; Biau and Scornet 2016).

3.4 Model Evaluation

Assessing the accuracy of a model is a pivotal stage for both developers and users alike. The subsequent section briefly outlines the statistical parameters employed to evaluate the performance of the models:

3.4.1 Coefficient of determination (R2)

The R2 metric is employed to assess the linear association between the observed and predicted datasets. Ranging from 0 to 1, a value of 1 indicates a robust linear relationship. Generally, an R2 value exceeding 0.5 is considered acceptable.

$${R}^{2}={\left(\frac{\frac{1}{n}{\sum }_{i=1}^{n}({y}_{i}-{\overline{y} }_{i})({\widehat{y}}_{i}-{\widehat{y}}_{i})}{{\sigma }_{y}{\sigma }_{\widehat{y}}}\right)}^{2}$$
(9)

In this context, \({y}_{i}\) denotes the observed value, \({\widehat{y}}_{i}\) is the predicted value for i = 1, 2,….n. \({\overline{y} }_{i}\) and \(\overline{{\widehat{y} }_{i}}\) is the mean of observed and predicted values, respectively. \({\sigma }_{y}\) and \({\sigma }_{\widehat{y}}\) is the standard deviation of actual and predicted values respectively.

3.4.2 Root mean square error (RMSE)

The Root Mean Square Error (RMSE) serves as a commonly employed metric to quantify the disparity between observed values from the environment and those predicted by the model. Utilizing RMSE allows for the measurement of the error existing between the two datasets. A lower RMSE value indicates superior model performance, while a higher value suggests poorer model performance. The RMSE is calculated using the following equation:

$$RMSE=\sqrt{\frac{{\sum }_{i=1}^{n}({y}_{i}-{\widehat{y}}_{i}{)}^{2}}{n}}$$
(10)

Here, \({y}_{i}\) is the observed value while \({\widehat{y}}_{i}\) is the predicted value and n shows the number of observations. The unit of RMSE is similar to the unit of observed or predicted values.

3.4.3 Normalized root mean square error (nRMSE)

The nRMSE also called as scatter index, is a statistical error indicator which can be calculated as:

$${\text{nRMSE}}= \frac{{\text{RMSE}}}{\overline{{{\text{y}} }_{{\text{i}}}}}$$
(11)

Here, \(\overline{{y }_{i}}\) is the mean of observed values. It helps to compare the models with different scales. The unit of nRMSE is percentage.

3.4.4 Nash sutcliffe model efficiency coefficient (NSME)

The NSME is a normalized statistic that determines the measure of likelihood or model performance in terms of its accuracy (Nash and Sutcliffe 1970). It can be expressed in terms of equation as:

$$NSME=1- \frac{{\sum }_{i=1}^{n}({y}_{i}-{\widehat{y}}_{i}{)}^{2}}{{\sum }_{i=1}^{n}({y}_{i}-\overline{{y }_{i}}{)}^{2}}$$
(12)

Here, \({y}_{i}\) is the observed value, \({\widehat{y}}_{i}\) is the predicted value and \(\overline{{y }_{i}}\) is the mean of observed values. The value of NSME ranges from -∞ to 1. A proximity of the NSME value to 1 signifies enhanced model efficiency, with a value of 0 indicating model accuracy comparable to the mean accuracy of the calculated observed data. Conversely, a negative value indicates a deficiency in the model's performance.

3.4.5 Correlation coefficient (CC)

This metric estimates the intensity of the linear association between observed and predicted data values, with the correlation coefficient (CC) spanning from -1 to + 1. A CC value of -1 indicates a robust negative relationship, while a + 1 value signifies a strong positive relationship. The computation of CC is expressed as:

$$CC=\frac{n{\sum }_{i=1}^{n}{y}_{i}{\widehat{y}}_{i}- ({\sum }_{i=1}^{n}{y}_{i})({\sum }_{i=1}^{n}{\widehat{y}}_{i})}{\sqrt{n({\sum }_{i=1}^{n}{{y}_{i}}^{2})-{({\sum }_{i=1}^{n}{y}_{i}) }^{2}} \sqrt{n({\sum }_{i=1}^{n}{{\widehat{y}}_{i}}^{2})-{({\sum }_{i=1}^{n}{\widehat{y}}_{i}) }^{2}}}$$
(13)

Here, \({y}_{i}\) is the observed value, \({\widehat{y}}_{i}\) is the predicted value.

3.4.6 Agreement index (d)

Conceived by Willmott (1981), this statistical measure serves as an accuracy assessment tool for models. The range of values for "d" extends from 0 to 1, with a value of 1 indicating a perfect match between observed and predicted values, and 0 signifying no alignment. However, it's important to note that "d" is particularly sensitive to extreme values, attributed to the squared differences. The expression for "d" is articulated as follows:

$$d=1-\left(\frac{{\sum }_{i=1}^{n}{{ ((y}_{i}-\widehat{{y}_{i}})}^{2})}{{{\sum }_{i=1}^{n}(\left|\widehat{{y}_{i}}-\overline{{y }_{i}}\right|+\left|{y}_{i}-\overline{{y }_{i}}\right| )}^{2}}\right)$$
(14)

Here, \({y}_{i}\) is the observed value, \({\widehat{y}}_{i}\) is the predicted value and \(\overline{{y }_{i}}\) is the mean of observed values.

3.4.7 Mean biased error (MBE)

The MBE value denotes the average bias in predictions, where a positive MBE signifies overestimation, and a negative MBE indicates underestimation from the datasets. The computation procedure for the MBE value is outlined as follows:

$$MBE=\frac{1}{n}{\sum }_{i=1}^{n}({y}_{i}-{\widehat{y}}_{i})$$
(14)

where, \({y}_{i}\) and \({\widehat{y}}_{i}\) is the observed and predicted value respectively.

4 Results and discussion

4.1 Correlation study between ET and input weather variables

Figure 3 displays the correlational diagram along with correlation coefficient values depicting the relationships among variables. The analysis reveals robust correlations between ET values and Rn (1.00), Temperature (0.51), Relative Humidity (-0.5), and Wind speed (0.44). Additionally, positive correlations emerge between Date and Temperature (0.61) as well as Net radiation and Temperature (0.49). Conversely, negative correlation coefficients are prominent, particularly between relative humidity and other meteorological variables. This trend is logical, as an increase in net radiation, temperature, and wind speed corresponds to a decrease in the relative humidity in the atmosphere. Additionally, it is noteworthy that high relative humidity in the atmosphere leads to a decrease in the evapotranspiration (ET) value. This can be attributed to the saturated nature of the atmosphere with water, limiting the potential for further evaporation and transpiration. These findings underscore the intricate relationships between meteorological parameters and their impact on ET, contributing valuable insights to the understanding of the dynamic processes governing agricultural water consumption. The examination of these correlation coefficients led to the formulation of three distinct scenarios for model development in this study. The first scenario incorporates all weather variables, including date and time, as inputs for model development. The second scenario utilizes only Rn as input to predict ET values. In the third and final scenario, all weather variables, along with date and time, are employed as inputs for comprehensive model development.

Fig. 3
figure 3

Correlation between the ET and different weather variables

Full size image

4.2 Evaluation of statistical (MLR) model performance

Table 2 presents the outcomes of the MLR model at both the calibration and validation stages, while Table 3 showcases the corresponding equations derived. The findings underscore the significance of net radiation (Rn) in predicting evapotranspiration (ET). Remarkably, the MLR model demonstrates outstanding performance when exclusively utilizing Rn as an input variable, achieving an impressive R2 value of 0.99 in both calibration and validation phases. The model's excellence is further evident in other key statistical parameters, with NSME values of 0.99 and 1, as well as nRMSE values of 8.6% and 4.8% during calibration and validation, respectively. This aligns with the findings of Chia et al. (2022), who also achieved highly accurate daily ET estimates by employing Rn as the sole input variable, attaining an R2 value of 0.96.

Table 2 Performance of MLR model to Forecast ET values
Full size table
Table 3 Equations developed in different scenarios of MLR model
Full size table

In the second scenario, where Rn was excluded as an input variable, there was a notable decline in model performance. The R2 values dropped to 0.41 and 0.4 during calibration and validation, respectively. Correspondingly, other statistical parameters exhibited diminished performance, with calibration values of NSME at 0.41, RMSE at 3.8, and nRMSE at 77.1%. During validation, these values were NSME = 0.16, RMSE = 4.85, and nRMSE = 91.4%. This emphasizes the limitations of employing a statistical model like MLR for accurate ET estimation when working with a restricted set of input data. In the third scenario, where all parameters were utilized as input variables, the model performances rebounded to excellence. However, a comparison between the results of the first scenario (Only Rn) and the third scenario (All parameters) revealed a marginal improvement during calibration and a slight deterioration during validation. This echoes findings by Sattari et al. (2021), who observed similar trends when using sunshine duration (n) as the sole input variable, generating superior ET estimates compared to multiple meteorological variables (T, WS, RH, n). The scatter plot diagram illustrating all MLR models is depicted in Fig. 4.

Fig. 4
figure 4

Scatter plot between observed ET and predicted ET of MLR model

Full size image

4.3 Evaluation of Penalized regression models performance

Ridge regression, LASSO, and ELNET represent penalized regression models, implying the imposition of penalties on input parameters when dealing with numerous input variables. In the first scenario when Only Rn is the input, the number of input variables is merely one, rendering the implementation of penalties impractical. Therefore, in these three penalized regression models, only the second scenario (All parameters except Rn) and the third scenario (All parameters) are applicable. The statistical parameters evaluating the performance of penalized regression models are detailed in Table 4. In the second scenario (All parameters except Rn), the performance of all penalized models was uniformly subpar, with consistent values across statistical metrics. The R2 value during calibration remained at 0.4 for all models, while during validation, it reached 0.27 for ridge regression and 0.4 for both LASSO and ELNET, indicating unsatisfactory model performance. Furthermore, the MBE values during validation displayed strong negative values, indicative of underestimation by all the penalized models. Consequently, caution is advised against employing penalized regression models for ET estimation when working with a limited set of input variables.

Table 4 Performance of Penalized regression models to estimate ET values
Full size table

In the preceding scenario where Rn was integrated as an input variable, there was a remarkable enhancement in the performance of the penalized models. The R2 and NSME values surpassed 0.98 for both calibration and validation across all penalized models, signifying an outstanding level of model performance. However, the nRMSE values indicated good performance (< 20%) for ridge regression, while LASSO and ELNET exhibited excellent performance (< 10%). During the validation stages, the MBE values were -0.15, -0.02, and -0.001 for ridge, LASSO, and ELNET, respectively, suggesting a minor underestimation. These findings align with the research of Zhou et al. (2020), which supports for the incorporation of Rn in combination with other weather variables to achieve superior results in arid and semi-arid regions. The scatter plot diagram illustrating all penalized regression models is presented in Fig. 5.

Fig. 5
figure 5figure 5

Scatter plot between observed ET and predicted ET of penalized (a) Ridge regression (b) LASSO and (c) ELNET regression models

Full size image

4.4 Evaluation of machine learning models performance

In the first and third scenarios, all machine learning models exhibited exceptional performance, boasting R2 values exceeding 0.95, except for the Support Vector Regression (SVR) model, which demonstrated subpar performance (R2 = 0.53) during the validation stage in the third scenario, possibly resulted due to data overfitting (Table 5). The additional statistical metrics of Artificial Neural Network (ANN), K-Nearest Neighbours (KNN), and Random Forest (RF) models, including nRMSE (< 10%) and NSME (> 0.98), consistently indicated outstanding model performance. With the inclusion of Rn as an input variable, any machine learning model, except SVR, proved suitable for accurate ET estimation across the study region. Comparable findings were reported by Üneş et al. (2020) when Rn was employed as the sole input variable for Support Vector Machines (SVM), resulting in more accurate ET estimates.

Table 5 Performance of machine learning models to estimate ET values
Full size table

In the second scenario, where input data for weather variables was limited, diverse outcomes were observed across different models. The Artificial Neural Network (ANN) model yielded moderate results, with R2 values of 0.58 and 0.61 during calibration and validation, respectively. However, the nRMSE values of 64.7% and 62.3% during calibration and validation stages indicated suboptimal model performance. Correspondingly, NSME values (0.58 and 0.61) suggested a fair level of model performance (Khaniya et al. 2020; Karunanayake et al. 2020; Ekanayake et al. 2021; Heddam et al. 2024). The Support Vector Regression (SVR) model displayed poor performance during the validation stage, registering an R2 value of 0. K-Nearest Neighbours (KNN) exhibited commendable performance during calibration, with an R2 value of 0.72, nRMSE of 10.2%, and NSME of 0.99. However, its performance diminished significantly during validation, with R2 and nRMSE values of 0.35 and 84.5%, respectively. Among all the machine learning models with limited input weather variables, the Random Forest (RF) model demonstrated the best performance. Its R2, nRMSE, and NSME values during calibration were 0.99, 10.2%, and 0.99, and during validation were 0.84, 48.3%, and 0.77, respectively. Similar results were reported by Shiri et al. (2014). The scatter plot diagram depicting all machine learning models is illustrated in Fig. 6.

Fig. 6
figure 6figure 6

Scatter plot between observed ET and predicted ET of machine learning: (a) ANN, (b) SVR, (c) KNNand (d) RF model

Full size image

Figure 7(a-b) show the Taylor diagram for observed and predicted ET at Pantnagar station. Taylor diagram represents the correlation coefficient (r), root mean square deviation (RMSD), and standard deviation (SD) (Markuna et al. 2023; Vishwakarma et al. 2023). In penalized regression, it is clear from Fig. 7a that the LASSO and ELNET exhibited excellent performance model has the highest correlation values while the lowest RMSD and SD values for both all input and without Rn parameter. While Fig. 7b show that ANN model exhibited excellent performance model has the highest correlation values while the lowest RMSD and SD values for both all input and without Rn parameter and Random Forest model show better performance in only Rn input.

Fig. 7
figure 7

Taylor Diagram of (a) penalized regression and (b) MLR and machine learning models

Full size image

Predicting future ET (evapotranspiration) under different climatic scenarios involves considering the potential impacts of climate change on key meteorological variables. Given the correlations identified in the analysis, the following considerations can be made regarding ET predictions for future climatic scenarios:

Temperature changes

If future climate scenarios involve temperature increases, it is likely to influence ET positively, as there is a positive correlation between temperature and ET. Elevated temperatures generally enhance the rate of evaporation and transpiration.

Net radiation

Changes in net radiation may also play a role in influencing ET. The identified positive correlation between Net radiation and Temperature suggests that alterations in net radiation could impact ET in tandem with temperature changes.

Relative humidity

Future scenarios with decreased relative humidity might further contribute to increased ET, given the negative correlation observed. Lower humidity implies a drier atmosphere, potentially facilitating higher rates of evaporation.

Wind speed

If future climates bring changes in wind speed, this could impact ET as well. The positive correlation with wind speed indicates that higher wind speeds might enhance ET.

5 Conclusion

Our comprehensive investigation into the relationships between various meteorological variables and evapotranspiration (ET) revealed robust correlations, highlighting the pivotal role of net radiation (Rn) in ET prediction. The multivariate linear regression (MLR) model excelled when solely utilizing Rn as an input, showcasing exceptional performance supported by key statistical parameters. However, limitations emerged when excluding Rn, emphasizing the need for a comprehensive set of input data. The incorporation of Rn enhanced the performance of penalized and machine learning models, demonstrating the importance of this variable. Penalized regression models, including ridge regression, LASSO, and ELNET, demonstrated improved performance with the inclusion of Rn, aligning with the findings of previous studies. In scenarios with limited input data, machine learning models showed varying performance, with the Random Forest (RF) model emerging as the most robust. However, caution is warranted when employing certain models, such as the Support Vector Regression (SVR), in limited-input scenarios due to potential performance issues. In summary, our study contributes valuable insights into the complex dynamics of ET estimation, emphasizing the importance of considering specific meteorological variables and the suitability of different modelling approaches based on data availability. The findings offer practical guidance for researchers and practitioners working in regions with varying data constraints, facilitating more accurate and reliable ET predictions.