1 Introduction

The Madden–Julian oscillation (MJO) is an essential intraseasonal oscillation in the tropical atmosphere (Madden and Julian 1971, 1972) with a slow eastward-propagating speed (about 5m/s on average), and its convection center usually prevails over the Indo-Pacific warm pool (Wang and Rui 1990; Hendon and Salby 1994). The MJO is the most energetic oscillation in the tropics that can be observed from the raw data without statistical filtering (Zhang 2005).

The MJO inspires many researchers to investigate its dynamics, but its simulation still remains a challenge for us (Hayashi and Golder 1986; Zhang et al. 2006; Jiang et al. 2015). To further investigate the MJO dynamics is not only crucial for the predictions of the tropical weather systems, like the tropical cyclones (Sobel and Maloney 2000), El Nino (Li et al. 2001), but also for the extratropical systems (Vitart and Molteni 2010). Since from the earliest notion of the MJO (Madden and Julian 1972), many theories have been established to investigate the MJO dynamical mechanisms and Zhang et al. (2020) discusses four popular theories in detail, including the skeleton theory (Majda and Stechmann 2009), moisture-mode theory (Adames and Kim 2016), gravity-wave theory (Yang and Ingersoll 2013), and trio-interaction theory (Wang et al. 2016). To sum up, all theories present their distinctive conclusions for the MJO propagating from different aspects. To be more specific, the skeleton theory considers that the positive lower-tropospheric moisture anomalies east of the convective center can cause the slow eastward-propagating. The moisture-mode theory draws the conclusion that the large-scale horizontal and vertical moisture advections maintain the eastward-propagating speed. The gravity theory holds that owing to the beta effect, the eastward inertia-gravity waves (EIG) travel faster than the westward inertia-gravity waves (WIG). In terms of the trio-interaction theory, the planetary boundary layer dynamic plays an important role in the MJO propagation. And further details of these theory conclusions and discussion can be found in Zhang et al. (2020), indicating that understandings of MJO are diverse and problems remain to be solved.

The cloud radiative feedback (CRF) is regarded as an important factor for the MJO dynamics. In the early findings, Hu and Randall (1995) proposed that the cloud, radiation, and evaporation could form the intraseasonal oscillations. Recent findings also show that the CRF has the important effect on the MJO dynamics (Fuchs and Raymond 2005; Wang et al. 2013; Adames and Kim 2016; Chen and Wang 2018) and can slow down the phase speed (Bony and Emanuel 2005; Andersen and Kuang 2012; Crueger and Stevens 2015; Chen and Wang 2018). Additionally, it is conducive for the climate model in correctly simulating the MJO (Kim et al. 2015). Moreover, in the moisture-mode theory, the MJO is regarded as a moisture mode based on the observed central role of the atmospheric convection in the MJO and the observed structural evolution of moisture throughout its life cycle (Hendon and Liebmann 1990; Jones and Weare 1996; Myers and Waliser 2003) and the CRF is also included to analyze the effects of this process. The results show that the CRF, an instable source for the MJO development, plays an important role in the maintenance of the intraseasonal precipitation anomalies. The CRF favors the planetary-scale selection because with the distance changing from the center of the convection, the magnitude of the precipitation declines in a faster way than the OLR. Detailed explanations can be found in Adams and Kim (2016). More evidence, however, is also needed to verify this conclusion (Zhang et al. 2020).

According to previous findings, the planetary boundary layer (PBL) and the moisture processes are thought to be important for the MJO. Therefore, in our research, the theoretical model used for investigating the role of the CRF is a modified version of the developed theoretical model for studying the MJO dynamics, which is called the trio-interaction model. This model integrates the wave-convection interaction, the planetary boundary layer (PBL) moisture convergence feedback, and a simple convection-moisture feedback in a united framework to investigate the MJO dynamics, including the MJO development, propagating speed, and horizontal structure.

To identify the role of the CRF in the MJO dynamics, the CRF is included into the trio-interaction model, which allows us to investigate the growth rate, frequency, and the horizontal structure under the CRF effects. Different from the previous work (Chen and Wang 2018), we consider the radiation coefficient as a function of the wavenumbers instead of the constant, which is consistent with the observations (Adames and Kim 2016). We want to find whether the different schemes of the radiative feedback can lead to the different results. To clarify the effects of CRF, we run the model under conditions with or without the PBL dynamics so that the CRF impact can be examined in isolation or in combination with the PBL feedback. The sensitivity experiments of the trio-interaction model are also conducted to show the CRF effects.

In Section 2, the theoretical models are introduced. In Section 3, the properties of the linear normal modes affected by the CRF are displayed. In Section 4, the energy analysis is made. In Section 5, the radiation coefficient is discussed. In Section 6, conclusions are drawn.

2 Model framework

2.1 Basic equations

The simplified Betts–Miller Relaxation Scheme (Betts 1986; Betts and Miller 1986; Frierson et al. 2004) is used to parameterize the large-scale precipitation heating in the theoretical model and the equations in non-dimensional units are also written. In the equation, the velocity scale of C = 50 m/s (the speed of the lowest internal gravity wave), the length scale of \( \sqrt{C/\beta }=1500\ km \) (the equatorial Rossby deformation radius), and the time scale of \( \sqrt{1/ C\beta}=8.5\ h \), while β = 2.3 × 10−11 m−1s−1 represents the leading-order curvature effect of the Earth at the equator. Therefore, the non-dimensional perturbation governing equations for the first baroclinic mode (Liu and Wang 2017) are written as follows:

$$ {\displaystyle \begin{array}{c}{u}_t=-{\phi}_x+y\\ {}{\mathrm{v}}_{\mathrm{t}}=-{\upphi}_{\mathrm{y}}-\mathrm{yu}\\ {}\begin{array}{c}{\phi}_t+\left({u}_x+{v}_y\right)-w=-\mathit{\Pr}-\mu \upphi \kern0.5em {}^{\circ}\\ {}{\mathrm{q}}_{\mathrm{t}}+\mathrm{Q}\left({\mathrm{u}}_{\mathrm{x}}+{\mathrm{v}}_{\mathrm{y}}\right)=-\Pr \\ {}\Pr =\left({\mathrm{q}}_{\mathrm{t}}+\upalpha \upphi \right)/\tau \end{array}\end{array}} $$
(1)

Among them, u and v are the horizontal winds; ϕ is the geopotential anomaly; and μ is the non-dimensional Newtonian cooling coefficient. Q is the non-dimensional vertical gradient of the tropospheric background moisture between the lower (900–500hPa) and the upper (500–100hPa) troposphere, which can be calculated by an empirical formula about SST (Wang 1988). Pr is the precipitation associated with the diabatic heating of the deep convection, which can be parameterized by the simplified Betts–Miller scheme. α is the coefficient of reference moisture profile measuring relative contribution of the environmental buoyancy to the Convective Available Potential Energy (CAPE) parameterization. τ in the BM scheme is the convective adjustment time, measuring the time length for the convection to release CAPE and relax moisture to its reference state (Neelin and Yu 1994). In our research, we select a slow adjustment τ = 12h to make it consistent with the observations (Bretherton et al. 2004), also used in the previous work (Liu and Wang 2017). Details of this model can be found in Liu and Wang (2017).

The cloud radiative feedback is parameterized in such a way that the heating in the deep convection zone due to the reduction of the radiative cooling is proportional to convective heating (Chen and Wang 2018):

$$ \mathrm{R}=\mathrm{rPr} $$
(2)

where r is the radiation coefficient, R is the cloud radiation anomaly, and Pr is the precipitation anomaly.

The constant r is set in many findings which hold that the CRF enjoys the same effect on different scale waves. The previous study, however, also shows that the coefficient r is zonal wavenumber dependent and r decreases as k increases. Consequently, the empirical relation for the r dependence on k is adopted (Adams et al. 2016):

$$ \mathrm{r}={\mathrm{r}}_0{\mathrm{e}}^{-{\mathrm{L}}_{\mathrm{r}}\mathrm{k}} $$
(3)

where r is the radiation coefficient, r0 is constant, which is set at 0.21 for wavenumber zero, and Lr = 243km is the length scale that characterizes the changes of r with the wavenumber k.

When the CRF is added, the original geopotential equation is replaced by

$$ {\upphi}_{\mathrm{t}}+\left({\mathrm{u}}_{\mathrm{x}}+{\mathrm{v}}_{\mathrm{y}}\right)-\mathrm{w}=-\Pr -\upmu \upphi -\mathrm{R} $$
(4)

By comparison, the PBL moisture convergence is included into the theoretical model and the longwave approximation (Wang and Li 1994) is also used here, where the movement is driven by the pressure anomaly that is presumed to be equal to the pressure anomaly in the lower troposphere. Therefore, the Ekman pumping ω (Liu and Wang 2017) has the form of

$$ \upomega =\mathrm{d}\left({\mathrm{d}}_1{\upphi}_{\mathrm{y}\mathrm{y}}+{\mathrm{d}}_3{\upphi}_{\mathrm{y}}\right) $$
(5)

where d1 = E/(E2 + y2) and d2 =  − 2Ey/(E2 + y2)2. The term d is the non-dimensional PBL depth and E is the Ekman number in the PBL. The PBL moisture convergence can moisten the lower troposphere, and then the PBL in the moisture equation is added:qt + Q(ux + vy) =  − Pr  + Qbw (Bony and Emanuel 2005)where Qb is the non-dimensional vertical gradient of the background moisture at the top of the PBL (900hPa).

2.2 The theoretical model with both cloud radiative feedback and PBL processes

The theoretical model with both the cloud radiative feedback and PBL processes can be written as follows:

$$ {\displaystyle \begin{array}{l}{u}_t=-{\phi}_x+ yv\\ {}{\mathrm{v}}_{\mathrm{t}}=-{\upphi}_{\mathrm{y}}-\mathrm{yu}\\ {}\begin{array}{c}{\mathrm{q}}_{\mathrm{t}}+\mathrm{Q}\left({\mathrm{u}}_{\mathrm{x}}+{\mathrm{v}}_{\mathrm{y}}\right)=-\Pr +{Q}_bw\\ {}{\upphi}_{\mathrm{t}}+\left({\mathrm{u}}_{\mathrm{x}}+{\mathrm{v}}_{\mathrm{y}}\right)-\mathrm{w}=-\Pr -\upmu \upphi -\mathrm{R}\\ {}\begin{array}{l}\Pr =\left({\mathrm{q}}_{\mathrm{t}}+\upalpha \upphi \right)/\tau \\ {}\upomega =\mathrm{d}\left({\mathrm{d}}_1{\upphi}_{\mathrm{y}\mathrm{y}}+{\mathrm{d}}_3{\upphi}_{\mathrm{y}}\right)\end{array}\end{array}\end{array}} $$
(7)

In the governing equations, the Ekman pumping is added to the temperature equation because of the continuity. The original wave dynamic-moisture (WM) model is obtained by neglecting the CRF and the PBL processes. The role of the CRF and the PBL can be observed by keeping a specific term in each test run. The values for the parameters in these theoretical models are listed in Table 1.

Table 1 Parameters and values used in models. Adopted from Liu and Wang (2017)
Full size table

2.3 The settings of the basic state and the model calculation

To calculate the role played by the CRF and PBL in the MJO dynamics, the basic states of the variables need to be set according to the observation. Based on the observations, the vertical profile of the basic-state specific humidity over the tropical ocean is assumed to decline exponentially with a water vapor scale height of 2.2 km (Wang 1988; Liu and Wang 2012). The surface specific humidity \( \overline{q_s} \) can be calculated by the empirical formula about SST and the standard value is set at 29.5.

$$ \overline{{\mathrm{q}}_{\mathrm{s}}}\left(\mathrm{SST}\right)=\left(0.94\times \mathrm{SST}-7.64\right)\times {10}^{-3} $$
(8)

Therefore, Q (the vertical seasonal-mean moisture gradient between the lower (900–500hPa) and upper (500–100hPa) troposphere) and Qb (the vertical seasonal-mean moisture gradient at the top of the PBL (900hPa)) are both obtained. Due to the background SST is maximum in the tropics, it becomes cold poleward and the e-folding damping scale is 30.

The linear governing equations can be calculated by solving the eigenvalue problems. We presume the solution has the form of e(ikx − ωt), where k is the wavenumber and ω is the frequency. Then, the phase speed and the growth rate of the perturbations are obtained. According to the assumptions, the governing equations can be written into the frequency-wavenumber field and the linear matrix of the five predicted variables is also realized. For each wavenumber, the eigenvalue and the eigenvector can be calculated through the matrix inversion. To simplify the calculation, the parabolic cylinder function is used to filter out the high-frequency waves and expand the meridional structure. With the first three lowest meridional modes kept, these modes form the orthogonal basis and the governing equations can be written into three modes. Details of the parabolic function can be found in Majda and Biello 2004). The sensitivity experiment shows that the higher modes included do not influence the results.

3 Linear analysis: instability and propagation

3.1 Effects of the CRF

The growth rate and the frequency for different wavenumbers by the model calculation are found and two models are kept to investigate the role played by the CRF in the MJO dynamics. The basic model is the WM model, where only the wave-moisture feedback is kept. As for the second model, the CRF is added to the basic model, and the effects of the CRF are identified by these two theoretical models.

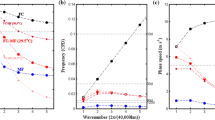
Without the CRF, the WM model only simulates damped eastward-propagating modes for all wavenumbers and the short waves are damped strongly (Fig. 1b). This result shows that the wave-moisture feedback mechanism alone cannot simulate the realistic modes of MJO. When the CRF is included, the growth rates of all wavenumbers are increased, showing that the CRF can destabilize the waves and serves as a significant unstable source for the wave development (Fig. 1b). The CRF, however, does not favor the planetary-scale selection because the growth rate caused by the CRF is greater at shorter wavelengths (red line).

Fig. 1
figure 1

Role of the cloud radiative feedback. (a) Frequency (cycles per day), (b) growth rate (day−1), and (c) phase speed (m/s) as a function of wavenumbers in the WM model (black) and the WM model with the CRF, the radiation coefficient dependent on wavenumbers (\( r=0.21{e}^{-{L}_rk} \), red). Another parameterization scheme of CRF (r = 0.21/k, blue) is also shown

Full size image

Moreover, when the frequencies of the wavenumbers in two models are focused on, the WM-damped mode is close to stationary, despite that all wavenumbers have the eastward-propagating speeds and the period is longer than 120 days (Fig. 1a). When the CRF is included, it makes the phase speeds of the wavenumber 1 slower and other wavenumbers faster compared with those in the WM model (Fig. 1a), although the changes of the short waves are less obvious than that of the wavenumber 1. The results show that the CRF has important effects on the growth rate and the phase speed. It is also worth mentioning that although the WM model with the CRF cannot make the planetary-scale wave unstable, the growth rate can be positive if the upper-level basic state moisture is ignored.

On the other hand, in our model, the CRF does not favor the planetary-scale selection. Therefore, after considering the condition when the CRF performs the planetary-scale selection and makes the long waves grow faster compared with the shorter waves, we make the assumption that the empirical relation for r dependence on k has the form as follows:

$$ \mathrm{r}={\mathrm{r}}_0/\mathrm{k} $$
(9)

The results of this parameterization are also shown in Fig. 1, that is, under this assumed parameterization scheme, the CRF in the theoretical model has the planetary-scale selection and the increase of growth rate for wavenumber 2 is the greatest, although the increases of growth rate for the wavenumbers 1 and 3 are not obviously different. The phase speed is also slowed down by the CRF in the wavenumber 1. Only under this assumption, our model can give the conclusion that the CRF prefers the planetary-scale selection.

3.2 Effects of the CRF in the presence of PBL dynamics

The aforementioned results coming from the two versions of the model show that the CRF process can influence both the growth rate and the phase speed of the waves. Therefore, what roles does the CRF play in the presence of PBL moisture convergence?

In order to solve that question, three versions of the original models are used to investigate the role of PBL and CRF in the presence of the PBL in the MJO dynamics. The first model is still the WM model and the second the model is the PBL model by adding only the PBL process into the WM model. The third model includes both the PBL and CRF processes.

In the second case, when the PBL is added, we can see that even though the growth rate of the planetary-scale is still negative, the long waves are damped less compared with the basic case and the short waves are damped more strongly, which shows the PBL moisture convergence is an important factor for the MJO development (Fig. 2b). In our study, the upper-level basic state moisture is considered, which is different from Liu and Wang (2017). Because in the previous work, the CRF is not considered in the model so neglecting the upper-level specific humidity can give a more unstable condition for the MJO development. In this paper, we want to give the more exact condition for the MJO development, so we consider the upper-level specific humidity. If the upper-level moisture is neglected, the PBL process alone can make the wavenumber 1 unstable, which is consistent with the previous work (Liu and Wang 2017). The red line in the figure shows that the combined effects of the PBL and CRF process can enhance the growth rate and the wavenumber 1 becomes unstable. Wavenumbers 2–5 are all damped (Fig. 2b). This model can simulate the characteristics of the planetary-scale mode and boost the large-scale wave development. The CRF, however, also performing the same characteristics, does not favor the large-scale waves and makes the shorter waves grow faster. The previous work shows, the CRF can change the ratio of the Rossby and the Kelvin wave components (Chen and Wang 2018). The CRF can increase the Rossby components which can decrease the MJO phase speed, which shows results are reasonable.

Fig. 2
figure 2

Role of the cloud radiative feedback in the presence of the PBL. (a) Frequency (cycles per day), (b) growth rate (day−1), and (c) phase speed (m/s) as a function of wavenumbers (\( r=0.21{e}^{-{L}_rk} \)) in the WM model (black), the WM model with the PBL (blue) and the WM with both the PBL and the CRF processes (red)

Full size image

As for the frequency, when the PBL process is added, the speeds for all wavenumbers are accelerated and the periods are between 30 and 90 days, which is the typical period for the intraseasonal oscillation (Fig. 2a). These results show the PBL, an important factor for the MJO, can accelerate the speed and increase the growth rate of the long waves. This result agrees with the conclusion of Liu and Wang (2017). When both processes are included, the period is between 30 and 120 days and the phase speeds of all wavenumbers are slower (Fig. 2c). The phase speed of the large-scale wave is decreased more by the CRF compared with the short waves.

3.3 The horizontal structure of the WM and the WM-CRF models

Because the MJO is viewed as a coupled Kelvin–Rossby wave structure, it is essential to investigate the horizontal structure and find whether the CRF can couple the Kelvin and Rossby waves, which can also be investigated by the eigenvector corresponding to the eigenvalue. First, the observed horizontal structures of the MJO signals are shown in Fig. 3. It is clear that the low-level geopotential height exhibits Matsuno–Gill-like pattern (Gill 1980), with a Kelvin wave low to the east of the convective heating center and a pair of equatorial Rossby wave lows to the west, which is consistent with the previous works (Adames and Wallace 2014). Also, the geopotential height at the upper level (200 hPa) shows the Matsuno–Gill-like pattern with opposite polarity in the vicinity of the convective heating center, indicating a first baroclinic mode.

Fig. 3
figure 3

Observed horizontal structures of MJO signals, namely, 850 hPa and 200 hPa geopotential height (contours, m) and OLR anomalies (shading, W/m2) with respect to the OLR index over 5 ° S − 5 ° N, 70 °  − 90 ° E during December–February from 1979 to 2016. The OLR index has been reversed prior to regression to present the precipitation anomaly. The negative OLR indicates the enhanced convection and the dashed contours indicate the negative values

Full size image

Figure 4 shows the horizontal structure of the eastward-propagating wavenumber 1. It can be found that when only the wave-moisture feedback is kept, the WM mode cannot simulate the realistic structure of MJO whether the upper-level specific humidity is considered or not. Although the WM can couple the Kevin wave and Rossby wave, the relationship between precipitation anomaly and the pressure anomaly is wrong. In the observations, the precipitation anomaly is in quadrature with the equatorial pressure anomaly. In this basic model, however, the positive geopotential anomaly is in phase with the positive precipitation anomaly, which is not a coupled Kelvin–Rossby wave structure (or the Gill pattern). When the CRF is included, the horizontal structure does not change, showing that the cloud radiative feedback cannot couple the Kelvin and Rossby waves to simulate the real MJO pattern.

Fig. 4
figure 4

The horizontal structure of the different models. Horizontal structures of normalized precipitation anomalies (shading), the lower-tropospheric geopotential height anomalies (contours) and the velocity anomalies (vectors) for wavenumber 1. The cloud radiative feedback has a function of wavenumbers (\( r=0.21{e}^{-{L}_rk} \)). Positive (negative) shading is dark (light) gray. Positive (negative) contours are solid (dashed). Contour interval is one-third of the magnitude, and the zero contours are not drawn

Full size image

3.4 The horizontal structure of the WM-PBL and the WM-PBL-CRF models

Figure 5 shows that when the PBL is added to the basic model, the different effect on the horizontal structure is displayed. The PBL can couple the Kelvin and Rossby waves and establish the relationship between the precipitation anomaly and the lower tropospheric pressure anomaly. The low-pressure anomaly now is leading the positive precipitation anomaly and the convergence of the low-pressure wind can lead to the occurrence of the precipitation. The results are consistent with the most characteristics of the observations. This result is consistent with the previous work (Liu and Wang 2017). However, this model can just couple the Rossby and the Kelvin waves, not the observed Gill-like pattern. When the upper-level specific humidity is considered to provide a more unstable environment (Liu and Wang 2017), the model can show a more realistic Gill-like structure, which indicates us to include other physical process. This is a model weakness, but this trio-interaction model is still useful for us to investigate the role of the CRF effects. When the CRF is included, the horizontal structure is more like Gill pattern. The low-pressure anomaly is stilling leading the positive precipitation anomaly. But the phase relation between the precipitation anomalies and the pressure anomalies is changed. This result confirms that the CRF can influence the horizontal structure with the PBL process, serving as an important instability source for the development of all wavenumbers and change the phase speed or frequency.

Fig. 5
figure 5

Horizontal structures of normalized precipitation anomalies (shading), the lower-tropospheric geopotential height anomalies (contours), and the velocity anomalies (vectors) for wavenumber 1. The cloud radiative feedback has a function of wavenumbers (\( r=0.21{e}^{-{L}_rk} \)). Positive (negative) shading is dark (light) gray. Positive (negative) contours are solid (dashed). Contour interval is one-third of the magnitude, and the zero contours are not drawn

Full size image

4 Energetic analysis

Positive eddy available potential energy (EAPE) is essential for destabilizing the atmosphere, which requires positive covariance between perturbation temperature and diabatic heating associated with large-scale precipitation anomalies. The EAPE is defined by \( -\overline{Pr\phi} \) averaged over one wavelength (Wang and Rui 1990). Keep in mind for the first baroclinic mode ϕ =  − θ, where θ is the non-dimensional temperature anomaly.

Figure 6 compares the EAPE in the aforementioned four models: WM, WM-CRF, WM-PBL, and WM-PBL-CRF model. For wavenumbers 1 and 2 in the WM model, the strongest negative EAPE is generated at the equator, while the negative EAPE is weaker when the CRF is included. And the wavenumber 2 is changed in a greater way compared with wavenumber 1. The weak positive EAPE is also shown in the 7 ° S and 7 ° N. When the PBL is added to the WM model, the weak positive EAPE is generated in the tropics while the wavenumber 2 is negative in this same region, showing the PBL makes the planetary-scale wave grow faster. When the CRF and the PBL processes are both included in the basic model, the wavenumbers 1 and 2 both have positive EAPE in the tropics and the EAPE is larger compared with the PBL in the WM model.

Fig. 6
figure 6

Zonally averaged EAPE of eastward-propagating wavenumber 1 and 2 in the (a) WM model, (b) the WM-CRF model, (c) the WM-PBL model, and (d) the WM-PBL-CRF model. The cloud radiative feedback has a function of wavenumbers (\( r=0.21{e}^{-{L}_rk} \))

Full size image

These results show the CRF can overwhelm the negative EAPE in the WM model for wavenumbers 1 and 2, although the EAPE for wavenumber 1 or 2 is still negative in the WM-CRF model. And the PBL can make the wavenumber 1 grow faster compared with the wavenumber 2.

In the WM model, the Betts–Miller precipitation scheme is a strong negative feedback and disturbances will be damped very quickly due to the consumption of the convective instability by convection, which is consistent with the previous work (Liu and Wang 2016). The PBL and the CRF can both give the unstable source for waves and generate the positive EAPE. The former is through pumping additional moisture in both equatorial and subtropical regions. The latter can benefit the free atmospheric moisture convergence (Chen and Wang 2018) and also generate the positive EAPE.

5 Sensitivity experiments

According to the aforementioned analysis, we can draw the conclusion that the CRF can destabilize waves and change speeds, which is an essential factor for the MJO dynamics. For the parameterization scheme of the CRF in the theoretical model, the radiation coefficient is significant because it can represent the strength of the CRF. Therefore, it is important for us to understand the CRF effect under different strengths. In our sensitivity experiments, the CRF is implemented into the WM-PBL-CRF model and the constant r0 is changed from 0.05 to 0.3 with the interval 0.05 and the rate of change for the wavenumbers is kept.

The results (Fig. 7) display the solutions under different CRF strengths. The strong and weak CRF can both destabilize the waves and make the growth rate larger compared with the WM-PBL model. The stronger CRF can reach more evident effects and the growth rate of the short waves is larger than the long waves when r0 reaches 0.3. In addition, all experiments can slow down the eastward-propagating speeds of all wavenumbers and the stronger CRF can make waves propagate more slowly. The change of the phase speed for the wavenumber 1 is most obvious in all wavenumbers. The stronger the CRF is, the ratio of the Rossby and Kelvin components is changed a lot, which makes the decrease more evident.

Fig. 7
figure 7

Sensitivity experiments about the CRF in the WM-PBL-CRF model. (a) Growth rate (day−1), (b) phase speed as a function of wavenumbers (\( r={r}_0{e}^{-{L}_rk} \)) with the r0 ranging from 0.05 to 0.3 with the interval 0.05. The solution of the WM-PBL model is also shown as a reference

Full size image

6 Conclusions and remarks

A basic theoretical model (Liu and Wang 2017) has been developed to investigate the role of the CRF in the MJO development, propagation, and scale selection. And the PBL process is also included into the MJO dynamics. This model is based on the WM model and the precipitation is used to parameterize the CRF. Different from the previous work, however, we do not use the same constant radiation coefficient to explain the relationship between the CRF and the precipitation anomaly under all wavenumbers (Bretherton and Sobel 2002; Chen and Wang 2018). Instead, we take into consideration the radiation coefficient dependent on the wavenumbers (Adames and Kim 2016) and study the role of the CRF effects with and without PBL process, which is also added for comparison. The parabolic cylinder function is also used to simplify the solution and obtain the linear mode.

In the WM and the WM-CRF models, the growth rates of all wavenumbers are negative and the waves are nearly stationary (Liu and Wang 2016) despite that the CRF can destabilize the waves and make the waves grow faster (Sobel and Maloney 2012; Adames and Kim 2016; Chen and Wang 2018). The CRF, however, does not favor the planetary-scale selection, which is different with the previous work (Adams et al. 2016). Therefore, we consider that the no planetary-scale selection of the CRF is corresponding with the rate of the change about the wavenumbers. When we presume that r has the form of the r = r0/k, the CRF can favor the planetary-scale oscillations. And the CRF can slow down the speed of wavenumber 1, which is consistent with the observations (Kim et al. 2015) and the previous works (Bony and Emanuel 2005; Andersen and Kuang 2012; Crueger and Stevens 2015).

By comparison, the PBL can accelerate the eastward-propagating speed, leading to the oscillation of 30–90 days and enable the long wave grow faster, which are consistent with the previous work (Liu and Wang 2016). And the combination of the CRF and the PBL processes can perform the unstable planetary-scale oscillation and the period is nearly 20–90 days, also consistent with the observations. It is worth noting that the WM-PBL model cannot simulate the unstable mode because we take into consideration the upper-level basic state moisture. If we neglect the upper-level moisture, the PBL process alone can simulate the developed mode (Liu and Wang 2017). The characteristics of the CRF effect are same for wavenumber 1 no matter whether the PBL is included or not.

The horizontal structure under these 4 models is also studied. The results show the WM and the WM-CRF model cannot simulate the realistic mode of coupled Kelvin–Rossby wave structure. These caveats can be remitted if we add the PBL into our model, for the PBL process can couple the Kelvin and Rossby waves and present the observed geopotential low in front of the convective center (Liu and Wang 2016). Besides, the WM-PBL and the WM-PBL-CRF both simulate the same mode, although the phase relation between the precipitation anomaly and the low-pressure anomaly is changed, which shows the CRF not only influences the horizontal structure but also changes the growth rate and the phase speed.

Sensitivity experiments are also designed to investigate the CRF effects. We make the constant r0 change from 0.05 to 0.3 with the interval of 0.05. The stronger CRF can make the waves grow faster and make the frequencies changed more evidently compared with the weaker CRF. In our study, the CRF can give the unstable source for the MJO development and decrease the phase speeds of the wavenumbers. These effects are consistent in many CMIP5 climate models (Kim et al. 2015). However, in our model, we only consider the CRF is linearized by the precipitation and neglect the different structures of the cloud. The different vertical structures of the cloud may have different radiation feedback on the MJO dynamics, which needs to be further investigated. The CRF is dependent on the wavenumbers and can give the unstable source for the MJO development and decrease the phase speed of the wavenumbers. However, many models still underestimate the CRF effect and neglect the CRF effects related to the wavenumbers. We need to focus on the CRF effect, which may help us to simulate the better MJO.