Prediction of Minimum Mud Weight for Prevention of Breakout Using New 3D Failure Criterion to Maintain Wellbore Stability

Abstract

Oil and gas extraction is difficult without understanding the subsurface formation up to the desired depth. Wellbore instability, such as lost circulation and pipe sticking, is an issue when drilling a well for a high-temperature, high-pressure reservoir. To maintain the stability of the borehole, optimum drilling mud should be simulated by preventing formation fracture or formation break-out. The main goal of this work is to propose a model with a 3D extended Mohr–Coulomb criterion that helps to achieve maximum wellbore stability using drilling fluid weight as a controlling parameter. This criterion includes the effect of the intermediate principal stress as a linear relation of principal stresses. this study also validated the extended Mohr–Coulomb criterion for in situ failure. To implement a new criterion on the wellbore for stability, a numerical mechanical earth model (NMEM) is developed as an empirical correlation of the wire-line well-log data. The mud weight is calculated using mechanical parameters derived from NMEM and lithology. The pore pressure, fracture pressure, and stress profile were also predicted by this NMEM, which gives insights into the subsurface formation's faulting regime. To achieve maximum wellbore stability, optimum mud weight is recommended based on the stress profile and faulting regime. One onshore and one offshore well is taken as a case study from the online dataset via the Dutch Oil and Gas Portal (NLOG) to simulate the NMEM. Mud weight using Mohr–Coulomb and Mogi–Coulomb criteria was also used to compare mud weight predicted by the proposed new 3D linear failure criterion. The treading line for the mud weight by the new 3D linear criterion is more accurate as a new criterion considering the effect of ${\sigma }_{2}$. The new criterion has been proved to be more specific, easy to compute, and a unique solution for estimating parameters using NMEM. This NMEM, which includes a new linear 3D criterion, can also solve sand production issues, hydrofracturing, and CO₂ sequestration.

Highlights

• A study about safe mud weight prediction using the new Extended Mohr–Coulomb criterion to prevent break-out and drilling-induced fracture with all six combinations of stress regimes.

• A numerical mechanical earth model is developed to stimulate appropriated reservoir conditions from actual well-log data.

• The prediction of mud weight to maintain wellbore stability is further compared with the Mohr–Coulomb and Mogi–Coulomb criteria results.

• A new 3D criterion with a numerical earth model has the potential to solve sand production issues and is also helpful for modeling hydrofracturing and CO₂ sequestration.

1 Introduction

Preventing a wellbore failure is challenging during drilling. Wellbore instability is mainly due to the mechanical effect and the chemical effect. The mechanical instability is due to the high in situ stresses around a wellbore, low formation rock strength, and inappropriate drilling practices. The chemical effect also causes wellbore instability due to the interaction between the formation rock and drilling fluid. Wellbore instability combines both effects, given as pipe sticking, tight sport, hole pack-off, lost circulation, and lost well during drilling. Wellbore instability due to the lack of proper planning and simulation will affect the repercussions of the industry to lose millions of dollars or even lives (Awal et al. 2001; Pašić et al. 2007; Zhang et al. 2010).

Simulation to maintain wellbore stability is most important for the exploratory well, the technically challenged well (high-pressure–high-temperature reservoir HPHT), or the horizontal and deviated well. Wellbore instability is mainly differentiated as pipe sticking or lost circulation. Pipe sticking is due to the pressure difference between hydrostatic and formation pressure or the formation break-out as a compressive failure of the formation in the direction of the minimum horizontal stress. Lost circulation is the phenomenon of drilling fluid moving into the formation through the drilling-induced fracture (DIF). The direction of the DIF is perpendicular to the minimum principal stress. Mud weight plays an essential role in the prevention of wellbore stability. As mud weight is inappropriate to prevent the pore pressure, a kick is possible due to the under-balance drilling. Most of the time, mud weight should be selected higher than the formation pressure to reduce the kick's possibility and prevent the blowout. Lost circulation also increases the possibility of kick as hydrostatic pressure is reduced, and it no longer resists the formation pressure. If the mud weight is far more than the pore pressure and near the yield strength of the formation rock, then it produces DIF. In the highly permeable reservoir or the naturally fractured reservoir, the mud went into the formation by fractures. Loss of the mud into the formation reduces the hydrostatic pressure as reducing the mud column's height leads to the kick and blowout (Fjaer et al. 2008).

An accurate wellbore stability analysis in planning and development shows the importance of drilling fluid programs, casing programs, and operating procedures for a stable wellbore (Zhang et al. 2010). Selection of optimum mud weight is made by simulation of a wellbore while considering the strength parameter of formation rock and stress concentration around the borehole. The well-log data estimate formation rock strength parameters and in situ stress. Estimated rock strength and near-wellbore stress are useful for optimum mud weight selection by failure criterion. Borehole instability due to the mechanical effect is a breakdown of formation by compressive failure or tensile formation fracture due to the inappropriate drilling mud weight.

Mud weight should be adequate to avoid compressive failure but not excessive to cause a drilling-induced fracture. For these two key wellbore instability issues, mud weight is essential in stabilizing a wellbore. Because predicted mud weight significantly impacts wellbore stability, several failure criteria have been established and used in the literature to determine a stable mud weight window (Culshaw 2015). Most failure criteria were used to predict wellbore instability without considering the effect of intermediated principal stress on rock failures, such as the Mohr–Coulomb criterion and the Hoek–Brown criterion (Hoek 1968; Murrell 1965; Franklin 1971; Hoek and Brown 1980; Hoek 2003; Benz et al. 2008).

The Mohr–Coulomb criterion is a well-known failure criterion considering major and minor principal stress (${\sigma }_{1}, {\sigma }_{3}$) and neglecting the intermediate principal stress $({\sigma }_{2})$. The Mohr–Coulomb criterion is one of the most applicable for the prediction of the failure of rock due to the meaningful physical parameters and linear mathematics relation between principal stresses. The Mohr–Coulomb failure criterion does not predict as accurately as the true-triaxial compression failure criteria, which were developed further based on the true-triaxial compression test data (McLean and Addis 1990) The Mohr–Coulomb failure criterion overestimates the mud weight to avoid the brack-out as the criterion neglects intermediate principles stress (Maleki et al. 2014; Das and Chatterjee 2017).

Experimental evidence shows intermediate principal stress influences rock material failure (Takahashi and Koide 1989). There are many failure criteria proposed as extended Mohr–Coulomb and extended Hoek–brown failure criteria with quantitative determination of the effect of intermediate principal stress on the strength of rock (Benz et al. 2008; You 2009; Singh et al. 2011; Chang and Haimson 2012; Meyer and Labuz 2012; Labuz et al. 2018; Feng et al. 2020). Mogi (1971) used a true-triaxial compression testing machine to investigate how rocks fail in three dimensions. Mogi derives a new failure criterion from the experimental results: a new failure criterion is the monotonic increasing function of octahedral shear stress and normal stresses. Al-Ajmi and Zimmerman (2005) developed the Mogi–Coulomb criterion from the Mohr–Coulomb by replacing normal shear stress with octahedral shear stress ${\tau }_{{\text{oct}}}$ called Mogi–Coulomb Criterion.

Haimson and Chang (2000), Haimson and Chang (2000), Takahashi and Koide (1989), Ma and Haimson (2016) validate the Mogi–Coulomb failure criterion on experiment data. Mogi (2006) published an experimental result on the true-triaxial compression test, which has served as the primary source for researchers developing a 3D failure criterion based on the experiment (You 2009; Lee et al. 2012; Jaiswal and Shrivastva 2012; Cai et al. 2021; Asem et al. 2021). Mogi–Coulomb failure gave a better result compared to another failure criterion. However, the Complexity of finding mud weight is significantly higher due to the function of the octahedral shear stress and normal principal stresses. Generally, failure criteria for finding the minimum stress for a stable borehole require many parameters and numerical equations for accurate results. In this paper, a new extended 3D failure criterion (Mahetaji et al. 2023) is implemented near the wellbore for the prediction of minimum mud weight to prevent break-out for wellbore stability problems. The extended Mohr–Coulomb criterion considers the effect of intermediate principal stress on the rock strength as a weighting (P) of ${\sigma }_{2}$ on the mean effective stress. As by Mahetaji et al. (2023), extended Mohr–Coulomb criteria are advisable for in situ conditions compared to existing failure criteria: Mogi–Coulomb and Mohr–Coulomb criteria. An extended Mohr–Coulomb criterion considers the effect of intermediate principal stress and is mathematically stable because the material parameter is also driven as a function of internal friction angle and cohesion coefficient.

A geomechanical parameter required for the mud weight window prediction is estimated with the help of a numerical mechanical earth model (NMEM). An NMEM for the geomechanics is done with the help of the well-log data concerning the depth. The empirical correlation for calculating the geomechanical parameter concerning the formation lithologies to get optimum output. This NMEM is also helpful for the simulation of the hydrofracturing operation, simulation for the sand production, and simulation for the carbon dioxide storage and sequestration, and various simulations enhance oil for recovery for optimum injection rate (Das and Chatterjee 2017; Moos et al. 2001; Rahmati et al. 2013). This study was only focused on the prevention of wellbore instability in terms of the geomechanical stress around the borehole.

2 3D Extended Mohr–Coulomb Criterion (Mahetaji et al. 2023)

In the conventional Mohr–Coulomb failure criterion, the effect of the intermediate stress is neglected during the rock failure prediction. Based on the experimental result of the triaxial compression failure test on the rock, there is an indication that the intermediate principal (${\sigma }_{2}$) stress impact ($\upgamma$) on the rock strength. An increment in the strength of the material is taken as a weighting ($\upgamma$) of the intermediated stress (${\sigma }_{2}$) on the mean effective stress (${\sigma }_{m}$).

The following equation gives the value of mean effective stress and maximum shear stress.

$${\sigma }_{m}=\frac{{(\sigma }_{1}+\upgamma *{\sigma }_{2}+{\sigma }_{3})}{\upgamma +2} {\text{and}} {\tau }_{m}=\frac{{\sigma }_{1}-{\sigma }_{3}}{2},$$

(1)

where $\upgamma$ is the weighting of the intermediate principal stress. The value of $\upgamma$ is contingent on rock property and calculated with the help of the Mohr–Coulomb criterion to find out UCS is given as

$$\gamma =\frac{\left(2-2{\text{sin}}\phi \right) {\text{UCS}}-4 c{\text{cos}}\phi }{(2 c{\text{cos}}\phi -{\text{UCS}})}.$$

(2)

Now based on the Mohr–Coulomb failure criterion

$$\tau =\sigma {\text{tan}}\left(\phi \right)+c$$

(3)

and

$$\sigma ={\sigma }_{m}-{\tau }_{m}{\text{sin}}\phi {\text{and}} \tau ={\tau }_{m}{\text{cos}}\phi .$$

(4)

The values of the ${\sigma }_{m}$ and ${\tau }_{m}$ are put in the to get the value of $\sigma$ and $\tau$, which is given by

$$\sigma =\frac{{(\sigma }_{1}+\upgamma \times {\sigma }_{2}+{\sigma }_{3})}{\upgamma +2}-\left(\frac{{\sigma }_{1}-{\sigma }_{3}}{2}\right){\text{sin}}\phi$$

(5)

And

$$\tau =\left(\frac{{\sigma }_{1}-{\sigma }_{3}}{2}\right){\text{cos}}\phi .$$

(6)

Now, put the value of $\sigma$ and $\tau$ in Eq. (3) and replace $\phi$ with friction angle in triaxial compression (${\phi }_{m })$,

$$\left\{\left(\frac{{\sigma }_{1}-{\sigma }_{3}}{2}\right){\text{cos}}{\phi }_{m} \right\}=\left\{\frac{{(\sigma }_{1}+\upgamma *{\sigma }_{2}+{\sigma }_{3})}{\upgamma +2}-\left(\frac{{\sigma }_{1}-{\sigma }_{3}}{2}\right){\text{sin}}{\phi }_{m}\right\}{\text{tan}}\left({\phi }_{m}\right)+c.$$

(7)

By Simplifying the above equation, we get the following new 3D extended Mohr–Coulomb criterion with a significant impact of ${\sigma }_{2}$ as proposed by Mahetaji et al., (2023) given.

$${\sigma }_{1}=\frac{2\mathrm{\gamma sin}c}{(2-2{\text{sin}}{\phi }_{m}+\upgamma )}{\sigma }_{2}+\frac{2+2{\text{sin}}{\phi }_{m}+\upgamma }{(2-2{\text{sin}}{\phi }_{m}+\upgamma )}{\sigma }_{3}+\frac{2\left(2+\gamma \right)\times c\times }{(2-2{\text{sin}}{\phi }_{m}+\upgamma )}$$

(8)

or

$${\sigma }_{1}={q}_{1}{\sigma }_{2}+{q}_{2}{\sigma }_{3}+UCS.$$

(9)

Here ${q}_{1}=\frac{2\mathrm{\gamma sin}{\phi }_{m}}{(2-2{\text{sin}}{\phi }_{m}+\upgamma )}$; ${q}_{2}=\frac{2+2{\text{sin}}{\phi }_{m}+\upgamma }{(2-2{\text{sin}}{\phi }_{m}+\upgamma )}$; $UCS=\frac{2\left(2+\upgamma \right)\times c\times {\text{cos}}{\phi }_{m}}{(2-2{\text{sin}}{\phi }_{m}+\upgamma )}$.

The amphibolite triaxial compression test data of the German Continental Deep Drilling Program (KTB) are taken from Colmenares and Zoback (2002) to show prediction failure by this criterion. As shown in Fig. 1, scatter data indicates the actual value of the failure at triaxial testing, and the continuous line indicates the prediction of the failure by the 3D extended Mohr–Coulomb criterion proposed failure criterion. In this prediction, the failure of the variable is taken as P = 0.21, ${\phi }_{m}$= 52, and C = 60.03 MPa. The prediction from the 3D linear criterion on the KBT amphibolite showed that the 3D extended Mohr–Coulomb criterion gave an appropriate result (RMSE = 55.02 MPa) with the actual triaxial test data. Wellbore stability is maintained by a 3D extended Mohr–Coulomb criterion with the help of the NMEM to calculate the required variable for the optimum mud weight by failure criterion.

Fig. 1

Validation of the failure criterion on the KBT amphibolite as $\upgamma$ =0.21, ${\upphi }_{{\text{m}}}$= 52 and C = 60.03 MPa (Mahetaji et al. 2023)

3 Numerical Mechanical Earth Model (NMEM)

A Numerical Mechanical Earth Model (NMEM) should be developed to represent the relationship between mechanical earth properties and geomechanical stresses. In the oil and gas industry, NMEM plays a vital role in understanding the drilling scenario and helps the drillers design a stable well. The NMEM characterizes formation properties regarding pore pressure, in situ stress, and formation strength (Allawi and Al-Jawad 2021; Gholami et al. 2014). The cross-relationship of petrophysical logs and their elastic and mechanical properties yields the formation property. The NMEM is the cross-disciplinary collaboration between astrophysicists, geologists, geomechanics and rock mechanics experts, and well engineers. The NMEM is created based on the output required by this research model and is prepared as an empirical correlation of petrophysical log data to formation properties. For the wellbore stability analysis, we required formation properties like pore pressure, uniaxial compressive strength, internal friction angle, cohesion, fracture pressure, and stresses around the wellbore for various drilling strategies.

Mechanical properties change with formation and lithology, taking depth and stress into account. Uniaxial compressive stresses are validated with the core data with uniaxial compressive testing or triaxial compressive testing on the core sample from various depths. Pore pressure will be validated with the field data measured during drilling, like a repeat formation tester (RFT). Fracture pressure derived from the NMEM is also validated with the actual fracture gradient data given for the field. Minimum horizontal stress is also validated with the leak-off-test data at casing shoe depth.

Rock mechanical properties like poison’s ratio, angle of internal friction, and uniaxial compressive strength may be calculated or derived from experiments on core samples, which should be collected from equal depth intervals of the well. Reservoir petro-mechanical properties exhibit heterogeneity and vary with both time and space. Since formation break-out can happen at any depth interval along the wellbore, it is essential to continuously monitor the entire well's petrophysical properties. The most effective approach to achieve a stable wellbore is estimating petrophysical parameters from well-log data while calibrating with actual data. The continued petrophysical parameter is driven by empirical co-relation of petrophysical log data giving better monitoring of the well from top to bottom. Petrophysical log data like spontaneous potential log (SP), calipers log, gamma-ray (GR), compressional transit time (DTCO), sonic shear transit time (DTSM), and bulk-density (${\rho }_{b}$) logs have an empirical relation to finding the rock's mechanical properties. This empirical relation is used for finding out the dynamic young modulus, Poisson’s ratio (ν), uniaxial compressive strength (UCS), cohesion (c), and internal friction angle ($\phi$). This property is used to predict the pore pressure, fracture pressure, and development of the stress profile with formation lithology.

The optimum mud weight is computed from the failure criterion with the help of geomechanical earth modeling for wellbore stability analysis. A detailed process for developing the NMEM is given in the flow diagram shown in Fig. 2. The empirical correlation involved in the construction of this NMEM is given below.

Fig. 2

Flow diagram for the numerical mechanical earth model

3.1 Young’s Modulus

Young modulus or modulus of elasticity can be estimated from the bulk-density (${\rho }_{b}$) log, sonic compression transit time (DTCO) log, and sonic shear transit time (DTSM) log. Young's modulus from sonic and density log, data by (Fjaer et al. 2008) as a relation of the ${V}_{p}$ and ${V}_{s}$ given as,

$${E}_{{\text{Dyn}}}=\frac{\rho {V}_{p}^{2}\left(3{V}_{p}^{2}-4{V}_{s}^{2}\right)}{{V}_{p}^{2}-{V}_{s}^{2}}.$$

(10)

The above equation is converted into the relation of DTCO and DTSM logs as

$${E}_{{\text{Dyn}}}=\frac{\rho \left(3{{\text{DTSM}}}^{2}-4{{\text{DTCO}}}^{2}\right)}{{{\text{DTSM}}}^{2}\left({{\text{DTSM}}}^{2}-{{\text{DTCO}}}^{2}\right)}.$$

(11)

The subscript $Dyn$ used in the above equations indicates these are dynamic properties (Zoback 2010).

3.2 Poisson’s Ratio ( ${\varvec{v}}$ )

Poisson’s ratio is the ratio of lateral expansion to longitudinal contraction.

$$v=-\frac{{\varepsilon }_{y}}{{\varepsilon }_{x}},$$

(12)

where ${\varepsilon }_{y}$ is the lateral expansion, and ${\varepsilon }_{x}$ is the longitudinal contraction. Poisson’s ratio given in the relation of ${V}_{p}$ and ${V}_{s}$ is given by the (Fjaer et al. 2008)

$$\upsilon =\frac{0.5{V}_{p}^{2}-{V}_{s}^{2}}{{V}_{p}^{2}-{V}_{s}^{2}}.$$

(13)

Poisson’s ratio is simplified into the relation of DTCO and DTSM logs as

$$\upsilon =\frac{0.5{\left(\frac{{\text{DTSM}}}{{\text{DTCO}}}\right)}^{2}-1}{{\left(\frac{{\text{DTSM}}}{{\text{DTCO}}}\right)}^{2}-1}.$$

(14)

3.3 The Angle of Internal Friction $({\varvec{\phi}})$

The friction angle is a term employed in the fields of mechanics and geotechnical engineering to characterize the degree of tilt concerning the horizontal axis of the Mohr–Coulomb shear resistance line (Barton 1973, 1976; Barton and Choubey 1977; Rahjoo 2019). The angle of internal friction $(\phi )$ depends on rock strength on confining pressure to the more excellent value of $\phi$, indicating a higher strength sensitivity to confining pressure. The coefficient of internal friction is given by $\mu ={\text{tan}}\phi$.

The empirical relation between friction angle and p-wave velocity is given by Lal (1999). They observed that $\phi$ increases monotonically from 0° to 45° as ${V}_{p}$ increase from 1000 to 6000 m/s. The above relation underestimates the $\phi$ for poorly consolidated or unconsolidated weak shale for ${V}_{p}$ less than 3000 m/s.

$$\phi ={{\text{sin}}}^{-1}\left(\frac{{V}_{p}-1000}{{V}_{p}+1000}\right).$$

(15)

The equation also re-written in the form of DTCO is given by

$$\phi ={{\text{sin}}}^{-1}\left(\frac{1-1000 {\text{DTCO}}}{1+1000 {\text{DTCO}}}\right).$$

(16)

The porosity for the sandstone-based empirical equation is given by Weingarten et al. (1995) that $\phi$ decreased with increasing porosity $\Phi$. That empirical equation was validated by (Handin et al. 1963; Murrell 1965; Gowd et al. 1977; Scott and Nielsen 1991; Wong et al. 2005).

$$\phi =57.8-105\Phi$$

(17)

The porosity may be estimated by bulk-density log or density-neutron log as given as

$$\Phi =\frac{{\rho }_{{\text{ma}}}-{\rho }_{b}}{{\rho }_{{\text{ma}}}-{\rho }_{f}}.$$

Matrix density for the sandstone, limestone, dolomite, salt, and anhydride is given as an average of 2.65, 2.71, 2.876, 2.977, and 2.032 g/cc simultaneously. Porosity from the density-neutron log is also given by,

$$\Phi ={\left(\frac{{\Phi }_{{\text{n}}}^{2}+{\Phi }_{D}^{2}}{2}\right)}^\frac{1}{2}$$

(18)

where $\Phi$ is the percent porosity, ${\Phi }_{{\text{n}}}$ is the neutron percent porosity, and ${\Phi }_{{\text{D}}}$ is the density percent porosity.

Internal friction angle ($\phi$) is given by Chang et al., (2006) for Shaley sedimentary rocks as an empirical relation of the gamma-ray log. From that correlation, it has been shown that the internal friction angle decreases gradually as the GR value increases.

$$\phi ={{\text{tan}}}^{-1}\left(\frac{\left({\text{GR}}-{{\text{GR}}}_{{\text{sand}}}\right){\mu }_{{\text{shale}}}+\left({{\text{GR}}}_{{\text{shale}}}-{\text{GR}}\right){\mu }_{{\text{sand}}}}{{{\text{GR}}}_{{\text{shale}}}-{{\text{GR}}}_{{\text{sand}}}}\right).$$

(19)

3.4 Uniaxial Compressive Strength (UCS)

Uniaxial compressive strength (UCS) is the failure point of the rock sample when the uniaxial compressive force is applied to the material. UCS is also calculated in the biaxial compressive test and triaxial compressive test. The uniaxial compressive strength is measured on the core sample taken from the targeted depth for the subsurface and in the simulation for the wellbore stability, sand production, and various EOR problems with NMEM required continuous value of UCS concerning depth (Moos et al. 2001). For the NMEM, UCS is estimated with the help of the empirical co-relation from well-log data. The value of UCS by empirical relation is continuous with depth, so the prediction of mud weight by UCS continues. The empirical co-relation must be validated, so the result should be appropriately done with experimental compression test data. Some of the empirical co-relation used in NMEM for calculating UCS are listed in Table 1. Based on the lithology and geological setting, the correlation should be changed. Empirical co-relation may not give the same result for each wellbore, so it needs to be calibrated for each well.

Table 1 Empirical co-relation for the uniaxial compressive (MPa) with the relation of DTCO (μs/ft), Sh (fraction), ${{\text{V}}}_{{\text{p}}}$(km/s), Is (fraction), ${{\text{E}}}_{{\text{dyn}}}$(GPa), Φ (fraction)

3.5 Cohesion

An empirical relation exists between cohesion (c) and UCS from the Mohr–Coulomb failure criterion as given in Miedema and Zijsling (2012),

$$C= \frac{{\text{UCS}}}{2}\left(\frac{1-{\text{sin}}\phi }{{\text{cos}}\phi }\right),$$

(20)

where UCS is taken from the correlation listed in Table 1. Estimation of in situ stress and pore pressure.

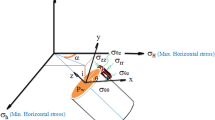
3.6 In Situ Stress Configuration

Three mutually orthogonal stresses are vertical (${\sigma }_{v}$), minimum horizontal stress (${\sigma }_{h}$), and maximum horizontal stress (${\sigma }_{H}$), acting near to wellbore at in situ conditions. In geomechanics, the magnitude and orientation of all three principal stresses affect wellbore stability (Zoback 2010). The behavior and magnitude of three principal stresses are responsible for two major wellbore stability problems: borehole break-out and induced fracture, leading to lost circulation. Among orthogonal stresses, one should be the greatest, one is intermediated, and one is the least stressed (Mitchell 2016). Faulting is classified as normal faulting, strike–slip faulting, and reverse faulting based on the magnitude of orthogonal stresses (Anderson 1953). If vertical stress is more significant among orthogonal stresses than a normal faulting regime or if vertical stress is intermediate stress among orthogonal stress, it is a strike–slip faulting regime or reverse faulting for the most negligible value of vertical stress. The first overburden pressure is taken as vertical stress to estimate the in situ stress profile. Fracture pressure is taken from minimum horizontal stress, and maximum horizontal stress is calculated with the help of Hook's law.

3.6.1 Overburden Pressure (Vertical Stress)

The overburden pressure is exerted by the total weight of overlying formations above the point of interest. Overburden pressure is the cumulative summation of the weight of formation from the top ($z=0$) to a depth of interest ($z=z$). The total weight is the combined weight of both the formation fluids in the pore space and formation solids as given as

$${P}_{{\text{ov}}}= \int_{0}^{z}{\rho }_{z} g {\text{d}}z.$$

(21)

In the NMEM, overburden pressure is taken as vertical stress, and density is derived from well logs. Vertical stress on the point of interest is generally due to the weight of the overlying formation. Vertical stress per unit interval of depth is a vertical stress gradient in the range of 0.8–1.0 psi/ft (18.1–22.6 kPa/m) (Fjaer et al. 2008).

3.6.2 Minimum Horizontal Stress (Fracture pressure)

Estimating the fracture pressure is only done with the idea of the pore pressure. Pore pressure should be estimated by Eaton's method.

3.7 Pore Pressure

Pore pressure or formation pressure gives pressure due to the fluid in the tarp in the pore space of rock. Pore pressure is sometimes taken as a summation of overlaying fluid weight in the absence of other processes. Pore pressure is a critically important parameter in the drilling and development of the hydrocarbon reservoir to prevent pressure kicks, blowouts, and fluid influx in the borehole. The impact of the pore pressure also influences the in situ stresses, which play an important role during the estimation of mud weight prediction for borehole stability. Nowadays, measurement while drilling also measures the pore pressure during drilling. Pore pressure detection in various phases of development is drill stem testing (DST), wire-line formation testing (RFT), and production testing (PT) (Mahetaji et al. 2020). The empirical correlation of seismic data is given by Ben Eaton (1975), Matthews et al. (1972), Sayers et al. (2002), Terzaghi and Peck (1996), Yan and Han (2012). Empirical co-relation of pore pressure from well-log data (shear sonic log, compressions sonic log, and resistivity log) is given by Ben Eaton (1975), Bowers (1995), Gardner et al. (1974), Hohmann et al. (1965).

Ben Eaton (1975) presented the following empirical equation for the pore pressure prediction from seismic velocity, resistivity, and sonic compressional transit time:

$${P}_{p}={P}_{{\text{ov}}}-\left({P}_{{\text{ov}}}-{P}_{p\mathrm{ Normal}}\right){\left(\frac{{V}_{{\text{observed}}}}{{V}_{{\text{Normal}}}}\right)}^{3}$$

(22)

$${P}_{p}={P}_{{\text{ov}}}-\left({P}_{{\text{ov}}}-{P}_{p\mathrm{ Normal}}\right){\left(\frac{{R}_{{\text{observed}}}}{{R}_{{\text{Normal}}}}\right)}^{1.2}$$

(23)

and

$${P}_{p}={P}_{{\text{ov}}}-\left({P}_{{\text{ov}}}-{P}_{p {\text{Normal}}}\right){\left(\frac{{{\text{DTCO}}}_{{\text{n}}}}{{\text{DTCO}}}\right)}^{3}.$$

(24)

${P}_{{\text{ov}}}$ is overburden pressure in the above equation due to the overlying formation and fluid above the exciting point. ${P}_{p {\text{Normal}}},$ commonly referred to as the normal pore pressure, typically represents the hydrostatic pressure of brine. ${{\text{V}}}_{{\text{observed}}}$, ${R}_{{\text{observed}}},$ and ${\text{DTCO}}$ is the observed value on the log data for the depth. ${V}_{{\text{Normal}}}$, ${R}_{{\text{Normal}}}$, and ${{\text{DTCO}}}_{{\text{n}}}$ are the normal compaction trend line data for that depth obtained by fitting a linear or non-linear curve to the compressional wave log data. The limitations of using P-wave velocity as an indirect method to estimate pore fluid pressure stems from its strong dependence on pressure and saturation, especially at low effective pressures. Nur and Simmons (1969) found that when pressures exceed 1 or 2 kilobars, all velocities show only minor variations with increasing stress. Consequently, the correlation between P-wave velocity and pore fluid pressure becomes non-linear and unsuitable for accurately estimating pore fluid pressure at higher pressures. Swarbrick (2012) states that pore pressure estimation is notably affected by rock properties, encompassing porosity, permeability, compressibility, lithology, and fluid characteristics.

Eaton's method has been widely used for pore pressure prediction in the last decades, but it has had limitations in application in the geological complicated area. This method is modified by including a factor of depth-dependent normal compaction trendline (Zhang 2011). To apply this method, there must be an idea about the normal sonic p-wave velocity, normal compaction shale resistivity, or normal compaction sonic compressional transit time.

3.8 Fracture Pressure

Empirical correlation to finding out the fracture pressure in the relation of poison ratio, pore pressure, overburden pressure, and stress anisotropy with depth given by Eaton (1969), Hubbert and Rubey (1959), Matthews et al. (1972). This research uses Matthews and Kelly's correlation and Eaton's method for fracturing pressure calculation. In the normal faulting regime, vertical stress is maximum, and two horizontal stresses. One should be intermediate, and one should be minimum principal stress. Minimum principal stress is obtained by a hydraulic fracturing test done to measure stress. Leak-of test (LOT) and extended leak-off test (ELOT) can be used to determine the minimum principal stress as a mini-frac test. Drilling mud weight should be less than the least principal stress or fracture gradient to prevent accidental mud loss due to hydraulic fracturing. LOT test data only show minimum principal stress at the casing shoe depth. The minimum horizontal principal stress for the hall wellbore cane is determined by the empirical co-relation listed in Table 2

Table 2 Empirical co-relation for the estimation of the minimum principal stress and maximum principal stress with the relation of z, ${{\text{P}}}_{{\text{p}}}$, ${{\text{P}}}_{{\text{h}}}, {\upsigma }_{{\text{v}}},\mathrm{ v},\Phi ,{{\text{E}}}_{{\text{h}}},{{\text{E}}}_{{\text{v}}},{{\text{v}}}_{{\text{h}}}$, ${{\text{v}}}_{{\text{v}}},$ and ${\upsigma }_{{\text{H}}}^{{\text{UB}}}$

3.8.1 Maximum Horizontal Principal Stress

The intermediate principle is maximum horizontal stress (${\sigma }_{H}$) in the normal and strike–slip faulting regime. ${\sigma }_{H}$ is not measured directly from the well; it has been making the most challenging component of the stress tensor to estimate the value of ${\sigma }_{H}$ accurately Determination of the ${S}_{H}$ is crucial for solving the problems related to wellbore stability like mud window selection, well trajectories selection, and selection of casing policy. Determination of ${\sigma }_{H}$ can be estimated from the Higgins-Borchardt et al. (2016) correlation and by Li and Purdy (2010) correlation listed in Table 2. Appendix Section-A presents a discussion of this derivation by Li and Purdy (2010), which correlates the maximum principal stress using Hook's law while disregarding strain in the minimum principal stress direction.

4 Implementation of Failure Criterion for Mud Weight for Wellbore Stability

Failure criteria are used to determine for which stress condition around the borehole that wellbore either break-out or induced failure occur. Stresses near to wellbore such as axial stress (${\sigma }_{z}$), radial stress (${\sigma }_{r}$), and tangential stress $({\sigma }_{\theta })$ are calculated using the Kirsch equation. The Kirsch equation is modified to determine stresses in the vicinity of the wellbore under specific conditions, where the radius (R) equals the distance (r) from the wellbore, and both the inclination angle and azimuth angle are set to zero for a vertical well, as described in Section B and Section C of the Appendix. The near-wellbore stresses, including axial stress (${\sigma }_{z}$), radial stress (${\sigma }_{r}$), and tangential stress $({\sigma }_{\theta })$, are dependent on various factors such as drilling mud properties, far-field stresses (${\sigma }_{H}, {\sigma }_{h}, and {\sigma }_{v}$), wellbore trajectory, and the ratio of (R/r), as described by the Kirsch equation. Here, R represents the distance from the wellbore axis to where these stresses are computed, and r is the wellbore radius. The Kirsch equation simplifies for vertical wells with zero polar angles, and the near-wellbore stresses become functions of mud weight and vertical stress. As a result, the stress profile changes concerning mud weight and vertical stress.

All possible combinations of near-wellbore stress for predicting mud weight to avoid both compressive and tensile failures are given as follows: $({\sigma }_{\theta }\ge {\sigma }_{z}\ge {\sigma }_{r}$); (${\sigma }_{r}\ge {\sigma }_{z}\ge {\sigma }_{\theta }$); (${\sigma }_{z}\ge {\sigma }_{\theta }\ge {\sigma }_{r}$); (${\sigma }_{r}\ge {\sigma }_{\theta }\ge {\sigma }_{z}$); (${\sigma }_{\theta }\ge {\sigma }_{r}\ge {\sigma }_{z}$) and (${\sigma }_{z}\ge {\sigma }_{r}\ge {\sigma }_{\theta }$).

Each stress profile combination has its implications: The presence of positive ${\sigma }_{z}$ and ${\sigma }_{\theta }$ in the stress profiles $({\sigma }_{\theta }\ge {\sigma }_{z}\ge {\sigma }_{r})$ and (${\sigma }_{\theta }\ge {\sigma }_{r}\ge {\sigma }_{z}$) leads to failure in the tangential direction. Profiles (${\sigma }_{z}\ge {\sigma }_{\theta }\ge {\sigma }_{r}$) and (${\sigma }_{z}\ge {\sigma }_{r}\ge {\sigma }_{\theta }$) cause axial compressive failure. Profiles (${\sigma }_{r}\ge {\sigma }_{z}\ge {\sigma }_{\theta }$) and (${\sigma }_{r}\ge {\sigma }_{\theta }\ge {\sigma }_{z}$) result in failure due to blasting or formation ballooning issues (Baldino and Meng 2021).

Table 2 represents the minimum and maximum mud weight limit using Mohr–Coulomb, Mogi–Coulomb, and 3D extended Mohr–Coulomb criterion. To prevent compressive break-out in the stress profile $({\sigma }_{\theta }\ge {\sigma }_{z}\ge {\sigma }_{r})$, mud weight given by criterion is considered as a lower limit to prevent compressive failure in the tangential direction. Similarly, for (${\sigma }_{z}\ge {\sigma }_{\theta }\ge {\sigma }_{r}$) and (${\sigma }_{z}\ge {\sigma }_{r}\ge {\sigma }_{\theta }$), the calculated mud weight serves as the lower limit to prevent break-out in the z-axis. When the values of ${\sigma }_{z}$ and ${\sigma }_{\theta }$ are negative, indicating tensile stress, the stress profiles ${\sigma }_{r}\ge {\sigma }_{z}\ge {\sigma }_{\theta }$; ${\sigma }_{r}\ge {\sigma }_{\theta }\ge {\sigma }_{z}$, and ${\sigma }_{\theta }\ge {\sigma }_{r}\ge {\sigma }_{z}$ can lead to formation fracture if the values of ${\sigma }_{\theta } and {\sigma }_{z}$ exceed the tensile strength of the formation. In this case, the upper limit for mud weight is calculated to prevent drilling-induced fractures (Gholami et al. 2014; Fjar et al. 2008).

Linear 3D failure criterion also re-writes in terms of effective principal stress ${\sigma }_{1}, {\sigma }_{2}, and {\sigma }_{3}$ is given by the equation here ${\sigma }_{1}\ge {\sigma }_{2}\ge {\sigma }_{3}$ in stress.

$${\sigma }_{1}={q}_{1}{\sigma }_{2}+{q}_{2}{\sigma }_{3}+{\text{UCS}}$$

(25)

For wellbore collapse, considering the situation ${(\sigma }_{\theta }\ge {\sigma }_{z}\ge {\sigma }_{r})$, the 3D extended Mohr–Coulomb criterion can be written as,

$${\sigma }_{\theta }={q}_{1}{\sigma }_{z}+{q}_{2}{\sigma }_{r}+{\text{UCS}}$$

(26)

The value of the ${\sigma }_{\theta }$ and ${\sigma }_{r}$ in the above equation from the Kirsch equation with the zero-inclination angle zero- azimuth angle. Stress near the wellbore is changed with the circumference angle as in minimum horizontal direction is minimum and at the maximum horizontal direction is maximum. Tangential stress and axial stress fluctuate formation around the borehole. To break-out prevention minimum value of this stress is taken for further calculations with zero polar angles with the maximum horizontal stress. Stresses near the wellbore based on the Kirsch equation (Appendix C) are given as

$${\sigma }_{\theta }=A-{P}_{w},$$

(27)

$${\sigma }_{r}={P}_{w}$$

(28)

$${\sigma }_{z}=B$$

(29)

where $A=3{ \sigma }_{h}{^\prime}-{\sigma }_{H}{^\prime}$; $B={\sigma }_{v}{^\prime}-2v\left({{\sigma }_{H}{^\prime}-\sigma }_{h}{^\prime}\right)$; ${\sigma }_{h}{^\prime}={ \sigma }_{h}-{P}_{o}$; ${\sigma }_{H}{^\prime}={ \sigma }_{H}-{P}_{o}$; ${\sigma }_{V}{^\prime}={ \sigma }_{V}-{P}_{o}$.

Substituting the value of the ${\sigma }_{\theta }, {\sigma }_{z,}$ and ${\sigma }_{r}$ in the above equation,

$$A-{P}_{w}={q}_{1}\left(B\right)+{q}_{2} {P}_{w}+{\text{UCS}}.$$

(30)

To avoid borehole collapse, the mud weight given by the linear 3D failure criterion is given as

$${P}_{w {\text{EMC}}} ={\text{abs}}\left(\frac{A-{q}_{1}B-{\text{UCS}}}{\left({q}_{2}+1\right)}\right),$$

(31)

Equation 31 represents the mud weight required to maintain wellbore stability in the stress profile when applying the 3D linear failure criterion ${(\sigma }_{\theta }\ge {\sigma }_{z}\ge {\sigma }_{r})$. For the remaining five combinations of the stress profile, the lower and upper mud weight limit needed to prevent failure is provided in Table 3. The derivation of the mud weight required to prevent failure using the Mohr–Coulomb and Mogi–Coulomb criteria can be found in Sections C and D of the appendix, respectively, and also listed in Table 3 with all six combinations of the stress profile.

Table 3 Minimum mud density for all six combinations of stress profile

5 Mud Weight Window Predictions to Maintain Wellbore Stability

5.1 Case A

Well-A is the Exploratory gas offshore well drilled up to the true vertical depth (TVD) of 2474.00 m concerning the rotary table. According to Boogaert and Kouwe (1993) and Munsterman et al. (2012), lithology around the wellbore is given mostly claystone, sandstone, limestone anhydrite, and dolomite as Interpreted lithology is given in Fig. 6 section from 7175 to 2350 mTVD is selected to implement the failure criterion for the mud weight selection for maximum wellbore stability. NMEM takes input as well-log data Fig. 3. (Caliper, GR, newton density, porosity, and deep resistivity). In the figure, the first track shows caliper and GR log; the second track shows DTCO (blue trend) and DTSM (orange trend); the third, fourth, and fifth tracks are newton porosity (NPHI) and density (RHOZ) log and deep resistivity, respectively. From the caliper log, it has been shown that nominal diameter changes around the depth of 2185 mTVD due to the casing policy change.

Fig. 3

Well log data taken as an input of the NMEM for case A. From a–e Gama ray. Sonic compression and sonic shear, porosity, density, and resistivity

Based on the NMEM, the mud density should be predicted using failure criteria required by the material parameter, pore pressure, and stress profile. Empirical correlations are used to derive the material parameter, as the NMEM discusses. Figure 5 shows the derived material parameter and predicted pore and fracture pressure. This figure derives the first track of dynamic young modulus from DTCO, DTSM, and RHOZ. The second track of Poisson's ratio is derived from the DTCO and DTSM. The internal friction angle is shown in the third track. Uniaxial compressive strength in the fourth track is calculated based on the correlation to lithology presented concerning depth. Pore pressure prediction is done with the help of the modified Eaton method based on the normal compaction trend line shown in the fifth track. Pore pressure prediction is done with the help of a sonic log or deep resistivity log. The normal compaction trend line for the pore pressure prediction by the sonic and resistivity is given in Fig. 4. Pore pressure prediction by the sonic compression trend line is better than that by the resistivity log. Pore pressure predictions are also validated with pore pressure from 2180 to 2205 m depth.

Fig. 4

Normal compaction trend line for pore pressure prediction by Eaton's method. a Sonic, b resistivity

The equation to finding the normal value of DTCO and RD for normal compaction trend line equation is

$${\text{log}}\left({{\text{DTCO}}}_{{\text{n}}}\right)=-0.0001619\times D+2.196$$

(32)

and

$${\text{log}}({{\text{RD}}}_{{\text{n}}})=0.001467\times D-2.351$$

(33)

The last track in Fig. 5 shows predicted fracture pressure using Eaton's equation. Fracture pressure is also validated with the actual fracture pressure. In this figure, the black dot shows the given fracture pressure and matches the predicted fracture pressure trend line.

Fig. 5

Estimated geomechanical property from the well-log data for case A. From a–f dynamic young modulus, Poisson’s ratio, angle of internal friction, UCS, pore pressure, and fracture pressure

Based on the value of the dynamic young modulus, Poisson’s ratio, UCS, friction angle, pore pressure and fracture pressure stress profile, and optimum mud weight are calculated as shown in Fig. 6. This figure shows the first track line in the interpreted lithology. The second track line shows the stress profile, where the saffron color shows the minimum horizontal stress, the red color shows vertical stress, and the blue color shows the maximum horizontal stress. In the second track minimum, horizontal stress is validated with LOT data at a depth of 2175 mTVD is 40 MPa, and at a depth of 2342 mTVD is 42 MPa. Based on the stress profile, vertical stress is the intermediated stress among all stresses, indicating the strike–slip faulting regime. The 3D extended Mohr–Coulomb criterion (red line), Mohr–Coulomb criterion (blue line), and Mogi–Coulomb criterion (green line) are used to calculate the lower mud density required to prevent break-out based on the stress profile, as shown in Fig. 6(c–h) with all possible stress profile combinations.

Fig. 6

Stress profile and mud density incorporates Mohr–Coulomb, Mogi-Coulomb, and new linear 3D criteria concerning lithology for case A. a interpreted lithology, b stress profile, c lower mud weight limit to prevent break-out in tangential direction when $({\upsigma }_{\uptheta }\ge {\upsigma }_{{\text{z}}}\ge {\upsigma }_{{\text{r}}}$), d upper mud weight to prevent fracture when (${\upsigma }_{{\text{r}}}\ge {\upsigma }_{{\text{z}}}\ge {\upsigma }_{\uptheta }$), e lower mud weight to prevent axial break-out when (${\upsigma }_{{\text{z}}}\ge {\upsigma }_{\uptheta }\ge {\upsigma }_{{\text{r}}}$), f upper mud weight to prevent axial fracture when (${\upsigma }_{{\text{r}}}\ge {\upsigma }_{\uptheta }\ge {\upsigma }_{{\text{z}}}$), g upper mud weight to prevent axial fracture when (${\upsigma }_{\uptheta }\ge {\upsigma }_{{\text{r}}}\ge {\upsigma }_{{\text{z}}}$), h lower mud weight limit to prevent axial break-out when (${\upsigma }_{{\text{z}}}\ge {\upsigma }_{{\text{r}}}\ge {\upsigma }_{\uptheta }$)

Figure 6 presents an extensive analysis of the stress profile and sediment density for case A, with a primary focus on lithological considerations. The figure incorporates three distinct criteria to investigate various aspects: Mohr–Coulomb, Mogi–Coulomb, and the new 3D extended Mohr–Coulomb criteria. The first track (a) illustrates the interpreted lithology, providing valuable insights into the geological formations within the study region. The lithology at specific intervals includes dolomite and limestone around 2200 mTVD, claystone at 2250 mTVD, claystone with sandstone between 2285 to 2350 mTVD, and claystone with minor stripes of sandstone from 2325 to 2350 mTVD.

The second track (b) showcases the stress profile, displaying the distribution and magnitude of stress along the investigated section, explicitly highlighting the minimum horizontal stress (depicted as a saffron line), vertical stress (maroon line), and maximum horizontal stress (blue line). The validation of the minimum horizontal stress is supported by LOT data 40 MPa at 2175 mTVD, 42 MPa at 2342 mTVD. The stress profile ${\sigma }_{H}(\mathrm{blue line})\ge {\sigma }_{V}(\mathrm{maroon line})\ge {\sigma }_{h}(\mathrm{saffron line})$ shows strike–slip faulting regime. Additionally, the figure explores specific mud weight limits using the 3D extended Mohr–Coulomb criterion (red line), Mohr–Coulomb criterion (blue line), and Mogi–Coulomb criterion (green line) under various stress conditions from track (c) to track (h).

The mud weight used for drilling this wellbore is approximately between 1.4 and 1.6 g/cc, at depths of 2185, 2211, 2268, and 2325 mTVD. In Fig. 3, the first track displaying the caliper log reveals that the wellbore failure profile experiences higher fluctuations showing unstable sections of the wellbore at depths between 2200, 2250, 2285 and 2305, and 2225 and 2350 mTVD.

The lower limit of mud weights to prevent tangential break-out in stress profile ${\sigma }_{\theta }\ge {\sigma }_{z}\ge {\sigma }_{r}$, axial break-out in stress profile ${\sigma }_{z}\ge {\sigma }_{\theta }\ge {\sigma }_{r},$ and stress profile ${\sigma }_{z}\ge {\sigma }_{r}\ge {\sigma }_{\theta }$ is shown in track (c), track (e), and track(h), respectively. The upper mud weight limit to prevent tensile fracture in stress profile ${\sigma }_{r}\ge {\sigma }_{z}\ge {\sigma }_{\theta }$, ${\sigma }_{r}\ge {\sigma }_{\theta }\ge {\sigma }_{z}$ and ${\sigma }_{\theta }\ge {\sigma }_{r}\ge {\sigma }_{z}$ in track (d), track(f), and track(g).

The lower limits for mud weight, as determined by the 3D extended Mohr–Coulomb criterion to prevent break-out (${\sigma }_{\theta }\ge {\sigma }_{z}\ge {\sigma }_{r}$), are generally set below the actual mud weight required. However, in the depth range of approximately 2200 m TVD (True Vertical Depth), the actual mud weight exceeds these lower limits, raising concerns about potential break-out occurrences. This break-out phenomenon is notably reflected in the caliper log and can be attributed to an incorrect choice of mud weight based on the lithological characteristics within that specific depth interval.

Furthermore, it is worth noting that the lower mud weight calculated using the Mohr–Coulomb criterion falls within the range of 0.1–0.4 g/cc for two distinct stress conditions: ${\sigma }_{\theta }\ge {\sigma }_{z}\ge {\sigma }_{r}$ and ${\sigma }_{z}\ge {\sigma }_{\theta }\ge {\sigma }_{r}$. However, this range proves inadequate for effectively preventing break-out. Conversely, the mud weight value of 1.9 g/cc prescribed for the σ_z ≥ σ_r ≥ σ_θ stress condition appears to be overestimated and not suitable to address any potential causes of break-out.

Interestingly, the lower limit for mud weight as determined by the Mogi–Coulomb criterion tends to be overestimated for the same stress conditions as the Mohr–Coulomb criterion, namely, ${\sigma }_{\theta }\ge {\sigma }_{z}\ge {\sigma }_{r}$ and ${\sigma }_{z}\ge {\sigma }_{\theta }\ge {\sigma }_{r}$. However, this overestimation is found to be justified when compared to the actual mud weight requirements in the ${\sigma }_{z}\ge {\sigma }_{r}\ge {\sigma }_{\theta }$ stress condition. These findings underscore the importance of selecting the appropriate mud weight criteria and values to maintain wellbore stability and prevent drilling complications in the given geological context.

The upper mud weight limits, as determined by the 3D extended Mohr–Coulomb criterion, to prevent drilling-induced fractures at various depth intervals (2250, 2285–2305, and 2325–2350 m TVD) are notably higher than the actual mud weight applied, potentially leading to wellbore failure. This discrepancy is further corroborated by observations in the caliper log, particularly in the stress profile where ${\sigma }_{r}\ge {\sigma }_{z}\ge {\sigma }_{\theta }$. In this specific stress condition, the excessive mud weight exceeds what is required, increasing the risk of complications.

Conversely, in stress profiles ${\sigma }_{r}\ge {\sigma }_{\theta }\ge {\sigma }_{z}$ and ${\sigma }_{\theta }\ge {\sigma }_{r}\ge {\sigma }_{z}$, the upper mud weight limits calculated using the 3D extended Mohr–Coulomb criterion do not show any signs of impending failure. This suggests that the mud weight is well within the safe range for these stress conditions.

However, when examining the upper mud weight limits using both the Mohr–Coulomb and Mogi–Coulomb criteria in stress conditions ${\sigma }_{r}\ge {\sigma }_{z}\ge {\sigma }_{\theta }$, ${\sigma }_{r}\ge {\sigma }_{\theta }\ge {\sigma }_{z}$, and ${\sigma }_{\theta }\ge {\sigma }_{r}\ge {\sigma }_{z}$, there appears to be significant fluctuation in the results, as indicated in Fig. 6. This variability underscores the importance of selecting the appropriate criterion for mud weight determination and highlights the complexity of the geological and stress conditions at play.

Taking into account these criteria and their respective mud weight limits, the analysis presented in Fig. 6 offers valuable insights into the intricate relationship between lithology, stress profiles, and mud density for case A. These insights are crucial for making informed decisions that promote the safe and efficient drilling and management of the well, helping to mitigate potential drilling-induced fractures and related challenges.

5.2 Case B

To validate our new 3D extended Mohr–Coulomb criterion, the second onshore exploratory well is chosen as a case study. Well B is an exploratory well for gas production with some technical failure during drilling. This technical failure may be due to improper selection of drilling mud. Then, a side-tracking method is used to drill a well up to the targeted depth. Figure 7 shows the input required to run the NMEM for the optimum mud weight selection to prevent the break-out. In this figure, the first track shows GR and caliper log. The caliper log indicates the irregularity of the drilled borehole due to the improper selection of mud. Based on the interpreted lithology, around 2305 mTVD–2360 mTVD and nearby 2790 MTVD–2850 mTVD have a rock-salt formation. The rock-salt formation is washout with drilling mud at the time of drilling. The second track shows the DTCO as an input. DTSM log is not run during the drilling, so Poisson's ratio should be kept constant (0.29) for the hall depth of the wellbore. The third and fourth tracks show the Newton porosity and density readings, respectively. Deep resistivity is shown in the last track of Fig. 7, which is helpful for the pore pressure prediction by the Eaton method. Formation rock properties such as dynamic young modulus, internal friction angle, and UCS are calculated based on the correlation given in the NMEM and presented in Fig. 9. Poisson’s ratio should be taken as a constant around near 0.29 based on the result of case A. In this figure: the first, second, and third tracks show the calculated result of the dynamic young modulus, angle of internal friction, and UCS, respectively. The fourth and fifth tracks presented the pore pressure by Eaton and fracture pressure by Mathews and Kelly. The sonic and resistivity methods are used for the pore pressure prediction, as shown in Fig. 8. The normal compaction trend line for both methods is given as

Fig. 7

Well log data were taken as an input of the NMEM for case B. From a–e Gamma-ray. Sonic compression slowness, porosity, density, and resistivity

Fig. 8

Normal compaction trend line for pore pressure prediction by Eaton's method for case B. a Using sonic, b using resistivity

$${\text{log}}\left({{\text{DTCO}}}_{{\text{n}}}\right)=-0.0007126\times D+1.51,$$

(34)

$${\text{log}}({{\text{RD}}}_{{\text{n}}})=0.009543\times {\text{D}}-1.354$$

(35)

Predicted pore pressure by the sonic method (blue line) shows near results to the actual pore pressure of the formation. Pore pressure by resistivity (red line) shows an overestimation of pore pressure (Fig. 9). The actual pore pressure of the formation at the depth of 2700 and 3100 mTVD is used to validate the result shown in the red dots. Measure pore pressure at the depth around 2700 mTVD is 17.7 MPa, and depth around 3100 mTVD is 21.9 MPa.

Fig. 9

Estimated geomechanical property from the well-log data for case B. From a–e dynamic young modulus, angle of internal friction, UCS, pore pressure, and fracture pressure

Figure 10 illustrates the outcomes derived from the mud weight calculations based on the determined pore and fracture pressures. In the initial part of the diagram, the inferred lithology is displayed, comprising claystone, sandstone, limestone, anhydrite, shale, siltstone, dolomite, and rock salt. The mechanical property correlation is altered in accordance with this lithological information, which in turn affects the precision of mud weight predictions.

Fig. 10

Stress profile and mud density incorporates Mohr–Coulomb, Mogi–Coulomb, and new linear 3D criteria concerning lithology for case B. a interpreted lithology, b stress profile, c lower mud weight limit to prevent break-out in tangential direction when $({\upsigma }_{\uptheta }\ge {\upsigma }_{{\text{z}}}\ge {\upsigma }_{{\text{r}}}$), d upper mud weight to prevent fracture when (${\upsigma }_{{\text{r}}}\ge {\upsigma }_{{\text{z}}}\ge {\upsigma }_{\uptheta }$), e lower mud weight to prevent axial break-out when (${\upsigma }_{{\text{z}}}\ge {\upsigma }_{\uptheta }\ge {\upsigma }_{{\text{r}}}$), f upper mud weight to prevent axial fracture when (${\upsigma }_{{\text{r}}}\ge {\upsigma }_{\uptheta }\ge {\upsigma }_{{\text{z}}}$), g upper mud weight to prevent axial fracture when (${\upsigma }_{\uptheta }\ge {\upsigma }_{{\text{r}}}\ge {\upsigma }_{{\text{z}}}$), h lower mud weight limit to prevent axial break-out when (${\upsigma }_{{\text{z}}}\ge {\upsigma }_{{\text{r}}}\ge {\upsigma }_{\uptheta }$)

The second section of the figure depicts a strike–slip faulting regime characterized by the stress conditions ${\sigma }_{H}(\mathrm{blue line})\ge {\sigma }_{V}(\mathrm{maroon line})\ge {\sigma }_{h}(\mathrm{saffron line})$. Using this stress profile, the mud density necessary to prevent break-out is determined through the application of the 3D extended Mohr–Coulomb criterion (red line), Mohr–Coulomb criterion (blue line), and Mogi–Coulomb criterion (green line) as shown in Fig. 10(c–h), encompassing all feasible combinations of stress profiles.

In Fig. 10, it is evident that the actual mud weight goes beyond the lower limit in track-c $({\sigma }_{\theta }\ge {\sigma }_{z}\ge {\sigma }_{r})$ and surpasses the upper limit in track-d (${\sigma }_{r}\ge {\sigma }_{z}\ge {\sigma }_{\theta }$). The mud weight utilized during drilling falls within the drilling mud window range according to both the Mogi-Coulomb and the 3D extended Mohr–Coulomb criteria. This range is crucial for preventing break-outs in tracks e and h (${\sigma }_{z}\ge {\sigma }_{\theta }\ge {\sigma }_{r}$ and ${\sigma }_{z}\ge {\sigma }_{r}\ge {\sigma }_{\theta })$, as well as drilling-induced fractures in tracks f and g (${\sigma }_{r}\ge {\sigma }_{\theta }\ge {\sigma }_{z}$ and ${\sigma }_{\theta }\ge {\sigma }_{r}\ge {\sigma }_{z}$). Nevertheless, deviations from the optimal mud weight range are noticeable in the caliper log and manifest as break-outs or drilling-induced fractures.

Specifically, in the depth range from 2200 to 2360 m below the vertical depth (mTVD), the actual mud weight exceeds the lower limit by new extended Mohr–Coulomb criterion, which is the primary factor behind the observed wellbore instability in that segment. Similarly, at depths ranging from 2770 to 2850 mTVD and from 2880 to 2950 mTVD, the actual mud weight surpasses the upper limit prescribed in track-d (${\sigma }_{r}\ge {\sigma }_{z}\ge {\sigma }_{\theta }$). This situation has the potential to induce instability in the wellbore, as evident in Fig. 7's first caliper log track. However, it is essential to highlight that the mud weight ranges established by the Mohr–Coulomb criterion are overestimated, which aligns with the conclusions drawn from the caliper log data.

6 Summary and Conclusion

Wellbore instability in geomechanical stress acting around the wellbore is due to the formation break-out, and drilling induces fracture. Wellbore stability is maintained with the help of the mud weight in the range between the pore pressure gradient and fracture pressure gradient. The optimum mud weight is calculated using the failure criterion by considering the inclination angle and formation lithology. The 3D extended Mohr–Coulomb criterion is applicable for in situ formation rock as it considers the effect of intermediated principal stress as a weighting (P) of the intermediated stress (${\sigma }_{2}$) on the mean effective stress (${\sigma }_{m}$). The material parameter (${q}_{1}, {q}_{2},\mathrm{ and UCS}$) is calculated as the relation of the friction angle ($\phi$), cohesion ($c$), and weighting ($\gamma$) on ${\sigma }_{2}$. This failure criterion is validated with true tri-axial compressive row data on the KBT amphibolite and applied to the wellbore to find the optimum mud weight with the help of the Kirsch equation and NMEM.

NMEM is developed with the help of the well-log data's empirical co-relation and the formation's geomechanical property. Dynamic young modulus is derived with the relation sonic log and density log. Poisson's ratio is estimated with the relation of shear and compressional sonic log data. Internal friction angle is calculated with the help of the DTCO or GR value or about porosity that can be derived by density-neutron log. UCS is estimated with the help of the number of empirical co-relations concerning the lithology, as listed in the table.

In situ stress profile estimation is difficult for heterogeneous behavior due to the pressure with depth and tectonic stress around the borehole. Overburden stress (${\sigma }_{v}$) is calculated with the help of density log data. ${\sigma }_{h}$ is nearly fracture pressure and estimated with the help of the Mathews and Kelly or Modified Eaton relation and validated with the help of the leek-of-test data. ${P}_{f}$ is estimated with the help of the ${P}_{p}$ in the equation ${\sigma }_{h}$ is predicted by the Eaton method of the normal compaction trend line of resistivity log data or DTCO log data. ${\sigma }_{H}$ is challenging to estimate directly. Li and Pudy estimate ${\sigma }_{H}$ as neglecting the minimum horizontal strain.

This study applies NMEM to two case studies that have faced technical difficulties at drilling. The input (well-logs) data are taken from the open-access data library (TNO) with lithology near the wellbore. Pore and fracture pressure estimated from the well-log data are also validated with actual filed data. The stress profile from NMEM suggests the strike–slip faulting regime. This NMEM is also applicable for the simulation of hydrofracturing operations, solution of sand production problems, and simulation of the carbon dioxide storage and sequestration in the formation. The mud weight limits for preventing break-out are determined based on the lithology and stress profile for different stress conditions, including ${\sigma }_{\theta }\ge {\sigma }_{z}\ge {\sigma }_{r}$, ${\sigma }_{z}\ge {\sigma }_{\theta }\ge {\sigma }_{r}$, and ${\sigma }_{z}\ge {\sigma }_{r}\ge {\sigma }_{\theta }$ for lower mud weight limits, and ${\sigma }_{r}\ge {\sigma }_{z}\ge {\sigma }_{\theta }$, ${\sigma }_{r}\ge {\sigma }_{\theta }\ge {\sigma }_{z}$, and ${\sigma }_{\theta }\ge {\sigma }_{r}\ge {\sigma }_{z}$ for upper mud weight limits. These limits are compared with those derived from the Mohr–Coulomb and Mogi–Coulomb criteria for each stress profile, as discussed in the results and discussion. Furthermore, the validity of these mud weight limits is confirmed by comparing them with the actual mud weight used during drilling. The caliper log is utilized to identify the failure profile, and it is concluded that if the actual mud weight exceeds the mud window limit, there is a possibility of wellbore instability, which is supported by evidence from the caliper log.

This research's uniqueness lies in applying the 3D extended Mohr–Coulomb criterion, which predicts both upper and lower mud weight limits in all six possible stress profiles to ensure wellbore stability. The study incorporates an updated mechanical earth model, focusing on considering the formation's lithology as the critical variable in this model. The mud weight prediction utilizing the 3D extended Mohr–Coulomb criterion demonstrates higher effectiveness by incorporating the intermediate principal stress and offering a simplified solution to overcome these limitations of the Mohr–Coulomb and Mogi–Coulomb criteria.

Appendices

Appendix A: Finding the Minimum Principal Based on the Strain Method

All three orthogonal stress follow Hook's law to keep stress–strain equilibrium. Strain in the minimum horizontal stress direction is given as

$${\varepsilon }_{h}=\frac{{\sigma }_{h}-v({\sigma }_{v}+{\sigma }_{H})}{E},$$

(36)

where ${\varepsilon }_{h}$ is the strain in the minimum horizontal stress direction, $E$ is Young's modulus ${\sigma }_{H},{\sigma }_{h}, {\text{and}} {\sigma }_{v}$ are orthogonal stress, and $v$ is the Poisson’s ratio. Equation 36 reduced the upper bound maximum horizontal stress by neglecting minimum horizontal strain about the vertical and maximum horizontal strain. Given by (Li & Purdy 2010)

$${\sigma }_{H}^{{\text{UB}}}=\left(\frac{({\sigma }_{h}-{P}_{p})}{v}\right)-{\sigma }_{v}+2{P}_{P}.$$

(37)

Appendix B: Local In Situ Stress for the Inclined Well

Local in situ stress for the incline well in a cross-section perpendicular to the wellbore axis can be expressed in the Fig. 

Fig. 11

Local in situ stress for the incline well redeveloped from the (Zhang 2019)

11.

$${\sigma }_{x}^{0}=\left({\sigma }_{H}{{\text{cos}}}^{2}\alpha +{\sigma }_{h}{{\text{sin}}}^{2}\alpha \right){{\text{cos}}}^{2}i+{\sigma }_{v}{{\text{sin}}}^{2}i$$

(38)

$${\sigma }_{y}^{0}=\left({\sigma }_{H}{{\text{sin}}}^{2}\alpha +{\sigma }_{h}{{\text{cos}}}^{2}\alpha \right)$$

(39)

$${\sigma }_{z}^{0}=\left({\sigma }_{H}{{\text{cos}}}^{2}\alpha +{\sigma }_{h}{{\text{sin}}}^{2}\alpha \right){{\text{sin}}}^{2}i+{\sigma }_{v}{{\text{cost}}}^{2}i,$$

(40)

$${\tau }_{xy}^{0}=\frac{\left({\sigma }_{h}-{\sigma }_{H}\right)}{2}{\text{sin}}2\alpha {\text{cos}}i,$$

(41)

$${\tau }_{xy}^{0}=\frac{\left({\sigma }_{h}-{\sigma }_{H}\right)}{2}{\text{sin}}2\alpha \mathrm{sin }i,$$

(42)

$${\tau }_{xz}^{0}=\frac{1}{2}\left({\sigma }_{H}{{\text{cos}}}^{2}\alpha +{\sigma }_{h}{{\text{sin}}}^{2}\alpha -{\sigma }_{v}\right){\text{sin}}2i.$$

(43)

Appendix C: Kirsch Equation

Near wellbore stresses in an inclined borehole by Bradley (1979) and Fjaer et al. (2008).

$${\sigma }_{r}=\frac{\left({\sigma }_{x}^{0}+{\sigma }_{y}^{0}\right)}{2}\left(1-\frac{{R}^{2}}{{r}^{2}}\right)+\frac{({\sigma }_{x}^{0}-{\sigma }_{y}^{0})}{2}\left(1-\frac{4{R}^{2}}{{r}^{2}}+\frac{3{R}^{4}}{{r}^{4}}\right){\text{cos}}2\theta +{\tau }_{xy}^{0}\left(1-\frac{4{R}^{2}}{{r}^{2}}+\frac{3{R}^{4}}{{r}^{4}}\right){\text{sin}}2\theta +{p}_{w}\frac{{R}^{2}}{{r}^{2}}$$

(44)

$${\sigma }_{\theta }=\frac{\left({\sigma }_{x}^{0}+{\sigma }_{y}^{0}\right)}{2}\left(1+\frac{{R}^{2}}{{r}^{2}}\right)-\frac{\left({\sigma }_{x}^{0}-{\sigma }_{y}^{0}\right)}{2}\left(1+\frac{3{R}^{4}}{{r}^{4}}\right){\text{cos}}2\theta +{\tau }_{xy}^{0}\left(1+\frac{3{R}^{4}}{{r}^{4}}\right){\text{sin}}2\theta -{p}_{w}\frac{{R}^{2}}{{r}^{2}},$$

(45)

$${\sigma }_{z}={\sigma }_{z}^{0}-2v\left(\left({\sigma }_{x}^{0}-{\sigma }_{y}^{0}\right)\right) \frac{{R}^{2}}{{r}^{2}}{\text{cos}}2\theta -4v{\tau }_{xy}^{0}\left(\frac{{R}^{2}}{{r}^{2}}\right){\text{sin}}2\theta ,$$

(46)

$${\tau }_{r\theta }=\left(-\frac{\left({\sigma }_{x}^{0}-{\sigma }_{y}^{0}\right)}{2}{\text{sin}}2\theta +{\tau }_{xy}^{0}\mathrm{cos }2\theta \right)\left(1+\frac{2{R}^{2}}{{r}^{2}}-\frac{3{R}^{4}}{{r}^{4}}\right)$$

(47)

$${\tau }_{rz}=\left({\tau }_{yz}^{0}{\text{sin}}\theta +{\tau }_{xz}^{0}\mathrm{cos }\theta \right)\left(1-\frac{{R}^{2}}{{r}^{2}}\right)$$

(48)

$${\tau }_{\theta z}=\left(-{\tau }_{xz}^{0}{\text{sin}}\theta +{\tau }_{yz}^{0}\mathrm{cos }\theta \right) \left(1+\frac{{R}^{2}}{{r}^{2}}\right)$$

(49)

At the borehole wall (r = R), Kirsch’s equations are simplified as follows:

Three possibilities arise for the determination of the allowable mud pressure such as (a) ${\sigma }_{z}\ge {\sigma }_{\theta }\ge {\sigma }_{r}$, (b) ${\sigma }_{\theta }\ge {\sigma }_{z}\ge {\sigma }_{r}$ and (c) ${\sigma }_{\theta }\ge {\sigma }_{r}\ge {\sigma }_{z}$ The magnitude of the wellbore stresses for the initiation of shear failure is:

$${\sigma }_{\theta }=A-{P}_{w},$$

(50)

$${\sigma }_{r}={P}_{w},$$

(51)

$${\sigma }_{z}=B,$$

(52)

where $A=3{ \sigma }_{h}-{\sigma }_{H}$ and $B={\sigma }_{v}-2v\left({{\sigma }_{H}-\sigma }_{h}\right)$

Appendix D: Mud Weight by the Mohr–Coulomb Criterion for Stable Well

Mohr–Coulomb failure criterion gives the linear relationship between material shear strength and normal stress. This relation is given by the equation below (Labuz et al. 2018)

$$\tau =\sigma {\text{tan}}\left(\phi \right)+c$$

(53)

where $\tau$ is the shear strength, $\sigma$ applied normal stress, c is the material cohesion, and $\phi$ is the internal friction angle.

Now from Mohr’s circle

$$\sigma ={\sigma }_{m}-{\tau }_{m}{\text{sin}}\phi \mathrm{ and }\tau ={\tau }_{m}{\text{cos}}\phi .$$

(54)

Here ${\sigma }_{m}$ (mean effective stress) and ${\tau }_{m}$ (maximum shear stress) define the relation of principal stresses is

$${\sigma }_{m}=\frac{{\sigma }_{1}+{\sigma }_{3}}{2}\mathrm{ and }{\tau }_{m}=\frac{{\sigma }_{1}-{\sigma }_{3}}{2}.$$

(55)

Mohr–Coulomb Eq. (25) is also re-written in terms of effective principal stress ${\sigma }_{1}, {\sigma }_{2}, and {\sigma }_{3}$ is given by the equation here ${\sigma }_{1}\ge {\sigma }_{2}\ge {\sigma }_{3}$ in biaxial stress.

$$\left({\sigma }_{1}{^\prime}\right)=q \left({\sigma }_{3}^{\mathrm{^{^\prime}}}\right)+{\text{UCS}},$$

(56)

where $q=\frac{\left(1+{\text{sin}}\phi \right)}{\left(1-{\text{sin}}\phi \right)}$ and UCS is the uniaxial compressive strength ${\text{UCS}}=\frac{2c{\text{cos}}\phi }{\left(1-{\text{sin}}\phi \right)}.$ For wellbore collapse, considering the situation ${(\sigma }_{\theta }\ge {\sigma }_{z}\ge {\sigma }_{r})$, the Mohr–Coulomb failure criterion can be written as,

$${\sigma }_{\theta }=q\times {\sigma }_{r}+{\text{UCS}}.$$

(57)

Substituting the value of the ${\sigma }_{\theta }$ and ${\sigma }_{r}$ in the above equation to avoid borehole collapse, the mud weight given by the Mohr–Coulomb failure criterion for ${(\sigma }_{\theta }\ge {\sigma }_{z}\ge {\sigma }_{r})$ is given as

$${P}_{w {\text{MC}}} ={\text{abs}}\left(\frac{A-{\text{UCS}}}{\left(q+1\right)}\right).$$

(58)

Appendix E: Mud Weight by Mogi–Coulomb Failure Criterion for Stable Well

Al-Ajmi and Zimmerman (2005) proposed a failure criterion by considering the Mogi criterion (1971) and the linear Mohr–Coulomb failure criterion called the Mogi–Coulomb criterion. The Mogi–Coulomb criterion is the linear relation between octahedral stress (${\tau }_{{\text{oct}}}$) and mean effective stress (${\sigma }_{m2}$).

$${\tau }_{{\text{oct}}}=a+b\times {\sigma }_{m2}$$

(59)

Here, ${\tau }_{{\text{oct}}}=\frac{\sqrt{{({\sigma }_{1}-{\sigma }_{2})}^{2}+{({\sigma }_{2}-{\sigma }_{3})}^{2}+{({\sigma }_{3}-{\sigma }_{1})}^{2}}}{3}$,${ \sigma }_{m2}=\frac{{\sigma }_{1}+{\sigma }_{3}}{2}.$

Material constant $a {\text{and}} b$ are related to the angle of internal friction ($\varnothing$), and cohesion (c) is given by

$$a=\frac{2\sqrt{2}}{3}\mathrm{ cos\varnothing }; b=\frac{2\sqrt{2}}{3}\mathrm{ sin\varnothing }.$$

Octahedral stress (${\tau }_{{\text{oct}}}$) and mean effective stress (${\sigma }_{m2}$) can be written in terms of stress invariants as

$${\tau }_{{\text{oct}}}=\frac{\sqrt{2}}{3} \sqrt{{I}_{1}^{2}-3{ I}_{2}}$$

(60)

and

$${\sigma }_{m2}=\frac{1}{2}\left({I}_{1}-{\sigma }_{2}\right),$$

(61)

where ${I}_{1}={\sigma }_{1}+{\sigma }_{2}+{\sigma }_{3}$ is the first stress invariant, and ${I}_{2}={\sigma }_{1}{\sigma }_{2}+{\sigma }_{2}{\sigma }_{3}+{\sigma }_{3}{\sigma }_{1}$ is the second invariant. Stress invariants can also write in terms of wellbore stresses as,

$${I}_{1}={\sigma }_{\theta }+{\sigma }_{z}+{\sigma }_{r}=A+B$$

(62)

$${I}_{2}={\sigma }_{\theta }{\sigma }_{z}+{\sigma }_{z}{\sigma }_{r}+{\sigma }_{\theta }{\sigma }_{r}=A {P}_{w}-{P}_{w}^{2}+AB$$

(63)

By considering the effective stress, the Mogi–Coulomb failure criterion is given as

$$\frac{\sqrt{2}}{3} \sqrt{{I}_{1}^{2}-3{ I}_{2}}=a+\frac{b}{2}\left({I}_{1}-{\sigma }_{2}\right)$$

(64)

or

$${I}_{1}^{2}-3{ I}_{2}={\left({a}^{\mathrm{^{^\prime}}}+\frac{{b}^{\mathrm{^{^\prime}}}}{2}\left({I}_{1}-{\sigma }_{2}\right)\right)}^{2}$$

(65)

where ${a}{^\prime}$=2c ${\text{cos}}\varnothing$ and b′=$2\mathrm{ sin}\varnothing .$ Now, ${I}_{2}$ is calculated from the above equation as

$${I}_{2}=\frac{{I}_{1}^{2}}{3}-\frac{1}{3}{\left({a}^{\mathrm{^{^\prime}}}+\frac{{b}^{\mathrm{^{^\prime}}}}{2}\left({I}_{1}-{\sigma }_{2}\right)\right)}^{2}$$

(66)

And mud density is given as

$${P}_{w {\text{mogi}}}={\text{abs}}\left(\frac{A\pm \sqrt{{A}^{2}-4\left({I}_{2}-AB\right)} }{2}\right)$$

(67)