Thermal Fracturing in Orthotropic Rocks with Superposition-Based Coupling of PD and FEM

Abstract

Thermally induced deformation and fracturing in rocks are ubiquitously encountered in underground geotechnical engineering and they are highly influenced by the material anisotropy. In the present manuscript, a superposition-based PD and FEM coupling approach is proposed for simulating thermal fracturing in orthotropic rocks. In this approach, the critical regions with possibility of cracks are encompassed by the non-ordinary state-based peridynamics (NOSBPD) model, while the entire problem domain is discretized by a fixed underlying finite element (FE) mesh. The thermal balance equation is fully approximated by the underlying finite elements without any contribution from the NOSBPD model. The NOSBPD model and FE model are coupled based on the superposition theory. The mechanical anisotropy, thermal anisotropy as well as the hindering effect of the insulated crack on the thermal diffusion are considered in this coupled model. A staggered solution scheme is employed to solve the coupled system. The performance of the coupled method for thermomechanical problems with and without damage is evaluated by two numerical examples. After validation, thermal fracturing in an orthotropic rock specimen under high surrounding temperature is systematically studied. The parametric study shows that the inclination angle of the cracks and the major axes of the elliptical shape of the isotherms are generally consistent with the principal material first axis. Both the mechanical and thermal anisotropy highly affect the thermal fracturing in orthotropic rocks.

Highlights

• A superposition-based coupling of non-ordinary state-based peridynamics and finite element method approach for thermal fracturing in orthotropic rocks is proposed.

• The mechanical anisotropy, thermal anisotropy as well as the hindering effect of the insulated crack on the thermal diffusion are all considered in the coupled model.

• The inclination angle of the cracks and the major axes of the elliptical shape of the isotherms are generally consistent with the principal material first axis.

• Both the mechanical and thermal anisotropy highly affect the thermal fracturing in orthotropic rocks.

1 Introduction

Composed of different mineral grains and crystals with different mechanical and thermal expansion features, the mechanical performances of rock or rock-like materials are closely related to the environmental temperatures (Wei et al. 2015). Thermal stress produced by the thermal load alters the mechanical deformation and consequently induces fracturing if it exceeds the strength of the rock materials. For example, for the disposal of high-level radioactive waste (Birkholzer et al. 2012; Zuo et al. 2017), a large amount of heat is released by the nuclear waste during the decay process and the temperature of the surrounding rock of repository is raised. Consequently, thermal cracking in the surrounding rocks may be generated. It should be carefully handled to prevent nuclide migration in fractured rocks. On the other hand, in the enhanced or engineered geothermal systems (EGS), thermally induced secondary cracks in the hot dry rock system are employed to generate effective fracture networks for water circulation (Breede et al., 2013). Recently, as specific development needs, some tunnels have to be constructed in complex geological regions with high ground temperature. For instance, the maximum temperature of rock even reaches 89.9 °C in Sangzhuling Railway Tunnel in China (Wang et al. 2019). The great temperature difference induced by the high ground temperature in surrounding rocks and air temperature in the tunnel could generate large temperature stress and subsequently cause cracks in the surrounding rocks or tunnel linings, which deteriorates the stability of the underground structures significantly (Hu et al. 2021).

As natural materials, rock masses contain numerous discontinuities as joints, cracks, bedding planes, and/or even faults, thus isotropic rocks are rare, instead, and anisotropy is a common phenomenon in rocks. Unlike in isotropic rocks, the preferential distribution of properties renders deformation and fracturing in anisotropic rocks more complex (Zhu and Arson 2014; Mohtarami et al. 2017). For instance, due to material anisotropy, experiments have shown that cracks in anisotropic rocks tend to propagates along the relatively weak bedding plane, rather than along the initial notch orientation as in isotropic rocks (Nejati et al. 2020). Sedimentary rocks can often be regarded as orthotropic media with different elastic properties in the bedding plane and perpendicular to this plane. Thus, in this study, we focus on the thermally induced deformation and fracturing in orthotropic rocks.

Thermally induced deformation and fracturing as well as mechanical properties variations influenced by the environmental temperature are extensively investigated by experimental tests (Heuze 1983; Jansen et al. 1993; Mahmutoglu 1998; Ke et al. 2009). In addition, analytical solutions are also available for some special thermomechanical problems (Nobile and Carloni 2005). However, the anisotropy effect is rarely taken into account in theses experimental or analytical studies. Furthermore, for engineering applications containing complicated geometries and boundary conditions, numerical methods are a more competitive option. So far, many advanced numerical approaches have been employed to study thermal fracturing in orthotropic materials. In simplified terms, these methods can be categorized into three groups: (1) continuum-based numerical methods, (2) discontinuum-based methods and (3) hybrid continuum–discontinuum methods. For the continuum-based numerical method, the extended finite element method (XFEM) is widely used for this purpose (Mohtarami et al. 2019). Bayesteh and Mohammadi (2013) compared different elastic tip enrichment functions for orthotropic functionally graded materials and the stress intensity factors (SIFs) were extracted to evaluate the performances of the specific orthotropic fracture propagation criterion. Bouhala et al. (2015) applied the XFEM to study the thermo-anisotropic crack propagation, where some temperature tip enrichment functions at the crack surface for temperature or heat flux discontinuities were used. Nguyen et al. (2019) employed the extended consecutive-interpolation four-node quadrilateral element method (XCQ4) with a novel enrichment approximation of discontinuous temperature field to study the thermomechanical crack propagation in orthotropic composite materials. Recently, a new set of tip enrichment functions for temperature field in anisotropic materials was proposed by Bayat and Nazari (2021), where their dependency on the thermal properties of the materials was considered. The typical discontinuous approaches for thermal fracturing in rocks are mainly based on the discrete element method (DEM). The particle discrete element method was used by Xu et al. (2022) to investigate the fracture evolution in transversely isotropic rocks considering the pre-existing flaws and weak bedding planes, but the temperature effect was ignored. A three dimensional DEM model for semi-circular bend (SCB) test under combined actions of thermal loading and material anisotropy in Midgley Grit sandstone was established by Shang et al. (2019) and a total of four fracture patterns were found. Hybrid approaches taking advantages of different methodologies, such as the combined finite-discrete element method (FDEM), have also been applied to deal with the thermal cracking in rocks considering anisotropy. A weakly coupled thermomechanical model taking into account the mechanical and thermal anisotropy in layered shale formation was proposed by Sun et al. (2020) using FDEM. Through these studies, there is a consensus that anisotropy plays an important role in the thermally induced deformation and fracturing of rocks and this effect should not be ignored.

Peridynamic (PD) theory, firstly proposed by Silling (2000), is a reformulation theory of classical continuum mechanics. Up to now, three types of peridynamics, namely bond-based peridynamics (BBPD), ordinary state-based peridynamics (OSBPD) and non-ordinary state-based peridynamics (NOSBPD) (Silling et al. 2007) have been proposed. Characterized by the integro-differential governing equation, the nonlocal PD model remains valid regardless of whether having the cracks or not and provides an effective tool for dealing with discontinuity problems in many areas. As far as thermomechanical analysis is concerned, numerous valuable attempts have been made in PD community. Nonlocal formulations for the thermomechanical coupled system were derived by Bobaru and Duangpanya (2012) and Oterkus et al. (2014). Thermal fracturing in many brittle or quasi-brittle materials has been investigated by using peridynamics (D’Antuono and Marco 2017; Yang et al. 2020; Bazazzadeh et al. 2020; Chen et al. 2021). Concerning thermal fracturing in rocks, several weakly coupled thermomechanical models based on BBPD (Wang et al. 2018), OSBPD (Wang and Zhou 2019) and NOSBPD (Shou and Zhou 2020) were established and rock fractures due to heating from boreholes or heterogeneity of rocks with different thermal expansion coefficients in different parts were successfully captured by these models. However, thermal fracturing in orthotropic rocks has rarely been studied by peridynamics. This raises the necessity to propose a thermomechanical coupled peridynamics model applicable for anisotropic rocks.

In this study, the PD-FEM coupling approach for thermomechanical problems proposed by the authors (Sun et al. 2021a) is generalized to consider mechanical and thermal anisotropy. To overcome the limit of high computational cost associated with peridynamics-based models, the orthotropic NOSBPD model is only applied in the critical regions around the cracks and it is coupled with the underlying FE model covering the entire problem domain based on the superposition theory. The work presented in this study is the first time for the superposition theory proposed by Fish (1992) and Sun et al. (2018, 2021b) to be applied in thermomechanical problems. The mechanical anisotropy, thermal anisotropy as well as the hindering effect of the insulated crack on the thermal diffusion are considered in this coupled model. After validation of this framework against relevant analytical or existent numerical solutions, the effects of mechanical and thermal anisotropy on the thermal fracturing in rocks are thoroughly studied.

The present article is organized as follows. In Sect. 2, the fundamental mechanism and numerical discretization for the superposition-based coupling of PD and FEM approach are presented in detail. The performance of the coupled method for thermomechanical problems with and without damage is evaluated in Sect. 3. In Sect. 4, thermal fracturing in an orthotropic rock specimen is parametrically studied. Summary and main conclusions are presented in Sect. 5.

2 The Superposition-Based Coupling of PD-FEM Approach for Thermal Fracturing in Orthotropic Rocks

2.1 Governing Equations

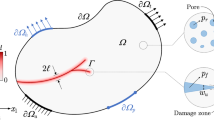
Herein, an orthotropic rock specimen occupying an open-bounded regular domain $\overline{\Omega }$, with the assumption of infinitesimal displacements and quasi-static state, under thermomechanical loadings is considered as shown in Fig. 1. The critical region(s) with possibility of cracks bounded by the boundary $\hat{\Gamma }$, where NOSBPD model is employed, is denoted by $\hat{\Omega }$. For notational consistency, quantities in the domain $\overline{\Omega }$ and $\hat{\Omega }$ will be denoted by $(\overline{*})$ and $(\hat{*})$, respectively, hereafter. Let $\overline{\Gamma }_{u}$, $\overline{\Gamma }_{t}$, $\overline{\Gamma }_{\Theta }$ and $\overline{\Gamma }_{J}$ denote the prescribed displacement, traction, temperature, and heat flux boundaries, respectively. The boundary of the domain $\overline{\Omega }$ is denoted by $\overline{\Gamma }$, which is partitioned into $\overline{\Gamma } = \overline{\Gamma }_{u} \cup \overline{\Gamma }_{t}$ and $\overline{\Gamma } = \overline{\Gamma }_{\Theta } \cup \overline{\Gamma }_{J}$ for mechanical deformation and heat transfer, respectively, which should satisfy $\overline{\Gamma }_{u} \cap \overline{\Gamma }_{t} = \overline{\Gamma }_{\Theta } \cap \overline{\Gamma }_{J} = \emptyset$. To describe material anisotropy, a local material coordinate system using two orthogonal axes 1 and 2 is established. The angle between the first axis-1 and the horizontal axis-x in the global coordinate system is defined as the material angle $\theta$ (see Fig. 1).

Fig. 1

Schematics of the superposition-based coupling of PD and FEM approach for thermal fracturing analysis in orthotropic rocks

In this work, only the thermal-elastic material under two-dimensional condition, including plane stress and plane strain scenarios, is considered. Two sets of equilibrium equations for this thermomechanical coupled problem are given as.

(1) Momentum balance equation

$$\nabla \cdot {\varvec{\sigma}}{ + }{\varvec{b}} = {\mathbf{0}},$$

(1)

where ${\varvec{b}}$ is the body force vector.

In the classical elasticity theory, the constitutive law for the orthotropic material can be expressed by using Hooke’s law as

$${\varvec{\sigma}} = {\mathbb{D}}:{\varvec{\varepsilon}}^{{\text{e}}} ,$$

(2)

where ${\mathbb{D}}$ is elastic stiffness tensor, ${\varvec{\varepsilon}}^{{\text{e}}}$ is the elastic strain, which is calculated as

$${\varvec{\varepsilon}}^{e} { = }{\varvec{\varepsilon}} - {\varvec{\varepsilon}}^{\Theta } .$$

(3)

The total strain tensor ${\varvec{\varepsilon}}$ in Eq. (3) with small deformation assumption is given by

$${\varvec{\varepsilon}}{ = }\frac{1}{2}(\nabla {\varvec{u}} + \nabla^{{\text{T}}} {\varvec{u}}).$$

(4)

For the orthotropic material, the thermal strain tensor ${\varvec{\varepsilon}}^{\Theta }$ in Eq. (3) is calculated as

$${\varvec{\varepsilon}}^{\Theta } { = }{\varvec{\alpha}}\Delta \Theta ,$$

(5)

where the thermal expansion coefficient tensor ${\varvec{\alpha}}$ in the global coordinate system is defined as

$${\varvec{\alpha}} = \left[ {\begin{array}{*{20}c} {\alpha_{1} \cos^{2} \theta + \alpha_{2} \sin^{2} \theta } & {(\alpha_{1} - \alpha_{2} )\sin \theta \cos \theta } \\ {(\alpha_{1} - \alpha_{2} )\sin \theta \cos \theta } & {\alpha_{1} \sin^{2} \theta + \alpha_{2} \cos^{2} \theta } \\ \end{array} } \right],$$

(6)

with $\alpha_{1}$ and $\alpha_{2}$ being the thermal expansion coefficients along the two principal material axes.

Using the Voigt notation, the stress–strain relation in the local coordinate system is given by

For the plane stress condition,

$$\left[ {\begin{array}{*{20}c} {\sigma_{11}^{{}} } \\ {\sigma_{22}^{{}} } \\ {\tau_{12}^{{}} } \\ \end{array} } \right]{ = }\underbrace {{\left[ {\begin{array}{*{20}c} {E_{1} E_{2} /\Lambda } & {E_{1} E_{2} v_{12} /\Lambda } & 0 \\ {} & {E_{2}^{2} v_{12} /\Lambda } & 0 \\ {{\text{syms}}} & {} & {G_{12} } \\ \end{array} } \right]}}_{{\varvec{s}}^{\prime}}\left[ {\begin{array}{*{20}c} {\varepsilon_{11}^{e} } \\ {\varepsilon_{22}^{e} } \\ {\gamma_{12}^{e} } \\ \end{array} } \right],$$

(7)

with

$$\Lambda = - E_{2}^{2} v_{23}^{2} + 2E_{1} E_{2} v_{12} v_{13} v_{23} + E_{1} E_{2} v_{13}^{2} + E_{1} E_{3} v_{12}^{2} .$$

(8)

For the plane strain condition,

$$\left[ {\begin{array}{*{20}c} {\sigma_{11}^{{}} } \\ {\sigma_{22}^{{}} } \\ {\tau_{12}^{{}} } \\ \end{array} } \right] = \underbrace {{\left[ {\begin{array}{*{20}c} { - E_{1} E_{2} \left( { - E_{2} v_{23}^{2} + E_{3} } \right)/\Lambda } & { - E_{1} E_{2} \left( {E_{3} v_{12} + E_{2} v_{13} v_{23} } \right)/\Lambda } & 0 \\ {} & { - E_{2}^{2} \left( { - E_{1} v_{13}^{2} + E_{3} } \right)/\Lambda } & 0 \\ {{\text{syms}}} & {} & {G_{12} } \\ \end{array} } \right]}}_{{\varvec{s}}^{\prime}}\left[ {\begin{array}{*{20}c} {\varepsilon_{11}^{e} } \\ {\varepsilon_{22}^{e} } \\ {\gamma_{12}^{e} } \\ \end{array} } \right],$$

(9)

with

$$\Lambda = - E_{2}^{2} v_{23}^{2} + 2E_{1} E_{2} v_{12} v_{13} v_{23} + E_{1} E_{2} v_{13}^{2} + E_{1} E_{3} v_{12}^{2} ,$$

(10)

where $E_{i}$, $v_{ij}$, $G_{ij}$ in the local elasticity stiffness matrix ${\varvec{s}}^{\prime}$ are Young’s modulus, Poisson’s ratio and shear modulus, respectively, in the principal material axes.

By a coordinate frame transformation, the constitutive matrix s in the global coordinate system is given by

$${\varvec{s}} = {\varvec{Ts}}^{\prime}{\varvec{T}}^{{\text{T}}} ,$$

(11)

where ${\varvec{T}}$ is the transformation matrix,

$${\varvec{T}} = \left[ {\begin{array}{*{20}c} {\cos^{2} \theta } & {\cos^{2} \theta } & { - 2\cos \theta \sin \theta } \\ {\cos^{2} \theta } & {\cos^{2} \theta } & {2\cos \theta \sin \theta } \\ {\cos \theta \sin \theta } & { - \cos \theta \sin \theta } & {\cos^{2} \theta - \sin^{2} \theta } \\ \end{array} } \right].$$

(12)

It is noted that throughout this paper, the classical sign convention of the continuum mechanics as the tensile stress being positive is adopted.

(2) Thermal balance equation

$$\rho c\dot{\Theta } + \nabla \cdot {\varvec{J}} = r{*,}$$

(13)

where constants $\rho$ and $c$ denote the mass density and the specific heat capacity of the material, respectively; $r{*}$ represents the internal heat source.

The heat flux ${\varvec{J}}$ is assumed to be controlled by the Fourier law (Zienkiewicz and Taylor 2000),

$${\varvec{J}} = - {\varvec{k}}\nabla \Theta ,$$

(14)

where the thermal conductivity tensor ${\varvec{k}}$ is given by

$${\varvec{k}} = \left[ {\begin{array}{*{20}c} {k_{1} \cos^{2} \theta + k_{2} \sin^{2} \theta } & {(k_{1} - k_{2} )\sin \theta \cos \theta } \\ {(k_{1} - k_{2} )\sin \theta \cos \theta } & {k_{1} \sin^{2} \theta + k_{2} \cos^{2} \theta } \\ \end{array} } \right],$$

(15)

with k₁ and k₂ being the thermal conduction coefficients in the axis-1 and axis-2 directions, respectively. It is noted that the anisotropy angle of the thermal conduction is assumed to be identical to the material angle $\theta$, for simplicity, as shown in Fig. 1.

The aforementioned balance equations, i.e., Eqs. (1) and (3), are coupled with the following initial and boundary conditions. The boundary conditions for the point ${\varvec{x}}$ are given by

$$\left\{ {\begin{array}{*{20}c} {{\varvec{u}}({\varvec{x}},0) = {\varvec{u}}_{0} ({\varvec{x}})} & {{\text{at}}\quad t = 0} \\ {\Theta ({\varvec{x}},0) = \Theta_{0} ({\varvec{x}})} & {{\text{at}}\quad t = 0} \\ {{\varvec{u}}({\varvec{x}},t) = \overline{\varvec{u}}({\varvec{x}},t)} & {{\text{on}}\quad \overline{\Gamma }_{u} } \\ {{\varvec{\sigma}}({\varvec{x}},t) \cdot {\varvec{n}}({\varvec{x}}) = \overline{\varvec{t}}({\varvec{x}},t)} & {{\text{on}}\quad \overline{\Gamma }_{t} } \\ {\Theta ({\varvec{x}},t) = \overline{\Theta }({\varvec{x}},t)} & {{\text{on}}\quad \overline{\Gamma }_{\Theta } } \\ {{\varvec{J}}({\varvec{x}},t) \cdot {\varvec{n}}({\varvec{x}}) = \overline{\varvec{J}}({\varvec{x}},t) + h_{{\text{s}}} (\Theta_{{\text{s}}} - \Theta_{{\text{a}}} )} & {{\text{on}}\quad \overline{\Gamma }_{J} } \\ \end{array} } \right.,$$

(16)

where ${\varvec{n}}$ is the unit normal vector; $h_{{\text{s}}}$ is the convection heat transfer coefficient; $\Theta_{{\text{s}}}$ is the body surface temperature, and $\Theta_{{\text{a}}}$ is the air temperature. It should be noted that for notation simplicity, the prescribed boundary conditions, such as prescribed displacement $\overline{\varvec{u}}$, prescribed traction force $\overline{\varvec{t}}$, prescribed heat flux $\overline{{\varvec{J}}}$ and prescribed temperature $\overline{\Theta }$, are assumed to be only applied on the boundary $\overline{\Gamma }$.

2.2 The Orthotropic NOSBPD Model Considering Thermal Effect

In the thermomechanical model considered herein, the fracturing in the orthotropic solid is described using the NOSBPD theory. Herein, an orthotropic NOSBPD model proposed by the first author (Sun et al. 2022) is extended to consider the thermal effect.

In the original NOSBPD theory, the conservation equation of linear momentum ignoring the inertial effect reads

$$\begin{gathered} \int_{{H_{{\varvec{x}}} }} {\left\{ {\omega (\left| {\varvec{\xi}} \right|){\rm{det}}({\varvec{F}}) \cdot {\varvec{F}}^{ - 1} \cdot {\varvec{\sigma}} \cdot {\varvec{B}}({\varvec{x}}) \cdot {\varvec{\xi}}} \right\}{\rm{d}}V_{{\varvec{x}}^{\prime}} - } \hfill \\ \int_{{H_{{\varvec{x}}} }} {\left\{ {\omega (\left| {\varvec{\xi}} ^{\prime} \right|){\rm{det}}(\varvec{F}^{\prime}) \cdot \left( {\varvec{F}}^{\prime} \right)^{ - 1} \cdot {\varvec{\sigma}}^{\prime} \cdot {\varvec{B}}(\varvec{x}^{\prime}) \cdot \varvec{\xi} ^{\prime}} \right\}{\rm{d}}V_{{\varvec{x}}^{\prime}} } + {\varvec{b}}(\varvec{x},t) = {\mathbf{0}}, \hfill \\ \end{gathered}$$

(17)

where the material point ${\varvec{x}}$ interacts with its surrounding points $\varvec{x}^{\prime}$ in the spherical neighborhood $H_{x}$ with a cutoff radius $\delta$. $\omega (\left| {\varvec{\xi}} \right|)$ is the weighting function incorporating the failure criterion of the bond ${\varvec{\xi}} = \varvec{x}^{\prime} - {\varvec{x}}$ as defined below. The nonlocal deformation ${\varvec{F}}$ and nonlocal shape tensor ${\varvec{B}}$ at material point ${\varvec{x}}$ are defined as

$${\varvec{F}}({\varvec{x}}) = \left[ {\int_{{H_{{\varvec{x}}} }} {\omega (\left| {\varvec{\xi}} \right|)(\underline{{\varvec{Y}}} \langle {\varvec{\xi}}\rangle \otimes {\varvec{\xi}}){\rm{d}}V_{{{\varvec{x}}^{\prime}}} } } \right] \cdot {\varvec{B}}({\varvec{x}})$$

(18)

$${\varvec{B}}({\varvec{x}}) = \left[ {\int_{{H_{{\varvec{x}}} }} {\omega (\left| {\varvec{\xi}} \right|)({\varvec{\xi}} \otimes {\varvec{\xi}}){\rm{d}}V_{{\varvec{\xi}}} } } \right]^{ - 1} .$$

(19)

Following Eq. (3), the governing equation of the NOSBPD theory considering thermal effect can be rewritten as

$$\begin{gathered} \int_{{H_{{\varvec{x}}} }} {\left\{ {\omega (\left| {\varvec{\xi}} \right|){\rm{det}}({\varvec{F}}) \cdot {\varvec{F}}^{ - 1} \cdot {\varvec{\sigma}}{\mathbf{(}}{\varvec{\varepsilon}} - {\varvec{\varepsilon}}^{\Theta } {\mathbf{)}} \cdot {\varvec{B}}({\varvec{x}}) \cdot {\varvec{\xi}}} \right\}{\rm{d}}V_{{\varvec{x}}^{\prime}} - } \hfill \\ \int_{{H_{{\varvec{x}}} }} {\left\{ {\omega (\left| {\varvec{\xi}} ^{\prime} \right|){\rm{det}}(\varvec{F}^{\prime}) \cdot \left( {\varvec{F}^{\prime}} \right)^{ - 1} \cdot {\varvec{\sigma}}^{\prime}{\mathbf{(}}{\varvec{\varepsilon}} - {\varvec{\varepsilon}}^{\Theta } {\mathbf{)}} \cdot {\varvec{B}}(\varvec{x}^{\prime}) \cdot \varvec{\xi} ^{\prime}} \right\}{\rm{d}}V_{{\varvec{x}}^{\prime}} } + {\varvec{b}}(\varvec{x},t) = {\mathbf{0}}. \hfill \\ \end{gathered}$$

(20)

For the orthotropic materials, the stress tensor ${\varvec{\sigma}}$ in Eq. (20) can be calculated using Eqs. (2)–(12). In other words, material and thermal anisotropy can be incorporated into the NOSBPD framework directly. However, two another issues, i.e., the numerical instability induced by zero-energy modes and the failure criterion, need to be discussed further.

For the numerical instability issue, an effective control method for anisotropic NOSBPD with a bond micromodulus continuously varying with the bond orientation proposed by the first author Sun et al. (2022) is employed herein.

For the thermal fracturing in orthotropic rocks considered herein, the failure criterion of ‘critical bond stretch’ is employed. The bond stretch considering temperature effect is given by

$$s_{{\varvec{\xi}}} = \frac{{\left| {\hat{\varvec{\xi }} + \hat{\varvec{\eta }}} \right| - \left| {\hat{\varvec{\xi }}} \right|}}{{\left| {\hat{\varvec{\xi }}} \right|}} - (\alpha_{1} \cos^{2} \varphi + \alpha_{2} \sin^{2} \varphi )\overline{\Theta }_{{{\text{avg}}}} ,\quad \overline{\Theta }_{{{\text{avg}}}} = \frac{{(\overline{\Theta } - \overline{\Theta }_{0} ) + (\overline{\Theta }^{\prime} - \overline{\Theta }_{0} )}}{2},$$

(21)

where $\hat{\varvec{\eta }}$ is the relative displacement vector; $\overline{\Theta }$ and $\overline{\Theta }^{\prime}$ are the temperature at the two ends of the bond $\hat{\varvec{\xi }}$; $\overline{\Theta }_{0}$ is the initial temperature; and $\varphi$ represents the orientation of the bond ${\varvec{\xi}}$ with respect to the principal material axis-1.

Consequently, the influence function $\omega (\left| \xi \right|)$ is defined as

$$\omega (\left| \xi \right|) = \left\{ {\begin{array}{*{20}c} 0 & {s_{{\varvec{\xi}}} > s_{0} } \\ 1 & {{\text{otherwise}}} \\ \end{array} } \right.,$$

(22)

where the critical stretch $s_{0}$ varies with the bond direction, of which definition can be found in Ghajari et al. (2014) and Sun et al. (2022).

2.3 Coupling Model

In the coupled model, the entire domain is discretized by a fixed underlying FE mesh representing the mechanical deformation and thermal diffusion, whereas the regions with a possibility of fracturing are encompassed by the NOSBPD model. It is noted that the thermal balance equation is fully approximated by the underlying finite elements without any contribution from the PD model. In other words, in the coupled model, the thermal balance Eq. (13) is only approximated by the FEM model, but the momentum balance Eq. (1) is approximated by the combination of NOSBPD (mainly focus on the fracturing) and FEM models.

The underlying FEM model on the entire domain and the PD patch are coupled by the superposition theory, where the displacement field ${\varvec{u}}$ is additively decomposed as

$${\varvec{u}} = \left\{ {\begin{array}{*{20}c} {\overline{\varvec{u}}} & {{\text{in}}\quad \overline{\Omega }\backslash \hat{\Omega }} \\ {\overline{\varvec{u}} + \hat{\varvec{u}}} & {{\text{in}}\quad \hat{\Omega }} \\ \end{array} } \right..$$

(23)

In addition, the homogenous boundary condition $\hat{\varvec{u}} = {0}$ should be applied to the boundary $\hat{\Gamma }$ for solution continuity.

In the limit of infinitesimal deformation, the total strain in the PD patch can also be linearly decomposed as

$${\varvec{\varepsilon}} = \overline{\varvec{\varepsilon }} + \hat{\varvec{\varepsilon }} \; {\text{in }}\hat{\Omega }.$$

(24)

To derive the variational statements for the momentum and thermal balance equations, the test functions ${\varvec{\eta}}$ and $\psi$ corresponding to the trial functions ${\varvec{u}}$ and $\Theta$, respectively, are introduced. In the coupling zone $\hat{\Omega }$, the test function ${\varvec{\eta}}$ can be decomposed as

$${\varvec{\eta}} = \overline{\varvec{\eta }}{ + }\hat{\varvec{\eta }}.$$

(25)

Taking into account of the equivalence between the internal work term expressed by using the peridynamics states and the classical continuum mechanics theory in the coupling zone (Sun et al. 2019), the resulting weak form of the momentum balance equation is given by

$$\begin{gathered} - \int_{{\overline{\Omega }\backslash \hat{\Omega }}} {\nabla^{s} \overline{\varvec{\eta }}:\sigma } \left( {\overline{\varvec{\varepsilon }} - {\varvec{\varepsilon}}^{\Theta } } \right){\text{d}}\Omega - \int_{{\hat{\Omega }}} {\nabla^{s} \overline{\varvec{\eta }}:\sigma \left( {\overline{\varvec{\varepsilon }} + \hat{\varvec{\varepsilon }} - {\varvec{\varepsilon}}^{\Theta } } \right)} {\text{d}}\Omega \hfill \\ + \int_{{\hat{\Omega }}} {\int_{{H_{{\varvec{x}}} }} {\hat{\varvec{\eta }} \cdot \left\{ \begin{gathered} \omega (|\hat{\varvec{\xi }}|){\rm{det}}(\hat{\varvec{F}}) \cdot \hat{\varvec{F}}^{ - 1} \cdot {\varvec{\sigma}}\left( {\overline{\varvec{\varepsilon }} + \hat{\varvec{\varepsilon }} - {\varvec{\varepsilon}}^{\Theta } } \right) \cdot \hat{\varvec{B}}(\hat{\varvec{x}}) \cdot \hat{\varvec{\xi }} \hfill \\ - \omega (|\hat{\varvec{\xi }^{\prime}}|){\rm{det}}(\hat{\varvec{F}^{\prime}}) \cdot \left( {\hat{\varvec{F}^{\prime}}} \right)^{ - 1} \cdot {\varvec{\sigma}}^{\prime}\left( {\overline{\varvec{\varepsilon }} + \hat{\varvec{\varepsilon }} - {\varvec{\varepsilon}}^{\Theta } } \right) \cdot \hat{\varvec{B}}(\hat{\varvec{x}^{\prime}}) \cdot \hat{\varvec{\xi }^{\prime}} \hfill \\ \end{gathered} \right\}} } {\text{d}}V_{{\varvec{x}}^{\prime}} {\text{d}}\Omega \hfill \\ + \int_{{\partial \overline{\Gamma }_{t} }} {\overline{\varvec{\eta t}}} {\text{d}}\Gamma + \int_{{\overline{\Omega }}} {\overline{\varvec{\eta }} \cdot {\varvec{b}}} {\text{d}}\Omega + \int_{{\hat{\Omega }}} {\hat{\varvec{\eta }} \cdot {\varvec{b}}} {\text{d}}\Omega = {\mathbf{0}}. \hfill \\ \end{gathered}$$

(26)

For the weak form of the thermal balance equation, it can be defined as

Find $\Theta \in {\mathcal{U}}^{\Theta }$, such that for all $\psi \in {\mathcal{W}}^{\Theta }$,

$$\int_{\Omega } {\rho c} \psi \dot{\Theta }{\text{d}}\Omega - \int_{\Omega } {\nabla \psi \cdot {\varvec{k}}} \cdot \left( { - \nabla \Theta } \right){\text{d}}\Omega + \int_{{\Gamma_{J} }} {\psi \overline{J} } {\text{d}}\Gamma + \int_{{\Gamma_{J} }} {\psi h_{{\text{s}}} \Theta_{{\text{s}}} } {\text{d}}\Gamma = \int_{\Omega } {\psi r{*}} {\text{d}}\Omega + \int_{{\Gamma_{J} }} {\psi h_{{\text{s}}} \Theta_{{\text{a}}} } {\text{d}}\Gamma ,$$

(27)

where $\psi$ is the test function of the temperature $\Theta$; the anisotropic heat conduction tensor ${\varvec{k}}$ is defined in Eq. (15).

It should be noted that a weak coupling between the thermal diffusion and mechanical deformation is assumed, that is, a variation of temperature field could cause a thermal strain affecting the mechanical behaviors (see Eq. (5)), and while on the contrary, the change of mechanical deformation cannot affect the heat transfer. However, when the stress ${\varvec{\sigma}}$ (see Eq. (2)) exceeds the material strength and a crack is formed, the hindering effect of the crack on the thermal diffusion should be taken into account. Herein, a degradation function $\overline{\varphi }$ for thermal conductivity tensor ${\varvec{k}}$ is introduced to ensure that no heat conduction occurs at the crack surface,

$${\varvec{k}} = {(1} - \overline{\varphi }{)}^{2} {\varvec{k}}_{0} ,$$

(28)

where ${\varvec{k}}_{0}$ denotes the inherent thermal conductivity tensor as expressed in Eq. (15) and $\overline{\varphi }$ is defined as

$$\overline{\varphi } = \left\{ {\begin{array}{*{20}c} 0 & {{\text{if }}\varphi \le c_{1} } \\ {\frac{{\varphi - c_{1} }}{{c_{2} - c_{1} }}} & {{\text{if }}c_{1} < \varphi \le c_{2} } \\ 1 & {{\text{if }}\varphi > c_{2} } \\ \end{array} } \right.,$$

(29)

with two threshold values $c_{1}$ and $c_{2}$ being 0.01 and 0.35, respectively (Sun et al. 2021a).

2.4 Discretization

The backward Euler method is employed for the temporal discretization of the PD-FEM coupled system. For the spatial discretization, the classical C⁰ continuous shape functions are used for the FEM model. A mesh-free method with a certain number of particles associated with specific volumes is employed to discretize the NOSBPD model, where the spatial integration over a horizon can be realized by summation over centroids of cells (Silling and Askari 2005).

Consequently, the PD force vector state in the coupling zone after discretization can be written as

$$\underline{{\hat{\varvec{T}}}} [\hat{\varvec{x}},t]\langle \hat{\varvec{x}^{\prime}} - \hat{\varvec{x}}\rangle = \omega (|\hat{\varvec{x}^{\prime}} - \hat{\varvec{x}}|)\hat{\varvec{Q}} \cdot {\varvec{\sigma}}(\overline{\varvec{\varepsilon } + \hat{\varepsilon }} - {\varvec{\varepsilon}}^{\Theta } ) + \hat{\varvec{E}}\left( {c(\varphi )} \right)\hat{\varvec{U}}_{{x_{i} }} ,$$

(30)

where for definitions of matrixes $\hat{\varvec{Q}}$, $\hat{\varvec{U}}_{{x_{i} }}$ and $\hat{\varvec{E}}\left( {c(\varphi )} \right)$, we refer to Sun and Fish (2021) and Sun et al. (2022).

The resulting internal force vectors for the mechanical deformation in different domains are given by

$${\varvec{f}}_{{}}^{{{\text{int}} ,\overline{u}}} = \int\limits_{{\overline{\Omega }\backslash \hat{\Omega }}} {\overline{\varvec{B}}^{\rm{T}} {\varvec{\sigma}}_{n + 1} \left( {\overline{\varvec{\varepsilon }} - {\varvec{\varepsilon}}^{\Theta } } \right)} {\rm{d}}\Omega { + }\int\limits_{{\hat{\Omega }}} {\overline{\varvec{B}}^{\rm{T}} {\varvec{\sigma}}_{n + 1} \left( {\overline{\varvec{\varepsilon }} + \hat{\varvec{\varepsilon }} - {\varvec{\varepsilon}}^{\Theta } } \right)} {\rm{d}}\Omega$$

(31)

$${\varvec{f}}_{{}}^{{{\text{int}} ,\hat{u}}} = \int\limits_{{\hat{\Omega }}} {\sum\limits_{j = 1}^{m} {\left( \begin{gathered} - \omega (|\hat{\varvec{\xi }}|)\hat{\varvec{Q}} \cdot {\varvec{\sigma}}_{n + 1} (\overline{\varvec{\varepsilon }} + \hat{\varvec{\varepsilon }} - {\varvec{\varepsilon}}^{\Theta } ) - \hat{\varvec{E}}\left( {c(\varphi )} \right)\hat{\varvec{U}}_{{x_{i} }} \hfill \\ + \omega (|\hat{\varvec{\xi }^{\prime}}|)\hat{\varvec{Q}^{\prime}} \cdot \varvec{\sigma^{\prime}}_{n + 1} (\overline{\varvec{\varepsilon }} + \hat{\varvec{\varepsilon }} - {\varvec{\varepsilon}}^{\Theta } ) + \hat{\varvec{E}}^{\prime}\left( {c(\varphi )} \right)\hat{\varvec{U}}_{{x_{i} }} \hfill \\ \end{gathered} \right)} } \hat{V}_{j} d\Omega ,$$

(32)

where m is the total number of material points $\hat{\varvec{x}}_{j}$ in the horizon of the material point $\hat{\varvec{x}}_{i}$; $\hat{V}_{j}$ is the volume of the cell occupied by the particle $\hat{\varvec{x}}_{j}$. The internal force vectors for the heat conduction characterizing by the underlying FEM model and external force vectors for the thermomechanical problem can be found in our previous study (Sun et al. 2021a).

The tangent stiffness matrix can be obtained by consistent linearization,

$${\varvec{K}} = \left[ {\begin{array}{*{20}c} {{\varvec{K}}^{{\overline{u}\overline{u}}} } & {{\varvec{K}}^{{\overline{u}\hat{u}}} } & {{\varvec{K}}^{{\overline{u}\overline{\Theta }}} } \\ {{\varvec{K}}^{{\hat{u}\overline{u}}} } & {{\varvec{K}}^{{\hat{u}\hat{u}}} } & {{\varvec{K}}^{{\hat{u}\overline{\Theta }}} } \\ {\mathbf{0}} & {\mathbf{0}} & {{\varvec{K}}^{{\overline{\Theta }\overline{\Theta }}} } \\ \end{array} } \right]$$

(33)

where submatrices in Eq. (33) are given by

$${\varvec{K}}^{{\overline{u}\overline{u}}} { = }\frac{{\partial {\varvec{r}}_{{}}^{{\overline{u}}} }}{{\partial {\varvec{d}}_{{}}^{{\overline{u}}} }} = \int_{{\overline{\Omega }}} {\overline{\varvec{B}}}^{{\text{T}}} {{\mathbb{D}}\overline{\varvec{B}}}{\text{d}}\Omega$$

(34)

$${\varvec{K}}^{{\overline{u}\hat{u}}} { = }\frac{{\partial {\varvec{r}}_{{}}^{{\overline{u}}} }}{{\partial {\varvec{d}}_{{}}^{{\hat{u}}} }} = \int_{{\hat{\Omega }}} {\overline{\varvec{B}}}^{{\text{T}}} {{\mathbb{D}}\hat{\varvec{C}}\hat{\varvec{G}}}{\text{d}}\Omega$$

(35)

$${\varvec{K}}^{{\overline{u}\overline{\Theta } }} { = }\frac{{\partial {\varvec{r}}_{{}}^{{\overline{u}}} }}{{\partial {\varvec{d}}_{{}}^{{\overline{\Theta } }} }} = - \int_{{\overline{\Omega }}} {\overline{\varvec{B}}^{{\text{T}}} {{\mathbb{D}}{\varvec{m}}\overline{\varvec{N}}}} {\text{d}}\Omega$$

(36)

$${\varvec{K}}_{{}}^{{\hat{u}\overline{u}}} = \frac{{\partial {\varvec{r}}_{{}}^{{\hat{u}}} }}{{\partial {\varvec{d}}_{{}}^{{\overline{u}}} }} = \int_{{\hat{\Omega }}} {\sum\limits_{j = 1}^{m} {\left( { - \omega (|\hat{\varvec{\xi }}|)\hat{\varvec{Q}{\mathbb{D}}\overline{B}} - \hat{\varvec{E}\overline{N}} + \omega (|\hat{\varvec{\xi }}|)\hat{\varvec{Q}}^{\prime}{\mathbb{D}}^{\prime}\overline{\varvec{B}}^{\prime} + \hat{\varvec{E}}^{\prime}\overline{\varvec{N}}^{\prime}} \right)\hat{V}_{j} } d\Omega }$$

(37)

$${\varvec{K}}_{{}}^{{\hat{u}\hat{u}}} = \frac{{\partial {\varvec{r}}_{{}}^{{\hat{u}}} }}{{\partial {\varvec{d}}_{{}}^{{\hat{u}}} }} = \int_{{\hat{\Omega }}} {\sum\limits_{j = 1}^{m} {\left( { - \omega (|\hat{\varvec{\xi }}|)\hat{\varvec{Q}}{\mathbb{D}}\hat{\varvec{CG}} - \hat{\varvec{E}} + \omega (|\hat{\varvec{\xi }}|)\hat{\varvec{Q}}^{\prime}{\mathbb{D}}^{\prime}\hat{\varvec{C}}^{\prime}\hat{\varvec{G}}^{\prime}{ + }\hat{\varvec{E}}^{^{\prime}} } \right)} \hat{V}_{j} {\rm{d}}\Omega }$$

(38)

$$\varvec{K}_{{}}^{{\hat{u}\overline{\Theta } }} = \frac{{\partial \varvec{r}_{{}}^{{\hat{u}}} }}{{\partial \varvec{d}_{{}}^{{\overline{\Theta } }} }} = \int\limits_{{\hat{\Omega }}} {\sum\limits_{{j = 1}}^{m} {\left( {\omega (|\hat{\varvec{\xi }}|)\hat{\varvec{Q}}{{\mathbb{D}}}{\varvec{m}}{\bar{\varvec{N}}} - \omega (|\hat{\varvec{\xi }^{\prime}}|)\hat{\varvec{Q}}^{\prime}\mathbb{D}^{\prime}{\varvec{m}}^{\prime}{\bar{\varvec{N}}}^{\prime}} \right)\hat{V}_{j} } } {\rm{d}}\Omega$$

(39)

$${\varvec{K}}_{{}}^{{\overline{\Theta } \overline{\Theta } }} = \frac{{\partial {\varvec{r}}_{{}}^{{\overline{\Theta } }} }}{{\partial {\varvec{d}}_{{}}^{{\overline{\Theta } }} }} = \int\limits_{{\overline{\Omega }}} {\overline{\varvec{N}}^{\rm{T}} \rho c\overline{\varvec{N}}} {\rm{d}}\Omega + \Delta t\int\limits_{{\overline{\Omega }}} {(\nabla \overline{\varvec{N}})^{\rm{T}} \cdot {\varvec{k}}\nabla \cdot \overline{\varvec{N}}{\rm{d}}\Omega } + \Delta t\int\limits_{{\overline{\Gamma }_{J} }} {\overline{\varvec{N}}^{\rm{T}} h_{\rm{s}} \overline{\varvec{N}}} {\rm{d}}\Gamma ,$$

(40)

with the definitions of matrices $\hat{\varvec{C}}$, $\hat{\varvec{G}}$ given in Sun et al. (2021a). ${\varvec{m}}{ = }\left[ {\alpha_{11} ,\alpha_{22} ,\alpha_{12} } \right]^{{\text{T}}}$, $\alpha_{ij}$ being the components of the matrix ${\varvec{\alpha}}$.

Herein, a staggered scheme is employed for updating the weakly coupled thermomechanical system. The thermal and mechanical problems are solved alternately and implicitly. Specifically, the thermal problem is solved firstly, and then the other two primary unknowns, $\overline{\varvec{u}}$, $\hat{\varvec{u}}$, are updated by using the obtained temperature field $\overline{\Theta }$.

3 Validation of the Proposed Method

In this section, two numerical examples are presented to assess the performance of the proposed method. To this end, the thermal-induced deformation problem in an orthotropic rock in the absence of damage with analytical solutions is analyzed in the first example. Then, the proposed method is applied to simulate the fracture propagation in an orthotropic plate induced by a certain thermal shock. Comparisons between the simulation results and previous numerical solutions for three cases with different material angles are presented. Plane stress conditions are assumed for the problems studied in this section. The ratio between the horizon and the grid spacing is always taken as $m = 3$ in this study, because it is sufficient to accurately predict the deformation and fracture in orthotropic media using the developed orthotropic NOSBPD model (Sun et al. 2022).

3.1 Transient Heat Conduction in Orthotropic Rock

The domain of interest is a $1 \times 1$ m² shale rock with a horizontal bedding plane, that is, the material angle is θ = 0°, as shown in Fig. 2a. Two cases with different boundary conditions are considered. In case 1, thermal loadings of $T_{1} = 100$ °C and $T_{2} = 0$ °C are applied instantaneously on the left and right edges, while other two edges are adiabatic. The thermal and mechanical constrains are illustrated in Fig. 2b. For case 2, the thermal loadings are prescribed on the top and bottom boundaries as shown in Fig. 2c. The initial temperature of the orthotropic rock is $T_{0} = {0}$ °C. The material properties listed in Table 1 are taken from Sun et al. (2020), which has been used to describe a shale formation in Switzerland. With these settings, the transient heat conduction in the square plate is idealized as a one-dimensional problem, where the heat conducts in the direction parallel or perpendicular to the bedding plane in case 1 and 2, respectively. Consequently, analytical solutions for temperature and stress distributions can be derived for these two scenarios (Chen et al. 2018; Sun et al. 2020). To simulate this problem, the plate is discretized into two models: FEM model having 2500 elements with element size of 0.02 m × 0.02 m and NOSBPD model consisting of 10,000 particles with grid size of 0.01 m. The time step increment is set as $\Delta t = 1_{{}} {\text{s}}$.

Fig. 2

Transient heat conduction in an anisotropic rock a geometry of the anisotropic rock; b case 1; c case 2

Table 1 Material parameters for the transient heat conduction in an anisotropic rock

Comparisons between the temperature distributions along the heat conduction direction, calculated by the proposed method and analytical solutions are depicted in Fig. 3. The corresponding stress distributions are illustrated in Fig. 4. It can be observed that heat transfers more rapidly along the direction parallel to the bedding plane than the perpendicular one, although temperature distributions at time t = 200,000 s reaching the steady state in these two scenarios are close to each other. However, the stress distribution is affected both by the thermal and mechanical anisotropy, thus they differ from each other even at the steady state. As expected, the numerical results agree with the analytical solutions well.

Fig. 3

Comparisons of the temperature distributions along the heat conduction direction obtained by the numerical and analytical models

Fig. 4

Comparisons of the stress distributions along the heat conduction direction obtained by the numerical and analytical models: a case 1; b case 2

3.2 Thermal Shock Fracturing in an Orthotropic Plate

In this section, thermal shock fracturing in an orthotropic plate is simulated to validate the proposed method for crack growth modeling. The geometry and boundary conditions of the plate are illustrated in Fig. 5. A perforated rectangle plate with dimensions of 3 mm × 1 mm is subjected to equal yet opposite thermal loadings ($- T$ and $T = 100$ °C) on its left and right edges. Thermally insulated conditions are assigned to the top and bottom boundaries. The upper and lower edges are constrained mechanically in the normal direction. The corner of the plate is constrained fully to remove rigid body motion. The initial notch is set to a = 0.15 mm and the radius of the perforation is R = 0.2 mm. The initial temperature of the plate is $T_{0} = 0$ °C. Three cases with different material angles, that is, θ = 0°, 60° and – 60°, are considered. Referring to Bayat and Nazari (2021), material parameters are listed in Table 2.

Fig. 5

Thermal shock fracturing in an anisotropic plate: a geometry and boundary conditions (units: mm); b computational model (units: mm)

Table 2 Material parameters for the thermal shock fracturing in an anisotropic plate

The configuration of the computational model is presented in Fig. 5b. Only the regions near the initial notch and the perforation, where the crack may nucleate or propagate, are encompassed by PD particles. Due to the two models being essentially independent, their discretizations are not necessarily compatible. Thus, a flexible discretization scheme for the perforated plate is employed herein, that is, uniformly distributed PD particles with grid spacing $\Delta x = 0.0167_{{}} {\text{mm}}$ being coupled with unstructured FE elements. The time step is set as $\Delta t = 1 \times 10^{{{ - }4}}_{{}} {\text{s}}$.

Simulation results obtained by the proposed method for three cases with different material angles are shown in Fig. 6. In the case of θ = 0°, the crack propagates straightforward to the right edge initially, but interestingly, when reaching the region near the hole, it tends to grow upward slightly. This phenomenon is also found in the previous studies (Nguyen et al. 2019; Bayat and Nazari 2021). In the case of θ = 60°, since the domination of material properties in the principal material axis-1 over those of axis-2, an upward straight crack with an angle approximately equaling to 46° with respect to the horizontal direction is obtained. While in the case of θ = − 60°, the crack propagates downward and the inclined angle is nearly – 40°. Moreover, the hindering effect of the insulated crack is readily to be found in Fig. 6. It is inferred from the observations that the crack propagation angle is determined conjunctly by the material angle and geometry conditions, i.e., the existence of the hole. Crack trajectories predicted by the current approach are sketched together for these three cases in Fig. 7, which are all in close agreement with previous solutions (Nguyen et al. 2019; Bayat and Nazari 2021). Distribution of shear stress obtained by the proposed method with material angle θ = 0° is compared with that calculated by the extended four-node consecutive-interpolation element method (Nguyen et al. 2019) in Fig. 8. Roughly speaking, they are in good agreement, and stress concentrations around the cracks and the hole are well captured by the proposed method.

Fig. 6

Simulation results obtained by the proposed method for three cases with different material angles: a crack patterns; b temperature distributions (units: °C)

Fig. 7

Crack trajectories obtained by different models: XFEM (Bayat and Nazari 2021; red lines), extended four-node consecutive-interpolation element method (Nguyen et al. 2019; blue lines) and the proposed method (green lines)

Fig. 8

Distribution of shear stress obtained by different models with material angle θ = 0°: a extended four-node consecutive-interpolation element method (Nguyen et al. 2019); b the proposed method (units: MPa)

4 Thermal Fracturing in an Orthotropic Rock Specimen Under High Surrounding Temperature

In this section, thermal fracturing in a perforated rock specimen induced by the temperature difference between the outer and inner surfaces is investigated. A parametric study with emphasize on discussing the effects of different factors’ anisotropy on the crack paths and thermal diffusion is conducted. In this section, the plane strain condition is considered. The 1–3 plane is taken as the plane of isotropy and Axis-2 is assumed to be perpendicular to the bedding plane.

The geometry and associated boundary conditions of the rock specimen are shown in Fig. 9. The specimen has a size of 1.5 m × 1.5 m with a hole of radius of 0.075 m at the center. The initial temperature of the specimen is $T_{0} = 100$ °C. The outer surface of the specimen is kept at $T_{0} = 100$ °C, while its inner surface is cooled gradually to a temperature of 20 °C, that is, the inner temperature is set as $T_{t} = 100(^{ \circ } {\text{C}}) - 0.36(^{ \circ } {\text{C/h}}) \times t({\text{h}})$ and $T_{t} \ge 20(^{ \circ } {\text{C}})$. The outer surfaces of the specimen are fully mechanically constrained. The material parameters are tabulated in Table 3, which are taken from the Mont Terri underground project (Sun et al. 2020). For the numerical simulation, the discretized model consists of 22,500 PD particles and 2961 FE elements as illustrated in Fig. 8. It is noted that PD particles are uniformly distributed, whereas the unstructured FE element is employed for adapting to the complex geometry in the presence of a hole. The time step is $\Delta t = 1_{{}} {\text{s}}$. The horizon is set as $\delta { = }3\Delta x$.

Fig. 9

Thermal fracturing in an orthotropic rock specimen under high surrounding temperature: a geometry and boundary conditions (units: m); b computational model

Table 3 Material parameters for thermal fracturing in an orthotropic rock specimen under high surrounding temperature

To reduce computational cost, an adaptive scheme proposed originally by the authors Sun et al. (2019) is employed herein. Initially, large portions of PD particles are dormant except for the particles near the hole. As the advancement of crack nucleation and propagation, PD particles are gradually activated on the condition that the distances of the particle to the ends of the broken bonds are no more than three times of the horizon $\delta$. The activation status of PD particles, damage and associated temperature distributions at typical moments in the case of material angle θ = 0° are shown in Fig. 10. For the steady state at time t = 1.2 × 10⁶ s, only 4448 PD particles are activated. The crack initiates around the inner surface of the specimen, and then propagates preferentially along the bedding plane. The isotherms have an approximately elliptical shape with a horizontal major axis since thermal conductivity coefficient k₁ dominates over k₂. In addition, the temperature distribution is also influenced by the hindering effect of the crack, which is well captured by the proposed method as shown in Fig. 10 (more obviously at time t = 1.2 × 10⁶ s).

Fig. 10

Thermal fracturing in an orthotropic rock specimen under high surrounding temperature using an adaptive scheme: a active PD particles drawing in red; b crack paths; c temperature distribution (units: °C)

In the following analysis, the effects of various factors, including the mechanical and thermal anisotropy of the rock, on the thermal fracturing in the aforementioned specimen under high surrounding temperature are thoroughly studied.

4.1 Effect of Material Direction

In this subsection, to investigate the effect of material direction on the fracture and thermal diffusion in this orthotropic medium, various cases with θ = 0°, θ = 30°, θ = 45°, θ = 60° and θ = 90° are simulated. Other material parameters are unchanged. The fracture patterns and temperature contours corresponding to each case at the steady state are shown in Fig. 11. For all cases, the crack nucleates around the hole and then multiple discrete cracks are formed as temperature difference increases. These cracks propagate approximately parallel to the bedding plane from the colder (inner) regions toward to the hotter (outer) regions. The inclination angle of the cracks increases as the increase of the material angle θ. The lengths of the crack slightly differ from each other. For the thermal diffusion, the major axes of the elliptical shape of the isotherms are also consistent with the principal material axis-1. Moreover, there is an obvious discontinuity for the temperature distribution around the cracks. The stress distributions for the case with material angle θ = 45° are shown in Fig. 12. An obvious stress concentration around the cracks can be found through this figure.

Fig.11

Thermal fracturing in an orthotropic rock specimen under high surrounding temperature with different material angles: a crack paths; b temperature distribution (units: °C)

Fig.12

Contours of stress in an orthotropic rock specimen under high surrounding temperature with material angle θ = 45°: a horizontal stress; b vertical stress; c shear stress. (units: Pa)

4.2 Effect of the Modulus Anisotropy

To study the effect of the modulus anisotropy, three cases with different values of the ratio of E₁/E₂ are considered. The modulus E₂ and other material parameters remain unchanged. The modulus E₁ is set to 1.3 GPa, 2.6 GPa and 5.2 GPa, which renders that E₁/E₂ = 1.0, 2.0 and 4.0, respectively. It is noted that either in this investigation or the following parametric studies, the material angle is fixed to θ = 45°. The fracture pattern and the temperature distribution at the steady state in these three cases with E₁/E₂ = 1.0, 2.0 and 4.0, are illustrated in Fig. 13. It is observed that the fracture propagation paths are not obviously influenced by the modulus anisotropy. Instead, the crack length is very sensitive to the ratio of E₁/E₂. When E₁/E₂ = 1.0, only a small crack with a length of nearly 0.5 m is formed. However, when E₁/E₂ = 4.0, the crack length increases a lot and a larger damage zone is achieved. For the heat conduction, the temperature distributions for the former two cases are similar to each other, but it exhibits a very different pattern for the last case due to the hindering effect of the discontinuities around the crack surfaces. The results indicate that increasing the differences of the modulus of the two principal material axes could decrease the deformation resistance of the orthotropic rock.

Fig. 13

Thermal fracturing in an orthotropic rock specimen under high surrounding temperature with different ratios of E₁/E₂: a crack paths; b temperature distribution (units: °C)

4.3 Effect of the Energy Release Rate Ratio

The energy release rate is another important factor determining the fracturing. Thus, the effect of the ratio of the energy release rate, that is, G_IC,1/G_IC,2, is investigated in this subsection. The energy release rate G_IC,2 is fixed to 20 N/m, while G_IC,1 is set to 20 N/m, 60 N/m and 100 N/m, respectively. Consequently, three cases with G_IC,1/G_IC,2 = 1.0, 3.0 and 5.0 are considered. Figure 14 shows the numerical results in this parametric study. Both the crack pattern and crack length are significantly influenced by the energy release rate ratio. For the case of G_IC,1/G_IC,2 = 1.0, the crack propagates in the direction almost perpendicular to the bedding plane and it bifurcates in the upper and lower parts of the specimen. While for other two cases, the crack follows opposite trends, that is, propagates along the bedding plane. In addition, with the increases of G_IC,1/G_IC,2, that is, increasing the resistance to fracture in the axis-1 direction, the crack length along the axis-2 direction increases a lot. For instance, for the case of G_IC,1/G_IC,2 = 5.0, when the temperature difference between the outer and inner surface reaches 50 °C, the crack even tends to penetrate through the diagonal line of the specimen. However, for the case of G_IC,1/G_IC,2 = 3.0, a considerably smaller fracture length is achieved. The temperature distributions and discontinuities are consistent with the fracture patterns. It is inferred from the results that decreasing the resistance to fracture in the direction parallel to the bedding plane could suppress the facture propagation along axis-1 direction, even induces the occurrence of the crack along the axis-2 direction.

Fig. 14

Thermal fracturing in an orthotropic rock specimen under high surrounding temperature with different ratios of G₁/G₂: a crack paths; b temperature distribution (units: °C)

4.4 Effect of Thermal Conduction Anisotropy

We now proceed to investigate effects of the thermal anisotropy. In this subsection, the thermal conduction anisotropy is quantitatively studied by setting the ratio of the thermal conduction coefficient, k₁/k₂, to 0.1, 2.0 and 10.0, respectively. It is noted that only k₁ are changed accordingly, while other parameters are identical to those listed in Table 3. Fracture patterns and temperature field at the steady state for these three cases with different k₁/k₂ are presented in Fig. 15. The corresponding heat flux field over two instances, that is prior to the crack initiation and the steady state, are plotted in Fig. 16. It is observed that the thermal conduction coefficient has a considerable influence on the thermal diffusion and consequently on the mechanical response. In the case of k₁/k₂ = 0.1, the major axis of the elliptical trajectory for the isotherm is in the local principal material axis-2 and the heat flux flows predominately in this direction. While for the case of k₁/k₂ = 10.0, it prohibits the heat flux flow in the axis-2 direction, instead, the heat preferentially transfers along the axis-1 direction. As a result, the crack initially propagates along such a path close to the axis-2 direction, although it turns to the path approximately parallel to the axis-1 direction finally. In addition, a zero heat flux around the crack is observed.

Fig. 15

Thermal fracturing in an orthotropic rock specimen under high surrounding temperature with different ratios of k₁/k₂: a crack paths; b temperature distribution (units: °C)

Fig. 16

Thermal fracturing in an orthotropic rock specimen under high surrounding temperature with different ratios of k₁/k₂: a heat flux directions at time t = 2.0 × 10⁵ s (prior to the crack initiation); b heat flux directions at the steady state

4.5 Effect of the Ratio of the Thermal Expansion Coefficient

In the weakly coupled thermomechanical model employed in this study, the thermal expansion coefficient is a key factor determining the effect of thermal field on the mechanical behaviors. Thus, in the last subsection, the effect of the ratio of the thermal expansion coefficient α₁/α₂ is discussed. Three ratios, that is, α₁/α₂ = 0.33, 0.67 and 1.0, are tested. It is realized by changing α₁ accordingly and remaining other parameters unchanged. As shown in Fig. 17, a larger α₁/α₂ gives rise to a longer crack due to the fact that increasing α₁ could increase the thermal stress. In addition, the damage is more serious with a larger α₁/α₂. As seen that in the case of α₁/α₂ = 1.0, there are four main cracks occurring, but for the other two cases, only two main cracks appear. It can be observed that the ratio of α₁/α₂ also has some influence on the crack angle. For the case of α₁/α₂ = 1.0, a nearly horizontal crack occurs at the right part of the specimen. It is inferred from the findings that increasing α₁ leads to the increases of thermal stress in the axis-1 direction, the crack length is significantly increased and the fracture path is also moderately changed.

Fig. 17

Thermal fracturing in an orthotropic rock specimen under high surrounding temperature with different ratios of α₁/α₂: a crack paths; b temperature distribution (units: °C)

5 Summary and Conclusions

A superposition-based coupling of PD and FEM approach is proposed to investigate quantitatively thermal fracturing in orthotropic rocks. In this approach, the NOSBPD model capable of effectively treating discontinuities is only used in the critical regions with the possibly of cracks and it is superimposed on the fixed underlying FE mesh spanning over the entire domain. The mechanical deformation, even fracturing, is simulated by the combination of NOSBPD and FEM models, while the thermal diffusion is solely approximated using FEM without resorting to PD. Mechanical anisotropy, thermal anisotropy as well as the hindering effect of an insulated crack on the thermal diffusion are considered in this weakly coupled thermomechanical model. The coupled model was seen to be able to simulate accurately the thermally induced deformation and fracturing in orthotropic rocks through comparing with either analytical or existing numerical solutions.

Thermal fracturing in an orthotropic rock specimen under high surrounding temperature is thoroughly studied considering the mechanical and thermal anisotropy. The main findings of the parametric study are as follows:

• (i) The inclination angle of the cracks and the major axes of the elliptical shape of the isotherms are generally along the bedding plane direction.

• (ii) The modulus anisotropy, that is, the differences of the Young’s modulus of the two principal material axes, has a little effect on the fracture propagation direction, but it affects the crack length significantly. The change of the distribution for the resistance to fracture may alter the crack propagation direction. The crack may propagate along the principal material axis-2 if the energy release rate in axis-1 direction decreases a lot.

• (iii) For thermal anisotropy, the thermal conduction coefficient has a considerable influence on the thermal diffusion pattern and consequently on the mechanical response. Increasing thermal expansion coefficient gives rise to a longer crack, and the fracture path is also moderately changed.