Study on Shear–Softening Constitutive Law of Rock–Concrete Interface

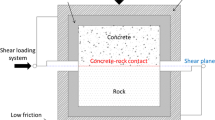
Abstract

To study fracture properties and establish a shear–softening constitutive law for rock–concrete interfaces, direct tension, three-point bending, and single shear push-out tests were conducted on composite rock–concrete specimens with different degrees of interface roughness. The relationships between tensile strength (f_t), average shear strength (τ_av), initial fracture toughness (Kini 1C), mode I fracture energy (G_If) and interfacial roughness were determined based on experimental results. A shear–softening constitutive law for rock–concrete interface was developed by measuring strain variations on rock surfaces under loading stages during single shear push-out tests and defined based on shear strength (τ_max) and mode II fracture energy (G_IIf). For practical applications, the relationships between τ_max and f_t and between G_If and G_IIf were determined by statistically fitting the experimental data in such a way that shear–softening constitutive law could be conveniently determined simply by measuring f_t and G_If parameters of rock–concrete interface. Also, numerical simulations were carried out to investigate crack propagation in rock–concrete interfaces under mixed mode I–II fractures. Predicted load versus crack mouth opening displacement (CMOD) curves agreed well with experimental findings and verified the shear–softening constitutive law for rock–concrete interfaces obtained in this study.

1 Introduction

In concrete structures built on rock foundations such as gravity concrete hydraulic dams, cracks tend to initiate and propagate along rock–concrete interfaces due to the weakness of these positions. Crack development under hydrostatic pressure can reduce the load-carrying capacity and threaten the integrity and stability of the whole structure. To ensure the operational safety of hydraulic dams under service loading conditions, it is essential to have a better understanding of the bonding mechanism and interfacial fracture behavior for rock–concrete interfaces.

Similar to other quasi-brittle materials, when a crack propagates along rock–concrete interface, a micro-crack zone, called fracture process zone (FPZ), is created at the tip of the crack contributing to the distinct nonlinearities of the interface. Fictitious crack model (FCM) was proposed by Hillerborg et al. (1976) and has been widely employed in numerical analyses of concrete fracture (Petersson 1981; Hans et al. 1986; Wittmann et al. 1988) to evaluate the cohesive effect of FPZ using a traction–separation law. In FCM, FPZ is regarded as a macroscopic crack with normal cohesive stress σ acting on crack surface. In mode I concrete fracture, the initiation and propagation of cracks are triggered by tension stress (Dong et al. 2016a) and cohesive stress in FPZ can be formulated with respect to crack opening displacement (COD), w. Accordingly, for mixed mode I–II fractures of concretes, cohesive stress in FPZ is formulated dividedly with respect to COD and crack slip displacement (CSD), w_s (Gálvez et al. 2002; Shi 2004; Dong et al. 2017), because crack propagation is driven by tension stress σ and shear stress τ. Due to heterogeneity and asymmetry of different materials on the two sides of rock–concrete interfaces, mixed mode I–II interfacial fracture is dominant in these structures even under mode I loading. Therefore, for exploring the bonding mechanism of dual-phase rock–concrete interfaces, it is essential to study their tension and shear constitutive laws.

Tension–softening at rock–concrete interface has been experimentally investigated and a simplified bilinear σ–w constitutive law has been proposed (Dong et al. 2016b) taking into account the effects of interfacial fracture energy and tensile strength. Due to the occurrence of brittle failure under mode II fracture, it is difficult to monitor the complete process of crack propagation and obtain the descending branches of load–displacement curves during tests. Various tests have been carried out to determine mode II fracture properties for different materials. End-notched flexure (ENF) specimens were employed to study the fracture energies of wood bonded joints under mode II loading (Silva et al. 2014). Moura and Morais (2008) conducted numerical simulations based on end-loaded split (ELS) tests at the endpoints of carbon/epoxy unidirectional laminate samples to evaluate mode II fracture energies. In addition, Iosipescu shear tests were conducted to study mode II fracture energies of concrete samples based on size effect law (Bažant and Pfeiffer 1986). Punch-through shear specimens were used to explore the shear strengths and crack patterns of ultra-high performance concretes under mode II fracture (Lukić and Forquin 2016). These testing methods have provided effective tools to investigate the fracture properties of different materials under mode II fracture. However, the complete process of crack propagation under mode II fracture when deriving τ–w_s constitutive law has not yet been fully understood. To address this problem, pull-out tests were conducted to determine shear–softening relationships at steel–concrete (Bouazaoui and Li 2008; Yang et al. 2016) and fiber-reinforced polymer–concrete (Ali-Ahmad et al. 2006; Wu and Jiang 2013; Lin and Wu 2016; Ghorbani et al. 2017) interfaces by measuring local interfacial strains during loading. Different bond stress–slip relationships such as tri-linear (Yang et al. 2016) and exponential (Lin and Wu 2016) relationships, have been developed to characterize interfacial shear–softening behaviors based on experimental results.

For rock–concrete interfaces, no shear–softening constitutive equations have been reported based on experimental results. To analyze the fracture process at rock–concrete interfaces, a shear–softening law of concrete has been introduced to characterize the relationship of τ–w_s. For example, Zhong et al. (2014) applied concrete shear–softening laws to simulate the propagation of rock–concrete interfacial cracks. It should be noted that, even for concrete samples, τ–w_s laws have been developed based on theoretical conclusions rather than experimental results. Therefore, a variety of τ–w_s laws have been applied in the numerical simulations of crack propagation in concrete samples. Combining with an extended fictitious crack model, Shi (2004) applied four τ–w_s curves to explore the crack propagation behavior of mixed I–II mode fracture in concrete samples. The effects of different τ–w_s curves on the fracture behavior of the samples were evaluated by comparing numerical and experimental results. Due to the different material properties of rock and concrete on the two sides of the interface, stress field at the interfacial crack tip is more complex than fracture in concrete. In addition, shear–softening relationship is usually determined based on shear strength and mode II fracture energy. At rock–concrete interfaces, fracture properties including fracture toughness (Yang et al. 2009), fracture energy (Sujatha and Kishen 2003; Kishen and Saouma 2004) and cracking pattern (Slowik et al. 1998; Zhong et al. 2014) are affected by the configurations and degrees of interfacial roughness. Therefore, in the design and analysis of rock–concrete structures, it is very important to experimentally derive shear–softening constitutive laws for different interfacial roughness degrees.

In line with this, a new experimental method, called the single shear push-out (SSP) test, was adopted in this study to obtain a shear–softening constitutive law for rock–concrete interfaces. Firstly, direct tension (DT) and three-point bending (TPB) tests were carried out on composite rock–concrete specimens with different interfacial roughness degrees to measure their uniaxial interfacial tensile strength, fracture toughness, and fracture energy. Then, a shear–softening constitutive law was derived based on experimental results obtained from SSP tests. Finally, the derived shear–softening constitutive law was employed to numerically simulate interfacial crack propagation under mixed I–II mode fracture. By comparing numerical and experimental curves of load versus crack mouth opening displacement (P–CMOD), the derived τ–w_s law was validated.

2 Experimental

2.1 Specimen Preparation

Three different types of composite specimens were used in this study: prism specimens for DT test, rock–concrete beams for TPB test and rock–concrete specimens for SSP test. The dimensions of composite prism specimens were 200 mm × 100 mm × 100 mm (length × width × depth) and composite beams had 500 mm × 100 mm × 100 mm dimensions with 400-mm span and 30-mm pre-crack length. Both beam and prism specimens consisted of two geometrically identical concrete and rock blocks. To form the pre-crack in the TPB specimen, a polyvinyl chloride (PVC) film was pasted on one side of the rock block in advance. SSP test specimens included a 150 mm × 150 mm × 150 mm concrete block and a 160 mm × 50 mm × 10 mm rock block with a bonding length of 100 mm between concrete and rock blocks. To prevent the concentration of stress at the two ends of rock blocks, two PVC films were attached onto the both ends of rock blocks with lengths of 25 mm and 35 mm. Thus, the dimensions of interfacial bonding area for SSP test specimens became 100 mm × 50 mm × 10 mm. Figure 1 illustrates composite rock–concrete beam and prism specimens.

Fig. 1

Geometries of composite rock–concrete specimens for various tests: a beams for TPB tests, b prisms for DT tests, and c specimens for SSP tests

To investigate the fracture properties of rock–concrete interfaces under different bonding conditions, six interfacial roughness levels were evaluated by producing artificial groove lines on the contact surfaces of rock blocks. It should be noted that, in a real project of hydraulic dams, the bedrock will be dealt with before casting concrete. The real interface between rock and concrete is different from the artificial grooving interface used in this study. The artificial grooving provides a simplified method to quantitatively investigate the effect of interfacial roughness on the bonding characteristic. By varying the number and depth of the grooving, a wide range of interfacial roughness can be obtained. Groove lines were 3 mm deep with 45° angle between grooving lines and rock block edges. The long sides of the rock blocks were equally divided by groove lines and six interfacial roughness profiles were created as 3 × 3, 4 × 4, 5 × 5, 7 × 7, 10 × 10 and 12 × 12. In this study, sand-fill method (Dong et al. 2018) was adopted to quantify the roughness degree of rock–concrete interface. To guarantee the sample similarity of rock–concrete interfaces, for the same operating condition, the relative error of sand volume filled in the grooving should be less than 5%. Taking TPB test composite beams as an example, Fig. 2 illustrates six different roughness profiles.

Fig. 2

Various interfacial roughness profiles on rock surface: a 3 × 3 profile, b 4 × 4 profile, c 5 × 5 profile, d 7 × 7 profile, e 10 × 10 profile, and f 12 × 12 profile

Granite rocks, obtained from Liaoning Province of China, were used in the preparation of composite specimens. Concrete mixture ratios were 1:0.60:2.01:3.74 (cement:water:sand:aggregate) by weight with maximum coarse aggregate size of 10 mm. Before casting, the rock block was firstly placed in one side of a steel mould, and then wet concrete mixture was filled in the remaining blank. A layer of plastic film was used to cover the surface of the composite specimens to avoid moisture evaporation. Composite specimens were released from molds 24 h after casting and were cured in a standard curing room at 23 °C and 95% relative humidity for 28 days.

For DT and TPB tests, three specimens were prepared for each roughness profile and loading condition. However, due to the large scatter of shear test, seven specimens were prepared for each SSP test. Concrete and rock material properties are listed in Table 1, where E is Young’s modulus, v is Poisson’s ratio, f_t is uniaxial tensile strength, f_c is uniaxial compressive strength, Kini 1C is initial mode I fracture toughness, and G_If is mode I fracture energy.

Table 1 Material properties of concrete and rock

2.2 Direct Tension (DT) Test

DT tests were conducted to measure rock–concrete interfacial tension strength for different roughness degrees. The loading rate of DT tests was 0.05 MPa/s. Interfacial tensile strength f_t can be calculated from

$$f_{{\text{t}}} = P_{{\max }} /A,$$

(1)

where P_max is peak load and A is interfacial area. It should be noted that, although the size effect can influence the tensile strength of quasi-brittle materials during DT test, it was not considered in this study.

2.3 Single Shear Push-Out (SSP) Test

SSP tests were performed under a 250 kN closed-loop servo-controlled testing machine with a displacement rate of 0.036 mm/min. To measure rock surface strains, 8 strain gauges 5 mm away from each other were successively attached on the middle part of the rock surface, as shown in Fig. 3a. Two clip gauges were arranged at the top and end edges of the bonding area to measure the relative displacements of concrete and rock blocks. A thick steel plate was attached to the base with two bolts to hold concrete cube specimens. Uniform load was applied on the top surface of the rock block. SSP test setup and loading condition are shown in Fig. 3b, c. Interfacial average shear strength τ_av can be calculated from

$$\tau _{{{\text{av}}}} = P_{{\max }} /A.$$

(2)

Fig. 3

Set-up of single shear push-out tests (unit: mm): a strain gauges on rock, b test set-up, and c loading condition

2.4 Three-Point Bending (TPB) Test

TPB tests were conducted to measure the initial fracture toughness of rock–concrete interface $K_{{1{\text{C}}}}^{{{\text{ini}}}}$ and mode I fracture energy G_If at different roughness degrees. Loading was applied at the displacement rate of 0.024 mm/min. Displacements at the loading-point and CMOD of composite beams were measured using two clip gauges. To measure initial cracking load, four strain gauges were vertically attached 5 mm away from the tip of pre-crack on both sides of composite beams. When the propagation of pre-crack along the interface was begun, a sharp drop occurred in the measured strain values due to the release of stored strain energy at the tip of pre-crack. Thus, the initial cracking load was determined according to the variations of measured strain values.

Stress intensity factors (SIFs) of rock–concrete interfacial cracks, K₁ and K₂, were calculated based on Eqs. (3) to (9), which are derived from displacement extrapolation method (Nagashima et al. 2003) with δ_x and δ_y being relative crack displacements along horizontal x and vertical y directions, respectively.

$$K_{1} = C\mathop {\lim }\limits_{{r \to 0}} \sqrt {\frac{{2\pi }}{r}} \left[ {\delta _{y} \left( {\cos Q + 2\varepsilon \sin Q} \right) + \delta _{x} \left( {\sin Q - 2\varepsilon \cos Q} \right)} \right],$$

(3)

$$K_{2} = C\mathop {\lim }\limits_{{r \to 0}} \sqrt {\frac{{2\pi }}{r}} \left[ {\delta _{x} \left( {\cos Q + 2\varepsilon \sin Q} \right) - \delta _{y} \left( {\sin Q - 2\varepsilon \cos Q} \right)} \right],$$

(4)

where

$$C = \frac{{2\cosh \left( {\varepsilon \pi } \right)}}{{\left( {\kappa _{1} + 1} \right)/\mu _{1} + \left( {\kappa _{2} + 1} \right)/\mu _{2} }},$$

(5)

$$Q = \varepsilon \ln \left( {{r \mathord{\left/ {\vphantom {r {2a}}} \right. \kern-\nulldelimiterspace} {2a}}} \right),$$

(6)

$$\varepsilon = \frac{1}{{2\pi }}\ln \left( {\frac{{\frac{{\kappa _{1} }}{{\mu _{1} }} + \frac{1}{{\mu _{2} }}}}{{\frac{{\kappa _{2} }}{{\mu _{2} }} + \frac{1}{{\mu _{1} }}}}} \right),$$

(7)

$$\mu _{i} = \frac{{E_{i} }}{{2(1 + v_{i} )}}\quad (i = 1,\;2),$$

(8)

$$\kappa _{i} = \left\{ {\begin{array}{*{20}c} {\left( {3 - v_{i} } \right)/\left( {1 + v_{i} } \right)} & {({\text{Plane}}\;{\text{stress}}),} \\ {\left( {3 - 4v_{i} } \right)} & {({\text{Plane}}\;{\text{strain}}),} \\ \end{array} } \right.$$

(9)

where δ_x and δ_y in Eqs. (3) and (4) are caused by the initial cracking load, K₁ and K₂ can be expressed as $K_{1}^{{{\text{ini}}}}$ and $K_{2}^{{{\text{ini}}}}$. Under mode I fracture, Kini 1 is equal to Kini 1C and Kini 2 is 0, where Kini 1C is the initial mode I fracture toughness.

3 Results and Discussion

3.1 Effect of Roughness on the Mechanical and Fracture Properties of Rock–Concrete Interface

The mean values of experimental results obtained from DT, TPB and SSP tests at different roughness degrees R_a, are listed in Tables 2, 3 and 4, respectively. R_a was defined as the volume of sand filled in a groove in the unit area of specimen cross-section (Dong et al. 2016b). Figures 4a, b and 5a show the relationships between f_t, τ_av and $K_{{1{\text{C}}}}^{{{\text{ini}}}}$ with R_a, respectively. It can be seen from the figures that all the above-mentioned parameters increased almost linearly with R_a. The averaged maximum values of f_t, τ_av and $K_{{1{\text{C}}}}^{{{\text{ini}}}}$ for rock–concrete interface were 2.306 MPa, 4.206 MPa and 0.528 MPa·m^1/2, corresponding to R_a values of 1.693 mm, 1.718 mm and 2.004 mm, respectively. The values of f_t and $K_{{{\text{IC}}}}^{{{\text{ini}}}}$ of the concrete samples used in this study were 2.49 MPa and 0.574 MPa·m^1/2, respectively. Tensile strength f_t and initial fracture toughness $K_{{1{\text{C}}}}^{{{\text{ini}}}}$ of the roughest interfaces studied here were close to those obtained for concrete. Therefore, it was concluded that the enhancement of interface roughness effectively increased its bonding and therefore prevented crack initiation. However, this is not the case for G_If. Figure 5b illustrates the relationship of G_If and R_a, where G_If was first linearly increased with R_a and then remained constant with a further increase of R_a above 1.673 mm. Fracture energy for the roughest interface was 44.24 N/m, which was much smaller than that obtained for concrete (103.4 N/m). Thus, the contribution to the enhancement of interfacial roughness was limited by increasing interfacial crack propagation resistance.

Table 2 Results from DT tests

Table 3 Results from TPB tests

Table 4 Results from SSP tests

Fig. 4

Effects of R_a on uniaxial tensile strength f_t and average shear strength τ_av: a f_t versus R_a, and b τ_av versus R_a

Fig. 5

Effects of R_a on initial fracture toughness $K_{{1{\text{C}}}}^{{{\text{ini}}}}$ and fracture energy G_If: a $K_{{1{\text{C}}}}^{{{\text{ini}}}}$ versus R_a, and b G_If versus R_a

3.2 Shear–Softening Constitutive Law of Rock–Concrete Interface

To derive shear–softening constitutive law for rock–concrete interfaces, interfacial strains were monitored using strain gauges according to Fig. 3a. Therefore, the evaluation of the effect of rock block thickness is necessary. Figure 6 illustrates the schematic diagram of the middle section along width direction, where t is rock block thickness, L is bonding length between rock and concrete, and q is a linear load applied on the top of rock block. A solid joint was assumed between rock and concrete.

Fig. 6

Sketch for rock block

The boundary conditions were given as

$$\sigma _{y} = - q\quad {\text{at}}\;y = - \frac{L}{2},$$

(10)

$$\sigma _{y} = 0\quad {\text{at}}\;y = \frac{L}{2},$$

(11)

where $\sigma _{y} = f(y)$ is stress along y-axis and could be expressed by the stress function Ф as

$$\sigma _{y} = \frac{{\partial ^{2} \Phi }}{{\partial x^{2} }} - y\,F_{y} .$$

(12)

Here Ф could be written as

$$\Phi = \frac{1}{2}x^{2} f\left( y \right) + xf_{1} \left( y \right) + f_{2} \left( y \right),$$

(13)

where F_y is forcing function, $f_{1} \left( y \right)$ and $f_{2} \left( y \right)$ are first-order and second-order derivatives of f(y), respectively. Substitution of Eq. (13) into compatibility equation $\nabla ^{2} \nabla ^{2} \Phi = 0$ gave

$$\frac{1}{2}x^{2} \frac{{d^{4} f}}{{dy^{4} }} + x\frac{{d^{4} f_{1} }}{{dy^{4} }} + \frac{{d^{4} f_{2} }}{{dy^{4} }} + 2\frac{{d^{2} f}}{{dy^{2} }} = 0.$$

(14)

Because Eq. (14) was applied for arbitrary x, the following equations were obtained

$$\frac{{d^{4} f}}{{dy^{4} }} = 0;\quad \frac{{d^{4} f_{1} }}{{dy^{4} }} = 0;\quad \frac{{d^{4} f_{2} }}{{dy^{4} }} + 2\frac{{d^{2} f}}{{dy^{2} }} = 0.$$

(15)

Therefore,

$$\begin{gathered} f\left( y \right) = Ay^{3} + By^{2} + Cy + D, \hfill \\ f_{1} \left( y \right) = Ey^{3} + Fy^{2} + Gy + R, \hfill \\ f_{2} \left( y \right) = - \frac{A}{{10}}y^{5} - \frac{B}{6}y^{4} + Hy^{3} + Ky^{2} + Ly + M, \hfill \\ \end{gathered}$$

(16)

where A, B, C, D, E, F, G, H, K, L and M are the coefficients to be determined. Substitution of Eq. (16) into Eq. (13) yielded

$$\Phi = \frac{1}{2}x^{2} \left( {Ay^{3} + By^{2} + Cy + D} \right) + x\left( {Ey^{3} + Fy^{2} + Gy} \right) + \left( { - \frac{A}{{10}}y^{5} - \frac{B}{6}y^{4} + Hy^{3} + Ky^{2} + Ly + M} \right).$$

(17)

Thus, σ_x, σ_y and τ_xy were obtained as

$$\sigma _{x} = \frac{{\partial ^{2} \Phi }}{{\partial y^{2} }} = x^{2} \left( {3Ay + B} \right) + x\left( {6Ey + 2F} \right) - 2Ay^{3} - 2By^{2} + 6Hy + 2K,$$

(18)

$$\sigma _{y} = \frac{{\partial ^{2} \Phi }}{{\partial x^{2} }} = Ay^{3} + By^{2} + Cy + D,$$

(19)

$$\tau _{{xy}} = - \frac{{\partial ^{2} \Phi }}{{\partial x\partial y}} = - x\left( {3Ay^{2} + 2By + C} \right) - \left( {3Ey^{2} + 2Fy + G} \right).$$

(20)

Equations for boundary conditions at $x = - \frac{t}{2}$ and $x = \frac{t}{2}$ were given as

$$\int\limits_{{ - L/2}}^{{L/2}} {\sigma _{x} \,{\text{d}}y = 0} \quad {\text{and}}\quad \mathop \int \limits_{{ - L/2}}^{{L/2}} \,\tau _{{xy}} \,{\text{d}}y = - qt\quad {\text{at}}\;x = \frac{t}{2},$$

(21)

$$\int\limits_{{ - L/2}}^{{L/2}} {\sigma _{x} \,{\text{d}}y = 0} \quad {\text{and}}\quad \mathop \int \limits_{{ - L/2}}^{{L/2}} \,\tau _{{xy}} \,{\text{d}}y = 0\quad x = - \frac{t}{2}.$$

(22)

Also, equations for boundary conditions at $y = - \frac{L}{2}$ and $y = \frac{L}{2}$ were given as

$$\sigma _{y} = - q\quad {\text{and}}\quad \tau _{{xy}} = 0\quad {\text{at}}\;y = - \frac{L}{2},$$

(23)

$$\sigma _{y} = 0\quad {\text{and}}\quad \tau _{{xy}} = 0\quad {\text{at}}\;y = \frac{L}{2}.$$

(24)

According to Eqs. (21) to (24), the coefficients A to K were found as

$$\begin{aligned} & A = - \frac{{2q}}{{L^{3} }};\quad B = 0;\quad C = \frac{{3q}}{{2L}};\quad D = - \frac{q}{2};\quad E = - \frac{{qt}}{{L^{3} }}; \\ & F = 0;\quad G = \frac{{3qt}}{{4L}};\quad H = - \frac{q}{{10L}} - \frac{{qt^{2} }}{{4L^{3} }};\quad K = 0. \\ \end{aligned}$$

(25)

By the substitution of these coefficients into Eqs. (18) to (20), σ_x, σ_y and τ_xy could be obtained as

$$\sigma _{x} = - \frac{{6q}}{{L^{3} }}y\left( {x^{2} + \frac{t}{4}^{2} } \right) + \frac{{4q}}{{L^{3} }}y^{3} - \frac{{3q}}{{5L}}y - \frac{{6qt}}{{L^{3} }}xy,$$

(26)

$$\sigma _{y} = - \frac{{2q}}{{L^{3} }}y^{3} + \frac{{3q}}{{2L}}y - \frac{q}{2},$$

(27)

$$\tau _{{xy}} = \frac{{6q}}{{L^{3} }}\left( {x + \frac{t}{2}} \right)y^{2} - \frac{{3q}}{{2L}}\left( {x + \frac{t}{2}} \right).$$

(28)

Strain along y-axis ε_y, and shear strain γ_xy, were determined as

$$\varepsilon _{y} = \left( {\sigma _{y} - \mu \sigma _{x} } \right)/E,$$

(29)

$$\gamma _{{xy}} = 2\left( {1 + \mu } \right)\tau _{{xy}} /E.$$

(30)

Rock block strains were determined by the substitution of Eqs. (29) and (30) into Eqs. (26) to (28). Taking points 1 to 6 of Fig. 6 as examples, ε_y at these positions were determined to be: $\varepsilon _{{y1}} = - \frac{{96}}{{100}}\frac{q}{E}$, $\varepsilon _{{y2}} = - \frac{{50}}{{100}}\frac{q}{E}$, $\varepsilon _{{y3}} = - \frac{4}{{100}}\frac{q}{E}$, $\varepsilon _{{y4}} = - \frac{{98.4}}{{100}}\frac{q}{E}$, $\varepsilon _{{y5}} = - \frac{{61}}{{100}}\frac{q}{E}$ and $\varepsilon _{{y6}} = - \frac{{1.6}}{{100}}\frac{q}{E}$. By comparing the values of ε_y at points with the same x value, i.e. points 1 and 4, points 2 and 5, and points 3 and 6, it was found that rock block thickness had an insignificant effect on ε_y. Particularly, this effect was small when the slip between rock and concrete was considered. Therefore, in this study, it was assumed that strains along rock thickness were approximately equal and those measured by strain gauges on rock surface could be used to approximate strain values at rock–concrete interface.

Figure 7a–f illustrate strain distributions of typical SSP specimens with six different interface roughness degrees and loading levels. It can be seen from the figures that strains near the loading end increased more rapidly than those near the free end during the initial loading stage. By increasing load, strains along the interface showed obvious nonlinear distributions which indicated the development of interfacial cracks. For a given specimen, the strain value obtained from the strain gauge located nearest to the loading point began to decrease after reaching a maximum value. The maximum strain point moved from the loading end towards the free end. When crack propagated to the middle point of interface, strain reached its maximum value and the applied load approached the ultimate interfacial bearing capacity. Subsequently, an abrupt failure occurred on the composite specimen because residual interfacial cohesive force could no longer resist the applied load. Meanwhile, with the increase of R_a, the maximum strain values of the tested points were gradually increased under the same load level, which indicated that the interfacial cohesive effect was stronger on rougher interfaces. Experimental average peak shear stresses for different R_a values are listed in Table 4. The cracking patterns of specimens SSP 5 × 5, SSP 10 × 10 and SSP 12 × 12 at failure are presented in Fig. 8 indicating that treatment by artificial grooving improved the bond between concrete and rock. For these specimens, failure in the artificial grooving interface was due to concrete shearing, while failure on the smooth interfacial surface between concrete and rock was due to a weak bond.

Fig. 7

Strain distribution curves for typical SSP specimens with various roughness degrees: a Specimen SSP 3 × 3-1, b Specimen SSP 4 × 4-1, c Specimen SSP 5 × 5-1, d Specimen SSP 7 × 7-1, e Specimen SSP 10 × 10-1, and f Specimen SSP 12 × 12-1

Fig. 8

Cracking patterns of rock–concrete interface: a Specimen SSP 5 × 5, b Specimen SSP 10 × 10, and c Specimen SSP 12 × 12

After obtaining strain distribution along the interface, average shear stress τ_i between two adjacent strain gauges i and i + 1 was

$$\tau _{i} = \frac{{E\left( {\varepsilon _{{y,i + 1}} - \varepsilon _{{y,i}} } \right)t}}{{\Delta L}},$$

(31)

where E is Young’s modulus of rock, t is rock block thickness, ΔL is the distance between the midpoints of two adjacent strain gauges, and ε_i and ε_i+1 are the strains of strain gauges i and i + 1 (i = 1, 2,…,7), respectively. Thus, the average slip displacement $\delta _{{{\text{s,i}}}}$ between two adjacent strain gauges was calculated from

$$\delta _{{{\text{s}},{\text{i}}}} = \frac{{\varepsilon _{{y,i + 1}} + \varepsilon _{{y,i}} }}{2}\Delta L + \delta _{{{\text{s}},{\text{i}} - 1}} .$$

(32)

Therefore, the relationships between τ and δ_s was determined by the substitution of the strain values measured for all SSP specimens into Eqs. (31) and (32) according to Fig. 9a–f. In Eq. (32), length scale ΔL was assumed as the distance between the midpoints of two adjacent strain gauges. It is well accepted that the lengths of strain gauges should be three times larger than granite grain size to ensure that the measured values represented real strains on the granite surface. In this study, the average granite grain size was 1 mm; therefore, strain gauges with 5 mm active gauge length and 8.5 mm gauge length were selected. To determine comprehensive strain distribution in the bonding zone at rock–concrete interface, 8 strain gauges 5 mm from each other were successively attached on the middle part of the rock surface (Fig. 3a) and the whole length of the bonding zone was 100 mm (Fig. 3b). As can be seen in Fig. 7, nearly smooth curves were obtained for strain distributions indicating that length scale ΔL was selected appropriately. The width of interfacial FPZ due to shear stress was not investigated in this study because the interfacial fracture was considered as a plane problem. In this way, interfacial FPZ along width direction was assumed to be constant and only strains in the middle part of the bonding zone were measured and analyzed.

Fig. 9

Relationships between shear stress and slip displacement for SSP series: a SSP 3 × 3 series, b SSP 4 × 4 series, c SSP 5 × 5 series, d SSP 7 × 7 series, e SSP 10 × 10 series, and f SSP 12 × 12 series

Figure 10 shows the bond–slip relationship derived through the linear fitting of experimental results shown in Fig. 9. Here, δ_s1 is crack slip displacement corresponding to the intersection point of the bilinear relationship, and δ_s0 is stress-free crack slip displacement which is δ_s0 = 1.5δ_s1. The area under the bilinear curve is mode II fracture energy G_IIf, which can be expressed as follows, with the average values of G_IIf corresponding to different R_a values listed in Table 3

$$G_{{{\text{IIf}}}} = \frac{1}{2}\tau _{{\max }} \delta _{{{\text{s}}0}} .$$

(33)

Fig. 10

Bond–slip relationship for rock–concrete interface

For practical applications, τ_max was replaced by f_t, and G_IIf was replaced by G_If by curve fitting based on their relationships. The relationships between f_t and τ_max, and between G_If and G_IIf are illustrated in Fig. 11a and b, respectively. To ensure the same interfacial roughness for curve fitting data, regression results of f_t and G_If were applied which corresponded to the same roughness for the measured τ_max and G_IIf values, respectively. Curve fitting on G_IIf and τ_max gave

$$G_{{{\text{IIf}}}} = 1.5G_{{{\text{If}}}} ,$$

(34)

$$\tau _{{\max }} = 3.5f_{{\text{t}}} .$$

(35)

Fig. 11

Relationships between G_IIf and G_If and between τ_max and f_t: a G_IIf versus G_If, and b τ_max versus f_t

Thus, bond–slip relationship could be expressed as

$$\tau = \frac{{(3.5f_{{\text{t}}} )^{2} }}{{2G_{{{\text{If}}}} }}\delta _{{\text{s}}} \quad {\text{for}}\;0 \le \delta _{{\text{s}}} < \delta _{{{\text{s}}1}} ,$$

(36)

$$\tau = \frac{{3.5f_{{\text{t}}} }}{{\delta _{{{\text{s}}0}} - \delta _{{{\text{s}}1}} }}\left( {\delta _{{{\text{s}}0}} - \delta _{{\text{s}}} } \right)\quad {\text{for}}\;\delta _{{{\text{s}}1}} \le \delta _{{\text{s}}} < \delta _{{{\text{s}}0}} ,$$

(37)

$$\tau = 0\quad {\text{for}}\;\delta _{{{\text{s}}0}} \le \delta _{{\text{s}}} ,$$

(38)

$${\text{with}}\;\delta _{{{\text{s}}0}} = \frac{{6G_{{{\text{If}}}} }}{{7f_{{\text{t}}} }},$$

(39)

$$\delta _{{{\text{s}}1}} = \frac{{4G_{{{\text{If}}}} }}{{7f_{{\text{t}}} }}.$$

(40)

Therefore, bond–slip relationship could be determined by measuring f_t and G_If values of rock–concrete interface. Since the effect of interfacial roughness was reflected in f_t and G_If, the proposed constitutive law was appropriate for different interfacial roughness degrees.

Figure 10 illustrates the bond–slip relationship, rather than shear–softening constitutive law, of rock–concrete interface. Shear–softening constitutive law, i.e., cohesive law, typically represents a traction–separation relationship and is assumed to characterize the cohesive effect of rock–concrete interface. The separation in the law is defined as fracturing displacement, i.e. the slip displacement of crack surface. The interfacial crack surface is formed after interfacial shear strength is reached and fracturing displacement becomes nonzero only in the post peak region of τ–δ_s relationship. Taking a typical τ–δ_s curve, as shown in Fig. 12, as an example, total displacement δ_s in the descending region of the curve included elastic deformation δ_e, plastic deformation δ_p and fracturing displacement w_s. Therefore, fracturing displacement w_s could be obtained by Eq. (41) as

$$w_{{\text{s}}} = \delta _{{\text{s}}} - \delta _{{\text{e}}} - \delta _{{\text{p}}} .$$

(41)

Fig. 12

Relationship of w_s, δ_s, δ_e and δ_p

For the bilinear τ–δ_s relationship derived in this study (Fig. 10), the displacements of δ_s and δ_e were obtained from curve of Fig. 12. However, plastic deformation δ_p could not be obtained because no cyclic loading was applied in the tests. Since the value of δ_p was very small and did not have significant effect on softening constitutive law, fracturing displacement w_s was approximated based on the difference of δ_s and δ_e. Accordingly, the shear–softening constitutive law of rock–concrete interface, i.e. τ–w_s relationship, was derived, as shown in Fig. 13 where, w_s0 is stress-free crack slip displacement and is equal to the value of δ_s0.

FPZ ahead of interfacial crack showed strain softening and strain localization behaviors. Both cohesive stress and corresponding crack slip displacement in FPZ are key parameters in determining the nonlinear behavior of rock–concrete interfaces. Based on the study conducted on shear–softening constitutive laws (τ–w_s relationships) of cementitious materials, a linear relationship could be assumed between these two parameters. Therefore, it was concluded that cohesive shear stresses were decreased with the increase of slip displacements until stress-free zone, i.e. macro-crack, was formed.

Fig. 13

Shear–softening constitutive law for rock–concrete interface

Similar tests were conducted to determine τ–δ_s relationships for steel–concrete (Bouazaoui and Li 2008; Yang et al. 2016) and fiber reinforced polymer–concrete (Ali-Ahmad et al. 2006; Wu and Jiang 2013; Lin and Wu 2016; Ghorbani et al. 2017) interfaces by measuring local interfacial strains during loading. As indicated in Eqs. (31) and (32), τ–δ_s relationship was obtained by measuring strains within the length ΔL. It was found that shear–softening constitutive law based on τ–δ_s relationship had to be unique if material properties on both sides of interface and interfacial bonding conditions were known. Thus, τ–δ_s relationships for rock–concrete interfaces could be uniquely determined by ensuring accurate distributions of strains. Hence, selecting small ΔL values in tests seemed to be more appropriate. However, under practical operation conditions in the laboratory, the lengths of strain gauges and their distances from each other had to have certain values. Therefore, to comprehensively explore the variations of cohesive shear stress and crack slip displacement, selecting a reasonable ΔL length in the tests was essential.

Since the aim of this experimental work was to determine the cohesive characteristics of FPZ, it was necessary to relate ΔL with the characteristic size of FPZ. However, FPZ evolution depended on the magnitude of load, i.e. FPZ length was increased from zero to full length during the loading stage. Meanwhile, the full length of FPZ was affected by specimen size and shear–softening constitutive law, which could be calculated using numerical methods (Dong et al. 2013). In this study, the length ΔL was associated with characteristic length l_ch proposed by Hillerborg (1976). Xu (2011) showed that there was a scaling relationship between the full length of PFZ and l_ch, which was appropriately 0.3 to 0.5. Characteristic length l_ch could be used to qualitatively determine the brittleness of a material as

$$l_{{\text{ch}}} = \frac{{EG_{{\text{If}}} }}{{f_{\text{t}}^{2} }} = \frac{{K_{{\text{IC}}}^{2} }}{{f_{\text{t}}^{2} }},$$

(42)

where K_IC is stress intensity factor or critical fracture toughness of mode I. Smaller characteristic lengths indicate that the material is more brittle. The characteristic length proposed by Hillerborg was appropriate for mode I fractures. Therefore, these parameters were adopted to reflect the tensile characteristics of materials. To the best of our knowledge, no characteristic length has been proposed for mode II fractures. Therefore, following the definition of characteristic length l_ch under mode I fractures, the characteristic length of mode II fractures was also proposed and employed in this study as

$$l_{{\text{ch - II}}} = \frac{{EG_{{\text{IIF}}} }}{{\tau _{{\text{av}}}^{2} }} = \frac{{K_{{\text{IIC}}}^{2} }}{{\tau _{{\text{av}}}^{2} }},$$

(43)

where l_ch-II is characteristic length for mode II fracture, and $K_{{{\text{IIC}}}}^{{}}$ is the critical stress intensity factor or fracture toughness of mode II. It should be noted that, for rock–concrete interface, the parameters K_IC and K_IIC had to be replaced with K_1C and K_2C. In a previous experimental study (Dong et al. 2016b), the ratio of $K_{{2{\text{C}}}}^{{{\text{ini}}}} /K_{{1{\text{C}}}}^{{{\text{ini}}}}$ was found to be about 1.6 for rock–concrete interfaces. Meanwhile, based on the experimental study conducted by Xu and Reinhardt (1999), the ratio of initial fracture toughness to unstable fracture toughness was obtained to be about 0.5. Therefore, K_2C could be approximated from the corresponding relationship for $K_{{1{\text{C}}}}^{{{\text{ini}}}}$, i.e. $K_{{2C}} = 2K_{{{\text{2C}}}}^{{{\text{ini}}}} = 3.2K_{{1{\text{C}}}}^{{{\text{ini}}}}$. The values of mode II characteristic length l_ch-II for six interfaces with different roughness degrees investigated in this study were 232, 140, 107, 112, 112 and 161 mm, giving an average value of 144 mm. In contrast, the value of ΔL was obtained to be 13.5 mm, which was approximately 10% of the corresponding value under mode II fracture. According to the experimental results illustrated in Fig. 7, strain variation distributions during loading stage can be reasonably represented based on length ΔL.

3.3 Crack Propagation of Rock–Concrete Interface Under Mixed Mode I–II Fracture

The obtained shear–softening constitutive laws were validated using numerical analyses conducted on crack propagation at rock–concrete interface under mixed mode I–II fractures using commercial finite element software ANSYS. A crack propagation criterion was introduced to determine the initiation and propagation of interfacial crack (Dong et al. 2018) as follows

$$\sqrt {\left( {\frac{{K_{1}^{{\text{P}}} - K_{1}^{{\sigma ,\tau }} }}{1}} \right)^{2} + \left( {\frac{{K_{2}^{{\text{P}}} - K_{2}^{{\sigma ,\tau }} }}{{1.6}}} \right)^{2} } = K_{{1{\text{C}}}}^{{{\text{ini}}}} ,$$

(44)

where $K_{{\text{1}}}^{{\text{P}}}$ and $K_{{\text{2}}}^{{\text{P}}}$ are SIFs of modes I and II caused by external loading and $K_{{{1}}}^{{{{\sigma ,\tau }}}}$ and $K_{{{2}}}^{{{{\sigma ,\tau }}}}$ are SIFs of modes I and II caused by cohesive tensile stress σ and shear stress τ in FPZ. A verified bilinear σ–w relationship was utilized to describe cohesive tensile stress in FPZ (Dong et al. 2016b) where breaking point coordinates on bilinear curve were set as (0.8G_If/f_t, 0.2f_t), and stress-free displacement was set as 6G_If/f_t. In addition, to compare different τ–w_s relationships, three shear–softening curves, including those reported by Zhong et al. (2014), Shi (2004) and our findings, were adopted to characterize cohesive shear stress in FPZ. Zhong used a bilinear τ–w_s relationship including ascending and descending stages where τ_max and w_s0 were set as 7f_t/4 and 4G_If/f_t, respectively, and breaking point coordinates on bilinear curve were set as (0.001 mm, 7f_t/4). Shi assumed that shear stress was related with crack opening displacement where τ_max and w_s0 were set as f_t/2 and 5G_If/f_t, respectively, and breaking point coordinates on the bilinear curve were set as (G_If/f_t, f_t/2). Meanwhile, there was another parameter w_s,ini in Shi’s model, which denoted crack opening displacement corresponding to shear stress initiation and was set as G_If/2f_t.

In numerical simulation on crack propagation of rock–concrete interface, the un-crack zone was assumed as perfectly bond and the fracture process zone was modeled as the discrete crack acting on cohesive stress. The rock–concrete interface under different conditions can be reflected by corresponding interfacial mechanics and fracture parameter, including tensile strength, shearing strength, fracture energy and fracture toughness. The flowchart of numerical simulation for the complete interfacial crack propagation is shown in Fig. 14, which can be summarized as follows:

• 1. Finite element model was established with crack length a_i,j = a₀ + (j − 1)⋅Δa (i = 1, 2,…; j = 2, 3,…), where a₀ is initial crack length, Δa is a specified increment of crack length, i represents load increment during iteration process with a fixed crack length, and j represents the increment of crack length during iterations.

• 2. Load P_i,j was applied and cohesive stresses σ_i,j and τ_i,j were calculated according to cohesive tension/shear traction–displacement relationships.

• 3. $K_{{\text{1}}}^{{\text{P}}}$, $K_{{{1}}}^{{{{\sigma ,\tau }}}}$, $K_{2}^{{\text{P}}}$ and $K_{2}^{{{{\sigma ,\tau }}}}$ were calculated by adjusting load P_i,j = P_i−1,j ± ΔP until Eq. (44) was satisfied, and P_i,j, a_i,j, CMOD(j) and CMSD(j) were saved.

• 4. Steps 1 and 3 were repeated for the next step of crack propagation.

• 5. Iterative process was terminated when a_i,j was equal to specimen height or P_i,j ≤ 0.

Fig. 14

Flowchart of numerical simulation for the complete interfacial crack propagation

By the implementation of the abovementioned iterations, the complete interface fracture process was numerically achieved. The details of the iteration process for numerical analysis of crack propagation can be found in the work of Dong et al. (2018).

Experimental results obtained from four-point shear (FPS) tests reported by Dong et al. (2018) were compared with numerical simulation results. The geometry of FPS beam is illustrated in Fig. 15. To obtain different ratios of Kini 2/Kini 1, different rock lengths LR of 225, 235, 240 and 250 mm were used. The calculated parameters of concrete-rock series specimens are listed in Table 5. Cracks propagated along rock-concrete interfaces in all specimens listed in Table 5.

Table 5 Calculated parameters used in the numerical simulations

Fig. 15

Geometry of the C–R specimen for FPS test

Figure 16a–c illustrate finite element mesh at different key fracture stages for specimen C–R-235. Meanwhile, P–CMOD curves obtained from experimental tests and numerical simulations are shown in Fig. 17a–d. It can be seen that the predicted peak loads using different τ–w_s relationships were different with the increase of the mode II components, i.e. Kini 2/Kini 1 ratios. For specimens C–R-225 and C–R-235 with Kini 2/Kini 1 ratios of 0.357 and 0.721, respectively, mode I fractures were dominant. Due to the insignificant effect of shear action on model I interfacial crack propagation, the predicated P–CMOD curves for different τ–w_s relationships were close to each other, as shown in Fig. 17a, b. For specimen C–R-240 with Kini 2/Kini 1 ratio of 1.137, crack propagation pattern was a typical mixed mode I–II fracture. Both the opening and shear actions had significant effects on interfacial crack propagation. In this case, the predicted peak load and critical CMOD using τ–w_s relationship derived in this study were slightly higher than those obtained using τ–w_s relationship reported by Zhong et al. (2014), as shown in Fig. 17c. For specimen C–R-250 with Kini 2/Kini 1 ratio of 16.238, the dominant crack propagation pattern was fairly mode II fracture. Due to the significant effect of shear action on interfacial crack propagation, the predicated peak load using τ–w_s relationship obtained in this study was obviously higher than those obtained using τ–w_s relationship reported by Zhong et al. (2014), as shown in Fig. 17d. In addition, the predicted peak loads obtained using τ–w_s relationship reported by Shi (2004) obviously underestimated numerical and experimental results. Therefore, τ–w_s relationships obtained from concrete, including non-zero shear stress initiation, were not appropriate for fracture analysis on rock–concrete interfaces. In general, numerical results obtained from derived shear–softening constitutive law proposed in this study agree well with experiment results, confirming that the derived τ–w_s relationship could be used in the simulation of mixed mode I–II fracture process at rock–concrete interfaces.

Fig. 16

Mesh and deformation of different fracture stages for Specimen C–R-235: a crack initiation, b critical crack propagation, and c failure of specimen

Fig. 17

Comparison of predicted P–CMOD curves with experimental results: a Specimen C–R-225, b Specimen C–R-235, c Specimen C–R-240, and d Specimen C–R-250

4 Conclusions

Direct tension (DT), three-point bending (TPB) and single shear push-out (SSP) tests were conducted to study the fracture properties of rock–concrete interfaces with different roughness degrees. Based on the experimental results obtained from SSP tests, a shear–softening constitutive law was developed and used in the numerical simulations of interfacial crack propagation under mixed mode I-II fractures. By comparing experimental results with those obtained from shear–softening constitutive laws, a new τ–w_s relationship was derived and validated. According to the experimental tests and numerical simulations, the following conclusions were drawn:

• Uniaxial tensile strength f_t, average shear strength τ_av and initial fracture toughness $K_{{1{\text{C}}}}^{{{\text{ini}}}}$ of rock–concrete interfaces were linearly increased with the increase of interfacial roughness R_a, when R_a was increased from 0.723 to 2.004 mm. Interfacial fracture properties, f_t and $K_{1}^{{{\text{ini}}}}$, were close to those of concrete at roughest interfaces indicating that the increase of interfacial roughness effectively prevented early crack initiation. However, the fracture energy G_f of rock–concrete interfaces was linearly increased until a peak value was reached at R_a equal to 1.673 mm. Maximum interfacial fracture energy G_f for the roughest interfaces became much smaller than the fracture energy of concrete, indicating that the contribution of increased interfacial roughness in increasing crack propagation resistance could be limited.

• A novel SSP testing method was proposed to experimentally develop shear–softening constitutive laws for rock–concrete interfaces. Linear τ–w_s relationship was derived based on experimental results which could be determined by measuring mode I interfacial fracture energy and tensile strength, regardless of the properties and the bonding conditions of concrete and rock. Accordingly, mode II interfacial fracture energy was obtained by calculating the area under the complete shear–softening curve, which was approximately 1.5 times larger than mode I fracture energy. Compared with shear–softening constitutive law for concrete, the peak shear stress determined based on the softening relationship developed in this study was higher, along with lower stress-free displacements, indicating larger brittleness for mode II interfacial fractures.

• By introducing derived shear–softening constitutive law in a verified numerical method, interfacial crack propagation under mixed mode I–II fractures were simulated. The difference between the peak loads predicted using τ–w_s relationship developed in this study and that obtained for concrete (Shi 2004; Zhong et al. 2014) was gradually increased with the increase of mode II SIF components. In general, the predicated P–CMOD curves agreed well with experimental findings, indicating that the τ–w_s relationship developed in this study can be applied to determine the shear–softening characteristics of rock–concrete interfaces.