Considerations Relevant to the Stability of Granite Boulders

Abstract

Granite boulders are characteristic geomorphological structures formed in granitic terrains. Due to their formation process associated with typical spheroidal weathering phenomena, they tend to show more or less ellipsoidal shapes prone to instability, and they often lie on small contact surfaces. Analyzing the stability of these boulders is not a straightforward task. First, these boulders may topple or slide. Additionally, their typically irregular geometry and uneven contact with the surface where they lie makes the analysis more complex. The authors have identified some critical issues that are relevant to characterize these boulders from a rock mechanics point of view, with the aim of estimating the stability of boulders. In particular, an accurate description of the geometry of the boulder is necessary to perform accurate toppling calculations. Additionally, the contact area and the features of the contact plane need to be known in detail. The study is intended to serve as a guideline to address the stability of these granite boulders in a rigorous way, since standard rock mechanics approaches (planar failure, toppling stability, standard rock joint strength criteria, etc.) may not be directly applicable to these particular cases.

1 Introduction

Large granite boulders are typical geomorphological structures formed in granitic terrains and are most common in temperate regions that are or have been humid on all continents. Accordingly, they can be found in the western part of Europe (Galicia in Spain, northern Portugal, UK), in southern Africa (Zimbabwe, Kenya or Namibia), in southern Asia including India or Thailand, Brazil, Australia and the USA (e.g. Yosemite or Joshua Tree National Parks), for example.

Due to their formation process, associated to differential weathering, they tend to show more or less ellipsoidal shapes, which in turn means that they often lie on a small contact surface, making these boulders prone to instability. Instability of these boulders can put people or property at risk, meaning this phenomenon should be studied in detail. Furthermore, the geometry of these blocks tends to be irregular, which contributes to making rigorous analyses of their stability difficult.

The authors have been involved in the stability analysis of some of these structures in the past and have developed approaches to analyze their stability (Alejano et al. 2010; Pérez-Rey et al. 2019a), either against sliding or toppling/overturning. At the same time, they have identified some critical issues that are relevant to characterize these boulders from a rock mechanics perspective to help quantify their stability.

Characterization of the contact surfaces of the boulders with the rock where they rest shows that they cannot typically be considered standard unfilled rough joints, in contrast to most of the joints usually found in rock masses. Their behavior is best represented by so-called mismatched joints, where the two contact surface roughness profiles differ.

It is also important to note that boulders are usually not regular or symmetric solids. Accordingly, to compute their stability against overturning, one has to analyze the projection of the center of gravity of the boulder on the resting plane in relation to the contact base. Rounded corners also play a role in stability computations.

In this paper, relevant features concerning the stability of these boulders against sliding and toppling based on practical experience will be briefly reviewed and illustrated with the help of physical models and actual case studies. Based on previous applied studies (Alejano et al. 2010; Pérez-Rey et al. 2019a, b), some improvements were incorporated and new analyses are provided to insight granite boulder stability behavior. This paper is ultimately intended to be of help in addressing the stability of granitic and other type of boulders for rock mechanics practitioners dealing with this type of problems, since standard rock mechanics approaches may not be directly applied to this particular type of stability analyses.

2 Granite Boulder Formation and Occurrence

This study addresses instability phenomena associated with irregular stone boulders in granitic terrains, illustrated in the context of the conditions encountered in the northwest of the Iberian Peninsula. These phenomena also take place in other regions of the globe where granitic basements are subjected (now or in the past) to intense weathering. A survey of granite landforms from a geomorphologic perspective was produced by Twidale (1982), where the author refers to four main groups of landform types including boulders, inselbergs, all-slopes topography and plains.

Disregarding the stable plains, three types of potentially unstable slope environments can be identified among these landforms, including typically large ellipsoidal individual granite boulders areas, whose stability is the main focus of this study, mid-slope regions formed by groups of medium-size granitic boulders in decomposed granite matrix (which can produce rockfall phenomena; Pérez-Rey et al. 2019b) and, finally, mild slopes formed by highly or completely decomposed granite (HDG or CDG) (Jiao et al. 2005; Alejano and Carranza-Torres, 2011; Jiao et al. 2012; Ohtsu et al. 2018) (Fig. 1). In all these cases, weathering of granitic materials plays an important role.

Fig. 1

Schematic diagram and accompanying pictures of different slope types in granitic terrain

Boulders are one of the most common and characteristic landforms of granitic terrains and they originate due to weathering (Durgin 1977; Fletcher et al. 2006). These structures form through the mechanism of spheroidal weathering and forward erosion of decomposed granite. Spheroidal weathering is a physical–chemical process that affects uniform rock masses with regular joint patterns, typical of granitic rocks, but also in volcanic tuffs or basaltic rock.

Weathering is the process by which rock deteriorates until it eventually breaks down to a soil. This process is highly dependent on climatic influences (Selby 1993). Often, weathering works from free surfaces where chemicals in water attack the parent rock (Figs. 2 and 3). Eventually it may leave a framework or core-stones of more or less fresh rock separated by weathered zones that can be easily eroded (Ollier 1975; Hack 2009; Wong 2012; Md Dan et al. 2016). Often, joint sets found in rock masses are orthogonal; two sets occur perpendicular to one another and perpendicular to some planar fabric such as bedding, foliation or flow banding in an igneous pluton (Taboada et al. 2005; Hencher 2012).

Fig. 2

Idealized sketches illustrating the evolution of granitic rock masses to produce boulder fields according to Linton (1955). a Original granite orthogonally fissured rock mass; b spheroidal penetration of weathering; c ultimate stage with saprolite and clay removal, unveiling spheroidal weathering

Fig. 3

Illustrative example of the tentative weathering and eroding process producing a group of granite boulders. a Intact fissured granitic rock mass. b Fissured granitic rock mass after weathering. c Fissured granitic rock mass after weathering and suffering erosion processes producing boulders and d actual photograph of the situation depicted in c

Linton (1955) theorized a two-stage process of formation (Fig. 2). The first stage involves deep penetration of weathering along joint surfaces, which produces a thick saprolite or completely decomposed granite (CDG) mantle interspersed with non-weathered core-stones. The second stage is brought on by exhumation either by tectonic uplift of these boulders or lowering of base level accompanied by erosive processes.

In the case of granites, rock erosion tends to produce boulder fields or the so-called tors or inselbergs, which are residual rock masses that display as isolated piles of boulders (Twidale and Vidal-Romaní 2005). This is consistent with the formation process suggested by Linton (1955).

Following weathering, granular saprolite or completely decomposed granite (CDG) is quickly eroded or removed by wind and water leaving behind the rounded core-stones or boulders. An example of one of these processes is illustrated in Fig. 3, where a structure of some granitic boulders eventually remains after weathering of a jointed rock granitic mass.

If these erosive processes persist until they reach the entire rock mass, a phenomenon typical of granite plains, the granite becomes completely decomposed, behaving like a soil material (HDG or CDG); this is also known in the NW of the Iberian Peninsula as “jabre” (Alejano and Carranza-Torres 2011), but has other local names according to geography (GEO 1988; Onitsuka et al. 1985). One defining aspect of CDGs in the context of geotechnical engineering is their heterogeneous spatial distribution and natural variability (Fig. 1c).

Since the original joints of a granitic mass are not necessarily orthogonal (though they tend to be), granite boulders occur in different shapes and sizes, from almost perfect spheres to ellipsoidal bodies, but also slender or irregular slabs. As previously noted, these boulders are common all over the world, but particularly in temperate humid regions (Fig. 4).

Fig. 4

Source: photos b and d by the authors and a, c, d and e taken from (https://commons.wikimedia.com)

Examples of granitic boulders in different parts of the world: a The 250 t Krishna butter ball in the Kancheepuram district in India b Kidney-shaped 100 t rocking stone in Abadín, Galicia (NW-Spain); c Devil’s marble in the North Territories (Australia); d Kit Mikayi or the stone of the first wife in Kisumu, Kenya, a 20 m high structure still attracting pilgrims, e Logan stone (a rock which, through weathering, has become disjoined from the parent-rock and is pivoted upon it…) at Thornworthy Tor in UK; f A 5 kt boulder in North Portugal.

3 Granite Boulder Instability Mechanisms

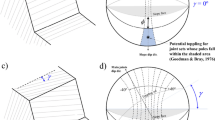
Granite boulders are effectively rock blocks with complex geometry lying on approximately planar resting surfaces. In the field of rock slope engineering, the stability of a rock block lying on an inclined plane should be studied against the two types of instability mechanisms hypothetically observable in these cases, namely, sliding and toppling/overturning (Sagaseta 1986). If we consider that a granite boulder is a block lying on such an inclined plane, both types of mechanisms should be considered (Fig. 5) to quantify its stability level.

Fig. 5

a Potential instability mechanisms of a boulder or a block lying on a tilted surface. b Point cloud and picture images of two granite boulders lying on inclined planar surfaces or basal planes, whose stability was considered in previous studies (Alejano et al. 2010; Pérez-Rey et al. 2019a)

Traditional rock slope engineering studies (Hoek and Bray 1974; Goodman and Bray 1976; Wyllie and Mah 2004) developed methodologies for analyzing the stability of rock blocks with simple shapes delimited by pre-existing rock joints or discontinuities, such as rock slabs, prisms, wedges or columns. These potentially unstable blocks tend to form when excavating man-made slopes or rock cuts. Stability against sliding or toppling of complex geometry boulders or blocks is not a straightforward task since adapting calculations to the observed geometries can be difficult. Additionally, contact zones between boulders and resting planes do not tend to behave like standard unfilled rough rock joints (further explained in Sect. 4.6), so traditional rock joint strength approaches may not be appropriate.

The stability against sliding, in case the contact plane is cohesionless (as is normally the case), is controlled by the plane dip (α) and the friction angle (ϕ) of the contact between the boulder and the basal plane according to Eq. 1:

$$FoS_{{{\text{sliding}}}} \; = \;\frac{\tan \phi }{{\tan \alpha }}$$

(1)

In the case of rough unfilled rock joints, the Barton–Bandis approach (Barton and Choubey 1977; Barton and Bandis 1982) can be used to compute the friction of the contact, but the authors’ experience is that the boulder–rock contact does not behave like this type of joint (Alejano et al. 2012).

The basic equation controlling the stability against toppling of a rigid block is presented in Eq. 2 and can be used to estimate the factor of safety, and accordingly, the stability of a block against toppling.

$$FoS_{{{\text{toppling}}}} \; = \;\frac{{\sum {M_{{{\text{stabilising}}}} } }}{{\sum {M_{{{\text{overturning}}}} } }}$$

(2)

This simple equation just considers the ratio of the stabilizing and overturning moments in relation to the corresponding rotation axis. In the simplest case, where the only driving force is the weight of the specimen, the factor of safety against toppling (FoS_toppling) can be computed according to the forces acting along x- and y-axes, in relation to a rotation axis located at the lower corner of the block in the direction of tilting (Fig. 5a).

The forces involved in the analysis of each specimen result from its own weight (and other external forces) and are typically applied at the center of gravity of the specimens. For slabs with simple geometry, the rotating axis is easily identified as the lower external corner, but when the corners of the slab or boulder are rounded or the boulder has complex geometry, the rotation axis should be chosen with care. Indeed, for boulders with an irregular base, the rotation point varies according to the projection of the center of gravity on this base.

The most likely failure mechanism (sliding or toppling) will be the one theoretically occurring at a lower tilting angle. Typically, slender boulders will be more prone to topple, whereas rounded blocks tend to slide, if the basal plane dip is larger than the apparent friction angle of the contact (Fig. 6).

Fig. 6

Different geometry boulders. Slender blocks are more prone to topple, particularly if they show rounded corners. Rounded blocks tend to be more stable but may slide if they lay on basal planes more inclined than the contact friction angle

With the aim of studying the stability of rock elements, it is possible to carry out simple tilt tests under controlled environmental conditions and constant lifting velocities to estimate analytically predicted angles in the laboratory (Alejano et al. 2015, 2018).

4 Relevant Issues Affecting Stability Calculations

In this section, the authors address a number of relevant issues to be considered when estimating boulder stability, adapting classic rock mechanics approaches to the types of cases under scrutiny.

4.1 Detailed Boulder Geometry

One of the reasons that has made it difficult in the past, if not impossible, to compute boulder stability was the unavailability of a detailed knowledge of the geometry of the boulders.

Advanced surveying techniques such as terrestrial laser scanning (TLS) and close range or drone (remotely piloted aircraft systems, RPAS) photogrammetry permits a very detailed record of the land geometry in the form of 3D point clouds (3DPC) (Armesto et al. 2009; Ferrero et al 2008; Riquelme et al. 2014).

Our experience is that it is better to apply TLS (generally more accurate) and RPAS photogrammetry together, since due to the shape and size of the boulders, their upper part is usually hidden from terrestrial views and their lower parts and contact zones are shadowed in top views typical of RPAS photogrammetry. By combining information recovered from both in-situ non-contact surveys, an accurate 3DPC can be obtained. This 3DPC can be processed using software like MeshLab or CloudCompare (Girardeau-Montaut 2018).

Figure 7.a illustrates the ‘Pena do Equilibrio’ boulder studied by Pérez-Rey et al. (2019a) and Fig. 7b shows the 3D point cloud derived from TLS and UAS imagery obtained for this boulder, where also its center of gravity and the relatively very small contact area are depicted. This information is critical for further sufficiently accurate calculations. Figure 7c. represents the top view of the boulder together with the contact zone and center of gravity (cog) projections (also enlarged). This projection is needed to compute stability against toppling of this block, as explained below.

Fig. 7

Modified from Pérez-Rey et al. (2019a)

a 3D photogrammetric model and b derived 3DPC of the ‘Pena do Equilibrio’ 350 t boulder in Spain, whose stability was studied by the authors. c, d Plan view of the point cloud with area enlarged.

4.2 Stability Against Toppling

Using detailed geometry data (e.g. a 3DPC) including contact area, the stability of the boulder against toppling can be reliably computed. FoS_toppling is computed according to Eq. 2. Application of this formula to an idealized slab geometry is straightforward as shown in Fig. 8, derived from the seminal Goodman & Bray (1976) approach.

Fig. 8

Formulation of the stability of slab like block against toppling, based on the Goodman and Bray (1976) approach

The location of the rotation axis is easily identified, as it is located on the lower outer corner of the rectangular-shaped slab. If the projection of the center of gravity (cog) falls within the base of the block, it will not topple, whereas when it falls out of this base, the block will topple.

To analyze the stability of a slab with rounded or eroded corners (Fig. 9), the situation becomes slightly more complicated. However, if the rounding corner radius (r) is known, computations can be performed according to Alejano et al. (2015) and the formulation presented in Fig. 9. Rounding of the corners contributes to making boulders more prone to toppling.

Fig. 9

Formulation of the stability analysis of slab like rounded corner block against toppling based on the Alejano et al. (2015) approach

To illustrate this effect of rounding corners, a slab-like solid with side lengths of 3, 4 and 5 cm and rounded corners with 1 cm curvature radius have been printed in a heavy plastic by means of a 3D printer (Fig. 10). This small block has been tilted in the 12 possible positions (4 corresponding to the slenderness ratio 5/3, 4 for 4/3 and 4 for 5/4). The average tilt angles obtained for every three groups of four tests, together with the theoretical value obtained applying the equations of Fig. 9 are compiled in Table 1, showing a very good agreement, confirming the validity of the round corner toppling stability computation approach.

Fig. 10

Printed plastic element with fixed dimensions and perfectly rounded 1 cm radius corners and tilt tests showing theoretical and average empirical results

Table 1 Results of toppling angle of a slab-like element with perfectly rounded corners

Remark that for the case of actual boulders the so-called curvature radius may vary along an edge and in different edges of the boulder, so the selection of a representative value of this parameter, tending to diminish in the middle of the edge, may slightly affect the stability computations (Alejano et al. 2015).

To further illustrate the influence of geometry on toppling stability, a number of increasingly complex geometrical elements are illustrated on the top row of Fig. 11 with the aim of analyzing their toppling behavior.

Fig. 11

Image of various 3D elements a, b, c and d to be subjected to tilt testing to illustrate the role of geometry on toppling. On the upper row 3D view of the elements resting on a horizontal base to be tilted. On the second row, initial top view with the projection including the cog. On the third row, top view of the surface after tilting and in the moment of toppling and on the last row, side view of platform and element when toppling

Figure 11a illustrates a simple rectangular prism with square base. If it is positioned on a flat surface, its center of gravity (cog) will project right on the center of its square base. If the surface where the prism stands is progressively tilted, at a particular tilt angle α, the projection of its cog will come out of its base (lower row of Fig. 11) so the prism will topple. The tilting angle α for toppling can be computed based on the formulation illustrated in Fig. 8.

To see the role of a more complex geometry, Fig. 11b shows a similar prism with a cube stuck to its upper back face. Note that when placed on a flat surface, its cog will not project on the center of the square base but somewhat backwards, due to the effect of the additional weight of the stuck cube. In this way, when tilting the plane on which this element stands, it will topple at a higher angle than the previous figure because the cog will project somewhat backwards. In this way the toppling angle in this case, β, will be steeper than the one observed for the first prismatic element (α).

Element c in Fig. 11 is like element b, but the added cube is now stacked on the upper left side face. Its cog will be at the same height as for element b (since it is the same element), but its projection on a horizontal plane will be moved leftwards in relation to element a (Fig. 11c, second row). When tilting the platform where element c rests, it will topple at a less steep angle than α, because its cog is located higher than in case “a”, so its projection will fall outside its base at a less steep angle γ, which will be also less steep than β.

Element d in Fig. 11 is a rectangular prism with square cross section that has cubes attached in the upper part of its lateral backward and leftward faces. In this case, the cog of the element will be even higher than for elements b and c and the cog projection on its base will be slightly moved backwards and a little bit leftwards in relation to the case of element a in Fig. 11. This will be clearly less stable than b (since the side-stuck cube moves the cog upwards), but more stable than c (since the back-stuck cube will increase its stability by moving the projection of its cog backwards).

One can then show that β > δ > α > γ. Based on this type of reasoning or equivalent computations, it is possible to develop an understanding of general toppling mechanics using the contact area and projection of the cog. This approach can be applied to better understand stability of granite boulders.

Note that when no external forces (e.g. water or seismic forces) are applied, the stability of these elements basically depends on the location of the vertical projection of the cog of the element on the contact base. When the projection of the cog is inside the contact base, the element is stable against toppling; when this projection falls out the contact base, the element will topple. External forces typically associated with seismic movements or water pressure can destabilize otherwise stable blocks.

Considering this, a factor of safety against toppling can be computed by relating the angle between the vertical line and the normal to the basal plane (denoted as α in Figs. 8, 9 and 12) and the angle formed by the normal to the basal plane and the line connecting the center of gravity and the rotation axis. Note that the rotation axis is the point where the projection of the cog will first come out of the contact area when tilting the basal plane (shown as β' in Figs. 9 and 12).

Fig. 12

On the left hand side grayscale photograph, the location of the cog and forces applied to the ‘Pena do Equilibrio’ boulder, whose stability was studied by the authors, is shown. On the right hand side, a force diagram and projection of the contact area of this boulder used to compute its stability against toppling are shown

This concept is illustrated for the ‘Pena do Equilibrio’ boulder studied by the authors (Pérez-Rey et al. 2019a) in the enlarged view of Fig. 7d and in Fig. 12. In both these figures, the projection of the cog normal to the basal plane (cog-p, in brown in the figures) falls out of the contact surface. This means that if the boulder were placed on a horizontal base, it would have toppled backwards. The vertical projection of the cog on the contact base (cog-v, in green color in Figs. 7c and 12) falls within this contact area, which explains the present stability of the boulder against toppling.

Moreover, the factor of safety of the boulder against toppling, denoted as FoS_toppling, can be computed as the relation of the tangents of the angles indicated above (shown as β' and α, respectively, in Figs. 9 and 12). This approach can be extended to the case where external forces such as water pressure, ice-jacking or a seismic force are applied to the boulder.

It should be noted, however, that such potential stability estimates depend on a very accurate description of the geometry of the boulder, including its contact area. Also, knowledge of the geometry of the basal plane (dip, dip direction and planarity) and the contact zone between the boulder and basal plane area and external forces acting is needed to assess stability. When the contact zone has a simple geometry (Figs. 8, 9 and 12), identifying the rotation axis is simple. However, for less regular contacts, as are usually found in nature, the situation is more complex, as illustrated in Sect. 4.4.

4.3 Positioning of the Rotation Axis for Toppling Estimates

Often, the location of the rotation axis enabling stability calculations of boulder toppling may not be known a priori. This is the case of the boulder illustrated on Figs. 7 and 12, or any other element that does not have an edge parallel to the strike of the basal plane.

To illustrate how to identify the rotation axis, a simple tilt test is performed with an element consisting of two pieces: a cylindrical rock specimen (with height twice its diameter) and a steel disk with the same diameter but much denser than the rock, which is positioned on the rock cylinder and moved a half radius leftwards as illustrated in Fig. 13a. In this way, the projection of the cog of the element moves towards the left and it does not project on the center of the rock cylinder base.

Fig. 13

Element formed by a rock cylinder and a steel disk positioned leftwards above subjected to a tilt test. a Side (left) and front views of the element and projection of its cog on its base and picture of the element; b side view of the element before starting the tilt test (left) and when toppling (right), and plan view illustrating the projection of its cog in both cases. A picture illustrates the observed toppling mechanism occurring in a direction forming β degrees with the dip direction

When this element is positioned on a tilting platform and increasingly tilted (Fig. 13b), the projection of the cog moves along the dip direction of the tilting table until it projects on the perimeter of the rock cylinder base. At this point, the whole setup will topple. This toppling will not occur in the dip direction, but in a direction forming an angle β with the dip direction as shown on Fig. 13b and demonstrated by Pérez-Rey et al (2019a).

This means that the toppling will occur in a direction marked by the point where the cog first projects outside the element base as shown in the lower left corner photograph in Fig. 13b. Accordingly, if the boulder illustrated on Fig. 12 topples, it will not do so in the dip direction, but in the direction marked by this intersecting point.

Additionally, the rotation axis necessary to compute stability against toppling will have to be identified based on this intersection. Pérez-Rey et al (2019a) illustrate how this is performed in greater detail.

4.4 Contact Zone Geometry

In all the reasoning above, we have assumed a fully planar contact surface between the element or boulder under scrutiny and the so-called basal plane. Even if this seems to be a reasonable assumption, it may not always hold true, which may positively or negatively affect the boulder stability. Specifically, a concave contact will improve stability against toppling, and a convex contact will be detrimental. However, the non-planarity of this contact is difficult to characterize in practice.

In theory, at least for specific tested geometries, the convex or concave contact geometries could be incorporated into stability computations against toppling. For illustrative purposes, the authors have checked this formulation for the elements shown in Fig. 14 and compare analytical results against actual tilt tests results, based on the force distribution and pictures of the two tested elements in Fig. 14.

Fig. 14

Force decomposition and picture of a cylindrical disk on a concave surface base and a disk with a lateral segment cut. Both these elements were tilt tested in the lab. Computation and results agree, showing increased stability for the concave case

The authors tentatively suggest that a convex contact can be associated with traditional rocking stones, also known as logan stones or logans. These are large stones that are so finely balanced that the application of just a small force causes them to rock. These rocks associated with popular traditions appear in the Atlantic European façade and elsewhere as pictured in Fig. 4b.

Not only the concavity of convexity of the base contact can affect stability, but also roughness may play a role. Indeed, typical roughness of rock joints could affect the critical value of the tilting angle, according to the wavelength and asperity amplitude, and particularly the asperity height in the potential rotation axis. Variations of a few degrees in the critical tilting angles and variations on the order of 10% of the FoS_toppling can be observed based on the roughness of the basal plane.

To illustrate this phenomenon from a theoretical point of view, a granitic composite specimen is considered with a regular rough base (Fig. 15). It has a height of 99.17 mm in the valleys and 93.64 mm in the peaks with a width of 46.36 mm. The roughness presents an inclination of 20° (equivalent JRC = 20) at a wavelength of 30.92 mm and an amplitude of 8.53 mm. When tilting this specimen in both possible directions, it topples at 20.9° when the toppling corner coincides with a valley, and at 23.6° when the rotation axis coincides with a peak. The corresponding theoretical estimates are 24.5º and 27.1°; once corrected considering a round corner with radius of 7.5% the width of the samples (a value selected to match the experimental values through back analysis), these values change to 21.1° and 23.5°, obviously quite close to those that were experimentally observed.

Fig. 15

Tilt tests on a composite rock sample with regular rough base. Representation and obtained experimental, theoretical and corrected theoretical angles for tilt tests in both directions

This simple study shows that the topology of the granite boulder base, if rough, could influence the stability condition of the boulder in relation to toppling. For the simple case introduced here, the variations introduced to the critical toppling angle are about 3º; this effect will be less significant for slenderer samples, and typically more significant when the contact zone size is small.

The boulders so far studied present rather smooth surfaces, so no significant roundness at the scale of the contact area was identified. However, it is suggested to investigate the effect of boulder roundness at the contact zone on the stability against toppling of granite boulders, particularly, for the case of slab-like granite blocks.

4.5 3D Printing of Boulders and Physical Modelling

Overturning of a constant density rigid body only depends on its geometry and its position on a basal plane. If the body is formed by materials with varying densities, it will also depend on the location of the cog. Therefore, if one can reproduce the geometry of a boulder with a different material, for instance any plastic as those used by 3D printers, it is possible to carry out physical models including tilt tests to analyze stability against toppling of the boulder. In the case that, as recommended, we have a detailed and accurate point cloud (3DPC) of the boulder available, it is now feasible to print a scaled 3D version of the boulder under consideration.

The authors have created a roughly 1:50 scaled plastic version of the ‘Pena do Equilibrio’ boulder illustrated in Fig. 7. Figure 16 shows the upper and lower plan views of the boulder, including the contact area and the boulder in the process of subjecting it to a tilt test. The polylactide (PLA) plastic replica of the boulder presented a plastic pattern inside, but we consider the assumption of uniform density to be reasonable. It is, therefore, an appropriate geometrical copy of the actual boulder for use in physical testing.

Fig. 16

3D printed 1:50 scaled reproduction of the ‘Pena do Equilibrio’ boulder. a Top view of the upper part; b top view of the lower part including the contact area with a piece of sandpaper to increase friction. c Tilt testing of the boulder reproduction on an expanded polyestyrene base, producing similar results to that derived from the theoretical calculations

3D printing of the boulder with concrete would make contact properties closer to reality but still different than those observed in reality. Since toppling behavior does only depend on the element shape, a plastic version is acceptable to study this instability mechanism. To avoid sliding before toppling, a sand paper element stuck in the corresponding contact area will avoid premature sliding due to poor friction of plastic contacts.

Tilt tests with this boulder, adequately positioned on an polyestirene surface and with sand paper in the contact area, provided tilt test toppling angles in the range of 30–31º, one degree (on average) less than the critical tilting angle estimated for the actual boulder based on analytical calculations.

As an alternative to the physical modeling demonstrated here, 3D point clouds may serve as a basis to create a grid able to simulate the behavior of the boulder by means of the discrete element method or any other suitable numerical modelling technique.

4.6 Contact Strength

The Barton and Bandis (1982) formulation has been widely used as a suitable approach to estimate the shear strength of rough unfilled rock joints. However, in the process of boulder formation associated with spheroidal weathering, the original joint typically erodes differently on its sides which tends to produce convex, and not planar, profiles. Accordingly, the final contact between the boulder and the basal plane behaves more like a so-called mismatched contact or joint (Fig. 17). In this case, the sides of the contact do not match, as each side presents a different roughness pattern (JRC) and shear behavior tends to depend more on the contact area than on the JRC.

Fig. 17

a Sketch of the evolution of a granitic rock mass where starting from slab-like blocks, ellipsoidal boulders eventually occur. b Detailed view of the small contact of a boulder with a basal plane and measurements taken (orientation, JRC and JCS). c Sketch of the ‘Pena do Equilibrio’ boulder and detail illustrating the mismatched nature of the contact

For illustrative purposes, Fig. 18 shows two natural rough joints (left hand side) and two block contacts (right hand side). Natural joints formed in a rock mass tend to present equal geometrical patterns in both sides, so they are matched joints and behave accordingly (Barton–Bandis); conversely, block contacts present different geometric patterns in both sides, so they are mismatched joints and behave as such.

Fig. 18

Natural rock joints, which are matched joints on the left hand side and block contacts, which are mismatched joints, on the right hand side. The contact geometry is sketched for each case in the center of the figure

Zhao (1997a, b) studied strength behavior of mismatched contacts and proposed a new version of Barton’s formula denoted the JRC-JMC shear strength model. This criterion accounts for an additional influence of the so-called joint matching coefficient (JMC), a parameter to be estimated based on the matching of the two joint sides:

$$\tau_{{{\text{JRC}}\; - \;{\text{JMC}}}} \; = \;\sigma_{n} \tan \left[ {\phi_{r} \; + \;{\text{JMC }} \cdot {\text{ JRC}}_{n} \log_{10} \frac{{{\text{JCS}}_{n} }}{{\sigma_{n} }}} \right]$$

(3)

Some studies have shown that JMC depends on the level of contact of the surfaces. Based on an estimation of potential contact of such a surface in case of granite blocks or granite boulders, previous experience developed by the authors with tilt tests carried out on large scale physical models (Alejano et al. 2012) and on the recommendation by Zhao (1997b), we tentatively suggest JMC = 0.3 as an initial estimate for this type of problem. The authors think that more detailed studies on the behavior of these mismatched joints will be necessary to better understand and bracket the shear strength behavior of these contacts.

4.7 External Forces

A detailed analysis of the external forces, including water pressures, ice-jacking and earthquakes potentially acting on the studied rock structures should be accounted for when analyzing the stability of boulders for different temporal horizons (Christianson et al. 1995; Alejano et al. 2010).

Most often, water pressure associated high rainfall periods can be considered, but seismic forces and ice-jacking are also typical external forces. When such forces are applied to boulders or rock elements at particular moments, they may cause the ultimate instability of the element under scrutiny (Wyllie and Mah 2004; Alejano et al. 2013).

Meteorological records informing on peak rainfall and lowest levels of temperatures and freezing periods can help to provide realistic assumptions regarding the magnitude and level of external forces associated to water on boulders. Additionally, seismic safety acts and earthquake damage mitigation policies could be of help to quantify the role of earthquakes on the stability of this type of structures.

Recent studies have put forward other potential external causes of ultimate instability (Vann et al. 2019). These include dynamic loads caused by construction equipment or seismic shaking, loss of downslope support, and human activity. All of these and other external influences should be considered in stability estimates.

4.8 Numerical Modeling

Numerical analysis can also be of help to carry out a realistic assessment on the stability of boulders with complex geometries. Some authors (Christianson et al. 1995; Shi et al. 1996; Purvance et al. 2009) have specifically addressed the stability of boulders in regard to seismic forces in regions particularly prone to earthquake activity.

The 3D geometry of boulders can be obtained in the form of a 3DPC. This 3DPC can be typically imported to 3D software to perform stability analysis. For the case of the ‘Pena do Equilibrio’ boulder, the 3DPC was imported to the finite-element software MIDAS GTS NX v.2019 (Midas 2019) to generate a 3D tetrahedral mesh with more than 20,000 elements (including boulder and basal rock where it stands). These elements were exported as individual blocks to the Discrete Element Method-based 3-Dimensional Distinct Element Code 3DEC v.5.20 (Itasca 2019) by means of an internal subroutine (Muñiz-Menéndez et al. 2020).

For these numerical studies, geomechanical parameters such as the normal and shear stiffness in the contact plane should be selected with care according to estimative techniques (Itasca 2019; Muñiz-Menéndez et al. 2020). Based on this approach, static, pseudo-dynamic and dynamic calculations have been performed. In the first and second cases, the obtained results coincide with analytical approaches. No analytical approach exists in the third case. Figure 19, illustrates the boulder toppling for the 3DEC model for a horizontal acceleration 0.105 g (Muñiz-Menéndez et al. 2020).

Fig. 19

Numerical result with code 3DEC of the toppling instability of the ‘Pena do Equilibrio’ boulder in a pseudo-dynamic analysis for the case of a large earthquake, illustrated by means of displacement vectors

The use of numerical approaches, provided they are applied in a rigorous manner, can be quite useful to carry out particular analyses on the stability of boulders and group of boulders (Christianson et al. 1995). This could include consideration of some dynamic and coupled processes that are difficult to address using standard approaches (Mendes et al. 2020; Lemos et al. 2011).

5 Conclusions

This paper is presented as an initial guideline for studies on granite boulder stability, or for other natural rock slope stability phenomena associated with irregular rock elements. Additionally, a number of issues still requiring further analysis are highlighted, with the aim of seeking improvement on our present capabilities to understand the actual instability behavior of granitic boulders.

A combination of different remote sensing techniques (UAS photogrammetry and TLS) has been successfully demonstrated with the aim of developing accurate geometric models of boulders. These techniques are critical in providing a detailed geometrical representation of the rock element whose stability is at stake.

The geometry and behavior of the contact zone of the boulder on the resting surface is another aspect that has shown to be important in the analysis of the stability of boulders against sliding or toppling. Sometimes it is not possible to fully constrain this geometry, so some assumptions regarding the geometry, roughness and strength of the contact are needed.

External forces associated with water, ice-jacking or earthquakes can be considered the final trigger of the instability of some boulders, so suggestions are provided on how to compute the effects of these forces on the boulder stability. Moreover, the use of numerical models is briefly described, which can be helpful to manage this type of analysis.

In summary, the authors have attempted to compile a number of aspects playing a relevant role on the stability of granitic boulders in this document, with the aim of aiding the rock mechanics community in better assessing and predicting the mechanical stability of these natural structures.