A Geomechanical Evaluation of Fault Reactivation Using Analytical Methods and Numerical Simulation

Abstract

One of the main problems related to mature oilfields is the decreased pore pressure due to hydrocarbon production. Therefore, to maintain the production rate of a reservoir, the lost pressure must be compensated. A very traditional method to increase the pressure is to inject natural gas into the reservoir. This technique is widely used in SW Iranian reservoirs because of the readily available supply of this type of gas. Reactivation of pre-existing faults and inducing new fractures into the reservoir and cap rock are some of the potential risks regarding gas injection. In this article, using data such as well logs, pore pressure estimates, and rock mechanical test results, the geomechanical simulation of the Asmari reservoir in the Gachsaran oilfield, SW Iran has been carried out. For this purpose, the current stress field was determined using elastic moduli of reservoir rocks and formation integrity test (FIT) results. Then, by applying analytical methods such as Mohr diagrams and slip tendency, the reactivation possibility of four faults in the field was analyzed, and the maximum sustainable pore pressures were estimated. In the next step, numerical simulations were conducted using ABAQUS software to investigate the injected gas flow path, leakage potential through the cap rock, possible fault reactivation due to gas injection, and shear stress build-up and plastic strain development in different parts of the reservoir. Results of Mohr diagrams and slip tendency showed that all the faults are stable in the current stress state, and fault F2 has the potential to sustain a maximum pore pressure of 55 MPa in the field. On the other hand, fault F3 has the proper conditions (i.e., strike and dip referring to σ_Hmax orientation) for reactivation. Results of numerical simulations suggested that an injection pressure of 30 MPa would not induce any new fracture or fault slip within 5 years of injection. In this period, the injected gas plume moves upward through the damage zone and reaches the shallower parts of the cap rock. It was also shown that by applying an injection pressure of 60 MPa, slip would occur on fault F4 after 10 days of injection.

1 Introduction

Gas injection is a common practice for maintaining reservoir pressure in mature oilfields. Hydrocarbon production will result in reduced pressure in the reservoir formation, and hydrocarbons will be replaced with other formation fluids (e.g., brines). Since the 1960s, it has been a regular practice to inject fluids into the reservoir to maintain the production rate (Verdon 2012).

Injection raises pore pressure in the target reservoir. This action reduces the effective stress, which causes the deformation of rocks. The amount of this geomechanical deformation is controlled by material properties of the formation and the magnitude of the pore pressure increase caused by the injection. The deformation may induce cap rock integrity issues. If pre-existing faults reactivate or new fractures develop, an escape path for injected gas will be introduced. Therefore, to ensure safe injection operations, it should be guaranteed that the deformation will not damage the cap rock. Zhang et al. (2006) demonstrated that gas leakage is due to hydraulic fracturing that is related to cap rock pressure increase or stress change in the system. As long as the reservoir pressure does not exceed the initial pressure of the formation, the risk of leakage through pre-existing fractures is low. Lithology and the structural setting of the reservoir and overburden are two significant factors that affect the gas migration through the cap rock.

Pre-existing faults and fractures in a reservoir may provide a conduit for leakage through fault reactivation. Therefore, investigations on the maximum sustainable injection pressure on sealing faults that act as structural traps are an integral part of geomechanical studies to ensure safe injection (Streit and Hillis 2004; Richey 2013). The initial sealing capacity of cap rocks may vanish by their reactivation (Wiprut and Zoback 2002; Gartrell et al. 2006; Langhi et al. 2010), which is induced by fluid injection into the reservoirs (Nicholson and Wesson 1990; Guha 2000; Cornet 2012; Evans et al. 2012; Keranen et al. 2013; McGarr et al. 2015).

Faults may assist the fluid flow at depth, based on the hypothesis of critically stressed faults. This hypothesis states that favorably oriented and critically stressed faults and fractures that are prone to frictional failure should control both fluid flow and reactivation potential (Barton et al. 1995; Sibson 1996; Ito and Zoback 2000; Ferrill et al. 2019). Increased pore pressure caused by injection may lead to shear slip failure of existing fractures when the maximum shear stress exceeds the shear strength. The resulting increase in fault roughness creates a potential leakage path, and thereby permeability enhancement. When an internally connected network of open fractures forms, it can act as a migration conduit for gas-rich fluids along the rough surface of faults. Therefore, one of the most critical parts of any investigation for a potential gas injection site is analyzing the risk of fault reactivation. In any injection project, identifying and characterizing faults is crucial, because their stability can be dramatically affected. Faults generally cannot be avoided in compartmentalized reservoirs (Castelletto et al. 2013). Reservoir compartmentalization is the segregation of a petroleum reservoir into a number of individual fluid or pressure compartments by bounding features (e.g., impermeable faults) which prevent hydrocarbon crossflow (Caine et al. 1996). Thus, they can be a restricting agent (by creating over-pressured segments caused by gas injection) that can reduce the safe injection operation (Fig. 1). For example, the excessive overpressure induced by low permeability faults in Snøvit, Norway, halted CO₂ injection operations after a few months (Hansen et al. 2013). Therefore, to minimize the risk of fault reactivation, injection wells should be located as far as possible from faults and thus avoid limitations on the injection rate (Vilarrasa et al. 2016).

Fig. 1

a Schematic illustration of pore pressure contours after injection, and b pressure-depth plot showing the excessive overpressures caused by a low permeable fault (Meng et al. 2016)

It is worth noting that even if fault reactivation does not lead to gas migration to the ground surface, such activities may reduce the sealing ability of nearby layers, which potentially lead to groundwater pollution.

We report in this paper the results of geomechanical modeling of the Asmari reservoir in the Gachsaran oilfield applied to an investigation of the potential for fault slippage and the creation of new fractures. The results of such studies can be used for locating safe injection points, identifying potential damage zones in the cap rock, and can be applied to the mitigation of other hazards related to gas injection with further geomechanical studies.

2 Geological Setting

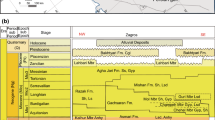
The Gachsaran oilfield is an asymmetric anticline structure located in Dezful-Embayment in the vicinity of Ahvaz city (Fig. 2a). This field is situated in the Iranian section of Zagros fold-thrust belt, a belt that stretches from Anatolian fault in eastern Turkey to the Minab fault near the Makran region in the southeast of Iran. This fold-thrust belt is a part of an active foreland basin complex, which was initiated in the Late Tertiary time by the collision between Iranian and Arabian Plates (Stocklin 1974; Berberian and King 1981). This field is an elongated doubly-plunging anticlinal structure with dimensions of 65 km length and 4–8 km width and is considered one of the most significant productive oilfields in the Oligocene–Lower Miocene carbonate horizons (Shaban et al. 2011). The Cretaceous to Early Miocene petroleum system of the field includes two carbonate reservoirs: Asmari (Early Miocene) and Bangestan (including the Cenomanian–Turonian aged Sarvak formation and the Santonian aged Ilam formation), which are sealed by the evaporitic Gachsaran (Miocene) and the marly Gurpi (Late Cretaceous) formations, respectively (Alizadeh et al. 2018).

Fig. 2

a Location of Gachsaran oil filed in Zagros fold-thrust belt (Shaban et al. 2011), b stratigraphic column of the field (Geological Society of Iran, GSI 2018)

The Asmari reservoir is one of the most well-known reservoirs in the world and produces almost 85% of total Iranian crude oil, which is characterized by its 30° API gravity and low sulfur content (Rezaie and Nogole-Sadat 2004). This reservoir was first discovered by the Anglo-Persian Oil Company in 1931 and had a peak production of 180 thousand barrels per day in 1976. The Asmari formation consists of cream to gray limestone, dolomitic limestone, and dolomite, and its thickness in the type section is 314 m (Darvishzadeh 2009). The cap rock of this oilfield is a Miocene aged formation called Gachsaran formation, which consists of seven members. This formation is composed of anhydrite, limestone, and bituminous shale, and its oldest and lowermost member, which is the cap rock of the Asmari reservoir, is referred to as Member 1 (James and Wynd 1965). The average thickness of Member 1 in this field is about 40 m (Darvishzadeh 2009). The lower contact of Asmari formation is the Pabdeh formation, which is the reservoir source rock with an age of Paleocene to Eocene. Figure 2b shows the Cenozoic era of the stratigraphic column in the Zagros fold-thrust belt.

In this study, we have investigated the stability of four faults of F1, F2, F3, and F4 located in the western sector of the field. Figure 3 shows the underground contour map of the faults and their cross section in the study area. All the faults are normal, and since there was no information about their cohesion (c) and friction coefficient (µ_s), these parameters were assumed to be zero and 0.6, respectively. Rock mechanics tests on a wide range of rocks have demonstrated that the coefficient of friction ranges between 0.6 and 1.0 (Byerlee 1978). A µ_s = 0.6 is a lower boundary value and a conservative assumption used by many researchers who have investigated fault stability (e.g., Rutqvist et al. 2007; Zoback 2007; Konstantinovskaya et al. 2012; Figueiredo et al. 2015). Zero cohesion is a reasonable assumption given the fault has already ruptured. The structural characteristics of the faults are summarized in Table 1.

Fig. 3

Underground contour map and the cross section of the study area in the Western part of the Gachsaran oilfield

Table 1 Structural properties of faults

3 Theory and Background

3.1 Introduction of Methodology

Generally, the first step in any geomechanical study is to identify the stress regime and the relationship among the three principal stresses. First, the static elastic moduli of the rocks were estimated using well logs and data obtained from core samples. The magnitude of the vertical stress was calculated using the overburden weight. Since the directly measured values of the two principal horizontal stresses were not available, these stresses were then estimated using elastic moduli, and the accuracy of the results was calibrated using data obtained from a formation integrity test (FIT) conducted in the field. An image log interpretation was used to determine the orientation of the principal horizontal stresses by specifying the orientation of drilling-induced tensile fractures. Utilizing the derived stress tensor in MohrPlotter software, we investigated the stability of the faults through Mohr diagram analysis of both the current stress state and the critical state of stress caused by the gas injection. Slip tendency, an analytical parameter was also calculated, and the results were compared with the Mohr diagrams. The maximum sustainable pore pressure was calculated for each one of the faults, as the final output of these two methods. Numerical simulations were then conducted using ABAQUS software, a finite element analysis tool that is widely used for geomechanical studies. A coupled pore fluid diffusion/stress analysis was performed to model the single-phase, fully saturated fluid flow through the porous media. In the numerical simulations, gas was injected for 5 years, and the possibility of plastic damage and fault slip was assessed.

3.2 Determining the In-Situ Stress Regime

Knowing the current state of stress is the key factor for building a comprehensive geomechanical model (Zoback 2007). For applying the stress concept in the Earth’s crust, it is useful to consider the magnitudes of the three principal stresses (σ₁, σ₂, and σ₃) in terms of vertical (σ_V), and horizontal (σ_Hmax and σ_hmin) stresses as first proposed by Anderson (1951). In this manner, an area can be characterized as being in a normal, strike-slip, or reverse faulting stress regime. The vertical stress (σ_V) is equal to the maximum principal stress (σ₁) in a normal faulting stress regime, the intermediate principal stress (σ₂) in strike-slip stress regime, and the minimum principal stress (σ₃) in reverse faulting stress regime. The magnitude of the vertical stress can be calculated by the integration of the densities of overburden rocks as follows:

$$\sigma_{{\text{V}}} = \mathop \int \limits_{0}^{z} \rho \left( z \right)g{\text{d}}z \approx \overline{\rho }gz.$$

(1)

In this equation, ρ(z) is the rock density as a function of depth, g is the gravitational acceleration constant, and ρ̄ is mean overburden density (Jaeger and Cook 1971).

Estimating the magnitudes of horizontal stresses is a major challenge in geomechanical modeling (Zang and Stephansson 2010). A common practice for determining the magnitude of the minimum horizontal stress is to conduct a leak-off test (LOT) or an extended leak-off test (XLOT). Limited test or the formation integrity test (LT or FIT) is another field test during which the leak-off point (LOP) (the pressure required to create a hydraulic fracture) is not reached. Formation integrity tests simply indicate a maximum pressure achieved during pumping. Since this pressure is insufficient to create a fracture or growing an initiated fracture away from the wellbore, the recorded pressure does not exceed the least principal stress (Zoback et al. 2003). The FIT does not provide any information about the magnitude of the least principal stress (Konstantinovskaya et al. 2012); however, it can be used as an indicator of the lower bound of σ_hmin, because the pressure of a FIT will always be less than the least principal stress (Zoback et al. 2003). Only one FIT is carried out in the field and is used to calibrate the log-derived magnitudes of the minimum and maximum horizontal stresses calculated by the poroelastic horizontal strain model of Blanton and Olson (1999), as follows:

$$\sigma_{{{\text{hmin}}}} = \frac{{\nu_{{\text{s}}} }}{{1 - \nu_{{\text{s}}} }}\sigma_{{\text{V}}} + \frac{{1 - 2\nu_{{\text{s}}} }}{{1 - \nu_{{\text{s}}} }}P_{{\text{P}}} \left( \alpha \right) + \frac{{E_{{\text{s}}} }}{{1 - \nu_{{\text{s}}}^{2} }}\varepsilon_{x} + \frac{{\nu_{{\text{s}}} E_{{\text{s}}} }}{{1 - \nu_{{\text{s}}}^{2} }}\varepsilon_{y} ,$$

(2)

$$\sigma_{{{\text{Hmax}}}} = \frac{{\nu_{{\text{s}}} }}{{1 - \nu_{{\text{s}}} }}\sigma_{V} + \frac{{1 - 2\nu_{{\text{s}}} }}{{1 - \nu_{{\text{s}}} }}P_{{\text{P}}} \left( \alpha \right) + \frac{{E_{{\text{s}}} }}{{1 - \nu_{{\text{s}}}^{2} }}\varepsilon_{y} + \frac{{\nu_{{\text{s}}} E_{{\text{s}}} }}{{1 - \nu_{{\text{s}}}^{2} }}\varepsilon_{x,}$$

(3)

where σ_V is the vertical stress, P_P is pore pressure (in MPa), α is the Biot’s coefficient (which was considered 1 to account for the brittle failure of rocks), E_s is the static Young’s modulus (in GPa), and ν_s is the static Poisson’s ratio. ε_x and ε_y are the magnitudes of the rock deformation in the x and y planes, which can be calculated as a function of the overburden stress as Eqs. 4 and 5:

$$\varepsilon_{x} = \frac{{\sigma_{{\text{V}}} \times \nu_{{\text{s}}} }}{{E_{{\text{s}}} }} \times \left( {\frac{1}{{1 - \nu_{{\text{s}}} }} - 1} \right),$$

(4)

$$\varepsilon_{y} = \frac{{\sigma_{{\text{V}}} \times \nu_{{\text{s}}} }}{{E_{{\text{s}}} }} \times \left( {1 - \frac{{\nu_{{\text{s}}}^{2} }}{{1 - \nu_{{\text{s}}} }}} \right).$$

(5)

The next step in determining the in-situ stress regime in an area is finding the orientation of horizontal stresses. Image logs provide a very useful tool for engineers to observe borehole breakouts and drilling-induced tensile fractures. The borehole breakouts and the drilling-induced tensile fractures are caused by wellbore hoop stress and radial stress, respectively (Zoback 2007). In vertical wells, the breakouts form at the azimuth of the minimum horizontal compressive stress, and drilling-induced tensile fractures form in the wall of the borehole at the azimuth of the maximum horizontal compressive stress when the circumferential stress acting around the well is locally in tension (Fig. 4).

Fig. 4

Schematic illustration showing the location of the borehole breakouts and drilling-induced tensile fractures in a vertical well (Alizadeh et al. 2015). Borehole breakouts form in the direction of σ_hmin and drilling-induced tensile fractures form in the direction of σ_Hmax

3.3 Estimating Pore Pressure and Permeability

Direct methods of measuring pore pressure include drill stem test (DST) and repeat formation test (RFT) (Rezaee 2014). However, these methods are only utilized in a limited number of wells in the study field. Therefore, using more effective and economical methods is essential for field-wide geomechanical reservoir simulations. In this paper, the pore pressure was estimated by the modified Eaton (1975) approach derived by Azadpour et al. (2015) as follows:

$$P_{{{\text{pg}}}} = S_{{\text{g}}} - \left( {S_{{\text{g}}} - P_{{{\text{ng}}}} } \right)\left( {\frac{{50 + \left( {185 - 50} \right){\text{e}}^{ - 0.00137z} }}{{{\Delta }t}}} \right)^{x}.$$

(6)

In this equation P_pg is the formation pressure gradient, P_ng is the hydrostatic pore pressure gradient, which equals 1.049 × 10^–2 MPa/m (0.464 psi/ft) for Iran, Δt is the measured sonic transit time by well logging, z is depth, and x is the exponent constant, which was determined as 0.5 by Azadpour et al. (2015) for gas fields in southern Iran. The overburden pressure gradient S_g can be calculated by the following equation:

$$S_{{\text{g}}} = 0.433 \times \rho_{{\text{b}}} ,$$

(7)

where the ρ_b is the bulk density. This pore pressure calculation was calibrated against repeat formation tests available from wells in this reservoir.

Permeability is one of the most important properties of a reservoir’s rocks, since it controls the rate of hydrocarbon recovery. The value of this property ranges considerably from 0.01 millidarcy (mD) to over 1 darcy. A permeability of 0.1 mD is generally considered the minimum for oil production. The permeability of reservoirs with a high production rate is in the Darcy range (Lucia 2007).

The best way to measure permeability is through direct test on core samples. In this study, a few core samples were only used for destructive rock mechanical tests, and determining porosity (n) and hydraulic conductivity (k). Instead of using porosity–permeability relationships, we used global permeability transform to avoid the averaging nature of these cross plots. Given the lack of core samples, and that permeability cannot be derived from well logs, it was estimated using indirect methods. It is common practice to estimate permeability using porosity–permeability transforms developed from core data. However, porosity–permeability cross plots for carbonate reservoirs too often average out the robust permeability variations that are characteristic of carbonate reservoirs. According to Lucia (2007), the more accurate method is to use the global permeability transform using petrophysical class or rock fabric number (rfn) and interparticle porosity (the pores that are connected). Rock fabric number is related to interparticle porosity and geologic descriptions of particle size and sorting called rock fabrics. rfn ranges from 0.5 to 4 and is defined by class-average and class-boundary porosity–permeability transforms (Jennings and Lucia 2001). The value of the rock fabric number depends on porosity and water saturation, as higher water saturation for a given porosity gives higher rfn, and lower permeability for a given porosity yields higher rfn (Crain 2017). This is a new method, designed especially for estimating the permeability in carbonates with different shapes of pores. In this approach the permeability can be calculated as follows:

$$\log \left( K \right) = \left( {a - b\log \left( {{\text{rfn}}} \right)} \right) + \left( {c - d\log \left( {{\text{rfn}}} \right)} \right)\log \left( {\phi_{{{\text{ip}}}} } \right).$$

(8)

In this equation, K is permeability (mD), rfn is the rock fabric number, Φ_ip is interparticle porosity, and a, b, c, and d are constant values (a = 9.7982, b = 12.0838, c = 8.6711, d = 8.2965). In this study, we used effective porosity log (PHIE) as Φ_ip. Rock fabric number can be calculated from spectral gamma ray and porosity logs using the following equation:

$$\log \left( {{\text{rfn}}} \right) = \left[ {A + B\log \left( \phi \right) + \lg \left( {S_{{{\text{wi}}}} } \right)} \right]/\left[ {C + D\log \left( \phi \right)} \right],$$

(9)

where rfn is the rock-fabric number ranging from 0.5 to 4 (petrophysical class may also be used), S_wi is the initial water saturation above the transition zone (The zone between water production and oil production), Φ is porosity, and A, B, C, and D are constants (A = 3.1107, B = 1.8834, C = 3.0634, and D = 1.4045). In this equation, total porosity log (PHIT) is used as Φ. S_wi is the saturation of an undisturbed reservoir with no prior production from any earlier well (Crain 2017). This parameter was available from an exploration well in the field.

The main advantage of this method is that the interparticle porosity (and not total porosity) is related to permeability (Lucia 2007).

3.4 Mechanical Properties

Evaluating the in-situ mechanical behavior of rocks requires appropriate input data such as stress state and pore pressure at the desired depth, elastic moduli, and mechanical parameters. The main data for this study come from core samples and the data recorded in the field (such as well logs, seismic data, and various well tests). In this research, we used the relationships derived by the NISOC for converting the dynamic Young’s modulus (E_d) and Poisson’s ratio (ν_d) to their static equivalents (E_s and ν_s), and calculating uniaxial compressive strength (UCS) and tensile strength (σ_t), as follows:

$$E_{{\text{s}}} = 0.7 \times E_{{\text{d}}} ,$$

(10)

$$\nu_{{\text{s}}} = \nu_{{\text{d}}} ,$$

(11)

$${\text{UCS}} = 2.27E_{{\text{s}}} + 4.7,$$

(12)

$$\sigma_{{\text{t}}} = 0.08 \times {\text{UCS}}\quad {\text{Limestone,}}$$

(13)

$$\sigma_{{\text{t}}} = 0.11 \times {\text{UCS}}\quad {\text{Anhydrite,}}$$

$$\sigma_{{\text{t}}} = 0.1 \times {\text{UCS}}\quad {\text{Shale}}.$$

The above parameters were obtained by testing core samples drilled out from the reservoir and establishing statistical correlations between them. Cohesion (c) and friction angle (φ) are two mechanical properties that describe the intrinsic properties of rocks. These parameters may be determined by performing a triaxial test on the core specimens. Moreover, there are empirical and theoretical relationships that can be used when there is no access to the triaxial test. For predicting the friction angle and cohesion, Plumb’s (1994) and Jaeger et al. (2009) equations were used, respectively:

$$\varphi = 26.5 - 37.4\left( {1 - {\text{NPHI}} - V_{{{\text{sh}}}} } \right) + 62.1(1 - {\text{NPHI}} - V_{{{\text{sh}}}} )^{2} ,$$

(14)

$$c = \frac{{{\text{UCS}}}}{2\tan \theta },$$

(15)

where NPHI is neutron porosity, and V_sh is shale volume. V_sh and θ can be calculated using Asquith et al. (2004) and Jaeger et al. (2009) equations, respectively:

$${\text{V}}_{{{\text{sh}}}} = \frac{{\left( {{\text{GR}}_{\log } - {\text{GR}}_{\min } } \right)}}{{\left( {{\text{GR}}_{\max } - {\text{GR}}_{\min } } \right)}},$$

(16)

$$\theta = 45 + \frac{\varphi }{2},$$

(17)

where GR is gamma ray. Equation 14 is a porosity based equation that predicts φ to decrease with increasing porosity and GR. Since GR is a measure of the amount of shale volume contained in a formation, this equation indicates that a rock with higher shale content has a lower internal friction angle (Chang et al. 2006). The cohesion equation (Eq. 15) is derived from UCS relationship in direct shear tests. In this equation, cohesion is a function of UCS and θ, which the latter one depends on the friction angle.

3.5 Analytical Methods of Fault Stability Evaluation

The possibility of fault reactivation to provide a flow path in faulted areas first was introduced by Sibson (1990), and the process is generally controlled by the Coulomb failure criterion. The three main approaches for evaluating this phenomenon are: analytical, semi-analytical, and numerical (Nacht et al. 2010). Mohr diagrams, slip tendency, and dilation tendency are some of the most common and widely used analytical methods.

One of the best ways to show the shear and normal stresses acting on arbitrarily oriented faults in three dimensions is the Mohr diagram (Zoback 2007). These diagrams are also applied to explain the mechanism of faulting and reactivation of pre-existing faults (Yin and Ranalli 1992; Jolly and Sanderson 1997; McKeagney et al. 2004; Streit and Hillis 2004; Xu et al. 2010).

The values of the three principal stresses σ₁, σ₂, and σ₃ are used to construct three Mohr circles. The largest Mohr circle is defined by the difference between σ₁ and σ₃, and the two smaller Mohr circles are defined by the differences between σ₁ and σ₂, and σ₂ and σ₃, respectively (Zoback 2007). Fault planes are represented in Mohr diagrams by their normal stress, σ_n, and shear stress, τ. These stresses are shown in Fig. 5 and can be readily calculated using the following equations:

$$\sigma_{{\text{n}}} = \sigma_{{\text{V}}} \left( {\cos \beta_{1} } \right)^{2} + \sigma_{{\text{H}}} \left( {\cos \beta_{2} } \right)^{2} + \sigma_{{\text{h}}} \left( {\cos \beta_{3} } \right)^{2} ,$$

(18)

$$\tau = \sqrt {\sigma_{{\text{V}}}^{2} \left( {\cos \beta_{1} } \right)^{2} + \sigma_{{\text{H}}}^{2} \left( {\cos \beta_{2} } \right)^{2} + \sigma_{{\text{h}}}^{2} \left( {\cos \beta_{3} } \right)^{2} - \sigma_{{\text{n}}}^{2} .}$$

(19)

Fig. 5

a Resolved normal (σ_n) and shear (τ) stress on plane A. b Orientation of the potential slip plane A in terms of three angles β1, β2, and β3 from the coordinate axes of the principal stresses (Schmitt 2014)

As shown in Fig. 5, β₁, β₂, and β₃ are the angles between the surface normal (n) and the axes of the greatest, intermediate, and least principal stresses, respectively. In this study, the open-source MohrPlotter software was used to calculate these angles and the stresses on the fault planes.

To estimate the maximum sustainable pore pressure on a fault, the fluid pressure increase required to induce failure on faults must be calculated. In a Mohr diagram, this pore pressure increase is the difference between the effective normal stress acting on a fault segment and the effective normal stress required to cause failure in this segment (Streit and Hillis 2004). For the case of a fault plane with cohesion (i.e., c ≠ 0), the critical pore pressure is measured as the difference between the initial and final states when the Mohr circle reaches the Griffith-Coulomb failure envelope. However, in most cases, the cohesion of the faults is assumed to be zero (i.e., c = 0); therefore, the Coulomb failure envelope is applied (Fig. 6).

Fig. 6

Maximum sustainable pore pressure for two states of faults with and without cohesion. ΔP_A–A1 and ΔP_A–A2 represent the maximum sustainable fluid pressures of incohesive and cohesive faults, respectively (Meng et al. 2016)

Simply reaching the failure envelope does not mean that the failure will occur, and the planes of weakness must lie within a range of specific orientations. To find these sets of orientations, failure envelopes for both intact rock (c ≠ 0) and pre-existing fractures (c = 0) must be defined (Fig. 6). In the rectangular core sample shown in Fig. 7, only the possible planes of weakness with orientations within the pink region will be reactivated; therefore, the reactivation angle (the angle between the σ₁ axis and the fault plane) should be calculated.

Fig. 7

Mohr diagram plotted for pre-existing fractures (red envelope), and new fractures (black envelope). Planes which their normal and shear stresses fall within the pink region will be reactivated (Allmendinger 2017) (color figure online)

To better explain the possible reactivation angles, we consider a Mohr diagram (Fig. 8), in which the red lines represent failure envelopes for a specific plane in the rock (e.g., pre-existing faults). In this case, some portions of the Mohr circle are above the failure envelope, because the orientation of the plane relative to the principal stresses is critical (critically stressed and favorably oriented faults). Consider, for example, the plane represented by the green line in Fig. 8. The associated shear and normal stress tractions associated with this plane (on the circle) are well below the failure envelope and so it is stable. If the plane was instead oriented in the range between the two orange lines (labeled as the unstable range) the shear stress would be above the failure envelope and slip should have occurred (Muvdi and McNabb 1991). In reactivation angle analysis we try to identify the unstable ranges as angles with respect to principal stresses orientations.

Fig. 8

Mohr circle showing the concept of reactivation angles as stable and unstable ranges for critically stressed and favorably oriented faults

Fault slip occurs when the maximum shear stress acting on the fault plane exceeds the shear strength of the fault plane. Slip tendency is a method that allows quick assessment of stress states and related potential fault activity (Morris et al. 1996). Using two-dimensional stress equations given by Jaeger and Cook (1969), the values of shear and normal stresses on the fault plane can be calculated as follows:

$$\sigma_{{\text{n}}} = \frac{{\left( {\sigma_{1} + \sigma_{3} } \right)}}{2} - \frac{{\left( {\sigma_{1} - \sigma_{3} } \right)}}{2}\cos 2\theta ,$$

(20)

$$\tau = \frac{{\left( {\sigma_{1} - \sigma_{3} } \right)}}{2}\sin 2\theta ,$$

(21)

where θ is the angle between the normal to the fracture plane of and σ₁.

The ratio of shear to normal stress acting on the surface is the slip tendency (T_S) and is defined as:

$$T_{{\text{s}}} = {\raise0.7ex\hbox{$\tau $} \!\mathord{\left/ {\vphantom {\tau {\sigma_{{\text{n}}}^{\prime } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sigma_{{\text{n}}}^{\prime } }$}}.$$

(22)

In this equation, τ is the shear stress, and σ′_n is the effective normal stress (σ_n − P_P). According to Rutqvist et al. (2007), for a cohesionless fault, the slip will occur when the following condition is met:

$${\raise0.7ex\hbox{$\tau $} \!\mathord{\left/ {\vphantom {\tau {\sigma_{n}^{\prime } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sigma_{n}^{\prime } }$}} \ge \mu_{{\text{s}}} ,$$

(23)

where µ_s is the static frictional coefficient.

In Mohr diagrams, the critical pore pressure is the pore pressure at which the effective normal stress decreases such that the point representing the fault plane reaches the failure envelope (Fig. 6). According to Eq. 23, the potential for fault slip can be expressed in terms of the fluid pressure required to induce slip. The critical pore pressure (P_C), can be calculated from effective stress law of Terzaghi (1923) (Eq. 24) and Coulomb failure criterion (Jaeger et al. 2009) (Eq. 25), as follows (Eq. 26):

$$\sigma_{{\text{n}}}^{\prime } = \sigma_{{\text{n}}} - P_{{\text{P}}} ,$$

(24)

$$\tau = c + \mu_{{\text{s}}} \sigma_{{\text{n}}}^{\prime } ,$$

(25)

$$P_{{\text{C}}} = \sigma_{{\text{n}}} - \frac{\tau }{{\mu_{{\text{s}}} }},$$

(26)

where P_P is pore pressure. By considering the Coulomb constitutive model for the fault, the shear slip potential can be expressed in terms of effective principal stresses as follows:

$$\sigma_{1}^{\prime } = c + q\sigma_{3}^{\prime } ,$$

(27)

where c is cohesion, σ′₁ is the maximum effective principal stress, σ′₃ is the minimum effective principal stress, and q is the slope of the line σ′₁ versus σ′₃, which is related to µ_s according to the following equation:

$$q = \left[ {\left( {\mu_{{\text{s}}}^{2} + 1} \right)^{\frac{1}{2}} + \mu_{{\text{s}}} } \right]^{2} .$$

(28)

By substituting a zero cohesion into Eq. 27 and a static coefficient of friction of 0.6 into Eq. 28, the following equation is obtained (Rutqvist et al. 2007):

$$\sigma_{1}^{\prime } = 3\sigma_{3.}^{\prime } .$$

(29)

Equation 29 indicates that the shear slip will be induced whenever the maximum principal effective stress exceeds three times the minimum compressive effective stress. Therefore, the critical pore pressure (P_C) required to induce slip on an arbitrarily oriented fault can be calculated as follows (Rutqvist et al. 2007; Figueiredo et al. 2015):

$$P_{{\text{C}}} = \frac{{3\sigma_{3} - \sigma_{1} }}{2}.$$

(30)

Taghipour et al. (2019) demonstrated that this simple 2D analysis could estimate the critical pore pressure with acceptable accuracy, and its results were consistent with the results of Mohr diagrams. Therefore, this method can be used as a substitute when there is no access to image logs for constructing a Mohr diagram.

Dilation tendency analysis, first introduced by Ferrill et al. (1999), investigates the ability of a fault to act as a fluid conduit by reactivation in the current stress field or intact rock to undergo tensile failure into the cap rock (hydraulic fracturing) (Kulikowski et al. 2016). In other words, this parameter highlights the faults or fault segments within a reservoir that are critically stressed, and therefore, likely to transmit fluids (Siler et al. 2016; Ferrill et al. 2019). This analysis is most useful in reservoirs that are fault sealing or have faults that cut both the reservoir and overlying cap rock, since it predicts the chance of tertiary migration of hydrocarbons through a permeable conduit away from the reservoir (Barton et al, 1995; Ferrill and Morris 2003; Jolie et al. 2015). The dilation of faults and fractures is mainly controlled by the resolved normal stress, which is a function of the lithostatic and tectonic stresses, and fluid pressure. Based on Eq. 18, the magnitude of normal stress can be computed for surfaces of all orientations within a known or suspected stress field. The normal stress can be normalized by the differential stress to give the dilation tendency (Moeck et al. 2009). Dilation tendency is calculated using the following equation:

$$T_{{\text{d}}} = \frac{{\sigma_{1}^{\prime } - \sigma_{n}^{\prime } }}{{\sigma_{1}^{\prime } - \sigma_{3}^{\prime } }},$$

(31)

where T_d is dilation tendency, σ′₁ is the maximum effective principal stress, σ′₃ is the minimum effective principal stress, and σ′_n is the effective normal stress acting on the fault plane. This relationship shows that as σ′_n approaches σ′₃, the tendency of the fault plane to dilate increases and remains open to potential fluid flow. The fault will have a higher dilation tendency as T_d approaches one. Dilation and fluid transmission ability of a fault or fracture is directly related to its aperture, which in turn is a function of the normal stress acting upon it. Faults or fractures with high normal stress are more likely to be closed than those with lower normal stress acting to close them (Ferrill et al. 2019). As a result, permeability perpendicular to the minimum principal stress direction (i.e., the σ₁–σ₂ plane) is relatively enhanced, because lower resolved normal stress results in less fracture aperture reduction (e.g., Carlsson and Olsson 1979). Dilation tendency is strongly controlled by resolved normal stress and can highlight which fracture orientations are most likely to dilate and hence transmit fluids. Higher dilation tendency values equate to a greater likelihood of fracturing causing dilation and hence a greater ability to allow fluid transmission (Grosser 2012). In general, the planes perpendicular to the minimum principal stress show the highest dilation tendency in a given stress field (Jolie et al. 2015). A schematic illustration of the dilation tendency in the Mohr diagram is shown in Fig. 9.

Fig. 9

Definition of dilation tendency (Mildren et al. 2005). T_d values range from 1, a fault plane that is ideally oriented to slip or dilate under current stress field to zero, a fault plane with no potential to slip or dilate

3.6 Numerical Approach of Fault Stability Evaluation

Although analytical methods are acceptable for a preliminary evaluation of fault stability, some of the simplifications characteristic of these methods cannot adequately represent the specifications of the reservoir. As observed in depleted reservoirs and validated by numerical modeling, the in-situ stress field does not remain constant during injection, but rather evolves in time and space, controlled by the evolutions of fluid pressure and temperature, and site-specific reservoir geometry (Hillis 2001; Rutqvist and Tsang 2005; Hawkes et al. 2005; Rutqvist et al. 2007).

In this study, numerical simulations were carried out using ABAQUS software, a finite element analysis code, which is widely used for geomechanical studies. The solver used in this study is Abaqus/Standard that is quite suitable for a wide range of geomechanical problems with coupled pore fluid-stress analysis. The main goals of these simulations include: (1) investigating the fluid flow in the reservoir-cap rock system, (2) the possibility of gas leakage through the cap rock, (3) possible fault reactivation, and (4) the propagation of shear stress and plastic strain in various parts of the reservoir.

The geometry of this 2D model is rectangular with dimensions of 7000 m length and 600 m width, which represents the layers of Gachsaran cap rock, Asmari reservoir, Pabdeh source rock, and the four faults F1–F4 within the depth range of 2000–2600 m (Fig. 10). The thickness of the reservoir was considered constant (nearly 300 m). To simulate fault throw (i.e., the amount of vertical displacement of rocks), the thickness of the cap rock was considered variable (50–200 m). The magnitude of the fault throw for each fault was measured in faulted wells in the field. An equivalent overburden is included in the model to the reservoir depth of 2000 m. The hydraulic boundary conditions of the model include a constant hydrostatic pressure at the outer boundary and no flow at the other boundaries. For the mechanical boundary conditions, a constant overburden pressure is applied on the upper boundary and displacement perpendicular to the other boundaries is fixed. The model mesh consists of quadratic pore fluid-stress elements with reduced integration (CPE8RP). A friction coefficient of µ = 0.6 is assumed for the faults, and the faults are simulated as fault zones (with a fault core in the middle of two adjacent damage zones). To simulate injection, constant pore pressure of 30 MPa was applied for 5 years through a vertical well located in the westernmost part of the model. The distance between the injection point and the nearest fault (F4) is about 560 m. The Coulomb failure criterion is used to indicate the onset of fault shear slip. The calculated horizontal/vertical stress ratios of 0.74 in the x–y plane, and 0.85 normal to this plane were considered. The hydraulic and mechanical properties of different parts of the model are summarized in Table 2. In this table E_s, ν_s, c, φ and σ_t were calculated using Eqs. 10–15, and k and n were obtained from laboratory tests carried on core samples by the NISOC. Note that the c values for fault core and damage zone in this table are related to the rocks of these regions and not to the fault surface, where its cohesion is considered zero.

Fig. 10

Schematic illustration of the 2D model (the red asterisk shows the location of the injection point) (color figure online)

Table 2 Hydraulic and mechanical properties of the model

No information was available to characterize the properties of the fault core and damage zone; therefore, their properties are mainly considered to be the same as the cap rock and reservoir, respectively. Due to the highly fractured nature of the rocks caused by shearing in the damage zone, the permeability of this zone is assumed to be an order of magnitude greater than the reservoir (Jeanne et al. 2014; Yoon et al. 2016).

4 Results and Discussion

4.1 Stress Magnitudes and Mechanical Properties

To investigate the stability of the faults in this reservoir, the current stress field was estimated using density logs and poroelastic equations, as described above. For this reservoir, the vertical stress (σ_V) is the maximum principal stress (σ₁), and the intermediate and minimum principal stresses (σ₂ and σ₃), are σ_Hmax and σ_hmin, respectively, and thereby classified as a normal faulting regime (i.e., σ₁ > σ₂ > σ₃) (Anderson 1951). Figure 11 shows the stress profile for the field. In this figure, σ_V, σ_H, σ_h and P_p are shown with the line of best fit (smooth scatter lines and points of these parameters are hidden). In this figure, the estimated P_p (red line) and directly measured P_p at 17 points within the reservoir (gray points) show a maximum difference of 2 MPa, which is consistent with an acceptable range for the accuracy when applying the Azadpour et al. (2015) method. In this field, the hydrostatic pressure (blue dashed line) is higher than the estimated pore pressure (red dotted line) (Fig. 11), which means that the field is under-pressured and confirms the necessity of gas injection. The interpreted image log showing the drilling-induced tensile fractures is illustrated in Fig. 12. In addition to interpreting the image log for the orientations of horizontal stresses, the population of natural fractures was measured. A total number of 32 fractures with a dominant azimuth of 52° were observed. Based on the fact that the existence of drilling-induced tensile fractures is 90° from borehole breakouts (Fig. 4), the azimuths of the two principal horizontal stresses were determined 52° for σ_Hmax and 142° for σ_hmin. Figure 13 shows the fault planes and in-situ stresses orientations in lower hemisphere stereographic projection.

Fig. 11

Stress-depth plot showing the stress state in Gachsaran oilfield (the principal stresses and pore pressure are plotted with the line of best fit). The gray points represent the formation fluid pressures (RFT), and triangles indicate FIT pressure (the stresses are calculated using the elastic moduli estimated by NISOC equation)

Fig. 12

Interpreted image log showing the locations of the drilling-induced tensile fractures (pink lines). These fractures show a dominant azimuth of 52° that corresponds to the direction of σ_Hmax (color figure online)

Fig. 13

Stereographic projection of fault planes and in-situ stresses orientations. The azimuths of σ_Hmax (S_H) and σ_hmin (S_h) are 52° and 142°, respectively

The mechanical properties of the rocks were estimated using Eqs. 10–17. Figure 14 shows these properties along a well. These properties were calculated for all the wells and were used for constructing Mohr diagrams and numerical models.

Fig. 14

Logs of static Young’s modulus, Poisson’s ratio, uniaxial compressive strength (UCS), friction angle and cohesion in a well. These properties are crucial for numerical modeling

4.2 Analytical Methods

Mohr diagrams were constructed for the four faults, and the maximum sustainable pore pressure calculated for each. Figure 15 shows the Mohr diagram plotted for F1 in the current stress conditions and Fig. 16 shows the Mohr diagram for the same fault at the pore pressure required to induce shear slip. The results of this analysis for all the faults are summarized in Table 3.

Fig. 15

Mohr diagram for the cohesionless F1 in the current stress field. As shown, this fault is stable in the current stress field (before injection). The red dot on the big circle (σ’₁–σ’₃) shows the shear and normal stresses for this fault

Fig. 16

Mohr diagram plotted for F1 for estimating critically stressed pore pressure. The pore pressure increase to cause failure (ΔP_p) for this fault is about 24.9 MPa

Table 3 Effective normal and shear stress, initial pore pressure (Ppi), the maximum sustainable pore pressure (Ppmax), pore pressure increase (ΔPp) and normal stress at failure point (σ'nf) for the faults

The results show that in the current stress field and pore pressure, all the faults are stable and lie below the failure envelope. In Table 3, σ'_ni and τ represent the current effective normal and shear stress acting on the faults. P_pi is the current pore pressure estimated for the field. P_pmax is the maximum sustainable pore pressure, calculated by increasing the pore pressure such that the Mohr circle reaches the failure envelope. ΔP_p is the difference between P_pi and P_pmax, and σ'_nf is the effective normal stress after increasing the pore pressure. The highest P_pmax was calculated for F2 (57 MPa), indicating this fault has the highest stability against injection.

For investigating the propagation of new fractures induced by injection (hydraulic fracturing), the Mohr failure envelope was constructed for intact rocks. The tensile strength and cohesion of the reservoir and cap rock were estimated using Eqs. 13 and 15, respectively. Figure 17 shows the injection pressure required to induce new fractures (intact rock) for the stress magnitudes in the vicinity of F1 (i.e., the pressure at which the effective normal stress is < 0). The remaining results for this analysis are summarized in Table 4.

Fig. 17

Mohr diagram of F1 and intact rocks in the current stress field. For this fault, the intact rock in the reservoir will undergo tensile fracturing at an injection pressure of 59 MPa

Table 4 Pore pressure required to induce new fractures in the stress condition around each fault

The results suggest that for the stress magnitudes around F1, intact rock in the reservoir will undergo tensile fracturing at an injection pressure around 59 MPa. It was also found that the pressure needed to create a fracture around F1 and F3 is less than F2 and F4, which divides the area into two regions, one with a lower strength (west to southwest) and the other higher strength (northwest). Using open-source MohrPlotter software, the potential angles for reactivation of these fractures were calculated (Table 5).

Table 5 Possible reactivation angles of new fractures

In Table 5, the reactivation angles calculated for F3 and F4 are nearly similar. The reason is that as shown in Fig. 13, these faults have similar strikes and orientations to the principal stresses, which means F3 and F4 are nearly two similar planes subjected to the in-situ stresses.

The slip tendency (T_s), the critical pore pressure (P_C), and dilation tendency (T_d) were calculated using Eqs. 22, 30, and 31. As shown in Table 6, again all the faults are stable in the current stress field, since their slip tendency is lower than the assumed frictional coefficient (µ = 0.6).

Table 6 Values of slip tendency (Ts), critical pore pressure (P_C), and dilation tendency (Td) for the faults

In a normal fault stress regime, the faults that are most likely to slip tend to have a strike sub-parallel to the intermediate in-situ principal stress (σ₂ = σ_Hmax) and dip at roughly 60 degrees (Hawkes et al. 2005). In the study area, F1, F3, and F4 have strikes nearly parallel to the σ_Hmax orientation, but only the dip of F3 is 59° (Table 1). Based on the results of both Mohr diagrams (Table 3) and slip tendency equation (Eq. 22 and Table 6), F3 is more likely to reactivate than the other faults, since its ΔP_p and P_pmax are lower. F3 also has the highest slip tendency value, which means it can reactivate with a lower pore pressure increase. On the other hand, F2 is the most stable fault based on both methods of Mohr diagrams and slip tendency parameter, with the lowest T_s and average maximum pore pressure of 55–57 MPa. The highest dilation tendency is computed for F3, which is perpendicular to the minimum horizontal stress. This means that this fault has a high potential to remain open against fluid flow. Since T_d also provides the potential for tensile failure, this potential is high for F3, because it will undergo tensile fracturing at lower injection pressures.

4.3 Numerical Modeling

The first step of the analysis is a geostatic step to equilibrate geostatic loading of the model. This step also establishes the initial distribution of pore pressure. Results of this step confirm that displacements are very small and the model is in geostatic equilibrium (Fig. 18). In this figure, the maximum magnitude of displacements (the resultant displacement of x and y directions) around F4 is 0.09 µm.

Fig. 18

Magnitude of the displacements (U is the resultant displacement of x and y directions) (m) in the geostatic step for F4. These displacements are very small, which confirms that the model is in geostatic equilibrium

The numerical simulation of gas injection into the reservoir was carried out, starting with a 30 MPa pressure for 5 years. The volume of the injected gas for this injection pressure and period is about 581.5 m³ (Fig. 19).

Simulation results using F4 geometry indicate that the injected gas plume moves both forward and upward over time. The ascending gasses are the main reason for hydraulic fracturing in the cap rock and can generate cap rock integrity issues. After two hours, the gas plume has traveled about 150 m away from the injection point in the reservoir (Fig. 20). Results show that the damage zone of the fault acts as a conduit because of its higher permeability than the fault core. Through this conduit, the pore pressure plume penetrates the Pabdeh source rock and the cap rock. Also, the ascending gasses from the reservoir infiltrate the lower part of the cap rock at the end of 5 years (Fig. 21). From this time forward, the gas plume will start to fully penetrate the cap rock from both the damage zone and the reservoir-cap rock interface. Generally, because the fault core is practically impermeable, gas injection in each block of the compartmentalized reservoir leads to the overpressures in that block and prevents the gas from infiltrating the other section beyond the fault (Fig. 22). And finally, this stored gas induces uplift (~ 11 cm) above the injection area (Fig. 23).

Fig. 19

Volume of the injected gas is about 581.5 m³ after 5 years for injection pressure of 30 MPa

Fig. 20

Progression of the injected gas plume in the reservoir after two hours of injection (pore pressure in Pa). After 2 h, the gas plume has travelled about 150 m away from the injection point in the reservoir

Fig. 21

source rock. Due to the higher permeability of the damage zone, the pore pressure plume first penetrates the Pabdeh source rock, and at the end of 5 years, it also infiltrates the cap rock (pore pressure in Pa). Furthermore, the ascending gasses from the reservoir-cap rock interface slightly infiltrate the lower part of the cap rock

Pore pressure build up through fault damage zone into Pabdeh

Fig. 22

Pore pressure increase (Pa) in the injected block. At the end of the 5 years, some parts of the cap rock have experienced pore pressure increase due to the moving gas from both the damage zone and reservoir-cap rock interface. At the same time, the other side of the fault has undergone a little change, since the fault core acts as a barrier and hinders the gas from moving forward

The pore pressure increase as a function of distance along a cross section perpendicular to F4 including the fault core and adjacent damage zone is shown in Fig. 24. As shown in this figure, the sharp decrease in pore pressure on the right side of the fault is due to the impermeable fault core that acts as a barrier and prevents the gas plume from spreading. The pressure evolution in the adjacent damage zone of F4 as a function of time is presented in Fig. 25. This figure also shows the importance of the impermeable fault core in preventing the pore pressure increase. The pore pressure on the left side of the fault (near the injection zone) reaches 30 MPa after a short time (~ 6 months), but on the right side, it shows a slight increase (~ 0.5 MPa) after 5 years. The maximum shear stress accumulated after injection is about 13 MPa on F4, and about 8 MPa on the other faults (Figs. 26, 27). This difference is because of the higher gas accumulation on the F4 surface, which is closer to the injection zone.

Fig. 23

Contours of displacement (m) over the injected area. The maximum induced uplift is about 11 cm above the injection area. This uplift is mainly because of reservoir compartmentalization by the impermeable fault core, which has trapped the gas in the injected block (left side of the fault)

Fig. 24

Pore pressure increase for a path perpendicular to F4, at the beginning and 1 week after injection. The impermeable fault core acts as a barrier and prevents the gas plume from spreading

Fig. 25

Pore pressure variations over time for two elements on the sides of F4. The pore pressure on the left side of the fault reaches 30 MPa after 6 months, but on the right side, it rises only about 0.5 MPa after 5 years

Fig. 26

Maximum shear stress accumulated on F4 is about 13 MPa after 5 years of injection. This stress is mainly accumulated in the injected block (left side). The accumulation and distribution of this shear stress will be the main reason of plastic strain growth and fault reactivation with higher injection pressures

In this study, the plastic plane strain was monitored. This is a two-dimensional state of strain in which all the shape changes of material happen on a single plane (the x–y plane in our case), and stress along z-direction is zero. Based on the findings, no plastic strain or fracture growth was initiated by applying an injection pressure of 30 MPa (Fig. 28). Therefore, this pressure can be assumed as the safe lower bound of injection pressure for this field. This result was also confirmed by the analytical methods.

Fig. 27

Maximum shear stress accumulated on F1, F2, and F3 is about 8 MPa after 5 years of injection. The magnitude of shear stress for these faults have not increased as much as for F4, since these areas have not experienced equal pore pressure increase due to F4 impermeability

We further investigated the effect of injection pressure increase on fault stability by increasing injection pressure to 50 MPa. After approximately 100 days of injection, the plastic strains started to develop on the fault plane (Fig. 29). These strains are directly related to the development of new fractures and imply the start of fault reactivation. According to the results of the geostatic step and injection pressure of 30 MPa, the model is stable, and no deformation was observed in these steps. Therefore, the only factor that can cause deformation in 50 MPa pressure is the pore pressure increase caused by injection. Since the gas was injected into the reservoir and these strains initiated in the cap rock, they seem to be the result of fault slip. These deformations are located near the fault plane, which is another proof for this claim. By increasing the injection pressure up to 60 MPa, the slip and resulting strains initiated after 12 days of injection. Also at this injection pressure, plastic strains developed at the reservoir-cap rock interface due to the accumulation of high pore pressure in this area (Fig. 30).

Fig. 28

No plastic strain was formed over time in the reservoir or cap rock for the injection pressure of 30 MPa. This implies that this pressure is safe for the reservoir, and cap rock integrity is not compromised

Fig. 29

Onset of plastic strains at the fault plane in the cap rock after 100 days of injection with an injection pressure of 50 MPa. These strains indicate the onset of fault reactivation and end of simulation

Finally, the effect of the friction angle on fault stability was examined by reducing the coefficient of sliding friction to 0.4 at an injection pressure of 60 MPa. The injection continued until the slip and the consequent plastic strains initiated. Figure 31 shows the magnitude of plastic strains for different frictional coefficients at injection pressure of 60 MPa. For the injection with µ = 0.6, the first plastic strains appeared after 12 days. By reducing µ to 0.4, the slip initiated only after 10 days of injection. It can also be inferred that by reducing µ, the accumulated plastic strain decreases, since the two blocks of rocks can slide more easily. These results indicate that the role of the frictional coefficient on fault stability can be more influential than injection pressure.

Fig. 30

Onset of plastic strains at the fault plane and reservoir-cap rock interface (caused by ascending gasses) after 12 days of injection with an injection pressure of 60 MPa

Fig. 31

Onset of plastic strain for frictional coefficients of µ = 0.6 and µ = 0.4 at the injection pressure of 60 MPa. By reducing the frictional coefficient, the slip initiated in 10 days. For µ = 0.4 the accumulated plastic strain decreases, since the two blocks of rocks can slide easier

5 Conclusions

In this study, a step by step procedure was followed to investigate the stability of four faults in Asmari reservoir, Gachsaran oilfield, SW Iran. To achieve this goal, the current stress field was determined using well logs and poroelastic equations. The field is in a normal faulting stress regime, which is confirmed by the presence of normal faults that cut the lower parts of the cap rock. By plotting Mohr diagrams, it was demonstrated that all the faults are stable in the current stress field and pore pressure. Mohr diagrams were also used to estimate the maximum sustainable pore pressure and the creation of new fractures. According to these analytical results, the most stable fault in the field is F2 which can support maximum pore pressures of 55–57 MPa. F3 was recognized to be the most prone to reactivation (P_pmax = 38.8 MPa). This low value may, however, be due to the short length of this fault within the reservoir and the numerical generation of anomalously large amounts of shear stress on the small fault segment. By comparing the injection pressures needed to create fractures in intact rocks around each fault, it was also recognized that the reservoir could be divided into two regions of low strength (west to southwest) and higher strength (northwest).

Numerical simulations were carried out to investigate the potential fluid flow, fault reactivation, and propagation of shear stress and plastic strain in different parts of the reservoir. A pressure of 30 MPa was recognized as the safe lower bound of injection pressure, since it did not induce hydraulic fractures or cause fault slip. Due to fault compartmentalization, the simulated injection resulted in overpressures leading to an uplift of about 11 cm at the end of 5 years. An increase in injection pressure up to 50 MPa and 60 MPa leads to fault slip in 100 and 12 days, respectively. For an injection pressure of 60 MPa, the onset of reactivation occurred earlier by reducing the frictional coefficient value from 0.6 to 0.4.

The results of both analytical methods and numerical simulations are consistent with each other and suggest an approximate safe injection pressure range of 30–50 MPa. One of the main uncertainties related to analytical methods is reservoir-cap rock system properties such as permeability, which plays a significant role in the injected gas flow pattern and imposing the location of accumulated plastic strains.