Applications of Digital Image Correlation (DIC) and the Strain Gage Method for Measuring Dynamic Mode I Fracture Parameters of the White Marble Specimen

Abstract

Digital image correlation (DIC) and the strain gage method are both widely used in characterizing the fracture mechanisms of materials. However, the quantitative comparisons of rock fracture parameters between the two methods have been studied insufficiently. In this paper, dynamic three-point bending impact tests were performed on white marble specimens using DIC and the strain gage method simultaneously. The complete cracking process was recorded by two high-speed cameras situated on either side of the specimen. The crack propagation velocities were obtained and the dynamic stress intensity factors (DSIFs) were calculated by both methods for analysis and comparison. The experimental results show that the crack propagation velocities almost remain constant during the cracking process, and the evolutions of strain values recorded by gages are consistent with the modified strain variations obtained theoretically. DSIFs calculated by DIC show good agreement with the results obtained from strain gages #1 to #4, while the size effect and the multiple stress waves interfere with the strain signals sensed in strain gage #5, causing a relatively larger deviation in the DSIF. In addition, the complete fracture process (including the variations in successive displacement and strain fields) can be obtained by the DIC method, while a rough changing trend in the DSIF can be given by the strain gage method with a limited number of strain gages.

1 Introduction

Dynamic fracture-mechanical behaviors of rock masses are closely related to geophysical processes and geological disasters, such as earthquakes, landslides and rock bursts. Thus, studying the dynamic fracture mechanism of rock masses is important for understanding rock mechanics. Key fracture parameters, including the crack propagation velocity and the dynamic stress intensity factor (DSIF), should be measured accurately to provide rock engineering applications with enough essential databases.

Various methods have been proposed to determine the fracture parameters of materials (Sanford and Dally 1979; Yao et al. 2003; Tippur 2010). Photomechanical testing methods such as the photoelastic method have been widely used to determine the stress intensity factor of materials (Sanford et al. 1981; Sanford 1989; Etheridge and Dally 1978) and can yield relative accurate experimental results. Caustics is another useful experimental method first proposed by Manogg (1965). Arakawa et al. (2000) investigated the dynamic fracture mechanism of polymethyl methacrylate (PMMA) material using the caustic method and revealed the characteristic evolution of DSIFs during the cracking process. Yao et al. (2008) and Yao and Xu (2011) employed the caustic method to study the dynamic fracture-mechanical behaviors (including crack initiation and propagation) of functionally graded materials. Liu et al. (2016) derived new governing equations based on the classic caustic theories to study the fracture mechanism of PMMA cylindrical shell specimens and obtained the corresponding fracture parameters. However, neither the photoelastic nor the caustic method seems to be suitable for studying the fracture behaviors of opaque materials such as rock. Even though the testing light path can be altered from transmission-type to reflection-type, it is uncertain whether the coating material planted on the specimen surface could deform consistently with the specimen itself (Zhang and Zhao 2014). In addition, the acoustic emission method is employed frequently to reveal the fracture behaviors of rock masses, and the related acoustic emission signal parameters (AESP) can be used for deformation identification of rock specimens (Cheon et al. 2011; Kim et al. 2015; Zhang et al. 2016). Zhang et al. (2017) used the acoustic emission method to investigate the related deformation characteristics of rock under different compressive loading rates.

Digital image correlation (DIC) is an optical full-field experimental technique widely used to obtain the successive displacement and strain fields of materials (Corr et al. 2007; Sutton et al. 2009; Pan et al. 2010a, b). DIC can be applied to both transparent and opaque materials due to its simple experimental setup. Zhao et al. (2018) observed the coalescence behaviors of two parallel cracks in rock-like specimens and concluded that there are three typical coalescence modes (shear, tensile and mixed coalescence mode) using DIC and the numerical method. Recently, DIC has been extended to fracture mechanism research and various fracture parameters were deduced from the original displacement and strain fields (McNeill et al. 1987; Durif et al. 2010; Zhang and He 2012). Rethore et al. (2005) computed the mixed mode stress intensity factors using DIC combined with a domain-independent integral. Gao et al. (2015) added a high-speed camera to the DIC method to accurately measure the complete cracking process of notched semicircular bend (NSCB) granite specimens and obtained the evolution of DSIFs and crack lengths with respect to time. Li and Einstein (2017) combined the DIC and acoustic emission methods to investigate the fracture behaviors of Barre granite specimens with pre-existing notches under four-point bending load.

Strain gages are broadly used for studying fracture-mechanical problems because of their low cost, convenience of use and ability to directly obtain and measure strains on the surface of the specimen (Sanford 2003). This method was first introduced by Irwin (1957) for the purpose of determining the stress intensity factor near the crack tip. Dally and Sanford (1987, 1990) studied the opening-mode stress intensity factor for stable and propagating cracks by using the strain gage method. Shukla et al. (1989) introduced the strain gage method to measure SIF in orthotropic composite material. More recently, Joudon et al. (2014) investigated the experimental process for the characteristic of mode I dynamic fracture toughness in advanced epoxy resins materials by using both the strain gage method and high-speed cinematography. Zhao et al. (2016) mounted several strain gages near the flaws of rock-like specimens to investigate the vertical and horizontal deformation fields of the tested specimens. Yue et al. (2017) combined the strain gage and the caustic method to compare the mode I DSIFs obtained from both approaches.

The strain gage method has rarely been employed to study the fracture behaviors of rock masses, and there is a lack of comparisons between the strain gage and the DIC method for determination of mode I DSIF. Hence, the objective of this work is to study the mode I fracture mechanism and measure the corresponding fracture parameters of a white marble rock using both DIC and the strain gage method. Two high-speed cameras were used to simultaneously record the typical DIC images and the complete cracking process for accurate determinations of crack tip positions at each moment. The crack propagation velocities were obtained and the successive displacement as well as strain field was calculated. Additionally, the DSIFs derived from both the strain gage and DIC method were analyzed and compared.

2 Experimental Theories

2.1 The Strain Gage Method

To obtain the constant mode I DISF variations of marble specimens, the strain gage was mounted along the cracking path with an orientation of $\alpha$ and a distance of $y_{\text{g}}$ (Fig. 1). A three-parameter model can express the strain sensed by the gage (Sarangi et al. 2012; Joudon et al. 2014; Yue et al. 2017):

$$2\mu \varepsilon_{\text{g}} = A_{0} f_{0} + A_{1} f_{1} + B_{0} g_{0} ,$$

(1)

where $\mu$ is the shear modulus of the specimen; $\varepsilon_{\text{g}}$ is the strain value recorded by the gage; and $A_{0}$, $A_{1}$ and $B_{0}$ are, respectively, constant parameters that are related to DSIF ($A_{0} = K_{\rm I}^{\text{d}} /\sqrt {2\pi }$), a nonsingular term and the constant stress of the nonsingular field along the cracking path. Based on the coordinate system for strain analysis (Fig. 2), the terms $f_{0}$, $f_{1}$ and $g_{0}$ can be given as follows:

$$\begin{aligned} f_{0} = \beta \times r_{1}^{ - 1/2} \times [\cos (\theta_{1} /2) \times \{ k(\lambda_{1}^{2} - \lambda_{2}^{2} ) + (1 + \lambda_{1}^{2} )\cos (2\alpha )\} + 2\lambda_{1} \sin (\theta_{1} /2)\sin (2\alpha )] \\ - \beta \times r_{2}^{ - 1/2} \times \left\{ {\frac{{4\lambda_{1} \lambda_{2} }}{{1 + \lambda_{2}^{2} }}\cos (\theta_{2} /2)\cos (2\alpha ) + 2\lambda_{1} \sin (\theta_{2} /2)\sin (2\alpha )} \right\}, \\ \end{aligned}$$

(2a)

$$\begin{aligned} f_{1} = \beta \times r_{1}^{1/2} \times [\cos (\theta_{1} /2) \times \{ k(\lambda_{1}^{2} - \lambda_{2}^{2} ) + (1 + \lambda_{1}^{2} )\cos (2\alpha )\} - 2\lambda_{1} \sin (\theta_{1} /2)\sin (2\alpha )] \\ - \beta \times r_{2}^{1/2} \times \left\{ {\frac{{4\lambda_{1} \lambda_{2} }}{{1 + \lambda_{2}^{2} }}\cos (\theta_{2} /2)\cos (2\alpha ) - 2\lambda_{1} \sin (\theta_{2} /2)\sin (2\alpha )} \right\}, \\ \end{aligned}$$

(2b)

$$g_{0} = \beta \times (\lambda_{1}^{2} - \lambda_{2}^{2} ) \times \left\{ {\kappa + \cos (2\alpha )} \right\}.$$

(2c)

Here, the coefficients $\beta$, $\kappa$, $\lambda_{1}$, $\lambda_{2}$ can be expressed as follows:

$$\beta = \frac{{1 + \lambda_{2}^{2} }}{{4\lambda_{1} \lambda_{2} - (1 + \lambda_{2}^{2} )^{2} }};\;\kappa = {{(1 - \nu )} \mathord{\left/ {\vphantom {{(1 - \nu )} {(1 + \nu )}}} \right. \kern-0pt} {(1 + \nu )}};\;\lambda_{1} = \sqrt {1 - (c/c_{1} )^{2} } ;\;\lambda_{2} = \sqrt {1 - (c/c_{2} )^{2} } ,$$

(3)

where $c$ is the propagation velocity of the running crack; $c_{1}$ and $c_{2}$ are the longitudinal and shear wave velocities, respectively; $\nu$ is the Poisson’s ratio of the specimen material. Equation (1) can be made into a two-parameter model by selecting a specific angle $\alpha$ to eliminate the $g_{0}$ term. Such selection needs satisfy:

$$\cos (2\alpha ) = - \kappa .$$

(4)

Fig. 1

Orientation and the rotated coordinate at the gage position

Fig. 2

Coordinate system for strain analysis

Therefore, the two-parameter model deduced from Eq. (1) can be written as:

$$2\mu \varepsilon_{\text{g}} = A_{0} f_{0} + A_{1} f_{1} .$$

(5)

The mechanical parameters of the marble used in this experiment are listed in Table 1. As is shown in Table 1, the Poisson’s ratio $\nu$ is 0.28. Thus, two specific orientation angles of the gage can be obtained (62° and 118°). Dally and Sanford (1990) and Yue et al. (2017) studied the influence from orientation angles on the experimental results and found that the obtuse orientation is more sensitive to the running crack tip, which may cause more testing errors. Therefore, the acute 62° is chosen as the orientation angle for the experiment.

Table 1 Mechanical parameters of marble specimens

To determine the parameters in Eq. (5), Eq. (5) is then rewritten as follows:

$$2\mu \varepsilon_{\text{g}} /A_{0} = f_{0} + (A_{1} /A_{0} )f_{1} .$$

(6)

Here, the term $2\mu \varepsilon_{\text{g}} /A_{0}$ is the modified strain. As $y_{\text{g}}$ is given when the gages are mounted, the r and x can be expressed by $y_{\text{g}}$ and angle $\theta$ as follows:

$$r = y_{\text{g}} /\sin \theta ;\;\;x = y_{\text{g}} /\tan \theta .$$

(7)

The modified strain is only related to $\theta$ and x when the crack propagation velocity c and the term $A_{1} /A_{0}$ are confirmed. In this experiment, the crack propagation velocity c measured by a high-speed camera is 210.5 m/s; $y_{\text{g}}$ is 2 mm. Therefore, given a series of $A_{1} /A_{0}$ (0, 20, 30 … 80), the variations of the modified strain $2\mu \varepsilon_{\text{g}} /A_{0}$ with respect to x are shown in Fig. 3a.

Fig. 3

Typical curves for variations of modified strain with crack position and the characteristic feature of strain–time response, $\alpha$ = 62°

To characterize the transit response of each strain gage and match the modified strain curve in Fig. 3a, the time interval $\Delta t$ when the modified strain reaches 75% of its peak value in each curve is calculated (as shown in Fig. 3b). It can be seen from Fig. 3b that $\Delta t$ represents the time interval when the $\varepsilon_{\text{g}} - t$ curve reaches its 75% peak value in either modified or testing strain–time response. The modified strain–time curve with a certain $A_{1} /A_{0}$ ratio is related to a corresponding time interval $\Delta t$. This relationship between $\Delta t$ and $A_{1} /A_{0}$ can be extracted from Fig. 3a and drawn out in Fig. 4. For experimental strain measurements, $\Delta t$ can be directly obtained from testing strain–time response. Thus, the corresponding $A_{1} /A_{0}$ for each experimental strain–time curve can be given by Fig. 4, and $K_{\rm I}^{d}$ is calculated using the strain gage method.

Fig. 4

Relationship between time interval $\Delta t$ and ${{A_{1} } \mathord{\left/ {\vphantom {{A_{1} } {A_{0} }}} \right. \kern-0pt} {A_{0} }}$ at crack propagation velocity c = 210.5 m/s

Figure 4 can help determine the $A_{1} /A_{0}$ ratio with the actual testing strain curve $\varepsilon_{\text{g}} - t$ obtained in the experiment. For example, if the time interval $\Delta t$ of a testing strain curve is 26.15 μs, the corresponding $A_{1} /A_{0}$ ratio can be read as 20 m⁻¹ in Fig. 4. Then, the similar modified strain variation curve to Fig. 3 can be drawn and the parameter $A_{0}$ is extracted for the determination of DSIF.

2.2 Digital Image Correlation Method and Extraction of DSIF

2.2.1 Digital Image Correlation

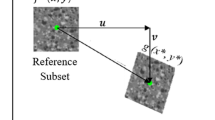
The process of comparing the features and extracting the estimated displacement is usually accomplished with an intensity pattern matching method known as DIC (Shukla and Dally 2014). Normally, by tracking and matching a subset of (2N+ 1) × (2N+ 1) pixels called subimage (Fig. 5) in both reference and deformed images using specific correlation function, the displacement of the considered point centered in the subimage can be determined. Similarly, the full field’s displacement components of the target area can be obtained by minimizing or maximizing the correlation coefficient.

Fig. 5

Schematic diagram of tracking and matching subimage in DIC method

Given the center-point coordinates of the subimage in the reference image as $O\left( {x_{0} ,y_{0} } \right)$, the corresponding point $P^{\prime}\left( {x^{\prime},y^{\prime}} \right)$ in deformed image can be expressed as (Sutton et al. 2009):

$$\begin{aligned} x^{\prime} = x_{0} + \Delta x + u + \frac{\partial u}{\partial x}\Delta x + \frac{\partial u}{\partial y}\Delta y \hfill \\ y^{\prime} = y_{0} + \Delta y + v + \frac{\partial v}{\partial x}\Delta x + \frac{\partial v}{\partial y}\Delta y, \hfill \\ \end{aligned}$$

(8)

where the parameters u, v represent the displacement components of the subimage center-point O in the horizontal and vertical directions, respectively; Δx and Δy denote the distances between point O and point P in the x and y directions, respectively; $\frac{\partial u}{\partial x}$, $\frac{\partial v}{\partial x}$, $\frac{\partial u}{\partial y}$ and $\frac{\partial v}{\partial y}$ represent the gradients of displacement components for subimage shown in Fig. 5. In addition, the correlation coefficient C employed in our tests can be expressed as follows:

$$C = \frac{{\sum {\left[ {f\left( {x,y} \right) - \bar{f}} \right] \times \left[ {g\left( {x,y} \right) - \bar{g}} \right]} }}{{\sqrt {\sum {\left[ {f\left( {x,y} \right) - \bar{f}} \right]^{2} } } \sqrt {\sum {\left[ {g\left( {x,y} \right) - \bar{g}} \right]}^{2} } }},$$

(9)

where $f\left( {x,y} \right)$ is the gray-level value of the considered point in the reference image; $g\left( {x,y} \right)$ is the gray-level value for the corresponding point in the deformed image; and $\bar{f}$ and $\bar{g}$ are the average gray-level values of the reference and deformed images, respectively.

2.2.2 Extraction of DSIF

Displacement fields obtained by the DIC method are used to deduce key fracture parameters in experiments, including DSIF and fracture toughness. By utilizing two high-speed cameras located on both sides of the specimen, the extraction of DSIF based on previous studies (Lin and Labuz 2013; Gao et al. 2015) can be optimized and the calculation routine is as follows: locating the crack tip positions during the cracking process; obtaining the full displacement and strain fields of the calculation area; and calculating DSIF using the least squares method. For an opening-mode fracture (mode I), the displacement fields around the crack tip shown in Fig. 1 can be described as (Yoneyama et al. 2006):

$$\begin{aligned} u = \sum\limits_{n = 1}^{\infty } {\frac{{C_{n} }}{2\mu }} r^{n/2} \left[ {\left( {\eta \cos \frac{n\theta }{2} - \frac{n}{2}\cos \left( {\frac{n}{2} - 2} \right)\theta + \left( {\frac{n}{2} + \left( { - 1} \right)^{n} } \right)\cos \frac{n\theta }{2}} \right)} \right] \\ v = \sum\limits_{n = 1}^{\infty } {\frac{{C_{n} }}{2\mu }} r^{n/2} \left[ {\left( {\eta \sin \frac{n\theta }{2} + \frac{n}{2}\sin \left( {\frac{n}{2} - 2} \right)\theta - \left( {\frac{n}{2} - \left( { - 1} \right)^{n} } \right)\sin \frac{n\theta }{2}} \right)} \right], \\ \end{aligned}$$

(10)

where u and v represent the displacement components in the x and y directions, respectively.$\eta = \left( {3 - \nu } \right)/\left( {1 + \nu } \right)$ for plane stress and $\eta = 3 - \nu$ for plane strain condition; $C_{n}$ is a parameter related to mode I dynamic stress intensity factors; and $K_{\text{I}}^{\text{d}}$ can be expressed as $K_{\text{I}}^{\text{d}} = C_{1} /\sqrt {2\pi }$. Taking possible rigid-body translation and rotation into account, Eq. (10) can be rewritten as:

$$\begin{aligned} u_{k} = \sum\limits_{n = 1}^{N} {C_{n} f_{{{\rm I}n}} \left( {r_{k} ,\theta_{k} } \right)} + T_{x} - Ry_{k} \hfill \\ v_{k} = \sum\limits_{n = 1}^{N} {C_{n} g_{{{\rm I}n}} \left( {r_{k} ,\theta_{k} } \right) + T_{y} } + Rx_{k} , \hfill \\ \end{aligned}$$

(11)

where

$$\begin{aligned} f_{{{\rm I}n}} \left( {r_{k} ,\theta_{k} } \right) = \frac{1}{2\mu }r_{k}^{n/2} \left[ {\left( {\eta \cos \frac{{n\theta_{k} }}{2} - \frac{n}{2}\cos \left( {\frac{n}{2} - 2} \right)\theta_{k} + \left( {\frac{n}{2} + \left( { - 1} \right)^{n} } \right)\cos \frac{{n\theta_{k} }}{2}} \right)} \right] \hfill \\ g_{{{\rm I}n}} \left( {r_{k} ,\theta_{k} } \right) = \frac{1}{2\mu }r_{k}^{n/2} \left[ {\left( {\eta \sin \frac{{n\theta_{k} }}{2} + \frac{n}{2}\sin \left( {\frac{n}{2} - 2} \right)\theta_{k} - \left( {\frac{n}{2} - \left( { - 1} \right)^{n} } \right)\sin \frac{{n\theta_{k} }}{2}} \right)} \right], \hfill \\ \end{aligned}$$

(12)

$T_{x}$, $T_{y}$ and $R$ represent the rigid-body translation and rotation. The unknown parameter $C_{n}$ can be determined using the least squares method and the related stress intensity factor can be obtained. The detailed expressions can be found in Gao’s (2015) work. It should be noted that the effect of the crack propagation velocity needs to be involved in the asymptotic expressions for the dynamic fracture process, and the distribution functions are given in previous references (Kirugulige and Tippur 2009) as:

$$\begin{aligned} f_{{{\rm I}n}} \left( {r_{1} ,r_{2} ,\theta_{1} ,\theta_{2} ,c} \right) = \frac{{B_{\rm I} \left( c \right)}}{2\mu }2\left( {n + 1} \right)\left[ {r_{1}^{n/2} \cos \frac{n}{2}\theta_{1} -\, h\left( n \right)r_{2}^{n/2} \cos \frac{n}{2}\theta_{2} } \right] \hfill \\ g_{{{\rm I}n}} \left( {r_{1} ,r_{2} ,\theta_{1} ,\theta_{2} ,c} \right) = \frac{{B_{\rm I} \left( c \right)}}{2\mu }2\left( {n + 1} \right)\left[ { - \lambda_{1} r_{1}^{n/2} \sin \frac{n}{2}\theta_{1} + \frac{h\left( n \right)}{{\lambda_{2} }}r_{2}^{n/2} \sin \frac{n}{2}\theta_{2} } \right], \hfill \\ \end{aligned}$$

(13)

where $B_{\rm I} \left( c \right) = \frac{{1 + \lambda_{2}^{2} }}{{4\lambda_{1} \lambda_{2} - \left( {1 + \lambda_{2}^{2} } \right)^{2} }}$; $\lambda_{1}$ and $\lambda_{2}$ are given in Eq. (3); $h\left( n \right) = \left\{ \begin{aligned} \frac{{2\lambda_{1} \lambda_{2} }}{{1 + \lambda_{2}^{2} }}:\;\;n{\text{ odd}} \hfill \\ \frac{{1 + \lambda_{2}^{2} }}{2}:\;\;n{\text{ even}} \hfill \\ \end{aligned} \right..$

However, the difference has been proven to be lower than 5% in the case of a lower crack propagation velocity ($c/c_{2} < 0.3$). Therefore, it is reasonable to analyze experimental results using quasi-static distribution functions in the least squares method.

3 Experimental Study

3.1 Specimen Preparation

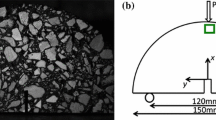
White marble specimens from Fangshan, Beijing, are used in the dynamic three-point bending impact experiments. The porosity of the marble specimen is 7.4%; the uniaxial compression strength is 149.70 MPa; the cohesion and internal friction angle of the tested marble specimen are 21.92 MPa and 57.35°, respectively. The dimensions of the white marble specimen are 200 mm × 50 mm × 5 mm (length × width × thickness). A pre-existing notch of 10 mm in length and 0.8 mm in width is perpendicularly set at the edge of the specimen. The notch tip is sharpened by a diamond wire saw to guarantee a typical mode I cracking path under the impact load.

A speckle pattern with the size range of 3–7 pixels is suggested by Sutton et al. (2009) in the speckle fabrication process. In addition, the mean intensity gradient proposed by Pan et al. (2010a, b) can be used for speckle optimization. In our tests, spray-painting was used to produce a matte white cover on specimen surfaces and dot printing was then used to generate a series of random speckles. The typical mode I fractured three-point bending white marble specimen with speckles is shown in Fig. 6.

Fig. 6

Fractured white marble specimen with typical speckle patterns and the crack path

A series of strain gages (with the size of 3.18 mm × 3.18 mm, resistance value of 120 ± 0.2 Ω and sensitivity coefficient of 2.08 ± 1%) numbered from 1 to 5 are mounted in a line on the back side of the specimen with the same orientation angle $\alpha$ of 62°. The perpendicular distance $y_{\text{g}}$ between the gage and the cracking path is set to 2 mm. The vertical space interval $\Delta x$ between each gage is 6 mm. Other detailed dimension parameters are shown in Fig. 7. Figure 8 shows the specimen surface where the strain gages were mounted.

Fig. 7

Schematic of marble specimens with strain gages

Fig. 8

The white marble specimen with strain gages

3.2 Experimental System

Figure 9 shows the schematic diagram of the complete experimental system used in our tests. The experimental system for measuring mode I fracture parameters of white marble specimens consist of an ultra-high-speed camera (Kirana-05 M, USA, maximum frame rate is 5 × 10⁶ fps), a camera adaptor, two flash lights, an impact-loading device, a high-speed camera (Photron Fastcam-SA5-16G, Japan, maximum frame rate is 2 × 10⁶ fps), a dynamic strain meter (brand: Sokki Kenkyujo, Japan; model: DC-97A), a strain data acquisition instrument, a time-delayed controller (16 trigger channels, minimum delayed time is 1 μs) and related computers.

Fig. 9

Schematic diagram of the experimental system

In the experiments, the Kirana camera is used to record the displacement variations of speckle patterns on white marble specimens for DIC analysis. To determine the crack tip position at each moment, the Photron camera is located at the back side of the specimen to record the cracking process. The frame rates of both Kirana and Photron high-speed cameras are set to 210,000 fps and the delayed time is 100 μs for the purpose of recording the complete cracking process. The sampling frequency and length of the dynamic strain meter are set to 4000 kHz and 800 K. The strain meter is connected to the data acquisition instrument and the external triggering mode is selected for data recording. The loading device, high-speed cameras and the strain meter are connected to the time-delayed controller by signal wires. When the hammer drops on the impactor from a vertical height of 400 mm, a closed circuit is formed between the loading device and the time-delayed controller. Furthermore, a pulse signal is emitted from the time-delayed controller to trigger the high-speed cameras and the dynamic strain meter simultaneously. The experimental system used in our tests can guarantee synchronicity of the data recording process (including the DIC images and the strain variations) and improve the accuracy in data processing.

4 Experimental Results and Analysis

4.1 Cracking Process

Figure 10 shows the cracking process and the related reaching moments obtained by the Photron camera at the back side of the specimen when the running crack propagates to each strain gage. The pre-existing crack initiates at t = 109.5 μs and reaches each testing area of the strain gages numbered 1–5 at the moments of 123.8 μs, 152.3 μs, 180.8 μs, 209.4 μs and 238.1 μs, respectively. The fracture process lasts for approximately 250 μs before the running crack completely propagates through the marble specimen. With the interval distance between each gage fixed to 6 mm, the propagation velocity is almost constant during the cracking path, and the mean propagation velocity of the running crack can then be calculated as $\overline{c}$ = 210.5 m/s. It should be noted that the running crack has to propagate through the gaps between internal grains in marble specimens during the fracture process, causing a relatively curved cracking path and a rough fracture surface. Nevertheless, mode I fracture is still the major failure mode in our three-point-bend marble specimens.

Fig. 10

Cracking process obtained by Photron camera

Figure 11 shows the region of interest (ROI) of the white marble specimen. The ROI, which determines the computational area around the crack tip during the DIC image processing and contains the possible cracking path, has an average dimension of 280 × 156 pixels in our tests. The image resolution is maintained as 924 × 768 pixels, so the ratio of actual length to pixel is 0.034 mm/pixel. The origin of the coordinate used in the experiments is set at the tip of the pre-existing crack. The main use of the Photron camera is to exactly locate the crack tip positions in DIC image processing. With the random speckles distributed on the marble specimen surface, it is difficult to distinguish cracking path and tip positions from DIC images. Therefore, fracture process obtained by the Photron camera in Fig. 10 can provide accurate cracking information for tracing the crack tip in DIC image processing. Based on Fig. 10, Fig. 12 shows successive evolution diagrams of horizontal u-displacement fields and the surface strain fields $\varepsilon_{x}$ of the white marble specimen obtained by DIC testing system. Distinct displacement gradients can be found in Fig. 12 at 109.5 μs when crack initiates. Furthermore, strain $\varepsilon_{x}$ concentrates around the pre-existing crack tip, forming flame-shaped strain localization. With the crack initiating and propagating through the specimen, the displacement gradients increase gradually. However, the degree of strain concentration decreases first due to the sudden dissipation of energy around the crack tip, and then increases as a consequence of crack development.

Fig. 11

Region of interest of the specimen for DIC data processing

Fig. 12

Evolution diagrams of displacement fields and strain fields for marble specimens

4.2 Dynamic Stress Intensity Factors

Figure 13 shows the strain data curves recorded by each strain gage. Good agreement in the variation characteristic can be found between the experimental testing results (Fig. 13) and the modified strain curves (Fig. 3). The positive peak values of each strain curve are 1455.10 με, 1474.63 με, 1289.08 με, 1318.38 με and 1044.93 με. Therefore, the corresponding time intervals $\Delta t$ at 75% peak values can be calculated directly from Fig. 13 (listed in Table 2). To improve the accuracy of the testing results from the strain gage method, the perpendicular distances $y_{\text{g}}$ for each gage are measured again and carefully because the cracking path is not strictly straight but slightly curved in gage areas. With the time interval $\Delta t$ obtained, $A_{1} /A_{0}$ ratios can be deduced from Fig. 4 and are listed in Table 2. In addition, the moments when each strain curve reaches its positive peak value are consistent with that when the running crack passes through each gage area in Fig. 11, which verifies the accuracy in the trace of cracking process.

Fig. 13

Evolution of strain recorded by strain gages with time

Table 2 Time interval at 75% peak values of each strain curve and relative $A_{1} /A_{0}$ ratio

Based on the fracture parameters obtained previously, evolutions of the modified strain for each $A_{1} /A_{0}$ ratio with respect to crack position x in our tests are shown in Fig. 14. To directly determine $A_{0}$ in experimental data processing, peak values $\varepsilon_{\text{max} }$ of modified strain curves are extracted for further calculations. For strain gages numbered from 1 to 5, the corresponding modified strain peaks $\varepsilon_{\text{max} }$ are 13.13 m^−1/2, 13.41 m^−1/2, 13.42 m^−1/2, 13.29 m^−1/2 and 12.24 m^−1/2. As $\varepsilon_{\text{max} }$ can be expressed as $2\mu \varepsilon_{\text{g}} /A_{0} = \varepsilon_{\text{max} }$, the parameter $A_{0}$ can be then deduced and DSIF $K_{\text{I}}^{\text{d}}$ can be rewritten as:

$$K_{\text{I}}^{\text{d}} = 2\mu \varepsilon_{\text{g}} \sqrt {2\pi } /\varepsilon_{\text{max} } .$$

(14)

Fig. 14

Evolution of modified strain in the experiment

Taking the strain gage #1 as an example: the strain peak value recorded by gage #1 in the experiment is $\varepsilon_{\text{g}}$ = 1455.1 με, and the corresponding modified strain peak $\varepsilon_{\text{max} }$ is 13.13 m^−1/2; with the crack propagation velocity c = 210.5 m/s and shear modulus $\mu$ = 30.06 GPa, the DSIF at gage #1 position can be obtained as $K_{\text{I}}^{\text{d}}$ = 16.70 MPa m^1/2. Consequently, DSIFs for other strain gages calculated similarly are 16.57 MPa m^1/2, 14.47 MPa m^1/2, 14.95 MPa m^1/2, and 12.86 MPa m^1/2, respectively.

Evolution of DSIF with time using DIC method and the strain gage method is given in Fig. 15. A series of images during the complete cracking process were selected and the relative fracture information is extracted to calculate DSIFs using the DIC method. It can be found from Fig. 15 that $K_{\text{I}}^{\text{d}}$ continuously increases before crack initiation at t = 109.5 µs and finally reaches the fracture initiation toughness of 7.18 MPa m^1/2. At the moment when the pre-existing crack initiates, the elastic energy stored at the vicinity of the crack tip dissipates simultaneously, causing the DSIF to decrease rapidly. Afterwards, stress concentration is reformed near the new crack tip until the DSIF reaches the toughness value again, the crack continues to propagate to strain gage #1 area at t = 123.8 μs, and the corresponding DSIF calculated by DIC system is 14.99 MPa m^1/2. Furthermore, the strain meter is triggered; the strain signals are sensed and the strain–time variations are recorded automatically (Fig. 13). Then, the variation of the $K_{\text{I}}^{\text{d}}$–t curve is relatively stable during the cracking period from 114.26 to 247.57 μs before the marble specimen is completely fractured and the mean value of DSIF in this period is 16.38 MPa m^1/2. DSIFs obtained by both the DIC method and the strain gage method are listed in Table 3. The deviations of the strain gage method relative to DIC method are also given in Table 3 for comparison. It can be seen that the counterpart DSIFs from the DIC method to those obtained by strain gages from #1 to #5 are 14.99 MPa m^1/2, 15.55 MPa m^1/2, 16.21 MPa m^1/2, 16.25 MPa m^1/2 and 16.38 MPa m^1/2. Based on the deviations given in Table 3, it can be deduced that the DSIFs obtained by the strain gage method and DIC method show a good agreement for gage areas from #1 to #4, and the average deviation of the strain gage relative to DIC is only 9.2%. The main reason for this difference may be related to the relatively curved cracking path of the white marble specimen. With the impact height known prior, the impact velocity can be calculated as nearly 3 m/s in our tests. Furthermore, the corresponding loading rate can be obtained as 119 GPa m^1/2/s on the basis of Fig. 15. Thus, it can be deduced that such an impact velocity and loading rate are relatively low for rock fracture, causing an intergranular fracture mode in white marble specimens. During the mode I fracture process of the white marble specimen, the running crack propagates through the gaps between marble grains, forming a slightly curved cracking path in the end. Therefore, the strain signals sensed by gages are relatively unstable because of the tiny changes in $y_{\text{g}}$, which is mainly responsible for the dispersion of strain data and the differences of $K_{\text{I}}^{\text{d}}$ between the DIC and the strain gage method. However, a deviation up to 21.49% can be found for the testing area of strain gage #5 and the variation of DSIF from the strain gage method is obviously not as stable as that from DIC calculations. These phenomena can be explained as follows. The stress waves generated by the impact load could slightly influence the acquisition process of strain data in gages. Especially when the running crack is approaching the top edge of the specimen, the size effect and interactions between multiple stress waves could aggravate the influence on strain data recording. Therefore, the DSIF calculated by the strain gage method fluctuates, and the deviation in gage #5 is relatively larger than the others. However, the extraction of DSIF using the DIC method is not influenced by stress waves, and it can be used for either dynamic or static fracture analysis. Thus, the DIC method is a more flexible and stable method in fracture analysis than the strain gage method. By contrast, as a testing approach based on the local field, the strain gage method only requires a limited number of gages situated along the cracking path, and can describe a rough variation of DSIF. This may provide a relatively simple experimental method when a quick measurement for mode I DSIF of rock mass is needed.

Fig. 15

Evolution of DSIF obtained by DIC and the strain gage method

Table 3 Comparisons of DSIF between strain gage method and DIC method

4.3 Error Analysis

The main error in this experiment is induced by the selection of $y_{\text{g}}$, which affects the testing results greatly. The strain field around a crack tip can be divided into three zones as shown in Fig. 16 (Dally and Sanford 1987). Theoretically, the singularity dominated area (Zone I in Fig. 16) is the ideal place for the strain gage to be mounted for obtaining accurate experimental results. Strains in Zone I can be directly expressed as a one-parameter equation, $2\mu \varepsilon_{\text{g}} = A_{0} f_{0}$ based on Eq. (1), which would keep the testing errors in the minimum range. However, some key factors including the plasticity effect, three-dimensional effect, strain gradients and limited gage size impose strong restrictions on direct testing in Zone I. Thus, the nonsingular area should be taken into account, and the strain expression is altered into a two-parameter model: $2\mu \varepsilon_{\text{g}} = A_{0} f_{0} + A_{1} f_{1}$. Sarangi et al. (2012) studied the optimum locations of strain gage when measuring the mode I stress intensity factor, and suggested the interval [0.25, 2.30] (unit: mm) for $y_{\text{g}}$ could provide adequate accuracy in experimental data processing. In addition, locations of gages in Zone III are not appropriate due to the large error in experiments. However, the experimental materials employed by Joudon and Sarangi were epoxy resin and polymethyl methacrylate (PMMA), which are obviously different from white marble. Therefore, it is necessary to analyze the error effect in out tests.

Fig. 16

Delimited zones for strain description around the crack tip

For the verification of $y_{\text{g}}$, a static three-point bending simulation is performed using ABAQUS software. The crack length is set to 18 mm, which is the same extended crack length as the experiment when the crack propagated to the second testing strain gage. The concentrated force is applied at the top of the model (which is shown as a blue arrow in Fig. 17) and the vertical displacements of two roller points (black triangles in Fig. 17) are fixed. The maximum $y_{\text{g}}$ in our tests is 2 mm, so the contour integral (J-integral) is employed in this simulation, and the diameter of singularity in J-integral is set to 2 mm. The model consists of 5460 8-node biquadratic plane-stress quadrilateral, reduced integration elements. The mesh of the model and the relative Mises stress field are shown in Figs. 17 and 18.

Fig. 17

Finite element mesh for the white marble specimen

Fig. 18

Mises stress field obtained by the numerical simulation method

The DSIF obtained by the simulation is 15.73 MPa m^1/2. The deviations of the strain gage method and DIC method relative to the numerical simulation result are 5.34% and 1.14%, respectively. Similarly, the other four simulation DSIFs are compared with the corresponding testing results obtained by the strain gage method and DIC method. The average relative deviations are 9.04% and 4.47%.

5 Conclusions

The DIC and the strain gage method have been employed jointly to investigate the deformation and fracture behaviors of a white marble specimen during three-point bending impact tests. The complete cracking process was recorded by two high-speed cameras and then the exact crack tip positions at each moment were determined. Full displacement and strain fields in the ROI of the white marble specimen were obtained using DIC image processing. Crack propagation velocities were given and variations of the DSIFs obtained by both DIC and the strain gage method were analyzed and compared. The key conclusions are as follows:

• 1. The high-speed camera situated at the back side of the specimen can exactly locate the crack tip positions at each moment during the cracking process. Thus, the crack propagation velocity, which is almost constant during the cracking process, can be obtained for DSIF calculations with the strain gage method.

• 2. With the crack tip positions known prior using the high-speed camera, the corresponding displacement and strain fields in the ROI can be obtained by DIC image processing. The displacement gradients increase continuously while the degree of strain concentration decreases after crack initiation due to the energy dissipation at the crack tip, and then rises with the development of the running crack.

• 3. The changing trend in strain responses sensed by the stain gages show agreement with the modified strain variations obtained theoretically. For the gages #1 to #4, the DSIFs obtained by the strain gage method are close to the corresponding results from the DIC method. However, the strain signal in gage #5 is influenced by the size effect and multiple stress waves, causing a larger deviation in DSIF compared with that obtained by the DIC method.

• 4. DIC is free from considerations of stress waves and its DSIFs change within relatively lower fluctuations, indicating that DIC is a flexible and stable method for studying fracture behaviors of rock materials. In contrast, the strain gage method can provide a quick measurement of fracture parameters of rock masses, and a rough changing trend in DSIFs during the cracking process can also be given by using a limited number of strain gages.