Methodology for Establishing Comprehensive Stress Paths in Rocks During Hollow Cylinder Testing

Abstract

We here systematically investigated the methodology for establishing comprehensive stress paths with the aim of developing hollow cylinder apparatuses for rock mechanics. The research was based on the stress combination in element of hollow cylinder sample with varied loading analysis treatment. For this purpose, we discussed the mechanism underlying the variations in principal stress magnitude and principal stress rotation. The orientation angle of the major principal stress was defined in an alternative prospect. Then a series of stress paths was introduced, including the hydrostatic pressure stress path, principal stress magnitude variation stress path on the deviatoric plane, pure principal stress rotation stress path, and the complex stress path coupling the variation in the magnitude of principal stress and principal stress rotation effect. The comprehensive stress paths were analyzed with rock mechanical theory and a mathematical approach. The suggested loading methods were examined using simulation loading tests, laboratory case tests and special case verification. The results showed successful completion of different stress paths. The proposed methodology was first investigated systematically in rock mechanics, contributing to development of the new hollow cylinder apparatus and complex rock engineering simulation.

1 Introduction

Geomaterial behavior is influenced by factors such as stress path, anisotropy, and type of loading (Lee et al. 1999). Any theoretical model for predicting the performance of engineering structures must consider these factors. Among the factors, the stress path is widely considered suitable for evaluating the safety of engineering construction. Practically, the change in the stress state is represented by principal stress magnitude variation (PSMV) and principal stress rotation (PSR). The PSMV effect has been fully investigated in previous works. Before tunnel construction, there is an equilibrium between the space ahead of the tunnel face and the surrounding ground. Early research showed that the excavation leads to discontinuous distribution of engineering structure, accompanied by the change in the value of radial stress and tangential stress (Fenner 1938). Several types of experiments have been performed to study the stress–strain behavior of the representative element under the PSMV effect. These include the triaxial test (Ding et al. 2016) and true triaxial test (Feng et al. 2016; He et al. 2010). In these tests, the magnitude of the principal stress changes to simulate similar stress paths in engineering projects.

To facilitate more generalized stress-path testing of soils, such as PSR testing, the more sophisticated hollow cylinder apparatus (HCA) was developed for use in soils. HCAs allow independent control of the magnitude of the three principal stresses and rotation of the principal stress axes. Hight et al. (1983) described both the design and principles of operation of a new HCA and its use in the investigation of PSR effects in sands and clays. Saada et al. (1983) introduced a thin hollow cylinder used in the soil laboratory for studies of soil strength and stability under both static and earthquake conditions. Vaid et al. (1990) used a new HCA to study the loose and dense sand behavior and assessed the stress nonuniformity across the wall of the specimen. Talesnick et al. (2000) determined five mechanical parameters with HCA to describe the elastic behavior of a transverse isotropic rock. O’Kelly and Naughton (2005) introduced a new and automated HCA and studied the stress–strain responses of Leighton Buzzard sand over the intermediate to failure strain range.

Although such soil apparatuses are still rare, their development and use have steadily increased. However, HCAs used in rocks are quite limited. Lee et al. (2002) used HCA to analyze the yield surface of Mu-San sandstone under a true triaxial stress path. Alsayed (2002) used the Hoek triaxial cell and hollow cylinder sandstone to conduct a series of triaxial and polyaxial compression tests. Yang (2016) investigated the deformation, peak strength, and crack damage behavior of hollow sandstone specimens under different confining pressures with various hole diameters. Based on the horizontal and vertical cross-sectional CT images, Yang (2018) evaluated the internal damage behavior of hollow-cylinder sandstone specimens under confining pressures. Although existing studies have attempted to use a hollow cylinder specimen in rocks, the test regarding the PSR effect has never been investigated. Alsayed (2002) found that the lack of suitable testing facilities and the cost and effort required for developing such facilities may have caused some hindrances. Recently, Zhou et al. (2018) successfully developed a new rock mechanical experimental technique and device, and firstly reported a simultaneous control of both stress magnitude variation and orientation in rock test. However, the methodology for establishing a generalized stress path with a versatile HCA taking into account the PSMV and PSR effects in rock mechanics has never been systematically studied.

In this paper, the stress paths used to simulate the PSMV and PSR and its methodology were systematically investigated. The equivalent stresses in the element representing the HCA sample and its role on the PSMV and PSR were studied. The orientation angle of major principal stress was defined in an alternative prospect. Additionally, the variations in stresses associated with the complex stress path were derived in detail. Our methodology contributes to the HCA development and engineering simulation in rock mechanics.

2 Motivation of Hollow Cylinder Test and Stress Path Design

PSR is a common stress path in geotechnical engineering, and it can be induced by dynamic loading events such as earthquakes, vehicular traffic, tunnel excavation, and ocean waves. After the rotation of the principal stress axes was proposed, more emphasis has been placed on the effect of PSR in soil tests and theories. Wang et al. (2016) took into account the impact of PSR under earthquake loading using an elastoplastic soil model. Lin et al. (2016) carried out a series of cyclic principal stress rotation tests and SEM techniques on intact clay to model the influence of traffic loading. Ishihara and Towhata (1983) explored the nature of cyclic loading in seabed soil deposits due to travelling waves. Most studies assessed the theoretical model approach using PSR. Furthermore, Yang and Yu (2013) used a typical and representative kinematic hardening soil model to reproduce soil responses under PSR. Gutierrez et al. (2009) developed a constitutive model for the behavior of sands during monotonic simple shear loading. Nishimura and Towhata (2004) proposed a three-dimensional stress–strain model of sand using the concept of multiple shear mechanisms.

There is no suitable test equipment with completing PSR effect for rock, so the research is limited to numerical simulation and theoretical analysis in rocks. Eberhardt (2001) explored near-field stress paths during the progressive advancement of a tunnel face using a three-dimensional finite-element approach, and proposed that the three-dimensional stress field encompasses a series of deviatoric stress and also increases or decreases across several rotations of the principal stress axes. Diederichs et al. (2004) performed a case study illustrating the influence of tunnel-induced stress rotation on crack propagation, interaction, and ultimately coalescence and failure. Zhou (2010) developed a micro-mechanics-based model to investigate microcrack damage mechanism of four stages of brittle rock under PSR. Lastly, Zhang et al. (2011) used the simulation methods of micro-mechanics and the 3D simulation of the excavation process to study the effect of PSR on layered fractures at the Jinping II Hydropower Station. For tunneling excavation, a spatial stress redistribution accompanied by deformation occurs around the working face (Cantieni and Anagnostou 2009). Here we summarized the evolution of principal stresses at tunnel roof during tunneling excavation in Fig. 1. As the tunnel face approaches and passes through a unit volume of surrounding rock, the spatial evolution of the stress field encompasses a series of PSMV as well as PSR.

Fig. 1

Evolution of principal stresses at tunnel roof during excavation: a Monitoring point is far away from the tunnel face, and basically undisturbed. b Monitoring point is getting closer to the tunnel face, and minor change in magnitude and orientation takes place. c Monitoring point is at the position of the tunnel face, and significant change in magnitude and orientation occurs. d Monitoring point is gradually away from the tunnel face, and minor change in magnitude and orientation takes place

From fracture mechanics for a single crack, wing crack initiates along principal stress direction at crack tip. The propagation of wing crack is restricted because of the influence of other principal stresses on the crack at the vertical direction. After the rotation of principal stress axis, the crack propagates along the direction of new principal stress and the depth of crack propagation increases. For the fracture network (see Fig. 2), when the principal stress reaches the threshold of yield strength, the micro-fractures mainly extend along the principal stress direction. With the rotation of the principal stress axis, the crack propagation turns to the new principal stress direction. The density of fractures increases and eventually leads to the intersection and penetration of new and old fissures, and the degree of destruction intensifies. It can be seen that compared with the non-rotation of principal stress axis, the failure characteristics of rock after rotation of principal stress axis are significantly changed, and the cracks are further penetrated during rotation.

Fig. 2

Conceptual model of damaged fracture network due to rotation of the principal stress axis over a successive series of critical angles (Eberhardt 2001)

From above analysis, both of PSMV and PSR play an important role in geotechnical engineering safety and mechanical properties. In fact, conventional geotechnical tests cannot take into account the PSR effect. Other than the hollow cylinder apparatus that works for it, nothing else has been reported. The hollow cylinder tests for soils have been successfully used to study the influence of the PSR effect on the strength and deformation behaviors of soils (Hight et al. 1983; Ishihara and Towhata 1983; Vaid et al. 1990; Sayao and Vaid 1991; O’Kelly and Naughton 2005), and it was demonstrated that strength and deformation parameters of soil are significantly stress-path dependent. However, almost all the traditional mechanical test techniques and devices in the field of rock mechanics can only control the stress magnitude variation, while the simultaneous control of both stress magnitude variation and orientation is actually impossible (Bieniawski 1967; Eberhardt et al. 1999; Ganne and Vervoort 2006; Amann et al. 2011, 2012). Thus, Zhou et al. (2018) developed a new rock experimental technique and device, which can take a simultaneous control of both stress magnitude variation and orientation in rock test.

Corresponding to the newly developed rock hollow cylinder apparatus, the stress path suitable for the test instrument should be developed. Table 1 lists the stress paths commonly used in the existing HCA tests for reference. It can be seen that most of these stress paths were not expressed in the form of stress invariants. Similarly, in the true triaxial test, most stress paths have not taken the form of stress invariants. The common stress path was criticized by Ma et al. (2017) that all three principal stress invariants, mean stress, octahedral shear stress, and Lode angle, change throughout the test. Consequently, an alternative stress path is desired to isolate the effects of stress invariants relative to the new HCA tests.

Table 1 Commonly used stress paths in the existing HCA tests

3 Principle of Hollow Cylinder Test

3.1 Test Setup and Theories

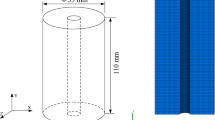
The hollow cylinder sample was used in the laboratory test. In soil tests, the selection of sample size mainly considers the following factors: (1) the stress and strain distribution is not uniform along the wall thickness due to the specimen curvature. The appropriate size should be chosen to reduce the nonuniformities of stress and strain distribution as much as possible. (2) Reduce the influence of the end effect on the representative element of the specimen. (3) There are enough soil particles along the wall-thickness direction. The wall thickness should be more than ten times of the particle size of the soil. Taking into account the above factors, Hight et al. (1983) defined the nonuniformity coefficient for each individual stress component. Sayao and Vaid (1991) recommended dimensions for HCA specimens: (1) wall thickness is 20–26 mm; (2) $0.65 \leqslant {R_{\text{i}}}/{R_{\text{e}}} \leqslant 0.82$; (3) the ratio of height to $2{R_{\text{e}}}$ is 1.8:2.2. Different from soil samples, the rock samples can be prepared by drilling core method, and the relevant experience can ensure the success of the sample preparation. The size of rock hollow cylinder specimen should be based on the principle of thin wall cylinder and minimum end effect. In this HCA test, a hollow cylinder specimen with the outer diameter of 50 mm, inner diameter of 30 mm, and height of 120 mm was selected. To prepare the hollow cylinder specimen more precisely and efficiently, a double-drill device was developed as shown in Fig. 3. As an alternative method, the samples can also be prepared by drilling the inner hole first and then the outer hole. If the influence of initial anisotropy on mechanical properties needs to be studied, the core can be drilled at different angles along the bedding planes. After the specimen was made, the inner wall was then coated with epoxy sealant, and both ends were bonded with the top cap and base pedestal using the adhesive, respectively, which was implemented with the assistance of a self-developed tooling device in this work. The outer wall was wrapped with a thermoplastic tube and sealed with epoxy sealant at both ends. Through these series of preparation, the internal and external surfaces of the specimen can withstand the confining pressure, and the two ends of the specimen can hold a torque. The whole system is schematized in Fig. 4.

Fig. 3

Sample preparation with drilling device and technique

Fig. 4

Schematic of HCA system for rock

Similar to conventional rock mechanical tests, in this study stress analysis was performed in an element in the middle of specimen vertical wall. The four types of surface traction, namely, vertical load F, torque M_t, external radial pressures P_e, and internal radial pressures P_i, respectively, acting on the hollow cylinder specimen are illustrated in Fig. 5a. These forces induce vertical stress ${\tilde {\sigma }_z}$, radial stress ${\tilde {\sigma }_r}$, circumferential stress ${\tilde {\sigma }_\theta }$, and shear stress ${\tilde {\tau }_{z\theta }}$ in the wall of the specimen. Referring to the study by Hight et al. (1983), distributions of these stresses are influenced by the curvature and end restraint, but they are basically similar for elastic and plastic materials. For simplicity, the linear elasticity theory was used in analysis. Therefore, ${\tilde {\sigma }_r}$ and ${\tilde {\sigma }_\theta }$ are expressed as follows:

Fig. 5

Stress conditions in a hollow cylinder element: a hollow cylinder sample and stresses on an element in the wall. b An element in the z–θ plane without τ_zθ. c Mohr circle representation of stress state before loading τ_zθ. d An element in the z–θ plane considering τ_zθ. e Mohr circle representation of stress state after loading τ_zθ

$${\tilde {\sigma }_r}=\frac{{{P_{\text{e}}}R_{{\text{e}}}^{2} - {P_{\text{i}}}R_{{\text{i}}}^{2}}}{{R_{{\text{e}}}^{2} - R_{{\text{i}}}^{2}}} - \frac{{\left( {{P_{\text{e}}} - {P_{\text{i}}}} \right)R_{{\text{e}}}^{2}R_{{\text{i}}}^{2}}}{{{r^2}\left( {R_{{\text{e}}}^{2} - R_{{\text{i}}}^{2}} \right)}}$$

(1)

$${\tilde {\sigma }_\theta }=\frac{{{P_{\text{e}}}R_{{\text{e}}}^{2} - {P_{\text{i}}}R_{{\text{i}}}^{2}}}{{R_{{\text{e}}}^{2} - R_{{\text{i}}}^{2}}}+\frac{{\left( {{P_{\text{e}}} - {P_{\text{i}}}} \right)R_{{\text{e}}}^{2}R_{{\text{i}}}^{2}}}{{{r^2}\left( {R_{{\text{e}}}^{2} - R_{{\text{i}}}^{2}} \right)}}$$

(2)

in which R_e and R_i are, respectively, the external and internal specimen radii. $r$ is the radius of any point in a hollow cylinder.

To simulate complex stress paths using hollow cylinder apparatus, the thin-wall approach was adopted in preparing specimen. Vaid et al. (1990) proposed that the uniform stress distribution assumption can be used across the wall of the specimen when its dimensions satisfy the conditions to decrease the effect of the curvature and restraint at its end. In this case, the average radial stress σ_r and circumferential stress σ_θ are obtained by averaging data collected across the wall, as follows:

$${\sigma _r}=\frac{{\int_{{{R_{\text{i}}}}}^{{{R_{\text{e}}}}} {{{\tilde {\sigma }}_r}{\text{d}}r} }}{{\int_{{{R_{\text{i}}}}}^{{{R_{\text{e}}}}} {{\text{d}}r} }}=\frac{{{P_{\text{e}}}{R_{\text{e}}}+{P_{\text{i}}}{R_{\text{i}}}}}{{{R_{\text{e}}}+{R_{\text{i}}}}}$$

(3)

$${\sigma _\theta }=\frac{{\int_{{{R_{\text{i}}}}}^{{{R_{\text{e}}}}} {{{\tilde {\sigma }}_\theta }{\text{d}}r} }}{{\int_{{{R_{\text{i}}}}}^{{{R_{\text{e}}}}} {{\text{d}}r} }}=\frac{{{P_{\text{e}}}{R_{\text{e}}} - {P_{\text{i}}}{R_{\text{i}}}}}{{{R_{\text{e}}} - {R_{\text{i}}}}}$$

(4)

From moment equilibrium and uniform stress distribution assumption, average shear stress τ_zθ is expressed as follows:

$${\tau _{z\theta }}=\frac{{3{M_{\text{t}}}}}{{2\pi \left( {R_{{\text{e}}}^{3} - R_{{\text{i}}}^{3}} \right)}}$$

(5)

For axisymmetric material and uniform vertical load, the vertical stress is not dependent on the material constitutive law, and is found only by equilibrium considerations as the following expression

$${\sigma _z}=\frac{{F+\pi \left( {{P_{\text{e}}}R_{{\text{e}}}^{2} - {P_{\text{i}}}R_{{\text{i}}}^{2}} \right)}}{{\pi \left( {R_{{\text{e}}}^{2} - R_{{\text{i}}}^{2}} \right)}}$$

(6)

As shown in Fig. 5a, σ_r is one principal stress. The other two principal stresses, σ′_z and σ′_θ, depend on σ_z, σ_θ, and τ_zθ in the 2-D stress plane. Without τ_zθ, the orientations of the principal stresses coincide with the coordinates z and θ. The 2-D element and Mohr circle representation of stress are shown in Fig. 5b, c. The 2-D element after τ_zθ starts to exist is shown in Fig. 5d. The corresponding Mohr circle is represented in Fig. 5e. The radius of the Mohr circle increases, which means the principal stresses increase. Furthermore, the stress point representing the stress state goes beyond coordinate σ, suggesting that the principal stresses rotate. In this way, the combination of the four stresses with hollow cylinder test would fulfill the loading capacity of PSMV and PSR.

3.2 Orientation of the Major Principal Stress

The orientation of the major principal stress is defined as the angle α rotated clockwise from the positive direction of the coordinate z to the major principal stress, as shown in Fig. 6. α ranges from 0 to π.

Fig. 6

Illustration of α

The radial stress σ_r is considered the intermediate principal stress in the element of the hollow cylinder specimen. The principal element, subjected to principal stresses, rotates in the vertical plane of σ_r, and α has no connection to the radial stress σ_r. Analysis of the 2-D element under the major principal stress and the minimum principal stress is shown in Fig. 7a. Throughout this paper, normal stresses are considered positive when they are compressive, and negative when they are tensile. Shear stresses are viewed positive when the element is rotated counterclockwise.

Fig. 7

Description of the link between principal stresses and plane stresses using two kinds of stress state representation: a 2-D element with an oblique section. b Mohr circle diagram with a semicircle for δ$\in$[–π/4 to π/4]

The plane ef in Fig. 7a divides the element into two parts. Block aef is here analyzed. It is subjected to four stresses: normal stress σ₁₃ and shear stress τ₁₃ on plane ef, σ₁ on plane ae, and σ₃ on plane af. δ is the angle with positive value rotating counterclockwise from the major principal stress σ₁ to the normal stress σ₁₃, and negative for clockwise rotation. δ ranges from − π/4 to π/4. If the area of the plane ef is assumed to be dA, then the areas of planes af and ae are dAsinδ and dAcosδ, respectively. In block aef, the equilibrium equations can be derived as follows:

$${\sigma _{13}}\sin \delta - {\sigma _3}\sin \delta - {\tau _{13}}\cos \delta =0$$

(7)

$${\sigma _1}\cos \delta - {\sigma _{13}}\cos \delta - {\tau _{13}}\sin \delta =0$$

(8)

From Eqs. (7) and (8), the stresses in Mohr circle are expressed as follows:

$${\sigma _{13}}=\frac{{{\sigma _1}+{\sigma _3}}}{2}+\frac{{{\sigma _1} - {\sigma _3}}}{2}\cos 2\delta$$

(9)

$${\tau _{13}}=\frac{{{\sigma _1} - {\sigma _3}}}{2}\sin 2\delta$$

(10)

For δ$\in$[–π/4 to π/4], the stress state of σ₁₃ and τ₁₃ can be represented by the semicircle in Fig. 7b. The following conclusions can be inferred: (a) if normal stress σ₁₃ rotates counterclockwise with the angle |δ| until aligning with direction of the major principal stress σ₁, and then the shear stress τ₁₃ < 0; (b) if normal stress σ₁₃ rotates clockwise with the angle δ until it aligns with major principal stress σ₁, then the shear stress τ₁₃ > 0.

According to Fig. 7, the expression of δ is derived as follows:

$$\delta =\frac{1}{2}\arctan \left[ {2{\tau _{13}}/\left( {{\sigma _1} - {\sigma _3}} \right)} \right]$$

(11)

In a hollow cylinder element, Eq. (11) could be rewritten as follows:

$$\left\{ \begin{gathered} \delta =\frac{1}{2}\arctan \left[ {2{\tau _{z\theta }}/\left( {{\sigma _z} - {\sigma _\theta }} \right)} \right]{\text{ }},{\text{ }}{\sigma _z}>{\sigma _\theta } \hfill \\ \delta =\frac{1}{2}\arctan \left[ {2{\tau _{\theta z}}/\left( {{\sigma _\theta } - {\sigma _z}} \right)} \right]{\text{ }},{\text{ }}{\sigma _z}<{\sigma _\theta } \hfill \\ \end{gathered} \right.$$

(12)

τ_zθ represents the negative ratio of τ_θz, which gives a generalized expression of δ as follows:

$$\delta =\frac{1}{2}\arctan \left[ {2{\tau _{z\theta }}/\left( {{\sigma _z} - {\sigma _\theta }} \right)} \right]$$

(13)

Therefore, based on the Mohr circle theory and limit equilibrium analysis method, δ is derived as Eq. (13) using the stresses consistent with hollow cylinder test. Further conclusions of the element rotation in Fig. 5 can be drawn by the inferences which we have made with Fig. 7b: (a) For the case σ_z > σ_θ, σ′_z is the major principal stress and σ′_θ is the minimum principal stress (Fig. 8a). When τ_zθ < 0, the element rotates counterclockwise by the angle of |δ|, and σ_z becomes σ′_z. When τ_zθ > 0, the element rotates clockwise by the angle of δ, and σ_z becomes σ′_z. (b) For the case σ_z < σ_θ, σ’_θ is the major principal stress and σ′_z is the minimum principal stress (Fig. 8b). When τ_θz < 0, the element rotates counterclockwise by the angle of |δ|, and σ_θ becomes σ′_θ. When τ_θz > 0, the element rotates clockwise by the angle of δ, and σ_θ becomes σ′_θ.

Fig. 8

Identification of the principal element with no shear stresses: a case of σ_z > σ_θ. b case of σ_z < σ_θ

From conclusions in Fig. 7, we can see that by controlling the magnitudes and directions of normal stress and shear stress, the corresponding principal element can be found by rotation of any plane element at a certain angle of δ. However, this angle is limited to − π/4 to π/4 in its definition. If the rotation angle of the major principal stress axis (α) in Fig. 6 is introduced, a more general theory of element rotation in hollow cylindrical test can be established.

The magnitude of δ is related to 2τ_zθ and (σ_z–σ_θ) according to Eq. (13). In this way, depictions of PSR in the 2τ_zθ– (σ_z–σ_θ) coordinate system can be sketched as shown in Fig. 9. Figure 9a, b show identification of the principal stress using the angle of δ and α, respectively. For the convenience of analysis, we take the stress point representing the initial stress state of the element in the positive (σ_z–σ_θ) coordinate. The stress point then passes through the first quadrant, the positive τ_zθ coordinate, the second quadrant, the negative (σ_z–σ_θ) coordinate, the third quadrant, the negative τ_zθ coordinate, the fourth quadrant in turn. For ease of understanding, the stress path is represented in Fig. 9 by the arrow and alphabetical order (a)–(h). In the diagram, we no longer use the element in a general stress state, but we use the principal element for representation. With the stress point changing in turn, the principal element rotates. Based on the above theoretical analysis, Table 2 complements Fig. 9 and shows the plane elements, principal elements and the expression of δ and α in various stress point location in alphabetical order in Fig. 9.

Fig. 9

Mechanism underlying PSR in an element of the hollow cylinder specimen in the 2τ_zθ- (σ_z–σ_θ) coordinate system: a Identification of the principal stress using the angle of δ. b Identification of the principal stress using the angle of α

Table 2 Illustrations of the element with the stresses (normal stresses and shear stresses, or principal stresses) and the expression of δ and α for various stress point locations in the 2τ_zθ– (σ_z–σ_θ) coordinate system

Combining Table 2 and Fig. 9, the stresses and angles of the element during rotation were analyzed with examples. Firstly, the stress point representing the initial stress state of the element is located at the positive (σ_z–σ_θ) coordinate, which suggests σ_z > σ_θ, then σ_z is the major principal stress σ₁, and σ_θ is the minimum principal stress σ₃. The corresponding alphabetic number is (a). In this case, δ = 0 and α = 0. After that, the stress point moves to the first quadrant, corresponding to the letter (b). σ_z > σ_θ and τ_zθ > 0. By the practice of Fig. 8, we can get that σ_z rotates clockwise by the angle of δ and finds the major principal stress σ₁ = σ′_z. In this case, δ = α and α$\in$(0, π/4). From Eq. (13), $\alpha =\frac{1}{2}\arctan \left[ {2{\tau _{z\theta }}/\left( {{\sigma _z} - {\sigma _\theta }} \right)} \right]$. When the stress point continues to move alphabetically to (c), it is located in the positive τ_zθ coordinate, which suggests τ_zθ > 0 and σ_z = σ_θ. This is a bit special for obtaining the value of δ. On one hand, when going from (a) to (c) in alphabetical order, σ_z rotates clockwise by π/4 and finds the maximum principal stress σ₁ = σ’_z, and δ = π/4; On the other hand, if we take the order (e) to (c), that is, in the second quadrant, σ_θ rotates counterclockwise by π/4 and finds the major principal stress σ₁ = σ′_θ. In this case, δ = − π/4. In any case, both approaches can yield consistent results, i.e., α = π/4. Referring to the above analysis, the rest of the results are obtained, as shown in Table 2 and Fig. 9, and are therefore not restated.

It is worth noting that Table 2 lists the values of α in each case, and the expression of α can be summarized based on the results of Table 2 as follows:

$$\alpha =\left\{ {\begin{array}{*{20}{l}} {\frac{1}{2}\arctan \frac{{2{\tau _{z\theta }}}}{{{\sigma _z} - {\sigma _\theta }}},}&{\quad {\text{if}}\;{\sigma _z}>{\sigma _\theta }\;{\text{and}}\;{\tau _{z\theta }} \geqslant 0{\text{ }}} \\ {\frac{1}{2}\arctan \frac{{2{\tau _{z\theta }}}}{{{\sigma _z} - {\sigma _\theta }}}+\frac{\pi }{2},}&{\quad {\text{if}}\;{\sigma _z}<{\sigma _\theta }} \\ {\frac{1}{2}\arctan \frac{{2{\tau _{z\theta }}}}{{{\sigma _z} - {\sigma _\theta }}}+\pi ,}&{\quad {\text{if}}\;{\sigma _z}>{\sigma _\theta }\;{\text{and}}\;{\tau _{z\theta }}<0{\text{ }}} \\ {\frac{\pi }{4},}&{\quad {\text{if}}\;{\sigma _z}=\sigma \;{\text{and}}\;{\tau _{z\theta }}>0} \\ {\frac{{3\pi }}{4},}&{\quad {\text{if }}\;{\sigma _z}={\sigma _\theta }\;{\text{and}}\;{\tau _{z\theta }}<0{\text{ }}} \end{array}} \right.$$

(14)

4 Methodology for Stress Path in HCA

4.1 Representation of Stress State

For a given stress state with three principal stresses σ₁, σ₂, and σ₃, there exists a point B in the principal stress space in Fig. 10a. Vector $\overline {{\mathbf{O}\mathbf{B}}}$ may be viewed as the operation of $\overline {{\mathbf{O}\mathbf{A}}}$ + $\overline {{{\mathbf{AB}}}}$. The vector $\overline {{\mathbf{O}\mathbf{A}}}$ aligns in the hydrostatic axis. When under hydrostatic pressure, geomaterial, especially rock, is vulnerable to yield. Therefore, the stress path along the hydrostatic axis is viewed a safe means of loading pressure. On the contrary, the vector $\overline {{{\mathbf{AB}}}}$ grows longer on the deviatoric plane and becomes limited in the yield envelope. The deviatoric plane is perpendicular to the hydrostatic axis. The stress path deviating from the hydrostatic axis on the deviatoric plane increases the instability of the material. In Fig. 10b, point C is on the yield envelop and defines the boundary of $\overline {{{\mathbf{AB}}}}$. Accordingly, the stress tensor σ_ij can be decomposed into two parts (Chen and Saleeb 2013) as follows:

Fig. 10

Description of stress state: a stress state representation in the principal stress space. b Stress point and yield envelop on the deviatoric plane. c Stress point and yield envelop on the meridian plane

$${{\mathbf{\sigma }}_{ij}}=p{{\mathbf{\delta }}_{ij}}+{{\mathbf{S}}_{ij}}$$

(15)

Here, pδ_ij represents the hydrostatic stress tensor. p is hydrostatic pressure defined as $p=\frac{1}{3}{{\mathbf{\sigma }}_{kk}}$. δ_ij is the Kronecker Delta. The value of δ_ij gets 1 when i = j and 0 on the contrary. S_ij is the stress deviator tensor.

${\theta _\sigma }$ is an important parameter in Fig. 10b, representing the following stress relationship:

$${\theta _\sigma }={\text{arctan}}\frac{{2{\sigma _2} - {\sigma _1} - {\sigma _3}}}{{\sqrt 3 \left( {{\sigma _1} - {\sigma _3}} \right)}}$$

(16)

The length of $\overline {{{\mathbf{AB}}}}$ equals to $\sqrt {2{J_2}}$ and ${J_2}$ is expressed as $\frac{{{{\mathbf{S}}_{ij}}{{\mathbf{S}}_{ij}}}}{2}$. Thus, the principal stress deviators are as follows:

$${S_1}=\frac{2}{{\sqrt 3 }}\sqrt {{J_2}} \cos \left( {{\theta _\sigma }{\text{+}}\frac{\pi }{6}} \right)$$

(17)

$${S_2}=\frac{2}{{\sqrt 3 }}\sqrt {{J_2}} \cos ({\theta _\sigma } - \frac{\pi }{2})$$

(18)

$${S_3}=\frac{2}{{\sqrt 3 }}\sqrt {{J_2}} \cos ({\theta _\sigma }{\text{+}}\frac{{5\pi }}{6})$$

(19)

As shown in Fig. 10c, q is the equivalent shear stress and $q=\sqrt {3{J_2}}$. There exists a relationship between the geometric length in Fig. 10a, c, such as $\left| {\overline {{\mathbf{O}{\mathbf{A}^\prime }}} } \right|$ = 1/$\sqrt 3 \left| {\overline {{\mathbf{O}\mathbf{A}}} } \right|$ and $\left| {\overline {{{\mathbf{A}^\prime }{\mathbf{B}^\prime }}} } \right|$ = $\sqrt {3/2} \left| {\overline {{\mathbf{A}\mathbf{B}}} } \right|$.

4.2 Hydrostatic Pressure Stress Path

In this case, the stress path represents the line OA in the principal stress space, point A on the deviatoric plane, and line A′B′ on the meridian plane (see Fig. 10). The three principal stresses are equal, as shown by

$${\sigma _z}={\sigma _r}={\sigma _\theta }=p$$

(20)

4.3 PSMV Stress Path on the Deviatoric Plane

The PSMV stress path in this section is discussed after the hydrostatic pressure is loaded as p₀. Presume the vertical stress σ_z, radial stress σ_r, circumferential stress σ_θ is loaded to p₀ + ∆σ_z, p₀ + ∆σ_r and p₀ + ∆σ_θ, respectively. In this case, the rotation angle of the maximum principal stress axis α, the Lode angle θ_σ, and the hydrostatic pressure p are constant. The equivalent shear stress q is loaded until yield. Its stress path can be represented in Fig. 10 as the line AB in the principal stress space and A′B′ on the meridian plane.

To assess the influence of the intermediate principal stress, intermediate principal stress coefficient b is widely used. b has the relationship with θ_σ as follows:

$$\sqrt 3 \tan {\theta _\sigma }=2b - 1$$

(21)

The expression of α and stress state corresponding to the stress point in the 2τ_zθ– (σ_z–σ_θ) coordinate system vary at different quadrants and coordinates, as shown in Table 2 and Eq. (14). The stress path was discussed with the 2τ_zθ– (σ_z–σ_θ) coordinate system.

If the stress state point is located at the first quadrant, then σ_z > σ_r > σ_θ and τ_zθ > 0. The major principal stress and minimum principal stress are expressed as follows:

$${\sigma _1} = \frac{{{\sigma _z}+{\sigma _\theta }}}{2}+\sqrt {\frac{{{{\left( {{\sigma _z} - {\sigma _\theta }} \right)}^2}}}{4}+\tau _{{z\theta }}^{2}}$$

(22)

$${\sigma _3} = \frac{{{\sigma _z}+{\sigma _\theta }}}{2} - \sqrt {\frac{{{{\left( {{\sigma _z} - {\sigma _\theta }} \right)}^2}}}{4}+\tau _{{z\theta }}^{2}}$$

(23)

The independent variables b, α, p, and q in the stress path can be expressed as follows:

$$b=\frac{{{\sigma _2} - {\sigma _3}}}{{{\sigma _1} - {\sigma _3}}}$$

(24)

$$\tan 2\alpha =\frac{{2{\tau _{z\theta }}}}{{{\sigma _z} - {\sigma _\theta }}}$$

(25)

$$p={\sigma _z}+{\sigma _\theta }+{\sigma _r}={\text{const}}.$$

(26)

$$q=\sqrt {3{J_2}}$$

(27)

From Eqs. (22) to (27), we have the following:

$$b=\frac{{\Delta {\sigma _r} - \frac{{\Delta {\sigma _z}+\Delta {\sigma _\theta }}}{2}+\left| {\frac{{\Delta {\sigma _z} - \Delta {\sigma _\theta }}}{{2\cos 2\alpha }}} \right|}}{{\left| {\frac{{\Delta {\sigma _z} - \Delta {\sigma _\theta }}}{{\cos 2\alpha }}} \right|}}$$

(28)

$$\tan 2\alpha =\frac{{2{\tau _{z\theta }}}}{{\Delta {\sigma _z} - \Delta {\sigma _\theta }}}$$

(29)

$$\Delta {\sigma _z}+\Delta {\sigma _\theta }+\Delta {\sigma _r}=0$$

(30)

$$q=\sqrt {\frac{{{{\left( {\Delta {\sigma _z} - \Delta {\sigma _\theta }} \right)}^2}+{{\left( {\Delta {\sigma _r} - \Delta {\sigma _\theta }} \right)}^2}+{{\left( {\Delta {\sigma _z} - \Delta {\sigma _r}} \right)}^2}}}{2}+3\tau _{{z\theta }}^{2}}$$

(31)

At the first quadrant σ_z > σ_θ and cos2α > 0, according to Eqs. (28) and (30) we have the following:

$$\Delta {\sigma _\theta }=\Delta {\sigma _r}\frac{{3\cos 2\alpha - 1+2b}}{{2\left( {1 - 2b} \right)}}$$

(32)

$$\Delta {\sigma _z}=\Delta {\sigma _r}\frac{{ - 3\cos 2\alpha - 1+2b}}{{2\left( {1 - 2b} \right)}}$$

(33)

From Eqs. (29) and (31) through (33), the variable q can be written as follows:

$$q=3\left| {\frac{{\Delta {\sigma _r}}}{{1 - 2b}}} \right|\sqrt {{b^2} - b+1}$$

(34)

If b < 0.5, according to Eq. (33) ∆σ_z∆σ_r < 0. Otherwise, according to Eq. (32) ∆σ_θ∆σ_r < 0. Therefore, ∆σ_r < 0 for b < 0.5 and ∆σ_r > 0 for b > 0.5. Then Eq. (34) can be rewritten as follows:

$$q=\frac{{3\Delta {\sigma _r}}}{{2b - 1}}\sqrt {{b^2} - b+1}$$

(35)

From Eqs. (29), (32), (33), and (35), the four stresses associated with the element in the hollow cylinder can be expressed as follows:

$$\Delta {\sigma _z}=\frac{{3\cos 2\alpha +1 - 2b}}{{6\sqrt {{b^2} - b+1} }}q$$

(36)

$$\Delta {\sigma _r}=\frac{{2b - 1}}{{3\sqrt {{b^2} - b+1} }}q$$

(37)

$$\Delta {\sigma _\theta }{\text{=}}\frac{{ - 3\cos 2\alpha +1 - 2b}}{{6\sqrt {{b^2} - b+1} }}q$$

(38)

$${\tau _{z\theta }}=\frac{{\sin 2\alpha }}{{2\sqrt {{b^2} - b+1} }}q$$

(39)

Similarly, at the other quadrants, we find the same equations as derived above. In the PSMV stress path, when the hydrostatic pressure is loaded as p₀, and we can load the variable q until rock yields at the given constants b and α = 0. The controlling methodology of PSMV stress path on the deviatoric plane is shown in Table 3.

Table 3 Variations in stresses in the PSMV stress path on the deviatoric plane

4.4 PSR Stress Path

The PSR stress path discussed in this section is a sequential load followed by PSMV stress path. Presume that, before PSR stress path, the four stresses in the element are σ_z, σ_r, σ_θ, and τ_zθ = 0. After PSR loading, the stresses change to σ_z + ∆σ_z, σ_r + ∆σ_r, σ_θ + ∆σ_θ, and ∆τ_zθ. In this situation, the principal stress magnitude remains constant but the orientation of principal stress axis changes. There is no variation in the intermediate principal stress.

$$\Delta {\sigma _r}=0$$

(40)

The hydrostatic pressure remains constant and, according to Eq. (40), we have the following:

$$\Delta {\sigma _z}+\Delta {\sigma _\theta }=0$$

(41)

Based on Eq. (41) and the expression of principal stresses in Eqs. (22) and (23), the validation that no change in the principal stress magnitude can be expressed as follows:

$$\Delta \tau _{{z\theta }}^{2}=\Delta {\sigma _\theta }\left( {{\sigma _z} - {\sigma _\theta }} \right) - \Delta {\sigma _\theta }^{2}$$

(42)

Notice that there is a generalized expression as derived from Table 2.

$$\tan 2\alpha =\frac{{2\Delta {\tau _{z\theta }}}}{{{\sigma _z}+\Delta {\sigma _z} - {\sigma _\theta } - \Delta {\sigma _\theta }}}$$

(43)

From Eqs. (41) to (43), we have the following:

$$\left| {\left( {{\sigma _z} - {\sigma _\theta }} \right)\cos 2\alpha } \right|=\left| {{\sigma _z} - {\sigma _\theta } - 2\Delta {\sigma _\theta }} \right|$$

(44)

At the PSMV loading stage before the PSR loading, the direction of the major principal stress α is equal to 0, and σ_z-σ_θ > 0. Moreover, during the PSR loading process, $\cos 2\alpha \left( {{\sigma _z}+\Delta {\sigma _z} - {\sigma _\theta } - \Delta {\sigma _\theta }} \right)>0$. Then Eq. (44) may be rewritten as follows:

$$\left( {{\sigma _z} - {\sigma _\theta }} \right)\cos 2\alpha ={\sigma _z} - {\sigma _\theta } - 2\Delta {\sigma _\theta }$$

(45)

According to Eqs. (41), (43), and (45), we have the following:

$$\Delta {\sigma _\theta }=\frac{{\left( {{\sigma _z} - {\sigma _\theta }} \right)\left( {1 - \cos 2\alpha } \right)}}{2}$$

(46)

$$\Delta {\sigma _z}=\frac{{\left( {{\sigma _z} - {\sigma _\theta }} \right)\left( {\cos 2\alpha - 1} \right)}}{2}$$

(47)

$${\tau _{z\theta }}=\frac{{\sin 2\alpha }}{2}\left( {{\sigma _z} - {\sigma _\theta }} \right)$$

(48)

The controlling methodology of PSR stress path is shown in Table 4.

Table 4 Stresses variations in the PSR stress path

4.5 Complex Stress Path Considering PSMV and PSR Effect

Assume there is no change in α before the discussed complex loading in this section. During the consequent loading process, hydrostatic pressure is kept constant, while the equivalent shear stress q and the orientation of the major principal stress α change. The loading of q and α corresponds to the PSMV and PSR process, respectively. Equations (36) to (39) show how the four stresses in the element change with q and α for a constant p. The controlling methodology of complex stress path considering PSMV and PSR effect is shown in Table 5.

Table 5 Stresses variations in the stress path coupling PSMV and PSR effect

5 Verifications

5.1 PSMV Stress Path

To simulate the PSMV stress path on the deviatoric plane, a numerical experimentation was conducted. First, hydrostatic pressure p was loaded at rate of 1 MPa/s until 30 MPa. Then the equivalent shear stress q was loaded at 1 MPa/s to 40 MPa. During the PSMV loading process, b was set to 0.3. The stresses in the test control are shown in Fig. 11. In this simulation, we see τ_zθ equals to zero in the whole process, which means the PSR effect does not work. In the hydrostatic pressure loading, q remains zero, while σ_z, σ_r, σ_θ and p rise equally to 30 MPa. Then, σ_z increases, and the other two principal stresses decrease at different rates. p keeps the value of 30 MPa and q increases from zero.

Fig. 11

Variations in the stresses in a PSMV loading simulation

Here we used a test case for verification. Different from the above numerical simulation, in the test, b equals to 0.5, thus θ_σ equals to zero referring to the Eq. (21). The expected stress path is set as shown in Fig. 12a. First, p was applied simultaneously from point O to A, and the stress state was σ_z = σ_r = σ_θ = p at point A according to the Eq. (20). Then, q was successively applied. From Table 3, Δσ_z = Δσ_θ, while σ_r remained constant.

Fig. 12

Loads and stress variations in PSMV stress path: a expected stress path. b Load paths in the test. c Principal stress paths in the test. d Stress invariant path in the test

Figure 12b–d showed the load paths, the principal stress paths and the stress invariant path in the test, respectively. During the test, to follow the prescribed stress path precisely, P_e, P_i and F were loaded to 30 MPa in increments. Then, P_e, P_i and F changed the values to make Δσ_z = Δσ_θ. In this process, σ_r and p were observed constant. It is worth noting that, the load curves of σ_z and q fluctuated a lot in several segments. This is because in Fig. 4, the force area of R is larger than that of F, which results in the vertical stress σ_z of the sample being about eight times that of the oil pressure at R. So the slight fluctuation of the oil pressure at R can cause the fluctuation of σ_z to be magnified. If the force area of the piston rod at R was similar to the vertical force area of the rock sample, the amplification effect of this fluctuation would be weakened, and the experimental results would be more satisfactory. In brief, through the designed methodology, PSMV effect can be achieved with a reasonable result.

5.2 PSR Stress Path

To exemplify a PSR stress path, a numerical experimentation was conducted as shown in Fig. 13. First, p was loaded at 30 MPa, followed by q at 40 MPa, and b at 0.3. During the PSR loading process, the orientation of the major principal stress axis α rotated at rate of π/400 per second. The principal stresses remained constant throughout the loading simulation. This process can be used to assess the PSR effect on rocks.

Fig. 13

The stresses variations in a PSR loading simulation

5.3 Stress Path Coupling PSMV and PSR Effect

With the equations in Table 5, if q is formulated with the function of α, the complex stress path considering the PSMV and PSR effect can be simulated. Take a numerical loading simulation for an example. Hydrostatic pressure p was first loaded to 30 MPa, followed by the PSMV loading on the deviatoric plane with q = 40 MPa, and b = 0.3. The complex loading considering PSMV and PSR was finally applied. Here, for simplicity, q was presumed to have a linear relationship with α:

$$q={k_1}\alpha +{k_2}$$

(49)

where k₁ and k₂ are constants determined by the on-site conditions. In this example, we take k₁ = 10 MPa and k₂ = 40 MPa. Based on Eqs. (36) through (39), and (49), the stresses increment in the process are expressed as follows:

$$\Delta {\sigma _z} = \frac{{3\cos 2\dot {\alpha }t+1 - 2b}}{{6\sqrt {{b^2} - b+1} }}\left( {{k_1}\dot {\alpha }t+{k_2}} \right)$$

(50)

$$\Delta {\sigma _r} = \frac{{2b - 1}}{{3\sqrt {{b^2} - b+1} }}\left( {{k_1}\dot {\alpha }t+{k_2}} \right)$$

(51)

$$\Delta {\sigma _\theta} = \frac{{ - 3\cos 2\dot {\alpha }t+1 - 2b}}{{6\sqrt {{b^2} - b+1} }}\left( {{k_1}\dot {\alpha }t+{k_2}} \right)$$

(52)

$${\tau _{z\theta }}=\frac{{\sin 2\dot {\alpha }t}}{{2\sqrt {{b^2} - b+1} }}\left( {{k_1}\dot {\alpha }t+{k_2}} \right)$$

(53)

where $\dot {\alpha }$ is the rotation rate of the major principal stress axis, and t is the loading time. In the loading test example, $\dot {\alpha }$ is set to π/400 per second. Figure 14 shows the controlling stresses and α in the coupling process. α and q increase in a linear manner over loading time. The principal stresses change throughout the process. This loading methodology can be used in engineering response simulations under complex stress application considering the coupling PSMV and PSR effect.

Fig. 14

Variations in stresses and α in a coupling loading simulation considering PSMV and PSR

5.4 An Argumentation Based on Existing Theories

In the PSMV stress path, the vertical stress σ_z, radial stress σ_r, circumferential stress σ_θ is loaded to p₀ + ∆σ_z, p₀ + ∆σ_r and p₀ + ∆σ_θ, respectively. In this way, assuming that the proposed methodology is correct, ∆σ_z, ∆σ_r and ∆σ_θ should equal to the three principal stress deviators ${S_1}$, ${S_2}$ and ${S_3}$, respectively.

From the Eqs. (16) and(21), the expression of ∆σ_z in Table 3 can be rewritten as:

$$\begin{aligned} \Delta {\sigma _z} & =\frac{{2 - b}}{{3\sqrt {{b^2} - b+1} }}q \\ & =\frac{{2 - \frac{{\sqrt 3 \tan {\theta _\sigma }+1}}{2}}}{{3\sqrt {{{\left( {\frac{{\sqrt 3 \tan {\theta _\sigma }+1}}{2}} \right)}^2} - \frac{{\sqrt 3 \tan {\theta _\sigma }+1}}{2}+1} }}q \\ & =\frac{2}{3}q\cos \left( {{\theta _\sigma }+\frac{\pi }{6}} \right) \\ & {\text{=}}\frac{2}{{\sqrt 3 }}\sqrt {{J_2}} \cos \left( {{\theta _\sigma }{\text{+}}\frac{\pi }{6}} \right) \\ \end{aligned}$$

(54)

By the calculation of Eq. (54), ∆σ_z in Table 3 is observed to be identical to the expression of ${S_1}$ in Eq. (17). Similarly, by calculating ∆σ_r and ∆σ_θ in Table 3, the same expressions as ${S_2}$ and ${S_3}$ in formulas (18) and (19) can be obtained, respectively. Therefore, the equations in Table 3 are verified suitable for PSMV stress path. Furthermore, because the expression in Table 3 is a special case of Table 5 when α = 0, the above analysis can indirectly prove the application of expressions in Table 5 to the stress path coupling PSMV and PSR effect. In other words, the methodology for stress path proposed in this paper is verified.

6 Conclusions

To address the dearth of research into stress control with HCA completing comprehensive stress path, we here investigated this methodology systematically. The elastic stresses distribution in the HCA sample and the equivalent stresses in the element were proposed. A mechanism for completing PSMV and PSR stress paths was sketched. The key to considering the PSR effect is applying a torque, which is represented by existence of a shear stress. Based on Mohr circle theory, the orientation angle of major principal stress was defined in an alternative prospect in Eq. (14). Using the above as foundation for the present work, the methodology for establishing comprehensive stress paths was investigated, including a hydrostatic pressure stress path [in Eq. (20)], PSMV stress path on the deviatoric plane (see Table 3), pure PSR stress path (see Table 4), and complex stress path coupling the PSMV and PSR effect (see Table 5). In the end, the proposed methodology for stress paths was verified using numerical simulations, case test and special case verification.

The methodology for establishing a comprehensive stress path with the HCA was investigated systematically with respect to rock mechanics, contributing to the development of new HCAs and rock engineering simulations in complicated geological projects. The methodology for a comprehensive stress path, isolating the effect of stress invariants, is of great significance for studying the failure characteristics and the failure evolution of geomaterials. It is worth noting that the rock HCA is particularly suitable for studying the anisotropic mechanical properties of rock. Generally speaking, anisotropy consists of initial anisotropy and stress-induced anisotropy. The former is formed by geological reasons, while the latter is caused by stress disturbance (e.g., induced by artificial excavation). For the former, mechanical tests of rock samples with initial anisotropy can be carried out, while for the latter, different stress paths can be used in mechanical tests of isotropic rocks or intact rocks. Based on the method proposed in this paper, the strength and deformation characteristics in HCA tests and the mechanical model considering PSMV and PSR effects need to be further studied.