1 Introduction

Rockbolting of caverns and tunnels is a routine practice to stabilize rock masses in civil and mining engineering as the bolts are cost-effective, flexible to apply in changing ground conditions, convenient and fast to install (Huang et al. 2002). Rockbolting assists the rock mass to form a self-supporting structure through supporting loosened blocks, contributing shear resistance to the rock joints or discontinuities, and formation of beams and arches.

For shallow excavations where in situ stresses are low, the main stability concern is rockfall under gravity. The principle of rockbolting in this case is to stabilize the loosened blocks. Therefore, the strength of the bolt is a crucial parameter in the rock bolt design. A fully grouted rebar is a good choice for this purpose since it fully utilizes the strength of the bolt steel.

At a greater depth where in situ stresses are high, rock failure (e.g., rock squeezing in soft and weak rock and rock burst in hard rock) occurs due to high in situ stresses, instead of loosening. Rock bursts are often observed in the mines at a depth of about 600–800 m below the ground surface and become more prevailing below 1000 m (Li 2010). Either strain or fault-slip rock bursts tend to release a great amount of energy, which must be dissipated to avoid rock ejection. In addition to energy transfer, momentum is also transferred during the interaction between the ejected rock and the support device (Li and Doucet 2012). A shorter transfer time implies higher loading on the support device and vice versa. If a rigid support system is used and the momentum transfer time is short, the load may exceed the bolt strength and premature failure may occur. In view of energy absorption and momentum transfer, the rock bolts need to be strong and ductile as well. This type of rock bolts is called the energy-absorbing (or dynamic) rock bolt. Conventional rock bolts such as the fully grouted rebar and the Split Set are not appropriate due to either small deformation capacity or small load-bearing capacity.

The cone bolt is a type of energy-absorbing bolt. It consists of a smooth steel bar and a flattened conical fare which can absorb energy by plowing through the grout when subjected to pulling load (Jager 1992). Durabar is evolved from the cone bolt. The anchor of the Durabar consists of a crinkled section and a smooth tail at the far end. When the face plate is loaded, the anchor slips in a wavy profile under pulling load (Li 2011). Swellex is a typical inflatable rock bolt, interacting with the rock mass through the friction between the cylindrical surface of the bolt and the wall of the borehole (Li and Håkansson 1999). Garford is another type of energy-absorbing bolt, consisting of a steel solid bar, an anchor and a coarse threaded steel sleeve at the end. The anchor is resin encapsulated in the borehole. The solid bar is pulled through the hole of the anchor with an approximately constant force when the rock dilates (Varden et al. 2008). Roofex has a similar mechanism with Garford, in which a smooth bar slips through the anchor, generating a constant frictional resistance (Charette and Plouffe 2007). D-bolt is a recently developed energy-absorbing bolt with a number of integrated anchors spaced along its length (Li 2010, 2011; Li and Doucet 2012). The anchors are firmly fixed in the grout, while the smooth bar sections between the anchors can deform so as to absorb energy.

Nowadays, mining goes deeper below 1000 m and even down to 3000 m. More rock burst events and problems related to large deformation are encountered. Although the concept of energy-absorbing support devices was raised back to early 1990s and a few types of rock bolts as mentioned above have been proposed, the reinforcement mechanism of rock bolts is not yet clear and the current energy-absorbing rock bolts still have some shortcomings which restrict their wide applications. Moreover, dynamic loading is not considered and the rock bolt type is usually not specified in the conventional rock bolting design based on empirical rules or rock classification systems (e.g., Q system or RMR).

In order to improve the rock bolting design, a good understanding of the rock bolt behavior under various scenarios is essential, which can be achieved through field monitoring, laboratory tests, analytical studies and numerical modeling. Nowadays, numerical modeling has been widely used because of its low cost, high efficiency and great adaptability.

Numerical methods for rock mechanics modeling can be categorized into two groups, i.e., the continuum-based methods and the discontinuum-based methods. To more accurately capture the behavior of the rock bolts in discontinuity-dominated situations such as joint opening/sliding, rock dilation and rock bursts, a discontinuum modeling method seems more appropriate. In this study, the discontinuous deformation analysis (DDA) method (Shi 1988) is adopted.

DDA was initially developed for analyses of jointed rock masses. It is an implicit method in which displacements are the unknowns and the equilibrium equations are solved in the same manner as that in the finite element method (FEM). Compared to the explicit distinct element method (DEM) [e.g., UDEC (Itasca 2004), 3DEC (Itasca 2007)], the DDA possesses strict postulate of equilibrium, correct energy consumption and higher computing efficiency for multiple discontinuity analysis. In the past two decades, researchers have made much efforts to improve and extend the DDA via sub-block discretization (Lin et al. 1996), high-order approximation (Hsiung 2001; Koo and Chern 1996) or a discretization of finite element mesh inside each block (Bao and Zhao 2013; Chang 1995; Shyu 1993), better contact algorithms (Bao and Zhao 2012; Lin et al. 1996), viscous boundary conditions (Bao et al. 2012; Gu and Zhao 2009; Jiao et al. 2007), hydromechanical coupling analysis (Jing et al. 2001; Kim et al. 1999; Koyama et al. 2011), excavation analysis (Kim et al. 1999) and various other rock engineering applications (Hatzor et al. 2010; MacLaughlin et al. 2001; Wu 2010; Wu et al. 2004, 2005; Yeung et al. 2003; Zhao et al. 2011).

Unfortunately, a comprehensive rock bolt model is absent under the DDA framework. The current rock bolt models are still preliminary and cannot cover the wide range of existing rock bolts in practice. For example, in the original DDA code, a rock bolt was oversimplified as a spring connecting two blocks. Moosavi and Grayeli (2006) implemented a fully grouted cable bolt element into the DDA algorithm based on the spring model. Nie et al. (2014) further extended their work by using a series of springs to represent the rock bolt. When the rock bolt crosses a joint plane, separated nodes are inserted by an artificial aperture. The limitation of this method is that the system matrix could be singular in most cases due to short springs/beams crossing each joint. If short springs are removed from the model, the interaction between rock bolt and rock joints cannot be modeled. Furthermore, as the displacement of rock bolt is interpreted from the displacement of rock instead of being independent from each other, its application is limited to small displacement problems. However, the DDA was initiated for large displacement or deformation problems. To overcome such limitations and take full advantage of the DDA method, this paper proposes an improved rock bolt model. The rock mass and the rock bolt contain independent degrees of freedom (DOFs), and their interactions are governed by proper constitutive models assigned to the anchored points. Different types of rock bolts can be realized within the unified framework. Different failure modes of bolts are available in the analysis procedure.

2 Brief Introduction to DDA

The basic formulation of DDA method and complete derivation refer to Shi (1988). In short, the most necessary equations are presented here. The displacement (u, v) of any point (x, y) within a block is represented by six deformation variables

$$ {\mathbf{D}}_{i} = \{ u_{0} , \, v_{0} , \, r_{0} , \, \varepsilon_{x} , \, \varepsilon_{y} , \, \gamma_{xy} \}^{T} $$
(1)

where (u 0, v 0) is the rigid body translation of a specific point (x 0, y 0) within the block; r 0 is the rotation angle of the block with the rotation center at (x 0, y 0), in radians; ɛ x , ɛ y , γ xy are the normal and shear strains of this block; (x 0, y 0) is usually chosen as the centroid of the block (x c , y c ).

The block displacement takes the following form

$$ \left( {\begin{array}{*{20}c} u \\ v \\ \end{array} } \right) = {\mathbf{T}}_{i} {\mathbf{D}}_{i} $$
(2)

where

$$ {\mathbf{T}}_{i} = \left[ {\begin{array}{*{20}c} 1 & 0 & { - (y - y_{0} )} & {(x - x_{0} )} & 0 & {(y - y_{0} )/2} \\ 0 & 1 & {(x - x_{0} )} & 0 & {(y - y_{0} )} & {(x - x_{0} )/2} \\ \end{array} } \right] $$
(3)

In DDA, individual blocks form a block system through contacts among blocks and displacement constraints on single blocks. Assuming n blocks in the block system, the simultaneous equilibrium equations can be written in matrix form as

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{11} } &\quad {{\mathbf{K}}_{12} } &\quad \cdots &\quad {{\mathbf{K}}_{1n} } \\ {{\mathbf{K}}_{21} } &\quad {{\mathbf{K}}_{22} } &\quad \cdots &\quad {{\mathbf{K}}_{2n} } \\ \vdots &\quad \vdots &\quad \ddots &\quad \vdots \\ {{\mathbf{K}}_{n1} } &\quad {{\mathbf{K}}_{n2} } &\quad \cdots &\quad {{\mathbf{K}}_{nn} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{1} } \\ {{\mathbf{D}}_{2} } \\ \vdots \\ {{\mathbf{D}}_{n} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{F}}_{1} } \\ {{\mathbf{F}}_{2} } \\ \vdots \\ {{\mathbf{F}}_{n} } \\ \end{array} } \right] $$
(4)

Since each block has six degrees of freedom (DOFs), each element \( {\mathbf{K}}_{ij} \) is a 6 × 6 sub-matrix and \( {\mathbf{D}}_{i} \) and \( {\mathbf{F}}_{i} \) are 6 × 1 sub-matrices, where \( {\mathbf{D}}_{i} \) represents the deformation variables of block i and \( {\mathbf{F}}_{i} \) is the loading on block i distributed to the six deformation variables. Sub-matrix \( {\mathbf{K}}_{ii} \) depends on the material properties of block i, and \( {\mathbf{K}}_{ij} \), where i ≠ j, is defined by the contacts and other links (e.g., bolts) between blocks i and j. Equation (4) can be rewritten into a more compact form as

$$ {\mathbf{KD}} = {\mathbf{F}} $$
(5)

The equilibrium equations are derived by the minimum potential energy principle. Details can refer to Shi (1988).

Both static and dynamic analyses can be conducted with the DDA method. For static analysis, the velocity of each block in the blocky system at the beginning of each time step is assumed to be zero. On the other hand, in the case of dynamic analysis, the velocity of the blocky system in the current time step is an accumulation of the velocities of previous time steps. Time integration is performed using an explicit, stepwise linear scheme, which is indeed the Newmark-β method with the collocation parameters β = 0.5 and γ = 1.0.

In each time step, Eq. (5) for the entire system is constructed and solved for the deformation variables, given properly defined initial and boundary conditions. The final displacement variables for a given time step are obtained by an iterative process, termed as open–close iteration (Shi 1988). A preliminary solution is first obtained, which is then checked to see whether the contact constraints are satisfied. If tension or penetration is detected at any contact, the constraints are adjusted and K and F in Eq. (5) are modified accordingly to find a new solution. This process is repeated until the contact constraints are satisfied for all contact pairs.

3 Basic Concepts of the Proposed Rock Bolt Model

In the proposed model, the rock mass and the rock bolt are treated separately.

3.1 Rock Mass

The rock mass is modeled as an assemblage of discrete rock blocks isolated by discontinuities. In the original DDA (Shi 1988), each block possesses a constant stress and strain based on the first order displacement assumption as in Eq. (2). Such an assumption is valid for the cases where the discontinuities dominate the failure modes. For continuous problems or the cases where the stress variation is crucial for the simulation results, each block can be further discretized into a set of sub-blocks [termed as sub-block DDA (Lin et al. 1996)], or a finite element mesh [termed as the NDDA (Bao and Zhao 2013; Chang 1995; Shyu 1993)], or a finite number of covers [termed as the NMM (An et al. 2011; He and Ma 2010; Ma et al. 2009; Shi 1992)] to resolve the stress variations.

3.2 Rock Bolt

Windsor (1997) proposed that a reinforcement system comprises four main components: the rock, the reinforcing element, the internal fixture and the external fixture. In the context of bolt reinforcement, the reinforcing element is the bolt and the external fixture element refers to the face plate and the nut (Li and Stillborg 1999). The internal fixture is either a medium, such as cement mortar or resin for grouted bolts, or a mechanical friction at the bolt interface for frictional bolts. The internal fixture provides a coupling condition at the interface.

With reference to the type of internal fixture, the reinforcement system can be categorized into three groups: continuously mechanically coupled (CMC), continuously frictionally coupled (CFC) and discretely mechanically/frictionally coupled (DMC/DFC) (Windsor 1997). According to this classification system, the fully grouted rebar belongs to the CMC bolts, the Split Set and Swellex belong to the CFC bolts, cone bolt, Durabar, Garford and Roofex belong to the DFC bolts, while Expansion Shell and D-bolts belong to the DMC bolts.

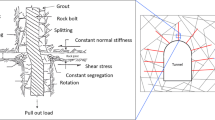
The framework of the proposed rock bolt model is sketched in Fig. 1.

Fig. 1
figure 1

Framework for the proposed rock bolt modeling in DDA

Full size image

3.2.1 Face Plate

The face plate is modeled as a simply deformable body described by the six deformation variables in Eq. (1), same to a normal rock block. It is also possible to further discretize the face plate into sub-blocks, or a finite element mesh or a finite number of covers to resolve the stress variation.

3.2.2 Bolt Shank

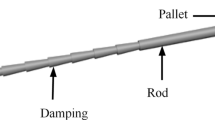
The bolt shank can sustain tension, shear and bending moment and thus can be represented by the beam elements. The bolt shank is discretized into a finite number of segments (Fig. 2), each of which is modeled as a beam element with the lumped mass and the degrees of freedoms (DOFs) represented at the two end nodes. The segments with negligible shear deformation are described by the Euler–Bernoulli beam model (Wang 2003), while the other segments across the joints with potential large shear deformation are described by the modified Euler–Bernoulli beam model considering the shear deformation (Wang 2003). Each beam element has two end nodes, and each node has three DOFs, namely the longitudinal displacement u, the deflection v and the rotation angle θ.

Fig. 2
figure 2

Proposed rock bolt model

Full size image

For dynamic and vibration analyses, it is essential to consider the mass. The total mass of each beam element is

$$ m^{e} = \frac{1}{2}\rho AL^{e} $$
(6)

where ρ is the density of the bolt material, A is the cross-sectional area of the bolt and L e is the length of the beam element. The mass is divided into two equal parts and assigned to two end nodes. The mass of each node will be the sum of the contributions from the elements sharing this node. Direct mass lumping used here results in a diagonal mass matrix. A master diagonal mass matrix can be stored simply as a vector. If all entries are nonnegative, it can be easily inverted, since the inverse of a diagonal matrix is also diagonal. Obviously, a lumped mass matrix entails significant computational advantages for calculations.

3.3 Interactions Between Rock Mass and Rock Bolt

3.3.1 Interactions Between Rock Mass and Face Plate

Interactions between the rock mass and the face plate are realized via the frictional contact obeying the Coulomb’s law. Detailed contact detection and modeling algorithms can refer to Shi (1988).

3.3.2 Interactions Between Rock Mass and Bolt Shank

The rock mass and the bolt shank contain independent DOFs and deform separately. Their interactions are enforced through a few anchored points (Fig. 3). The anchored points can be arbitrarily located along the bolt length. For convenience, the nodes in the bolt shank are chosen as the anchored points. A normal spring and a tangential spring are applied at each anchored point. The normal spring is used to restrict the relative movement between the rock mass and the bolt shank in the direction perpendicular to the bolt. The tangential spring is assigned with a proper constitutive model to represent the shear behavior of the bolt/rock interface. Once debonding at the interface occurs, the tangential spring is removed and replaced by a pair of forces (i.e., the residual strength for the CMC bolts or the frictional forces for the CFC bolts) acting on both the rock and the bolt shank.

Fig. 3
figure 3

Illustration of interaction between the rock mass and the rock bolt: the face plate interacting with the rock mass via contact, the bolt shank interacting with the rock mass via a few (real or artificial) anchored points

Full size image

Another important concept in the proposed rock bolt model in Fig. 1 is the borehole slot. It represents the borehole segment in each block and is used to record the topology relationship between the bolt shank and the rock blocks. As in Fig. 2, the borehole segment in DDA has been defined as a pair of line segments, which represents the upper-and-lower surface (2D) for the inner side of the borehole. This is to control the possible movement in between for the node of the bolt shank. In simple words, it can be treated as another two boundaries, except for the external surface of the rock mass, which also follows the Coulomb friction criterion.

  1. 1.

    When the controlled node of bolt shank only moves along the borehole segment direction, the research finding in the literature (Ivanović and Neilson 2009) has adapted.

  2. 2.

    When shearing displacement occurs in the bolt along the joint, compressive pressure is generated between the controlled node of the shank and the borehole segment, and the tangential behavior between the bolt and borehole conforms to the Coulomb relations.

In fact, the above two situations can be unified under the Coulomb criterion, by converting the peak strength into the combination of equivalent conferment force and corresponding friction angle, which can be realized by the model proposed in this paper.

An artificial example in Fig. 4 is used to illustrate the concept of the borehole slot and automatic update of the topological relationship between the bolt and rock mass. The model consists of two rock blocks: The upper block is numbered as Block 1 and the lower block is numbered as Block 2. A complete debonding along the rock/bolt interface is assumed. A pulling load is applied to the face plate to pull the bolt out with an angle to the right. If the anchored point is not inside any rock block, the index is set to 0; otherwise, the index is set to be the block number which it interacts with. The top 5 nodes initially interact with Block 1, thus indexed as 1. The next five nodes interact with Block 2, thus indexed as 2. The bottom node does not interact with any block, thus indexed as 0. During the pulling-out process, the interaction between the bolt shank and the rock blocks is automatically detected and the indices are updated accordingly. When the two blocks are separated, a gap is formed in between. The indices for the top five nodes are changed to 0 when passing through the gap, then to 2 when interacting with Block 2 and finally to 0 again when they are completely outside the blocks. The indices of other nodes are updated in a similar way. With the updated indices, the constraints between the bolt shank and the rock blocks can be conveniently realized and the resulted sub-matrices can be easily arranged into the global matrices. One unique feature of the proposed rock bolt model, as illustrated by the above example, is that the rock bolt and the rock blocks are independent of each other. Therefore, the bolt can be completely pulled out from the rock blocks, which is impossible in many existing rockbolting modeling codes.

Fig. 4
figure 4

An example illustrating automatic update of topology relationship between the bolt and the rock mass

Full size image

3.4 Realization of Different Failure Modes

As summarized in Fig. 1, the face plate may lose its containment capacity if the rock immediately contacting with it crushes or the connection between the bolt shank and the face plate fails. The bolt shank may experience both tensile failure and shear failure. The coupling between the rock mass and the bolt shank may lose in either one of the following four cases: (1) debonding between the bolt shank and the grout material; (2) breaking of the grout material; (3) debonding between the grout material and the rock; (4) breaking of the attached rock material. Among all the possible failure modes, the actual failure depends on which one is the weakest.

In the proposed rock bolt model, the above-mentioned potential failure modes are categorized into four groups, namely tensile failure of the bolt shank (Fig. 5a), shear failure of the bolt shank (Fig. 5b), debonding along the bolt/rock interface (Fig. 5c) and loss of the face plate (Fig. 5d). Criteria for each mode of failure are provided as follows:

Fig. 5
figure 5

Four types of failure modes: a tensile failure of bolt shank; b shear failure of bolt shank; c debonding along bolt/rock interface; d loss of face plate

Full size image

3.4.1 Tensile Failure of the Bolt Shank

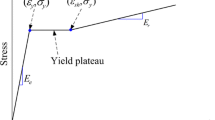
The axial behavior of the bolt shank is governed by a piecewise constitutive model (Fig. 6). Once the axial strain exceeds an ultimate value ɛ u, tensile failure of the bolt shank occurs and the corresponding beam element is removed. The yield strain ɛ y , the yield strength σ y and the ultimate strain ɛ u depend on the steel material used in the bolt shank. Both loading and unloading are considered in order to perform a full dynamic analysis. The Young’s modulus is assumed the same for both the loading and unloading processes.

Fig. 6
figure 6

Constitutive model for axial behavior of bolt shank steel material

Full size image

  • Shear failure of the bolt shank Refer to Spang and Egger (1990) and the Industrial Fastener Institute (2003), the shear strengths of the carbon steel fasteners can be assumed to be 60 percent of their specified minimum tensile strengths. Once the shear strength of the bolt shank reaches its ultimate value, the shear failure occurs and the corresponding beam element is removed.

  • Debonding along the bolt/rock interface Once the shear force at an anchored point exceeds the shear strength, the anchored point is removed and debonding along the bolt/rock interface occurs. For DMC/DFC bolts, the shear strength of each real anchored point is directly obtained through tests, while that of each artificial anchored point is set to zero (no constraint in the tangential direction). For CMC/CFC bolts, the shear strength of the interface can be obtained through tests or found in the specifications of the bolt. The shear strength of each anchored point is the sum of the contributions from the beam elements sharing it. For CMC bolts, when debonding occurs, the shear strength of the adhesive component is first mobilized, followed by the mechanical interlock, and finally the frictional component. The shear strength of the interface decreases during this process. The shear strength after the loss of some strength components is usually referred to as the residual shear strength, with the value determined by tests. For DMC bolts, when debonding occurs, the residual strength is set to zero. For CFC/DFC bolts, the shear strength of the interface comprises one or two components, i.e., either friction or mechanical interlock and friction. The friction still exists in spite of deformation incompatibility across the interface. In another word, the residual shear strength of the interface is approximately the same as the peak shear strength.

  • Loss of the face plate When the normal or shear stress at the connecting point between the bolt and the face plate exceeds a critical value, which can be determined by tests, the face plate is lost.

3.5 Realization of Different Rock Bolt Types

Different types of rock bolts are realized by specifying proper constitutive models to each anchored point. Details are provided as follows.

  1. (a)

    Fully grouted rebar (Fig. 7a) Each anchored point is constrained in two directions: (1) no relative movement between the rock and the bolt shank in the direction perpendicular to the bolt; (2) the tangential behavior of each anchored point is governed by a constitutive model determined through tests to represent the rock/grout/bolt coupling; once debonding occurs, the shear strength for each anchored point is updated as the residual shear strength.

    Fig. 7
    figure 7

    Realization of different types of rock bolts (solid circle—real anchored point, open circle—artificial anchored point). a Rebar, shear strength of each anchored point representing the grout coupling between rock and rock bolt. b Split Set/Swellex, shear strength of each anchored point representing the frictional coupling between rock and rock bolt. c Expansion Shell, shear strength of real anchored point representing the mechanical coupling at the end. d D-bolt, shear strength of each real anchored point representing the grout coupling between rock and bolt. e Cone bolt, shear strength of the real anchored end point representing the cone plowing through grout. f Roofex/Garford, shear strength of the real anchored points is constant, representing the mechanical coupling in the anchor

    Full size image
  2. (b)

    Split Set/Swellex (Fig. 7b) The constitutive model is similar to that for the fully grouted rebar, except that the shear strength remains unchanged when debonding occurs.

  3. (c)

    Expansion Shell (Fig. 7c) Only the two end anchored points are termed as the real anchored points, which are constrained in a way similar to the fully grouted rebar. Once the anchored point at the far end fails, the whole bolt is lost. Other anchored points are termed as the artificial anchored points, which are constrained only in the direction perpendicular to the bolt to enforce the displacement compatibility.

  4. (d)

    D-bolt (Fig. 7d) Only a few anchored points are assigned as the real anchored points, which are constrained in a way similar to the fully grouted rebar. Once debonding occurs, the shear strength of the corresponding anchored point is set to zero. The artificial anchored points are constrained in a way similar to the expansion shell.

  5. (e)

    Cone bolt (Fig. 7e) The anchored point connecting to the face plate is constrained in a way similar to the fully grouted rebar. The far-end anchored point is also constrained in two directions: (1) no relative movement between the rock and the bolt shank perpendicular to the bolt; (2) the tangential behavior of the anchored point is governed by a constitutive model obtained by tests to represent the plowing of the cone through the grout. The artificial anchored points are constrained in a way similar to the expansion shell.

  6. (f)

    Roofex (Fig. 7f) The anchored point connecting the face plate is constrained in a way similar to the fully grouted rebar. The last few anchored points (the range determined by the length of the Garford anchor) at the far end of the bolt shank are also constrained in two directions: (1) no relative movements between the rock and the bolt shank perpendicular to the bolt; (2) the tangential behavior of the anchored point is represented by a constant frictional resistance with the value provided in the specification of Roofex. The artificial anchored points are constrained in a way similar to the expansion shell.

  7. (g)

    Garford (Fig. 7f) The anchored points are constrained in a way similar to Roofex.

4 Formulations of the Rock Bolt Models

The global governing equation for a system with n rock blocks, m face plates and l beam nodes has the form of

$$ \begin{aligned} \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{11} } &\quad \cdots &\quad {{\mathbf{K}}_{1n} } &\quad {{\mathbf{K}}_{1(n + 1)} } &\quad \cdots &\quad {{\mathbf{K}}_{1(n + m)} } &\quad {{\mathbf{K}}_{1(n + 1)} } &\quad \cdots &\quad {{\mathbf{K}}_{1(n + 1)} } \\ \vdots &\quad \ddots &\quad \vdots &\quad \vdots &\quad \ddots &\quad \vdots &\quad \vdots &\quad \ddots &\quad \vdots \\ {{\mathbf{K}}_{n1} } &\quad \cdots &\quad {{\mathbf{K}}_{nn} } &\quad {{\mathbf{K}}_{n(n + 1)} } &\quad \cdots &\quad {{\mathbf{K}}_{n(n + m)} } &\quad {{\mathbf{K}}_{1(n + 1)} } &\quad \cdots &\quad {{\mathbf{K}}_{1(n + 1)} } \\ {{\mathbf{K}}_{(n + 1)1} } &\quad \cdots &\quad {{\mathbf{K}}_{(n + m)n} } &\quad {{\mathbf{K}}_{(n + 1)(n + 1)} } &\quad \cdots &\quad {{\mathbf{K}}_{(n + 1)(n + m)} } &\quad {{\mathbf{K}}_{1(n + 1)} } &\quad \cdots &\quad {{\mathbf{K}}_{1(n + 1)} } \\ \vdots &\quad \ddots &\quad \vdots &\quad \vdots &\quad \ddots &\quad \vdots &\quad \vdots &\quad \ddots &\quad \vdots \\ {{\mathbf{K}}_{(n + m)1} } &\quad \cdots &\quad {{\mathbf{K}}_{(n + m)n} } &\quad {{\mathbf{K}}_{(n + m)(n + 1)} } &\quad \cdots &\quad {{\mathbf{K}}_{(n + m)(n + m)} } &\quad {{\mathbf{K}}_{1(n + 1)} } &\quad \cdots &\quad {{\mathbf{K}}_{1(n + 1)} } \\ {{\mathbf{K}}_{1(n + 1)} } &\quad \cdots &\quad {{\mathbf{K}}_{1(n + 1)} } &\quad {{\mathbf{K}}_{1(n + 1)} } &\quad \cdots &\quad {{\mathbf{K}}_{1(n + 1)} } &\quad {{\mathbf{K}}_{(n + m + 1)(n + m + 1)} } &\quad \cdots & \quad{{\mathbf{K}}_{(n + m + 1)(n + m + l)} } \\ \vdots &\quad \ddots &\quad \vdots &\quad \vdots &\quad \ddots &\quad \vdots &\quad \vdots &\quad \ddots &\quad \vdots \\ {{\mathbf{K}}_{1(n + 1)} } &\quad \cdots &\quad {{\mathbf{K}}_{1(n + 1)} } &\quad {{\mathbf{K}}_{1(n + 1)} } &\quad \cdots &\quad {{\mathbf{K}}_{1(n + 1)} } &\quad {{\mathbf{K}}_{(n + m + l)(n + m + 1)} } &\quad \cdots &\quad {{\mathbf{K}}_{(n + m + l)(n + m + l)} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{1} } \\ \vdots \\ {{\mathbf{D}}_{n} } \\ {{\mathbf{D}}_{n + 1} } \\ \vdots \\ {{\mathbf{D}}_{n + m} } \\ {{\mathbf{D}}_{n + m + 1} } \\ \vdots \\ {{\mathbf{D}}_{n + m + l} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{F}}_{1} } \\ \vdots \\ {{\mathbf{F}}_{n} } \\ {{\mathbf{F}}_{n + 1} } \\ \vdots \\ {{\mathbf{F}}_{n + m} } \\ {{\mathbf{F}}_{n + m + 1} } \\ \vdots \\ {{\mathbf{F}}_{n + m + l} } \\ \end{array} } \right] \hfill \\ \hfill \\ \end{aligned} $$
(7)

Equation (7) can be written in a more compact form as

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{aa} } & {{\mathbf{K}}_{ab} } & {{\mathbf{K}}_{ac} } \\ {{\mathbf{K}}_{ba} } & {{\mathbf{K}}_{bb} } & {{\mathbf{K}}_{bc} } \\ {{\mathbf{K}}_{ca} } & {{\mathbf{K}}_{cb} } & {{\mathbf{K}}_{cc} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{a} } \\ {{\mathbf{D}}_{b} } \\ {{\mathbf{D}}_{c} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{F}}_{a} } \\ {{\mathbf{F}}_{b} } \\ {{\mathbf{F}}_{c} } \\ \end{array} } \right] $$
(8)

where \( {\mathbf{K}}_{aa} ,{\mathbf{K}}_{bb} \) and \( {\mathbf{K}}_{cc} \) represent the stiffness matrices formed by the rock blocks, the face plates and the bolt shanks, respectively; \( {\mathbf{K}}_{ab} \) and \( {\mathbf{K}}_{ba} \) are the stiffness matrices formed by the interactions between the rock blocks and the face plates; \( {\mathbf{K}}_{ac} \) and \( {\mathbf{K}}_{ca} \) are the stiffness matrices formed by the interactions between the rock blocks and the bolt shanks; \( {\mathbf{K}}_{bc} \) and \( {\mathbf{K}}_{cb} \) are the stiffness matrices formed by the interactions between the bolt shank and the face plate; \( {\mathbf{D}}_{a} ,{\mathbf{D}}_{b} \) and \( {\mathbf{D}}_{c} \) are the unknown vectors of the rock blocks, the face plates and the beam nodes, respectively; \( {\mathbf{F}}_{a} ,{\mathbf{F}}_{b} \) and \( {\mathbf{F}}_{c} \) are the force vectors corresponding to the rock blocks, the face plates and the beam nodes, respectively. Each rock block or face plate has six unknown variables; thus, the element \( {\mathbf{K}}_{ij} ,i = 1 \sim n + m,j = 1 \sim n + m \) is a 6×6 sub-matrix and \( {\mathbf{D}}_{i} , \, {\mathbf{F}}_{i} , \, i = 1 \sim n + m \) are 6×1 sub-matrices. Each node of the beam elements has three unknowns; thus, the element \( {\mathbf{K}}_{ij} ,i = n + m + 1 \sim n + m + l,j = n + m + 1 \sim n + m + l \) is a 3×3 sub-matrix, the elements \( {\mathbf{K}}_{ij} ,i = n + 1 \sim n + m,j = i + 1 \sim n + m \) and \( {\mathbf{K}}_{ij} ,j = n + 1 \sim n + m,i = n + 1 \sim j - 1 \) are 6×3 sub-matrices, and \( {\mathbf{D}}_{i} , \, {\mathbf{F}}_{i} , \, i = n + m + 1 \sim n + m + l \) are 3×1 sub-matrices. \( {\mathbf{K}}_{aa} ,{\mathbf{K}}_{bb} ,{\mathbf{K}}_{ab} \) and \( {\mathbf{K}}_{ba} \) are the stiffness matrices of the rock blocks, the face plates and their interactions, respectively. More details can refer to Shi (1988). Constructions of other elements will be presented in the following subsections.

4.1 Sub-Matrices of Beam Elements

A typical Euler–Bernoulli beam element with the local and global coordinate system is shown in Fig. 8. The beam element has two end nodes 1′ and 2′ with the coordinates (x i′,y i′), and each node has three DOFs: the normal displacement u i′, the deflection w i′ and the rotation θ i′ in the local coordinate system. Thus, the unknown vector for a beam element is

$$ {\mathbf{d}}^{{\prime }} = \left[ {\begin{array}{*{20}c} {u_{{1^{{\prime }} }} } & {w_{{1^{{\prime }} }} } & {\theta_{{1^{{\prime }} }} } & {u_{{2^{{\prime }} }} } & {w_{{2^{{\prime }} }} } & {\theta_{{2^{{\prime }} }} } \\ \end{array} } \right]^{T} $$
(9)

The force vector is

$$ {\mathbf{f}}^{{\prime }} = \left[ {\begin{array}{*{20}c} {f_{{1^{{\prime }} }} } & {S_{{1^{{\prime }} }} } & {M_{{1^{{\prime }} }} } & {f_{{2^{{\prime }} }} } & {S_{{2^{{\prime }} }} } & {M_{{2^{{\prime }} }} } \\ \end{array} } \right]^{T} $$
(10)

where f, S and M are the axial force, the shear force and the bending moment, respectively.

Fig. 8
figure 8

Euler–Bernoulli beam model

Full size image

Based on the Euler–Bernoulli beam theory, the stiffness matrix for a beam element is derived as (Wang 2003)

$$ {\mathbf{k}}^{'} = \left[ {\begin{array}{*{20}c} {\frac{EA}{L}} & 0 & 0 & {\frac{EA}{L}} & 0 & 0 \\ {} & {\frac{12EI}{{L^{3} }}} & {\frac{6EI}{{L^{2} }}} & 0 & { - \frac{12EI}{{L^{3} }}} & {\frac{6EI}{{L^{2} }}} \\ {} & {} & {\frac{4EA}{L}} & 0 & { - \frac{6EI}{{L^{2} }}} & {\frac{2EI}{L}} \\ {} & {} & {} & {\frac{EA}{L}} & 0 & 0 \\ {} & {{\text{sym}} .} & {} & {} & {\frac{12EI}{{L^{3} }}} & { - \frac{6EI}{{L^{2} }}} \\ {} & {} & {} & {} & {} & {\frac{2EI}{L}} \\ \end{array} } \right] $$
(11)

where E is the Young’s modulus and I is the moment of inertia.

When considering the shear deformation, the stiffness matrix in Eq. (11) is modified into (Wang 2003)

$$ {\mathbf{k}}^{{\prime }} = \left[ {\begin{array}{*{20}c} {\frac{EA}{L}} & 0 & 0 & {\frac{EA}{L}} & 0 & 0 \\ {} & {\frac{12EI}{{L^{3} }}} & {\frac{6EI}{{L^{2} }}} & 0 & { - \frac{12EI}{{L^{3} }}} & {\frac{6EI}{{L^{2} }}} \\ {} & {} & {\frac{{\left( {4 + b} \right)EA}}{L}} & 0 & { - \frac{6EI}{{L^{2} }}} & {\frac{{\left( {2 - b} \right)EI}}{L}} \\ {} & {} & {} & {\frac{EA}{L}} & 0 & 0 \\ {} & {{\text{sym}} .} & {} & {} & {\frac{12EI}{{L^{3} }}} & { - \frac{6EI}{{L^{2} }}} \\ {} & {} & {} & {} & {} & {\frac{{\left( {4 + b} \right)EI}}{L}} \\ \end{array} } \right] $$
(12)

where b is the modifier to consider the shear deformation effect, taking the form of

$$ b = \frac{12EIk}{{GAL^{2} }} $$
(13)

where k is another modifier, k = 3/2 and 4/3 for rectangular and circular cross sections, respectively. When the depth-to-length ratio is small, b tends to be zero. Then, the shear deformation effect can be neglected, and the stiffness matrix in Eq. (12) reduces to Eq. (11).

The unknown vectors in the global coordinate system is

$$ {\mathbf{d}} = \left[ {\begin{array}{*{20}c} {u_{1} } & {v_{1} } & {\theta_{1} } & {u_{2} } & {v_{2} } & {\theta_{2} } \\ \end{array} } \right]^{T} $$
(14)

Then, the elemental stiffness matrix and the elemental force vector are transformed into the global coordinate system as

$$ {\mathbf{k}} = {\mathbf{T}}^{T} {\mathbf{k}}^{{\prime }} {\mathbf{T}} $$
(15)
$$ {\mathbf{f}} = {\mathbf{T}}^{T} {\mathbf{f}}^{{\prime }} $$
(16)

where T is the transformation matrix, taking the form of

$$ {\mathbf{T}} = \left[ {\begin{array}{*{20}c} c &\quad s & 0 &\quad 0 &\quad 0 &\quad 0 \\ { - s} &\quad c &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 1 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad c &\quad s &\quad 0 \\ 0 &\quad 0& 0 &\quad { - s} &\quad c &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 1 \\ \end{array} } \right] $$
(17)

where

$$ c = \frac{{x_{2} - x_{1} }}{L} $$
(18)
$$ s = \frac{{y_{2} - y_{1} }}{L} $$
(19)

where \( x_{i} ,y_{i} ,\quad i = 1,2 \) are the coordinates of the nodes 1′ and 2′ in the global coordinate system.

Assume the global indices for the two nodes are l 1, l 2, 1 ≤ l 1, l 2 ≤ l. The elemental matrices are assembled into the global matrices as

$$ \begin{aligned} {\mathbf{k}}\left( {1:3;1:3} \right) \to {\mathbf{K}}_{{(n + m + l_{1} )(n + m + l_{1} )}} \hfill \\ {\mathbf{k}}\left( {1:3;4:6} \right) \to {\mathbf{K}}_{{(n + m + l_{1} )(n + m + l_{2} )}} \hfill \\ {\mathbf{k}}\left( {4:6;1:3} \right) \to {\mathbf{K}}_{{(n + m + l_{2} )(n + m + l_{1} )}} \hfill \\ {\mathbf{k}}\left( {4:6;4:6} \right) \to {\mathbf{K}}_{{(n + m + l_{2} )(n + m + l_{2} )}} \hfill \\ \end{aligned} $$
(20)

4.2 Sub-Matrices of Lumped Mass Matrix

The lumped mass matrix for each beam element is derived as

$$ {\mathbf{m}} = \frac{W}{2}\left[ {\begin{array}{*{20}c} 1 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 & \quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 1 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ \end{array} } \right] $$
(21)

where

$$ W = \rho LA, $$
(22)

where \( \rho , \, L, \, A \) are the density, the length and the cross-sectional area of the beam element, respectively.

The lumped mass matrix is assembled into the global matrices as

$$ \begin{aligned} {\mathbf{m}}\left( {1:3;1:3} \right) \to {\mathbf{K}}_{{(n + m + l_{1} )(n + m + l_{1} )}} \hfill \\ {\mathbf{m}}\left( {1:3;4:6} \right) \to {\mathbf{K}}_{{(n + m + l_{1} )(n + m + l_{2} )}} \hfill \\ {\mathbf{m}}\left( {4:6;1:3} \right) \to {\mathbf{K}}_{{(n + m + l_{2} )(n + m + l_{1} )}} \hfill \\ {\mathbf{m}}\left( {4:6;4:6} \right) \to {\mathbf{K}}_{{(n + m + l_{2} )(n + m + l_{2} )}} \hfill \\ \end{aligned} $$
(23)

4.3 Sub-matrices of Interactions Between Rock Mass and Bolt Shank

It is assumed that the node P 1 of beam element l 1 interacts with the borehole slot P 2 P 3 in rock block n 1, and (x k , y k ) and (u k , v k ) are the coordinates and displacement of P k , k = 0–3, respectively. Constraints are applied between the node P 1 and the borehole slot P 2 P 3 in both the normal and tangential directions. The normal constraint is used to enforce the displacement compatibility of the rock and the bolt shank in the direction perpendicular to the bolt. The tangential constraint is to enforce the tangential behavior of the bolt/rock interface.

Based on the minimum potential energy principle, the sub-matrices due to the normal constraint and assemblage into the global matrices are derived as

$$ \begin{aligned} &k_{n} {\mathbf{AA}}^{T} \to {\mathbf{K}}_{{(n + m + l_{1} )(n + m + l_{1} )}} \hfill \\ &k_{n} {\mathbf{AB}}^{T} \to {\mathbf{K}}_{{(n + m + l_{1} )n_{1} }} \hfill \\ & k_{n} {\mathbf{BA}}^{T} \to {\mathbf{K}}_{{n_{1} (n + m + l_{1} )}} \hfill \\ & k_{n} {\mathbf{BB}}^{T} \to {\mathbf{K}}_{{n_{1} n_{1} }} \hfill \\ & - k_{n} \left( {\frac{{A_{0} }}{l}} \right){\mathbf{A}} \to {\mathbf{F}}_{{(n + m + l_{1} )}} \hfill \\ & - k_{n} \left( {\frac{{A_{0} }}{l}} \right){\mathbf{B}} \to {\mathbf{F}}_{{n_{1} }} \hfill \\ \end{aligned} $$
(24)

where k n is the normal spring stiffness and

$$ {\mathbf{A}} = \frac{1}{l}\left\{ {\begin{array}{*{20}c} {y_{2} - y_{3} } \\ {x_{3} - x_{2} } \\ 0 \\ \end{array} } \right\} $$
(25)
$$ {\mathbf{B}} = \frac{1}{l}{\mathbf{N}}_{{n_{1} }} (x_{2} ,y_{2} ) \cdot \left\{ {\begin{array}{*{20}c} {y_{3} - y_{1} } \\ {x_{1} - x_{3} } \\ \end{array} } \right\} + \frac{1}{l}{\mathbf{N}}_{{n_{1} }} (x_{3} ,y_{3} ) \cdot \left\{ {\begin{array}{*{20}c} {y_{1} - y_{2} } \\ {x_{2} - x_{1} } \\ \end{array} } \right\} $$
(26)
$$ A_{0} = \left( {x_{1} y_{2} - x_{2} y_{1} } \right) + \left( {x_{3} y_{1} - x_{1} y_{3} } \right) + \left( {x_{1} y_{2} - x_{2} y_{1} } \right) $$
(27)

The sub-matrices due to tangential constraint and the assemblage into the global matrices are

$$ \begin{aligned} k_{s} {\mathbf{CC}}^{T} \to {\mathbf{K}}_{{(n + m + l_{1} )(n + m + l_{1} )}} \hfill \\ & k_{s} {\mathbf{CD}}^{T} \to {\mathbf{K}}_{{(n + m + l_{1} )n_{1} }} \hfill \\ & k_{s} {\mathbf{DC}}^{T} \to {\mathbf{K}}_{{n_{1} (n + m + l_{1} )}} \hfill \\ & k_{s} {\mathbf{DD}}^{T} \to {\mathbf{K}}_{{n_{1} n_{1} }} \hfill \\ & - k_{s} \left( {\frac{{A_{0} }}{l}} \right){\mathbf{C}} \to {\mathbf{F}}_{{(n + m + l_{1} )}} \hfill \\ & - k_{s} \left( {\frac{{A_{0} }}{l}} \right){\mathbf{D}} \to {\mathbf{F}}_{{n_{1} }} \hfill \\ \end{aligned} $$
(28)

where k s is the tangential spring stiffness and

$$ {\mathbf{C}} = \frac{1}{l}\left\{ {\begin{array}{*{20}c} {x_{3} - x_{2} } \\ {y_{3} - y_{2} } \\ 0 \\ \end{array} } \right\} $$
(29)
$$ \begin{aligned} {\mathbf{D}} = \frac{1}{l}{\mathbf{N}}_{{n_{1} }} (x_{2} ,y_{2} )^{T} \left( {\begin{array}{*{20}c} { - x_{1} + 2(1 - t_{0} )x_{2} - (1 - 2t_{0} )x_{3} } \\ { - y_{1} + 2(1 - t_{0} )y_{2} - (1 - 2t_{0} )y_{3} } \\ \end{array} } \right) \hfill \\ \begin{array}{*{20}c} {} & + \\ \end{array} \frac{1}{l}{\mathbf{N}}_{{n_{1} }} (x_{3} ,y_{3} )^{T} \left( {\begin{array}{*{20}c} {x_{1} + (2t_{0} - 1)x_{2} - 2t_{0} x_{3} } \\ {y_{1} + (2t_{0} - 1)y_{2} - 2t_{0} y_{3} } \\ \end{array} } \right) \hfill \\ \end{aligned} $$
(30)

where t 0 is the time when the beam node aligns on the borehole slot.

Once debonding occurs, the tangential constraint is replaced by a pair of forces (i.e., the residual shear strength for the CMC/DMC bolts or the frictional force for the CFC/DFC bolts), with the values provided in the specifications of each type of bolt or obtained through experiments. The sub-matrices and assemblage into the global matrices are

$$ -\, f{\mathbf{C}} \to {\mathbf{F}}_{{(n + m + l_{1} )}} $$
(31)
$$ -\, f{\mathbf{E}} \to {\mathbf{F}}_{{n_{1} }} $$
(32)

where f is the magnitude of the force and

$$ {\mathbf{E}} = \frac{1}{l}{\mathbf{N}}_{{n_{1} }} (x_{0} ,y_{0} )\left\{ {\begin{array}{*{20}c} {x_{3} - x_{2} } \\ {y_{3} - y_{2} } \\ \end{array} } \right\}. $$
(33)

5 Numerical Examples

In this section, one typical conventional rock bolt (fully grouted rebar) and one typical energy-absorbing rock bolt (D-bolt) (see Fig. 9) are simulated by the proposed unified numerical rock bolt model. In order to evaluate the efficiency and robustness of the model, the numerical results are compared with the theoretical derivation (Li and Doucet 2012; Li and Stillborg 1999) and experimental results (Chen 2014; Chen and Li 2015a, b) separately.

Fig. 9
figure 9

Two-block model with the left block fixed while the second block connected to the left block via a bolt. a 3D sketch of rock bolt test bed (for numerical studies and experiment setup). b Front view of the test rig in NTNU/SINTEF bolt testing. c Detailed illustration on two types of rock bolts (rebar bolt and D-bolt) (Chen and Li 2015a)

Full size image

The verification process is divided into three steps in the following subsections:

  1. 1.

    In the first subsection, no failure is considered within the bolt system (no shank material failure and no debonding failure on rock/grout/shank interfaces). The numerical results and the theoretical solutions for inner force distribution under axial loading are compared.

  2. 2.

    In the second subsection, only debonding is considered. The inner stress distribution of the rebar shank actually changes along the different stress level according to the threshold value of bond strength, which matches the corresponding theoretical foundation in literatures (Li and Stillborg 1999).

  3. 3.

    In the third subsection, the experimental parameters in Chen and Li (2015a) are adopted as the input parameters, which simplify the defined nonlinear constitutive model for the bolt shank material. Furthermore, the overall “displacement and load curves” under the pullout testing scenarios are compared with the experiment results.

Based on the NTNU/SINTEF experimental setup, the numerical model is simplified into a two-block system, as illustrated in Fig. 9. The dimension of each block is 1 m × 1 m. The left block is fixed, while the right block is subjected to the controlled force or displacement. Both the shanks of rebar bolt and the D-Bolt specimens are d = 20 mm in diameter and L = 2 m in length, with the yield strength and ultimate tensile strength at 490 and 630 MPa, respectively. The bolt is elongated elastically until the strain reaches 0.23%, the yielding process continues until the strain reaches 2.1%, and the hardening phenomena can be over-served afterward, the ultimate tensile strength reaches by approximately 16%. As shown in Fig. 6, since the bolt shank is relatively slim and the loading condition is not complex, a simplified piecewise linear constitutive model (which is divided into 10 linear sections) is introduced in the numerical simulation. The material properties used in this study are summarized in Table 1.

Table 1 Material properties used in the calculation
Full size table

In the numerical model, the bolt shank is installed across two rock blocks. It is discretized into 60 bar/beam elements with 61 nodes uniformly distributed along the bolt length. The anchored points (sharing the common location with element nodes) are coupled with a pair of independent nonlinear bond connections to equivalently represent the mechanical interactions among the rock–grout–shank interface.

For the fully grouted rebar, all the 60 anchored points are tied in both normal and tangential directions with proper discretized connections (an interfacial constitutive threshold and residual stress are applied). According to the experimental setup (Chen and Li 2015a), for the D-bolt, only the anchored points located at 0.10, 0.43, 1.23 and 1.80 m starting from the far end of the bolt are assigned as the real bonds. These anchored points are constrained in both normal and tangential directions, while the others are constrained to the normal direction of bolt length only. Therefore, the effective spacing of D-bolt specimens is 0.8 m. The rock blocks and the face plate are assumed to be linearly elastic in this study.

Step 1:

Internal force distribution within elastic limit of bolt system

As the design of the bolt systems is usually based on the inner stress distribution in the bolt shank and along the bonding interface, most theoretical studies tried to describe the stress distribution in the rock bolt precisely. In this subsection, the simulation results by the proposed numerical models will be verified by comparison with the analytical results.

  1. (a)

    Rebar bolt

The axial load on the right blocks is set to 200 kN, so as to keep both the bolt shank and the shank-grout-rock interface within the elastic range. Then, the shear stiffness of the bonding interface is gradually changed, which helps to observe the distribution pattern of axial force in the shank and shear force along the interfaces.

Figure 10 shows that the shear movement along the bonding surface increases when the equivalent stiffness of grout material decreases. The softened rock–grout–shank interface relies on the face plate to provide more resistance against the axial pulling force. Hence, the inner stresses of the shanks within the blocks asides would become more and more asymmetric (both axial force in shank and shear force along the interfaces). The value at the segment No. 60 indicates the loading on the face plate. The inner stress distribution pattern is highly consistent with the theoretical solution in the previous studies (He et al. 2015; Li and Stillborg 1999).

Fig. 10
figure 10

Inner force distribution of rebar bolt. a Axial force distribution along the bolt shank under different tangent stiffness of grouting material. b Shear force on the anchored points

Full size image
  1. (b)

    D-bolt

As shown in Fig. 11, the inner stress distribution of the D-bolt also differs for various shear stiffness values. The resultant force in the bolt shank within the left block (with face plate) is affected relatively slightly by different shear stiffness setting, compared with the rebar model. Simultaneously, it is observed that the tensile force in the shank is constant between the anchored points, indicating that the D-bolt has longer efficient–deformable segment than the rebar. The reason is that the D-bolt has a smoother surface profile and the shank diameter tends to shrink under tension. In a D-bolt, the effectively grouted range is relatively narrow. Therefore, the external force of 200 kN results in larger shear force on the limited number of equivalent anchored points. More specifically, the resultant shear force is about 3–5 times in the rebar under the same loading condition. In field practices, the strong cement mix or resin with high strength is recommended for D-bolt installation.

Fig. 11
figure 11

Internal axial force and shear force on shank interface

Full size image
Step 2-1:

Inner force distribution during the debonding process of the rock–grout–shank interface subject to the axial loading (resistant capabilities of bolts to weight of loosen block)

  1. (a)

    To confirm reasonable shear (bond) stiffness and strength of the interfaces:

As shown in the previous section, it is quite obvious that, even in the elastic stage, the equivalent shear stiffness of rock–grout–shank interface (bond stiffness) has a significant effect on the internal force distribution profile. For the ultimate pullout resistance capacity of the whole rock bolt system, the bond stiffness also plays a crucial role. Large amount of experiments and field tests on different rock bolts have also demonstrated such tendencies (Jalalifar 2006; Jalalifar and Naj 2010). However, no sufficient mechanical parameters for the grout material were given in the literature (Chen and Li 2015a).

In order to transfer the unstable rock movement to a stable zone through the rock bolt, each bond section/anchorage (Fig. 12) has two discontinuous interfaces: the bolt–grout interface and the grout–rock interface. The lateral displacement/failure might occur along a weaker interface in the bolt system, or even both interfaces (failure by splitting of grout and rock annulus). To determine the mechanical properties for the bond is a complicated analytical process, as many controlling factors (some of them are even uncertain) should be taken into account for the interlocking mechanism, such as the geometry of borehole and bolt, rock roughness, the mechanical properties of bolt, grout and rock and the confining pressure induced by in situ stress or experimental setup.

Fig. 12
figure 12

Load transfer mechanism (after Jalalifar 2006)

Full size image

A comprehensive deductive approach is designed to confirm the bond constitutive behavior in this study, in order to overcome the data insufficiency. The deduction process starts from the charts recommended by Yazici and Kaiser (1992), who carried out a series of pullout test to investigate the relationship between the ultimate bond strength and the relevant factors. Based on the experimental setup, “the strength of the cement mortar is about 65 MPa after three days curing” (Chen 2014), and the high-strength concrete with Young’s modulus of 50 GPa, and the borehole “pneumatically drilled with 33 mm drill bit” (Chen and Li 2015a), the equivalent ultimate bond strength against the debonding on bolt–grout–rock interface is estimated to be 45.39 MPa. Therefore, the equivalent ultimate load on each anchored point (on 60 divisions) is about 24.56 kN in the proposed numerical models. Thus, Young’s modulus can be derived as 8.8 GPa according to Yazici and Kaiser (1992). Assume that the elastic component of shear displacement along the shank interface is generated by the deformation of the grouting material, the equivalent shear stiffness of each anchored point is about 84.78 kN/mm in the proposed numerical models. In addition, the residual frictional force after bond failure is another important factor in resisting shear along the bolt shank. As suggested by Li and Stillborg (1999) for a practical case, the residual friction, which is set to 9.12% of the peak strength (2.24 kN), is reasonable compared to the field test data. With the above deductive parameters, the numerical results of a rebar bolt match well with the experimental observation of 206–209 kN at a total displacement of 32.4 mm.

Through the trial numerical experiments, it is found that the gap between the blocks due to axial loading is majorly contributed by four components, namely the deformation of fully grouted rebar, deformation of rock and grout material and the embedding deformation of the face plate. Although not all the factors are considered in the deductive bond stiffness, it is believed that the deduced value should fall into certain reliable intervals after verified by the experimental results.

  1. (b)

    Inner force distribution during the debonding process

In shallow underground excavation where the in situ stresses are low, the main stability concern is falling of the loosened blocks under gravity. The function of the rock bolt is therefore to maintain the loosened blocks at their original positions so as to keep the surrounding rock blocks in place. In this case, the dead weight of loosen blocks can be represented by a constant load applied on the right block at its geometrical center. With the bond stiffness, strength and residual friction as mentioned in the previous section, a typical constitutive profile of combined bond interfaces from Cai et al. (2004) and Ivanović and Neilson (2009) is introduced into the DDA simulation, as shown in Fig. 13a. Along with the increased external forces, the bolt shank is initially intact, then partially debonded, until fully debonded from the right block, as shown in Fig. 13b. It is worth noting that the residual strength on the interfaces plays an important role in symmetrical debonding among the joints between two blocks.

Fig. 13
figure 13

Debonding process of the bolt bonding interface. a Simplified constitutive model of bond (Modified after Ivanović and Neilson 2009). b Debonding process subjected the axial force

Full size image

Figure 14 presents the inner stress distribution in the shank and the shear force in the bolt–grout–rock interface under different external stresses. This is in agreement with the theoretical results (e.g., He et al. 2015; Li and Stillborg 1999). As the bond failure is not considered in the D-bolt model, the internal force distribution is the same as in the previous step.

Fig. 14
figure 14

Force distribution in the bolt system during the debonding process due to constant axial tensile force

Full size image
Step 2-2:

Inner force distribution during the debonding process of the rock–grout–shank interface subject to the displacement boundary condition (resistant capabilities to rock dilation)

One of the most significant phenomena observed in deep underground excavations is tensile fracturing of brittle rocks (Cho et al. 2004). Micro- and macro-fractures occur as a result of superficial tangential stress concentrations after excavation. The brittle rock failure around underground openings reveals that the tensile fracture exhibits great dilation phenomena. In the mining industry, the process is often referred to as “spalling” or “dog-earing.” In the petroleum industry, the problem is often to cast as “well-bore breakouts.” Most laboratory tests on rock dilation involve two rock or concrete blocks, among which one is fixed and another one is allowed to move with a small constant velocity (to ensure a quasi-static condition). In this subsection, the fully grouted rebar and the D-bolt are simulated to compare their capability in sustaining rock dilation.

Figure 15a shows the variation of the maximum axial tensile load in the bolt shank (i.e., the axial tensile load in the beam element crossing over the joint) with varying degrees of rock dilation. According to the parameters of bond connection determined in the earlier section, the maximum tensile load initially increases linearly to 121.96 kN before the rock dilation reaches 0.05875 mm, followed by a zigzag increase from 121.96 to 164.58 kN with the rock dilation between 0.05875 and 0.3345 mm, and then a sudden drop from 164.58 to 67.20 kN until the rock dilation is 0.345 mm. It finally keeps at a constant value of 67.20 kN when the rock dilation is larger than 0.345 mm. The zigzag range indicates the debonding process along the bolt/grout/rock interface. Each drop in the zigzag range represents the debonding at an anchored point (numerical format), following with redistribution of tensile load until another anchored point is debonded with increasing degree of rock dilation. The process is repeated until the bolt/rock interface in the left block is debonded completely, i.e., the final drop in Fig. 15a. The constant tensile load in the final range represents the residual shear strength at each debonded point. The residual shear capacity is 67.20 kN, which is exactly the same as the theoretical prediction of 2.24 kN × 30 = 67.20 kN.

Fig. 15
figure 15

Variation of maximum axial tensile load and debonded range in the rebar system with rock dilation. a Variation of maximum axial tensile force in the shank with rock dilation. b Variation of debonded range in the shank with rock dilation

Full size image

The results imply that the rebar can only sustain a rock dilation of 0.345 mm, given the assumed bolt length and peak/residual shear strength along the bolt/rock interface. The bolt shank is still within the elastic range and the rebar fails due to debonding along the bolt/rock interface.

Figure 15b depicts the debonded range in both left and right blocks induced by rock dilation. A discrete point represents the debonding of a particular anchored point, thus corresponding to a drop-and-rise cycle in the zigzag range in Fig. 15a. The debonding of the bolt/grout/rock interface starts, closed to the insert joint, then gradually and symmetrically moves toward two sides until the complete debonding in the left block. The debonded range increases almost linearly with rock dilation. With the correlation equation, the rock dilation, which can be sustained by a specific rebar, can be easily predicted.

Figure 16 shows the variation of the axial tensile load in the smooth section crossing over the interface with increasing degree of rock dilation for the D-bolt. The anchors are loaded when the rock dilates and then the smooth section between the anchors is stretched. The axial tensile load in the smooth section increases quickly and linearly with a small increase in the rock dilation until 172.24 kN corresponding to rock dilation of 4.93 mm. After that, the smooth section elongates plastically and the axial tensile load maintains approximately at 200 kN until the rock dilation increases to 154.48 mm, where tensile failure occurs.

Fig. 16
figure 16

Comparison of axial displacement curves obtained by modeling and experiments for two typical rock bolt systems

Full size image

The D-bolt absorbs the rock dilation energy through fully mobilizing the strength and deformation capacities of the steel. Its behavior depends solely on the material properties (i.e., yield strain, ultimate strain and yield strength) of the bolt shank, given reliable anchored points.

Step 3:

Comparison with experimental results

In order to fully examine the efficiency and robustness of the proposed bolt model, the numerical results are compared with the experiment results in this section. The boundary conditions, the applied displacement curve, the bolt profile and other conditions of the numerical model are set exactly the same as the experiment. A series of complicated processes, such as rock material deformation, shank deformation, slipping of the bond interfaces, debonding, bolt shank failure and interaction between the rock block and the face plate, take place simultaneously during the numerical simulation. The loading profile of the bolt and the numerical model for both rebar and D-bolt subject to axial displacement are shown in Fig. 16. The key features of bolt performance, including elastic range, yield point, elasto-plastic range and failure range, are captured and compared with the experiment results. It is found that the ultimate load-bearing capacity of rebar and D-bolt is consistent, since it is mainly controlled by the shank properties, and both the rebar and D-bolt have the same shank material and dimension.

As mentioned before, the D-bolt has longer efficient–deformable segment than the rebar. Therefore, for a given ultimate strain, the D-bolt has significantly larger value of ultimate elongation. This phenomenon has been demonstrated in both numerical simulations and experiments. The initial self-adoptive process can be observed in the initial stage, and the rest parts of curves approach the input constitutive profile in Fig. 6. As the interlocking mechanism of the rebar is much complicated than of the D-bolt, it is susceptible to any local factors, such as the bonding quality and local clamp effect. Therefore, as shown in Fig. 6, the bias between numerical results and experimental results of the rebar is larger than that of D-bolt.

In summary, the proposed rock bolt model incorporated in the DDA method can reflect the mechanical behavior of two typical bolts very well, and it is also verified that the derivation method for unknown parameters of bond constitutive model is acceptable. The numerical results can match well with the experiment results.

6 Discussion and Summary

This paper proposes and implements an advanced rock bolt model into the 2D DDA method. The formulations are based on the (modified) Euler–Bernoulli beam elements with the unknowns represented at the end nodes. The rock mass and the bolt shank are modeled separately, and they interact with each other through the anchored points (control node of shank) and borehole segments. Different types of rock bolts are simulated within the unified framework by specifying the corresponding constitutive models for the anchored points. Four modes of bolt failures, namely tensile failure and shear failure of the bolt shank, debonding along the bolt/rock interface and loss of the face plate, are possible in the analysis procedure.

Based on the proposed bolt model in DDA, the interaction among “bolt–grout–rock” to capture the major aspects of real functional mechanism of the bolt system is demonstrated with as less degrees of freedom (DOF) as possible. The large displacement between the shank and borehole, as well as the debonding process, can be realized. However, due to the limited data from direct experiments on various types of bolts, only two simple block examples, a typical conventional rock bolt (rebar) and a typical energy-absorbing rock bolt (D-bolt), have been completely verified with the available analytical predictions and experimental observations. The most challenging part for the proposed model is determination of the constitutive relations and parameters. A comprehensive trial procedure to determine the parameters is introduced, and the numerical results are demonstrated to be in good agreement with the overall bolt performance obtained by physical tests.

The proposed model has potential applications in numerical experiments to investigate the performance of rock bolts in the scenarios where experiments are tremendously expensive or even impossible. More specifically, it could be used to: (1) reveal the mechanism of each type of rock bolt in various scenarios; (2) identify their applicability, advantages and limitations; (3) propose any modifications to achieve better performance; (4) provide site-specific and problem-specific rock bolting design, especially in dynamic situations; (5) better interpret the monitoring data since nowadays the rock bolts are used not only as rock support but also as monitoring instruments.

On another hand, it is worth mentioning that the accuracy of proposed bolt system would be inevitably mesh-dependent in the DDA code. Different mesh sizes may be required according to the accuracy demand for different practical problems. For instance, whether the pure pullout condition or emphasis on shear forces is considered in the orthogonal jointed rock mass, the required DOFs of bolt are different. Normally, when considering the latter case, more anchored points shall be used for higher accuracy. Taking the bolt with a length of 2 m as an example, about 50–100 divisions (default value 60 in our in-house code) could satisfy the general requirement with relatively acceptable computing cost. From our experiences, if only pure tension is considered, up to 30 divisions are far more sufficient to obtain convergent numerical results. However, if wave propagation within the bolt (e.g., ultrasonic wave, normally used in applications such as health monitoring of bolts) is considered, up to 1000 divisions might be required in order to achieve reasonable results.