The Influence of Fracturing Fluids on Fracturing Processes: A Comparison Between Water, Oil and SC-CO₂

Abstract

Conventional water-based fracturing treatments may not work well for many shale gas reservoirs. This is due to the fact that shale gas formations are much more sensitive to water because of the significant capillary effects and the potentially high contents of swelling clay, each of which may result in the impairment of productivity. As an alternative to water-based fluids, gaseous stimulants not only avoid this potential impairment in productivity, but also conserve water as a resource and may sequester greenhouse gases underground. However, experimental observations have shown that different fracturing fluids yield variations in the induced fracture. During the hydraulic fracturing process, fracturing fluids will penetrate into the borehole wall, and the evolution of the fracture(s) then results from the coupled phenomena of fluid flow, solid deformation and damage. To represent this, coupled models of rock damage mechanics and fluid flow for both slightly compressible fluids and CO₂ are presented. We investigate the fracturing processes driven by pressurization of three kinds of fluids: water, viscous oil and supercritical CO₂. Simulation results indicate that SC-CO₂-based fracturing indeed has a lower breakdown pressure, as observed in experiments, and may develop fractures with greater complexity than those developed with water-based and oil-based fracturing. We explore the relation between the breakdown pressure to both the dynamic viscosity and the interfacial tension of the fracturing fluids. Modeling demonstrates an increase in the breakdown pressure with an increase both in the dynamic viscosity and in the interfacial tension, consistent with experimental observations.

1 Introduction

As an important product from unconventional reservoirs, shale gas has been produced commercially and recognized as a “game changer” for the US natural gas and energy markets (EIA 2015; Gensterblum et al. 2015). The extraction of shale gas, which was previously considered inaccessible in ultra-low permeability formations, has become economically feasible through the advent of horizontal drilling and massive hydraulic fracturing (Vidic et al. 2013; Vengosh et al. 2014). Shale gas is trapped inside formations with low permeability that limit the extraction of the gas, and more than 90% of gas wells drilled in recent years have been hydraulically fractured to achieve economical flow rates (Wang et al. 2016; Jarvie et al. 2004).

However, conventional water-based fracturing treatments do not perform to full potential in many shale gas reservoirs due to the impairment of productivity, of which the major cause may be the effects of water retention. In many shale gas formations, water is the wetting phase and the initial water saturation is less than the equilibrium capillary irreducible water saturation (Gupta 2009; Friehauf 2009). Water from conventional water-based fracturing fluids will be trapped in the near-wellbore region during the fracturing processes, which may limit the ability of gas to flow to the wells. This adverse effect is observed in many reservoirs (Al-Anazi et al. 2002; Mahadevan et al. 2007; Parekh and Sharma 2004). Another cause of the productivity impairment is the swelling of clay minerals. Clays within the walls of fractures will expand after the water invades the formation, resulting in a decrease in permeability and an increase in entry pressures. Additionally, some areas rich in shale gas suffer from a water deficit and the water supply may also limit the use of water-based fracturing fluids (Gallegos et al. 2015). In addition, deep reinjection of the contaminated flow-back water is a possible cause for induced seismicity that results in low-level earthquakes (Ellsworth 2013; Elsworth et al. 2016). As an alternative to water-based fluids, gaseous stimulants not only avoid this potential impairment in productivity, but also conserve water as a resource and may additionally sequester greenhouse gases underground (Middleton et al. 2015).

Recent experimental observations of hydraulic fracturing in PMMA (Alpern et al. 2012; Gan et al. 2015) indicate that the fracture path and breakdown pressure vary with the composition and state of the fracturing fluid. Fluid-driven fracturing experiments in shale and granite (Ishida et al. 2004, 2016; Chen et al. 2015; Li et al. 2015), using fluids of different viscosities, show that supercritical CO₂ results in the lowest breakdown pressure, the most fracture branches and the highest fracture tortuosity—possibly due to the reduced viscosity of supercritical fluids. So far, the dependence of breakdown pressures and of the resulting fracture complexity on fluid composition or state remain partly unexplained. Thus, the task of determining this relation appears to be important for capturing the principal features of gaseous stimulation for in situ demonstrations. In this work, we investigate mechanisms of hydraulic fracturing driven by three kinds of fluids: water, viscous oil and supercritical CO₂. Coupled models of rock damage and fluid flow are developed for both slightly compressible (water and oil) and compressible fluids (CO₂). These models are used to simulate the fracturing processes driven by pressurization of fluids within a borehole under isothermal conditions. The differences in fracture evolution process and fracture topology between these three kinds of fluids are detailed. Finally, the effect of dynamic viscosity and interfacial tension on the breakdown pressure is examined.

2 Governing Equations

During the fracturing process, fracturing fluids will penetrate into the rock around borehole driven by the injection pressure. Thus, the initiation and evolution of the resulting fractures is a coupled phenomenon involving fluid flow, solid deformation and damage. In the following, a set of governing equations for rock deformation and fluid flow are derived at the macroscopic scale with a damage evolution law defined by a micromechanical model.

2.1 Governing Equation for Rock Deformation

The strain–displacement relation of the rock is expressed as

$$\varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right)\quad i = 1,2,3;\;j = 1,2,3,$$

(1)

where $\varepsilon_{ij}$ is the strain, $u_{i}$ is the displacement, $i,j$ denote the space coordinates, and the subscripted comma followed by a subscripted “i” indicates partial differentiation with respect to each coordinate x _i .

The equilibrium equation is defined as

$$\sigma_{ij,j} + f_{i} = 0,$$

(2)

where $\sigma_{ij}$ is the stress and $f_{i}$ is the body force in the ith direction.

According to poroelastic theory, the constitutive relation for the deformed rock is expressed as

$$\varepsilon_{ij} { = }\frac{1}{2G}\sigma_{ij} - \left( {\frac{1}{6G} - \frac{1}{9K}} \right)\sigma_{kk} \delta_{ij} { + }\frac{\alpha }{3K}p\delta_{ij} ,$$

(3)

where G is the shear modulus of the rock, K is the bulk modulus, p is the pore pressure, $\alpha$ is the Biot coefficient, and $\delta_{ij}$ is the Kronecker delta.

Combining Eqs. (1)–(3) yields the Navier-type equation expressed as

$$Gu_{i,kk} + \frac{G}{1 - 2v}u_{k,ki} - \alpha p_{,i} + f_{,i} = 0,$$

(4)

where Eq. (4) is the governing equation for deformation under the influence of fluid pressures.

2.2 Governing Equation for Fluid Flow

Rock is composed of the solid matrix, which contains interstitial pore space between the framework of grains. In order to describe the fluid transport through the connected porosity, it is necessary to introduce the governing equation for fluid flow. However, compressible CO₂ exhibits transport behavior different from water and oil (slightly compressible fluids) due to the large compressibility and phase change under certain pressures and temperatures. Therefore, the transport equations for slightly compressible fluids and CO₂ are established, respectively, in this section.

2.2.1 Slightly Compressible Fluids

The governing equation for fluid flow is based on the mass balance equation of fluid, which is defined as

$$\frac{\partial m}{\partial t} + \nabla \cdot \left( {\rho {\mathbf{q}}} \right) = Q_{\text{s}} ,$$

(5)

where m is the fluid content in the rock, $\rho$ is the fluid density, ${\mathbf{q}}$ is the Darcy velocity vector, and $Q_{\text{s}}$ is the gas source or sink.

Neglecting the effect of gravity, which will be small, the Darcy velocity can be expressed as

$${\mathbf{q}} = - \frac{k}{{\mu_{g} }}\nabla p,$$

(6)

where k is the permeability of the rock, $\mu_{\text{g}}$ is the dynamic viscosity of the fluid, and p is the fluid pressure.

Assuming that the rock is saturated by the fluid, the fluid content per unit volume can be expressed as $m = \rho \phi$, where $\phi$ is the porosity. Slightly compressible fluids often exhibit exceedingly small compressibility, for which the partial derivative of m with respect to time can be written as

$$\frac{\partial m}{\partial t} = \phi \frac{\partial \rho }{\partial t} + \rho \frac{\partial \phi }{\partial t} = \rho \left( {\frac{\phi }{{K_{\text{f}} }} + \frac{1 - \phi }{{K_{\text{s}} }}} \right)\frac{\partial p}{\partial t}$$

(7)

where $K_{\text{f}}$ is the bulk modulus of fluid and $K_{\text{s}}$ is the bulk modulus of rock grains.

Combining Eqs. (5)–(7) yields the governing equation for slightly compressible fluid flow through the rock expressed as

$$\left( {\frac{\phi }{{K_{\text{f}} }} + \frac{1 - \phi }{{K_{\text{s}} }}} \right)\frac{\partial p}{\partial t} + \nabla \cdot \left( { - \frac{k}{\mu }\nabla p} \right) = Q_{\text{s}} .$$

(8)

2.2.2 Compressible Fluids (SC-CO₂)

The compressibility of CO₂ is significantly larger than that of either water or oil and further changes markedly in the phase change from gaseous state to supercritical state. This change occurs at the critical point, which for CO₂ is at temperature and pressure greater than 304.1 K and 7.38 MPa. This transition in compressibility must be accommodated in models below and above this phase change, where it exists as a gas, evolving into a supercritical fluid (described later in this section). Therefore, the governing equation for slightly compressible fluid flow [Eq. (8)] is not generally applicable for CO₂. The generalized flow equation can be written as

$$\frac{{\partial \left( {\rho \phi } \right)}}{\partial t} + \nabla \cdot \left( { - \frac{k}{\mu } \cdot \rho \cdot \nabla p} \right) = Q_{\text{s}} ,$$

(9)

where the density $\rho$ of the CO₂ varies significantly with pressure under isothermal condition, which can be described by the equation of state (EOS). One applicable and robust model for the EOS of CO₂ is that of Span and Wagner (1996) defined in terms of Helmholtz free energy, referred to as the Span–Wagner (S–W) equation of state (EOS). The density of CO₂ is only related to the residual part of the full expression, which can be written as

$$\begin{aligned} \varphi^{r} \left( {\delta ,\tau } \right) = & \sum\limits_{i = 1}^{7} {n_{i} \delta^{{d_{i} }} \tau^{{t_{i} }} } + \sum\limits_{i = 8}^{34} {n_{i} \delta^{{d_{i} }} \tau^{{t_{i} }} \text{e}^{{ - \delta^{{c_{i} }} }} } + \sum\limits_{i = 35}^{39} {n_{i} \delta^{{d_{i} }} \tau^{{t_{i} }} \text{e}^{{ - \alpha_{i} \left( {\delta - \varepsilon_{i} } \right)^{2} - \beta_{i} \left( {\tau - \gamma_{i} } \right)^{2} }} } , \\ & \quad + \sum\limits_{i = 40}^{42} {n_{i} \Delta^{{b_{i} }} \delta \text{e}^{{ - C_{i} \left( {\delta - 1} \right)^{2} - D_{i} \left( {\tau - 1} \right)^{2} }} } \\ \end{aligned}$$

(10)

where $\delta = {\rho \mathord{\left/ {\vphantom {\rho \rho }} \right. \kern-0pt} \rho }_{\text{c}}$ is the reduced density and $\tau = {{T_{\text{c}} } \mathord{\left/ {\vphantom {{T_{\text{c}} } T}} \right. \kern-0pt} T}$ is the inverse reduced temperature, $\Delta = \{ {\left( {1 - \tau } \right) + A_{i} \left[ {\left( {\delta - 1} \right)^{2} } \right]^{{{1 \mathord{\left/ {\vphantom {1 {\left( {2\beta_{i} } \right)}}} \right. \kern-0pt} {\left( {2\beta_{i} } \right)}}}} }\}^{2} + B_{i} \left[ {\left( {\delta - 1} \right)^{2} } \right]^{{a_{i} }}$, $\rho_{\text{c}}$ is the critical density, $T_{\text{c}}$ is the critical temperature, and the other parameters are all constant. The relation between the CO₂ density and the pressure can be defined by the following implicit function

$$p = \left( {1 + \delta \varphi_{\delta }^{r} } \right)\left( {\rho RT} \right)$$

(11)

where $\varphi_{\delta }^{r}$ is the derivative of the residual part of the Helmholtz free energy with respect to the reduced density and R is the universal gas constant. As an illustration, the evolution of CO₂ density with pressure at three specified temperatures is shown in Fig. 1. Below the critical temperature (31.1 °C), there is a discontinuity in the density of CO₂ indicating the liquefaction of gaseous CO₂ (the blue dashed line with the blue dot represents the liquefaction point). Above the critical temperature, as shown by the green (45 °C) and red (65 °C) lines, the CO₂ density increases continuously with variable compressibility as the pressure increases (the green dot and red dot represent corresponding critical points).

Fig. 1

Evolution of CO₂ density with pressure at three specified temperatures simulated by the S–W equation of state. The blue, green and red lines represent cases with temperature T = 25, 45 and 65 °C, respectively. The blue dots indicate the liquefaction point with T = 25 °C, while the green and red dots indicate the critical points with T = 45 and 65 °C, respectively (color figure online)

Combining Eqs. (9)–(11) yields the governing equation for CO₂ flow in porous media expressed as

$$\frac{\phi }{N}\frac{\partial p}{\partial t} + \nabla \cdot \left( { - \frac{k}{\mu } \cdot \rho \cdot \nabla p} \right) = Q_{\text{s}} ,$$

(12)

where $N = RT\left( {\delta^{2} \varphi_{\delta \delta }^{r} + 2\delta \varphi_{\delta }^{r} + 1} \right)$ is a variable only related to the density of CO₂ under isothermal conditions, and $\varphi_{\delta }^{r}$ and $\varphi_{\delta \delta }^{r}$ are the first and second derivatives of $\varphi_{{}}^{r}$ with respect to $\delta$, respectively. For the purpose of fast numerical evaluation of CO₂ density through Eqs. (10) and (11), the values of CO₂ density are first calculated accurately for a set of pressures and then stored. This enables the use of interpolation to map values according to the pressure distribution at each time step in a fast and accurate manner. In other words, for a given time step, the CO₂ density is determined and updated based on the pressure distribution from the last time step by using an interpolation function, and remains unchanged within the current time step.

2.3 Damage Evolution Law

During the fracturing process, the heterogeneity of the rock has an influence on determining the fracture paths and the resulting fracture patterns (Kim and Yao 1995; Tang 1997; Fang and Harrison 2002). In order to characterize this intrinsic heterogeneity, the macroscopic description of the rock is composed of an overlay of microscopic square elements that each equals a representative elemental volume (REV). The mechanical parameters for each of the REVs, such as strength and elastic modulus, are assumed to conform to the widely used Weibull distribution, which is justified as a means of characterizing the strength variations of rocks (Weibull 1951; Hudson and Fairhurst 1969; Wong et al. 2006) and follows the probability density function:

$$f\left( u \right) = \frac{m}{{u_{0} }}\left( {\frac{u}{{u_{0} }}} \right)^{m - 1} \exp \left( { - \frac{u}{{u_{0} }}} \right)^{m} ,$$

(13)

where u is any applicable characteristic mechanical parameter (strength or elastic modulus) for the REV, the scaling parameter $u_{0}$ is the average value of that characteristic parameter, and the parameter m describes the shape of the distribution function. According to Eq. (13), heterogeneous mechanical parameters for each of the REVs can be generated by a Monte-Carlo simulation.

In this study, we use the damage evolution law defined at the microscopic scale (Tang 1997; Zhu and Tang 2004). The nonlinear stress–strain relation of the REV under the conditions of uniaxial tension and compression can be simplified as a piecewise function, as shown in Fig. 2 (positive for compression). Damage in tension or in shear is initiated when the stress state of an REV satisfies the maximum tensile stress criterion or the Coulomb shear failure criterion, respectively, as defined by

$$\left\{ {\begin{array}{*{20}l} {F_{1} = - \left( {\sigma_{3} - \alpha p} \right) - f_{{{\text{t}}0}} = 0} \hfill \\ {F_{2} = \left( {\sigma_{1} - \alpha p} \right) - \frac{1 + \sin \theta }{1 - \sin \theta }\left( {\sigma_{3} - \alpha p} \right) - f_{{{\text{c}}0}} = 0} \hfill \\ \end{array} } \right.,$$

(14)

where $\sigma_{1}$ and $\sigma_{3}$ are the maximum and minimum principal stresses, respectively, $f_{{{\text{t}}0}}$ and $f_{{{\text{c}}0}}$ are the uniaxial tensile and compressive strength, respectively, $\theta$ is the internal friction angle, $\alpha$ is the Biot coefficient, and $F_{1}$ and $F_{2}$ are two damage threshold functions. Figure 3 shows the two criteria with red and blue Mohr’s circles representing stress states where tensile failure and shear failure occur, respectively.

Fig. 2

Constitutive law for rock under a uniaxial tensile stress and b uniaxial compressive stress

Fig. 3

Maximum tensile stress criterion and the Coulomb shear failure criterion used in the model. The red and blue Mohr circles represent stress states where tensile failure and shear failure are imminent, respectively. The yellow dashed Mohr circle shows the case when the two criteria are simultaneously met (color figure online)

The elastic modulus of an REV decreases monotonically with the evolution of damage and can be expressed as

$$E = \left( {1 - D} \right)E_{0}$$

(15)

where $E_{0}$ and E are the elasticity modulus of an REV before and after the initiation of damage, respectively, D is the damage variable that varies from 0 to 1.

When the REV is under uniaxial tension, the constitutive relationship illustrated in Fig. 2a is adopted where power function softening is used to describe the softening process in the post-peak region. Since no initial damage is incorporated in this model, the initial stress–strain curve is linearly elastic, and thus no damage occurs (D = 0) when $\varepsilon \ge \varepsilon_{{{\text{t}}0}}$, where $\varepsilon_{{{\text{t}}0}}$ is the tensile strain at the elastic limit. When the maximum tensile stress criterion is met, the REV begins to degrade according to the specified power-law softening function until the stress attains the residual strength f _tr, which is given as $f_{\text{tr}} = \lambda f_{{{\text{t}}0}} = \lambda E_{0} \varepsilon_{{{\text{t}}0}}$. Herein, $\lambda$ is the residual strength coefficient, which is equal to the ratio of the residual tensile strength f _tr to initial tensile strength of the rock f _t0. When the strain exceeds the ultimate tensile strain $\varepsilon_{\text{tu}}$, the REV would be completely damaged in the tensile mode (D = 1). The ultimate tensile strain is defined by $\varepsilon_{\text{tu}} = \eta \varepsilon_{{{\text{t}}0}}$, where $\eta$ is the ultimate strain coefficient. Therefore, the damage variable D can be defined as

$$D = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\varepsilon > \varepsilon _{{{\text{t}}0}} } \hfill \\ {1 - \left( {\varepsilon _{{{\text{t}}0}} {/}\varepsilon } \right)^{2} } \hfill & {\varepsilon _{{{\text{t}}0}} \ge \varepsilon > \varepsilon _{{{\text{tr}}}} } \hfill \\ {1 - \left( {\lambda \varepsilon _{{{\text{t0}}}} {/}\varepsilon } \right)} \hfill & {\varepsilon _{{{\text{tr}}}} \ge \varepsilon > \varepsilon _{{{\text{tu}}}} } \hfill \\ 1 \hfill & {\varepsilon _{{{\text{tu}}}} \ge \varepsilon } \hfill \\ \end{array} } \right.$$

(16)

According to the method of extending one-dimensional constitutive laws under uniaxial tensile stress to complex tensile stress conditions, as proposed by Mazars and Pijaudier-Cabot (1989) for a constitutive law of elastic damage, the constitutive law for uniaxial tension described above [Eq. (16)] can be easily extended to a three-dimensional stress state. Under a multiaxial stress state, the element is still damaged in tension when the equivalent maximum tensile strain attains the threshold strain $\varepsilon_{{{\text{t}}0}}$. Therefore, the constitutive law of an element subjected to multiaxial stresses can be obtained by substituting the strain $\varepsilon$ in Eq. (16) with the equivalent principal tensile strain $\varepsilon_{\text{t}}$, which is defined as $\varepsilon_{\text{t}} = \sqrt {\sum\nolimits_{1}^{3} {\left( {{{\left| {\varepsilon_{i} } \right|} \mathord{\left/ {\vphantom {{\left| {\varepsilon_{i} } \right|} 2}} \right. \kern-0pt} 2} - {{\varepsilon_{i} } \mathord{\left/ {\vphantom {{\varepsilon_{i} } 2}} \right. \kern-0pt} 2}} \right)}^{2} }$.

The constitutive relationship for REVs under uniaxial compression is illustrated in Fig. 2b. Similarly, the damage variable D for the uniaxial compression condition can be obtained as

$$D = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\varepsilon < \varepsilon_{{{\text{t}}0}} } \hfill \\ {1 - \left( {{{\varepsilon_{{{\text{c}}0}} } \mathord{\left/ {\vphantom {{\varepsilon_{{{\text{c}}0}} } \varepsilon }} \right. \kern-0pt} \varepsilon }} \right)^{2} } \hfill & {\varepsilon_{{{\text{c}}0}} \le \varepsilon < \varepsilon_{\text{cr}} } \hfill \\ {1 - \left( {{{\lambda \varepsilon_{{{\text{c}}0}} } \mathord{\left/ {\vphantom {{\lambda \varepsilon_{{{\text{c}}0}} } \varepsilon }} \right. \kern-0pt} \varepsilon }} \right)} \hfill & {\varepsilon_{\text{cr}} \le \varepsilon < \varepsilon_{\text{cu}} } \hfill \\ \end{array} } \right. ,$$

(17)

where $\varepsilon_{{{\text{c}}0}}$ is the maximum compressive strain at the peak stress state and $\varepsilon_{\text{cr}}$ is the corresponding compressive strain when stress attains the specified residual strength. For the multiaxial compression condition, the maximum compressive principal strain $\varepsilon_{1}$ of a damaged element is used to substitute the uniaxial compressive strain $\varepsilon$ in Eq. (17), and the maximum compressive principal strain $\varepsilon_{{{\text{c}}0}}$ at the peak value of maximum compressive principal stress is calculated as follows to consider the effect of all principal stresses:

$$\varepsilon_{c0} = \frac{1}{{E_{0} }}\left[ {f_{c0} + \frac{1 + \sin \theta }{1 - \sin \theta }\sigma_{3} - \mu \left( {\sigma_{1} + \sigma_{2} } \right)} \right].$$

(18)

Validation against typical laboratory observations have demonstrated that, under a variety of static and dynamic loading conditions, this model can effectively simulate the key features of deformation and failure in rock. This includes nonlinearity in the stress–strain response, localization of deformation, strain softening, and the crack propagation process (Tang 1997; Tang and Kaiser 1998; Zhu and Tang 2004, 2006; Zhu et al. 2005).

As shown in Fig. 3, the Mohr circle may move in either direction, and damage can occur either in tension or in shear, according to the stress states of the REVs. There remains the slight possibility that the stress state of an REV simultaneously meets the maximum tensile stress criterion and the Coulomb shear failure criterion (the yellow circle in Fig. 3), and the damage could be either in tension or in shear. In the numerical implementation, the damage variable D in tensile mode has primacy for this case. This constraint has no influence on the simulation results since: (1) the damage variable is a scalar in this model, and (2) a stepwise loading is used to apply the fluid pressure on the boundary, which limits the increment of the damage variable magnitude to a small value within a single iteration step, and changes in stress state/damage variable will shift the Mohr circle from this position (the yellow circle in Fig. 3) in the next iteration step). According to Eq. (15), the elastic modulus of the damaged REV is reduced with an increase of the damage variable. If the tensile equivalent principal strain exceeds the ultimate tensile strain, the damage variable is set to unity and the REV is considered to be fully ruptured and thus a small residual magnitude of the elastic modulus is assigned to it. In addition, the permeability also evolves as function of damage. Since the evolution of permeability with damage is complex, we describe this relation as the following exponential function (Zhu et al. 2013)

$$k = k_{0} \exp \left( {\alpha_{k} D} \right)$$

(19)

where $k_{0}$ is the initial permeability and $\alpha_{k}$ is a constant (set at 5) referred to as the damage-permeability coefficient to indicate the effect of damage on the permeability. Note that this expression gives k = k ₀ at D = 0 and a large k for any significant D. It is likely that during hydraulic fracturing in low permeability formations, even limited damage will increase k by many orders of magnitude, which can be captured by Eq. (19). Analyses with different magnitudes of the multiplier $\alpha_{k}$ larger than 5 give similar results. This is because the material transits from impermeable ($k_{0}$) to permeable once $D > 0$, and this binary transformation is the essence of the coupling of the propagating fracture. Any nuance in behavior that results from finessing the magnitude of the multiplier $\alpha_{k}$ is irrelevant as long as $\alpha_{k}$ is sufficiently large to allow fluid penetration.

2.4 Numerical Implementation of the Model

Since the established model is nonlinear both in space and time, it is not possible to obtain an analytical solution. Therefore, the complete set of coupled equations is solved by the finite element method. Additionally, this approach requires that the damage variable and the damage-induced alteration of elastic modulus and permeability are continually updated as the loads increase. The basic procedure is shown in Fig. 4 and is summarized as follows:

• (i) After establishing the model geometry, the model is discretized into a set of REVs. Then, the initial mechanical and hydraulic properties are defined and the initial boundary conditions are applied.

• (ii) A fully coupled analysis is performed by FEM through the solver of COMSOL, and the stress, strain and pore pressure for each of the REVs are obtained.

• (iii) Effective stresses defined over the REVs are then calculated according to Biot theory, and they are used to check whether the REVs are damaged by exceeding the damage threshold functions [Eq. (14)].

• (iv) Effective stresses in the damaged REVs are substituted into Eqs. (16) and (17) to calculate the damage variable. Then, the elastic modulus and permeability of these REVs are modified following Eqs. (15) and (19).

• (v) If the convergence condition, i.e., $E_{\text{step + 1}} - E_{\text{step}} \le 10^{ - 3} {\text{ Pa}}$, is satisfied, then the solution cycles to step (vi)—otherwise steps (iii)–(v) are repeated with the updated material parameters.

• (vi) The boundary conditions are updated in the next load increment.

The above procedures are implemented in MATLAB to obtain the parameters related to damage and implemented into COMSOL Multiphysics, a powerful PDE-based multiphysics modeling environment, to complete the FEM analysis.

Fig. 4

Procedure for the numerical implementation of the model

3 Numerical Simulation

In this section, the physical processes for several 2D hydraulic fracturing problems with different fracturing fluids (water, oil and SC-CO₂) are simulated and the simulation results are compared with available experimental observations. The influence of dynamic viscosity and surface tension of the fracturing fluids on the breakdown pressure is examined.

3.1 Model Geometry

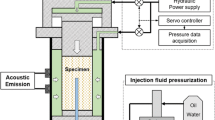
The 2D hydraulic fracturing problem considered here is a 2D plane cross-section through a cubical specimen containing a central borehole and subjected to an initial anisotropic stress field. The pressurizing fluids are injected into the borehole at a constant pressurization rate C until the breakdown pressure is reached and the fracture propagates without increasing the hydraulic pressure (unstable fracture propagation occurs). The problem is simulated as plane strain with transient state fluid flow.

Referring to the configuration of the experiments conducted by Chen et al. (2015), the geometries and loading conditions of the model are defined as shown in Fig. 5. The square rock specimen is 170 mm on each side, and the borehole at its center is 20 mm in diameter. The geometry is divided into a grid of elements $340 \times 340 = 115{,}600$ microscopic elements (REVs). The boundary conditions are $\sigma_{1} = 6\;{\text{MPa}}$ applied on the top boundary and $\sigma_{3} = 3\;{\text{MPa}}$ applied on the right boundary with rollers along the left and bottom sides. All boundaries are no-flux boundaries except for the borehole on which a monotonically increasing fluid injection pressure is applied. The fluid pressurization rate is ${{R = \Delta p} \mathord{\left/ {\vphantom {{R = \Delta p} {\Delta t}}} \right. \kern-0pt} {\Delta t}} = 0.5\;{\text{MPa/s}}$, where $\Delta p = 0. 5\;{\text{MPa}}$ and $\Delta t = 1\;{\text{s}}$ are the pressure increment and time increment, respectively. For the simulation of hydraulic fracturing with SC-CO₂, the system is isothermal (318.15 K) to ensure that the gas is supercritical before the breakdown pressure is reached. The other physico-mechanical parameters of the rock and fluids are assigned according to Table 1. Zhu and Tang (2004) investigated the effect of constitutive parameters on the numerical solutions and concluded that the ultimate strain coefficient, $\eta$, and the residual strength coefficient, $\lambda$, develop similar fracture geometries and failure strengths in numerical specimens as long as they are in the ranges $2 \le \eta \le 5$ and $0 < \lambda \le 0.1$, respectively. Note that an appropriate Biot coefficient should be used since the simulated breakdown pressure may be affected by the Biot coefficient. This may result from fluid infiltration into the borehole wall prior to fracture initiation and changes the effective stress in that region.

Fig. 5

Geometry of gas fracturing experiments used in the modeling

Table 1 Physico-mechanical parameters of rock and fluids

3.2 Evolution of Fractures

We now focus on the evolution of fractures driven by pressurization of the three kinds of fracturing fluids. Figure 6 displays the traces of injection pressure from the simulations as a function of normalized time in comparison with the experimental data (Ishida et al. 2004, 2012). In order to eliminate the influence of the difference of the pressurization rates and model parameters, normalized time $t^{\prime}$ is introduced in Fig. 6. Here, $t^{\prime} = t/t_{\text{c}}$, where t denotes the actual time and $t_{\text{c}}$ is the critical time when breakdown occurs. The values of t _c for experimental data are cited from Ishida et al. (2012, 2004), while those for numerical data are recorded during the simulation. In Fig. 6, the solid lines and the dotted lines indicate the injection pressure recovered from the numerical simulations and experiments, respectively. It can be seen that the injection pressures of both the numerical simulations and experimental observations peak when the breakdown pressure is reached, and the breakdown pressures of the experiments are also characterized by a rapid drop in the injection pressure. In the numerical simulations, hydraulic fracturing with SC-CO₂ returns the lowest breakdown pressure (9.0 MPa), followed by water (12.0 MPa), and with oil exhibiting the highest breakdown pressure (13.5 MPa). This may be due to the SC-CO₂ having the lowest dynamic viscosity which allows it to readily infiltrate into the matrix around the borehole and to elevate the average effective stress over the REVs in the vicinity of the borehole more rapidly before the fracture initiation—this thus ruptures these REVs at a lower injection pressure than for water and oil, leading to a lower breakdown pressure. The experimental breakdown pressures for SC-CO₂-, water- and oil-induced fracturing are 8.44 MPa, 12.8 MPa and 13.0 MPa, respectively. It should be noted that the experiment for hydraulic fracturing with SC-CO₂ was conducted under a confining pressure of $\sigma_{1} = \sigma_{3} = 1{\text{ MPa}}$; therefore, the equivalent breakdown pressure under the confining pressure of $\sigma_{1} = 2\sigma_{3} = 6{\text{ MPa}}$ is calculated by adding the compressive stress difference at the fracturing point along the borehole wall using Kirsch’s solution (Kirsch 1898) and the result is 9.44 MPa (Ishida et al. 2012). This estimate is acceptable when the rock is still in the elastic regime and is therefore representative. It can be seen that the simulation results and experimental data are in close agreement.

Fig. 6

Simulation results of injection pressure as a function of normalized time in comparison with experimental data (Ishida et al. 2004, 2012) with blue, red and green lines representing water, viscous oil and SC-CO₂, respectively. The solid lines and the dotted lines indicate the injection pressure from the numerical simulations and experiments, respectively (color figure online)

Figure 7a shows the distribution of ruptured REVs for a particular computation step at the breakdown pressure in the simulation of hydraulic fracturing with SC-CO₂, with differently colored symbols denoting ruptured REVs generated at different times: the blue symbols are for the ruptured REVs generated before breakdown pressure is reached (the normalized time is less than 1 in Fig. 6c), the red symbols are for the ruptured REVs generated under the breakdown pressure (the normalized time is equal to 1 in Fig. 6c) and the white background is for unruptured REVs. It is seen that most of the REVs rupture at the breakdown pressure and ultimately connect to coalesce into a contiguous hydraulic fracture. Although the figures of ruptured REVs distribution with time for water and oil are not shown here, a similar phenomenology is observed. Furthermore, Fig. 7b, c shows the pore pressure distribution and the associated CO₂ state for the same computational step as Fig. 7a. As can be seen from Fig. 7b, during fracture propagation, the pore pressure in the hydraulic fractures is close to the injection pressure applied at the borehole, which indicates that a connected flow path is formed and that the fluid transits from the borehole to the open fractures directly, and with only a slight loss of pressure. It is also interesting to note from Fig. 7c that, below the breakdown pressure, the CO₂ is in a supercritical state in the vicinity of the borehole and changes to a gaseous state in the field far away from the borehole due to the decrease in pressure. Such phase changes closely resemble observations during SC-CO₂-based fracturing experiments (Ishida et al. 2012) where a gas escapes from the fracture as it intersects the exterior of the sample.

Fig. 7

Simulated a distribution of ruptured REVs due to hydraulic fracturing with SC-CO₂, b distribution of pore pressure and c CO₂ state in the specimen for a particular computational step for borehole pressure at the breakdown pressure

3.3 Fracture Topology

In order to enhance the extraction of hydrocarbons from unconventional gas reservoirs, it is desirable to produce complex fractures with large surface area to volume ratio. In the 2D problems considered here, the “surface area” can be measured by the length of the fractures. Now, we focus on the fracture geometries and complexity for the simulation results of hydraulic fracturing individually with water, oil and SC-CO₂.

Figure 8 displays the simulation results for the fracture geometries resulting from fracturing with the three fluids. The fracture geometries are defined by the ruptured REVs which are connected to the borehole through a path composed of other ruptured REVs; as can be seen by the comparison between Figs. 8c and 7a the “isolated ruptured REVs” around the main fractures in Fig. 7a are eliminated from Fig. 8c. It is apparent that the fractures grow progressively in the direction of the maximum principal stress. However, due to the heterogeneity of the mechanical properties of the rock, the fracture geometries are relatively irregular. To evaluate the complexity of the fractures, the tortuosity is defined as (Chen et al. 2015)

$$C = \frac{{L_{\text{t}} }}{{L_{\text{d}} }}$$

(20)

where C is the tortuosity; $L_{\text{t}}$ is the total fracture length along a pathway; and $L_{\text{d}}$ is the linear length of the two ends of a pathway. The fracture tortuosity of simulated fractures induced by SC-CO₂, water and viscous oil is calculated using Eq. (20), respectively, and is shown in Fig. 9 with the positive signs representing fractures above the borehole (+Y direction) and negative signs representing fractures below the borehole (−Y direction). As a comparison, the experimental data from Chen et al. (2015) are also plotted in Fig. 9 (open circles and open triangles represent +Y and −Y directions, respectively). It is seen that the SC-CO₂-induced fractures exhibit the largest tortuosity, followed by water-induced fractures and then the oil-induced fractures, and the simulation results agree well with the experimental data.

Fig. 8

Fracture geometries induced by a water, b oil and c SC-CO₂

Fig. 9

Simulation results of fracture tortuosity of hydraulic fracturing with water, oil and SC-CO₂ in comparison with experimental data (Chen et al. 2015). The positive (+) signs and negative (−) signs represent fractures either above (+Y direction) or below the borehole (−Y direction), respectively. As a comparison, the experimental data from Chen et al. (2015) are represented by open circles (+Y direction) and open triangles (−Y direction)

3.4 Effect of Dynamic Viscosity

We now focus on the problem related to the dependence of the critical breakdown pressure on the dynamic viscosity of the fracturing fluid. The dynamic viscosity of the fracturing fluid has an effect on the fluid flow behavior within the rock and affects the evolution of the poroelastic stress around the borehole that is caused by fluid pressurization. The poroelastic response in the region near the borehole, and at early times, is simulated to explore the effect of dynamic viscosity on poroelastic stress distribution, and the simulation results are compared to the analytical solutions (Detournay and Cheng 1988; Lu et al. 2013). This set of simulation assumes that no damage occurs in the rock (the rock strength is assigned a very large value) and that the external stresses are set to be the same as those in Fig. 5, i.e., $\sigma_{1} = 6 {\text{ MPa}}$ and $\sigma_{3} = 3 {\text{ MPa}}$. The fluids are assumed to be slightly compressible and fluid pressure in the borehole is retained at $P = 5.0{\text{ MPa}}$. Note that the fluid viscosity affects the fluid flow process around the borehole by governing the mobility, which is independent of the fluid compressibility; thus, gases should show similar behavior with slightly compressible fluids regarding the influence of fluid viscosity on breakdown pressure. Figure 10 shows the distribution of pore pressure and tangential effective stress with radius along the direction of the vertical diameter for three values of dynamic viscosity ($\mu = 1{\text{E}} - 3\;{\text{Pa}}\;{\text{s}}$, $1{\text{E}} - 4{\text{ Pa}}\;{\text{s}}$ and $1{\text{E}} - 5{\text{ Pa}}\;{\text{s}}$) and a specified early time ($t = 0.01{\text{ s}}$). Note that the x coordinate of ${{\left( {r - R_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {r - R_{0} } \right)} {R_{0} }}} \right. \kern-0pt} {R_{0} }}$ ranges from 0 to 0.25, which is in the vicinity of the borehole. It can be seen that the pore pressure and tangential effective stress on the borehole wall are not affected by the dynamic viscosity, but the interior stresses increase with a decrease in dynamic viscosity in the vicinity of the borehole, implying that a lower dynamic viscosity might result in a lower breakdown pressure. Also, the numerical results agree well with the analytical predictions, which provide a further validation for the modeling of coupled hydraulic-mechanical processes.

Fig. 10

Simulated and analytical poroelastic stress around the borehole with radius along the direction of the vertical diameter for three values of dynamic viscosity at a specified early time (t = 0.01 s): a pore pressure and b tangential effective stress

Furthermore, a set of simulations of hydraulic fracturing are performed with various dynamic viscosities, which range from $10^{ - 10}$ to $10^{5} \;{\text{Pa}}\;{\text{s}}$. To facilitate comparison between models, the numerical specimens are assumed to be homogenous in mechanical properties. Figure 11 illustrates the influence of dynamic viscosity on the breakdown pressure. It is apparent that the breakdown pressure first remains constant in the lower dynamic viscosity regime ($\le 10^{ - 7} \;{\text{Pa}}\;{\text{s}}$), then increases gradually with an increase in dynamic viscosity, and finally reaches an asymptote at a limiting dynamic viscosity ($\ge 10^{1} \;{\text{Pa}}\;{\text{s}}$). This tendency is consistent with results stated in Sect. 3.2. There are two classical formulae to predict breakdown pressure in terms of far-field stresses (Hubbert and Willis 1957, 23; Haimson and Fairhurst 1967): one is for impermeable rocks (the Hubbert–Willis solution), and the other is for permeable rocks (the Haimson–Fairhurst solution), which can be written as

$$\left\{ {\begin{array}{*{20}c} {P_{\text{HW}} = \sigma_{\text{T}} - 3\sigma_{3} + \sigma_{1} } \\ {P_{\text{HF}} = \frac{{\sigma_{\text{T}} - 3\sigma_{3} + \sigma_{1} }}{{2 - {{\alpha \left( {1 - 2\nu } \right)} \mathord{\left/ {\vphantom {{\alpha \left( {1 - 2\nu } \right)} {\left( {1 - \nu } \right)}}} \right. \kern-0pt} {\left( {1 - \nu } \right)}}}}} \\ \end{array} } \right.,$$

(21)

where $P_{\text{HW}}$ and $P_{\text{HF}}$ are the breakdown pressures related to H–W and H–F solutions, respectively, $\sigma_{\text{T}}$ is the tensile strength of the rock, and $\sigma_{1}$ and $\sigma_{3}$ are the far-field principal stresses. The two dashed lines in Fig. 11 represent the two theoretical breakdown pressures with the H–W and the H–F solution representing the upper and lower limits of the breakdown pressure, respectively. Lu et al. (2013) also obtained similar results by using a microcrack-based coupled damage and flow numerical model.

Fig. 11

Influence of dynamic viscosity on breakdown pressure. The dashed line and the dashed-dotted line represent the H–W solution and the H–F solution, respectively. These comprise the upper and lower limits of the breakdown pressure

3.5 Effect of Fluid Interfacial Tension

Experimental observations have demonstrated that the fluid interfacial tension can influence the breakdown pressure by controlling whether fluid invades the pore space at the borehole wall (Gan et al. 2015). Here, we focus on this interesting problem to examine the dependence of breakdown pressure on fluid interfacial tension.

We invoke the invasion pressure (Gan et al. 2015) to describe the response of the borehole wall to the injection of fluid. Invasion pressure is defined as the minimum pressure which is required to overcome capillary exclusion and to force fluid into the pore space through the largest available pore throat. If the injection pressure exceeds the invasion pressure, the fluid will penetrate into the borehole wall and then the effective stress around the wellbore will be correspondingly changed. The relation between the invasion pressure and the interfacial tension can be expressed by the Leverett J-function, which is defined as

$$J = \frac{{P_{\text{c}} }}{\sigma }\sqrt {\frac{k}{\phi }} ,$$

(22)

where $P_{\text{c}}$ is the invasion pressure; $\sigma$ is the interfacial tension; k is the permeability; and $\phi$ is the porosity. Here, the function J, the permeability k and the porosity $\phi$ are constants; thus, the critical invasion pressure $P_{\text{c}}$ is proportional to the interfacial tension $\sigma$. Therefore, the model is able to follow the evolution of breakdown pressure with interfacial tension that conditions an appropriate invasion pressure according to Eq. (22), i.e., the governing equation for fluid flow [Eq. (8)] is not involved in the computation until the fluid injection pressure is larger than invasion pressure. In the following, a set of simulations of hydraulic fracturing with slightly compressible fluids are reported in which various invasion pressures $P_{\text{c}}$ (ranging from 5.0 to 17.0 MPa) are considered, and the corresponding interfacial tensions can be calculated through Eq. (22) for a given J value. The mechanical parameters are assumed to be homogeneous and uniform, and the dynamic viscosity of the injection fluids is retained at $\mu = 1{\text{E}} - 5\;{\text{Pa}}\;{\text{s}}$. Figure 12 displays the variation of injection pressure with time for three specified values of invasion pressure ($P_{\text{C}}$ = 6.0, 12.0 and 16.0 MPa). When invasion pressure is lower than the H–F solution, the simulated breakdown pressure is approximately equal to that of the H–F solution (see Fig. 12a). When invasion pressure is intermediate between the H–F solution and the H–W solution, the simulated breakdown of the specimen occurs at the critical invasion pressure (see Fig. 12b). When the invasion pressure is larger than the H–W solution, the breakdown pressure is close to the H–W solution (see Fig. 12c). Figure 13 presents the simulated results of the breakdown pressure as a function of invasion pressure. The traces of the invasion pressure to breakdown pressure curves AB, BC and CD in Fig. 13 correspond to Fig. 12a–c, respectively. It is noted that the H–W and H–F solutions give upper and lower bound values for the simulated breakdown pressure, respectively. This is because an invasion pressure lower than the H–F solution corresponds to the permeable condition (fluid has infiltrated into the matrix before breakdown occurs), while the case of invasion pressure larger than the H–W solution corresponds to the impermeable condition (fluid remains excluded from the borehole wall when breakdown occurs). If the invasion pressure is intermediate between these bounding behaviors, the simulated breakdown pressure is equal to the invasion pressure. Such results are consistent with experimental observations (Gan et al. 2015). Note that the invasion pressure is governed by the interfacial tension only and is independent of the fluid compressibility, as indicated by Eq. (22). Although slightly compressible fluid is used to perform the simulations in this section, for the large pressures assumed here, this is applicable to compressible fluids (gases).

Fig. 12

Variation of injection pressure with time for three specified magnitudes of invasion pressure: a $P_{\text{c}} = 6.0{\text{ MPa}}$, b $P_{\text{c}} = 12.0\;{\text{MPa}}$, and c $P_{\text{c}} = 16.0\;{\text{MPa}}$. The dashed line and the dashed-dotted lines represent the H–W and H–F solutions, respectively

Fig. 13

Influence of invasion pressure on breakdown pressure. The dashed lines and dashed-dotted lines represent the H–W and the H–F solutions, respectively. The traces of AB, BC and CD in this figure correspond to Fig. 10a–c, respectively

4 Conclusions

Conventional hydraulic fracturing may not be optimal for the effective extraction of shale gas in many shale gas reservoirs. This is because shales may be significantly more sensitive to the presence of water due to the influence of capillary effects and due to high clay contents. In this study, coupled models of rock damage mechanics and gas flow for slightly compressible fluids and CO₂ are proposed, respectively, to simulate the processes of hydraulic fracturing with water, viscous oil and supercritical CO₂. The following conclusions can be drawn from the results of the numerical simulations.

Hydraulic fracturing with SC-CO₂ exhibits the lowest breakdown pressure, followed by water and then the oil. This progression in responses results since the SC-CO₂, with the lowest dynamic viscosity, can invade the borehole wall more easily and elevates the average effective stress over the REVs in the vicinity of the borehole more rapidly, and thus ruptures these REVs at a lower injection pressure than water and oil, returning a lower breakdown pressure.

Fractures grow progressively in the direction of the maximum principal stress. The fracture geometries are relatively irregular due to the heterogeneity of the rock mechanical properties in space. Fracture geometries induced by SC-CO₂ show higher tortuosity than those induced by water and oil—i.e., SC-CO₂ returns a more complex fracture with greater surface area than either water or oil.

The dynamic viscosity of the fracturing fluid influences the breakdown pressure by affecting the fluid flow behavior and the evolution of the poroelastic stress around the borehole. The breakdown pressure and fracture initiation pressure increase with an increase in the dynamic viscosity. Moreover, the H–W and the H–F solutions comprise the upper and lower bound limits of the fracture initiation pressure, respectively.

Fluid interfacial tension influences breakdown pressure by controlling whether fluid invades the pore space at the borehole wall. The H–W solution and H–F solution give upper and lower bounding values for the simulated breakdown pressure. When the invasion pressure is intermediate between these two magnitudes, the simulated breakdown pressure is equal to the invasion pressure.