Numerical Investigation of Dynamic Rock Fracture Toughness Determination Using a Semi-Circular Bend Specimen in Split Hopkinson Pressure Bar Testing

Abstract

The International Society for Rock Mechanics (ISRM) has suggested a notched semi-circular bend technique in split Hopkinson pressure bar (SHPB) testing to determine the dynamic mode I fracture toughness of rock. Due to the transient nature of dynamic loading and limited experimental techniques, the dynamic fracture process associated with energy partitions remains far from being fully understood. In this study, the dynamic fracturing of the notched semi-circular bend rock specimen in SHPB testing is numerically simulated for the first time by the discrete element method (DEM) and evaluated in both microlevel and energy points of view. The results confirm the validity of this DEM model to reproduce the dynamic fracturing and the feasibility to simultaneously measure key dynamic rock fracture parameters, including initiation fracture toughness, fracture energy, and propagation fracture toughness. In particular, the force equilibrium of the specimen can be effectively achieved by virtue of a ramped incident pulse, and the fracture onset in the vicinity of the crack tip is found to synchronize with the peak force, both of which guarantee the quasistatic data reduction method employed to determine the dynamic fracture toughness. Moreover, the energy partition analysis indicates that simplifications, including friction energy neglect, can cause an overestimation of the propagation fracture toughness, especially under a higher loading rate.

1 Introduction

Rock dynamic loading and subsequently induced dynamic rupture are widely observed in tectonic activities and geotechnical engineering applications. As an inherent attribute representing the capability of rocks to resist fracturing under dynamic circumstances, rock dynamic fracture toughness has acquired extensive applications as diverse as rock classification, structure design, seismic events, rock bursts control and prevention, explosive storage, etc. (Chen et al. 2008). In these cases, rocks often damage under a rather high loading rate, and, thus, the dynamic characteristics of rocks differ significantly from their static counterparts. To determine the fracture toughness of rocks under high strain rates, the split Hopkinson pressure bar (SHPB) or Kolsky bar system has been widely used in conjunction with several sample configurations commonly extended from static fracture tests, including cracked straight-through Brazilian disk (CSTBD) (Wang et al. 2011), cracked chevron notched Brazilian disk (CCNBD) (Dai et al. 2010a), short rod (SR) (Zhang et al. 2000), single edge notch bending (SENB) (Zhao et al. 2013), notched semi-circular bend (NSCB) (Chen et al. 2009; Dai et al. 2010b; Zhang and Zhao 2013), cracked chevron notched semi-circular bend (CCNSCB) (Dai et al. 2011), etc. Among these methods, the NSCB specimen in combination with SHPB techniques has been recommended as the suggested method for determining mode I dynamic fracture toughness of rock materials by the International Society for Rock Mechanics (ISRM) in 2012 (Zhou et al. 2012), due to its distinct advantages such as easy sample preparation from core-based rock mass, simple loading, as well as easy adaptability to anisotropy studies, etc. (Dai and Xia 2013).

Compared with substantial static researches regarding rock fracture toughness determination in recent decades however, studies associated with rock dynamic fracture were fewer in number, resulting in a limited understanding of dynamic fracturing characteristics of rocks. Due to the transient nature of loading and the complexity of rock mass, rock dynamic fracture tests remain challenging and to be improved in the following problems: (1) some vital micromechanisms, such as wave propagation, failure process, force equilibrium, and so on, are still unclear; (2) although numerous detecting techniques have been developed, the time to fracture remains challenging to capture because of the three-dimensional failure process of specimens with complex configurations; (3) the measurement on energy partitions is far from consummate and, thus, the propagation fracture toughness based on the energy analysis is only roughly determined due to the lack of sophisticated monitoring techniques under high-speed loading (Zhang et al. 2000; Chen et al. 2009; Li et al. 2014; Zhang and Zhao 2014).

Numerical simulation, by contrast, provides an efficient access to the experiment implementation and data analysis, since: (1) repeated simulations with exactly identical numerical samples can be performed, eliminating the interference of geometrical errors or material heterogeneity; (2) a first approximation can be achieved before laboratory experiments for a guidance; and (3) details at any arbitrarily instantaneous moment are available, even in dynamic cases. Among commonly used numerical methods to simulate dynamic problems, e.g., finite element analysis (FEA) (Li et al. 2009), discrete element method (DEM) (Li et al. 2014), distinct lattice spring method (DLSM) (Zhao et al. 2011), numerical manifold method (NMM) (Wu et al. 2014), DEM features: (1) reproducing fracturing of brittle materials, since microcracks initiate, coalesce, and form macrofractures as a result of breakage of bonds cemented between particles; (2) bypassing the development of sophisticated constitutive laws and simulating the physical micromechanisms directly; (3) generating the actual dynamic impact process due to the application of Newton’s second law and the real-time tracking of contact forces (Cundall and Strack 1979; Potyondy and Cundall 2004). Indeed, DEM is believed to be an efficient tool for simulating the dynamic failure process of rocks (Li et al. 2014).

In this paper, a numerical model based on DEM was first developed to simulate the ISRM-suggested NSCB method for determining dynamic mode I fracture toughness of rocks. Section 2 gives a brief summary of the NSCB specimen and SHPB techniques, and the DEM fundamental principles as well as the numerical model are introduced in Sect. 3. In Sect. 4, efforts are devoted to the comprehensive numerical verification with the experimental results involving wave propagation in the Hopkinson bars, dynamic force equilibrium, and failure process of the rock specimen, as well as the rate dependence of fracture toughness. The energy partitions along with the propagation fracture toughness determination are given in Sect. 5. Furthermore, two crucial experimental conditions, i.e., the incident wave form and the interfacial friction condition, are numerically assessed in Sect. 6. Section 7 summarizes the whole study.

2 The NSCB-SHPB Method for Mode I Fracture Toughness Measurements

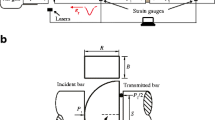
Figure 1a shows the geometry of the NSCB specimen, where: R is the radius of the NSCB sample; B is the thickness of the semi-disk; a is the crack length; S is the span of the supporting pins; P ₁ is the force applied on the incident end of the sample; and P ₂ is the force exerted on the transmitted end, with P ₂/2 on each pin.

Fig. 1

Schematics of: a the notched semi-circular bend (NSCB) specimen and b the split Hopkinson pressure bar (SHPB) system (ε denotes strain, and the subscripts i, r, and t refer to the incident, reflected, and transmitted waves, respectively)

The dynamic loading is implemented by the SHPB test system (Fig. 1b), which mainly consists of a striker, an incident bar, a transmitted bar, with a specimen sandwiched between them, and a data acquisition unit. The impact of the striker upon the free end of the incident bar produces a longitudinal compressive stress wave (incident wave ε _i), which then propagates along the incident bar to the bar–specimen interface, resulting in a reflected tensile wave (ε _r) and a transmitted compressive wave (ε _t). With a pair of strain gauges glued diametrically at the middle section of the incident bar and the transmitted bar, these three wave signals can be captured. Based on the one-dimensional stress wave assumption, the dynamic forces on both ends of the specimen are calculated as (Kolsky 1953):

$$P_{ 1} = A_{\text{b}} E_{\text{b}} \left( {\varepsilon_{\text{i}} + \varepsilon_{\text{r}} } \right),P_{ 2} = A_{\text{b}} E_{\text{b}} \varepsilon_{\text{t}}$$

(1)

where A _b is the cross-section area of the pressure bars and E _b is the Young’s modulus of the bar material.

As long as the dynamic force balance on both ends of the sample is achieved, i.e., P ₁ ≈ P ₂ or ε _i + ε _r ≈ ε _t, the evolution of mode I stress intensity factor (SIF) K _I(t) can be calculated by virtue of a quasistatic data reduction method as follows (Zhou et al. 2012):

$$K_{\rm I} (t) = \frac{P(t)S}{{BR^{3/2} }}Y(\alpha_{a} )$$

(2)

where P(t) is the load; α _a is the dimensionless crack length, α _a = a/R; and Y(α _a) is a dimensionless function which can be calibrated independently before the experiments via numerical tools.

3 Numerical Model in DEM

3.1 Brief Description of DEM

The DEM open source code ESyS-Particle (Abe et al. 2004; Utili et al. 2015; Weatherley et al. 2011) is employed herein for the simulations. The numerical model is an assembly of rigid particles that interact only at the soft contacts with finite normal and shear stiffness (Cundall and Strack 1979). The calculations performed in DEM iterate through the application of Newton’s second law to the individual particles and an alternative force–displacement relationship at each contact. To reproduce the mechanical behavior of rocks, a bonded particle model (BPM) is supposed, in which the bonds serving as cements are added to particles at their contact points (Potyondy and Cundall 2004). When the load is applied on the BPM, microcracks are represented explicitly as broken bonds, which coalesce and form the macroscopic fractures in an intuitive way. The feasibility of DEM in fracture problems, such as crack nucleation and propagation during compressive loading (Hazzard et al. 2000), rock cutting induced fracture (Huang 1999), acoustic emission (Hazzard and Young 2000), etc., has been validated. In addition, since dynamics is an inherent feature of DEM, explicit algorithms are utilized to simulate dynamic problems, as evidenced by elastic wave propagation modeling (Holt et al. 2005), induced seismicity (Hazzard and Young 2004), dynamic loading at a high rate (Hentz et al. 2004), etc.

3.2 Model Setup

The numerical model established in this work consists of two materials which possess distinct mechanical behaviors. For the rock specimen, an initial particle aggregate is created via the built-in radius expansion method, and then compacted to an isotropic stress state with floating balls eliminated. Bonds with limited strength are added to reproduce brittle failure. For the Hopkinson bar, regularly arranged particles bonded with extremely high strength are generated to simulate the elastic deformation. The geometry of the numerical NSCB model is detailed in Table 1, corresponding to the laboratory experiments (Chen et al. 2009), while the incident and transmitted bars are 1500 and 1000 mm long, respectively, with a diameter of 25 mm.

Table 1 Geometry of the notched semi-circular bend (NSCB) specimen

A calibration of microscopic parameters to match macroscopic mechanical responses is conducted via sufficient trial and error tests. The calibration results as well as the microscale properties of the specimen and the bars are listed in Tables 2 and 3, respectively. On the one hand, the deformability (i.e., Young’s modulus and Poisson’s ratio) is calibrated through numerical static uniaxial compression tests. On the other hand, as for the failure resistance, the bond strength of the numerical bars is assumed to be extremely large since the pressure bars never break, while the bond strength of the numerical specimen is calibrated based on the dynamic mode I fracture toughness, for which a comprehensive interpretation will be given in Sect. 4.3.

Table 2 Calibration results of the numerical specimen and Laurentian granite

Table 3 Calibration results of the numerical bar and the maraging steel bar

Consequently, the whole numerical SHPB test system is established, as shown in Fig. 2. The ramped stress wave (depicted in Fig. 2a) is derived from experiments and applied directly at the free end of the incident bar. Measuring circles A–D and E–F (illustrated in Fig. 2b) are embedded in the incident and transmitted bars, respectively, acting as strain gauges in laboratory tests to monitor strain and stress histories at each circle position. Details of the numerical specimen sandwiched between the incident and transmitted bar are shown in Fig. 2c. Either supporting pin consisting of three particles forms a contacting line of 2 mm long with the specimen to ensure enough transmitting access. The contact forces of the blue balls are used to calculate the forces on both ends of the specimen.

Fig. 2

The numerical split Hopkinson pressure bar (SHPB) test system, partially enlarged at: a the loading end, b one measurement circle, and c the NSCB specimen

4 Validation for the Numerical Simulation

4.1 Wave Propagation Process

The radial and axial stress signals obtained by the measuring circles are exhibited in Figs. 3 and 4, respectively, with curves A–D standing for incident waves (before 306 μs) and reflected waves (after 306 μs) at typical points A–D in the incident bar and curves E–F for the transmitted waves at points E–F in the transmitted bar.

Fig. 3

Radial stress histories at two typical points in the incident and transmitted bars

Fig. 4

Axial stress histories at several points in the incident and transmitted bars

For the radial stress, the incident value is nearly zero, while the reflected and transmitted values fluctuate with rather low amplitude compared to the axial stress, suggesting that the one-dimensional premise (Eq. 1) is approximately satisfied in this numerical model. For the axial stress, a trifling attenuation of the wave propagation is observed, as amplitudes of the incident wave propagating though points A–D along the incident bar are, in order, 61.77, 61.71, 61.67, and 61.63 MPa, while amplitudes of the transmitted wave propagating though points E–F along the transmitted bar are, in order, 27.85 and 27.70 MPa. On the other hand, the distribution of contact forces between particles in the same cross-section of the bar is nearly uniform from a detailed local view (the black line denotes compressive contact force). The above two points indicate that this numerical SHPB test system is valid, with no apparent wave dispersion. Note that the distinct loss of the amplitude of the reflected wave A is caused by the superposition of the initial reflected (tensile) stress wave and the corresponding secondary reflected (compressive) stress wave near the free end of the incident bar. This confirms that strain gauges used in a SHPB test should be cemented far away from both ends of bars to avoid the wave superposition.

In addition, according to the principle of the contact force transformation in particles, the contact force network in the bars can feature the stress wave propagation intuitively, as shown in Fig. 5 (the black line denotes compressive contact force and the red line represents tensile contact force) of wave propagation at typical moments along the bars. A ramped stress wave lasting for 208 μs is generated via exerting axial velocity directly on the free end of the incident bar. When the compressive incident wave reaches the bar–specimen incident interface (306 μs), one part of it reflects back as a tensile wave and the remainder transmits through the specimen to the bar–specimen transmitted interface (326 μs), resulting in a reflected wave moving backwards and a compressive transmitted wave propagating forwards along the transmitted bar. After several reverberations in the specimen, the dynamic force equilibrium is reached (357 μs). Note that the ramp-up-and-down outline of the contact force network configuration is in favorable accordance with the stress wave.

Fig. 5

Stress wave propagation in bars

4.2 Force Equilibrium and Failure Process

Force equilibrium is a prerequisite to the determination of dynamic SIF using the quasistatic method (Zhou et al. 2012). The distinct unbalance of the loading force will lead to significant inertial effects in a specimen (Weerasooriya et al. 2006), and, thus, the SIF history derived from far-field force cannot represent the real SIF history in the vicinity of the crack tip. Therefore, the force equilibrium is essential to the reasonability of the SHPB dynamic fracture test, which has been evaluated by two methods in this section.

The incident, reflected, and transmitted strain signals obtained via measurement circles D and E are converted into force histories by Eq. 1, respectively, and then shifted to the corresponding bar–specimen contact interfaces as shown in Fig. 6. According to the SHPB theory, the force of the specimen on the transmitted end can be expressed by transmitted wave (T), while the force on the incident end can be represented by the superposition of the incident wave and the reflected wave (I+R). A pleasurable consistency can be observed between the black and red curves during the whole load–unload process, demonstrating that the force equilibrium has been approximately fulfilled and that the inertial effect has been efficiently eliminated.

Fig. 6

Dynamic force balance on both ends of the specimen (I incident wave, R reflected wave, T transmitted wave)

The above indirect approach to acquire the force of the specimen on both ends is commonly employed in the SHPB laboratory test, due to the difficulties in directly monitoring the axial forces of the specimen. In DEM simulations, on the contrary, a variety of transient microscopic concerns [including contact force, acoustic emission (AE), displacement, etc.] at any designated position can be conveniently captured. Most importantly, a direct measurement method is proposed herein to calculate the axial forces on both ends of the specimen from contact forces as:

$$F_{\text{Ic}} = \sum\limits_{m = 1}^{{N_{\text{I}} }} {f_{\text{Im}} \cos \theta_{\text{m}} } ,\quad F_{Tc} = \sum\limits_{n = 1}^{{N_{\text{T}} }} {f_{\text{Tn}} } \cos \theta_{\text{n}}$$

(3)

where F _Ic and F _Tc are the forces on the specimen’s incident end and transmitted end, respectively, with the subscript c representing this direct measurement method; N _I and N _T denote the number of contacts on the bar–specimen incident interface and transmitted interface, respectively; f _Im and f _Tn are the values of the contact force m and n, while θ _m and θ _n are the absolute angles between the bar axis and the direction vector of the contact forces m and n, respectively.

To clarify the reliability of this contact force monitoring approach, forces obtained via the conventional wave method (Eq. 1) and the direct measurement method (Eq. 3) are compared in Fig. 7. In general, the results from both approaches match well. Note that, in the vicinity of the peak region, forces derived from contact forces of particles fluctuate slightly, but still form a clear outline in agreement with the curves calculated by the theoretical method. The oscillation around the peak region reveals that some microdamages occur in the specimen, to which the direct measurement without wave shifting along the time axis and superposition in the strain signals is more sensitive than the conventional wave method. Indeed, the direct measurement approach is more convenient and precise in characterizing the forces on the two ends of the specimen, and, thus, being adopted in the following studies.

Fig. 7

Comparison of the two methods: force histories on the specimen’s a incident end and b transmitted end (F _Iw and F _Tw denote forces attained via the conventional wave method, while F _Ic and F _Tc denote forces obtained by the direct measurement method)

Figure 8 depicts the dynamic force evolution obtained by the direct measurement method. By introducing the force equilibrium coefficient μ (calculated by Eq. 4) featuring the force balance level, the failure process of the specimen can be divided into six stages marked by six typical moments: t _i, t _t, t _b, t _p, t _d, and t _e, with the subscripts i, t, b, p, d, and e denoting incident, transmitted, balanced, peak, destroyed, and ending, respectively. Combining the evolution of three microcharacteristics (velocity vector field, contact force path, and AE distribution) shown in Fig. 9, the failure process can be analyzed as follows:

$$\mu = \frac{{2(F_{Ic} - F_{Tc} )}}{{F_{Ic} + F_{Tc} }}$$

(4)

Fig. 8

Force equilibrium and the six typical stages divided by force equilibrium coefficient

Fig. 9

Microscopic evolution of specimen: a velocity field (the green arrows denote the velocity vector); b contact force network (the black and red lines denote compressive and tensile contact force, respectively); c acoustic emission (AE) distribution (the red and blue spots denote the tensile and shear induced microcracks, respectively)

(1) At time t _i (306 μs), the incident wave reaches the bar–specimen incident interface (as depicted by the compressive contact force streaming up to the incident end of the specimen), resulting in a reflected wave back into the incident bar and a transmitted wave through the specimen. From time t _i to time t _t (326 μs), F _Tc remains zero and the force equilibrium coefficient μ remains at 2 until the transmitted wave reaches the transmitted end of the specimen.

(2) At time t _t, the transmitted wave arrives at the other bar–specimen interface, partially transmitting into the transmitted bar, and the rest moving back and forth in the specimen. It can be seen from the contact force network that only one pin serves as the passing access for the stress wave. The reason for this may be that the numerical specimen is not symmetric at a microscopic level due to a normal distribution of the particle size. In reality, the rock sample is far from perfectly symmetric because of the inevitable geometrical errors and material heterogeneity, so the poor contact in the early stage is common in NSCB experiments. From time t _t to time t _b (357 μs), the drastic oscillation of the force equilibrium reveals that the unbalanced force state and the axial inertial effect cannot be neglected.

(3) At time t _b, after undergoing several wave reverberations, the specimen reaches a force balance state. The force equilibrium coefficient reaches zero, and the uniform contact force distribution on both ends of the specimen can be observed. From time t _b to time t _p (381 μs), the force equilibrium coefficient undulates slightly around zero, indicating that the force equilibrium is sustained to a certain degree in this period. Meanwhile, the forces on the two ends of the specimen increase with the incident pulse at a constant rate, based upon which the loading rate can be calculated.

(4) At time t _p, the forces on the two ends of the specimen increase to the peak value. It is worth noting that, from the AE distribution, microcracks have initiated from the crack tip and propagated radially towards the incident end of the NSCB for a rather short distance. In addition, the time to fracture is measured to be 5.46 μs ahead of the peak force by a real-time search for the AE occurrence, which can also be obtained from the energy analysis given in Sect. 5. A similar phenomenon has been observed in the laboratory tests (Dai et al. 2010b), and this small time difference between the peak far-field load and the fracture initiation was partially explained as the time difference of the released waves emitted from the crack tip to the supporting pins at the sound speed of the rock material. This tiny time difference indicates that the fracture onset near the prefabricated notch tip almost synchronizes with the peak force, and, thus, the critical dynamic SIF can be determined by the peak force based on the applicable method. From time t _p to time t _d (402 μs), the cracking continually propagates towards the specimen’s incident end in the direction of the loading. Meanwhile, the bearing capacity slowly decreases due to the increasingly accumulated damage in the specimen.

(5) At time t _d, the rapid extending fracture ultimately splits up the whole NSCB specimen, forming a mode I tensile fracture as shown by red spots in the AE distribution. From time t _d to time t _e (426 μs), there is a sharp decline of the force on both ends of the specimen. This can be explained by the follows: as the specimen cannot bear the load as an entirety, the stress wave has difficulties in transmitting through the damaged specimen and, instead, is mostly reflected. Thereafter, the force equilibrium coefficient fluctuates in large amplitudes, and the force balance cannot be fulfilled.

(6) At time t _e, the force on the transmitted end declines to zero and the force equilibrium coefficient rises to 2 abruptly, depicting the end of the failure process.

In summary, the acceptable agreement between the experimental and numerical results confirms the capability of this DEM model in reproducing the dynamic failure process of the NSCB specimen in an SHPB test. Particularly, the force equilibrium of the specimen can be effectively achieved by virtue of a ramped incident pulse, and the fracture onset in the vicinity of the crack tip is precisely measured to synchronize with the peak force, both of which guarantee the quasistatic data reduction method employed to determine the dynamic fracture toughness

4.3 Initiation Fracture Toughness and Rate Dependence

To determine the dynamic mode I fracture toughness of the NSCB under a certain loading rate, the bearing force of the specimen is taken as the average value of the forces on both ends of the specimen via the direct measurement method, and the corresponding SIF is calculated by Eq. 2. For the case of calibration, the SIF history curves obtained from the simulation and the experiment (Chen et al. 2009) under the equivalent incident stress wave are compared in Fig. 10. The slope of the approximately linear prepeak region and the peak value of the SIF history are evaluated, which relate to the loading rate and the corresponding critical SIF (referred to as the initiation fracture toughness K ^d_IC ), respectively. It can be seen that the two peak values remain highly consistent, and that, in the relatively linear prepeak region, the two curves perfectly match each other. The agreement between the simulated and experimental results confirms the capacity of the numerical model with carefully selected microparameters (see Table 2) to reproduce the actual dynamic response under the same loading rate as the laboratory tests.

Fig. 10

Comparison of the stress intensity factor (SIF) history obtained by experiment and simulation under the equivalent incident stress wave

Similarly, the dynamic fracturing of the numerical specimen under various impact conditions can be realized by varying the amplitude or the duration of the incident stress wave. In each case, the force equilibrium has been well achieved, and the time to fracture is precisely measured. In particular, the fracture initiation moments are compared with the peak points in Table 4, demonstrating a favorable simultaneity. Therefore, the initiation fracture toughnesses under different loading rates are obtained by the applicable method and compiled in Fig. 11 along with the experimental results (Chen et al. 2009). With increasing loading rates, the initiation fracture toughness increases accordingly (Fig. 11). It can be seen that this rising trend approximates to the experimentally attained rate dependence of toughness values, further verifying the reliability of microscopic parameters in the numerical model and the validity of this numerical NSCB-SHPB testing system.

Table 4 Characteristic time under different loading rates

Fig. 11

Comparison of the rate dependency of the initiation fracture toughness obtained by simulations and experiments

5 Energy Partitions and Propagation Fracture Toughness

Upon the occurrence of a new crack, the strain energy stored in rock mass partially releases and transforms to the relevant surface energy. The critical state of a crack propagation can be described as (Griffith 1921):

$$G = \frac{{{\text{d}}U}}{{{\text{d}}A}} = \frac{{{\text{d}}W}}{{{\text{d}}A}}$$

(5)

where dA denotes the increment of the fracture area, and dU and dW denote the corresponding decrement of the strain energy and increment of the surface energy, respectively. G is defined as the fracture energy (dissipated per unit fracture area dA created) and the fracture toughness can be calculated as (Irwin 1957):

$$G = \left\{ {\begin{array}{*{20}l} {\frac{{K_{\text{IC}}^{2} }}{E}} \hfill & { ( {\text{plane}}} \hfill & {\text{stress)}} \hfill \\ {\frac{{(1 - \nu^{2} )K_{\text{IC}}^{2} }}{E}} \hfill & { ( {\text{plane}}} \hfill & {\text{strain)}} \hfill \\ \end{array} } \right.$$

(6)

where K _IC is the fracture toughness, E is the Young’s modulus, and $\nu$ is the Poisson’s ratio.

In experiments, the measurement of the dynamic fracture energy is challenging at high loading rates owing to the limitations of measuring techniques. Some attempts have been made to partition energies in the SHPB system, and, thus, the fracture energy and the propagation fracture toughness (Zhang et al. 2000; Chen et al. 2009; Zhang and Zhao 2014) can be calculated. The energy absorbed by the specimen, calculated as the difference of the elastic energy carried by the incident, reflected, and transmitted stress waves, consists of three main parts: the fracture energy dissipated by fracture surface and microcracks, the residual kinetic energy of the flying fragments, and other energies, such as friction-induced thermal energy. Since the elastic wave energy can be precisely calculated via strain histories retrieved from strain gauges (Lundberg 1976) and the residual kinetic energy can be approximately obtained by the relative high-speed photographs, the fracture energy can be determined by virtue of the first law of thermodynamics.

Numerical simulation, comparatively speaking, provides a more straightforward access to tracing all kinds of energies in the concerned system. For an accurate analysis, the bond energy, friction energy, kinetic energy, and strain energy of the whole numerical SHPB system are recorded based on Eqs. 7–10:

$$_{{E_{\text{b}} }} = \frac{1}{2}\sum\limits_{{N{\text{b}}}} {\left( {\left( {F_{\text{bi}}^{\text{n}} } \right)^{2} /k_{\text{bi}}^{\text{n}} + \left( {\text{FE}} \right)^{2} /k_{\text{bi}}^{\text{s}} + \left( {M_{\text{bi}} } \right)^{2} /\left( {I_{\text{bi}} k_{\text{bi}}^{\text{n}} } \right)} \right)}$$

(7)

where E _b denotes the total potential energy stored in all bonds; N _b denotes the number of bonds, and for each bond individual i, M _bi is the moment applied; F ⁿ_bi and F ^s_bi are the normal and shear force, respectively; k ⁿ_bi and k ^s_bi are the normal and shear stiffness; and I _bi is the moment of inertia;

$$E_{\text{f}} = \sum\limits_{{N{\text{t}}}} {\left( {\sum\limits_{{N{\text{broken}}}} {{\text{d}}F_{\text{s}} {\text{d}}s} } \right)}$$

(8)

where E _f denotes the energy dissipated by friction; N _t and N _broken denote the number of total steps and broken bonds, respectively. Note that the friction energy E _f is calculated by an incremental method, where dF _s and ds denote the increments of the shear component of the contact force and the relative displacement, respectively;

$$E_{\text{k}} = \frac{1}{2}\sum\limits_{{N{\text{p}}}} {\left( {m_{i} v_{i}^{2} + I_{i} \omega_{i}^{2} } \right)}$$

(9)

where E _k denotes the total kinetic energy; N _p denotes the number of particles; m _i , I _i , v _i , and ω _i are mass, moment of inertia, and translational and rotational velocities of particle i, respectively;

$$E_{\text{p}} = \frac{1}{2}\sum\limits_{{N{\text{c}}}} {\left( {\left( {F_{i}^{n} } \right)^{2} /k_{i}^{n} + \left( {F_{i}^{s} } \right)^{2} /k_{i}^{s} } \right)}$$

(10)

where E _p denotes the total potential energy stored in all contacts; N _c denotes the number of contacts, and for each contact individual i, F ⁿ_i and F ^s_i are the normal and shear force, respectively; k ⁿ_i and k ^s_i are the mean values of the normal and shear stiffness of the two particle constituents.

Figure 12 depicts the evolution of the energy partitions ranging from 300 to 500 μs, as well as the total energy defined as the sum of the above four equations. It can be seen that, upon the impact of the incident wave on the specimen, the kinetic energy starts to increase while the strain energy decreases, and that the bond energy of the specimen slowly increases due to the increasing bearing force. Note that the total energy is maintained at a constant level, indicating no distinct fracture events. At time 375.72 μs, an abrupt drop emerges in the total energy evolution, following a progressive decline and, ultimately, a balance. The decline phase of the total energy evolution agrees well with the fracture process discussed in Sect. 4.2, since the fracturing of rocks consumes energy. The peak point of the bond energy however, lags behind the drop point for 5.46 μs, which verifies the minute time lag obtained in Sect. 4.2. Furthermore, it is worth noting that, during the fracture process, the friction energy has increased continually by a rather large amount with respect to the total energy decrement. If the bar–specimen interfaces are ideally lubricated with a friction coefficient of zero, the friction energy increment should be the consequence of a relative movement of the fractured surface with a certain roughness under dynamic loading. In the experiments however, thermal energy dissipated by friction has been commonly assumed to be small and negligible when the loading rate is not high. Therefore, the propagation fracture toughness determined based on these simplifications is inevitably overestimated (Chen et al. 2009).

Fig. 12

Evolution of the concerned energy partitions and the total energy

According to the initial and eventual balance state of the total energy, the total released strain energy U to generate fracture surface can be obtained by the difference shown in Fig. 12. For simplification, the actual area of the fractured surface A _s and the total released strain energy U are used to calculate the average fracture energy G = U/A _s; thus, the average propagation fracture toughness can be obtained via Eq. 6. Similarly, propagation fracture toughnesses under varied loading rates are obtained and compared with the experimental results (Chen et al. 2009) in Fig. 13. Note that the friction energy is carefully considered in the numerical simulations, of which the results are in a perfect accordance with the propagation fracture toughness from experiments under lower loading rates but smaller than those under higher loading regimes. Further, the residual kinetic energy of the flying fragments consists of two parts (rotation and translation), but in previous experiments (Chen et al. 2009), only the rotation kinetic energy was incorporated in the calculations. The simplifications partially explain the difference in the propagation fracture toughness between simulations and experiments.

Fig. 13

Comparison of the effect of loading rate on the initiation and propagation fracture toughness obtained by experiments and simulations

6 Discussions on Two Experimental Conditions

6.1 Effects of Wave Forms on Force Equilibrium

In a conventional SHPB test, a direct impact of the striker bar with a uniform cross-section upon the incident bar yields a rectangular incident stress wave with high-frequency oscillation. Researches (Böhme and Kalthoff 1982; Dai et al. 2010b) indicate that the sharp rising edge of the rectangular incident stress wave will induce huge inertia effects in the specimen. And, consequently, for the NSCB sample, the peak far-field load on the sample boundary fails to synchronize with the fracture initiation near the crack tip (Dai et al. 2010b).

In this section, a typical rectangular wave (depicted in Fig. 14) derived from the laboratory test (Dai et al. 2010b) is applied directly on the free end of the numerical incident bar to evaluate the loading-induced inertia effects. The dynamic forces on both ends of the numerical specimen measured by the direct measurement method, along with the force equilibrium coefficient μ calculated by Eq. 4, are shown in Fig. 15. It is evident that the dynamic forces on either side of the bar fluctuate drastically, resulting in a severe force unbalance, as demonstrated by the force equilibrium coefficient severely deviating from zero. To further investigate the failure process, the fracture onset is captured to be 6.2 and 15.4 μs ahead of the peak force on the transmitted end and the incident end, respectively. In addition, the differences in the corresponding forces are up to 6.9 and 3.8 KN, respectively. Therefore, it is absolutely invalid to determine the dynamic fracture toughness by stress wave loading with a rectangular incident wave shape.

Fig. 14

Different incident wave forms: rectangular wave and ramped wave

Fig. 15

Dynamic forces on both ends of the numerical NSCB specimen under a rectangular impact pulse

Identical results obtained from simulations and experiments confirm the loading inertia effect inevitably induced by the steep rising edge of the rectangular incident wave. A ramped incident wave, by contrast, facilitates the force equilibrium, as discussed in Sect. 4.2. To minimize the inertia effects, a pulse-shaping technique should be used in the SHPB experiments to generate a ramped loading pulse (Zhou et al. 2012).

6.2 Effects of Interfacial Friction on Fracture Toughness Determination

The interfacial friction effects have been widely confirmed in SHPB experiments on rocks for both compression tests (Dai et al. 2010c; Lu et al. 2015) and fracture tests (Xia et al. 2013). In dynamic NSCB tests, the resistance to dynamic fracture can be enhanced due to the friction between the supporting pins and the specimen, which, thus, significantly affects the fracture toughness measurement results (Xia et al. 2013).

In this section, friction coefficients of particles beside the bar–specimen interface are taken into account to investigate the friction effects. For a given loading rate of 98 GPa m^1/2/s, the SIF histories are obtained considering different levels of friction coefficients ranging from 0.0 to 1.0, as shown in Fig. 16. It can be seen that the nominal fracture toughness increased by 200 % as the friction coefficient increased up to 0.5, and varied little as the friction coefficient continually increased. Furthermore, a real-time detection of the fracture process and the force evolution shows that the fracture onset occurs significantly ahead of the peak force. This phenomenon illustrates, to some extent, the necessity to lubricate the bar–specimen interface in the laboratory NSCB-SHPB tests.

Fig. 16

Simulated SIF history curves under varied friction conditions

7 Conclusion

Due to myriads of merits over other counterparts, the notched semi-circular bend (NSCB) specimen has been recommended by the International Society for Rock Mechanics (ISRM) as a suggested method to determine the dynamic mode I fracture toughness of rocks by virtue of the split Hopkinson pressure bar (SHPB) technique. However, a comprehensive understanding of the dynamic fracture mechanism associated with energy partitions is plagued by the transient nature of dynamic loading and the limited experimental techniques. In this study, a discrete element method (DEM) model is developed to numerically simulate and analyze the dynamic fracturing process of the NSCB specimen in SHPB testing.

The results show that the stress wave propagation satisfies the two fundamental assumptions and the force equilibrium can be approximately achieved, thus validating the feasibility of the numerical SHPB system for dynamic loading. The typical failure process characterized in multiple viewpoints, including force history, velocity field, contact force chain fabric, and acoustic emission (AE) distribution, exhibits a pleasant conformance with experiments. Most importantly, multiple dynamic rock fracture parameters, including initiation fracture toughness, fracture energy, and propagation fracture toughness, are simultaneously measured during dynamic fracturing, and results under varied loading rates are obtained, of which the rate dependence approximates that in experiments. The agreement between numerical and experimental results confirms the validity of this DEM model to simulate the dynamic fracturing of the NSCB specimen under high loading rates.

In particular, in spite of the complex configuration of the NSCB specimen, the force equilibrium can be effectively achieved by virtue of ramped incident pulses. Both the AE monitoring and the energy analysis reveal that the fracture onset of the prefabricated notch tip almost synchronizes with the peak force. The above two points guarantee the quasistatic data reduction method employed to determine the dynamic fracture toughness. Furthermore, an apparent overestimation of the propagation fracture toughness with respect to the simulated results is observed under higher loading rates. The reason for the difference may be the neglect of friction energy and other simplifications, which calls for more accurate monitoring techniques to directly measure rock fracture toughness values in physical tests.