1 Introduction

Rock is an extremely heterogeneous material that contains many flaws such as joints, holes, fissures, and cracks. Rock masses surrounding underground structures usually have nonlinear mechanical responses to loading and strong irreversible behaviors. Understanding this rock failure process is of significant interest to those involved with underground construction for mining engineering, geotechnical engineering, and petroleum geosciences. Experimental investigations over a broad range of temperatures and pressures have been performed in the past decades to understand this failure process. In particular, the strength and deformation behaviors of rocks or rock masses at different stages of deformation have been addressed (e.g., Brace and Byerlee 1966; Hoek 1968; Scholz 1968; Wawersik and Fairhurst 1970; Yang et al. 2012; Xue et al. 2014; Zhang et al. 2014). These responses were almost always measured using conventional material testing systems. However, anisotropy and heterogeneity of rock materials lead to complexities in the rock mechanics; For example, the physical properties of rock materials can vary with deformation stage or loading level. As Young (1993) pointed out, these testing systems can only provide limited characterization of the responses to load because they can only obtain the accumulated force–displacement curve in experiments. They cannot detect the formation and evolution of heterogeneity for the whole deformation process. Acoustic emission (AE) technologies provide a feasible and effective way to detect such formation and evolution through the measurement of energy releases during fracturing.

AE technology is an effective, nondestructive evaluation tool that has been widely used in rock mechanics and rock engineering. AE signals are generated throughout the rock failure process. On the one hand, these signals carry abundant information on crack propagation and fracture energy release. As a result, AE technology has been widely employed to investigate rock failure processes quantitatively. Analysis of these signals can capture the evolution of the inner structure and detect deformation stages. On the other hand, large quantities of AE signals are produced during the fracturing process. Therefore, elegant and efficient methods for signal processing and treatment are required for recognition and identification of this dynamic process. AE signal analysis technologies can be grouped into three categories: AE signal parameter (AESP) analysis based on the statistical characteristics of AE signals, AE source localization using multichannel data acquisition systems, and waveform analysis approaches that employ signal-processing methods.

The purpose of the AESP approach is to simplify the analysis of transient AE signals. AESP illustrate aspects of AE signals that can be represented as functions of time (e.g., amplitude, counts, duration, energy, and rise time). The AESP approach has been widely applied to rock mechanics (e.g., Colombo et al. 2003; Chang and Lee 2004; Cheon et al. 2011; Kim et al. 2014; Wasantha et al. 2014). As the rock fracturing process is a multiscalar, nonlinear, and nonstationary phenomenon (He and Qian 2010), traditional AESP methods face various difficulties. Various AESP represent different features of rock materials under load. The values of AESP depend on the selected properties of the AE signals, so they are unable to describe the rock failure process completely. Moreover, rock fracturing is a dynamic process, and this simple statistical approach cannot illustrate changes of characteristics at different rock deformation stages. Thus, AESP techniques need to be improved.

AE localization technology is an important category that uses multichannel signal acquisition systems to detect nucleation and progression of fractures in rock material. The advantage of this technology is that the space–time distribution of cracks can be traced during the experiment, thereby explaining the details of the mechanism evolution with load; For example, Lockner et al. (1991), Lockner and Byerlee (1992), Lockner (1993), Lei et al. (2000), and Ponomarev et al. (2010) all successfully investigated the growth of failure processes in intact and precracked rock specimens at laboratory scale by studying the spatial and temporal patterns of AE sources with different loading. Lin et al. (2009) observed the initiation of failure under three-point bending. The localization indicates that microcrack hypocenters form an intrinsic zone. Li et al. (2010) presented the three-dimensional location of AE events in granite and marble specimens under uniaxial compression. They detected stress redistribution phenomena and characterized the spatial correlation length of AE events during the deformation stages. Their work can better describe precursory information associated with the nonlinear processes of rock failure. All this research shows that the AE signal is strongly associated with rock failure.

It is clear that AE signals change with the rock fracturing process. These signals include abundant time–frequency information that is helpful for understanding rock failure processes if appropriate mathematical methods are employed to process the AE signals (Sejdić et al. 2009). AE signals are obviously digital signals that can be investigated by signal-processing methods. Much research has addressed the time–frequency properties of AE signals; For example, Benson et al. (2010) investigated the microstructure of basalt at confining pressure of 40 MPa, and found a correlation between low-frequency events and earthquakes. Liu et al. (2011) investigated the spectral characteristics of microseismic signals observed during rupture of coal. Li et al. (2012a) investigated the propagation of microseismic signals transmitted parallel and vertical to bedding in the process of coal rock rupture under uniaxial compression. Gon et al. (2013) obtained instantaneous frequencies of granites under uniaxial loading. They carried out a waveform-based investigation on AE signals. Cai et al. (2013) developed a real-time microseismic monitoring system using a wavelet transform algorithm. In all of these studies, investigations of the relationship between spectral characteristics and rock deformation behaviors are rare.

Technically, AE signals are nonlinear and nonstationary; they do not satisfy the crucial restrictions of traditional spectral analysis; For example, for the Fourier transform, signals must be linear and strictly periodic or stationary; otherwise, the resultant spectra make little physical sense. Similarly, spectral characteristics of serial data based on the wavelet method depend on the selection of a wavelet function, therefore these results highly depend on the experience of the analyst. The Hilbert–Huang transform (HHT) has been developed to solve these problems. The HHT method extracts instantaneous frequencies and amplitudes of signals by performing a Hilbert transform of the intrinsic mode functions (IMFs), which are decomposed from the original signals by using the empirical mode decomposition (EMD) [or improved ensemble empirical mode decomposition (EEMD)] process. The arithmetic of the HHT method is fixed, so the results are insensitive to the experience of the analyst. Moreover, different IMFs with instantaneous frequencies from high to low correspond to the properties of signals that trend from short to long. This paper selects the HHT method as a signal analysis tool for investigating the dynamic properties of AE signals.

A schematic of the HHT-based AE processing approach is shown in Fig. 1. Both AE signals and calculated AESP are selected for analysis using this approach. AESP are statistical results of AE signals changing over time. This can be considered to be a type of signal that illustrates macroscopic-scale trends in the rock failure process as well, whereas instantaneous properties of a rock specimen can be captured by analyzing high-frequency AE signals. Therefore, a combined processing approach using both AE signals and AESP is natural. In this approach, the Hilbert spectra present two types of useful information: instantaneous frequencies and amplitudes, both of which change continuously. The instantaneous amplitudes represent the strength of energy released from the rock sample, and the instantaneous frequencies are related to the attenuation that correlates with the development of rock damage caused by loading. Therefore, these features of the Hilbert spectra are sensitive to the physical properties of the sample and can be used in rock mechanics analysis.

Fig. 1
figure 1

Schematic diagram of the HHT-based AE processing approach

Full size image

This paper is organized as follows: An introduction is presented in Sect. 1. Section 2 describes the experimental procedures and test specimens in detail. Section 3 summarizes the HHT method. Section 4 profiles the AE effective energy rate as the AESP. The relationships between fracture energy, selected AESP, and spectral amplitude are also explored in this section, showing that the process of rock fracturing could be investigated using this approach. The next section presents the analysis results based on the HHT for the AE processing approach. Both the AE signals and AESP are analyzed using the HHT method. The results show that rock deformation stages can be distinguished by using both of those signals. Two important processes during rock deformation have been investigated thoroughly. Moreover, rock fracture is shown to be predictable when employing the HHT-based AE processing approach. The conclusions of this study are drawn in Sect. 6.

2 Laboratory-Based Experimental Procedures

The specimens in this experiment were made from sandstone sourced in Xingguo, Jiangxi Province, China. Six samples with rectangular prismatic shape of 25 × 60 × 150 mm3 were cut from the same rectangular block. To remove any effect of anisotropy on the experimental results with the sandstone, the cutting directions were kept constant. All tests were performed in natural and dry conditions. Furthermore, the suggestion of the International Society for Rock Mechanics is that the height-to-width ratio of tested samples should be in the range of 2.0–3.0 to minimize the effects of end friction on test results; in this test, the ratio was set to 2.5. A schematic of the experimental apparatus is shown in Fig. 2.

Fig. 2
figure 2

Schematic diagram of experimental setup

Full size image

All experiments were performed in a DLL500 material testing system made by the Changchun Research Institute for Mechanical Science Corp. This servo-controlled system can be controlled by either load or displacement, while both load and deformation are recorded and analyzed in real time. The loading capacity of the system is 500 kN in axial force and 7 mm in deformation. A series of uniaxial compression experiments were performed using a displacement rate of 0.05 mm/min until the specimen failed completely. Load and deformation of the tested sandstone samples were recorded simultaneously throughout the experiment. The front face was also monitored by a JVC GC-PX100BAC high-speed camera. Using the digital image correlation technique, full-field displacements and strains could be directly computed by processing grayscale digital images of the specimen surface recorded by this camera. The AE signals were recorded by a PCI-2 AE measuring system that employed a commercially available piezoelectric sensor (Physical Acoustic Corporation, type Nano30). The test parameters of the AE measuring system are given in Table 1. Six tests were carried out in the experiment. Figure 3 shows the failure patterns of the specimens after testing. Because of the similar AE signals among different specimens, only specimen no. 1 is presented below.

Table 1 Test parameters of AE measuring system
Full size table
Fig. 3
figure 3

Images of sandstone specimens after uniaxial tests

Full size image

3 Hilbert–Huang Transform

The HHT method that was previously briefly introduced is explored more fully in this section. The HHT consists of EMD (or improved EEMD) and Hilbert spectral analysis (HSA) (Huang et al. 1998, 1999). The EMD and EEMD are powerful processing tools that can decompose a signal into various IMF components, the Hilbert transform of which can be used to deduce two physically meaningful instantaneous quantities: frequency and amplitude. The IMF follows two principles:

  1. 1.

    The value of the absolute difference of the number of extremes and the number of zero crossings should be either zero or one.

  2. 2.

    The mean values of the local maxima envelope and local minima envelope should be zero for the whole data series.

3.1 Empirical Mode Decomposition

Data preprocessing follows the procedure below (Huang et al. 1998). This study combined two MATLAB codes written by Rilling et al. (2003) and Wang et al. (2014) to implement the following EMD process:

  1. 1.

    Compute the local maxima values \( e_{\hbox{max} } (t) \) and local minima values \( e_{\hbox{min} } (t) \) of the input signals \( x_{0} (t) \) at each point via interpolation and form the lower and upper envelopes of these signals by using the cubic spline method.

  2. 2.

    Compute the mean values \( m(t) \) of \( e_{\hbox{max} } (t) \) and \( e_{\hbox{min} } (t) \) of the series. Then, compute the differences between \( x_{0} (t) \) and \( m(t) \) to obtain the component \( h(t) \) at each point.

  3. 3.

    Check if \( h(t) \) is an IMF. If not, set \( h(t) \) as the input signal and continue the above search until the first IMF \( c_{1} (t) \) is found.

  4. 4.

    Once the first IMF has been found, subtract it from the original signals; i.e., \( x_{1} (t) = x_{0} (t) - c_{1} (t) \). Take \( x_{1} (t) \) as the input signal and repeat the above procedure to obtain the second IMF \( c_{2} (t) \). Similarly, the i-th IMF \( c_{i} (t) \) is obtained.

  5. 5.

    Continue the above steps until no more IMFs are extracted. The remaining component is called the monotonic function. Then, n empirical modes \( c_{i} (t), i = 1-n \), and one monotonic function \( r(t) \) are obtained.

The original signals are then rewritten as

$$ x_{0} (t) = \sum\limits_{i = 1}^{n} {c_{i} (t)} + r(t), $$
(1)

where \( x_{0} (t) \) is the original data series, \( c_{i} (t) \) are the empirical modes, and \( r(t) \) is the monotonic function.

3.2 Ensemble Empirical Mode Decomposition

The amplitudes of AE signals increase immediately when rock failure events happen. However, the EMD process may cause a mode-mixing problem when faced with burst signals. The mode-mixing problem is the result of the intermittent characteristic of signals at a certain scale. This causes serious aliasing in time–frequency analysis and hides the physical meaning of the individual IMFs. Wu and Huang (2009) proposed an EEMD method to alleviate this mode-mixing problem. In their EEMD method, k white-noise series are first added to the original signals. The j-th amalgamation of the signals \( x(t) \) and white-noise series is denoted by \( x^{(j)} (t) \). Then, for each series of mixed signals \( x^{(j)} (t) \), several IMFs \( c_{i}^{(j)} (t) \) can be obtained by using the EMD method. Note that \( c_{i}^{(j)} (t) \) means the i-th IMF component of the j-th series. Finally, the i-th IMF\( c_{i} (t) \) of the original data series \( x(t) \) is the ensemble mean of all the i-th IMFs \( c_{i}^{(j)} (t),\;j = 1-k \) obtained previously.

3.3 Hilbert Spectral Analysis

HSA is used to compute instantaneous properties such as frequency and amplitude. The Hilbert transform is expressed as

$$ y(t) = H(x(t)) = \frac{1}{\pi }\int_{ - \infty }^{\infty } {\frac{x(\tau )}{t - \tau }} {\text{d}}\tau . $$
(2)

By means of this transform, any time series can be represented as an analytic signal,

$$ z(t) = x(t) + \text{i}y(t) = a(t)\text{e}^{{\text{i}\int {\omega (t)} {\text{d}}t}} . $$
(3)

The instantaneous frequency \( \omega (t) \) and the instantaneous amplitude \( a(t) \) are thus obtained as

$$ \omega (t) = \frac{{{\text{d}}\theta (t)}}{{{\text{d}}t}},\quad a(t) = \sqrt {\left( {x(t)^{2} + y(t)^{2} } \right)} , $$
(4)

where

$$ \theta (t) = \arctan \left( {\frac{y(t)}{x(t)}} \right) . $$
(5)

4 Effective Energy Rate of Acoustic Emissions

Previous studies have defined various AESP. This study selected the effective energy rate of AE as the AESP parameter.

The AE effective energy \( E_{\text{AE}} \) is defined as

$$ E_{\text{AE}} = \int_{0}^{\infty } {V(t){\text{d}}t} , $$
(6)

where \( V(t) \) is the voltage of the signal at time t.

Fracture energy is released when rock failure events happen. Because AE signals are generated by the release of elastic energy from an event, a correlation between the AE effective energy and fracture energy may exist. One goal of AE effective energy analysis is to measure the instantaneous release of fracture energy in rock. Accordingly, characteristics of AE signals were considered to simplify the analysis approach. AE signals are caused by rock failure events, the duration of which is only about 10 ms. The signals are transient, and their amplitudes quickly attenuate to below the threshold of the instrument. Here, only one rock failure event is assumed to occur at a time, therefore AE signals are considered separately. The AE effective energy of the i-th rock failure event \( E_{\text{AE}}^{i} \) is then calculated as

$$ E_{\text{AE}}^{i} = \int_{t}^{{t + \Delta t_{i} }} {V(t){\text{d}}t} , $$
(7)

where \( \Delta t_{i} \) is the duration of each rock failure event.

If n events happen in unit time, the AE effective energy rate \( \bar{E}_{\text{AE}} \) is calculated as

$$ \bar{E}_{\text{AE}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {E_{\text{AE}}^{i} } . $$
(8)

After the HHT process, the AE effective energy rate of the tested specimen is decomposed into many components and a residue. The AE effective energy rate is expressed as

$$ \bar{E}_{\text{AE}} = \sum\limits_{j = 1}^{n} {a_{j} (t)\exp \left( {\text{i}\int {\omega_{j} (t)} {\text{d}}t} \right) + r(t)} , $$
(9)

where \( a_{j} (t) \) and \( \omega_{j} (t) \) are the instantaneous amplitude and frequency of the j-th IMF, and n is the number of components.

The rock material laboratory experiment is a thermodynamic process in an open system. Energy is transferred from the material testing system to the rock specimen continuously, a transformation that can be associated with three types of energy: elastic energy, plastic energy, and “disappeared” energy. Elastic deformation generates elastic energy that can be released totally while unloading. In contrast, plastic deformation generates plastic energy that cannot be released after the load disappears. Additionally, some energy disappears as part of a complex phenomenon involving radiation, phase transformation and chemical energy, fracturing energy, and other effects. To simplify the analysis approach, we assume that the disappeared energy is equal to the fracture energy generated from the elastic energy. Previous studies have revealed that the AE effective energy rate is linearly related to the fracture energy release rate during the entire failure process, whether the material is metal or nonmetal and the observation is on either macroscopic or microscopic scales (e.g., Gerberich and Hartbower 1967; Curtis 1975; Cai et al. 1992; Bahr and Gerberich 1998; Landis and Whittaker 2000; Landis and Baillon 2002; Puri and Weiss 2006; Raghu Prasad and Vidya Sagar 2008). Moreover, the value of the AE effective energy rate can be reflected in the instantaneous amplitude as illustrated in Eq. 9. Therefore, the failure process of rocks can be investigated using the AE effective energy rate and the HHT method.

5 Experimental Results and Analysis

Rock samples are homogeneous at macroscales but highly heterogeneous at microscales. This is the result of two aspects. First, natural flaws reduce the effective area of local elements within rocks. Second, mineral constituents and physical properties in different local elements change in different ways. This heterogeneity changes the mechanical properties of the rock and complicates the mechanics of the rock. Figure 4 presents a typical stress–strain curve for brittle sandstone and three images corresponding to points C, D, and E.

Fig. 4
figure 4

Stress–strain curve of sandstone sample

Full size image

The failure process of a rock under compressive load can be divided into three stages according to this stress–strain curve: a nonlinear compaction stage (OA), a linear deformation stage (AC), and a nonlinear deformation stage (CE). The basic deformation mechanism in both the linear and nonlinear deformation stages can be described as follows (e.g., Lockner et al. 1991; Lei et al. 2000; Zuo et al. 2007; Ponomarev et al. 2010): During the linear deformation stage, the occurrence of microflaw closures is rare. Instead, the phenomena of irreversible deformation and local stress concentration occur, and the generation and progression of microcracks are random. The stress–strain curve is nonlinear in the last stage, and the propagation and coalescence of microcracks happen while the load is steadily increased, and finally macrocracks are generated at point D. This point is the peak stress point of the stress–strain curve.

The blue curve in Fig. 5 presents the tangent modulus synchronized with strain. The black scatter plots are the AE effective energy rate with strain. The strain range of interest is the last one-third of the strain curve (between points B and E in Fig. 4). Here, the tangent modulus is defined as

$$ E = \frac{\text{d}\sigma }{\text{d}\varepsilon } , $$
(10)

where \( \sigma \) is the stress and \( \varepsilon \) is the strain in the rock sample. The red points indicate strong signals at various stages. The tangent modulus is the instantaneous stiffness of specimens; it can roughly indicate the degree of damage. The value of the AE effective energy rate increased immediately at point C, and the tangent modulus decreased at the same time. However, this figure cannot illustrate the dynamic transformation between the linear and nonlinear deformation stages. Similarly, during the softening process (Fig. 5), the scatter plots have difficulty describing the decrease of the tangent modulus. The characteristics of these two process are discussed using a HHT-based AE processing approach below.

Fig. 5
figure 5

Tangent modulus–strain curve and AE effective energy rate–strain scatter plots of sandstone sample

Full size image

5.1 Hilbert Spectral Characteristics for AESP

The Hilbert spectrum is presented in a color map format for the AESP at the linear deformation stage and the nonlinear deformation stage in Fig. 6a and b, respectively. The amplitude of the Hilbert spectrum lies in the range \( 10^{ - 2}-10^{4} \), which is too wide to display. Therefore, a variable is defined as

$$ a^{\prime}_{j} (t) = \log (a_{j} (t)) , $$
(11)

where \( a_{j} (t) \) is the instantaneous amplitude of the j-th IMF. The colors in these spectra represent the order of magnitude of the AESP, which also illustrates the moment release of elastic energy for the rock specimen. The instantaneous amplitude is obviously weak in the linear deformation stage but becomes strong in the nonlinear deformation stage. The spectrum at point E is chaotic and obscure, as shown in Fig. 6b, owing to the end boundary effect (Huang et al. 1998). The trend of the instantaneous amplitude is similar to those presented in previous research based on the AESP directly.

Fig. 6
figure 6

AE effective energy rate signals and their Hilbert spectra: a at linear deformation stage; b in transition process and at nonlinear deformation stage

Full size image

The upper parts of Figs. 6 and 7 show the AESP spectra for various specimens. The scatter plots in the lower parts of those figures show the AESP synchronized with strain. The red arrows on the spectra indicate increases of the instantaneous amplitude as indicated by the transform process. The red points in the lower part of Fig. 6 indicate the strong signal selected in the analysis. The blue lines in the lower part of Fig. 7 are the stress–strain curve. The color bar on the right side of those figures indicates the order of magnitude of the instantaneous amplitude of the Hilbert spectra.

Fig. 7
figure 7

Hilbert spectral characteristics in transition process

Full size image

The spectral characteristics of AESP are observed to shift at the various stages. The AESP has instantaneous frequencies of around 0.5 Hz in the linear deformation stage and around 1–1.5 Hz, attributed to the deformation mechanism, in the nonlinear deformation stage (Fig. 6). Moreover, it is difficult to observe a difference in the AESP before and after the generation of macrocracks (Fig. 5). In fact, the highest instantaneous frequency is approximately 1 Hz before the generation of macrocracks and then generally 1.5 Hz after. The separation of rock failure events at points C, I, and J is clear in Fig. 6b. Nevertheless, a frequency fluctuation of around 0.2 Hz between points D and E indicates that fracture energy releases continuously as indicated by the green rectangle. Furthermore, the shape of the instantaneous frequency spectrum at points C, I, and J is symmetric, whereas it is asymmetric at points D, L, and E. The physical meaning of these phenomena is explored below. The effect of each rock failure event at the first three points is temporary, and the increase in damage is stable and ordered. However, following the generation of the first macrocrack at point D, the influence of rock failure events becomes sustained. The development of damage is random, and macrocrack propagation is unstable. Thus, the execution of a HHT-based AESP analysis process provides a better distinction between the different stages. This has advantages over those methods based only on AE signals and, in particular, can be used to predict the failure of a rock specimen.

The current method can readily predict the transition process between different deformation stages. The transition process refers to the period of change between linear and nonlinear deformation stages. Energy transformation and damage progression during the transition process are described in Fig. 6b. Three rock failure events are continuous around point H, and one strong event occurred immediately at point C (Fig. 5). As a result, the highest instantaneous frequencies for these four events increase linearly from 0.5 to 1.5 Hz during this process. Because of the differences between the new HHT method and those methods that use a constant threshold, the HHT can separate the linear and nonlinear deformation stages from the whole rock failure process with a variable threshold. Moreover, the Hilbert spectra illustrate that the transformation between these two stages is transitional but short in duration. The increase of the instantaneous frequencies indicates that this transformation is a dynamic process. Large numbers of AE signals were received during this process. This indicates that most of the energy was rapidly released. However, the generation of a macroscopic crack did not take place during this transition process (Fig. 4). Figure 7 gives the Hilbert spectra of the other five rock specimens in the test. Similar phenomena were observed in these tests as well, with the exception of Fig. 7b, which shows a macrocrack that was generated in the linear deformation stage.

A further explanation of the transition process using Ncorr (open-source two-dimensional digital image correlation software) (Blaber et al. 2015) is presented in Fig. 8. At point H, the rock deformation is highly asymmetric. After the transition process, high strain inhomogeneity (in the circle at point H) was released at point C owing to a significant release of elastic energy. A more detailed understanding of rock deformation properties during the failure process as well as a comparison between the analysis results using the HHT-based AE technique and a digital image correlation method will be discussed in the future.

Fig. 8
figure 8

Evolution of apparent normal strain ε x at points H (a) and C (b) obtained by digital image correlation method

Full size image

5.2 Hilbert Spectral Characteristics for AE Signals

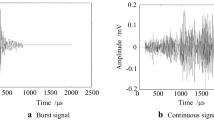
AE signals are damped with a sinusoidal oscillation. Their amplitudes vary with the release of fracture energy (Mitraković et al. 1985). Rock can be described as a heterogeneous viscoelastic material. Elastic waveforms change as they spread into a specimen. These changes are the result of the attenuation effect and can be portrayed by a Hilbert spectrum. The attenuation is clearly frequency dependent, which reflects the nature of the fractures generated in the specimen (Cai and Zhao 2000; Zhao et al. 2006; Wang et al. 2010). Therefore, the attenuation of rock specimens can be investigated using a HHT-based processing method; For example, the monitor received 19,692 AE signals during the test, of which 269 were classified as strong (i.e., their maximum amplitudes were greater than 1 V). Figure 9 presents the analytical results of the HHT-based AE processing approach. Each image contains two parts: the AE signals are shown in the lower part of the figure, and the related Hilbert spectrum is presented in the upper part. Figure 9a–e shows the moments at points F, G, H, C, and I, respectively. Three typical moments in the softening process are shown in Fig. 9f–h. A macrocrack was generated at point D as shown in Fig. 4, and the amplitudes of the AE signals are high at this moment. Therefore, three typical AE signals are presented separately in Fig. 9i–k. The AE signal in Fig. 9l corresponds to the moment of rock failure at point L. The results presented in Fig. 9j, k were received continuously starting at point E. All characteristics of interest concerning the AE signals are summarized in Table 2.

Fig. 9
figure 9figure 9

Original AE signals and their Hilbert spectra at points F (a), G (b), H (c), C (d), I (e), D (i–k), L (l), and E (m, n), and in the softening process (f–h)

Full size image
Table 2 Characteristics of AE signals at different points
Full size table

The frequency characteristics of Hilbert spectra distributions highlight some differences in the linear and nonlinear deformation stages (Fig. 9). They are mainly distributed over the range of 100–400 kHz in the linear deformation stage. In contrast, various characteristics show that those frequencies form two or three clusters in the nonlinear deformation stage. Thus, the analysis of a Hilbert spectrum of AE signals represents a novel way to identify deformation stages in rock specimens.

The Hilbert spectra of AE signals during the transition process (at points H and C) highlight the transformation from linear to nonlinear deformation. The characteristics of the spectra for this process suggest a combination of both linear and nonlinear deformation. The attenuation of elastic waves results in similar features in the spectra. Meanwhile, the distribution of clusters of instantaneous frequencies in the spectra also has some features in common with both the transition process and the nonlinear deformation stage. Thus, the transformation from linear to nonlinear deformation stages could be illustrated by using the HHT-based AE processing approach. In addition, the transition process has some special characteristics. Although points F, G, and H occurred at the same stage, Fig. 9c presents features that are different from the other two spectra. The instantaneous frequencies of this spectrum are distributed in two clusters, whereas in the first two spectra, the instantaneous frequencies are distributed over a wide range. This phenomenon indicates that the deformation mechanism of the rock specimen was changing at point H. Moreover, the lower-frequency cluster is distributed over a broad range of 10–150 kHz in the transition process, but with few components below 100 kHz in the previous stage. Larger numbers of microcracks propagated and coalesced during this process, and volume dilation followed. The voids resulted in a decrease in the tangent modulus of the rock specimen and affected the instantaneous frequencies of the AE signals. One section of typical AE signals from the nonlinear compaction stage and their corresponding Hilbert spectrum is shown in Fig. 10, where the lower frequencies are also distributed over the 10–150 kHz range owing to the existence of natural voids. The spectra in Fig. 9c, d also differ. The higher-frequency components of the spectrum disappeared quickly at point H, but they lasted for about 2.5 × 10−4 s at point C. AE signals become more complex than before at this stage.

Fig. 10
figure 10

Typical original AE signal and its Hilbert spectrum at the nonlinear compaction stage

Full size image

A more thorough examination of the data presented in Fig. 9 shows that the Hilbert spectra in the softening process are more complex than in other processes. More clusters exist during this process than in other processes. The values of the higher primary frequencies of different AE signals change during the softening process to around 300 kHz in Fig. 9f, h, and 400 kHz in Fig. 9g. Likewise, the clusters of middle frequencies are centered at approximately 200 kHz in Fig. 9f, h, and 250 kHz in Fig. 9g. These changes are the result of the propagation of fractures and affect the tangent modulus of the rock (Fig. 5). The changeable frequency property of the AE signals is a response of the attenuation of the rock specimen that varies during the softening process, implying that the deformation mechanism is unstable.

The attenuation of the elastic wave spreading in the sample could be investigated by using this approach. Obviously, this attenuation is frequency dependent. On the one hand, the higher frequencies quickly disappear owing to the attenuation of rock samples in the linear deformation stage. Figure 9a, b shows this phenomenon, where each rock fracture event is simple and can be distinguished from the AE signals. The red arrows in the spectra of those figures highlight the attenuation of the rock specimen from higher to lower frequencies as a function of time and frequency. On the other hand, the decrease of the lowest instantaneous frequency indicates a change in the deformation mechanism. During the transformation from linear to nonlinear deformation stages, the value of the lowest instantaneous frequency dropped from 100 to 10 kHz. Similarly, the instantaneous frequency of approximately 100 kHz observed during the softening process tailed off to 50 kHz at point D when the first macrocrack was generated, then dipped to 10 kHz at point E when the rock failed. These two decreases have a common feature: a dramatic transformation in the rock specimen. Strain softening of rock happens when the rock is damaged (Read and Hegemier 1984; Li et al. 2012b), and manifests as a decrease of frequencies (Pride et al. 2004). Thus, the HHT-based AE processing approach is sensitive to attenuation in a rock.

The attenuation of the lowest frequencies corresponds to the damage accumulating in the rock and enables the exploration of rock failure trends. A more accurate prediction of rock failure could be forecasted by analyzing the Hilbert spectra in detail. Figure 9i shows the moment before macrocrack generation, and Fig. 9m is just prior to the rock breaking. These figures have similar features. The distribution of instantaneous frequencies covers a wide range without a centralized cluster. This phenomenon is unique in the nonlinear deformation stage, and major failure events could occur in milliseconds. Therefore, this approach represents a possible way to predict the failure of a rock specimen.

The amplitudes of different Hilbert spectra develop during the rock failure process. The main trend of the spectrum amplitudes is close to that obtained by the AESP from Fig. 5. The only incompatibility occurs at point C, where the AESP value is high but the instantaneous amplitudes are low. This phenomenon can be interpreted as described below. The energy release rate is much lower than others at point C. Three strong AE signals were monitored continuously at that moment with signal amplitudes of approximately 1 V. To save space, only one typical result is presented in Fig. 9. Meanwhile, the AESP is the integral of AE signals, the values of which are the sum of the influences of all AE signals in a short period. Therefore, even though the amplitudes of each section of these AE signals are small, the accumulated effect is large.

6 Conclusions and Further Work

This study has presented a HHT-based AE processing approach, in which two types of signals have been analyzed. The approach provides an effective way to interpret nonlinear and nonstationary signals by decomposing them into different intrinsic mode function components and then obtaining the Hilbert spectra. The advantage of this approach is that the damage and attenuation of rocks under load can be investigated at both macroscopic and microscopic scales. In this approach, AESP are selected to describe the trend of the rock failure process, whereas instantaneous information about rock deformation is illustrated by using AE signals. The analysis results show that both are related to the rock failure process, and present a similar trend that is synchronized with the damage process. From these investigations, the following main conclusions can be drawn:

  1. 1.

    Different deformation stages can be distinguished by this approach. On the one hand, the spectrum of AESP before macrocrack generation is symmetric, whereas it is chaotic following generation. This illustrates a change in the propagation of cracks from stable to unstable. Meanwhile, the distribution of instantaneous frequencies of AE signals extends over a broad range during the linear deformation stage, whereas it is concentrated in several clusters during the nonlinear deformation stage.

  2. 2.

    The transformation from linear to nonlinear deformation stages is short. The Hilbert spectra of AESP show that the instantaneous frequencies increase linearly from 0.5 to 1.5 Hz during this process. These dynamic processes illustrate the gradual release of fracture energy as the load increases.

  3. 3.

    Attenuation in rock can be presented by the Hilbert spectra of AE signals. Lower-frequency clusters are generally around 100 kHz at first, which is representative of two attenuations: one during the transition process caused by the existence of voids, and the other during the softening process caused by a decrease of the tangent modulus.

  4. 4.

    The scatter distribution of instantaneous frequencies is related to the degree of rock damage. Three clusters of instantaneous frequencies are identified to be related to the softening process, implying that a complex mechanism exists. Thus, rock failure is predictable using a HHT-based AE processing approach. The AESP analysis provides an approximation range, and the results based on AE signals are sensitive.

  5. 5.

    The methods presented here constitute an improved technique for signal characterization and provide a new way to study mechanism changes associated with rock failure processes. This study does not involve AE location identification, which is an important characteristic of AE signals. Indeed, the combination of a HHT-based AE processing approach and an AE source localization technique could provide detailed information about rock deformation mechanisms; For instance, the HHT could improve the accuracy of AE source localization, and the joint interpretation of various series of AE data (and the calculation of the moment tensors of AE signals) may result in a more detailed understanding of the mechanisms driving individual rock fracture events. Thus, both knowledge of the rock failure process and prediction of rock fracturing could be improved.