1 Introduction

Fragmentation is an important yardstick for wide variety of processes such as blasting in mines, tunnel and slopes as well as for structural demolition. In a blasting processes, solid masses are damaged and fragmented by detonating explosive confined within spaces inside a solid medium. It is well known that rock damage and fragmentation by blasting occurs due to detonation-induced stress wave and product gas driven fracture propagation. To achieve an efficient numerical procedure, it is required to understand detonation mechanism of explosive and subsequent failure process of surrounding rock material.

Detonation of explosive involves a rapid chemical decomposition of explosive molecules under the action of a shock wave. The exothermic chemical reaction takes place in a reaction zone which travels through the explosive charge at a velocity, depending on the type of explosive, its density and energy that expend in the sustaining process. Detonation wave propagates in free space if explosion occurs in unconfined conditions. On the other hand, in confined blasting condition, wave propagates in the rock medium and causes fracture initiation. Subsequently, high pressure gas penetrates into the developed cracks near the blast holes causing extension of fracture, which leads to fragmentation depending upon the charge and blast hole diameter. Therefore, a comprehensive understanding of dynamics of explosion process in confined as well as unconfined system benefits optimization of explosive energy in rock fragmentation and thereby, casting of broken material. In addition, prediction of characteristics of high gas pressure behind detonation waves assists in designing appropriate blasting patterns in mining and allied applications.

Continuum damage mechanics is considered to be appropriate to describe the failure process of rock under such high-amplitude stress wave. Based on this approach, several theoretical models have been developed to analyze the dynamic damage of brittle material such as rock and concrete with microstructure (Taylor et al. 1986; Yazdchi et al. 1996; Wu et al. 2004; Chen 1999; Seaman et al. 1976). These models are mostly based on the theory of damage mechanics or fracture mechanics with some statistical treatment to incorporate random distribution of microcracks. In the application of fracture mechanics theory, sometimes it is difficult to estimate the micromechanical parameters such as crack density and fracture toughness in different modes. In this study, damage in rock material is evaluated according to the earlier model developed by Grady and Kipp (1980), which is a fracture model coupled with a material description for stress wave propagation to predict quantitatively fracture and fragmentation under explosive loading conditions.

Analytical solution to the above-complicated phenomenon is rare in the literatures and limited to only some simple cases. Experimental studies often require expensive and time consuming series of test to elucidate the complex phenomena of blasting process. Sometimes certain physical characteristics related to explosion cannot be scaled to practical experimental set up. Computational methods are the most economical and efficient tool to investigate the complicated phenomena (Mader 1998; Shin and Chisum 1997). However, it is generally difficult to simulate the very process using grid base numerical methods (FEM, FDM). In this case, a thin reaction zone separates the domain into two inhomogeneous parts and produces large deformation. In addition, the outward moving gaseous products disperses and enters into the cracked spaces or moving interfaces. Recent development of meshless or meshfree methods has advantage for simulating large deformation, large inhomogeneities, fracture propagation and fragmentation that may occur during failure process under static or dynamic loading conditions. Among the meshfree methods, smoothed particle hydrodynamics (SPH) has shown the promises to simulate large deformation behavior of rock medium by including elasto-plastic or damage theories (Deb and Pramanik 2013; Das and Cleary 2010; Pramanik and Deb 2013; Bui et al. 2008). SPH was first developed to simulate nonaxisymmetric phenomena in astrophysical dynamics, in particular polytropes (Gingold and Monaghan 1977; Benz et al. 1989). Due to its flexibility of meshless Lagrangian nature, ease of implementation is well employed within numerous branches of computational physics (Liu and Liu 2003; Vignjevic and Campbell 2009). Liu et al. (2003) applied the smoothed particle hydrodynamics to simulate the detonation process of high explosive on the behavior of gas jet. However, they have ignored the effect of physical reaction zone in explosive between inert unreacted shock point to the reacted sonic point.

The dynamic fracture mechanism in a circular rock medium under stress wave loading has been investigated by Zhu et al. (2007). In their study, penetration of high pressure gaseous product into developed crack spaces is neglected. To simulate post detonation gas flow into rock fracture and subsequent fragmentation process, combined finite-discrete element method is successfully adopted by various researchers (Munjiza 2004; Minchinton and Lynch 1997; Munjiza 2004; Munjiza et al. 2013; Vyazmensky et al. 2010). In this method, it is assumed that detonation process completes instantaneously due to high detonation velocity of explosive. With this assumption, the simulation starts with a blast hole filled with gaseous product at high pressure. The initial gas flow occurs into the existing cracks and voids. After that, secondary flow roots develop due to the cracking process, fracturing and eventually fragmentation of the solid medium. However, it is also mentioned in the literature that the approach is not concerned with a full scale model of gas flow including detonation process of explosive.

In this paper, a methodology in the SPH framework is implemented to investigate the key physical phenomena that occur in detonation process of explosive and failure in surrounding rock media under blast-induced stress wave and expansion, and penetration of high pressure gaseous product. For detonation dynamics of explosive, SPH formulation of the Euler equation is implemented with Jones–Wilkins–Lee (JWL) equation of state with a reaction zone. A pressure-based program burn algorithm is applied to modify the equation of state of the burning particle in the reaction zone. The proposed method of detonation process is applied in TNT explosive for both one- and two-dimensional cases to predict detonation wave as well as dispersion process of product gas. Numerically predicted results are compared with those obtained from theoretical solutions and similar AUTODYN model. The developed procedure is further applied to elucidate dynamic failure mechanism of rock under blast-induced stress wave and subsequently, by high pressure gas expansion process. For this purpose, a SPH model is developed by considering a square shape rock medium with centrally located emulsion explosive in a blast hole. The model is simulated by assuming all four sides of the rock medium as free surfaces. A procedure is developed to treat the dynamic behavior of rock–gas interface as the gaseous product expands and penetrates into the fractured space of rock medium. The paper elaborates the propagation of stress wave, expansion dynamics of gaseous products, and development of fracture and fragmentation of the medium. The results of peak pressure are also validated with those obtained from AUTODYN and are found to be in good agreement.

2 Formation of the Problem

In this section, the governing equations for detonation-induced gas and brittle rock deformation are briefly summarized.

2.1 Detonation Process of Explosive

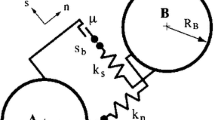
Explosion within a confined space of rock mass consists of two distinct processes (1) detonation process through explosive and (2) interaction of detonation-induced high pressure gas with surrounding rock mass. A detonation refers to a shock wave that advances through the explosive with a constant velocity driven by the chemical reactions initiated at the shock front. Figure 1a depicts a schematic diagram of the detonation process in which three zones appear due to chemical reaction. In the steady-state detonation process, the reaction rate is essentially infinite and the chemical equilibrium is attained. Detonation process follows two Hugoniot curves, first the Hugoniot of the unreacted explosive and second, the Hugoniot of gaseous products of the reaction as shown in Fig. 1b. Consider a shock front is advancing through an explosive with a detonation velocity D that compresses the explosive from an original status point A \((p_0, V_0)\) to another specific status point C \((p_1, V_1)\) along the Hugoniot of the unreacted explosive. The point C (called the von Neumann spike or the chemical peak) is an unreacted state at very high temperature and pressure that initiates the chemical reaction within a thin zone and the state of the point C transforms to gaseous state. As a result, volume expands and pressure drops by proceeding along the Rayleigh line, derived from the conservation of mass by assuming that \(D=D_{\rm CJ}\), to the C–J point at B. According to the experimental evidence (Sheffield et al. 1984), the pressure falls due to release of chemical energy into the reaction zone. Chemical reaction in the reaction zone leads to the reacted gaseous products of the detonation. The end point of the reaction zone is the Chapman and Jouguet (C–J) point or the sonic point. Chapman and Jouguet’s hypothesis states that for a steady plane detonation wave propagation, the Rayleigh line must be the tangent at the C–J point to the Hugoniot curve of the gaseous detonation products. After completion of the detonation, the rarefaction wave disperses the product gas from C–J state to the expanding state along the downhill path of the Hugnouit curve of gaseous product.

Fig. 1
figure 1

a Schematic of the detonation process of explosive; b Hugoniot curves of detonation from the unreacted state to the C–J state on p-V plane

Full size image

2.2 Explosive Burn

A traditional program burn model has been implemented in many hydrocodes (Bdzil et al. 2001) of explosive engineering to describe a detonation process. In this case, each SPH particle is pre-assigned its burn time, \(t_b\) based on the detonation velocity, \(D_{\rm CJ}\) and its distance from the detonating point. If the current time is below the particle burn time, \(t<t_b\), then the particle will not be allowed to burn at this time and the burn fraction \(Y\) for this particle is assigned to be zero. If \(t>t_b\), then burn fraction is calculated base on the Eq. (1). The burn fraction is usually assigned to be the volume fraction of the particle that belongs to the reaction zone behind the detonation shock wave and computed value lies between 0 and 1. The program burn model assumed that explosive detonates at a given time and detonation wave propagates with constant positive speed, \(D_{\rm CJ}\). The burn fraction is updated according to the rule

$$\begin{aligned} Y({\mathbf {x}})=\left\{ \begin{array}{lll} 0 &{}\text{ for } &{} t\le t_{b}\\ \frac{t({\mathbf{ x}})-t_d({\mathbf {x}}_d)}{\Delta t} &{} \text{ for } &{} t_b < t < t_b+\Delta t\\ 1 &{} \text{ for } &{} t\ge t_b+\Delta t \end{array}\right. \end{aligned}$$
(1)

where \(t_b=\left| \mathbf {x}-\mathbf {x}_d \right| /D_{\rm CJ}\) is the burn time, \(\mathbf {x}_d\) is the position of the detonation point at time \(t\) and \(\Delta t\) is the burning interval, given by

$$\begin{aligned} \Delta t=\left\{ \begin{array}{lll} n_b\frac{\Delta x}{D_{\rm CJ}} &{}\text{ for } &{} {{\text1}-D }\\ n_b\frac{\Delta x \Delta y}{D_{\rm CJ}\sqrt{\Delta x^2+\Delta y^2}} &{} \text{ for } &{} {{\text2}-D } \end{array}\right. \end{aligned}$$
(2)

where \(n_b=3-6\), \(\Delta x\) and \(\Delta y\) are the initial spacing of the explosive particles in \(x\) and \(y\) directions, respectively.

2.3 Equation of State

The Jones–Wilkins–Lee (JWL) equation of state is adopted to describe the pressure of gaseous products of the explosive and given as

$$\begin{aligned} p_{_{JWL}}=A\left( 1-\frac{\omega \theta }{R_1}\right) e^{-R_1/\theta }+B\left( 1-\frac{\omega \theta }{R_2}\right) e^{-R_2/\theta }+\omega \theta \rho _0E \end{aligned}$$
(3)

where \(A\) and \(B\) are constants in GPa pressure units, \(R_1\), \(R_2\) and \(\omega\) are real numbers, \(\theta =\rho /\rho _0\), \(\rho _0\) is the initial density of the explosive, and \(E\) is the initial internal energy per unit volume in J/kg. The JWL parameters of explosives used in this paper are given in Table 1.

By incorporating the above program burn model (1) in Eq. (3), the modified equation of state is given by

$$\begin{aligned} p(\rho , E, Y)=p_0+[p]Y \end{aligned}$$
(4)

where \(p_0\) is the initial pressure of the unreacted explosive and \([p]=p_{_{\rm JWL}}(\rho , E) - p_0\). The above scheme replaces the pressure with partial pressure in the reaction zone according to the burn fraction. The modified equation of state also helps to increase the pressure in such a way that internal energy is assumed to be finite and the effective reaction zone structure begins from the unreacted state at the ambient pressure. It should be noted that non-ideal detonation process can also be used in SPH framework for dynamic finite length reaction zones (Kirby et al. 2014; Schoch et al. 2013).

Table 1 Reaction products parameters for high explosives: JWL form
Full size table

2.4 Governing Equations

The interaction between product gas and rock medium is a multi-physics phenomenon in which high pressure of the detonation-induced gas causes a considerable deformation in rock medium. In this paper, detonation-induced gas is considered as compressible fluid that interacts with surrounding brittle rock material when explosion occurs in confined conditions. As shown in Fig. 2, the domain occupied by gas is denoted by \(\Omega _{t}^{\rm g}\) and the rock by \(\Omega _{t}^{\rm r}\) at time \(t\in [0,T]\).

Fig. 2
figure 2

Schematic of the domains occupied by gas and rock in rock blasting phenomenon

Full size image
Fig. 3
figure 3

Support domain of particle \(a\) and weight function

Full size image

The governing equations of motion of gas and rock in combined form can be written as

$$\begin{aligned} \frac{D\rho }{Dt}&= -{\rho }\frac{\partial v^{\alpha }}{\partial x^{\alpha }} \end{aligned}$$
(5)
$$\begin{aligned} \frac{Dv^{\alpha }}{Dt}&= \frac{1}{\rho }\frac{\partial \sigma ^{\alpha \beta }}{\partial x^{\beta }}\end{aligned}$$
(6)
$$\begin{aligned} \frac{De}{Dt}&= \frac{\sigma ^{\alpha \beta }}{\rho }\frac{\partial v^{\alpha }}{\partial x^{\beta }} \end{aligned}$$
(7)

where \(\alpha\) and \(\beta\) denote the Cartesian components; \(v^\alpha\) is the velocity component; \(e\) is the internal energy; \(D/Dt\) denotes the material derivative following the motion. The stress components, \(\sigma ^{\alpha \beta }\) for gas and elastic solid are defined by

$$\begin{aligned} \sigma ^{\alpha \beta } = \left\{ \begin{array}{ll} -p\delta ^{\alpha \beta } &{} \forall \,{{\mathbf {x}}}\in \Omega _t^{\rm g}\\ 2G\varepsilon _{\rm d}^{\alpha \beta } +K\varepsilon _{\rm v}\delta ^{\alpha \beta } &{} \forall \,{\mathbf {x}}\in \Omega _{t}^{\rm r} \\ \end{array}\right. \end{aligned}$$
(8)

where the pressure of detonation gas, \(p\) is evaluated from Eq. (4); \(G\) and \(K\) are shear and bulk modulus of rock, respectively; \(\varepsilon _{\rm d}\) and \(\varepsilon _{\rm v}\) are the deviatoric and volumetric strain of rock material. It should be noted that as the detonation-induced gas has high pressure and high dispersion speed. The product gas is treated as inviscid in adiabatic process. The boundary conditions at interface of gas–rock is discussed in Sect. 3.3.

2.5 Inelastic Behavior of Rock Medium

Under dynamic loads, rock exhibits an inelastic brittle material response. The inelastic behavior arises principally due to stress-induced microcracks. The growth of these microcracks renders portions of the rock volume unable to carry loads, which is then reflected in decrease of the stiffness of material. During stress wave propagation, tensile stresses or shear stresses do occur and cause rock material to fail in tension or in shear, respectively. In this study, generalized Grady and Kipp (1980) damage model for higher dimension is incorporated to determine damage variable, \(D\) (\(0\le D\le 1\)) for tensile failure (Melosh et al. 1992). After evaluation of damage variable, the common approach is to scale the entire stress tensor by the factor \((1-D)\). However, this approach equally modifies compressive components along with tensile components of the total stress tensor which should not be the case if failure occurs due to tensile stress. In this paper, a rational approach similar to that of Das and Cleary (2010) is adopted to treat only the tensile stress components keeping the compressive part unaltered.

Total stress tensor \((\varvec{\sigma })\) is decomposed into tensile \((\varvec{\sigma }^{+})\) and compressive \((\varvec{\sigma }^{-})\) parts as

$$\begin{aligned} \varvec{\sigma }^{+}&= \mathbf {P}^+:\varvec{\sigma }\end{aligned}$$
(9)
$$\begin{aligned} \varvec{\sigma }^{-}&= \varvec{\sigma }-\varvec{\sigma }^{+}=\mathbf {P}^-:\varvec{\sigma } \end{aligned}$$
(10)

where the fourth-order projection tensors \(\mathbf {P}^+\) and \(\mathbf {P}^-\) expressed as (Faria et al. 1998)

$$\begin{aligned} \mathbf {P}^+&= \sum _iH(\sigma _i)\mathbf {p}_{ii}\otimes \mathbf {p}_{ii}\end{aligned}$$
(11)
$$\begin{aligned} \mathbf {P}^-&= \mathbf {I}-\mathbf {P}^+ \end{aligned}$$
(12)

where \(\mathbf {I}\) is the fourth-order identity tensor; \(H\,(\sigma _i)\) denotes the Heaviside function computed for the ith eigenvalue \(\sigma _i\) of \(\varvec{\sigma }\); the second-order symmetric tensor \(\mathbf {p}_{ij}\) is defined as

$$\begin{aligned} \mathbf {p}_{ij}=\mathbf {p}_{ji}=\frac{1}{2}(\mathbf {n}_i\otimes \mathbf {n}_j+\mathbf {n}_j\otimes \mathbf {n}_i) \end{aligned}$$
(13)

where \(\mathbf {n}_i\) is the ith normalized eigenvector corresponding to \(\sigma _i\).

Now, the tensile part \(\varvec{\sigma }^{+}\) is only scaled down by the factor \((1-D)\) and added with compressive part \(\varvec{\sigma }^{-}\) to have the modified stress tensor for tensile damage. Under compressive loads, pressure-dependent inelastic response is also observed for rock medium. Therefore, the material is treated with the context of Drucker–Prager strength theory for elaso-plastic response (Deb and Pramanik 2013).

3 The SPH Method

SPH methodology overcomes the disadvantages of traditional mesh-based numerical methods in treating large deformations, large inhomogeneities, tracing free surfaces and moving boundaries in transient analysis under explosive-induced stress wave. In this section, a brief summary of the SPH method is presented for solving the equations of motion (5–7). For more comprehensive details on SPH method one can refer to Monaghan (1992) and Vignjevic and Campbell (2009).

3.1 Numerical Approximation

In SPH, the state of particles is represented by a set of points with fixed volume, which posses material properties interact with the all neighboring particles by a weight function or smoothing function or smoothing kernel (Gingold and Monaghan 1977). This function required to be continuously differentiable and satisfies the normalization, delta function, and compactness properties. Each particle has a support domain, \(\Lambda _a, \forall a\in \Omega\), specified by a smoothing length, \(h_a\) (Fig. 3). The value of a function at a typical particle is obtained by interpolating values of that function at all particles in his support domain weighted by smoothing function. Gradients that appear in the flow equation are obtained via analytic differentiation of the smoothing kernel.

The smoothed particle technique involve replacing grid-based approximation to an arbitrary collection of interpolating points. The basic idea of this method is kernel estimate, which start with the following identity

$$\begin{aligned} A(\mathbf {x})=\int _{\Omega }{A(\mathbf x')W(\mathbf {x'}-\mathbf {x})}d\Omega _{\mathbf {x'}},\,\,\,\,\,\,\,\,\forall \,\mathbf {x}\in \Omega \subset \mathbb {R}^{d}\,\,\,\,\,\, \end{aligned}$$
(14)

where \(A\) is a vector function of the position vector of \(\mathbf {x}\), \(\Omega\) is a volume of the integral containing the point \({\mathbf {x}}\), and \(W(\mathbf {x-x'},h)\) is smoothing kernel or weight function. The value interpolated for a function \(A\) at the position \(\mathbf{x_a}\) of particle \(a\) can be expressed using SPH smoothing as

$$\begin{aligned} A(\mathbf {x}_a)=\sum _{b\in \Lambda _{a}}A_{b}\frac{m_b}{\rho _{b}}W(\mathbf {x}_a-\mathbf {x}_{b},h). \end{aligned}$$
(15)

where \(m_b\) and \(\rho _{b}\) are the mass and the density of particle \(b\). \(\Lambda _{a}=\{b\in \mathbb {N}\mid \left| \mathbf {x}_{a}-\mathbf {x}_{b} \right| \le k(h_{a}+h_b)/2\}\) is the set of neighbor particles of the particle \(a\) in its defined support domain. The gradient of the function \(A\) at the position of the particle \(a\) is given by differentiating kernel \(W\) in Eq. (15)

$$\begin{aligned} \nabla A\,(\mathbf {x}_a)=\sum _{b\in \Lambda _{a}}A_{b}\frac{m_b}{\rho _{b}}\nabla _a W\,(\mathbf {x}_a-\mathbf {x}_{b},h). \end{aligned}$$
(16)

where

$$\begin{aligned} \nabla _a W(\mathbf {x}_a-\mathbf {x}_{b},h)=\frac{\partial W_{ab}}{\partial \mathbf {x}_a}=\left( \frac{\mathbf {x}_a-\mathbf {x}_{b}}{r}\right) \frac{\partial W_{ab}}{\partial r} \end{aligned}$$
(17)

with \(r\) is the relative distance between particle \(a\) and \(b\) and it is defined as \(r=\left| \mathbf {x}_a-\mathbf {x}_{b} \right|\).

The interpolating kernel or smoothing function most widely used in SPH is the cubic B-spline

$$\begin{aligned} W(s,h) = \Gamma _d{\left\{ \begin{array}{ll} \frac{2}{3}-s^2+\frac{1}{2}s^3 &{} 0\le s \le 1\\ \frac{1}{6}(2-s)^3 &{} 1\le s < 2\\ 0 &{} s\ge 2 \end{array}\right. } \end{aligned}$$
(18)

where \(\Gamma _{d}= \frac{1}{h}, \frac{15}{7\pi h^2}, \frac{1}{2\pi h^3}\) for one, two- and three-dimensional space respectively and s = r/h. Cubic spline function has a computational advantage as a potentially small number of neighboring particles contributes in the sum over the particles due to its compact support.

3.2 SPH Approximation of the Governing Equations

The transformation of the set of governing Eqs. (5–7) into particle approximation yields the following set of SPH equations

$$\begin{aligned} \frac{D\rho _a}{Dt}&= \sum _{b\in \Lambda _{a}}m_{b}(v^{\alpha }_{a}-v^{\alpha }_{b})\frac{\partial W_{ab}}{\partial x^{\alpha }_a} \end{aligned}$$
(19)
$$\begin{aligned} \frac{Dv_{a}^\alpha }{Dt}&= \sum _{b\in \Lambda _a}m_{b}\left( \frac{\sigma ^{\alpha \beta }_{a}}{\rho _{a}^{2}}+\frac{\sigma ^{\alpha \beta }_b}{\rho _b^2}-\Pi _{ab}\delta ^{\alpha \beta }\right) \frac{\partial W_{ab}}{\partial x^{\beta }_a}\end{aligned}$$
(20)
$$\begin{aligned} \frac{De_{a}}{Dt}&= \frac{1}{2}\sum _{b\in \Lambda _a}m_{b}\left( \frac{\sigma ^{\alpha \beta }_{a}}{\rho _{a}^{2}}+\frac{\sigma ^{\alpha \beta }_b}{\rho _b^2}-\Pi _{ab}\delta ^{\alpha \beta }\right) (v^{\alpha }_{b}-v^{\alpha }_{a})\frac{\partial W_{ab}}{\partial x^{\beta }_a} \end{aligned}$$
(21)

where \(\Pi _{ab}\) represents the artificial viscous pressure presented below. It is useful to note that above representations of the governing equations are not unique. Several alternative forms can be derived, but these are most often appear in the literatures.

The modeling of physical phenomena having shock wave with Euler equations in the framework of any method at finite resolution without some sort of viscosity and low-order diffusion or a Riemann solver, a strong unphysical oscillation generates from the downward of the shock. In the case of SPH, it is easiest to introduce an artificial viscosity, though it is possible to use Riemann solver (Monaghan 1997). Many form of artificial viscosity has been introduced in the literature, but most commonly used Monaghan’s (Monaghan 1992) type of artificial viscosity. The detailed formulation is as follows

$$\begin{aligned} \Pi _{ab}={\left\{ \begin{array}{ll} \frac{-{\alpha _{\Pi }}_{ab}\mu _{ab}(\bar{c}_{ab}-2\mu _{ab})}{\bar{\rho }_{ab}}&{} \mathbf {v}_{ab}\cdot \mathbf {x}_{ab}<0\\ 0 &{} \mathbf {v}_{ab}\cdot \mathbf {x}_{ab}\ge 0 , \end{array}\right. } \end{aligned}$$
(22)

where

$$\begin{aligned} \mu _{ab}=\frac{h_{ab}\mathbf {v}_{ab}\cdot \mathbf {x}_{ab}}{\left| r_{ab} \right| ^2+0.01h^2} \end{aligned}$$
(23)

and \(\bar{c}_{ab}=\frac{1}{2}(c_{a}+c_{b})\), \(\bar{\rho }_{ab}=\frac{1}{2}(\rho _{a}+\rho _{b})\), \(\mathbf {v}_{ab}=\mathbf {v}_a-\mathbf {v}_b\), \(h_{ab}=\frac{1}{2}(h_{a}+h_{b})\), \({\alpha _{\Pi }}_{ab}=\frac{1}{2}({\alpha _{\Pi }}_{a}+{\alpha _{\Pi }}_{b})\) and \(c_{a}\) denotes the sound’s speed at a particle \(a\). Every particle evolves its own viscosity parameter, \({\alpha _{\Pi }}_{a}\), with time as

$$\begin{aligned} \frac{d{\alpha _{\Pi }}_{a}}{dt}=-\frac{{\alpha _{\Pi }}_{a}-\alpha ^*}{\tau }+\varrho _a. \end{aligned}$$
(24)

The above relation causes \({\alpha _{\Pi }}_{a}\) to decay to a critical value, \(\alpha ^*=0.1\) with e-folding time \(\tau\). The second term, \(\varrho _a=\max (-\nabla \cdot \mathbf {v}_a,0)\) is a source term which cause \({\alpha _{\Pi }}_{a}\) to grow as the particle approaches to shock.

3.3 Rock–Gas Interface Treatment in SPH

The fluid–structure interaction problems consist of the description of fluid, in this case gaseous product and solid, the surrounding rock, with stress and velocity continuity conditions at the interface boundary, \(\Gamma _t^d\). One of the most straightforward solution strategies is to decouple the problems into solid part and fluid part, each of these parts can be solved separately; then the interaction process is introduced as an external boundary conditions in each sub-domains. However, in spite of its simplicity, treatment  at the interface and the interaction is problematic due to stiffness difference and sensitivity. Also, such treatment causes a lag in the evaluation process of interfacial forces which leads to some instability problems.

In this paper, a general methodology is developed to treat the stress continuity at the interface between rock and gas particles using kernel interpolation technique. In this approach, gas particles near the interface are treated as dummy particles (Pramanik and Deb 2014) of a rock particle located adjoining to the interface. To transmit the pressure of a gas particle to the neighboring rock particles, an interfacial stress tensor at the dummy gas particles is introduced in the momentum Eq. (20). Suppose a rock particle \(a^{\rm r}\) has a dummy gas particle \(b^{\rm g}\) in its neighborhood as shown in Fig. 4, the interfacial stress tensor of the dummy gas particles is to be applied as boundary condition on the rock particle \(a^{\rm r}\). To achieve this objective, first, stress tensors of the rock particles are extrapolated to the position of dummy particle \(b^{\rm g}\) as

$$\begin{aligned} \acute{\varvec{\sigma }}_{b^{\rm g}}=\frac{\sum _{c^r\in \Lambda _{b^{\rm g}}^{\rm r}}\frac{m_{c^{\rm r}}}{\rho _{c^{\rm r}}}{\varvec{\sigma }_{c^{\rm r}}}W_{c^{\rm r}b^{\rm g}}}{\sum _{c^{\rm r}\in \Lambda _{b^{\rm g}}^{\rm r}}\frac{m_{c^{\rm r}}}{\rho _{c^{\rm r}}} W_{c^{\rm r}b^{\rm g}}} \end{aligned}$$
(25)

where \(\Lambda _{b^{\rm g}}^r\) is the sub-support domain of particle \(b^{\rm g}\) containing all neighboring rock particles and \(\Lambda _{b^{\rm g}}=\Lambda _{b^{\rm g}}^{\rm r}\cup \Lambda _{b^{\rm g}}^{\rm g}\).

Fig. 4
figure 4

Rock particle interact with gas particle in the interface using kernel interpolation

Full size image

Then, the interfacial stress tensor, \(\tilde{{\sigma }}_{b^{\rm g}}^{\alpha \beta }\) is estimated as

$$\begin{aligned} \tilde{{\sigma }}_{b^{\rm g}}^{\alpha \beta }&= 2{\sigma }_{b^{\rm g}}^{\alpha \beta }-\acute{\sigma }_{b^{\rm g}}^{\alpha \beta } \,\,\text{ if }\,\,\,\alpha =\beta \end{aligned}$$
(26)
$$\begin{aligned} \tilde{\sigma }_{b^g}^{\alpha \beta }&= \acute{\sigma }_{b^g}^{\alpha \beta }\,\,\text{ if }\,\,\,\alpha \ne \beta \end{aligned}$$
(27)

where \({\sigma }_{b^{\rm g}}^{\alpha \beta }\) is the estimated stress tensor of gas particle \(b_{\rm g}\) at time \(t\) (Eq. 8). Now, interfacial stress, \(\tilde{{\sigma }}_{b^{\rm g}}^{\alpha \beta }\) is incorporated into momentum equation of \(a^{\rm r}\) as follows:

$$\begin{aligned} \frac{D v^\alpha _{a^{\rm r}}}{Dt}&\, =\sum _{b^{\rm r}\in \Lambda ^{\rm r}_{a^{\rm r}}}m_{b^{\rm r}}\left( \frac{{\sigma }^{\alpha \beta }_{a^{\rm r}}}{\rho _{a^{\rm r}}^{2}}+\frac{{\sigma }^{\alpha \beta }_{b^{\rm r}}}{\rho _{b^{\rm r}}^2} -\Pi _{a^{\rm r}b^r}\delta ^{\alpha \beta }+( {R}^{\alpha \beta }_{\epsilon _{a^{\rm r}}}+{R}^{\alpha \beta }_{\epsilon _{b^{\rm r}}})f_{a^{\rm r}b^{\rm r}}^{n}\right) \frac{\partial W_{a^rb^{\rm r}}}{\partial x^{\beta }_{a^{\rm r}}}\nonumber \\&\quad +\sum _{b^{\rm g}\in \Lambda ^{\rm g}_{a^{\rm r}}}m_{b^{\rm g}}\left( \frac{{\sigma }^{\alpha \beta }_{a^{\rm r}}}{\rho _{a^{\rm r}}^{2}}+\frac{{\tilde{\sigma }}^{\alpha \beta }_{b^{\rm g}}}{\rho _{b^{\rm g}}^2} -\Pi _{a^{\rm r}b^{\rm g}}\delta ^{\alpha \beta }+( {R}^{\alpha \beta }_{\epsilon _{a^{\rm r}}}+\tilde{R}^{\alpha \beta }_{\epsilon _{b^{\rm g}}})f_{a^{\rm r}b^{\rm g}}^{n}\right) \frac{\partial W_{a^{\rm r}b^{\rm g}}}{\partial x^{\beta }_{a^{\rm r}}} \end{aligned}$$
(28)

where \({R}^{\alpha \beta }\) denotes the artificial stress tensor with correction parameter \(\epsilon\) (Gray et al. 2001); \(n\) is the exponent dependent on the smoothing kernel; \(f_{ab}\) is defined as

$$\begin{aligned} f_{ab}=\frac{W_{ab}}{W(\Delta d,h)} \end{aligned}$$
(29)

where \(\Delta d\) is the initial particle spacing. The above procedure transmits explosive-induced pressure into the surrounding rock medium by maintaining the traction continuity condition in the interface. It is to be mentioned that simultaneous integration of the governing equations for rock and gas particle is required to be performed in a same time step. This procedure is not enough for velocity continuity at the interface as reaction occurs between detonation-induced high pressure gas and surrounding brittle rock material, that leads to unphysical particle penetration in the interfacial damaged zone. To avoid this situation, XSPH approximation developed by Monaghan (1992) has been applied in the framework that ensure velocity continuity as well as forbid unphysical particle penetration.

3.4 Time Integration

To integrate SPH approximation of the governing equations in the form of ordinary differential equations, standard integration techniques such as the second-order Leapfrog (LF), predictor–corrector (PC) and Runge–Kutta (RK) schemes can be employed to calculate the field variables for each particle. The LF scheme offers a simplified algorithm with low memory requirements and appears to be well suited for large-scale simulations.

The stability of the above LF integration scheme is governed by the Courant–Friedrichs–Lewy (CFL) condition. This condition requires the time step to be proportional to the spatial particle resolution, which in SPH is represented by the smallest smoothing length. In this work, time integration of the governing equations for gas particle and rock particle has been performed in a same time step. For this purpose, following condition is used to determine the time step:

$$\begin{aligned} \Delta t=\xi \min (\Delta t^{\rm g},\Delta t^{\rm r}) \end{aligned}$$
(30)

where \(\xi\) is the Courant number, taken to be 0.3,

$$\begin{aligned} \Delta t^{\rm g}=\min _{a^{\rm g}}\left( \frac{h_{a^{\rm g}}}{c_{a^{\rm g}}+h_{a^{\rm g}}\nabla \cdot \mathbf {v}_{a^{\rm g}}+1.2(\alpha _{\pi } c_{a^{\rm g}}+\beta _{\pi }h_{a^{\rm g}}\left| \nabla \cdot \mathbf {v}_{a^{\rm g}} \right| )}\right) \end{aligned}$$
(31)

and

$$\begin{aligned} \Delta t^{\rm r}=\min _{a^{\rm r}}\left( \frac{h_{a^{\rm r}}}{c_{a^{\rm r}}}\right) . \end{aligned}$$
(32)

4 Numerical Results and Discussions

Three numerical examples are presented below to show the efficacy of the proposed methodology. First two examples deal with the one- and two-dimensional detonation process of TNT explosive slab. The initial pressure of unreacted SPH explosive particle is assumed to be zero. The third example deals with dynamic failure mechanism of rock under blast-induced stress waves followed by high pressure gas expansion.

4.1 One-Dimensional Detonation

One-dimensional detonation process is a simple benchmark problem and often been simulated in the literature to verify a developed methodology. In this study, 0.1-m-long TNT charge is considered in the simulation with free surface at the detonating end so that detonation-induced gas can freely move outward. Initially, a total of 4000 SPH particles are regularly distributed along the TNT slab. The smoothing length is taken to be twice of the initial particle separation of 0.05 mm. After detonation, the planar detonation wave produces along the charge and according to the detonation velocity of TNT, it takes about 14.4 μs to reach at the other end of the charge.

Figures 5a–c represent density, pressure and velocity profiles along the charge length at time 3, 6 and 12  μs, respectively, after the detonation. Due to the free boundary condition at the detonating end, product gas disperses outward with decrement of density and pressure. The solid lines represent theoretical solution derived by Dykema et al. (2002). It can be seen that SPH results of density, pressure and velocity profiles are in good agreement with those obtained from the theoretical solution. The distribution of burn fraction during detonation process is shown in Fig. 5d. The values of burn fraction between 0 and 1 represent the presence of the corresponding particles into the reaction zone. Since the length of the reaction zone is four times of the initial spacing, at least five particles belong to the reaction zone at a given time.

Fig. 5
figure 5

Density, pressure, velocity and burn fraction distribution at 2, 6 and 10 μs, respectively, of the detonation wave along the TNT explosive

Full size image

The product Hugoniot and the Rayleigh line in p–V space are depicted in Fig. 6. Theoretical Hugoniot curve and the Rayleigh line are depicted based on JWL equation of state. Results obtained from SPH are compared with these theoretical curves by considering no reaction zone and a reaction zone of length 0.0001 m. It can be observed that for no reaction zone, a strong shock produces at the upstream of the detonation wave and diverts from the theoretical solution as the detonation wave propagates forward. For reaction zone of 0.0001 m, detonation pressure converges to the tangential point of the Hugoniot curve and the Rayleigh line at the CJ state. These results strongly confirm the efficacy of the proposed method in simulating detonation process of explosive in one dimension. To further validate the results, sensitivity analysis is conducted by varying the length of reaction zone from 0 to 0.0001 m. Figure 7 represents the change of peak pressure for different reaction zone length in a 0.1-m-long TNT charge. It can be seen that the peak pressure in the detonation precess having reaction zone greater than \({\rm d}x\,= 2.5\times 10^{-5} {\rm m}\) converges near to the CJ pressure.

Fig. 6
figure 6

Hugoniot and Rayleigh line of product gas at the upstream of the shock

Full size image
Fig. 7
figure 7

Peak pressure variation with time for different reaction zone length where \({\rm d}x\,= 2.5\times 10^{-5} {\rm m}\)

Full size image

4.2 Two-Dimensional Detonation

In this example, a two-dimensional TNT slab is detonated as shown in Fig. 8. The aim is to determine the velocity and pressure variation of product gas behind the detonation front. The external boundaries of the explosive slab are considered as free surfaces to model the expansion of induced gas behind the detonation shock. The explosive slab has a width of 0.01 m and a length of 0.1 m. A total of 64,000 square particles of spacing 0.125 mm are used to model explosive region with an initial smoothing length of 0.15 mm. The detonation process consists of a reaction zone of width 0.6 mm preceded by a spherical shock and propagates into a quiescent explosive at a constant velocity of 6,930 m/s. In the model, four gauge points are marked to track the pressure and velocity profiles with time. Points 1, 2 and 3 are located at the middle of the explosive at a distance 20, 50 and 90 mm from the detonation point, respectively, and point 4 is at the boundary of the initial explosive surface. A similar model is developed in AUTODYN for comparison of results with those of the proposed method.

Fig. 8
figure 8

A schematic representation of a two-dimensional steady-state detonation in TNT explosive

Full size image

Figure 9a, b show the history of pressure and velocity of the product gas with time at gauge points, 1, 2, and 3, respectively, obtained from SPH method and AUTODYN. The peak pressure is attained to the C–J pressure of 21 GPa at gauge point 3 suggesting that it takes time to develop steady state in the detonation process of explosive. The similar phenomenon is observed in one-dimensional detonation as shown in Fig. 5b. However, peak pressure at the gauge point 4 is found to be 4.7 GPa (Fig. 10) in the presence of free surface of the explosive. Therefore, it can be observed that a non-uniform pressure profile occurs at the detonation front. SPH results agree well with those obtained from AUTODYN at four gauge points. Similar to the one-dimensional example, gas particles reach to a peak velocity of 1,800 m/s at gauge point 3 and afterward, it decreases gradually due to freely dispersion of the gas particles to the opposite direction of detonation wave.

Fig. 9
figure 9

Pressure and velocity profiles with time at three different gauge points, 1, 2 and 3, respectively, and their comparison with results of AUTODYN

Full size image
Fig. 10
figure 10

Pressure–time profile at surface gauge point 4

Full size image

Figure 11a–d show the pressure profile of all particles during the detonation process after 0.72, 4.27, 11.3 and 14.6 ms, respectively. The detonation wave, rarefaction wave and dispersion process of product gas can clearly be observed from those figures. It can be seen that pressure is generated to a maximum value along the centerline of the explosive. For the presence of free surface, pressure of the particles along the boundary is relatively lower. It means that in gas expansion process, pressure gradually decreases due to inward propagation of the rarefaction wave.

Fig. 11
figure 11

Pressure distribution in the TNT slab at four different time steps during detonation

Full size image

4.3 Explosion in Rock Medium

The objective of this example is to analyze rock failure mechanism and understand how the damaged and fractured zones develop under dynamic stress wave and latter, due to expansion of high pressure gas.

A two-dimensional rock medium of dimension 0.1 m \(\times\) 0.1 m is loaded with emulsion explosive at a center blast hole having a diameter of 0.01 m as shown in Fig. 12. The parameters of emulsion explosive for JWL equation is given in Table 1. Simulation is performed in 2D plain strain condition. The rock medium has density of 2,261 kg/m3, elastic modulus of 17.83 GPa, Poisson’s ratio of 0.271, compressive strength of 106 MPa and tensile strength of 5 MPa. However, it is well known that loading rate plays an important role in dynamic failure mechanism. The dynamic strength of rock varies with a cube-root dependency on the strain rate (Grady and Lipkin 1980). Therefore, dynamic fracture simulation under high strain rate requires correction in strength values so that material strength increases with increasing strain rate. For this example, a semi-log relation described by Zhao (2000) between uniaxial compressive strength and loading rate is implemented to correct compressive strength of the rock medium, whereas dynamic tensile strength modifies according to the Grady–Kipp damage model (Grady and Kipp 1980).

Fig. 12
figure 12

Schematic of rectangular rock medium containing centrally located explosive

Full size image

A total of 62,500 square particles with spacing 0.4 mm are used to discretize the rectangular domain with an initial smoothing length of 0.48 mm. The particles inside the blast hole represent emulsion explosive and the rest represents rock particles that surround the explosive. Free surface boundary conditions are assumed for the outside surfaces of the rock medium.

At time 1.280.5 and 1.28 μs after detonation, the pressure developed in explosive particles inside the blast hole is shown in Fig. 13. It can be seen that the maximum compressional pressure can be as high as 5.25 GPa around the blast hole. This compressional stress causes an intensive outward propagating shock wave from the blast hole towards the free surface. Figure 14 illustrates the development of major and minor principal stresses, and the corresponding damage growth in the rock medium after 4.14, 17.7, 26.9 and 97.9 μs, respectively. The high stress wave near blast hole (Fig. 14a, b) causes an initial damage zone around the blast hole (Fig. 14c). A high crack density region is developed around the blast hole due to several microcrack nucleations. After 17.7 μs of initiation, several intersecting radial crack zones have formed extending damage zone in the middle of the rock medium (Fig. 14f). At the same time, stress wave reflects from free surfaces (Fig. 14d, e). It can be seen that at time 26.9 μs, the reflected stress wave causes a thin damage zone along the free surfaces, commonly termed as ‘spalling’ (Fig. 14i). At this stage, radial cracks are extended towards the spalling zone. The extent of spalling zone appears after the formation of radial cracks and depends on the dynamic tensile strength of the rock and the distance of free surface from the blast hole. It may be possible not to have such spalling zone in case of large-dimensional rock medium or rock having much higher tensile strength. At time 97.9 μs, further extension of cracks can be observed in Fig. 14l. It is worth mentioning that major cracks are developed in the radial directions, however, spalling zone is parallel to the free surface. The amplitude of stress waves (or the reflected stress wave) gradually decreases with time and after a while, they are no longer capable of creating further cracks in rock. The subsequent fragmentation in the rock medium occurs due to expansion and penetration of high pressure product gas into void space generated by radial cracks. This is evident from Fig. 15 that gas penetrates into the radial cracks near the blast hole and causes further displacement of rock fragments.

Fig. 13
figure 13

Pressure distribution of explosive particle before impact on explosive at different time

Full size image
Fig. 14
figure 14

Distribution of major principal stress (left), minor principal stress (middle), damage (right) in the rock medium at four different time step. a Time = 4.14 μs. b Time = 4.14 μs. c Time = 4.14 μs. d Time = 17.7 μs. e Time = 17.7 μs. f Time = 17.7 μs. g Time = 26.9 μs. h Time = 26.9 μs. i Time = 26.9 μs. j Time = 97.9 μs. k Time = 97.9 μs. l Time = 97.9 μs

Full size image
Fig. 15
figure 15

Failure pattern and development of damage in the rock at different time scale. a Time = 124.9 μs. b Time = 167.3 μs. c Time = 213.4 μs. d Time = 340.06 μs

Full size image

A similar model is developed in AUTODYN to validate the results of the proposed method in term of pressure distribution. Figure 16 depicts the distribution of peak pressure from blast hole wall to free surface (along line BA). It is found that results predicted by SPH method agree well with those determined from AUTODYN. Three gauge points (Fig. 12) are also marked inside the rock medium to analyze stresses during failure process. The distance of the gauge points, 1, 2 and 3 are 0.01, 0.024 and 0.04 m, respectively, from the detonation point. The time history of stress components, \(\sigma _{xx}\) and \(\sigma _{yy}\) at those gauge points are shown in the Fig. 17a and b, respectively. These two figures clearly show the attenuation of peak stresses at three gauge points. The radial stress \(\sigma _{xx}\) at gauge point 1 always remains compressive due to proximity of the blast hole with a peak value of 2 GPa (Fig. 17a). From Fig. 17b, it can be seen that the tangential stress \(\sigma _{yy}\) at this point is initially compressive in nature and then it changes to tensile attending to a maximum tensile strength about 100 MPa. At the same point, the tangential stress again becomes compressive after 0.037 ms due to the fact that product gases penetrate into the radial crack. The radial stress, \(\sigma _{xx}\) at the gauge points 2 and 3 reaches to a maximum compressive value of 150 MPa and 121 MPa, respectively. The reflected stress waves return from the free surface after 0.025 and 0.017 ms at these two locations, respectively (Fig. 17a).

Fig. 16
figure 16

Comparison between peak pressure obtained in SPH and AUTODYN from the blast hole wall to free surface along the line BA

Full size image
Fig. 17
figure 17

Profile of stress components. a \(\sigma _{xx}\). b \(\sigma _{yy}\) with time for three different gauge points

Full size image

5 Conclusion

This paper has mainly focused on the numerical simulation of detonation of explosive and interaction of product gas with the surrounding brittle rock material within SPH framework. A pressure-based program burn algorithm is applied in the detonation process of explosive to modify the equation of state of the burning particle in the reaction zone. Numerical examples of detonation process in one- and two-dimensional problems have shown the promises to predict detonation wave as well as dispersion process of product gas. It has been demonstrated that von Neumann spike, which sometimes causes instability in the numerical simulation can be taken care of by considering appropriate reaction zone length.

Explosion in rock medium emphasizes the role of stress wave loading on crack initiation and propagation if explosive is detonated in a blast hole. The final failure pattern and the extent of damage in the rock medium depend on the detonation-induced stress wave and the subsequent expansion, and penetration of gas in the developed crack zones. The numerical example presented in this paper shows the potentiality to estimate blast-induced crack initiation and propagation. The failure process of the rock medium can be separated into three failure zone namely, high crack density zone around the blast hole, several intersecting radial cracks zone and spalling cracks zone parallel to free surface. The results show that intensive compressive stress in the blast hole causes high crack density zone in the immediate vicinity of the blast hole. The major principal stress (tensile) is responsible to form intersecting radial crack zone. The reflected stress wave from the free surface causes spalling zone. It should be noted that major cracks remain in the radial directions even if spalling zone is parallel to the free surface.

Finally, the proposed methodology have shown the promises for analyzing complex phenomenon of dynamic failure and fragmentation mechanism under blast-induced stress wave propagation and high pressure gas expansion, and penetration into the crack spaces. It is worth mentioning that SPH framework is computationally expensive. To obtain final failure pattern, time of execution is taken about 6 hours for parallel computation on shared memory OpenMP interface in PowerEdge R720, a server with two E5-2650 processors (2.00 GHz) and 16 GB memory. However, issues relating to the applicability and performance of the procedure to even more complicated classes of problems involving different types of discontinuity planes, multiple blast holes with time delay, non-ideal detonation process of explosive, etc., are yet to be investigated. This will be the subject of additional research work in near future.