Dynamical Vortex Production and Quantum Turbulence in Perturbed Bose–Einstein Condensates

Abstract

Dynamical vortex production and quantum turbulence emerging in periodic perturbed quasi-two-dimensional (q2D) Bose–Einstein condensates are reported by considering two distinct time-dependent approaches. In both cases, dynamical simulations were performed by solving the corresponding 2D mean-field Gross-Pitaevskii formalism. (1) In the first model, a binary mass-imbalanced system is slightly perturbed by a stirring time-dependent elliptic external potential. (2) In the second model, for single dipolar species confined in q2D geometry, a circularly moving external Gaussian-shaped obstacle is applied in the condensate, at a fixed radial position and constant rotational speed, enough for the production of vortex–antivortex pairs. Within the first case, vortex patterns are crystalized after enough longer period, whereas in the second case, the vortex pairs remains interacting dynamically inside the fluid. In both cases, the characteristic Kolmogorov spectral scaling law for turbulence can be observed at some short time interval.

1 Introduction

Within the going on experimental and theoretical Bose–Einstein condensates (BECs) studies, in more recent years a lot of attention has been done on the possibilities to consider atomic BECs to get a more deep understanding on the classical well-known phenomenon known as turbulence [1], in view of some similarities in the dynamics of vortices being generated in BECs [2,3,4,5]. Particularly, the interest was enhanced by the reported experiments in Ref. [6] on the observation of quantum turbulent regime in BEC. This interest also follows previous long-time investigations related to the Helium superfluidity phase transition, with the corresponding possible similarities with the Bose–Einstein condensate phase transition. In order to trace the related bibliography, several works and reviews are already available; among the reviews, we can select Refs [7,8,9,10] as appropriate.

The present report is contemplating two approaches in the dynamical vortex production in BECs, which can lead to the so-called quantum turbulence, by examining the corresponding incompressible part of the kinetic energy spectrum. Both approaches to produce vorticity in the system rely on the solution of extended Gross-Pitaevskii formalisms, in which external periodic time-dependent interactions are included. In the first approach, the dynamical production of stable vortices and quantum turbulence is verified by assuming two component mass-imbalanced atomic condensates confined by a quasi-two-dimensional (quasi-2D) pancake-like trap potential slightly perturbed elliptically by a time-dependent periodic potential, with periodicity given by a parameter $\nu _E$ [11], which induces rotation in the confined system with final vortex patterns being crystalized. This approach follows closely a previous study [12] in which a single condensate was considered; extended to binary system as to verify possible effects due to mass-imbalanced atomic mixtures. In the second approach we consider a condensed dipolar system, also confined in quasi-2D geometry, under the effect of an external circularly moving Gaussian-type penetrable obstacle, which is simulating a blue-detuned laser stirring mechanism. In this case, the first task is to verify the critical frequencies of the obstacle in order to start producing vortex pairs. By considering dipolar atoms, in a quasi-2D pancake-like confined condensate, another related purpose is to explore the possibilities to manipulate the strength of the atom-atom interactions, from repulsive to attractive, via magnetic applied field, by considering the dipole orientations. As to manipulate the two-body interaction, this approach came as an additional useful mechanism that can be used for dipolar systems, in addition to the already well-known procedure via Feshbach resonance techniques. In both cases, the time evolution of the incompressible kinetic energy contributions is studied, within a semi-classical analysis, as to distinguish turbulent from non-turbulent flows, guided by the corresponding expected classical behavior. Following these analyses, transient turbulent regimes with the characteristic $k^{-5/3}$ Kolmogorov behavior are identified in both model approaches, with the main difference being related to the transient time intervals at which turbulence behavior can be identified.

2 Vortex Patterns Induced by Periodic Elliptical Perturbation

The vortex nucleation dynamics with corresponding characterization of turbulent flows ws recently studied in Ref. [11], following previously related studies [12], by assuming a coupled mass-imbalanced BEC confined in quasi-2D geometry +perturbed elliptically. For that, two easily accessible and controllable systems in cold-atom experiments were assumed, by considering mixtures of $^{85}$Rb-$^{133}$Cs and $^{85}$Rb-$^{87}$Rb, both in the miscible regime (implying that the two species atom-atom scattering lengths $a_{ij}$, assumed being repulsive, are such that $a_{12}^2<|a_{11}| |a_{22}|$).

Next, we follow the essential dimensionless formalism provided in Ref. [11], in which the units are given in terms of transversal trap frequency of the first species, $\omega _\rho \equiv \omega _{1,\perp }$, with energies being in units of $\hbar \omega _\rho$, time in units of $1/\omega _\rho$, and length units given by $\ell _\rho = 1\mu$m$\approx 1.89\times 10^4 a_0$. Within the quasi-2D pancake-like system, the 2D harmonic trap $V_0(x,y)\equiv (x^2+y^2)/2$, is slightly perturbed elliptically by the time-dependent stirring interaction: $V_s(x,y,t)=(\epsilon /{2})\big [(x^2-y^2) \cos (2\nu _E t)-2xy\sin (2\nu _E t)\big ]$, where $\nu _E$ is the laser stirring oscillating parameter, with $\epsilon$ the corresponding strength. As one may find convenient, the total perturbed trap potential can be written in the usual polar coordinates, as

$$\begin{aligned} V_{\epsilon }(\rho ,\theta ,t;\nu _E)= & {} \frac{\rho ^2}{2}\left[ 1+\epsilon \;\cos \left( 2\theta +2\nu _E t\right) \right] , \end{aligned}$$

(1)

where $x=\rho \cos \theta$, $y=\rho \sin \theta$ and $\rho ^2=x^2+y^2$. As detailed in [11], the same formal expression for the confinement can be applied for both species 1 and 2, by first adjusting their confining trap frequencies with the corresponding masses, such that ${m_2\omega _{2,\perp }^2}={m_1\omega _{1,\perp }^2}$. Therefore, conveniently, the mass relations appear in the coupled formalism only in the kinetic energy term and the non-linear interactions. The corresponding 2D coupled Gross-Pitaevskii formalism can be expressed by

$$\begin{aligned} \textrm{i}\frac{\partial \psi _{i} }{\partial t }=\Big [\frac{-m_{1}}{2m_{i}}{\nabla ^2 }+V_{\epsilon }(\rho ,\theta ,t;\nu _E)+\sum _{j}g_{ij}|\psi _{j} |^{2} \Big ]\psi _{i}, \end{aligned}$$

(2)

where $-\textrm{i}\nabla$ is the 2D momentum operator, with the two-component wave functions, $\psi _{i}\equiv \psi _{i}(\rho ,\theta ,t)$ being normalized to one, such that $\int d^2\rho \,|\psi _{i}|^{2}=1$. The parameters $g_{ij}$ are the 2D reduction of the corresponding three-dimensional parameters related to the intra- and inter-species two-body scattering lengths (respectively $a_{ii}$ and $a_{12}$), given by $g_{ij}\equiv \sqrt{2\pi \lambda } \frac{m_1 a_{ij} N_j}{\mu _{ij}\ell _\rho },$ where $\mu _{ij} \equiv m_im_j/(m_i+m_j)$ is the reduced mass, $\lambda \gg 1$ is the shape-aspect parameter of the pancake-like trap (assumed identical for both species), with $N_j$ being the number of atoms of the species j.

The perturbation is applied in the coupled condensate, as given in (1), by considering a very small strength $\epsilon \approx 0.025$, with oscillating parameter $\nu _E=1.25$, analogously as in a previous [12] with single component condensate, such that the original trap remains approximately with spherical format, besides the small time-dependent elliptical oscillation.

In the dynamics, the system goes through different stages of instability, starting with shape deformation of the cloud, followed by symmetry breaking involving vortex nucleation, with a final stage approaching rotating frame equilibrium, in which crystallization of vortex patterns are verified. In order to characterize vortex nucleation in the coupled BEC system, a full analysis of vortex formation is performed in Ref. [11], where the time evolutions of the relevant dynamical observables are presented for each one of the two components of the mixture, including the total and kinetic energies, the current densities, and torques. The kinetic energy injected is primarily compressible, when the system is in the shape deformation regime, switching to incompressible energy when vortex nucleation begins. The effective time-dependent rotational frequency of each component i, $\Omega _i(t)$, is estimated from the classical rotational relation, obtained from the expected values of the angular momenta and moment of inertia operators, as

$$\begin{aligned} \Omega _i(t)\equiv & {} \frac{\langle L_z(t)\rangle _i }{\langle I(t)\rangle _i } =\frac{\int d^2\rho \;\psi _i^\star \left( {-\mathrm i} \frac{\partial }{\partial \theta }\right) \psi _i}{\int d^2\rho |\psi _i|^2\;\rho ^2}. \end{aligned}$$

(3)

As shown in [11], by comparing two different mass-imbalanced mixtures, larger mass-imbalanced systems provide larger rotational frequency than lower mass-imbalanced mixtures, a result being reflected in the visible number of vortices shown in the final vortex patterns.

Fig. 1

(Color online) The main panel shows the time evolutions of the rotational frequencies $\Omega _1(t)$, for $^{85}$Rb (solid-red line); $\Omega _2(t)$, for $^{133}$Cs (dot-dashed-green line); with the corresponding averaging, $\Omega _{av}(t)\equiv [\Omega _1(t)+\Omega _2(t)]/2$ (dashed-blue line). The vertical lines are approximately separating three time regimes: (I) shape deformation; (II) turbulent regime, with starting vortex nucleations; and (III) when vortex patterns are settled. In the inset of main panel, we also show time snap-shots for the two coupled densities, $|\psi _1|^2$ [from (a$_1$) to (d$_1$)] and $|\psi _2|^2$ [from (a$_2$) to (d$_2$)], corresponding to the three stages in the time evolution. The intermediate turbulent region is represented by the panels (b$_{1,2}$) and (c$_{1,2}$), respectively for $t=3600$ and 4000. The stirring parameters are $\epsilon =0.025$ with $\nu _E=1.25$. In a separate box, in the right-hand-side, for a comparison with the final patterns (d$_i$), we have independent respective results (a$_{i,0}$) obtained from direct ground-state calculations of the GP equation, with the stirring interaction replaced by $\Omega _0 L_z = -\textrm{i}\Omega _0 \frac{\partial }{\partial \theta }$, assuming the same $\Omega _0=0.63$ for both species. This figure is combining partial results presented in Ref. [11]. All quantities are dimensionless, considering the units as defined in the text

In Fig. 1, the main results for the dynamics are shown by considering the larger mass-imbalanced mixture studied in Ref. [11], being $^{85}$Rb and $^{133}$Cs. In the principal panel, we present the long-time evolution results obtained for the time-dependent rotation $\Omega _i(t)$, together with some representative snap-shot panels of the densities in the inset. The densities in the inset are contemplating the three different regimes of the evolution, with (a$_i$) being for the shape deformation stage, (b$_i$) and (c$_i$) for the turbulent regime, with (d$_i$) for the final stage, with vortex-pattern crystallization. For comparison of the final vortex patterns obtained with the stirring perturbation, in a separate box of Fig. 1 we are also presenting results for the densities of the two species, obtained by direct ground-state calculations of the GP equation, when the stirring interaction is replaced by $\Omega _0 L_z = -\textrm{i}\Omega _0 \frac{\partial }{\partial \theta }$. In this case, for simplicity, we are assuming the same frequency $\Omega _0$ for both species, which is consistent with an averaging of the asymptotic limiting obtained in $\Omega _i(t)$.

Fig. 2

(Color online) In panel (a), for each component of the mixture, $^{85}$Rb ($i=$1, solid-blue lines) and $^{133}$Cs ($i=$2, dashed-red lines), the time evolutions are presented (in the laboratory frame) for the compressible and incompressible parts of the kinetic energies, respectively, $E^{c}_i$ (indicated with bullets) and $E^{nc}_i$ (indicated with triangles). In panels (b $_1$) and (b $_2$) we show, respectively, the incompressible kinetic energy spectra, $E^{nc}\equiv E^{nc}(k,t)$, for the $^{85}$Rb-$^{133}$Cs mixture, obtained by averaging over 50 samples in the turbulent time-interval (II) indicated in Fig. 1, which approximately agree with the classical Kolmogorov $k^{-5/3}$ power-law behavior in the shown interval $0.1<k\xi <1$ (red-dashed lines), being modified to the $k^{-3}$ in the ultraviolet region. In the stirring perturbation, the parameters are $\epsilon =0.025$ with $\nu _E=1.25$. This figure is combining partial results reported in Ref. [11]. All quantities are dimensionless, considering the units as defined in the text

By verifying possible characterization of turbulent behavior in the dynamics of the coupled condensate, the results obtained for the incompressible kinetic energy spectra of the two species were investigated, with the corresponding main results resumed in the three panels of Fig. 2. When computing the incompressible kinetic energy, as a measure for the vortex energy, a care was taken to subtract the uninteresting rigid body velocity field associated with the rotation. The time evolutions for the compressible (c) and incompressible (nc) parts of the kinetic energies are shown in the main panel, in which the starting time of the turbulent regime (near $t\approx 3000$) can be identified by the splitting between the two parts of the kinetic energies for both species. See also by the vertical dashed line between regions I and II, in the main panel of Fig. 1. As noticed by the results shown in the panels (b$_1$) and (b$_2$) of Fig. 2, in this regime of the time evolution, the incompressible kinetic energy presents evidence of the Kolmogorov $k^{-5/3}$ scaling, for values of the $k\xi$ momenta (where $\xi$ is the healing length corresponding to the respective species i) smaller than 1, which is modified to a $k^{-3}$ power-law behavior in the ultraviolet regime determined by the vortex core structure [13]. While the Kolmogorov scale range appears somewhat limited, the spectrum is consistent with energy transport to large scales as disordered vortices enter the system and begin to organize. The vortices in this stage are close to the boundary of the condensate, and the Kolmogorov power-law scaling vanishes once stable vortex configurations develop. As comparing two kind of mass-imbalanced systems in [11], for $^{133}$Cs$^{85}$Rb and $^{85}$Rb$^{87}$Rb, it was noticeable that larger mass-imbalance system shows the approximate $k^{-5/3}$ power-law behavior for a longer time window. Also, the dynamical production of stable patterns of vortices is verified to be a much faster process for larger mass-imbalanced systems than for smaller mass-imbalanced ones.

In the following section, instead of a small time-dependent perturbation, another approach is reported to generate vorticity in a dipolar BEC system, by considering direct external obstacle moving periodically inside a single condensed system.

3 Vortex–Antivortex Dynamical Production in Dipolar BEC Under Circularly Moving Obstacle

In this section, within another approach which is being considered experimentally to produce vorticity in a condensate [14], an external penetrable Gaussian-type moving obstacle is considered to generate vortex–antivortex pairs, following a recent study detailed in [15], in which Bose–Einstein condensed dipolar atoms were considered. Applied to a dipolar condensate confined by a quasi-2D pancake-like harmonic trap, two variants of a circularly moving Gaussian-shaped penetrable obstacle were assumed in [15], following previous related investigations with linearly-moving obstacle [16, 17]. In the first variant, the obstacle moves with constant rotational frequency at a fixed given radius inside the condensed fluid, with its amplitude $A_0$ assumed to be close to 90% of the stationary chemical potential $\mu$. For the second variant, it was verified the effect of an additional dynamics provided by a vibrating amplitude with frequency larger than the stirring rotational one. By having in mind that the most significant results can be appreciated through the simpler model, here we discuss the case in which the shape parameters (amplitude and width) of the circularly moving obstacle remain constant in the condensate. Within this approach, vortex–antivortex pairs are generated by the obstacle, once the rotational speed is larger than a critical threshold one. Therefore, instead of the stirring time-dependent perturbation, here we assume a penetrable Gaussian-shaped obstacle, moving circularly at a fixed radius $r_0$ and rotation speed $\nu$, having amplitude $A_0$ and width $\sigma$,

$$\begin{aligned} V_{G}(x,y,t)\equiv & {} A_0 \exp \left( -\frac{\left[ x-x_0(t)\right] ^2+ \left[ y-y_0(t)\right] ^2}{2\sigma ^2}\right) , \end{aligned}$$

(4)

where $x_0(t)\equiv r_0 \cos (\nu \,t)$ and $y_0(t) \equiv r_0 \sin (\nu \,t)$ are the instant positions of the obstacle in the 2D plane, with $\sigma$ being the corresponding standard radial deviation (close to half-width of the distribution).

The study of vorticity in BEC was extended from non-dipolar to dipolar atomic systems motivated by several previous studies followed by different experimental realizations of dipolar BECs in recent years [18,19,20,21,22,23,24], in which the atoms have large magnetic dipole moments, as discussed in the topical review [9]. The interest, in this case, relies on the fact that dipolar condensates can combine properties of superfluidity (having quantized circulation vortices) with ferrofluidity, in which the long-range dipolar interactions can induce new effects due to the interplay of magnetism with vorticity. In response to the magnetic field, basic properties of vortex and vortex patterns are expected to be affected, leading to shape deformations and/or new patterns. Dipolar condensates are also opening new possibilities to manipulate the atom-atom interactions, not only through Feshbach resonance mechanism, but also by controlling of magnetic moment orientations between atoms in relation to the trap geometry. Along the present communication, before submitting the system to a circularly moving obstacle, we assume net repulsive contact plus dipolar nonlinear interactions, in order to keep the system in stable configuration. By following [25], for the formalism reduction from three- to 2D, as also detailed in [15, 26,27,28], with the dipolar term in the Fourier-transformed momentum space, the effective equation for the dipolar BEC is given by

$$\begin{aligned} \textrm{i}\frac{\partial \psi }{\partial t}= & {} \left\{ -\frac{1}{2}\nabla _{\rho }^2+\frac{\rho ^2}{2}+ V_{G} +g_{s}|\psi |^2 +g_{dd}\int \frac{d^2k_{\rho }}{4\pi ^2} e^{i \textbf{k}_{\rho }.\tilde{\rho }}\tilde{n}(\textbf{k}_{\rho }) \widetilde{{V}}^{(d)}(\mathbf{k_\rho }) \right\} \psi , \end{aligned}$$

(5)

which corresponds to the single-condensate formalism version of (2) for dipolar system, with $\psi \equiv \psi (\varvec{\rho }, t)$ normalized to one, $g_s\equiv \sqrt{8\pi \lambda } {a_s N}/{\ell _\rho }$ (N the number of atoms) and $V_G\equiv V_{G}(\varvec{\rho },t)$ given by (4). In the above 2D Eq. (5), $\tilde{n}(\textbf{k}_{\rho })$ and $\widetilde{{V}}^{(d)}(\mathbf{k_\rho })$ are the Fourier transforms of the 2D density and dipolar potential, respectively. As shown in Ref [15], as well as by following Refs. [25, 29], the dipole-dipole interaction in momentum space, after an averaging of the polarization rotating field in the $(k_x,k_y)$ plane, can be expressed by

$$\begin{aligned} {\widetilde{V}}^{(d)}(\mathbf{k_\rho }) = \frac{3\cos ^2\alpha -1}{2} \left[ 2-3\sqrt{\frac{\pi }{2\lambda }}k_\rho \exp {\left( \frac{k_{\rho }^{2}}{2\lambda }\right) } \textrm{erfc}\left( \frac{k_{\rho }}{\sqrt{2\lambda }}\right) \right] \end{aligned}$$

(6)

where $\textrm{erfc}(x)$ is the complementary error function of x, with $\alpha$ defining the inclination of the dipole moments relative to the perpendicular $z-$direction. Therefore, as show above, the strength of the atom-atom long-ranged dipolar interaction is guided by the factor $g_{dd}\left( 3\cos ^2\alpha -1\right) /2$ (which goes from $g_{dd}$ for $\alpha =0$ to $-\frac{g_{dd}}{2}$ for $\alpha =90^\circ$, being cancelled out for $\alpha \approx 54.7^\circ$. )

In the dynamical vortex production simulation, studied in [15], the circularly moving obstacle inside the condensed fluid was assumed with frequency $\nu$, at a given fixed radius $r_0$ (which, obviously is restricted to the size of the condensate), such that the obstacle velocity is $v=\nu r_0$. Given that, by first observing that the corresponding critical velocity $v_c=\nu _c r_0$ to produce vortex–antivortex pairs remains close to a constant value when varying $\nu$ and $r_0$, one can verify that $r_0$ cannot be near the maximum unperturbed trapped density ($r_0=0$), where vortex production needs unrealistic too-large values of $\nu$, as well as not close to the low-density region of the condensate. By assuming an intermediate value, $r_0=3.5\ell _\rho$, the critical rotation was verified being near $\nu _c=0.6\omega _\rho$, when considering the Gaussian obstacle parameters $A_0=36\hbar \omega _\rho$ and $\sigma =1.5\ell _\rho$, for the nonlinear short-ranged contact interactions (SCI) fixed by the scattering length $a_s=50a_0$, with the corresponding dipole-dipole interactions (DDI) fixed by $a_{dd}=66a_0$, with $\alpha =0$. The choice of $a_s$ and $a_{dd}$ parameters were directly associated to the dipolar erbium isotope $^{168}Er$. Therefore, the observed dynamical results reflect effects due to both nonlinear atom-atom contact and dipolar interactions, which can be distinguished by switching off one of them. As known, the SCI can be modified by using Feshbach resonance techniques to increase or decrease $a_s$. Similarly, the DDI can be modified by manipulating the polarization angle $\alpha$, being reduced to zero for $3\cos ^2\alpha =1$ ($\alpha =\alpha _M\approx 54.7^\circ$, known as the magic angle), as well as changing the DDI to be attractive for $54.7^\circ<\alpha < 90^\circ$.

As a complement to the dynamical production of vortex–antivortex pairs investigated in Ref. [15], as well as to appreciate the effect of the long-ranged DDIs in contrast to some well-known effects verified with pure the short-ranged contact interactions, we show in Fig. 3 a few set of sample results obtained in our simulations, related to the vortex production and their dynamics, by considering pure-contact (when DDI=0) or pure-dipolar (when SCI=0) effects. For this comparison, taken the Gaussian obstacle with identical parameters in both cases, we need to adjust the parameters such that in both the cases we have similar condensates with about the same root-mean-square (rms) radius and chemical potentials.

By taking as reference the dipolar condensate with $^{168}Er$, the parameters and physical quantities considered in Fig. 3 are provided in the following Table 1.

Table 1 Parameters and physical quantities assumed in the simulations shown in Fig. 3. The Gaussian obstacle, which is circularly moving with frequency $\nu =0.8\omega _\rho$, at a fixed radial position $r_0=3.5\ell _\rho$ in the condensate, have identical parameters in all the panels, ($a_{j}$) and ($b_{j}$), represented in Fig. 3, being $A_0=36 \hbar \omega _\rho$ and $\sigma = 1.5 \ell _\rho$

Fig. 3

Comparative snap-shot results of densities $|\psi (x,y,t)|^2$ (units defined in the text) obtained in the dynamics of vortex–antivortex production, for the circularly rotating obstacle (large shadowing circle) at $r_0=3.5\ell _\rho$, with frequency $\nu =0.8\omega _\rho$. As indicated, the panels (a$_j$) and (b$_j$), in the left two columns, are from $\nu t=0\; (j=1)$ upto $1.5\pi \; (j=4)$; and, in the right two columns, from $\nu t=2\pi \;(j=5)$ upto $3.5\pi \;(j=8)$. In the first and third columns we have pure dipolar interactions (SCI=0), with $a_{dd}=66a_0$ ($\alpha =0$) and $a_s=0$. In the second and forth columns are for pure contact interactions (DDI=0), with $\alpha =54.7^\circ$ and $a_s=177a_0$. Density levels vary from zero (black) to maximum (yellow), with the small black circles being the vortex and antivortex (produced in pairs), which are moving inside the fluid

The results for zero nonlinear contact interactions (SCI=0) are represented in the eight panels ($a_{j}$) of Fig. 3, implying results for pure-dipolar long-ranged interacting systems. They are in the first and third columns of Fig. 3, with $\nu t$ varying anti-clockwise from 0 to 3.5$\pi$, as indicated. For the case of DDI=0, we simply adjust the orientation angle such that $\alpha =54.7^\circ$, increasing the repulsive contact interaction using $a_s=177a_0$, such that the chemical potential and rms values remain fixed. Similarly, the results are shown in the eight panels (b$_{j}$), in the second and forth columns of Fig. 3, with the same variation of $\nu t$. Therefore, the associated animated results can be visualize comparatively in this figure, such that one can separate the short-ranged and long-ranged net effect interactions in the production and dynamical behavior of vortex–antivortex pairs inside the fluid. In this dynamics, differently from the case that the obstacle moves linearly passing through the center [17], the vortex and antivortex of a single pair emerge at slightly different times, which can be understood by the fact that the fluid in one side of the moving obstacle is denser than the opposite side. For an anti-clockwise circular movement of the obstacle, a clockwise vortex emerges (at the right side of the obstacle) at a slightly shorter time than the corresponding anti-clockwise anti-vortex. A related interesting aspect, observed in the dynamics of vortex–antivortex in the fluid, is their tendency to persist longer time moving inside the fluid without being dissipate or annihilate, in which the non-annihilation can be related to the fact that both vortex and anti-vortex of a given pair emerge with slightly different kinetic energy in a superfluid with almost no viscosity.

It is being noticeable in this comparison of pure-DDI condensate with pure-SCI condensate that the long-range repulsive dipolar interactions are affecting not only the subsequent dynamics of the vortex pairs interacting inside the fluid, but also the initial emission of vortex pairs, indicating that the critical velocities in case of pure dipolar system are slightly lower than in the case of pure contact interactions. In principle, one could expect the initial vortex production relying mainly in the obstacle position and its shape. But apparently this is not the case, which can be attributed to the different fluid characteristics related to range interactions. On this regard, as discussed in Ref. [9], following cited related works, by comparing vortex-free solutions with DDI, using Thomas-Fermi approximation in the general 3D case, it was noted that, besides the fact that non-dipolar BECs have the same aspect ratio as given by the harmonic trap, for dipolar case the aspect ratio is modified. In view of these observations, a more detailed analysis is required by considering different increasing rotational velocities of the obstacle.

As verified in the dynamics represented by the snap-shots given in panels (b$_j$) of Fig. 3, the condensed cloud remains approximately uniformly distributed in case with pure SCI, without DDI, even after the started production of vortices. However, within a pure dipolar system (no SCI), shown in panels (a$_j$) of Fig. 3, one can observe not only the slightly increasing number of vortex pairs, but also the production of stripes and fluctuations in the fluid, which can be taken as clear signs of the long-range interactions between atoms. More clearly, the effect of long-ranged DDI as compared with the short-ranged SCI, can be appreciated in the second loop ($\nu t \ge 2\pi$) shown in Fig. 3. These results are also compatible with experimental observations [23], as well as in line with previous numerical calculations in [30, 31], performed for 2D pancake-like dipolar condensate where, for perpendicular polarized dipoles they observe, in case of a single vortex, that density ripples form about the vortex core for large trap ratios ($\lambda \sim 100$). This kind of density behavior can also be observed within our results when more vortices are emerging inside the fluid. In case of pure DDI, it is noticeable the occurrence of stripes and vortex ripples, which are clearly in contrast with the SCI case.

These different rich dynamics, observed by comparing the short-ranged with long-ranged atom-atom interactions in a condensate, as well as the subsequent interactions between vortices and antivortices inside the fluid, deserve more detailed analyses by simulating different conditions and obstacle velocities. In the present contribution, our study will be limited to the above discussion related to our direct results obtained from the solution of the GP formalism, and by the following analysis of possible quantum turbulence behavior.

Fig. 4

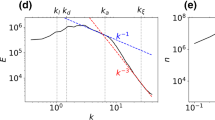
Incompressible kinetic energy spectrum $E^{(i)}$ as function of the the momentum k (in units of the healing length $\xi$), for two rotational frequencies of the obstacle [$\nu =0.8\omega _\rho$ (a) and $1.5\omega _\rho$ (b)], located at $r_0=3.5\ell _\rho$, considering $\alpha =0^\circ$ (where repulsive DDI is maximized). The results are obtained by time averaging over 10 samples within the interval of vortices emission ($2< \omega _\rho t< 10$). As shown, the Kolmogorov-kind behavior $k^{-5/3}$, indicated between the vertical dashed lines, starts at lower values of k for higher obstacle rotation. The contact and dipolar interactions are set to $a_s=50a_0$ and $a_{dd}=66a_0$, respectively

By considering the kinetic energy spectrum, along the same procedure as done in Ref. [11], as outlined in the previous section 2, a time interval is also verified in such case with the incompressible part of the kinetic energy behavior following approximately the Kolmogorov classical law. This dynamical process occurs in this case within a shorter time interval in which the vortex pairs are being emitted. As the vortex pairs are not produced at the same time, in the present case, summarized in two panels of Fig. 4, we consider two different velocities of the obstacle, given by $\nu =0.8\omega _\rho$ [panel (a)] and $\nu =1.5\omega _\rho$ [panel (b)]. The behavior of $E^{(i)}$, as function of $k\xi$ (where $\xi$ is the healing length), is extracted from time averaging the corresponding time-dependent behavior, in the time interval started when the incompressible part of the kinetic energy deviates from the corresponding compressible part, within a short time interval till vortex pairs have been dynamically interacting in the fluid. As also verified in the present case, the classical Kolmogorov power-law behavior $k^{-5/3}$ is being characterized for the two different velocities of the obstacle, providing indication for quantum turbulence, within the momentum spectral analysis of the incompressible kinetic energy. On this regard, our analyses are still under more detailed investigation, considering different combinations of dipolar and contact interactions, and also by assuming different rotational frequencies of the obstacle inside the fluid. As one can noticed by a visual analysis of the dynamical production and vortex–antivortex interactions inside the fluid, as shown in Fig. 3 for the limited two cycles with $\nu =0.8\omega _\rho$, the dipolar fluid starts to present stronger fluctuations and stripes affecting the vortex–antivortex dynamics, which may require further investigation. It should also be noticed the quite interesting aspects previously revealed in Ref. [32] of quantum turbulence arising in dipolar Bose gas from highly non-equilibrium thermal states, without external forces. In such case, quantum turbulence emerges strongly polarized when the contact and dipolar interactions are of the same order. As considering our present case, with an external circularly moving obstacle applied to the Bose system, a more detailed comparative analysis of non-dipolar and dipolar systems can be implemented by varying the obstacle speed, in which for higher speeds vortex clusters can also be emitted.

4 Conclusions

Within a comparative analysis, two recent investigations are reported in this communication, considering production of vorticity with eventual turbulence behavior. In Sect. 2, a binary mass-imbalanced BEC system under periodic small elliptically perturbation was analyzed by considering some results extracted from Ref. [11] for a particular large mass-imbalanced coupled system. In Sect. 3, another approach was considered for vortex–antivortex production, with a single dipolar condensate under circularly periodic Gaussian-shaped obstacle, simulating a laser stirring mechanism. In both the cases, the dynamics of vortex production is further explored by kinetic energy spectral analysis, in which the characterization of turbulent dynamics is verified in a time regime preceding the stable vortex formations. As follows from classical fluid dynamics, it is understood that vortex tangles are usually signatures of turbulence associated with the flow of incompressible viscous fluids. Therefore, by concentrating the spectral analysis on the incompressible kinetic energy part, obtained by averaging over several samples in the time evolution, the characterization of the turbulence behavior was possible to be established by verifying that the incompressible kinetic energy $E^{(i)}(k)$ follows approximately the classical Kolmogorov power-law $k^{-5/3}$ [1] in the momentum region $k\xi \lesssim 5$ (where $\xi$ is the healing length), changing to $k^{-3}$ as k goes to the ultraviolet region, consistent with previous studies [13]. A common feature in our analysis is that the time interval observed for the turbulence behavior is initiated when the compressible and incompressible parts of the kinetic energy start deviating from each other. In the case of small elliptically perturbation discussed In Sect. 2, this happens when vortex formations start migrating from low-density regions to the internal part of the condensate. However, for the case in which the condensate is being affected by circularly moving obstacle, as analyzed In Sect. 3, such dynamics occurs immediately before vortex–antivortex pairs are being produced. In both cases, such turbulent behavior occurs during a limited time interval as compared with the full period of vortex dynamics, but with the Kolmogorov spectral law being verified within similar intervals in momentum space, as seen in panels (b$_i$) of Fig. 2 and Fig. 4. In the case the fluid is under the influence of a moving obstacle, the dynamics can be modified significantly by varying the velocity of the obstacle, also with production of vortex clusters, it is also required a more detailed investigation in order to establish possible time intervals where Kolmogorov criterium may be applied.

Apart from the above discussed turbulent behavior, when assuming a pure-dipolar condensate under rotating Gaussian-shaped obstacle, it is also shown a rich dynamics that occurs inside the condensate, which is quite different from the dynamics following the case of pure-contact nonlinear interactions. This dynamics, which follows the vortex–antivortex production, is exemplified in a specific case in which the rotational frequency is $\nu =0.8\omega _\rho$ of the obstacle at a fixed radial position $r_0=3.5\ell _\rho$. It is represented by a series of eight pair of panels, considering two extreme cases as related to the nonlinear interactions: One case, in which the contact interactions are set to zero ($a_s=0$, or SCI=0), such that the non-linear interactions are purely due to dipolar interactions; with the other case in which dipolar interactions are cancelled out, by taking $\alpha =54.7^\circ$ (DDI=0). In this case, the SCI is given by $a_s=177a_0$, in order to keep both condensates having the same rms radius and chemical potentials. Within these comparative simulations, the vortex–antivortex dynamics became clearly evidenced in both the cases (pure dipolar, or pure contact interactions). By considering the dynamical movement and interactions of the vortices and antivortices inside the fluid, as well as the observed density fluctuations, one can clearly verify the richer dynamics of dipolar systems in comparison with the case that dipolar interactions are cancelled out. Finally, relevant to say is that all the interesting observed dynamics inside the fluid are verified within the simpler mean-field approach with cubic non-linear interactions, without the addition of other nonlinearities brought by quantum fluctuations.