Medium Effect in S-shell Double-$\Lambda$ Hypernuclei and Hyperon Superfluidity in Neutron Star Cores

Abstract

The effective $\Lambda$-$\Lambda$ interaction energies in s-shell double-$\Lambda$ hypernuclei, $^{6}_{\Lambda \Lambda }\text {He}$, $^{5}_{\Lambda \Lambda }\text {He}$ and $^{5}_{\Lambda \Lambda }\text {H}$ have been investigated by solving three-body system ($\Lambda$ + $\Lambda$ + core) within the framework of coupled rearrangement channel Gaussian basis treatment. The Nijmegen soft-core potential models, NSC97d, NSC97e and NSC97f, have been applied for free-space $\Lambda$-$\Lambda$ interaction. By taking into account the medium effects, it was adjusted to fit the experimental $\Lambda$-$\Lambda$ interaction energies of $^{6}_{\Lambda \Lambda }\text {He}$ (0.67 ± 0.17 MeV). The effective $\Lambda$-$\Lambda$ interaction energies of $^{5}_{\Lambda \Lambda }\text {He}$ are 0.92 MeV, 0.88 MeV, 0.86 MeV for each potential model and that of $^{5}_{\Lambda \Lambda }\text {H}$ is 0.6 MeV for all potential modes. Moreover, the $\Lambda$-superfludity in the neutron star cores which is related to cooling process has also been investigated by applying our constructed effective $\Lambda$-$\Lambda$ NSC97e potential of $^{6}_{\Lambda \Lambda }\text {He}$. It is found that $\Lambda$ superfludity begins to appear when the interaction strength is 1.5 times more attractive than our constructed interaction. The $\Lambda$-superfluidity in the neutron star cores might occur at the hyperon percentage $Y_\Lambda$ (1%–5%), and vanish at $Y_\Lambda$ (15%– 20%).

1 Introduction

The study of baryon-baryon interaction is closely related to many phenomena occurring in neutron star matter and it is an important issue for the understanding of high density nuclear matter inside the neutron stars. The population of constituent particles strongly depends upon the density of neutron stars and hyperons may appear in its inner core at densities of about 2-3$\rho _0$  [1]. From the theoretical point of view, the characteristic of neutron stars is studied by solving the equation of state (EoS). The presence of hyperon in the neutron stars has been studied by many authors  [2,3,4,5]. The hyperon mixing in the core of a neutron stars can cause it to be cooled much faster due to neutrino emission process; $\Lambda \rightarrow p + e^- + \overline{\nu }_e$, $\Sigma ^-\rightarrow \Lambda + e^- + \overline{\nu }_e$  [6]. If there is a hyperon (Y) mixing in the neutron stars, two problems arise; (1) too-soft EoS which is incompatible with 2M$_\odot$ from neutron star observations and (2) too-rapid cooling which is inconsistent with surface temperature. Takatsuka et al. discussed to solve the first problem by introducing the universal 3-body force  [7]. The hyperon composition and the cooling process in the neutron star cores are closely related to cooper pair, superfluidity and hyperon-hyperon interaction which might solve the second problem. Thus the neutron stars are the excellent matters to test our present understanding of strong interacting matters and they could give an interesting relationship between nuclear processes and astrophysical observables.

2 Three-body Calculation and Effective $\Lambda$-$\Lambda$ Potential

In this research work, double-$\Lambda$ hypernuclei were considered as three-body systems; ($\Lambda$ + $\Lambda$ + core). The non-relativistic three-body Hamiltonian in Jacobi coordinate is expressed as

$$\begin{aligned} \hat{H}=-\frac{\hbar ^{2}}{2M_c} \Delta _{R_c}^{2} - \frac{\hbar ^{2}}{2\mu _c} \Delta _{r_c}^{2} + V_{23} (\mathbf {r}_1) + V_{13} (\mathbf {r}_2) + V_{12} (\mathbf {r}_3), \end{aligned}$$

(1)

where $V_{23}$ $(\mathbf {r}_1)$, $V_{13}$ $(\mathbf {r}_2)$ and $V_{12}$ $(\mathbf {r}_3)$ are the potentials between the corresponding particles. $r_c$ is the relative distance between two particles and $R_c$ is the relative distance between third particle and the center of mass of the first two particles. $\mu _c$ and $M_c$ are the reduced masses corresponding to the Jacobi coordinate $r_c$ and $R_c$ respectively. The total wave function of a three-body system is

$$\begin{aligned} \Psi (\mathbf {r}_c, \mathbf {R}_c)= \displaystyle \sum _{c=1}^{3} \sum _{i,j}^{N} A_{ij}^{c}\exp (-\frac{r_c^2}{b_{ic}^2})\exp (-\frac{R_c^2}{B_{jc}^2}), \end{aligned}$$

(2)

and the range parameter can be expanded as the geometric progressive series as $(\frac{b_N}{b_1})^{\frac{1}{(N-1)}}b_{i}$, $b_{1}$=0.2 fm, common ratio c=1.4 and number of basis N=11 for each three channel. In this calculation, it is necessary to know the $\Lambda$-nucleus potential and $\Lambda$-$\Lambda$ potential. For the $\Lambda$-nucleus interaction, two-range Gaussian potential which can reproduce the experimental binding energies of s-shell $\Lambda$-hypernuclei ($B_{\Lambda }$) was used  [8]. As the first step for the $\Lambda$-$\Lambda$ potential, the single-channel $\Lambda$-$\Lambda$ interaction in free space has been constructed from Shinmura’s S=-2 interactions which are phase-shift equivalents to Nijmegen potential, NSC97d, NSC97e and NSC97f. As the second step, the medium effect is taken into account as follow.

In three-body calculation of $^{6}_{\Lambda \Lambda }\text {He}$, when the two $\Lambda$-hyperons transform to the $\Lambda \Lambda -\Xi N$ channel, Pauli suppression effect might appear between one of the nucleon in the nuclear medium and converted nucleon from $\Lambda \Lambda -\Xi N$ conversion process. Thus Pauli suppression effect in $^{6}_{\Lambda \Lambda }\text {He}$ must be taken into account in this calculation.

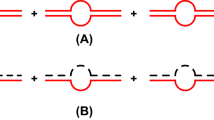
In the case of five-body double-$\Lambda$ hypernuclei, $^{5}_{\Lambda \Lambda }\text {He}$ and $^{5}_{\Lambda \Lambda }\text {H}$, it is necessary to consider both Pauli suppression effect and $\alpha$ formation effect. Figure 1 (a), (b) and (c) are the Pauli suppression effect and $\alpha$ formation effect in s-shell double-$\Lambda$ hypernuclei. The detailed calculations and discussion for the $\Lambda$-$\Lambda$ potential are described in reference  [9].

Fig. 1

Medium effects in a $^{6}_{\Lambda \Lambda }\text {He}$ b $^{5}_{\Lambda \Lambda }\text {He}$ and c $^{5}_{\Lambda \Lambda }\text {H}$

After solving three-body Schrödinger equation by considering the medium effect, the effective $\Lambda$-$\Lambda$ interaction energy $\Delta B_{\Lambda \Lambda }$=$B_{\Lambda \Lambda }({}^{A}_{\Lambda \Lambda }\text {Z})$-$2B_{\Lambda }({}^{A-1}_{\Lambda }\text {Z})$ is obtained. Our constructed effective $\Lambda$-$\Lambda$ interaction which can reproduce the experimental binding energy ($B_{\Lambda \Lambda }$) and $\Lambda$-$\Lambda$ interaction energy of $^{6}_{\Lambda \Lambda }\text {He}$, 6.91 ± 0.16 MeV and 0.67 ± 0.17 MeV  [10], is three-range Gaussian form.

3 $\Lambda$-Superfluidity in Neutron-star Matter

The hyperon superfluidity in the cores of neutron star matter will be examined by studying the gap equation which is based on BCS theory and it is described by

$$\begin{aligned} \Delta (k)= -\frac{1}{\pi }\int \frac{ V_{\Lambda \Lambda }(k,k') \Delta (k')}{[\xi ^2(k')+\Delta ^2(k')]^{1/2}}k'^2 dk'. \end{aligned}$$

(3)

The potential matrix element $V_{\Lambda \Lambda }(k,k')$ is expressed as

$$\begin{aligned} V_{\Lambda \Lambda }(k,k')=\langle k|V_{\Lambda \Lambda }(k,k') ({}^{1}S_0)|k'\rangle = \int r^2 dr j_0(kr) V_{\Lambda \Lambda }(r) j_0(k'r), \end{aligned}$$

(4)

where $j_0$ is the spherical Bessel function $j_{0}(kr)=\frac{sin (kr)}{kr}$. In equation (3), $\Delta (k)$ denotes the gap energy for $\Lambda$, $V_{\Lambda \Lambda }(k,k')$ is the potential matrix element, $V_{\Lambda \Lambda }(r)$ is the $\Lambda$-$\Lambda$ interaction in neutron star matter and $\xi (k')$ is the single particle energy, $\xi (k')=\frac{k^{2}-k^2_f}{2M^*_\Lambda }$, $k_f$ is the fermi momentum of $\Lambda$ in terms of density $k_f$=$(3\pi ^2 Y_{\Lambda } \rho )^\frac{1}{3}$ and $Y_\Lambda$ is the percentage of $\Lambda$-hyperon in the neutron star. $M^*_{\Lambda }$ is the effective mass and effective mass parameter $m^*_{\Lambda }$ is $m^*_{\Lambda }$=$\frac{M^*_{\Lambda }}{ M_\Lambda }$. Our constructed effective $\Lambda$-$\Lambda$ interaction which is based on Nagara event data will be applied in this calculation. The effective interaction is the three-range Gaussian form, $V(r)= \displaystyle \sum _{i=1}^{3} V_i \exp (-\frac{r^2}{\mu ^2})$. Thus the analytical solution of potential energy matrix element is expressed as

$$\begin{aligned} \langle k|V|k'\rangle =\displaystyle \frac{1}{2kk'} \sum _{i=1}^{3} \frac{V_i}{2} \sqrt{\pi _{i}\mu ^2_{i}} [\exp (\frac{-(k'-k)^2\mu ^2_{i}}{4}) -\exp (\frac{-(k'+k)^2\mu ^2_{i}}{4})]. \end{aligned}$$

(5)

In order to solve the gap equation, it has been replaced without any approximation by two equivalent equations.

$$\begin{aligned}&\chi (k)=\phi (k)-\frac{1}{\pi }\int \frac{W(k,k')\chi (k')}{ [\xi ^2(k')+\Delta ^2_f\chi ^2(k')]^{1/2}} k'^2dk', \end{aligned}$$

(6)

$$\begin{aligned}&-\frac{1}{\pi } V_f \int \frac{\phi (k')\chi (k')}{[\xi ^2(k')+\Delta ^2_f\chi ^2(k')]^{1/2}} k'^2dk'=1, \end{aligned}$$

(7)

where $\phi (k)=\frac{V(k,k_f)}{ V(k_f,k_f) }$ and $W(k,k')= V(k,k') -\frac{V(k,k_f) V(k',k_f)}{ V(k_f,k_f) }$. The dimensionless shape function can be defined as $\chi (k)=\frac{\Delta (k)}{\Delta (k_F)}= \frac{\Delta (k)}{\Delta _{F}}$. Equation (6) is solved with the use of matrix inversion by a very small constant scaling factor $\Delta _{0} (\Delta _{f}\chi (k_f) \rightarrow \Delta _{0})$. After getting the first iteration, the shape function $\chi ^{(1)}_i$ is obtained. To get first approximation of $\Delta ^{(1)}_f$ for the scaling factor $\Delta _f$, equation (7) is solved by applying Newton-Raphson method. In our numerical calculation, we used a very small constant scaling factor $\Delta _0 =0.01$ MeV and the initial value $\Delta ^{(1)}_f=0.1$ MeV for Newton-Raphson method. The gap energy ($\Delta _f$) is obtained after solving the above two equations iteratively. It is closely related to the critical temperature $T_{c}\sim 0.66 \Delta \times 10^{10}$ K and the $\Lambda$-superfluidity in neutron stars can be occurred when $T_{c} > T_{i}$ which is internal temperature of neutron stars approximately $T_{i}\sim 10^8$ K. It disappears when $T_{c}$ becomes lower than the internal temperature of neutron stars.

4 Results and Dicussions

In this research work, $\Lambda$-$\Lambda$ interaction energies of s-shell double-$\Lambda$ hypernuclei, $^{6}_{\Lambda \Lambda }\text {He}$, $^{5}_{\Lambda \Lambda }\text {He}$ and $^{5}_{\Lambda \Lambda }\text {H}$ have been investigated. The medium effects have also been implicitly taken into account and the effective $\Lambda$-$\Lambda$ interaction in three-range Gaussian form have been deduced from the three-body calculation. The interaction strength and range parameter for NSC97d, NSC97e and NSC97f are described in Table 1. $V^{Sc}_{\Lambda \Lambda }$ is the effective $\Lambda$-$\Lambda$ interaction for $^{6}_{\Lambda \Lambda }\text {He}$ and $V^{Sc1}_{\Lambda \Lambda }$ is the free-space $\Lambda$-$\Lambda$ interaction.

Table 1 The strength and range parameter of $\Lambda$-$\Lambda$ interaction for $^{6}_{\Lambda \Lambda }\text {He}$

In order to calculate $\Lambda$-$\Lambda$ interaction energies of $^{5}_{\Lambda \Lambda }\text {He}$ and $^{5}_{\Lambda \Lambda }\text {H}$, the free-space $\Lambda$-$\Lambda$ interaction is applied together with the medium effects. The $\Lambda$-$\Lambda$ interaction energies and the medium effects of these double-$\Lambda$ hypernuclei are described in Table 2. From these results, $\Lambda$-$\Lambda$ interaction energies in $^{5}_{\Lambda \Lambda }\text {He}$ is the largest among the s-shell double-$\Lambda$ hypernuclei due to the strongest $\alpha$ formation effect. Pauli suppression effect is not negligible for these hypernuclei.

Table 2 The $\Lambda$-$\Lambda$ interaction energies and medium effects of double-$\Lambda$ hypernuclei

Moreover, the $\Lambda$-superfluidity in neutron star core has been explored with the use of our constructed effective $\Lambda$-$\Lambda$ interaction, NSC97e ($V^{SC}_{\Lambda \Lambda } (97e)$), in $^{6}_{\Lambda \Lambda }\text {He}$ by solving the gap equation. Therefore, the gap energy and critical temperature of the core of neutron stars have been investigated and the results are described in Table 3. In this paper, all the effective mass of $\Lambda$ and hyperon percentage are taken from Takatsuka’s paper  [6].

Table 3 Gap energy and critical temperature by using effective $\Lambda$-$\Lambda$ interaction

According to this results, our constructed effective $\Lambda$-$\Lambda$ interaction in $^{6}_{\Lambda \Lambda }\text {He}$ is no attractive enough to support the occurrence of hyperon superfluidity. Therefore, we fit the long-range attractive interaction strength ($V_2$) of this potential by multiplying factor(F) 1.1–1.5 to check the gap energy. Figure 2 (a) and (b) are the variation of $\Lambda$-$\Lambda$ scattering phase shift with the center of mass energy and the gap energy versus the fermi momentum which is closely related with the density and hyperon percentage in the neutron star cores.

Fig. 2

a The $\Lambda$-$\Lambda$ scattering phase shift with the center of mass energy b Variation of gap energy with fermi momentum

We have also checked under which condition $\Lambda$-superfluidity would occur and it is shown in Table 4. From this result, $\Lambda$-superfluidity can be observed at 1.5 times of attractive part of effective $\Lambda$-$\Lambda$ interaction in $^{6}_{\Lambda \Lambda }\text {He}$. According to our results, the superfluidity of $\Lambda$-hyperon in the neutron star cores appears at the hyperon percentage $Y_\Lambda$ (1%–5%) and disappears at $Y_\Lambda$ (15%– 20%).

Table 4 Gap energy and critical temperature ($T_c\times 10^8$ K) by using effective $\Lambda$-$\Lambda$ interaction

5 Conclusion

In this paper, s-shell double-$\Lambda$ hypernuclei have been theoretically investigated within three-body frame work to determine effective $\Lambda$-$\Lambda$ interaction energies. Nijmegen soft-core potentials, NSC97d, NSC97e and NSC97f, have been used for the free-space $\Lambda$-$\Lambda$ interaction and the medium effects have been taken into account. Then, the effective $\Lambda$-$\Lambda$ interaction which is closely related to hyperon superfluidity in neutron star cores has been deduced by fitting the experimental data of $^{6}_{\Lambda \Lambda }\text {He}$ observed from the Nagara event. The effective $\Lambda$-$\Lambda$ interaction energies of $^{5}_{\Lambda \Lambda }\text {He}$ are found to be 0.92 MeV, 0.88 MeV and 0.86 MeV for NSC97d, NSC97e and NSC97f potential model and that of neutron-rich $\Lambda$-hypernucleus, $^{5}_{\Lambda \Lambda }\text {H}$ is 0.6 MeV for each potential model. In addition, the $\Lambda$-superfludity in the neutron star cores has also been investigated by applying our constructed effective $\Lambda$-$\Lambda$ NSC97e potential of ${}^{6}_{\Lambda \Lambda }\text {He}$. We found that the $\Lambda$-superfluidity in the neutron stars can be observed only when the interaction strength is 1.5 times the attractive part of effective $\Lambda$-$\Lambda$ interaction in $^{6}_{\Lambda \Lambda }\text {He}$. The $\Lambda$-superfluidity might be starting to occur in the core of neutron star at the hyperon percentage $Y_\Lambda$ (1%–5%) and disappear at $Y_\Lambda$ (15%–20%).