Electromagnetic Production of Kaon in All Isospin Channels: Summary of the Progress and Application

Abstract

We report on the improvement of our isobar models for elementary kaon photo- and electroproduction, $\gamma _\mathrm{r,v}+N\rightarrow K+Y$, during the last two decades. Our effort started with the investigation of kaon photoproduction near threshold, followed by the construction of new models which were intended to explain all $K\Lambda$ and $K\Sigma$ data from threshold up to $W\approx 3$ GeV by using two approaches, i.e., the partial waves and the fully covariant isobar models. Both approaches yield nice agreement with the presently available experimental data. A number of applications of the models in nuclear and particle physics area are presented. We also discuss our effort to use the pure spin-3/2 and spin-5/2 propagators in meson scattering and meson photoproduction processes.

1 Introduction

The electromagnetic production of kaon has drawn attention from the hadronic physics community for more than five decades. This is due to the production of explicit strangeness degrees of freedom in the final state of the process. As a consequence, kaon photo- or electroproduction provides a number of important phenomenological applications in nuclear and particle physics, which are not possible in the case of pion and eta productions. In this paper, we briefly review some applications of kaon photo- and electroproduction that we have explored during the last two decades. Nevertheless, we understand that accurate models that can precisely describe all available experimental observables is indispensable to this end. Thus, we will start the discussion in this paper with the progress we have achieved to improve our previous models, including the Kaon-Maid.

2 Isobar Model

By imposing the conservation of quantum numbers we have six possible reaction channels for kaon photo- or electroproduction off the nucleon as listed in Table 1. From the isospin point of view, we can divide these reactions to the isoscalar ($K\Lambda$) and isovector ($K\Sigma$) hyperon productions. Therefore, in principle, all channels can be coupled by using isospin symmetry. However, since we have fixed the leading coupling constants, $g_{K \Lambda N}$ and $g_{K \Sigma N}$, to the SU(3) prediction, the isoscalar and isovector production channels are decoupled. Therefore, we have two phenomenological isobar models to this end. Both models can be constructed by using a fully covariant formalism (Feynman diagrams) or partial wave analysis.

Table 1 Six possible isospin channels of kaon photoproduction (using $\gamma _\mathrm{r}$) and electroproduction (using $\gamma _\mathrm{v}$) with their total c.m. threshold energies

2.1 Progress in the Isobar Model for $K\Lambda$ Photoproduction

Table 1 obviously indicates that the threshold energies of kaon productions are much higher than those of the pion and eta ones. With these energies at least three nucleon and two delta resonances can be excited before kaon and hyperon are created. Therefore, before we can construct a model that works in the energy range covered by the present experimental data, it is important to investigate the production properties near the threshold. We performed this investigation a decade ago for the $K\Lambda$ photoproduction with the energy 50 MeV above threshold. It was found that the use of pseudovector coupling leads to a better $\chi ^2$ and the hyperon resonance $\Lambda (1800)S_{01}$ plays an important role [1]. Note that although three nucleon resonances are possible to this end, only the $N(1650)S_{11}$ was included. Extension of the model to the electroproduction case was not easy due to the large contribution of the $K^*$ and $K_1$ exchanges, unless special electromagnetic form factor was introduced.

An improvement to Kaon–Maid in $K^+\Lambda$ channel was achieved after the use of spin-3/2 and -5/2 nucleon resonances in the covariant isobar model [2]. More than 7000 data points were successfully fitted by using 17 nucleon resonances and the best model achieved $\chi ^2/N_\mathrm{dof}=1.58$. Further improvement was made by adding four nucleon resonances with spins 7/2 and 9/2, where the $\chi ^2/N_\mathrm{dof}$ can be reduced to 1.25 [3]. The latest improvement was made by incorporating the $K^0\Lambda$ channel [4], for which new data have been recently available from the CLAS [5] and MAMI [6] collaborations. In this coupled analysis the number of experimental data used is more than 9400 points with the best $\chi ^2/N_\mathrm{dof}=1.53$. Further development has been made by including spin-11/2 up to -15/2 resonances and the report will be published soon [7].

In the partial wave analysis the resonant electric and magnetic multipoles are parameterized by using, e.g., the Breit-Wigner form. This approach has a clear advantage, i.e, the resonance formalism is much simpler than the covariant one. However, its application in the nuclear sectors is difficult, since analytical continuation to the energy region below threshold is complicated. We started this approach not long after the problem of Kaon–Maid appeared. By using 15 nucleon resonances and nearly 2500 data points the obtained $\chi ^2/N_\mathrm{dof}$ is between 0.98 and 1.31, depending on the data set used [8]. Note that the SAPHIR and CLAS data used in the fit had the problem of data consistency. Moreover, the extracted resonance properties are significantly different from the PDG estimates. Recently, we have revisited the partial wave model by incorporating newer data and PDG information [9]. The model was improved by including 22 nucleon resonances and fitting nearly 9000 data points. Although the obtained $\chi ^2/N_\mathrm{dof}$ increased to 1.63, the resonance properties could be constrained within the error bars of PDG estimates.

2.2 Progress in the Isobar Model for $K\Sigma$ Photoproduction

When Kaon–Maid was created, experimental data were only available for the $K^+\Sigma ^0$ and $K^0\Sigma ^+$ channels with very limited number. At present, all isospin channels of $K\Sigma$ photoproduction listed in Table 1 have experimental data. Therefore, all parameters inside the models can now be fixed by fitting the calculated observables to the data. We have started the analysis near threshold by using an isobar model that includes four baryon resonances, the $N(1700)D_{13}$, $\Delta (1700)D_{33}$, $N(1710)P_{11}$, and $N(1720)P_{13}$ states. All available data with total c.m. energy W up to 50 MeV above threshold were fitted, including the electroproduction ones. Furthermore, all resonance properties were constrained within the PDG error bars. Interestingly, this analysis confirms the validity of $P_\Lambda =-(1/3)P_\Sigma$ relation derived in the past.

A more comprehensive analysis has been performed within the framework of partial waves one, where nearly 8000 experimental data points from all four isospin channels with W from threshold up to 2.8 GeV were fitted [10]. By using 19 nucleon and 13 delta resonances, whose properties were constrained within the PDG estimates, the model achieved the best $\chi ^2/N_\mathrm{dof}$ of 1.74. The analysis also showed that the artificial spike in the $K^+\Sigma ^-$ channel found in the previous work does not exist and the $N(1895)S_{11}$ and $\Delta (1900)S_{31}$ resonances are indispensable for the $K\Sigma$ photoproductions.

A fully covariant model that fits the same number of experimental data has been also constructed [11]. In this model all nucleon and delta resonances with at least two-star PDG status and spins up to 9/2 have been taken into account. The resonance masses and widths are given at their pole positions, besides using the Breit-Wigner definition. Thus, the result is model independent and can be compared with those obtained from other studies.

2.3 Kaon Electroproduction

Having finished the analysis of kaon photoproduction, we are ready to extend the models to the electroproduction regime. Two more terms are required to this end, i.e., the longitudinal terms of the production amplitudes and the electromagnetic form factors. The former have been already derived but automatically vanish when we calculate photoproduction amplitude, while the latter will be selected according to the need to accurately fit the electroproduction data. Recently, we have reported the preliminary result that used simple dipole form factors and fitted more than 1200 data points of $K^+\Lambda$ electroproduction [12]. A nice agreement with experimental data was obtained. Extension of this work to include all six isospin channels is in progress.

3 Phenomenological Applications

The covariant isobar model constructed to describe kaon photo- and electroproduction off the nucleon has unique but indispensable applications in the particle and nuclear physics researches. In the followings we briefly review few applications we have made in the last two decades.

3.1 Missing Resonance

A number of nucleon resonances have been predicted to have considerably large branching ratios only to the kaon–hyperon channels [13]. Since the cross section of kaon production is much smaller than that of pion and eta productions, these resonances are less probable to be identified by the PDG. One of the earliest investigations of missing resonance by making use of kaon photoproduction was reported in Ref. [14]. By fitting the experimental data obtained from SAPHIR collaboration [15], it was obtained that the $N(1895)D_{13}$ resonance is responsible for the existence of the second peak in the total cross section. Since the resonance was not included in the PDG listing, it was concluded that the $N(1895)D_{13}$ is one of the searched missing resonances (Fig. 1a).

Fig. 1

a Total cross section predicted by Kaon–Maid [16] (dashed line), isobar models given in Refs. [17] (dotted line) and [4] (solid line), and measured by SAPHIR 2004 [15] and CLAS 2006 [18] collaborations. b Differential cross sections predicted by the three models given in a compared with the new data from BGOOD 2021 collaboration [19]

However, newer data from CLAS collaboration [18] show sizable discrepancy with the SAPHIR data. By using the CLAS data it was shown that the second peak in the total cross section originates from the $N(1900)P_{13}$ resonance, instead the $N(1895)D_{13}$ one [17]. Comparison between total cross sections obtained from fitting to the SAPHIR and CLAS data is displayed in Fig. 1a, where the result from latest analysis [4] is also shown.

Very recently, new data at very forward angles have been obtained by the BGOOD collaboration [19]. As shown in Fig. 1b, the data show a clear structure at $W\approx 1.83$ GeV and all models shown in Fig. 1a cannot reproduce this structure. This could be a hint that there is a possibility of resonance existence with Breit-Wigner mass nearly 1830 MeV.

3.2 Narrow Resonance

The existence of the narrow resonance was predicted by the chiral soliton model [20] as a member of the ten antidecuplet baryons shown in Fig. 2a with $J^p=1/2^+$. It was originally presumed to be the $N(1710)P_{11}$ listed by the PDG [21], but it was soon realized as the origin of the substantial enhancement in the $\gamma n\rightarrow \eta n$ quasi-free cross section [22]. Since the narrow resonance is predicted to have a considerably large branching ratio to the KN channel, it is also possible to use kaon photoproduction to investigate this resonance.

Fig. 2

a Antidecuplet baryons predicted by the chiral soliton model [20]. b Effects of the inclusion of $P_{11}$ narrow resonance on the differential cross section of the $\gamma +p\rightarrow {K^+}+\Lambda$ process for three different kaon scattering angles [23]

The existence of this resonance has been investigated by including it in an isobar model and scanning its mass, width, and spin-parity to search for significant improvement in the $\chi ^2$ [23]. The result indicates that the most probable candidate is the $N(1650)P_{11}$. Other candidates with different masses and spin-parities are less probable, since the $\chi ^2$ improvement is less significant. The effect of $N(1650)P_{11}$ inclusion on differential cross section is exhibited in Fig. 2b. Note that the effects at forward and backward angles have different signs. As a consequence, the net effect is negligible on the total cross section. Thus, future experiments should focus on scrutinizing differential cross section and $\Lambda$ polarization at this kinematics, i.e., $1640\le W \le 1660$ MeV.

In a recent investigation [4], it was shown that the effect of this narrow resonance is more apparent in the neutron channel, i.e., $\gamma n \rightarrow K^0\Lambda$. This result corroborates the similar finding that the resonance only appears in the quasi-free neutron target ($\gamma n\rightarrow \eta n$) [22]

3.3 Hadronic Coupling Constant

One of the challenging problems in this case is the coupling strength of the $N(1535)S_{11}$ resonance. The existence of this resonance faces the mass reverse problem, since the constituent quark model predicts that this resonance should have the lowest mass state [13], whereas according to the PDG the lowest state is occupied by the $N^*(1440)P_{11}$ resonance with $J^p=1/2^+$ [21]. Furthermore, by using an isobar model it was obtained that the coupling of this resonance to $K\Lambda$ channel is larger than that to $\eta N$ channel, i.e., $R\equiv |g_{N^*(1535) \Lambda K}/g_{N^*(1535)\eta p}|=1.3\pm 0.3$ [24]. As a consequence, the mass and width of this resonance should be 1400 and 270 MeV, respectively, in contrast to the PDG estimate for this resonance [21].

We note that the mass of this resonance is located below the $K^+\Lambda$ production threshold. Nevertheless, the inclusion of this resonance still influences both the background and resonance sectors due to the relatively large resonance width. We have investigated the effect of including this resonance in an isobar model and extracted the ratio R [25]. It was found that the coupling ratio is $R =0.460\pm 0.172$, which is significantly smaller than that obtained from the isobar model of the $J/\psi$ decays reported in Ref. [24]. However, this result is consistent with that of unitary chiral approach, i.e., $R=0.5\sim 0.7$ [26]. Recent update by using newer PDG data yields $R=0.360\pm 0.076$ [10].

3.4 Electromagnetic Form Factor of Kaon

Unlike the neutral pion, the difference between the strange and non-strange quark masses inside a neutral kaon $K^0$ (see Fig. 3a) creates a non-uniform charge distribution. As a consequence, the $K^0$ has an explicit charge form factor. Since the t-channel in $K^0\Lambda$ electroproduction exchanges a neutral kaon (Fig. 3b), we have the possibility to asses the charge distribution inside this meson. Note that, the charged kaon $K^+$ is exchanged in the $K^+\Lambda$ electroproduction and it is obvious that we can also investigate the $K^+$ form factor by using this process. However, the neutral form factor is more interesting, since it could become an alternative test to phenomenological models that attempt to describe nonperturbative QCD.

Fig. 3

a The difference between strange- and down-quark masses creates charge distribution inside the $K^0$. b The $K^0$ charge form factor enters the $K^0$ electroproduction reaction via the t-channel exchange. c Effect of the $K^0$ inclusion on the longitudinal cross section, where the quark meson vertex (QMV) and light cone quark (LCQ) models are used [27]

Figure 3c shows the effect of two different $K^0$ form factors, quark meson vertex (QMV) and light cone quark (LCQ) models [28], on the neutral kaon electroproduction cross section. Clearly, the effect is visible for the experiment of $K^0$ electroproduction. For $\theta _K\approx 70^\circ$ the LCQ model increases the longitudinal cross section to nearly 50%. Note that, such phenomenon occurs only if the background terms in the model are not severely suppressed by the hadronic form factors. From Fig. 3c we may conclude that experimental data with uncertainties of 10% would make this effect visible [27].

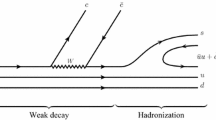
3.5 Hypernuclear Production

A hypernucleus is a nucleus that contains one or more hyperons in addition to the protons and neutrons. A hypernucleus can be produced by replacing a nucleon inside a conventional nucleus with a hyperon. One of the possible methods is by using kaon photoproduction, as shown in Fig. 4a, assuming that the photon interacts with only one nucleon inside the nucleus. Let us consider the electroproduction of hypertriton for instance. In this case the nuclear transition matrix can be written in terms of three-body wavefunction of the initial $|\mathrm{^3He}\rangle$ and final $|\mathrm{^3_\Lambda H}\rangle$ states [29],

$$\begin{aligned} \langle \, \mathrm{^3_\Lambda H} \left| \, J^\mu \, \right| \mathrm{^3 He} \,\rangle= & {} \sqrt{3}\,\int d^{3}{\varvec{p}}~d^{3}{\varvec{q}}~ \mathrm{\Psi _{f}}^{*}({\varvec{p}}, {\varvec{q}}') ~ J^\mu \, ({\varvec{k}},{\varvec{p}}_{N}, {\varvec{p}}_Y) ~ \mathrm{\Psi _{i}}({\varvec{p}},{\varvec{q}})~ ,~ \end{aligned}$$

(1)

where the elementary operator $M_\mathrm{fi}=\epsilon _\mu \, J^\mu$ is taken from Kaon–Maid [16] and the integrations are performed over the three-body momentum coordinates ${\varvec{p}} = \frac{1}{2}\,({\varvec{k}}_2 - {\varvec{k}}_3)$ and ${\varvec{q}} = {\varvec{k}}_1$. Since the baryons inside both nuclei are off-shell, in contrary to the case of the constructed elementary operator, a number of off-shell assumptions should be made. The effect of different off-shell assumptions is shown in Fig. 4b. Interestingly, the effect is in agreement with the fact that the $\Lambda$ binding energy in hypertriton is weak; it is almost on-shell.

Fig. 4

a A hypernucleus can be excited by using kaon photo- or electroproduction (using a real or virtual photon) off a nucleus target. b Off-shell effects on the differential cross sections of hypertriton electroproduction as a function of the kaon scattering angle [29]. Experimental data are obtained from Ref. [30]

Very recently, kaon electroproduction off a tritium target has been measured at Jefferson Lab Hall A (JLab E12-17-003) [31]. This reaction is very interesting because the final state consists of $nn\Lambda$. There was a speculation that the $nn\Lambda$ system could be bound or at least lead to a resonant state. Meanwhile, an accurate experiment of hypertriton electroproduction has been conditionally approved as the JLab C12-19-002 experiment [31]. It is expected that this experiment can solve the problem of $\Lambda$ binding energy in the hypertriton, since previous measurement obtained a stronger binding energy [32]. Thus, an accurate theoretical calculation of the kaon electroproduction on $^3$H and $^3$He nuclei is urgently required at present.

4 Pure-Spin Formalism

In the previous works we have shown that it is possible to construct a pure-spin propagator that is completely free from the background problems [33, 34]. However, care must be taken to ensure that the constructed scattering amplitude exhibits the expected resonance structure in the cross section.

Theoretically, a particle with spin 3/2 can be represented by the pure spin-3/2 representation, $(3/2,0) \oplus (0,3/2)$. However, this is not easy because the formulation requires an eight-dimensional spinor since the corresponding operator is given by $4 \times 4$ matrices. Acosta et al. [35] proposed the solution by embedding the components of the 8-dimensional spinor in a totally antisymmetric tensor of second rank, which is called the antisymmetric tensor spinor (ATS) representation, formed by the product of an antisymmetric tensor and the Dirac field. In the practical form the propagator of pure-spin 3/2 particle with momentum p and mass m can be written as [35]

$$\begin{aligned} S_{\alpha \beta \gamma \delta }(p) = \frac{1}{p^2 - m^2 + i\epsilon } \left\{ \frac{p^2}{m^2} {\mathcal {P}}_{\alpha \beta \gamma \delta } - \frac{p^2-m^2}{m^2} \, \mathbf{I }^{\mathrm{(ATS)}}_{\alpha \beta \gamma \delta }\right\} , \end{aligned}$$

(2)

where the projection operator ${\mathcal {P}}_{\alpha \beta \gamma \delta } = {\textstyle \frac{1}{8}} \left( \sigma _{\alpha \beta } \sigma _{\gamma \delta } + \sigma _{\gamma \delta } \sigma _{\alpha \beta } \right) - {\textstyle \frac{1}{12}} \sigma _{\alpha \beta } \sigma _{\gamma \delta }$, with $\sigma _{\alpha \beta } = {\textstyle \frac{i}{2}}\left[ \gamma _\alpha , \gamma _\beta \right]$, and the ATS identity $\mathbf{I }^{\mathrm{(ATS)}}_{\alpha \beta \gamma \delta } = {\textstyle \frac{1}{2}} \left( g_{\alpha \gamma }g_{\beta \delta } - g_{\alpha \delta }g_{\beta \gamma }\right)$.

In the previous work [33] we calculated the contribution of $\Delta$-exchange in elastic $\pi N$ scattering amplitude by using this representation. Using the gauge invariant interaction ${\mathcal {L}}_{\pi N \Delta } = g_{\pi N \Delta } {\bar{N}} \gamma _5 \gamma _\mu {\tilde{\Psi }}^{\mu \nu }\partial _\nu \pi + \mathrm{H.c.}$ we obtained

$$\begin{aligned} {{{\mathcal {M}}}} = \frac{g_{\pi N \Delta }^2 \left( q^2-m_\Delta ^2 \right) }{m_\Delta ^2 (q^2 - m_\Delta ^2 + i\epsilon )} \left( g^{\nu \sigma } + {\textstyle \frac{1}{2}} \gamma ^\nu \gamma ^\sigma \right) k'_\nu k_\sigma \, , \end{aligned}$$

(3)

which does not exhibit the contribution of a resonance, since instead of being maximum, the amplitude equals to zero at resonance pole ($q^2 = m_\Delta ^2$). To overcome this problem we replace the $\gamma$ matrix in the interaction with a partial derivative, i.e., ${\mathcal {L}}_{\pi N \Delta } = \left( {g_{\pi N \Delta }}/{m_\Delta } \right) {\bar{N}} \gamma _5 \partial ^\mu \Psi _{\mu \nu }\partial ^\nu \pi + \mathrm{H.c.}$, so that

$$\begin{aligned} {{{\mathcal {M}}}} = \frac{g_{\pi N \Delta }^2 k'^\nu k^\sigma }{q^2 - m_\Delta ^2 + i\epsilon } \left\{ \frac{q^4}{4m_\Delta ^4} P^{(3/2)}_{\nu \sigma }(q) - \left( \frac{q^2 - m_\Delta ^2}{2m_\Delta ^4} \right) \left( q^2 g_{\nu \sigma } - q_\nu q_\sigma \right) \right\} , \end{aligned}$$

(4)

where $P_{\mu \nu }^{(3/2)}$ is the projection operator of spin-3/2 in the RS field [33]. Equation (4) obviously shows the expected resonance structure at its pole.

For the application in photo- or electroproduction we slightly modified the hadronic interaction to ${\mathcal {L}}_{\pi N \Delta } = \left( {g_{\pi N \Delta }}/{m_\Delta } \right) {\bar{N}} \gamma _5 {\mathcal {P}}_{\mu \nu \rho \sigma } \partial ^\rho \psi ^{\mu \nu } \partial ^\sigma \pi + \mathrm{H.c.}$, whereas the electromagnetic interaction reads ${\mathcal {L}}_{\gamma N \Delta } = {\bar{N}} (g_1 {\mathcal {P}}_{\rho \sigma \mu \nu } + g_2 \gamma _\rho {\mathcal {P}}_{\sigma \alpha \mu \nu } \partial ^\alpha ) \psi ^{\mu \nu } F^{\rho \sigma } + \mathrm {H. c.}$ [34]. As a result we obtain the contribution of $\Delta$-exchange to the amplitude of pion photoproduction [34]

(5)

where $G_1$ and $G_2$ are the coupling constants that can be extracted from fitting to experimental data. By using Eqs. (4) and (5) we can calculate the cross sections of the $\pi N$ elastic scattering and photoproduction. Both cross sections are shown in Fig. 5, where we also compare the results obtained from the Rarita-Schwinger formulation. Note that a dipole form factor has been inserted in the hadronic vertices to avoid the divergence of the amplitudes at high energies. Figure 5 shows that the pure spin-3/2 formulation combined with the consistent hadronic and electromagnetic interactions yield the correct behavior of a resonance as in the Rarita-Schwinger one. Thus, the formulation can be used directly in the hadronic physics sector, such as meson photoproduction and meson-nucleon scattering.

Fig. 5

Total cross sections of a $\pi N$ elastic scattering and b $\pi N$ photoproduction obtained from the Rarita–Schwinger and pure-spin-3/2 formulations [34]. Note that the cross sections were calculated from the $\Delta (1232)$ contribution only

The propagator of the pure spin-5/2 particle is clearly more complicated. For the particle with momentum p and mass m the propagator reads [36]

$$\begin{aligned} S_{\alpha \beta \gamma \delta \rho \sigma \kappa \eta }(p)= \frac{m^2}{p^{2}-m^{2}+i\epsilon } \left\{ \frac{p^{2}}{m^{2}}\, \wp ^{(5/2,0)}_{\alpha \beta \gamma \delta \rho \sigma \kappa \eta }-\frac{p^{2}-m^{2}}{m^{2}}\, \mathbf{I }^\mathrm{(ATATS)}_{\alpha \beta \gamma \delta \rho \sigma \kappa \eta }\right\} . \end{aligned}$$

(6)

The complicated forms of the projection operator $\wp ^{(5/2,0)}_{\alpha \beta \gamma \delta \rho \sigma \kappa \eta }$ and the ATATS identity $\mathbf{I }^\mathrm{(ATATS)}_{\alpha \beta \gamma \delta \rho \sigma \kappa \eta }$ are given explicitly in Refs. [36, 37]. By using the propagator given in Eq. (6) and the appropriate hadronic and electromagnetic interaction vertices for spin-5/2 particle we can calculate the contribution of pure spin-5/2 resonance in the isobar model. The result will be published soon.

5 Conclusion

We have reviewed the progress that we have achieved in improving the performance of our isobar models during the last 20 years. It is shown that the photoproduction models can nicely describe the presently available data in all six isospin channels. The electroproduction model is still in progress. The presented applications of our isobar models show that kaon photo- and electroproduction processes are very powerful tools for exploring physical properties of hadrons and nuclei that contain strangeness degrees of freedom.